Aromaticity: what does it mean?
T M Krygowski
H Szatylowicz
Corresponding author.
Received 2015 Feb 7; Accepted 2015 May 19; Issue date 2015.
Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Abstract
Aromaticity/aromatic belongs to one of the most useful and popular terms in organic chemistry and related fields. However, aromaticity is not an unambiguous term; therefore, its definition is enumerative. The criteria are based on energy (increased stability), molecular geometry (very low bond lengths alternation), magnetism (induction of the diatropic ring current by external magnetic field) and reactivity (tendency to maintain π-electron structure in chemical reactions). The energetic criterion is based on resonance energy and aromatic stabilization energy, whereas harmonic oscillator model of aromaticity—on molecular geometry. Magnetism-based criteria are illustrated by local indicators (for individual rings): nucleus independent chemical shifts and proton nuclear magnetic resonance chemical shifts as well as the global aromaticity index—exaltation of the magnetic susceptibility. For selected homo- and hetero-cyclic compounds, illustrative data are presented in tables, which allow the comparison of the above-mentioned indices. Finally, examples of agreements or disagreements between these various aromaticity indices are presented for few representative cases.
Electronic supplementary material
The online version of this article (doi:10.1007/s40828-015-0012-2) contains supplementary material, which is available to authorized users.
Keywords: Aromaticity, HOMA, NICS, Resonance energy, Pi-electron delocalization, Ring current
Introduction
Aromaticity is a very frequently used term in chemistry and in related fields. Statistically, every day ~30 papers appear in which the terms ‘aromatic/aromaticity’ are used in either their titles or abstracts or the keywords [1]. Numerous organic compounds are either aromatic or contain aromatic fragments. The definition of aromaticity is enumerative in nature,i.e. it is described by a collection of physicochemical properties determining specific features of cyclic or polycyclic π-electron molecules [2–4]. The following features are accepted as decisive for defining a molecule to be aromatic (Fig. 1):
Scheme 1.
Homodesmotic reaction
as already mentioned it has to be cyclic or polycyclic;
its bond lengths exhibit very low bond lengths alternation;
it should be more stable than its acyclic analogue;
in external magnetic field it shows an increased diamagnetic susceptibility and diatropic (low field) chemical shifts of exocyclic protons in1H NMR spectra, due to magnetic field induced ring current;
it more easily undergoes substitution reactions than the addition ones.
Fig. 1.
Aromaticity as a problem of π-electron delocalization
These criteria of aromaticity presented above may have some numerical representation, very often termed “aromaticity indices”.
Energetic measure of aromaticity
Already in the nineteenth century, it was known that aromatic compounds (mainly benzene) are much more resistant to chemical reactions than their acyclic analogues [5]. First quantitative description of aromaticity was proposed in 1933 by introduction of a thermodynamic term, namely the resonance energy, RE [6]i.e. the energy by which the aromatic compound is more stable than its virtual olefinic analogue. In the case of benzene, this analogue is a virtual compound with three single and three double bonds. Estimated RE for benzene amounts to 36 kcal/mol. A very similar value was experimentally determined by Kistiakowsky et al. [7] through calorimetric measurements of heats of hydrogenation of benzene and cyclohexene [8].
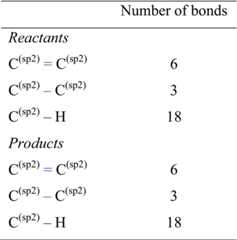
Later, the term RE was replaced by more precisely defined aromatic stabilization energy (ASE) which is estimated by the use of either isodesmic [9] or more precise homodesmotic [10,11] reactions. The latter is defined as a virtual reaction leading to products with the same number of CH bonds and the same numbers of atoms in the appropriate hybridization states (see Scheme 1; Table 1 in which representative cases of homodesmotic reactions are presented).
Table 1.
Types of bonds for homodesmotic reaction shown in Scheme 1
C6H6 + 3 CH2CH2 = 3trans CH2CHCHCH2
C6H6 + 3 CH2CH2 = 3cis CH2CHCHCH2
ASE = 23.2 kcal/mol
ASE = 33.6 kcal/mol
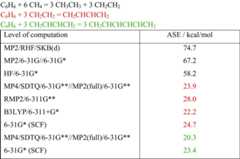
Here the problem of an appropriate reference for the stability of aromatic molecules arises. Table 2, data taken from [12], shows that ASE values depend dramatically on the choice of the computation method of computation and of the selection of the reference system [12].
Table 2.
Stabilization energiesa of ISODESMIC and reactions:
reactions:
aData taken from [12]
Apart from these limitations, the ASE approaches are mostly applied to π-electron hydrocarbons. They are much less effective in the case of heterocyclic systems where the problem of the reference system is much more complicated.
For tautomers and isomers yielding reliable information on energetic relations between different chemical species, a direct comparison of energy is possible, without the necessity of applying any kind of ASE procedure.
Undoubtedly the energetic criterion is very important but it describes only stability of the whole molecule. However, it is well known that in polycyclic π-electron molecules, rings of different stability can co-exist. Phenanthrene is a good example here, since its central ring is more reactive. Addition to the C9C10 bond of the central ring is relatively easy, whereas all positions in the two other rings are chemically more inert. Several procedures were proposed for determining energetic characteristics of individual rings, which are based on their geometry [13–15], for review see [16].
HOMA: geometry-based aromaticity index
The next criterion of aromaticity is directly based on the molecule geometry. In strongly aromatic compounds the bond lengths either do not alternate or their alternation is very weak. Quantitatively it was first considered by Julg and Francois [17] who defined a numerical characteristic of aromaticity as a function of variance of the perimeter bond lengths in a molecule. Unfortunately application of this approach was limited to hydrocarbons only, since there is no possibility to estimate an averaged bond length for heterocyclic molecules. Hence an improvement was necessary to make the concept more general. It was done by replacing the averaged bond lengthRav by a hypothetical optimal bond lengthRopt proper for fully aromatic molecules [18,19]. This geometry based aromaticity index has the form expressed by equation:
| 1 |
where αj is a parameter (normalization constant) dependent on the type of a given bond (j stands for CC, CN, CO, CP, CS, NN, NO, etc.) and is estimated empirically from the lengths of their optimal (Ropt), single (Rs) and double (Rd) bonds. TheRopt denotes the length of the bond for which extension to the single bond and compression to the double bond costs energetically the same. Energy of compression or extension is estimated by the use of a harmonic oscillator approach. Table 3 presents all data necessary for the HOMA model application [16] to molecules with heteroatoms involving bonds.
Table 3.
Reference bond lengthsRs andRd, and appropriateRopt and α values used in the HOMA index
| Type of bond | Rs/Å | Rd/Å | Ropt/Å | α | References |
|---|---|---|---|---|---|
| BBa | 1.6474 | 1.5260 | 1.5665 | 244.147 | [20] |
| BBw a | 1.6474 | 1.5260 | 1.5693 | 250.544 | [20] |
| BCexp b | 1.5472 | 1.3616 | 1.4235 | 104.507 | [21] |
| BCtheo b | 1.5542 | 1.3796 | 1.4378 | 118.009 | [21] |
| BCtheo/w b | 1.5542 | 1.3766 | 1.4386 | 118.618 | [21] |
| BNc | 1.564 | 1.363 | 1.402 | 72.03 | [22] |
| CCd | 1.467 | 1.349 | 1.388 | 257.7 | [23] |
| CNe | 1.465 | 1.269 | 1.334 | 93.52 | [23] |
| COf | 1.367 | 1.217 | 1.265 | 157.38 | [23] |
| CPg | 1.814 | 1.640 | 1.698 | 118.91 | [23] |
| CSh | 1.807 | 1.611 | 1.677 | 94.09 | [23] |
| CSei | 1.959 | 1.7591 | 1.8217 | 84.9144 | [24] |
| NNj | 1.420 | 1.254 | 1.309 | 130.33 | [23] |
| NOk | 1.415 | 1.164 | 1.248 | 57.21 | [23] |
Reference systems used:a H2B-BH2 and HB=BH;b H3C-BH2 and H2C=BH;c H3B-NH3 and (isoPr)2N=B=C(SiMe3)2, H3B-NH3 and H2B=NH2;d buta-1,3-diene;e H2N-CH3 and HN=CH2;f HCOOH monomer;g H2C=P-CH3;h S(CH3)2 and H2C=S,i H3C-SeH and H2C=Se;j (CH3)2C=N–N(CH3)2 and H3C–N=N–CH3; k CH3–O–N=O
It follows from the data of Table 1 that all π-electron systems with bonds presented there can be treated with the HOMA approach, provided that their reliable geometry is known.
Term (1) can be analytically transformed into a more detailed form [25] as (2), (3) and (4)
| 2 |
where
| 3 |
and
| 4 |
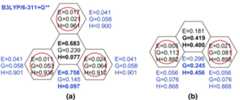
Formulae (3) and (4) describe two structural factors deciding about aromaticity of a molecule in question. The GEO term describes the degree of bond length alternation—the greater GEO, the greater loss of the aromatic character due to an increase of alternation. This term is equivalent to Julg’s definition of aromaticity [17]. The second term, EN describes the loss of aromaticity due to lengthening of bonds over the mean length. According to Eq. (2) both terms lead to a decrease of the HOMA value. Figure 2 presents the results of the application of Eqs. (1), (2), (3) and (4) to phenanthrene and triphenylene [26].
Fig. 2.
Dependence of the aromatic character of benzene ring on its topological environment in benzenoid hydrocarbons:a triphenylene andb phenanthrene; E, G and H denotes EN, GEO and HOMA parameters, respectively; values inside of the ring (taken from [26]) were obtained for experimental structures
Few interesting findings should be pointed out. First, the HOMA, EN and GEO terms based on experimental geometry are different for symmetrically equivalent rings. This is due to specific conditions of the molecular geometry determination by X-ray diffraction. If a molecule in a crystal lattice lies in a special position,i.e. coincides with a symmetry element, then its symmetrical property is maintained. However, if the position of the molecule and the symmetry element do not coincide, then its molecular environment in the crystal is no more symmetrical and hence different intermolecular interactions act on this molecule which would be symmetrical in the free state [27]. In Fig. 2 EN (E), GEO (G) and HOMA (H) values calculated from the experimental data are compared with those derived from purely computational (B3LYP/6-311 + G**) geometry. The observed differences seem to be significant in some cases, but the overall picture in both approaches is very similar.
In both molecules the central rings are significantly less aromatic than the peripheral ones. The HOMA values of the latter reach 0.9 and in the case of triphenylene even exceed this value. However, the decrease of HOMA in the phenanthrene central ring is predominantly associated with a greater value of the GEO than the EN term. This means that the dominant contribution to dearomatization comes from an increase of the bond length alternation. Definitely, this ring has a low aromatic character in line with its significant reactivity: addition to 9, 10 positions, for example. An opposite trend is observed for the central ring of triphenylene. Here the GEO term is much smaller than the EN term and the low HOMA value is due to lengthening of the central ring bonds. The central ring is then non-aromatic, and is known in Clar’s classification [28,29] as the empty one,i.e. exhibiting a deficiency of pi electrons in the ring. Interestingly, when the geometry based estimation of energy of individual rings is applied [30], then the central rings in phenanthrene and triphenylene show bond energy (BE) values equal to 699.4 and 668.9 kcal/mol, respectively. All other rings in these molecules have the BE values between 715.6 and 725.2 kcal/mol. Definitely, the central rings have a lower energy content than the other ones, in line with the predictions resulting from their HOMA values. It is important to note that Eqs. (1)–(4) give an additional information of the reason of the observed aromaticity decrease. HOMA, EN and GEO values for selected homo- and heterocyclic compounds are presented in Table 4.
Table 4.
HOMA EN and GEO values for selected homo- and heterocyclic compounds
Magnetic-based aromaticity descriptors
Other criteria of aromaticity are based on specific magnetic properties of π-electron molecules. It is known from1H NMR that chemical shifts for external protons in aromatic molecules are deshielded. Figure 3 illustrates it taking benzene as an example.
Fig. 3.
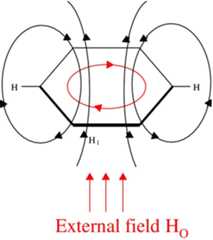
External magnetic field inducing an internal ring current, leading to characteristic “aromatic”1H NMR shifts. Reprinted with permission from [12] Copyright 2005 American Chemical Society
A term “aromatic chemical shifts” was even introduced for aromatic protons, which are larger (~7 ppm) than those measured for olephinic (~5 ppm) or for aliphatic (~1 ppm) protons [37].1H NMR chemical shifts may differ for various positions of protons as shown in the case of phenanthrene [38], see Table 5. This means that to some extent1H NMR chemical shifts may serve as a local measure of aromaticity, having in mind that these data depend on the medium used for the measurements [38].
Another local measure of aromaticity was introduced by Schleyer et al. [29,40]. These authors introduced a purely theoretical concept of nucleus independent chemical shift (NICS) that has later become one of the most popular characteristics of aromaticity. NICS is defined as a negative value of the absolute shielding measured in the center of a given ring [NICS(0), one angstrom above the center NICS(1)] or, alternatively, as the value of the perpendicular component of the tensor describing the shielding, NICS(1)zz. Table 6 presents NICS values for some π-electron ring systems; the more negative value of NICS, the more aromatic is the system [39]. As it can be easily noticed in some cases NICS values are in opposition to ASE or HOMA indices. For example, according to its NICS index, naphthalene is more aromatic than benzene. This problem arises from the fact, that NICS values depend on the size of a system being examined. Inspection of the data presented in Table 6 also leads to a conclusion that heterocyclic compounds such as pyrrole, thiophene and furan are inadequately described by this index since according to NICS values they are more aromatic than benzene—again against all other evidences (compare results Tables 4,6).
Table 5.
1H NMR characteristics of phenanthrene; spectrum recorded in CDCl3 [38]
| Hydrogen | Chemical shift/ppm | |
|---|---|---|
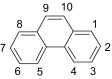 | 1 | 7.901 |
| 2 | 7.606 | |
| 3 | 7.666 | |
| 4, 5 | 8.702 | |
| 9, 10 | 7.751 |
Table 6.
Magnetic susceptibility exaltation (Λ) and NICS(0) values for selected homo- and heterocyclic compounds
| Λ/cgs ppm | Refs. for Λ | NICS(0)/ppm | Refs. for NICS(0) | |
|---|---|---|---|---|
| Pyrrole | −6.5 | [32] | −15.1 | [39] |
| Phosphole | −1.7 | [32] | −5.35 | [40] |
| Thiophene | −7.0 | [32] | −13.6 | [39] |
| Furan | −2.9 | [32] | −12.3 | [39] |
| Benzene | −10.47 | [41] | −9.7 | [39] |
| Naphthalene | −20.98 | [41] | −9.9 | [39] |
 | −13.81 | [41] | −7.6 | [39] |
| Cyclopentadiene | −2.4 | [39] | −3.2 | [39] |
| Cyclohexane | −0.7 | [39] | −2.2 | [39] |
| Pentalene | 34.59 | [41] | 18.1 | [39] |
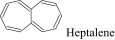 | 76.6 | [39] | 22.7 | [39] |
| Cyclobutadiene | 17.20 | [41] | 27.6 | [39] |
Apart from the above-mentioned local aromaticity characteristics, there are well known whole-molecule characteristics (named also as global aromaticity measures), accessible both experimentally and theoretically. The most important are: (1) anisotropy of magnetic susceptibility Δχ, [42] Eqs. (5), and (2) magnetic susceptibility exaltation Λ [43] Eq. (6).
| 5 |
and
| 6 |
where χcc, χaa and χbb are the elements of the diagonalized magnetic susceptibility tensor andc is the out of plane direction for the planar molecule.
Both characteristics are relative in character. The former is a difference between the out of plane and the average in plane components (as reference) of the magnetic susceptibility tensor. The magnetic susceptibility exaltation is estimated in reference to the value for some non-aromatic (M′), artificial systems. The latter case resembles the resonance energy concept, where energy of a real system is related to some value for an artificial “olefinic analogue”.
Mills and Llagostera [41] found that the summation of aromatic and antiaromatic hydrocarbons values of NICS(1)zz yields a very good correlation with the magnetic susceptibility exaltation.
Effect of intra- and inter-molecular interactions on aromaticity of the ring
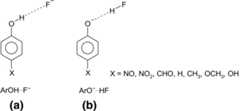
The dependence of benzene ring aromaticity on the substituent type and on the strength of intermolecular interactions in the case of phenol and phenolates is an interesting exemplification of the factors which can influence this property. It can be demonstrated by a computational model of approaching the hydroxyl group by F− and the anionic (phenolate) form by HF [44] (see Fig. 4).
Fig. 4.
Structural scheme of the computational model
As it can be seen from the data presented in Fig. 5 the obtained HOMA indices for the benzene ring in substituted phenols and phenolates clearly correlate with the strength of the hydrogen bond, determined by the C–O bond length. Moreover, theoretically calculated and experimentally determined (data taken from Cambridge Structural Data Base) C–O bond lengths yield qualitative very similar pictures [45,46]. Thus, strengthening of the H-bond inp-X-PhOH…F− complexes (shortening of the C–O bond length) results in lowering of aromaticity, whereas forp-X-PhO−…HF systems the opposite trend is observed.
Fig. 5.
Dependence of aromaticity of phenyl ring (HOMA) on hydrogen bond strength,a X-ray data (CSD, 664 geometries) andb B3LYP/6-311 + G** results. Reprinted with permission from [45,46]. Copyright 2004 and 2005 American Chemical Society
One of the most important problems in organic chemistry is impact of the substituents on the system in question. The classical approach to these problems is strongly related to substituted benzene derivatives and described by the fundamental theory introduced by Hammett [47], the most recent review is given in [48]. Application of the Hammett ideas forpara substituted phenols, phenolates and their equilibrium H-bonded complexes is presented in Fig. 6.
Fig. 6.
Dependence of aromaticity of phenyl ring (HOMA) ona the C–O bond length,dC–O, andb a substituent constant, σp (for electron accepting substituents σ−p are used) forpara substituted phenols, phenolates, and their H-bonded equilibrium complexes (p-X-PhO−…HF). Parta reprinted with permission from [46]. Copyright 2005 American Chemical Society
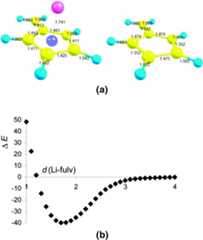
It should be stressed that in some cases a qualitative agreement is encountered in the estimation of aromaticity by means of geometry based HOMA, energy and NICS’s indices. Interactions between fulvene lithium can be considered as an instructive example here [49]. Figure 7 presents energy the potential well obtained as a result of approaching the center of fulvene ring by Li. Fulvene is known as a nonalternant π-electron hydrocarbon [50,51]. If the Li atom gets closer to its ring the stability of the resulting complex increases, up to ~40 kcal/mol in the equilibrium state. This is also manifested by the increase of aromaticity as evidenced by the change of HOMA from ~−0.3 to ~0.6 and NICS(0) from 0.94 to −11.15.
Fig. 7.
a Computed structures of the Li-fulvene complex and the free fulvene molecule [B3LYP/6-311++G(d,p) level].b Relative energy, ΔE (kcal/mol), of the Li-fulvene complex relative to neutral fragments, as a function of the distance from Li to the ring center,d(Li-fulv) (Å). Reprinted with permission from [49]. Copyright 2010 American Chemical Society
Multidimensional character of aromaticity
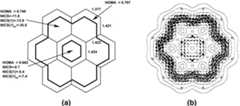
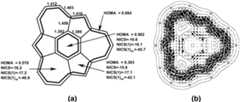
However, it is worth to mention that in some cases the criteria of aromaticity may show different trends. An interesting disagreement between the magnetic and energetic criteria of aromaticity was found for coronene and isocoronene [52], as presented in Figs. 8 and9, respectively.
Fig. 8.
a Bond lengths and the aromaticity descriptors: HOMA, NICS, NICS(1) (calculated 1 Å above the molecular plane), and NICS(1)zz (the component of NICS(1) corresponding to the principal axis perpendicular to the ring plane) for fragments of coronene.b Map of π-current density in coronene. Diatropic and paratropic circulations are shown anticlockwise and clockwise, respectively. Reprinted with permission from [52]. Copyright 2010 American Chemical Society
Fig. 9.
a Bond lengths and the aromaticity descriptors: HOMA, NICS, NICS(1), and NICS(1)zz for isocoronene.b Map of π-current density in isocoronene. The NICS descriptors follow the notation used in Fig. 7. Reprinted with permission from [52]. Copyright 2006 American Chemical Society
These two compounds are isomers, thus direct comparisons of “whole molecule” properties are allowed. Using energetic criteria it follows that coronene is more aromatic than its isomer since it is more stable by 105 kcal/mol. This is in contradiction to the magnetic susceptibility exaltation parameters which show the opposite picture: isocoronene exceeds coronene by 51.4 cgs ppm. This is, in turn, in line with the HOMA values calculated for the outer and inner envelopes: for isocoronene HOMA(out) = 0.864, HOMA(inn) = 0.982, whereas for coronene they amount to 0.797 and 0.662, respectively. Computation of the ring current density map by the use of the ipsocentric approach [53] explains these results. Isocoronene shows a clear diatropic circulation on the perimeter reinforced by a weak central circulation in the same sense instead of the paratropic central circulation of coronene, see Fig. 8.
The problem of the disagreement between various criteria of aromaticity was first formulated by Katritzky et al. [54] and then discussed in many subsequent papers in the past two decades [30,55,56]. Application of various aromaticity indices to nearly 100 π-electron systems [32] allowed to conclude that aromaticity is a statistically multidimensional phenomenon and various criteria may sometimes present non-equivalent pictures.
The other indices of aromaticity
In addition to the above-presented characteristics of aromaticity it is necessary to briefly mention some other measures, which do not their origin in the enumerative definition presented in the beginning of this paper. The Bader quantum theory of atoms in molecules (QTAIM) [57–59] allows to analyze charge distribution in molecules. Among many properties accessible by the use of this method, the most useful for structural studies are the charges in the atomic basins and properties in the critical point of bonds and rings. The critical points are characterized by the local extreme of electron density, being a minimum charge density in direction of the bond and maximum in directions perpendicular to the bond (a saddle point). This is the so-called the bond critical point (BCP), moreover, the ring critical point (RCP) can also be determined [60]. In addition, it is also possible to compute the density of electron energy (as a whole and also as its potential and kinetic components) in the critical point. It was shown that for polycyclic benzenoid hydrocarbons the QTAIM parameters in RCPi.e. charge, total, kinetic and potential energies very well correlate with HOMA (correlation coefficient,cc, always better than 0.98) and with NICS(0) withcc = 0.909 [61].
QTAIM also allows to describe ellipticity of a bond in its BCP. It is known that the more double is the bond, the higher is its ellipticity. Thus the next aromaticity parameter based on elipticity, EL was proposed [62] which successfully correlated with other aromaticity indices like HOMA, EN, GEO, PDI [63] FLU [64] and NICS’s. Similar approach was earlier presented [65], although not so well documented.
There are several aromaticity descriptors based directly on atomic charges. For example, FLU (aromatic fluctuation index) [64] describes the fluctuation of electronic charge between adjacent atoms in a given ring. Its good correlation with other aromaticity indices as HOMA, EN, GEO, NICS’s and PDI allowed to accept it as a valuable measure of the aromatic character. PDI (para-delocalization index) is defined [63] as the average of all the Bader delocalization indices between thepara-related atoms in six-membered rings. A good review on various aromaticity indices based on atomic charges is presented in a paper of Bultinck [66] which shows their mutual intercorrelations.
Therefore, comparison with the traditional aromaticity indices as well as with some more recently developed ones should be considered as a rule in establishing of any new aromaticity measure.
Conclusions
In summary, the critical discussion of aromaticity presented above clearly indicates that it is not a single property of chemical compounds, and hence none of criterion alone is sufficient to unequivocally characterize it. Thus, only the multidimensional view on aromaticity-related chemical properties of a given compound can be reliable. As already stated Tetrahedron Report 520 [4], aromatic compounds are only those which fulfil all criteria (i)–(v) presented in the definition, whereas those compounds that fulfil only some of them are described as partly aromatic compounds.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
The authors are deeply indebted to Jarek Kucharczyk for preparing the graphical “picture of aromaticity”, presented in Fig. 1. T.M.K. thanks Warsaw University, whereas H.S., Warsaw University of Technology, for supporting this work.
Abbreviations
- ASE
Aromatic stabilization energy
- BCP
Bond critical point
- BE
Bond energy
- cc
Correlation coefficient
- EL
Aromaticity index based on ellipticity of bonds
- FLU
Aromatic fluctuation index
- HOMA
Harmonic oscillator model of aromaticity
- NICS
Nucleus independent chemical shifts
- NMR
Nuclear magnetic resonance
- PDI
Para-delocalization index
- QTAIM
Quantum theory of atoms in molecules
- RCP
Ring critical point
- RE
Resonance energy
Footnotes
In memory of our friends and co-workers, Professors Alan R. Katritzky and Paul von Rague Schleyer.
Contributor Information
T. M. Krygowski, Email: tmkryg@chem.uw.edu.pl
H. Szatylowicz, Email: halina@ch.pw.edu.pl
References
- 1.ISI Web of Science, retrieved in December 2014
- 2.Elvidge JA, Jackman LM (1961) J Chem Soc, pp 859–866
- 3.Sondheimer F. Pure Appl Chem. 1964;7:363–388. [Google Scholar]
- 4.Krygowski TM, Cyrański MK, Czarnocki Z, Haefelinger G, Katritzky AR. Tetrahedron Report 520. Tetrahedron. 2000;56:1783–1796. doi: 10.1016/S0040-4020(99)00979-5. [DOI] [Google Scholar]
- 5.Kekule FA. Lehrbuch der organischen Chemie. Erlangen: F. Enke Verlag; 1866. [Google Scholar]
- 6.Pauling L, Sherman J. J Chem Phys. 1933;1:606–617. doi: 10.1063/1.1749335. [DOI] [Google Scholar]
- 7.Kistiakowsky GB, Ruhoff JR, Smith HA, Vaughan WE. J Am Chem Soc. 1936;58:146–153. doi: 10.1021/ja01292a043. [DOI] [Google Scholar]
- 8.Pauling L. The Nature of Chemical Bond. Ithaca: Cornell Univ. Press; 1960. p. 193. [Google Scholar]
- 9.Hehre WJ, Ditchfield R, Radom L, Pople JA. J Am Chem Soc. 1970;92:4796–4801. doi: 10.1021/ja00719a006. [DOI] [Google Scholar]
- 10.Hehre WJ, McIver RT, Pople JA. Schleyer PvR. J Am Chem Soc. 1974;96:7162–7163. doi: 10.1021/ja00829a087. [DOI] [Google Scholar]
- 11.Radom L (1974) J Chem Soc Chem Commun, pp 403–404
- 12.Cyranski MK. Chem Rev. 2005;105:3773–3811. doi: 10.1021/cr0300845. [DOI] [PubMed] [Google Scholar]
- 13.Krygowski TM, Ciesielski A, Bird CW, Kotschy A. J Chem Inf Comput Sci. 1995;35:203–210. doi: 10.1021/ci00024a006. [DOI] [Google Scholar]
- 14.Howard ST, Cyranski MK, Stolarczyk LZ (2001) Chem Comm, pp 197–198
- 15.Cyranski MK, Howard ST, Chodkiewicz ML. Chem Comm. 2004;10:2458–2459. doi: 10.1039/b408903k. [DOI] [PubMed] [Google Scholar]
- 16.Krygowski TM, Szatyłowicz H, Stasyuk OA, Dominikowska J, Palusiak M. Chem Rev. 2014;114:6383–6422. doi: 10.1021/cr400252h. [DOI] [PubMed] [Google Scholar]
- 17.Julg A, Francois P. Theor Chim Acta. 1967;7:249–259. doi: 10.1007/BF00527311. [DOI] [Google Scholar]
- 18.Kruszewski J, Krygowski TM. Tetrahedron Lett. 1972;13:3839–3842. doi: 10.1016/S0040-4039(01)94175-9. [DOI] [Google Scholar]
- 19.Krygowski TM. J Inf Comput Sci. 1993;33:70–78. doi: 10.1021/ci00011a011. [DOI] [Google Scholar]
- 20.Zborowski KK, Alkorta I, Elguero J, Proniewicz LM. Struct Chem. 2013;24:543–548. doi: 10.1007/s11224-012-0109-9. [DOI] [Google Scholar]
- 21.Zborowski KK, Alkorta I, Elguero J, Proniewicz LM. Struct Chem. 2012;23:595–600. doi: 10.1007/s11224-011-9907-8. [DOI] [Google Scholar]
- 22.Madura ID, Krygowski TM, Cyranski MK. Tetrahedron. 1998;54:14913–14918. doi: 10.1016/S0040-4020(98)00933-8. [DOI] [Google Scholar]
- 23.Krygowski TM. J Chem Inf Comput Sci. 1993;33:70–78. doi: 10.1021/ci00011a011. [DOI] [Google Scholar]
- 24.Zborowski KK, Proniewicz LM. Polish J Chem. 2009;83:477–484. [Google Scholar]
- 25.Krygowski TM, Cyranski MK. Tetrahedron. 1996;52:1713–1722. doi: 10.1016/0040-4020(95)01007-6. [DOI] [Google Scholar]
- 26.Krygowski TM, Cyrański M, Ciesielski A, Świrska B, Leszczyński P. J Chem Inf Comput Sci. 1996;36:1135–1141. doi: 10.1021/ci960367g. [DOI] [Google Scholar]
- 27.Bunn CW. Chemical Crystallography. Oxford: Clarendon Press; 1961. [Google Scholar]
- 28.Clar E (1964) Polycyclic Hydrocarbons. Vol. 1 and 2. Academic Press, London and New York; Springer Verlag, Berlin and Goettingen
- 29.Clar E. The Aromatic Sextet. Chichester: J Wiley; 1972. [Google Scholar]
- 30.Krygowski TM, Ciesielski A, Bird CW, Kotschy A. J Chem Inf Comput Sci. 1995;35:203–210. doi: 10.1021/ci00024a006. [DOI] [Google Scholar]
- 31.Zborowski KK, Alkorta I, Elguero J, Proniewicz LM. Struct Chem. 2012;23:595–600. doi: 10.1007/s11224-011-9907-8. [DOI] [Google Scholar]
- 32.Cyranski MK, Krygowski TM, Katritzky AR. Schleyer PvR. J Org Chem. 2002;67:1333–1338. doi: 10.1021/jo016255s. [DOI] [PubMed] [Google Scholar]
- 33.Zborowski KK, Proniewicz LM. Polish J Chem. 2009;83:477–484. [Google Scholar]
- 34.Krygowski TM, Cyrański M. Tetrahedron. 1996;52:10255–10264. doi: 10.1016/0040-4020(96)00560-1. [DOI] [Google Scholar]
- 35.Alonso M, Herradon B. Phys Chem Chem Phys. 2010;12:1305–1317. doi: 10.1039/B917343A. [DOI] [PubMed] [Google Scholar]
- 36.Cyranski MK (1998) Analysis of the aromatic character of π-electron systems by separating geometric and energetic contributions. Ph.D. Thesis (in Polish), University of Warsaw, Warsaw
- 37.Bruice PY. Organic chemistry. Pearson Prentice Hall: Upper Saddle River; 2007. p. 580. [Google Scholar]
- 38.Abraham RJ, Canton M, Reid M, Griffiths L. J Chem Soc Perkin Trans. 2000;2:803–812. doi: 10.1039/a907830d. [DOI] [Google Scholar]
- 39.Schleyer PVR, Maerker C, Dransfeld H, Jiao H, van Eikemma Hommes NJR. J Am Chem Soc. 1996;118:6317–6318. doi: 10.1021/ja960582d. [DOI] [PubMed] [Google Scholar]
- 40.Chen Z, Wannere CS, Corminboeuf C, Puchta R, Schleyer Pvr. Chem Rev. 2005;105:3842–3888. doi: 10.1021/cr030088+. [DOI] [PubMed] [Google Scholar]
- 41.Mills NS, Llagostera KB. J Org Chem. 2007;72:9163–9169. doi: 10.1021/jo7013609. [DOI] [PubMed] [Google Scholar]
- 42.Flygare WH. Chem Rev. 1974;74:653–687. doi: 10.1021/cr60292a003. [DOI] [Google Scholar]
- 43.Dauben HJ, Jr, Wilson JD, Laity JL. J Am Chem Soc. 1968;90:811–813. doi: 10.1021/ja01005a059. [DOI] [Google Scholar]
- 44.Krygowski TM, Zachara JE, Szatylowicz H. J Phys Org Chem. 2005;18:110–114. doi: 10.1002/poc.875. [DOI] [Google Scholar]
- 45.Krygowski TM, Szatylowicz H, Zachara JE. J Chem Inf Comput Sci. 2004;44:2077–2082. doi: 10.1021/ci049817s. [DOI] [PubMed] [Google Scholar]
- 46.Krygowski TM, Zachara JE, Szatylowicz H. J Chem Inf Model. 2005;45:652–656. doi: 10.1021/ci049633d. [DOI] [PubMed] [Google Scholar]
- 47.Hammett LP. Physical Organic Chemistry. 1. New York: McGraw-Hill; 1940. [Google Scholar]
- 48.Krygowski TM, Stepien BT. Chem Rev. 2005;105:3482–3512. doi: 10.1021/cr030081s. [DOI] [PubMed] [Google Scholar]
- 49.Ozimiński WP, Krygowski TM, Fowler PW, Sonchi A. Org Lett. 2010;12:4880–4883. doi: 10.1021/ol102037e. [DOI] [PubMed] [Google Scholar]
- 50.Streitwieser A. Molecular orbital theory for organic chemists. New York: Wiley; 1961. p. 237f. [Google Scholar]
- 51.Skanke A. In: Aromaticity, pseudoaromaticity, antiaromaticity, proceedings of an international symposium held in jerusalem 1970. Bergmann ED, Pullman B, editors. Jerusalem: Israel Academy of Science and Humanities; 1971. [Google Scholar]
- 52.Ciesielski A, Cyrański MK, Krygowski TM, Fowler PW, Lillington M. J Org Chem. 2006;71:6840–6845. doi: 10.1021/jo060898w. [DOI] [PubMed] [Google Scholar]
- 53.Fowler PW, Steiner E. J Phys Chem A. 1997;101:1409–1413. doi: 10.1021/jp9637946. [DOI] [Google Scholar]
- 54.Katritzky AR, Barczyński B, Musumurra G, Pisano D, Szafran M. J Am Chem Soc. 1989;111:7–15. doi: 10.1021/ja00183a002. [DOI] [Google Scholar]
- 55.Jug K, Koester A. J Phys Org Chem. 1991;4:163–169. doi: 10.1002/poc.610040307. [DOI] [Google Scholar]
- 56.Katritzky AR, Karelson M, Sild S, Krygowski TM, Jug K. J Org Chem. 1998;63:5228–5231. doi: 10.1021/jo970939b. [DOI] [Google Scholar]
- 57.Bader RFW. Atom in molecules. A quantum theory. Oxford: Oxford University Press; 1992. [Google Scholar]
- 58.Bader RFW. Chem Rev. 1991;91:893–928. doi: 10.1021/cr00005a013. [DOI] [Google Scholar]
- 59.Popelier P. Atoms in molecules. An introduction. Englewood Cliffs: Printice Hall; 2000. [Google Scholar]
- 60.Howard ST, Krygowski TM. Can J Chem. 1997;75:1174–1181. doi: 10.1139/v97-141. [DOI] [Google Scholar]
- 61.Palusiak M, Krygowski TM. Chem Eur J. 2007;13:7996–8006. doi: 10.1002/chem.200700250. [DOI] [PubMed] [Google Scholar]
- 62.Dominikowska J, Palusiak M. Struct Chem. 2012;23:1173–1183. doi: 10.1007/s11224-011-9941-6. [DOI] [Google Scholar]
- 63.Poater J, Fradera X, Duran M, Sola M. Chem Eur J. 2003;9:400–406. doi: 10.1002/chem.200390041. [DOI] [PubMed] [Google Scholar]
- 64.Matito E, Duran M, Sola M. J Chem Phys. 2005;122:014109. doi: 10.1063/1.1824895. [DOI] [PubMed] [Google Scholar]
- 65.Matta CF, Hernandez-Trujillo J. J Phys Chem A. 2005;109:10798. doi: 10.1021/jp055864r. [DOI] [Google Scholar]
- 66.Bultinck P. Faraday Discuss. 2007;135:345–365. doi: 10.1039/B609640A. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.