
The evolution of recombination rates in finite populations during ecological speciation
James Reeve
Daniel Ortiz-Barrientos
Jan Engelstädter
e-mail:j.engelstaedter@uq.edu.au
Electronic supplementary material is available online athttps://dx.doi.org/10.6084/m9.figshare.c.3518952.
Received 2016 Jun 5; Accepted 2016 Oct 4.
Abstract
Recombination can impede ecological speciation with gene flow by mixing locally adapted genotypes with maladapted migrant genotypes from a divergent population. In such a scenario, suppression of recombination can be selectively favoured. However, in finite populations evolving under the influence of random genetic drift, recombination can also facilitate adaptation by reducing Hill–Robertson interference between loci under selection. In this case, increased recombination rates can be favoured. Although these two major effects on recombination have been studied individually, their joint effect on ecological speciation with gene flow remains unexplored. Using a mathematical model, we investigated the evolution of recombination rates in two finite populations that exchange migrants while adapting to contrasting environments. Our results indicate a two-step dynamic where increased recombination is first favoured (in response to the Hill–Robertson effect), and then disfavoured, as the cost of recombining locally with maladapted migrant genotypes increases over time (the maladaptive gene flow effect). In larger populations, a stronger initial benefit for recombination was observed, whereas high migration rates intensify the long-term cost of recombination. These dynamics may have important implications for our understanding of the conditions that facilitate incipient speciation with gene flow and the evolution of recombination in finite populations.
Keywords: adaptive divergence, Hill–Robertson effect, maladaptive gene flow, mathematical model, random genetic drift, recombination modifier
1. Introduction
Ecological speciation is the evolution of reproductive isolation between populations adapting to contrasting environments [1–5]. Gene flow is a major impediment to this as it allows maladapted migrant alleles to infiltrate the local population [5–8]. A major factor determining the extent to which migrant alleles penetrate a population is recombination [9–11]. During ecological speciation with gene flow co-adapted gene complexes break down in recombined hybrids, resulting in chromosomes comprised of both adaptive and maladaptive alleles. Natural selection is not able to efficiently remove these maladaptive alleles because they are ‘hidden’ between adaptive alleles on the chromosome. As a result, alleles conferring local adaptation are expected to accumulate in regions of reduced recombination, such as population-specific chromosomal inversions [12–15].
The presence of maladaptive gene flow between populations is predicted to favour the suppression of recombination within populations (reviewed in [16]). Mathematical models aimed at understanding the evolution of sex demonstrate that a modifier allele reducing the recombination rate between selected loci (the modifier approach [17]) is generally favoured in the presence of maladaptive gene flow [18–20]. This can be interpreted as a mechanism of reinforcement [7,16] because reduced recombination rates will promote the genetic clustering of diverging populations. Similarly, models investigating the origin of species have shown that inversions that capture locally beneficial alleles should also be favoured by natural selection and thus spread within a population [14,21].
Empirical support for these theoretical predictions has only recently accumulated. For example, two host races of the North American apple maggot (Rhagoletis pomonella) diverged following the spread of a chromosomal inversion due to natural selection in one host race [22,23]. Additional evidence comes from theDrosophila genus where closely related sympatric species are more often genetically separated by inversions than their allopatric relatives [24]. More broadly, chromosomal inversions have been implicated in many cases of divergence with gene flow, including sunflowers [25], monkeyflowers [26] and wild rabbits [27]. The capturing of adaptive loci in genomic regions of reduced recombination may be one mechanism that triggers the speciation process [12]. Overall, both theoretical and empirical data indicate that recombination antagonizes speciation, and that there is selection for mechanisms suppressing recombination in the presence of maladaptive gene flow that facilitate both the origin and maintenance of species.
Nevertheless, mechanisms increasing the rate of recombination can also be favoured in local populations adapting to new environments, as a consequence of Hill–Robertson interference [28,29]. This causes selection at one locus to reduce the efficacy of natural selection at another linked locus. This interference relies on stochastic processes (drift and mutation) operating in finite populations and hence is absent in idealized, infinitely large populations [28,29]. Linked modifier alleles that increase recombination between the selected loci will reduce Hill–Robertson interference and can spread through genetic hitchhiking [30–35]. A number of evolution experiments have demonstrated an advantage for sexual reproduction in adapting populations implicating variants of the Hill–Robertson effect as a cause [36–40], but definite evidence is still lacking.
Recombination thus would appear to have contrasting effects during ecological speciation with gene flow: on the one hand, recombination reduces Hill–Robertson interference and may therefore accelerate local adaptation, but on the other hand, recombination homogenizes diverging populations and thereby reduces local adaptation. As a consequence, modifier alleles that increase recombination rates can be favoured during local adaptation because of the Hill–Robertson effect [30–35], but disfavoured because of the maladaptive gene flow effect [18–20]. However, to date these two effects have only been investigated in isolation. A better understanding of the relative contribution and timing of these mechanisms when operating jointly may afford new insights into how recombination rate evolution can affect the early stages of ecological speciation with gene flow [16].
Here, we investigate a mathematical model of two finite populations exchanging migrants while adapting to two contrasting environments. We are interested in the spread of modifier alleles that affect the recombination rate between the loci under direct selection. Specifically, we ask whether the Hill–Robertson effect prevents the evolution of recombination suppression during the early stages of ecological speciation with gene flow. As expected, our model shows that migration selects for reduced recombination whereas finite population sizes can produce selection for increased recombination. However, these two effects operate at different times: selection for recombination through the Hill–Robertson effect is pronounced during the early phase of adaptation, whereas selection against recombination through the maladaptive gene flow effect predominates once the two populations have diverged. Our results suggest that depending on the migration rate and size of the populations, recombination rate evolution may affect both the early and late stages of ecological speciation.
2. Material and methods
(a). The genetic setting
We consider two populations of haploid organisms experiencing contrasting selection pressures while still connected by migration. Within a population, individuals have two biallelic loci (A andB), with a different allele favoured in each environment (A andB in population 1,a andb in population 2). In addition, a biallelic modifier locusM alters the recombination rate betweenA andB, without being directly affected by selection [17,20,41]. The loci are arranged in the orderMAB. The resulting genotype frequencies (pi andqi in populations 1 and 2, where ) were predicted each generation through a series of five recursion equations corresponding to migration, selection, mutation, recombination and random genetic drift. All parameters and variables of the model are summarized intable 1.
) were predicted each generation through a series of five recursion equations corresponding to migration, selection, mutation, recombination and random genetic drift. All parameters and variables of the model are summarized intable 1.
Table 1.
The notation of parameters and variables used in this model. Unless otherwise stated all parameters apply to theA andB locus.
| parameter | description | standard values |
|---|---|---|
| m | migration rate | 0.01 |
| s | selection coefficient | 0.05 |
| μ | mutation rate | 1 × 10−5 |
| rM | recombination rate determined byM allele | 0.0005 |
| rm | recombination rate determined bym allele | 0.005 |
| ρ | recombination rate betweenM andA locus | 0 |
| N | population size | 100 000 |
| variable | description | |
|---|---|---|
| pi | genotype frequencies in population 1a | |
| qi | genotype frequencies in population 2a |
aThe subscripti takes values
 .
.
(b). Migration, selection and mutation steps
The migration step follows the classic two-island model where each generation a fractionm of individuals are replaced by migrants from the other equally sized population
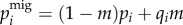 | 2.1a |
and
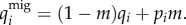 | 2.1b |
After migrating, the genotype frequencies are selected in the local environment according to their fitness values (wi) in the respective population
 | 2.2a |
and
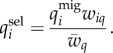 | 2.2b |
Here, the average population fitness is in population 1, and
in population 1, and in population 2. For fitness values, we assume that beneficial alleles confer a fitness of 1 +s relative to a fitness of 1 in genotypes with the other allele, wheres is the selection coefficient in both populations. The genotype fitness is calculated by multiplying the values of its composite alleles (i.e. we assume that there is no epistasis).
in population 2. For fitness values, we assume that beneficial alleles confer a fitness of 1 +s relative to a fitness of 1 in genotypes with the other allele, wheres is the selection coefficient in both populations. The genotype fitness is calculated by multiplying the values of its composite alleles (i.e. we assume that there is no epistasis).
The mutation step is a two-locus extension of the single-locus reversible mutation model. We assume that the lociA andB mutate at the same rateμ. Furthermore, to eliminate any effects not attributable to recombination, the modifier locus is assumed not to mutate. Thus, the genotype frequencies after mutation are
 | 2.3a |
and
 | 2.3b |
Here, the subscripts refer to different genotypes; withi1 being the focal genotype,i4 the genotype that differs at both theA andB loci, andi2 andi3 being the genotypes one mutation step away at theA orB locus. For example, wheni =MAB, we have
refer to different genotypes; withi1 being the focal genotype,i4 the genotype that differs at both theA andB loci, andi2 andi3 being the genotypes one mutation step away at theA orB locus. For example, wheni =MAB, we have .
.
(c). Recombination step
The effects of recombination were calculated each generation according to a mating table of the outcomes of all possible crosses, assuming there is random mating between all genotypes. Three different recombination rates are required to cover every potential cross:rM,rm andρ. The parametersrM andrm determine recombination rates between theA andB locus, depending on the allelic state at theM locus. Recombination takes place during a brief period of diploidy immediately following syngamy. We assume additive effects of theM andm alleles so that for example, the recombination rate inMm heterozygotes is equal torM +rm.ρ is the recombination rate betweenM andA.
Recombination is incorporated into the model through an 8 × 8 × 8 tensorT, whose elementsTjki give the fraction of offspringi that are generated from a cross between parentsj andk (see [17] for a full derivation of a similar tensor). The genotype frequencies after recombination were then calculated by the sum of all possible parental genotype frequencies multiplied by their corresponding element in the tensor
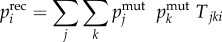 | 2.4a |
and
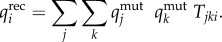 | 2.4b |
(d). Random genetic drift
Random genetic drift was incorporated into the model by randomly sampling variants from a multinomial distribution. Specifically, we assume that the genotype abundances after drift follow a multinomial distribution with parameters (genotype frequencies before drift, corresponding to probabilities of drawing these genotypes from an infinitely large pool of juveniles), and population sizeN (number of samples drawn). These genotype abundances are then normalized byN to yield the genotype frequencies after drift. Removing this drift step from the model allowed us to compare our full model with a deterministic model that does not involve the Hill–Robertson effect (as studied in [18,20]).
(genotype frequencies before drift, corresponding to probabilities of drawing these genotypes from an infinitely large pool of juveniles), and population sizeN (number of samples drawn). These genotype abundances are then normalized byN to yield the genotype frequencies after drift. Removing this drift step from the model allowed us to compare our full model with a deterministic model that does not involve the Hill–Robertson effect (as studied in [18,20]).
(e). Computation and analysis
Recursion equations were solved numerically using the Mathematica 10 software package (Wolfram Research, Inc., Champaign, Illinois, USA). All simulations started with both modifier alleles in equal frequency and with thea andb alleles fixed in both populations (i.e. all other frequencies are equal to zero). This corresponds to a situation where population 2 is already fully adapted and a new habitat is colonized by population 1. Moreover, equal modifier allele frequencies correspond to standing genetic variation in recombination rates, a situation frequently reported in natural populations [42–45]. Simulations were run for 10 000 generations with 2000 replicate runs. Throughout, only results for population 1 are presented, as population 2 was treated as an ancestral gene pool.
all other frequencies are equal to zero). This corresponds to a situation where population 2 is already fully adapted and a new habitat is colonized by population 1. Moreover, equal modifier allele frequencies correspond to standing genetic variation in recombination rates, a situation frequently reported in natural populations [42–45]. Simulations were run for 10 000 generations with 2000 replicate runs. Throughout, only results for population 1 are presented, as population 2 was treated as an ancestral gene pool.
3. Results
To put our work into context, we first briefly summarize previously derived analytical results for two infinitely large populations connected by migration and subject to divergent selection at two loci. Pylkovet al. [18] provided approximations for both the equilibrium allele frequencies and linkage disequilibrium ( ) under the resulting migration–selection balance. Using our notation and ignoring mutation, those approximations read
) under the resulting migration–selection balance. Using our notation and ignoring mutation, those approximations read
 | 3.1 |
Note that will always be positive, meaning there will be disproportionately many extreme genotypes (AB andab) relative to intermediate ones (aB andAb). Moreover,
will always be positive, meaning there will be disproportionately many extreme genotypes (AB andab) relative to intermediate ones (aB andAb). Moreover, is inversely proportional tor and is maximized at intermediate values ofm. This is because with higher migration rates the allele frequencies in the two populations become increasingly similar. These approximations assume loose linkage between the loci and hence are in reasonable agreement with our simulation results, only for high recombination rates (not shown). We were able to derive an exact solution for the migration–selection balance accounting for arbitrary linkage, but the resulting formulae are long and uninformative and therefore not given here (Mathematica notebook available upon request).
is inversely proportional tor and is maximized at intermediate values ofm. This is because with higher migration rates the allele frequencies in the two populations become increasingly similar. These approximations assume loose linkage between the loci and hence are in reasonable agreement with our simulation results, only for high recombination rates (not shown). We were able to derive an exact solution for the migration–selection balance accounting for arbitrary linkage, but the resulting formulae are long and uninformative and therefore not given here (Mathematica notebook available upon request).
Both Pylkovet al. [18] and Lenormand & Otto [20] also derived an approximation for the strength of selection acting on a rare modifier allelem that increases recombination, entering a population at migration–selection balance. Again using our notation, this approximation can be expressed as
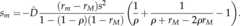 | 3.2 |
As both and the other two factors in this equation are positive there is always selection against a modifier increasing recombination rates, and the strength of this selection is directly proportional to
and the other two factors in this equation are positive there is always selection against a modifier increasing recombination rates, and the strength of this selection is directly proportional to . We will now explore how the ‘maladaptive gene flow effect’ quantified by these approximations interacts with the Hill–Robertson effect in our full, stochastic model.
. We will now explore how the ‘maladaptive gene flow effect’ quantified by these approximations interacts with the Hill–Robertson effect in our full, stochastic model.
We first performed simulations of our model for fixed recombination rates (no modifier). These simulations provided evidence for both the Hill–Robertson effect and the maladaptive gene flow effect (figure 1). In particular, using our standard set of parameters (table 1), we observed a faster spread of the optimalAB genotype with recombination; as predicted by the Hill–Robertson effect, this was only seen in finite populations. However, recombination also led to a lower equilibrium frequency of theAB genotype, as predicted by the maladaptive gene flow effect (figure 1). A stronger maladaptive gene flow effect occurred when either the migration rate was increased or the strength of selection was decreased (electronic supplementary material, figure S1b,c). By contrast, altering the mutation rate (electronic supplementary material, figure S1d) or the population size (electronic supplementary material, figure S1e,f) only affected the speed of adaptation and the magnitude of the Hill–Robertson effect.
Figure 1.

Change in the frequency of the fittest genotypeAB in the presence and absence of recombination. Starting from the standard conditions (table 1), the genotype frequency ofAB was tracked for 500 generations. The red lines represent simulations without recombination (r = 0), and the blue lines simulations withr = 0.1. The dashed lines are the deterministic model results (N = ∞). The faded lines are 2000 individual simulation runs with the solid line being the mean of all runs. See electronic supplementary material, figure S1 for similar dynamics with different parameters.
We next investigated the full model including the modifier locus. Based on our initial simulations, we expected both selection for and against theM allele which reduces recombination. Indeed, simulations with our standard parameter set demonstrated that on average, the frequency ofM declined initially, but then rose almost to fixation in the long term (electronic supplementary material, figure S2). To investigate the generality of this effect, we performed extensive simulations varying all six parameters of our model. The dynamics of each simulation were summarized by focusing on the range of the frequency ofM for each set of parameters (figure 2). Increases to the population sizeN led to a more pronounced reduction in the minimum frequency ofM, indicating that selection for recombination through the Hill–Robertson effect becomes stronger forN up to 106 (figure 2a). On the other hand, the maximum frequency ofM also increased with increasingN, reflecting more efficient selection forM through the maladaptive gene flow effect. We also observed that the Hill–Robertson effect was most notable when the migration rate was low and the selection pressure was strong, corresponding to the lowest frequencies ofM (figure 2b,c).
Figure 2.
The range of the modifier frequency of theM allele for different parameters. Each panel shows the maximum and minimum frequency of the modifier through time, averaged across 2000 replicate simulations (solid lines; shading represents the range). In each panel (except panel (a)), the deterministic results from simulations that run without genetic drift (N = ∞) are shown as dashed lines. The vertical lines are the standard values for the focal parameter (table 1); note that because of the logarithmic scale, the standard value ofρ = 0 could not be indicated in panel (f). (Online version in colour.)
The maladaptive gene flow effect was maximized at high migration rates, as recombination needs to be suppressed to prevent the populations rapidly homogenizing (figure 2b). Intriguingly, the maladaptive gene flow effect was maximized under intermediately strong selection, as weaker selection permits maladaptive alleles to persist in the population with little impact on the recombination modifier, while stronger selection would rapidly sweep maladaptive genes out of the population limiting the opportunities for recombining them onto resident backgrounds (i.e. pre-zygotic extrinsic reproductive isolation [3]).
The Hill–Robertson effect was maximized at intermediate mutation rates, as shown by the minimum frequency ofM (figure 2d). This is because either mutations arise too rarely in the population to segregate simultaneously, or mutations arise too frequently rapidly producing double mutants and never creating linkage disequilibrium. By contrast, the maximum frequency ofM increased with mutation rate (figure 2d), presumably because the migration–selection balance was reached more rapidly. The degree to which theM allele reduced recombination only had minor effects on the range of frequencies (figure 2e; values ofrM <rm). WhenrM >rm,M enhanced recombination compared tom, leading to a reversal of selection through the Hill–Robertson and maladaptive gene flow effects. However, in line with Barton [46], selection for increased recombination became much weaker when the recombination rate was initially high (see right-hand side offigure 2e). Finally, as the genetic distance increased between theM andA locus (ρ), indirect selection on the modifier through both the Hill–Robertson and the maladaptive gene flow effect was weakened ([20,35]figure 2f; see also [46]).
Although the range of the frequency of theM allele is informative about the relative strength of the Hill–Robertson and the maladaptive gene flow effect, it tells us nothing about the relative timing of these two effects. Therefore, we investigated the frequency ofM at four explanatory time points over a range of values for the migration rate and population size (figure 3; electronic supplementary material, figure S3). Starting from equal frequencies, the first 100 generations were governed by random genetic drift (figure 3a), with reduced variance in the frequency ofM in larger populations (electronic supplementary material, figure S3a). The variance in this frequency expanded by the 250th generation (roughly around the time when theAB genotype arose, which varies between simulation runs). This time also corresponded to the earliest evidence for a Hill–Robertson effect, except in the presence of frequent gene flow (figure 3b). The Hill–Robertson effect became strongest roughly by the time theAB genotype reached equilibrium (figure 3c). Once at equilibrium, selection for recombination suppression through the maladaptive gene flow effect became dominant, resulting in an increased frequency ofM with stronger migration rates (figure 3d).
Figure 3.
Distribution of the frequency of a modifier alleleM reducing recombination over a range of migration values at four time points. The charts show the frequencies of the modifierpM at four different time points that describe the evolution of recombination. They-axis of each chart is split up into 20 equally sized bins (horizontal lines) covering all frequencies from 0 to 1, in increments of 0.05. The shading of each cell indicates the fraction of runs, out of 2000 replicates, that the modifier frequency was in that bin at any given migration rate (see legend). The left-most value for migration rate (left of the thick vertical line) representsm = 0. The solid red line shows the mean of all replicates for a given migration rate, and the dashed orange line indicates the result of the deterministic simulation (N = ∞).
To explore the combined effects of two key parameters of our model, the migration rate and selection coefficient, we performed additional simulations for nine combinations of these parameters (figure 4). These simulations clearly show the limits of the maladaptive gene flow effect, as the rapid suppression of recombination only evolved when bothm ands were high. This is because whenm was high buts was not, allele frequencies in the two populations became very similar and the populations were close to linkage equilibrium, reducing selection for recombination suppression (see also the discussion of equations (3.1) and (3.2)). Conversely, whenm was low buts was high, the few maladaptive migrant alleles that entered a population were very efficiently purged so that again there was only little linkage disequilibrium and hence selection for recombination suppression. In combination, the maladaptive gene flow effect can therefore be strongest at intermediate migration rates or selection coefficients when the other parameter is kept fixed (compare plots in left column or plots in middle row infigure 4). By contrast, early selection for increased recombination through the Hill–Robertson effect became stronger with increasing selection, but was diminished with increasing migration rates because this produces an earlier and stronger maladaptive gene flow effect.
Figure 4.
Changes in the frequency of a modifier alleleM reducing recombination depending on the strength of migration and selection. Simulations were run using three different migration rates (rows) and three different selection coefficients (columns); other parameters were maintained at standard conditions (table 1). The faded lines show 1000 replicate runs for each simulation, with the solid line showing the average and the dashed line the deterministic result (N = ∞). (Online version in colour.)
4. Discussion
It has long been recognized that recombination antagonizes adaptive divergence and speciation with gene flow [9–11]. This is because recombination homogenizes migrant and resident genotypes that have diverged by natural selection. Theoretical studies of speciation with gene flow have often found that natural selection favours the spread of suppressors of recombination (e.g. chromosomal inversions and modifier alleles; reviewed in [16]) due to maladaptive gene flow [14,15,18–21]. However, these studies have ignored the stochastic processes that operate in finite populations and that are known to produce selection for increased recombination via the Hill–Robertson effect [29–32,35,47]. Here, we have investigated the interplay between these two effects and demonstrated that the Hill–Robertson effect favours increased recombination between adaptive loci during the early stages of adaptive divergence, whereas the maladaptive gene flow effect leads to suppression of recombination after populations have diverged.
Our results caution against the view that suppressors of recombination will always spread in the presence of maladaptive gene flow. Although in our two-locus model selection for increased recombination is only transitory, the magnitude of the Hill–Robertson effect is expected to increase with a larger number of loci under selection [30,31,33,47]. We would also expect the duration of the Hill–Robertson effect to be extended relative to the maladaptive gene flow effect if there is ongoing selection acting on many loci. In addition, even after the population has reached a fitness peak, selection for increased recombination may continue as a consequence of the mutation–selection balance [33]. Finally, selection for the suppression of recombination can be opposed or even reversed if there is negative epistasis between the selected loci [20]. More generally, the evolution of supressed recombination during the early stages of ecological speciation with gene flow depends on a number of factors including not only genetic architecture (e.g. number of loci and epistatic interactions) and migration rate, but also mutation rate and population size. Whether or not the initial conditions that favour the evolution of reproductive isolation between locally adapted populations in the face of gene flow are common in nature remains an empirical problem.
The strength of the Hill–Robertson and the maladaptive gene flow effect as well as the timing of the transition between these effects was determined by the parameters we used. We selected our standard parameters so that both effects were observed, including complete linkage between the modifier locus and the loci under selection (asfigure 2f indicates, this does not seem to be crucial though as long as linkage is reasonably tight). Relatively large populations and strong selection were required for increased recombination rates to evolve under the Hill–Robertson effect, whereas strong migration and selection were necessary for recombination suppression to evolve under the maladaptive gene flow effect. We expect that both of these conditions should be met in many systems. In particular, in hybrid zones between populations with large effective population size recombination suppression should evolve readily. For example,Helianthus sunflowers andDrosophila species that occur in sympatry are often separated by chromosomal inversions [24,25] and strong selection [48,49]. These taxa also frequently haveNe values above one million [48,50,51] and are experiencing, or have experienced, extensive gene flow [50,52,53]. Across other systems, regions of suppressed recombination also separate hybridizing species or locally adapted populations [54–56], but whether these regions evolved during speciation with gene flow or are ancestral genomic landscapes (e.g. [57]) remains to be determined (see [22] for a more detailed discussion).
If populations exposed to maladaptive gene flow can establish suppressed recombination, then it is possible that they might also continue to diverge, becoming new species. However, the specific conditions for continued divergence can be restrictive. For example, Flaxmanet al. [58] found that recombination suppression aids speciation when selection is weak but migration is high, presumably because selection effects acting upon each locus are extended to larger regions of the genome [59]. In our model, the recombination rate itself evolves and the levels of migration and selection that lead to its suppression appear to partially differ from those favouring divergence in these speciation models. For instance, under moderate selection and strong migration, the modifier of recombination did not spread. However, whens andm were both high and of similar magnitude, the modifiers of recombination spread easily (figure 4). This disjunction between models might suggest that cases of speciation with gene flow where migration is stronger than selection might be unlikely because the required recombination landscape is difficult to evolve in the first place. Conversely, cases of speciation with gene flow where selection is strong are likely to proceed without the suppression of recombination, although recombination suppression is nonetheless expected to evolve. We therefore speculate that the evolution of suppressed recombination might not be required in some cases, but nonetheless will be a signature of speciation with gene flow. This is because the most favourable conditions for speciation with gene flow are also the most favourable conditions for the spread of modifier alleles that suppress recombination (i.e. when selection is strong). Overall, cases of sympatric and parapatric speciation might require strong selection, and they will generally be characterized by coldspots of recombination.
A number of studies have also investigated the reduction of recombination by chromosomal inversions during speciation with gene flow [14,21,22,24,25,27]. For instance, Kirkpatrick & Barton [14] showed that a chromosomal inversion would spread when it captures loci under divergent selection, as an inversion will prevent hybridization with maladapted migrants. Such an inversion and the modifier model we used in this study are similar, except for one key difference: inversions only prevent recombination in heterokaryotypes. As a consequence, shuffling between resident and migrant alleles is prevented but shuffling of different resident alleles can still occur. Therefore, we would expect the extent to which the Hill–Robertson effect opposes the maladaptive gene flow effect to be reduced, making an inversion a powerful mechanism that simultaneously allows efficient local adaptation and limits maladaptive gene flow between populations during speciation with gene flow. In addition, populations separated by fixed chromosomal inversions might be able to diverge further during secondary contact even if gene flow was very high and selection was weak. As noted by Flaxmanet al. [58], these are the conditions where recombination suppression has the greatest contribution to speciation driven by divergent natural selection.
In order to isolate the specific effects on recombination modifiers caused by gene flow as opposed to population size, we intentionally kept our model as simple as possible. Future models should consider a larger number of loci and integrate additional factors that are not part of our model. These could include different types of recombination modifiers (local versus global allelic modifiers and also chromosomal rearrangements), epistasis, diploidy and multiple populations with variable spatial selection and migration rates. It would also be interesting to construct models that explore the interplay between selection on recombination rates and other mechanisms of reinforcement such as selection for assortative mating or migration rate in response to maladaptive gene flow [7,16].
In conclusion, our model indicates that the dynamics of recombination rate evolution during adaptive divergence are governed not only by deterministic evolutionary forces such as selection and migration, but also by stochastic forces such as random genetic drift and mutation. Much of the theoretical literature on adaptive speciation with gene flow has overlooked the interplay between these forces, and consequently often saw recombination as a hindrance to adaptive divergence and speciation. The fact that the benefits of recombination in finite populations are well established within the research community studying the evolution of sex highlights the need of increased dialogue between these fields.
Supplementary Material
Acknowledgements
We would like to thank the anonymous reviewers for their helpful comments on our manuscript. We are also grateful to Mohamed Noor, Patrik Nosil and Sam Yeaman for useful discussions on speciation with gene flow.
Authors' contribution
J.R. and J.E. created the model and ran simulations. All authors planned the study and wrote the manuscript. All authors gave final approval for publication.
Competing interests
We have no competing interests.
Funding
This research was supported by an Australian Research Council Discovery grant no. (DP140103774) to J.E. and D.O.-B.
References
- 1.Schluter D.2009. Evidence for ecological speciation and its alternative. Science323, 737–741. (doi:10.1126/Science.1160006) [DOI] [PubMed] [Google Scholar]
- 2.Nosil P, Harmon LJ, Seehausen O. 2009. Ecological explanations for (incomplete) speciation. Trends Ecol. Evol.24, 145–156. (doi:10.1016/j.tree.2008.10.011) [DOI] [PubMed] [Google Scholar]
- 3.Rundle HD, Nosil P. 2005. Ecological speciation. Ecol. Lett.8, 336–352. (doi:10.1111/J.1461-0248.2004.00715.X) [Google Scholar]
- 4.Schluter D.2001. Ecology and the origin of species. Trends Ecol. Evol.16, 372–380. (doi:10.1016/S0169-5347(01)02198-X) [DOI] [PubMed] [Google Scholar]
- 5.Nosil P.2012. Ecological speciation, 280Oxford, NY: Oxford University Press. [Google Scholar]
- 6.Nosil P, Vines TH, Funk DJ. 2005. Perspective: reproductive isolation caused by natural selection against immigrants from divergent habitats. Evolution59, 705–719. (doi:10.1111/j.0014-3820.2005.tb01747.x) [PubMed] [Google Scholar]
- 7.Lenormand T.2012. From local adaptation to speciation: specialization and reinforcement. Int. J. Ecol.2012, 508458 (doi:10.1155/2012/508458) [Google Scholar]
- 8.Bolnick DI, Nosil P. 2007. Natural selection in populations subject to a migration load. Evolution61, 2229–2243. (doi:10.1111/j.1558-5646.2007.00179.x) [DOI] [PubMed] [Google Scholar]
- 9.Felsenstein J.1981. Skepticism towards Santa Rosalia, or why are there so few kinds of animals. Evolution35, 124–138. (doi:10.2307/2407946) [DOI] [PubMed] [Google Scholar]
- 10.Butlin RK.2005. Recombination and speciation. Mol. Ecol.14, 2621–2635. (doi:10.1111/J.1365-294x.2005.02617.X) [DOI] [PubMed] [Google Scholar]
- 11.Bürger R, Akerman A. 2011. The effects of linkage and gene flow on local adaptation: a two-locus continent-island model. Theor. Popul. Biol.80, 272–288. (doi:10.1016/j.tpb.2011.07.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Faria R, Navarro A. 2010. Chromosomal speciation revisited: rearranging theory with pieces of evidence. Trends Ecol. Evol.25, 660–669. (doi:10.1016/J.Tree.2010.07.008) [DOI] [PubMed] [Google Scholar]
- 13.Navarro A, Barton NH. 2003. Accumulating postzygotic isolation genes in parapatry: a new twist on chromosomal speciation. Evolution57, 447–459. (doi:10.1554/0014-3820(2003)057[0447:Apigip]2.0.Co;2) [DOI] [PubMed] [Google Scholar]
- 14.Kirkpatrick M, Barton N. 2006. Chromosome inversions, local adaptation and speciation. Genetics173, 419–434. (doi:10.1534/Genetics.105.047985) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feder JL, Nosil P. 2009. Chromosomal inversions and species differences: when are genes affecting adaptive divergence and reproductive isolation expected to reside within inversions?Evolution63, 3061–3075. (doi:10.1111/j.1558-5646.2009.00786.x) [DOI] [PubMed] [Google Scholar]
- 16.Ortiz-Barrientos D, Engelstädter J, Rieseberg LH. 2016. Recombination rate evolution and the origin of species. Trends Ecol. Evol.31, 226–236. (doi:10.1016/j.tree.2015.12.016) [DOI] [PubMed] [Google Scholar]
- 17.Nei M.1967. Modification of linkage intensity by natural selection. Genetics57, 625–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pylkov KV, Zhivotovsky LA, Feldman MW. 1998. Migration versus mutation in the evolution of recombination under multilocus selection. Genet. Res.71, 247–256. (doi:10.1017/S0016672398003243) [DOI] [PubMed] [Google Scholar]
- 19.Charlesworth D, Charlesworth B. 1979. Selection on recombination in clines. Genetics91, 581–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lenormand T, Otto SP. 2000. The evolution of recombination in a heterogeneous environment. Genetics156, 423–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Trickett AJ, Butlin RK. 1994. Recombination suppressors and the evolution of new species. Heredity73, 339–345. (doi:10.1038/hdy.1994.180) [DOI] [PubMed] [Google Scholar]
- 22.Feder JL, Xie XF, Rull J, Velez S, Forbes A, Leung B, Dambroski H, Filchak KE, Aluja M. 2005. Mayr, Dobzhansky, and Bush and the complexities of sympatric speciation inRhagoletis. Proc. Natl Acad. Sci. USA102, 6573–6580. (doi:10.1073/pnas.0502099102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Michel AP, Sim S, Powell THQ, Taylor MS, Nosil P, Feder JL. 2010. Widespread genomic divergence during sympatric speciation. Proc. Natl Acad. Sci. USA107, 9724–9729. (doi:10.1073/pnas.1000939107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Noor MAF, Grams KL, Bertucci LA, Reiland J. 2001. Chromosomal inversions and the reproductive isolation of species. Proc. Natl Acad. Sci. USA98, 12 084–12 088. (doi:10.1073/pnas.221274498) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rieseberg LH, Whitton J, Gardner K. 1999. Hybrid zones and the genetic architecture of a barrier to gene flow between two sunflower species. Genetics152, 713–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lowry DB, Willis JH. 2010. A widespread chromosomal inversion polymorphism contributes to a major life-history transition, local adaptation, and reproductive isolation. PLoS Biol.8, e1000500 (doi:e100050010.1371/journal.pbio.1000500) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carneiro M, Ferrand N, Nachman MW. 2009. Recombination and speciation: loci near centromeres are more differentiated than loci near telomeres between subspecies of the European rabbit (Oryctolagus cuniculus). Genetics181, 593–606. (doi:10.1534/genetics.108.096826) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hill WG, Robertson A. 1966. Effect of linkage on limits to artificial selection. Genet. Res.8, 269–294. (doi:10.1017/S0016672300010156) [PubMed] [Google Scholar]
- 29.Felsenstein J.1974. Evolutionary advantage of recombination. Genetics78, 737–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Otto SP, Barton NH. 2001. Selection for recombination in small populations. Evolution55, 1921–1931. (doi:10.1017/S0016672300010156) [DOI] [PubMed] [Google Scholar]
- 31.Iles MM, Walters K, Cannings C. 2003. Recombination can evolve in large finite populations given selection on sufficient loci. Genetics165, 2249–2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Barton NH, Otto SP. 2005. Evolution of recombination due to random drift. Genetics169, 2353–2370. (doi:10.1534/genetics.104.032821) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Keightley PD, Otto SP. 2006. Interference among deleterious mutations favours sex and recombination in finite populations. Nature443, 89–92. (doi:10.1038/nature05049) [DOI] [PubMed] [Google Scholar]
- 34.Martin G, Otto SP, Lenormand T. 2006. Selection for recombination in structured populations. Genetics172, 593–609. (doi:10.1534/genetics.104.039982) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Roze D, Barton NH. 2006. The Hill–Robertson effect and the evolution of recombination. Genetics173, 1793–1811. (doi:10.1534/Genetics.106.058586) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Becks L, Agrawal AF. 2012. The evolution of sex is favoured during adaptation to new environments. PLoS Biol.10, e1001317 (doi:10.1371/Journal.Pbio.1001317) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cooper TF.2007. Recombination speeds adaptation by reducing competition between beneficial mutations in populations ofEscherichia coli. PLoS Biol.5, 1899–1905. (doi:10.1371/journal.pbio.0050225) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Goddard MR, Godfray HCJ, Burt A. 2005. Sex increases the efficacy of natural selection in experimental yeast populations. Nature434, 636–640. (doi:10.1038/nature03405) [DOI] [PubMed] [Google Scholar]
- 39.Colegrave N.2002. Sex releases the speed limit on evolution. Nature420, 664–666. (doi:10.1038/nature01191) [DOI] [PubMed] [Google Scholar]
- 40.McDonald MJ, Rice DP, Desai MM. 2016. Sex speeds adaptation by altering the dynamics of molecular evolution. Nature531, 233–236. (doi:10.1038/nature17143) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Karlin S, McGregor J. 1974. Towards a theory of evolution of modifier genes. Theor. Popul. Biol.5, 59–103. (doi:10.1016/0040-5809(74)90052-5) [DOI] [PubMed] [Google Scholar]
- 42.Smukowski CS, Noor MA. 2011. Recombination rate variation in closely related species. Heredity107, 496–508. (doi:10.1038/hdy.2011.44) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kong A, et al. 2010. Fine-scale recombination rate differences between sexes, populations and individuals. Nature467, 1099–1103. (doi:10.1038/nature09525) [DOI] [PubMed] [Google Scholar]
- 44.Bauer E, et al. 2013. Intraspecific variation of recombination rate in maize. Genome Biol.14, R103 (doi:10.1186/gb-2013-14-9-r103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gion JM, Hudson CJ, Lesur I, Vaillancourt RE, Potts BM, Freeman JS. 2016. Genome-wide variation in recombination rate in Eucalyptus. BMC Genomics17, 590 (doi:10.1186/s12864-016-2884-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Barton NH.1995. A general-model for the evolution of recombination. Genet. Res.65, 123–144. (doi:10.1017/S0016672300033140) [DOI] [PubMed] [Google Scholar]
- 47.Hartfield M, Otto SP, Keightley PD. 2010. The role of advantageous mutations in enhancing the evolution of a recombination modifier. Genetics184, 1153–1164. (doi:10.1534/genetics.109.112920) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sambatti JB, Strasburg JL, Ortiz-Barrientos D, Baack EJ, Rieseberg LH. 2012. Reconciling extremely strong barriers with high levels of gene exchange in annual sunflowers. Evolution66, 1459–1473. (doi:10.1111/j.1558-5646.2011.01537.x) [DOI] [PubMed] [Google Scholar]
- 49.Ortiz-Barrientos D, Counterman BA, Noor MA. 2004. The genetics of speciation by reinforcement. PLoS Biol.2, e416 (doi:10.1371/journal.pbio.0020416) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Strasburg JL, Rieseberg LH. 2008. Molecular demographic history of the annual sunflowers Helianthus annuus andH. petiolaris—large effective population sizes and rates of long-term gene flow. Evolution62, 1936–1950. (doi:10.1111/j.1558-5646.2008.00415.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ortiz-Barrientos D, Chang AS, Noor MA. 2006. A recombinational portrait of theDrosophila pseudoobscura genome. Genet. Res.87, 23–31. (doi:10.1017/S0016672306007932) [DOI] [PubMed] [Google Scholar]
- 52.Schaeffer SW, Miller EL. 1992. Estimates of gene flow inDrosophila pseudoobscura determined from nucleotide sequence analysis of the alcohol dehydrogenase region. Genetics132, 471–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Machado CA, Kliman RM, Markert JA, Hey J. 2002. Inferring the history of speciation from multilocus DNA sequence data: the case ofDrosophila pseudoobscura and close relatives. Mol. Biol. Evol.19, 472–488. (doi:10.1093/oxfordjournals.molbev.a004103) [DOI] [PubMed] [Google Scholar]
- 54.Saether SA, et al. 2007. Sex chromosome-linked species recognition and evolution of reproductive isolation in flycatchers. Science318, 95–97. (doi:10.1126/science.1141506) [DOI] [PubMed] [Google Scholar]
- 55.White BJ, Cheng C, Simard F, Costantini C, Besansky NJ. 2010. Genetic association of physically unlinked islands of genomic divergence in incipient species of Anopheles gambiae. Mol. Ecol.19, 925–939. (doi:10.1111/j.1365-294X.2010.04531.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Berg PR, Star B, Pampoulie C, Sodeland M, Barth JM, Knutsen H, Jakobsen KS, Jentoft S. 2016. Three chromosomal rearrangements promote genomic divergence between migratory and stationary ecotypes of Atlantic cod. Sci. Rep.6, 23246 (doi:10.1038/srep23246) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Renaut S, Grassa CJ, Yeaman S, Moyers BT, Lai Z, Kane NC, Bowers JE, Burke JM, Rieseberg LH. 2013. Genomic islands of divergence are not affected by geography of speciation in sunflowers. Nat. Commun.4, 1827 (doi:10.1038/ncomms2833) [DOI] [PubMed] [Google Scholar]
- 58.Flaxman SM, Wacholder AC, Feder JL, Nosil P. 2014. Theoretical models of the influence of genomic architecture on the dynamics of speciation. Mol. Ecol.23, 4074–4088. (doi:10.1111/mec.12750) [DOI] [PubMed] [Google Scholar]
- 59.Rieseberg LH.2001. Chromosomal rearrangements and speciation. Trends Ecol. Evol.16, 351–358. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


