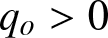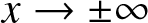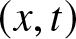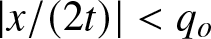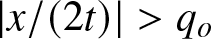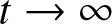Refine listing
Actions for selected content:
- View selected items
- Save to my bookmarks
- Export citations
- Download PDF (zip)
- Save to Kindle
- Save to Dropbox
- Save to Google Drive
Save content to
To save this undefined to your undefined account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your undefined account.Find out more about saving content to.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle.Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about theKindle Personal Document Service.
Please be advised that item(s) you selected are not available.You are about to saveJournal of Nonlinear Waves- ISSN:
- EISSN: 3033-4268
- URL: /core/journals/journal-of-nonlinear-waves
Volume2 - 2026
Research Article
Numerical inverse scattering transform for the defocusing nonlinear Schrödinger equation with box-type initial conditions on a nonzero background
- Aikaterini Gkogkou,Barbara Prinari,Thomas Trogdon
- Published online by Cambridge University Press:
- 09 January 2026, e1
- Article
- You have access
- Open access
- HTML
- Export citation
We present a method to solve numerically the Cauchy problem for the defocusing nonlinear Schrödinger (NLS) equation with a box-type initial condition (IC) having a nontrivial background of amplitude
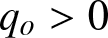 $q_o \gt 0$ as
$q_o \gt 0$ as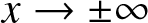 $x\to \pm \infty$ by implementing numerically the corresponding inverse scattering transform (IST). The Riemann–Hilbert problem associated with the inverse transform is solved numerically by means of appropriate contour deformations in the complex plane following the numerical implementation of the Deift–Zhou nonlinear steepest descent method. In this work, the box parameters are chosen so that there is no discrete spectrum (i.e., no solitons). The numerical method is demonstrated to be accurate within the two asymptotic regimes corresponding to two different regions of the
$x\to \pm \infty$ by implementing numerically the corresponding inverse scattering transform (IST). The Riemann–Hilbert problem associated with the inverse transform is solved numerically by means of appropriate contour deformations in the complex plane following the numerical implementation of the Deift–Zhou nonlinear steepest descent method. In this work, the box parameters are chosen so that there is no discrete spectrum (i.e., no solitons). The numerical method is demonstrated to be accurate within the two asymptotic regimes corresponding to two different regions of the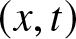 $(x,t)$-plane depending on whether
$(x,t)$-plane depending on whether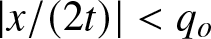 $|x/(2t)| \lt q_o$ or
$|x/(2t)| \lt q_o$ or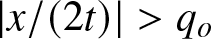 $|x/(2t)| \gt q_o$, as
$|x/(2t)| \gt q_o$, as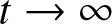 $t \to \infty$.
$t \to \infty$.
A plethora of fully localized solitary waves for the full-dispersion Kadomtsev–Petviashvili equation
- Part of:
- Mats Ehrnström,Mark D. Groves
- Published online by Cambridge University Press:
- 28 January 2026, e2
- Article
- You have access
- Open access
- HTML
- Export citation
The KP-I equation arises as a weakly nonlinear model equation for gravity-capillary waves with Bond number
 $\beta \gt 1/3$, also called strong surface tension. This equation has recently been shown to have a family of nondegenerate, symmetric ‘fully localized’ or ‘lump’ solitary waves which decay to zero in all spatial directions. The full-dispersion KP-I equation is obtained by retaining the exact dispersion relation in the modelling from the water-wave problem. In this paper, we show that the FDKP-I equation also has a family of symmetric fully localized solitary waves which are obtained by casting it as a perturbation of the KP-I equation and applying a suitable variant of the implicit-function theorem.
$\beta \gt 1/3$, also called strong surface tension. This equation has recently been shown to have a family of nondegenerate, symmetric ‘fully localized’ or ‘lump’ solitary waves which decay to zero in all spatial directions. The full-dispersion KP-I equation is obtained by retaining the exact dispersion relation in the modelling from the water-wave problem. In this paper, we show that the FDKP-I equation also has a family of symmetric fully localized solitary waves which are obtained by casting it as a perturbation of the KP-I equation and applying a suitable variant of the implicit-function theorem.