fractal, inmathematics, any of a class of complex geometric shapes that commonly have “fractional dimension,” aconcept first introduced by the mathematician Felix Hausdorff in 1918. Fractals are distinct from the simple figures of classical, or Euclidean, geometry—the square, the circle, the sphere, and so forth. They are capable of describing many irregularly shaped objects or spatially nonuniform phenomena in nature such as coastlines andmountain ranges. The termfractal, derived from the Latin wordfractus (“fragmented,” or “broken”), was coined by the Polish-born mathematician Benoit B. Mandelbrot. See the animation of the Mandelbrot fractalset.

Although the key concepts associated with fractals had been studied for years by mathematicians, and many examples, such as the Koch or “snowflake” curve were long known, Mandelbrot was the first to point out that fractals could be an ideal tool in applied mathematics for modeling a variety of phenomena from physical objects to the behavior of thestock market. Since its introduction in 1975, the concept of the fractal has given rise to a new system ofgeometry that has had a significant impact on suchdiverse fields asphysical chemistry, physiology, andfluid mechanics.

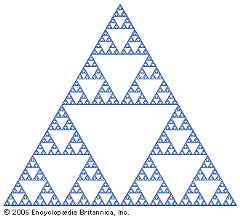
Many fractals possess the property ofself-similarity, at least approximately, if not exactly. A self-similar object is one whose component parts resemble the whole. This reiteration of details or patterns occurs at progressively smaller scales and can, in the case of purely abstract entities, continue indefinitely, so that each part of each part, when magnified, will look basically like a fixed part of the whole object. In effect, a self-similar object remains invariant under changes of scale—i.e., it has scalingsymmetry. This fractal phenomenon can often be detected in such objects as snowflakes and tree barks. All natural fractals of this kind, as well as some mathematical self-similar ones, are stochastic, or random; they thus scale in a statistical sense.

Britannica Quiz

Numbers and Mathematics

Another key characteristic of a fractal is a mathematicalparameter called itsfractal dimension. Unlike Euclidean dimension, fractal dimension is generally expressed by a noninteger—that is to say, by a fraction rather than by awhole number. Fractal dimension can be illustrated by considering a specific example: thesnowflake curve defined byHelge von Koch in 1904. It is a purely mathematical figure with a six-fold symmetry, like a natural snowflake. It is self-similar in that it consists of three identical parts, each of which in turn is made of four parts that are exact scaled-down versions of the whole. It follows that each of the four parts itself consists of four parts that are-scaled down versions of the whole. There would be nothing surprising if the scaling factor were also four, since that would be true of aline segment or a circular arc. However, for the snowflake curve, the scaling factor at each stage is three. The fractaldimension,D, denotes the power to which 3 must be raised to produce 4—i.e., 3^D= 4. The dimension of the snowflake curve is thusD = log 4/log 3, or roughly 1.26. Fractal dimension is a key property and an indicator of thecomplexity of a given figure.

Fractal geometry with its concepts of self-similarity and noninteger dimensionality has been applied increasingly instatistical mechanics, notably when dealing with physical systems consisting of seemingly random features. For example, fractal simulations have been used to plot the distribution of galaxy clusters throughout the universe and to study problems related to fluid turbulence. Fractal geometry also has contributed tocomputer graphics. Fractalalgorithms have made it possible to generate lifelike images of complicated, highly irregular natural objects, such as the rugged terrains of mountains and the intricate branch systems of trees.