


7 Rules and Style Conventions for Expressing Values of Quantities
7.1 Value and numerical value of a quantity
Thevalue of a quantity is its magnitude expressed as the product of a number and a unit, and thenumber multiplying the unit is thenumerical value of the quantity expressed in that unit.
More formally, the value of quantityA can be written asA = {A}[A], where {A} is the numericalvalue ofA when the value ofA is expressed in the unit [A]. The numerical value can therefore be written as{A} =A / [A], which is a convenient form for use in figures and tables. Thus, to eliminate the possibility ofmisunderstanding, an axis of a graph or the heading of a column of a table can be labeled t/°C instead oft (°C) or Temperature (°C). Similarly, an axis or column heading can be labeled E/(V/m) instead ofE (V/m) or Electric field strength (V/m).
Examples:
1) In the SI, the value of the velocity of light in vacuum is c = 299 792 458 m/s exactly. The number299 792 458 is the numerical value of c when c is expressed in the unit m/s, and equals c/(m/s).
2) The ordinate of a graph is labeled T/(103 K), where T is thermodynamic temperature and K is theunit symbol for kelvin, and has scale marks at 0, 1, 2, 3, 4, and 5. If the ordinate value of a pointon a curve in the graph is estimated to be 3.2, the corresponding temperature is T / (103 K) = 3.2 orT = 3200 K. Notice the lack of ambiguity in this form of labeling compared with Temperature(103 K).
3) An expression such as ln(p/MPa), where p is the quantity symbol for pressure and MPa is the unitsymbol for megapascal, is perfectly acceptable, because p/MPa is the numerical value of p when pis expressed in the unit MPa and is simply a number.
Notes:
1) For the conventions concerning the grouping of digits, see Sec.10.5.3.
2)An alternative way of writingc/(m/s) is {c}m/s, meaning the numerical value ofc whenc is expressed in the unit m/s.
7.2 Space between numerical value and unit symbol
In the expression for the value of a quantity, the unit symbol is placed after the numerical value anda space is left between the numerical value and the unit symbol.
The only exceptions to this rule are for the unit symbols for degree, minute, and second for planeangle: °, ', and ", respectively (seeTable 6), in which case no space is left between the numerical value andthe unit symbol.
Example: α = 30°22'8"
Note: α is a quantity symbol for plane angle.
This rule means that:
(a) The symbol °C for the degree Celsius is preceded by a space when one expresses the values of Celsiustemperatures.
Example: t = 30.2 °C but not: t = 30.2°C or t = 30.2° C
(b) Even when the value of a quantity is used as an adjective, a space is left between the numerical valueand the unit symbol. (This rule recognizes that unit symbols are not like ordinary words orabbreviations but are mathematical entities, and that the value of a quantity should be expressed in away that is as independent of language as possiblesees Secs.7.6 and7.10.3.)
Examples: a 1 m end gauge but not: a 1-m end gauge
a10kΩ resistor but not: a 10-kΩ resistor
However, if there is any ambiguity, the words should be rearranged accordingly. For example, thestatement the samples were placed in 22 mL vials should be replaced with the statement the sampleswere placed in vials of volume 22 mL.
Note: When unit names are spelled out, the normal rules of English apply. Thus, for example, a roll of35-millimeter film is acceptable (see Sec.7.6, note 3).
7.3 Number of units per value of a quantity
The value of a quantity is expressed using no more than one unit.
Example::l = 10.234 m but not: l = 10 m 23 cm 4 mm
Notes: Expressing the values of time intervals and of plane angles are exceptions to this rule. However, it is preferable to divide the degree decimally. Thus one should write 22.20° rather than 22°12′, except in fields such as cartography and astronomy.
7.4 Unacceptability of attaching information to units
When one gives the value of a quantity, it is incorrect to attach letters or other symbols to the unit inorder to provide information about the quantity or its conditions of measurement. Instead, the letters orother symbols should be attached to the quantity.
Example:Vmax = 1000 V but not: V = 1000 Vmax
Note: V is a quantity symbol for potential difference.
7.5 Unacceptability of mixing information with units
When one gives the value of a quantity, any information concerning the quantity or its conditions ofmeasurement must be presented in such a way as not to be associated with the unit. This means thatquantities must be defined so that they can be expressed solely in acceptable units (including the unitone see Sec.7.10).
Examples:
| the Pb content is 5 ng/L | but not: | 5 ng Pb/L or 5 ng of lead/L |
| the sensitivity for NO3 molecules is 5 × 1010/cm3 | but not: | the sensitivity is 5 × 1010 NO3 molecules/cm3 |
| the neutron emission rate is 5 × 1010/s | but not: | the emission rate is 5 × 1010 n/s |
| the number density of O2 atoms is 3 × 1018/cm3 | but not: | the density is 3 × 1018 O2 atoms/cm3 |
| the resistance per square is 100 Ω | but not: | the resistance is 100 Ω/square |
7.6 Symbols for numbers and units versus spelled-out names of numbers and units
ThisGuide takes the position that the key elements of a scientific or technical paper, particularly theresults of measurements and the values of quantities that influence the measurements, should be presentedin a way that is as independent of language as possible. This will allow the paper to be understood by asbroad an audience as possible, including readers with limited knowledge of English. Thus, to promote thecomprehension of quantitative information in general and its broad understandability in particular, valuesof quantities should be expressed in acceptable units using
— the Arabic symbols for numbers, that is, the Arabic numerals, not the spelled-out names of theArabic numerals; and
— the symbols for the units,not the spelled-out names of the units.
Examples:
| the length of the laser is 5 m | but not: | the length of the laser is five meters |
| the sample was annealed at a temperature of 955 K for 12 h | but not: | the sample was annealed at a temperature of 955 kelvins for 12 hours |
Notes:
1. If the intended audience for a publication is unlikely to be familiar with a particular unit symbol, itshould be defined when first used.
2. Because the use of the spelled-out name of an Arabic numeral with a unit symbol can causeconfusion, such combinations must strictly be avoided. For example, one should never write thelength of the laser is five m.
3. Occasionally, a value is used in a descriptive or literary manner and it is fitting to use the spelledoutname of the unit rather than its symbol. Thus, this Guide considers acceptable statements such as the reading lamp was designed to take two 60-watt light bulbs, or the rocket journeyeduneventfully across 380 000 kilometers of space, or they bought a roll of 35-millimeter film fortheir camera.
4. The United States Government Printing Office Style Manual (Ref.[3], pp. 181-189) gives the rulethat symbols for numbers are always to be used when one expresses (a) the value of a quantity interms of a unit of measurement, (b) time (including dates), and (c) an amount of money. Thispublication should be consulted for the rules governing the choice between the use of symbols fornumbers and the spelled-out names of numbers when numbers are dealt with in general.
7.7 Clarity in writing values of quantities
The value of a quantity is expressed as the product of a number and a unit (see Sec.7.1). Thus, toavoid possible confusion, thisGuide takes the position that values of quantities must be written so that it iscompletely clear to which unit symbols the numerical values of the quantities belong. Also to avoidpossible confusion, thisGuide strongly recommends that the word to be used to indicate a range ofvalues for a quantity instead of a range dash (that is, a long hyphen) because the dash could bemisinterpreted as a minus sign. (The first of these recommendations once again recognizes that unitsymbols are not like ordinary words or abbreviations but are mathematical entitiessee Sec.7.2.)
| 51 mm × 51 mm × 25 mm | but not: | 51 × 51 × 25 mm |
| 225 nm to 2400 nm or (225 to 2400) nm | but not: | 225 to 2400 nm |
| 0 ºC to 100 ºC or (0 to 100) ºC | but not: | 0 ºC - 100 ºC |
| 0 V to 5 V or (0 to 5) V | but not: | 0 - 5 V |
| (8.2, 9.0, 9.5, 9.8, 10.0) GHz | but not: | 8.2, 9.0, 9.5, 9.8, 10.0 GHz |
| 63.2 m ± 0.1 m or (63.2 ± 0.1) m | but not: | 63.2 ± 0.1 m or 63.2 m ± 0.1 |
| 129 s - 3 s = 126 s or (129 - 3) s = 126 s | but not: | 129 - 3 s = 126 s |
Note: For the conventions concerning the use of the multiplication sign, see Sec.10.5.4.
7.8 Unacceptability of stand-alone unit symbols
Symbols for units are never used without numerical values or quantity symbols (they are notabbreviations).
Examples:
| there are 106 mm in 1 km | but not: | there are many mm in a km |
| it is sold by the cubic meter | but not: | it is sold by the m3 |
| t/°C, E/(V/m), p/MPa, and the like are perfectly acceptable (see Sec.7.1). | ||
The selection of the appropriate decimal multiple or submultiple of a unit for expressing the value ofa quantity, and thus the choice of SI prefix, is governed by several factors.
These include:— the need to indicate which digits of a numerical value are significant,
— the need to have numerical values that are easily understood, and
— the practice in a particular field of science or technology.
A digit is significant if it is required to express the numerical value of a quantity. In the expressionl = 1200 m, it is not possible to tell whether the last two zeroes are significant or only indicate themagnitude of the numerical value ofl. However, in the expression l = 1.200 km, which uses the SI prefixsymbol for 103 (kilo, symbol k), the two zeroes are assumed to be significant because if they were not, thevalue ofl would have been writtenl = 1.2 km.
It is often recommended that, for ease of understanding, prefix symbols should be chosen in such away that numerical values are between 0.1 and 1000, and that only prefix symbols that represent thenumber 10 raised to a power that is a multiple of 3 should be used.
Examples:
3.3 × 107 Hz may be written as 33 × 106 Hz = 33 MHz
0.009 52 g may be written as 9.52 × 10-3 g = 9.52 mg
2703 W may be written as 2.703 × 103 W = 2.703 kW
5.8 × 10-8 m may be written as 58 × 10-9 m = 58 nm
However, the values of quantities do not always allow this recommendation to be followed, nor is itmandatory to try to do so.
In a table of values of the same kind of quantities or in a discussion of such values, it is usuallyrecommended that only one prefix symbol should be used even if some of the numerical values are notbetween 0.1 and 1000. For example, it is often considered preferable to write the size of the sample is10 mm × 3 mm × 0.02 mm rather than the size of the sample is 1 cm × 3 mm × 20 μm.
In certain kinds of engineering drawings it is customary to express all dimensions in millimeters.This is an example of selecting a prefix based on the practice in a particular field of science or technology.
7.10 Values of quantities expressed simply as numbers: the unit one, symbol 1
Certain quantities, such as refractive index, relative permeability, and mass fraction, are defined asthe ratio of two mutually comparable quantities and thus are of dimension one (see Sec.7.14). The coherentSI unit for such a quantity is the ratio of two identical SI units and may be expressed by the number 1.However, the number 1 generally does not appear in the expression for the value of a quantity of dimensionone. For example, the value of the refractive index of a given medium is expressed asn = 1.51 × 1 = 1.51.
On the other hand, certain quantities of dimension one have units with special names and symbolswhich can be used or not depending on the circumstances. Plane angle and solid angle, for which the SIunits are the radian (rad) and steradian (sr), respectively, are examples of such quantities (see Sec.4.2.1).
7.10.1 Decimal multiples and submultiples of the unit one
Because SI prefix symbols cannot be attached to the unit one (see Sec.6.2.6), powers of 10 are usedto express decimal multiples and submultiples of the unit one.
Example: μr = 1.2 × 10-6 but not: μr = 1.2 μ
Note: μr is the quantity symbol for relative permeability.
7.10.2 %, percentage by, fraction
In keeping with Ref. [4: ISO 31-0], thisGuide takes the position that it is acceptable to use theinternationally recognized symbol % (percent) for the number 0.01 with the SI and thus to express thevalues of quantities of dimension one (see Sec.7.14) with its aid. When it is used, a space is left between the symbol % and the number by which it is multiplied [4: ISO 31-0]. Further, in keeping with Sec.7.6, thesymbol % should be used, not the name percent.
Example: xB = 0.0025 = 0.25 % but not: xB = 0.0025 = 0.25% or xB = 0.25 percent
Note: xB is the quantity symbol for amount-of-substance fraction of B (see Sec.8.6.2).
Because the symbol % represents simply a number, it is not meaningful to attach information to it(see Sec.7.4). One must therefore avoid using phrases such as percentage by weight, percentage bymass, percentage by volume, or percentage by amount of substance. Similarly, one must avoidwriting, for example, % (m/m), % (by weight), % (V/V), % (by volume), or % (mol/mol). Thepreferred forms are the mass fraction is 0.10, or the mass fraction is 10 %, or wB = 0.10, or wB =10 % (wB is the quantity symbol for mass fraction of Bsee Sec.8.6.10); the volume fraction is 0.35, orthe volume fraction is 35 %, or φB = 0.35, or φB = 35 % (φB is the quantity symbol for volumefraction of Bsee Sec.8.6.6); and the amount-of-substance fraction is 0.15, or the amount-of-substancefraction is 15 %, or xB = 0.15, or xB = 15 %. Mass fraction, volume fraction, and amount-of-substancefraction of B may also be expressed as in the following examples:wB = 3 g/kg; φB = 6.7 mL/L;xB =185 mmol/mol. Such forms are highly recommended (see also Sec.7.10.3).
In the same vein, because the symbol % represents simply the number 0.01, it is incorrect to write,for example, where the resistancesR1 andR2 differ by 0.05 %, or where the resistance R1 exceeds theresistanceR2 by 0.05 %. Instead, one should write, for example, whereR1 =R2 (1 + 0.05 %), or define aquantity Δ via the relation Δ = (R1 -R2) /R2 and write where Δ = 0.05 %. Alternatively, in certain cases,the word fractional or relative can be used. For example, it would be acceptable to write the fractionalincrease in the resistance of the 10 kΩ reference standard in 2006 was 0.002 %.
In keeping with Ref. [4: ISO 31-0], thisGuide takes the position that the language-dependent termspart per million, part per billion, and part per trillion, and their respective abbreviations ppm, ppb, andppt (and similar terms and abbreviations), are not acceptable for use with the SI to express the values ofquantities. Forms such as those given in the following examples should be used instead.
Examples:
| a stability of 0.5 (μA/A)/min | but not: | a stability of 0.5 ppm/min |
| a shift of 1.1 nm/m | but not: | a shift of 1.1 ppb |
| a frequency change of 0.35 × 10-9 f | but not: | a frequency change of 0.35 ppb |
| a sensitivity of 2 ng/kg | but not: | a sensitivity of 2 ppt |
the relative expanded uncertainty of the resistance R is Ur = 3 μΩ/Ω | ||
| or | ||
| the expanded uncertainty of the resistanceR isU = 3 × 10-6R | ||
| or | ||
| the relative expanded uncertainty of the resistance R is Ur = 3 × 10-6 | ||
| but not: | ||
| the relative expanded uncertainty of the resistance R is Ur = 3 ppm | ||
Because the names of numbers 109 and larger are not uniform worldwide, it is best that they beavoided entirely (in many countries, 1 billion = 1 × 1012, not 1 × 109 as in the United States); the preferredway of expressing large numbers is to use powers of 10. This ambiguity in the names of numbers is one ofthe reasons why the use of ppm, ppb, ppt, and the like is deprecated. Another, and a more important one, isthat it is inappropriate to use abbreviations that are language dependent together with internationallyrecognized signs and symbols, such as MPa, ln, 1013, and %, to express the values of quantities and inequations or other mathematical expressions (see also Sec.7.6).
Note: ThisGuide recognizes that in certain cases the use of ppm, ppb, and the like may be required by alaw or a regulation. Under these circumstances, Secs.2.1 and2.1.1 apply.
It is unacceptable to use Roman numerals to express the values of quantities. In particular, oneshould not use C, M, and MM as substitutes for 102, 103, and 106, respectively.
7.11 Quantity equations and numerical-value equations
A quantity equation expresses a relation among quantities. An example isl =νt, wherel is thedistance a particle in uniform motion with velocityν travels in the timet.
Because a quantity equation such as l =νt is independent of the units used to express the values ofthe quantities that compose the equation, and becausel, ν, andt represent quantities and not numericalvalues of quantities, it is incorrect to associate the equation with a statement such as wherel is in meters,νis in meters per second, andt is in seconds.
On the other hand, a numerical value equation expresses a relation among numerical values ofquantities and therefore does depend on the units used to express the values of the quantities. For example,{l}m = 3.6-1 {ν}km/h {t}s expresses the relation among the numerical values of l, ν, and t only when thevalues ofl, ν, andt are expressed in the units meter, kilometer per hour, and second, respectively. (Here{A}X is the numerical value of quantityA when its value is expressed in the unit Xsee Sec.7.1, note 2.)
An alternative way of writing the above numerical value equation, and one that is preferred becauseof its simplicity and generality, isl/m = 3.6-1 [ν/(km/h)](t / s). NIST authors should consider using thispreferred form instead of the more traditional form l = 3.6-1 νt, where l is in meters, ν is in kilometers perhour, and t is in seconds. In fact, this form is still ambiguous because no clear distinction is made betweena quantity and its numerical value. The correct statement is, for example, l* = 3.6-1 ν*t *, wherel* is thenumerical value of the distance l traveled by a particle in uniform motion whenl is expressed in meters, ν*is the numerical value of the velocity ν of the particle when ν is expressed in kilometers per hour, andt* isthe numerical value of the time of travel t of the particle when t is expressed in seconds. Clearly, as isdone here, it is important to use different symbols for quantities and their numerical values to avoidconfusion.
It is the strong recommendation of this Guide that because of their universality, quantity equationsshould be used in preference to numerical-value equations. Further, if a numerical-value equation is used, itshould be written in the preferred form given in the above paragraph, and if at all feasible the quantityequation from which it was obtained should be given.
Notes:
1. Two other examples of numerical-value equations written in the preferred form are as follows,where Eg is the gap energy of a compound semiconductor andk is the conductivity of anelectrolytic solution:
Eg/eV = 1.425 - 1.337x + 0.270x2, 0 ≤x ≤ 0.15,wherex is an appropriately defined amount-of-substance fraction (see Sec.8.6.2).
k /(S / cm) = 0.065 135 + 1.7140 × 10-3(t / °C) + 6.4141 × 10-6(t / °C)2 - 4.5028 × 10-8(t / °C)3,0 °C ≤ t ≤ 50 °C, wheret is Celsius temperature.
2. Writing numerical-value equations for quantities expressed in inch-pound units in the preferredform will simplify their conversion to numerical-value equations for the quantities expressed in SIunits.
7.12 Proper names of quotient quantities
Derived quantities formed from other quantities by division are written using the words divided by or perrather than the words per unit in order to avoid the appearance of associating a particular unit with thederived quantity.
Example: pressure is force divided by area or pressure is force per area but not: pressure is force per unit area
7.13 Distinction between an object and its attribute
To avoid confusion, when discussing quantities or reporting their values, one should distinguishbetween a phenomenon, body, or substance, and an attribute ascribed to it. For example, one shouldrecognize the difference between a body and its mass, a surface and its area, a capacitor and its capacitance,and a coil and its inductance. This means that although it is acceptable to say an object of mass 1 kg wasattached to a string to form a pendulum, it is not acceptable to say a mass of 1 kg was attached to a stringto form a pendulum.
Any SI derived quantityQ can be expressed in terms of the SI base quantities length (l ) , mass (m),time (t), electric current (l ) , thermodynamic temperature (T ) , amount of substance (n), and luminousintensity (Iv ) by an equation of the form
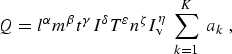
 εζη,
εζη,where L, M, T, I, θ, N, and J are thedimensions of the SI base quantities length, mass, time, electriccurrent, thermodynamic temperature, amount of substance, and luminous intensity, respectively. Theexponents α, β, γ, . . . are called dimensional exponents. The SI derived unit of Q is mα·kgβ sγ·Aδ·Kε molζ cdη, which is obtained by replacing the dimensions of the SI base quantities in the dimension of Qwith the symbols for the corresponding base units.
Example: Consider a nonrelativistic particle of massm in uniform motion which travels a distancel in atimet . Its velocity isν =l /t and its kinetic energy is Ek =mν2 / 2 =l2mt.-2 / 2. Thedimension ofEk is dimEk = L2MT-2 and the dimensional exponents are 2, 1, and -2. The SIderived unit ofEk is then m2·kg·s-2, which is given the special name joule and specialsymbol J.
A derived quantity of dimension one, which is sometimes called a dimensionless quantity, is onefor which all of the dimensional exponents are zero: dimQ = 1. It therefore follows that the derived unit forsuch a quantity is also the number one, symbol 1, which is sometimes called a dimensionless derivedunit.
Example: The mass fractionwB of a substance B in a mixture is given bywB =mB / m, wheremB is themass of B andm is the mass of the mixture (see Sec.8.6.10). The dimension ofwB is dimwB = M1M-1 = 1; all of the dimensional exponents of wB are zero, and its derived unit iskg1·kg-1 = 1 also.
 | |
 |  |