I currently need to implement efficiently a quantum comparator, with one of the values that is known at generation-time.
In other words, I am searching for a quantum routinecompare(n, rhs) that will produce a circuit taking as input
- a quantum register$\vert a \rangle$ of size
nthat should be interpreted as a unsigned integer. - a single qubit initialised to$\vert 0 \rangle$ that will store the result of$a < rhs$ at the end of the routine.
- at most one ancilla qubit, and preferably no ancilla qubit at all.
There are a lot of quantum comparators in the wild (for example[1],[2] or[3]) but all of them are designed to compare values stored in two quantum registers, not one value from a quantum register and the other known at compile time.
I tried to modify[1] in order to be able to remove the need for the quantum register$\vert b \rangle$, but I ended up proving it was not possible (seemy question).
Even if I have no rigorous proof, I think a similar argument applies to[2]. My "intuition" comes from the fact that in[2], both$\vert a \rangle$ and$\vert b \rangle$ are used to store intermediate results, which is impossible if we remove one of them.
On the other hand,[3] is relatively easy to adapt. The only operation involving$\vert b \rangle$ is a controlled-Phase, so we can easily "remove" the control and just apply a Phase gate when the corresponding bit of$b$ (known at generation-time) is$1$.
Draper's adder ([3]) is nice on multiple points:
- No ancilla qubit needed.
- Only QFT and phase gates, which should be easy to implement on hardware.
- A depth in$O(n)$.
But an ideal implementation would also:
- have a number of gates that grows in$O(n)$. Draper's adder is$O(n^2)$ because of the QFT.
- have more room for optimisation with respect to the number of gates / depth (for example a very low cost when the constant is$\vert 00000\rangle$ or has a lot of$0$.
- be based on a logic/arithmetic approach like[1] or[2]. One of the problem with Draper's adder is that it requires very precise rotations angle, and it is hard to compute the error introduced if one of the rotations is only approximated and not exact.
My question: do you know any paper that introduce an algorithm that may interest me, based on the lists above?
1 Answer1
You can do this with two ancillae and$O(n \lg n)$ operations by using the comparator fromhttps://arxiv.org/abs/1706.07884.
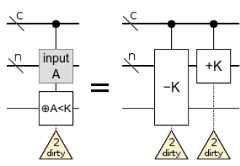
The constant comparator uses two constant adders:
The constant adders are a recursive construction fromhttps://arxiv.org/abs/1611.07995 which uses an incrementer and a carry signal propagator:
The incrementer uses a normal adder with same-sized input and target registers:
The same-sized input/target adder can be done with no ancillae:
And the carry propagation uses linear dirty ancillae:
If you're feeling really ambitious, you can remove at least one of the ancillae by using phasing operations in this way:
- $\begingroup$Really interesting! At first glance, this seems like what I was searching for. I will take a look at the papers and implement the algorithms to test them. I come back to you once done. Thank you for your answer.$\endgroup$Adrien Suau– Adrien Suau2019-08-23 08:11:24 +00:00CommentedAug 23, 2019 at 8:11
- $\begingroup$@Nelimee There is code implementing the operations atgithub.com/Strilanc/PaperImpl-2017-DirtyPeriodFinding specificallygithub.com/Strilanc/PaperImpl-2017-DirtyPeriodFinding/blob/…$\endgroup$Craig Gidney– Craig Gidney2019-08-24 01:38:30 +00:00CommentedAug 24, 2019 at 1:38
- $\begingroup$Thank you for your answer, it helped me a lot. I only had to implement the carry propagation to compute the high-bit of $a - c = (a' + c)'$ where ' is the bitwise complementation. Once this done, the comparator is built as the high-bit of $a - c$ is $1$ only if $a < c$. I will implement the adder in the few next days (following your links and the papers) to compare its practical implementation to Draper's one (with QFT).$\endgroup$Adrien Suau– Adrien Suau2019-08-29 08:10:34 +00:00CommentedAug 29, 2019 at 8:10
- $\begingroup$@AdrienSuau Did you finish the comparison with Draper-based adder? I am interested in a similar application.$\endgroup$V. Patel– V. Patel2025-05-19 21:17:44 +00:00CommentedMay 19 at 21:17
- $\begingroup$@CraigGidney Are the constant adders you mentioned still optimal compared to the conditionally clean ancillae approach in your new paper? Also, any thoughts onquantumcomputing.stackexchange.com/q/41829/36359 ?$\endgroup$V. Patel– V. Patel2025-05-19 21:19:54 +00:00CommentedMay 19 at 21:19
Explore related questions
See similar questions with these tags.