Movatterモバイル変換

[0]ホーム
URL:

Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
Thehttps:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

NIH NLM Logo
Log inShow account info
Access keysNCBI HomepageMyNCBI HomepageMain ContentMain Navigation
pubmed logo
Advanced Clipboard
User Guide

Full text links

Atypon full text link Atypon Free PMC article
Full text links

Actions

Share

.2022 May 27;50(13):2701-2716.
doi: 10.1080/02664763.2022.2078289. eCollection 2023.

Bayesian models for spatial count data with informative finite populations with application to the American community survey

Affiliations

Bayesian models for spatial count data with informative finite populations with application to the American community survey

Kai Qu et al. J Appl Stat..

Abstract

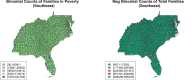
The American Community Survey (ACS) is an ongoing program conducted by the US Census Bureau that publishes estimates of important demographic statistics over pre-specified administrative areas. ACS provides spatially referenced count-valued outcomes that are paired with finite populations. For example, the number of people below the poverty line and the total population for each county are estimated by ACS. One common assumption is that the spatially referenced count-valued outcome given the finite population is binomial distributed. This conditionally specified (CS) model does not define the joint relationship between the count-valued outcome and the finite population. Thus, we consider a joint model for the count-valued outcome and the finite population. When cross-dependence in our joint model can be leveraged to 'improve spatial prediction' we say that the finite population is 'informative.' We model the count given the finite population as binomial and the finite population as negative binomial and use multivariate logit-beta prior distributions. This leads to closed-form expressions of the full-conditional distributions for an efficient Gibbs sampler. We illustrate our model through simulations and our motivating application of ACS poverty estimates. These empirical analyses show the benefits of using our proposed model over the more traditional CS binomial model.

Keywords: Bayesian statistics; conjugate; generalized linear models; official statistics; spatial statistics.

© 2022 Informa UK Limited, trading as Taylor & Francis Group.

PubMed Disclaimer

Conflict of interest statement

No potential conflict of interest was reported by the author(s).

Figures

Figure 1.
Figure 1.
ACS poverty count data: the observed families counts in poverty (left) and the total families number (right).
Figure 2.
Figure 2.
Simulated binomial and negative binomial counts and true proportions.
Figure 3.
Figure 3.
The first panel presents the true values and estimated values of{πi} by method withi on thex-axis. Similarly, the right panel presents the credible bands for{πi} by method.
Figure 4.
Figure 4.
MSPE versus prior specification for ACS binomial data mixed effects model.
Figure 5.
Figure 5.
Trace plots of the JBWBIN model for ACS binomial training data (898).
Figure 6.
Figure 6.
Testing (50) models for binomial data: the first row displays the predicted logit of poverty proportions and their associated MSPE (on the logit-scale for visualization purposes); the second row displays the estimated proportions versus the observed proportions; and the third row displays the 95% lower and upper credible limits for estimated proportions.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Ahlburg D.A., Population growth and poverty, in The Impact of Population Growth on Well-Being in Developing Countries, D.A. Ahlburg, A. C. Kelley, and K. O. Mason eds., Berlin-Heidelberg: Springer, 1996, pp. 219–258.
    1. Bradley J., Wikle C., and Holan S., Spatio-temporal change of support with application to American community survey multi-year period estimates, Statistics 4 (2015), pp. 255–270.
    1. Bradley J.R., Wikle C.K., and Holan S.H., Bayesian spatial change of support for count-valued survey data with application to the American community survey, J. Am. Stat. Assoc. 111 (2016), pp. 472–487.
    1. Bradley J.R., Wikle C.K., and Holan S.H., Spatio-temporal models for big multinomial data using the conditional multivariate logit-beta distribution, J. Time Ser. Anal. 40 (2019), pp. 363–382.
    1. Bradley J.R., Holan S.H., and Wikle C.K., Bayesian hierarchical models with conjugate full-conditional distributions for dependent data from the natural exponential family, J. Am. Stat. Assoc. 115 (2020), pp. 2037–2052.

Grants and funding

Jonathan R. Bradley's research was partially supported by the U.S. National Science Foundation (NSF) [NSF grant SES-1853099] and the National Institute of Health (NIH) [grant 1R03AG070669-01].

LinkOut - more resources

Full text links
Atypon full text link Atypon Free PMC article
Cite
Send To

NCBI Literature Resources

MeSHPMCBookshelfDisclaimer

The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.

[8]ページ先頭
©2009-2025 Movatter.jp