Modeling the spatiotemporal spread of beneficial alleles using ancient genomes
- PMID:36537881
- PMCID: PMC9767474
- DOI: 10.7554/eLife.73767
Modeling the spatiotemporal spread of beneficial alleles using ancient genomes
Abstract
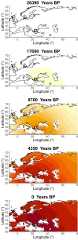
Ancient genome sequencing technologies now provide the opportunity to study natural selection in unprecedented detail. Rather than making inferences from indirect footprints left by selection in present-day genomes, we can directly observe whether a given allele was present or absent in a particular region of the world at almost any period of human history within the last 10,000 years. Methods for studying selection using ancient genomes often rely on partitioning individuals into discrete time periods or regions of the world. However, a complete understanding of natural selection requires more nuanced statistical methods which can explicitly model allele frequency changes in a continuum across space and time. Here we introduce a method for inferring the spread of a beneficial allele across a landscape using two-dimensional partial differential equations. Unlike previous approaches, our framework can handle time-stamped ancient samples, as well as genotype likelihoods and pseudohaploid sequences from low-coverage genomes. We apply the method to a panel of published ancient West Eurasian genomes to produce dynamic maps showcasing the inferred spread of candidate beneficial alleles over time and space. We also provide estimates for the strength of selection and diffusion rate for each of these alleles. Finally, we highlight possible avenues of improvement for accurately tracing the spread of beneficial alleles in more complex scenarios.
Keywords: ancient DNA; diffusion; evolution; evolutionary biology; human; lactase persistence; natural selection; spatiotemporal inference.
Plain language summary
Analyzing the genomes of our ancient ancestors can reveal how certain traits spread through the human population over the course of evolution. Mutations that make individuals better equipped to survive their environment are more likely to be passed on to the next generation and become more common. For example, a genetic variant that enables adult people to digest sugars in dairy products has become more common in humans over time. Yet evolution does not only happen across time: it transverses space as well. Modeling the geographic spread of such genetic mutations is challenging using existing methods. To overcome this, Muktupavela et al. developed a new computational method that uses modern and ancient human genomes to study the evolution of specific genetic variants across space and time. The tool can determine where certain variants first emerged, how quickly they spread across geographic areas, and how rapidly they became prevalent in human populations. Muktupavela et al. applied their new method, which was based on a previously published framework, to track the spread of two common genetic variations that have previously been reported to be subject to natural selection: one that allows adult humans to digest dairy products, and another associated with skin pigmentation. They found that the mutation that enabled dairy consumption originated around what is now southwestern Russia or eastern Ukraine. The variation then spread westward, becoming increasingly more common over the course of the Holocene. The mutation related to skin pigmentation emerged further south than the dairy-related variation, and then also spread westward. Massive human migrations during the Neolithic and Bronze Age eras may have helped disperse both variants. The model developed by Muktupavela et al. could help scientists track the geographic spread of other genetic variants in human populations, as well as provide new insights into how humans adapt to changing environmental conditions. Incorporating major events into the model, like mass migrations or glacial retreats, may lead to even more insights.
© 2022, Muktupavela et al.
Conflict of interest statement
RM, MP, LS, TK, JN, FR No competing interests declared
Figures



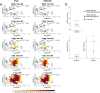




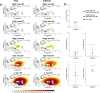




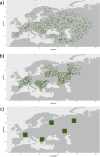















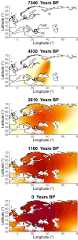














Similar articles
- Balancing selection on genomic deletion polymorphisms in humans.Aqil A, Speidel L, Pavlidis P, Gokcumen O.Aqil A, et al.Elife. 2023 Jan 10;12:e79111. doi: 10.7554/eLife.79111.Elife. 2023.PMID:36625544Free PMC article.
- Native American genetic ancestry and pigmentation allele contributions to skin color in a Caribbean population.Ang KC, Canfield VA, Foster TC, Harbaugh TD, Early KA, Harter RL, Reid KP, Leong SL, Kawasawa Y, Liu D, Hawley JW, Cheng KC.Ang KC, et al.Elife. 2023 Jun 9;12:e77514. doi: 10.7554/eLife.77514.Elife. 2023.PMID:37294081Free PMC article.
- A method for low-coverage single-gamete sequence analysis demonstrates adherence to Mendel's first law across a large sample of human sperm.Carioscia SA, Weaver KJ, Bortvin AN, Pan H, Ariad D, Bell AD, McCoy RC.Carioscia SA, et al.Elife. 2022 Dec 7;11:e76383. doi: 10.7554/eLife.76383.Elife. 2022.PMID:36475543Free PMC article.
- Adaptations to local environments in modern human populations.Jeong C, Di Rienzo A.Jeong C, et al.Curr Opin Genet Dev. 2014 Dec;29:1-8. doi: 10.1016/j.gde.2014.06.011. Epub 2014 Aug 15.Curr Opin Genet Dev. 2014.PMID:25129844Free PMC article.Review.
- Quantitative Human Paleogenetics: What can Ancient DNA Tell us About Complex Trait Evolution?Irving-Pease EK, Muktupavela R, Dannemann M, Racimo F.Irving-Pease EK, et al.Front Genet. 2021 Aug 4;12:703541. doi: 10.3389/fgene.2021.703541. eCollection 2021.Front Genet. 2021.PMID:34422004Free PMC article.Review.
Cited by
- slendr: a framework for spatio-temporal population genomic simulations on geographic landscapes.Petr M, Haller BC, Ralph PL, Racimo F.Petr M, et al.Peer Community J. 2023;3:e121. doi: 10.24072/pcjournal.354. Epub 2023 Dec 15.Peer Community J. 2023.PMID:38984034Free PMC article.
- Resource-explicit interactions in spatial population models.Champer SE, Chae B, Haller BC, Champer J, Messer PW.Champer SE, et al.bioRxiv [Preprint]. 2024 Jan 15:2024.01.13.575512. doi: 10.1101/2024.01.13.575512.bioRxiv. 2024.Update in:Methods Ecol Evol. 2024 Dec;15(12):2316-2330. doi: 10.1111/2041-210x.14432.PMID:38293045Free PMC article.Updated.Preprint.
- Population genetic models for the spatial spread of adaptive variants: A review in light of SARS-CoV-2 evolution.Steiner MC, Novembre J.Steiner MC, et al.PLoS Genet. 2022 Sep 22;18(9):e1010391. doi: 10.1371/journal.pgen.1010391. eCollection 2022 Sep.PLoS Genet. 2022.PMID:36137003Free PMC article.Review.
References
- Allentoft ME, Sikora M, Sjögren K-G, Rasmussen S, Rasmussen M, Stenderup J, Damgaard PB, Schroeder H, Ahlström T, Vinner L, Malaspinas A-S, Margaryan A, Higham T, Chivall D, Lynnerup N, Harvig L, Baron J, Della Casa P, Dąbrowski P, Duffy PR, Ebel AV, Epimakhov A, Frei K, Furmanek M, Gralak T, Gromov A, Gronkiewicz S, Grupe G, Hajdu T, Jarysz R, Khartanovich V, Khokhlov A, Kiss V, Kolář J, Kriiska A, Lasak I, Longhi C, McGlynn G, Merkevicius A, Merkyte I, Metspalu M, Mkrtchyan R, Moiseyev V, Paja L, Pálfi G, Pokutta D, Pospieszny Ł, Price TD, Saag L, Sablin M, Shishlina N, Smrčka V, Soenov VI, Szeverényi V, Tóth G, Trifanova SV, Varul L, Vicze M, Yepiskoposyan L, Zhitenev V, Orlando L, Sicheritz-Pontén T, Brunak S, Nielsen R, Kristiansen K, Willerslev E. Population genomics of bronze age Eurasia. Nature. 2015;522:167–172. doi: 10.1038/nature14507. - DOI - PubMed
- Alonso S, Izagirre N, Smith-Zubiaga I, Gardeazabal J, Díaz-Ramón JL, Díaz-Pérez JL, Zelenika D, Boyano MD, Smit N, de la Rúa C. Complex signatures of selection for the melanogenic loci Tyr, TYRP1 and DCT in humans. BMC Evolutionary Biology. 2008;8:1–14. doi: 10.1186/1471-2148-8-74. - DOI - PMC - PubMed
- Bélisle CJP. Convergence theorems for a class of simulated annealing algorithms on rd. Journal of Applied Probability. 1992;29:885–895. doi: 10.2307/3214721. - DOI
- Bergström A, McCarthy SA, Hui R, Almarri MA, Ayub Q, Danecek P, Chen Y, Felkel S, Hallast P, Kamm J, Blanché H, Deleuze J-F, Cann H, Mallick S, Reich D, Sandhu MS, Skoglund P, Scally A, Xue Y, Durbin R, Tyler-Smith C. Insights into human genetic variation and population history from 929 diverse genomes. Science. 2020;367:eaay5012. doi: 10.1126/science.aay5012. - DOI - PMC - PubMed
Publication types
MeSH terms
Related information
Grants and funding
LinkOut - more resources
Full Text Sources
