Movatterモバイル変換

[0]ホーム
URL:

Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
Thehttps:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

NIH NLM Logo
Log inShow account info
Access keysNCBI HomepageMyNCBI HomepageMain ContentMain Navigation
pubmed logo
Advanced Clipboard
User Guide

Full text links

Atypon full text link Atypon Free PMC article
Full text links

Actions

Share

.2019 Jul 23;116(30):14813-14822.
doi: 10.1073/pnas.1905164116. Epub 2019 Jul 8.

Characteristic disruptions of an excitable carbon cycle

Affiliations

Characteristic disruptions of an excitable carbon cycle

Daniel H Rothman. Proc Natl Acad Sci U S A..

Abstract

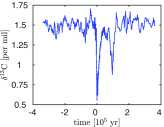
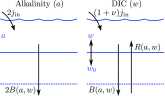
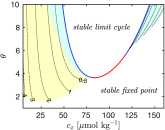
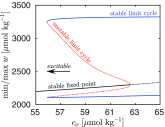
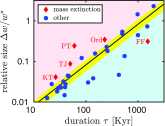
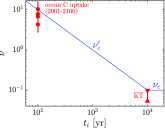
The history of the carbon cycle is punctuated by enigmatic transient changes in the ocean's store of carbon. Mass extinction is always accompanied by such a disruption, but most disruptions are relatively benign. The less calamitous group exhibits a characteristic rate of change whereas greater surges accompany mass extinctions. To better understand these observations, I formulate and analyze a mathematical model that suggests that disruptions are initiated by perturbation of a permanently stable steady state beyond a threshold. The ensuing excitation exhibits the characteristic surge of real disruptions. In this view, the magnitude and timescale of the disruption are properties of the carbon cycle itself rather than its perturbation. Surges associated with mass extinction, however, require additional inputs from external sources such as massive volcanism. Surges are excited when [Formula: see text] enters the oceans at a flux that exceeds a threshold. The threshold depends on the duration of the injection. For injections lasting a time [Formula: see text] y in the modern carbon cycle, the threshold flux is constant; for smaller [Formula: see text], the threshold scales like [Formula: see text] Consequently the unusually strong but geologically brief duration of modern anthropogenic oceanic [Formula: see text] uptake is roughly equivalent, in terms of its potential to excite a major disruption, to relatively weak but longer-lived perturbations associated with massive volcanism in the geologic past.

Keywords: carbon cycle; carbon isotopic events; dynamical systems; excitable systems; mass extinctions.

PubMed Disclaimer

Conflict of interest statement

The author declares no conflict of interest.

Figures

Fig. 1.
Fig. 1.
Fluctuations of the isotopic composition of carbonate carbon (δ13C) during the Eocene period, about 54 Ma (26). Time advances to the right and is given with respect to the minimum of the first abrupt downswing, an event known as Eocene Thermal Maximum 2 (ETM2) or H1. The second event, about 100 ky later, is called H2. The timescale is derived from astrochronology (26).
Fig. 2.
Fig. 2.
Schematic diagram of the model (not drawn to scale).Left andRight panels represent, respectively, the evolution of total alkalinity,a, and total dissolved inorganic carbon (DIC),w. The wavy line represents the air–sea interface, the upper horizontal thick line divides the shallow ocean from the deep sea, and the lower horizontal dashed line represents the sediment–seawater interface. Concentration fluxes are indicated by unidirectional arrows. The sediment–seawater interface is dashed to indicate that there is no dynamical distinction between the deep sea and sediments.
Fig. 3.
Fig. 3.
(A–C) Stability in the planes ofμ andb (A),μ andcx (B), andμ andθ (C). Values of fixed parameters are given inSI Appendix, Table S1. Crossing the red and blue boundaries results in supercritical and subcritical Hopf bifurcations, respectively. The fixed point is stable only where indicated. However, the region of stability of the limit cycle extends into the region of the stable fixed point adjacent to the subcritical bifurcation. Fig. 6 maps the bistable region in the plane ofcx andθ.
Fig. 4.
Fig. 4.
A stable limit cycle in the phase plane of theCO32− concentrationc and the DIC concentrationw. Values of parameters are given inSI Appendix, Table S1. The dotted curves represent the nullclinesċ=0 andw˙=0.
Fig. 5.
Fig. 5.
Evolution following perturbations below and above the excitations threshold. (A–D) Phase-plane representation and the time seriesw(t) for a subthreshold perturbation withν=0.35 (A andB) and an above-threshold perturbation withν=0.40 (C andD). The initial condition and all other parameters are the same in each simulation. The crossoverCO32− concentrationcx=55 μmol⋅kg−1; other parameters are given inSI Appendix, Table S1. The larger value ofν in the above-threshold case increases the DIC fixed pointw* by0.05μ=12.5 μmol⋅kg−1 inC compared withA, which is nearly imperceptible in the plots.
Fig. 6.
Fig. 6.
Contours ofνc (dotted) in the region of excitations (pale yellow) and jumps to the stable limit cycle in the region of bistability (pale blue) in the plane ofcx andθ. The blue and red portions of the stability boundary correspond to a subcritical and a supercritical Hopf bifurcation, respectively. Fixed parameters are specified inSI Appendix, Table S1. Excitations or jumps are defined to occur if there exists aν for whichdΔw/dν>103, whereΔw=wmax−w*. The thresholdνc is the value ofν where that derivative is greatest.
Fig. 7.
Fig. 7.
Bifurcation diagram for the parametercx, the crossoverCO32− concentration for the ballast feedback. The solid and dotted black line respectively represents the stable and unstable fixed pointw*. The solid blue line indicates the maximum and minimum values ofw in the stable limit cycle and the dashed red line represents the same extremes of the unstable limit cycle. The subcritical Hopf bifurcation occurs where the radius of the unstable limit cycle goes to zero, atcx=62.61 μmol⋅kg−1. The saddle-node bifurcation of cycles occurs where the unstable and stable limit cycles collide, atcx=55.89 μmol⋅kg−1. Excitations occur at smaller values ofcx, to the left of the arrowhead. Fixed parameters are specified inSI Appendix, Table S1.
Fig. 8.
Fig. 8.
Phase-space trajectories in the bistable regime. Herecx=58 μmol⋅kg−1 and all other parameters are the same as in Fig. 5C andD. The red dashed limit cycle is unstable; thus trajectories initialized inside it return to the (stable) fixed point. Trajectories initialized outside the unstable limit cycle evolve to the stable limit cycle.
Fig. 9.
Fig. 9.
The relationship between the relative size and duration of 31 disruptions of the global carbon cycle during the last 542 My (7). The relative sizeΔw/w* is obtained from changes in the isotopic composition of carbonate carbon that occur in time series similar to that of Fig. 1. The yellow region contains characteristic events; these events satisfy Eq.20 withα∼0.1. The events in the pale red region, which include 4 of the 5 mass extinction events, grow faster than characteristic events. The light blue region contains minor events with relatively slow growth rates. The labeled events are associated with the end-Cretaceous (KT), end-Triassic (TJ), end-Permian (PT), end-Ordovician (Ord), and Frasnian–Famennian (FF) mass extinctions. Ref. provides descriptions of each event and a discussion of uncertainties.
Fig. 10.
Fig. 10.
Equivalence, with respect to the excitation threshold, of the perturbations of the modern and end-Cretaceous carbon cycles, expressed in terms of the dimensionlessCO2 injection rateν. The straight line labeledνc′ is the threshold’s upper bound predicted by Eq.24, assuming the modern damping timescaleτw=104 y; the segment labeledνc (Eq.22) provides the upper bound for timesti>104 y. The circles represent projected 21st-century ocean carbon uptake rates for a range of plausible scenarios (77); the vertical line indicates their uncertainty. The symbols labeledKT¯ provide the median and upper limit of the 68% confidence interval estimated for the period of peak Deccan volcanism tens of thousands of years before the end-Cretaceous extinction (24). Because the excitation threshold scales like1/ti, both the modern and end-Cretaceous perturbations potentially lie near the threshold’s upper bound despite the 2 orders of magnitude that separate their rates.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Berner R. A., The Phanerozoic Carbon Cycle: CO2 and O2. (Oxford University Press, New York, 2004).
    1. Sarmiento J. L., Gruber N., Ocean Biogeochemical Dynamics (Princeton University Press, Princeton, NJ, 2006).
    1. Emerson S. R., Hedges J. I., Chemical Oceanography and the Marine Carbon Cycle (Cambridge University Press, New York, NY, 2008).
    1. Rothman D. H., Earth’s carbon cycle: A mathematical perspective. Bull. Am. Math. Soc. 52, 47–64 (2015).
    1. Walliser O. H., Ed., Global Events and Event Stratigraphy in the Phanerozoic (Springer, Berlin, Germany, 1996).

Publication types

LinkOut - more resources

Full text links
Atypon full text link Atypon Free PMC article
Cite
Send To

NCBI Literature Resources

MeSHPMCBookshelfDisclaimer

The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.

[8]ページ先頭
©2009-2025 Movatter.jp