Possible Worlds
Anne is working at her desk. While she is directly aware only of herimmediate situation — her being seated in front of her computer,the music playing in the background, the sound of her husband's voiceon the phone in the next room, and so on — she is quite certainthat this situation is only part of a series of increasingly moreinclusive, albeit less immediate, situations: the situation in herhouse as a whole, the one in her neighborhood, the city she lives in,the state, the North American continent, the Earth, the solar system,the galaxy, and so on. On the face of it, anyway, it seems quitereasonable to believe that this series has alimit, that is,that there is a maximally inclusive situation encompassing all others:things, as a whole or, more succinctly,the actualworld.
Most of us also believe that things, as a whole, needn't have beenjust as they are. Rather, things might have been different incountless ways, both trivial and profound. History, from the verybeginning, could have unfolded quite other than it did in fact: thematter constituting a distant star might never have organized wellenough to give light; species that survived might just as well havedied off; battles won might have been lost; children born might neverhave been conceived and children never conceived might otherwise havebeen born. In any case, no matter how things had gone they would stillhave been part of a single, maximally inclusive, all-encompassingsituation, a single world. Intuitively, then, the actual world is onlyone among manypossible worlds.
The idea of possible worlds is evocative and appealing. However,possible worlds failed to gain any real traction among philosophersuntil the 1960s when they were invoked to provide the conceptualunderpinnings of some powerful developments in modal logic. Only thendid questions of their nature become a matter of the highestphilosophical importance. Accordingly, Part 1 of this article willprovide an overview of the role of possible worlds in the developmentof modal logic. Part 2 explores three prominent philosophicalapproaches to the nature of possible worlds.[1] Although many of the finer philosophical points of Part 2 dopresuppose the technical background of Part 1, the generalphilosophical landscape laid out in Part 2 can be appreciatedindependently of Part 1.
- 1. Possible Worlds and Modal Logic
- 2. Three Philosophical Conceptions of Possible Worlds
- 2.1 Concretism
- 2.2 Abstractionism
- 2.3 Combinatorialism
- 2.3.1 The Basic Ontology of Combinatorialism
- 2.3.2 States of Affairs and Recombination
- 2.3.3 Structural States of Affairs and Supervenience
- 2.3.4 Combinatorial Possible Worlds and Existence Therein
- 2.3.5 Analytic and Emergent Modalities; Essential Properties
- 2.3.6 Fewer Things and Other Things: Modified Combinatorialism
- 2.3.7 A Brief Assessment of Combinatorialism
- Bibliography
- Academic Tools
- Other Internet Resources
- Related Entries
1. Possible Worlds and Modal Logic
Although ‘possible world’ has been part of thephilosophical lexicon at least since Leibniz, the notion became firmlyentrenched in contemporary philosophy with the development ofpossible world semantics for the languages of propositional andfirst-order modal logic. In addition to the usual sentence operatorsofclassical logic such as ‘and’ (‘∧’), ‘or’(‘∨’), ‘not’ (‘¬’),‘if...then’ (‘→’), and, in thefirst-order case, the quantifiers ‘all’(‘∀’) and ‘some’(‘∃’), these languages contain operators intended torepresent the modal adverbs ‘necessarily’(‘□’) and ‘possibly’(‘◇’). Although a prominent aspect of logic in bothAristotle's work and the work of many medieval philosophers, modallogic was largely ignored from the modern period to the mid-20thcentury. And even though a variety of modal deductive systems had infact been rigorously developed in the early 20th century, notably byLewis and Langford (1932), there was for the languages of thosesystems nothing comparable to the elegant semantics that Tarski hadprovided for the languages of classical first-order logic.Consequently, there was no rigorous account of what it means for asentence in those languages to betrue and, hence, no accountof the critical semantic notions of validity and logical consequenceto underwrite the corresponding deductive notions of theoremhood andprovability. A concomitant philosophical consequence of this void inmodal logic was a deep skepticism, voiced most prominently by Quine,toward any appeal to modal notions in metaphysics generally, notably,the notion of an essential property. (See Quine 1953 and 1956, and theappendix to Plantinga 1974.) The purpose of the following twosubsections is to provide a simple and largely ahistorical overview ofhow possible world semantics fills this void; the final subsectionpresents two important applications of the semantics. (Readersfamiliar with basic possible world semantics can skip to §2 withno significant loss of continuity.)
1.1 Extensionality Lost
Since the middle ages at least, philosophers have recognized asemantical distinction betweenextension andintension. The extension of a denoting expression, orterm, such as a name or a definite description is itsreferent, the thing that it refers to; the extension of a predicate isthe set of things it applies to; and the extension of a sentence isits truth value. By contrast, the intension of an expression issomething rather less definite — itssense, ormeaning, the semantical aspect of the expression thatdetermines its extension. For purposes here, let us say that alogic is a formal language together with a semantic theory forthe language, that is, a theory that provides rigorous definitions oftruth, validity, and logical consequence for the language.[2] A logic isextensional if the truth value of every sentenceof the logic is determined entirely by its form and the extensions ofits component sentences, predicates, and terms. An extensional logicwill thus typically feature a variety of validsubstitutivityprinciples. A substitutivity principle says that, if twoexpressions are coextensional, that is, if they have the sameextension, then (subject perhaps to some reasonable conditions) eithercan be substituted for the other in any sentencesalvaveritate, that is, without altering the original sentence's truthvalue. In anintensional logic, the truth values of some sentences are determined by something overand above their forms and the extensions of their components and, as aconsequence, at least one classical substitutivity principle istypically rendered invalid.
Extensionality is a well known and generally cherished feature ofclassical propositional and predicate logic. Modal logic, by contrast,is intensional. To illustrate: the substitutivity principle forsentences tells us that sentences with the same truth value can besubstituted for one anothersalva veritate. So suppose thatJohn's only pets are two dogs, Algol and BASIC, say, and consider twosimple sentences and their formalizations (the predicates in questionindicating the obvious English counterparts):
| All John's dogs are mammals: ∀x(Dx →Mx). |
| All John's pets are mammals: ∀x(Px →Mx) |
As both sentences are true, they have the same extension. Hence, inaccordance with the classical substitutivity principle for sentences,we can replace the occurrence of (1) with (2) in the false sentence
| Not all John's dogs are mammals: ¬∀x(Dx→Mx) |
and the result is the equally false sentence
| Not all John's pets are mammals: ¬∀x(Px→Mx). |
However, when we make the same substitution in the true sentence
| Necessarily, all John's dogs are mammals:□∀x(Dx →Mx), |
the result is the sentence
| Necessarily, all John's pets are mammals:□∀x(Px →Mx), |
which is intuitively false, as John surely could have had anon-mammalian pet. In a modal logic that accurately represents thelogic of the necessity operator, therefore, the substitutivityprinciple for sentences will have to fail.
The same example illustrates that the substitutivity principle forpredicates will have to fail in modal logic as well. For, according toour example, the predicates ‘D’ and‘P’ that are true of John's dogs and of John'spets, respectively, are coextensional, i.e.,∀x(Dx ↔Px). However, whilesubstituting the latter predicate for the former in (3) results in asentence with the same truth value, the same substitution in (5) doesnot.
Modal logic, therefore, is intensional: in general, the truth value ofa sentence is determined by something over and above its form and theextensions of its components. Absent a rigorous semantic theory toidentify the source of its intensionality and to systematizeintuitions about modal truth, validity, and logical consequence, therewas little hope for the widespread acceptance of modal logic.
1.2 Extensionality Regained
The idea of possible worlds raised the prospect of extensionalrespectability for modal logic, not by rendering modal logic itselfextensional, but by endowing it with an extensional semantic theory— one whose own logical foundation is that of classicalpredicate logic and, hence, one on which possibility and necessity canultimately be understood along classical Tarskian lines. Specifically,inpossible world semantics, the modal operators areinterpreted asquantifiers over possible worlds, as expressedinformally in the following two general principles:
| Nec | A sentence of the form⌈Necessarily,φ⌉(⌈◻φ⌉) is true if and onlyif φ is true in every possible world.[3] |
| Poss | A sentence of the form⌈Possibly,φ⌉(⌈◇φ⌉) is true if and onlyif φ is true in some possible world. |
Given this, the failures of the classical substitutivity principlescan be traced to the fact that modal operators, so interpreted,introduce contexts that require subtler notions of meaning forsentences and their component parts than are provided in classicallogic; in particular, a subtler notion (to be clarified shortly) isrequired for predicates than that of the set of things they happen toapply to.
Tarskian Semantics. Standard model theoretic semantics for thelanguages of predicate logic deriving from the work of Tarski (1933,1944) is the paradigmatic semantic theory for extensional logics.Given a standard first-order language ℒ, a TarskianinterpretationIfor ℒ specifies a setD for the quantifiers of ℒ to range over (typically, someset of things that ℒ has been designed to describe) and assigns,to each term (constant or variable) τ of ℒ, a referentaτ ∈D and, to eachn-placepredicate π of ℒ, an appropriate extensionEπ — a truth value (TRUE or FALSE) ifn = 0, a subset ofD ifn = 1, and a set ofn-tuples of members ofD ifn > 1. Given theseassignments, sentences are evaluated as true under the interpretationI — trueI, for short — accordingto a more or less familiar set of clauses. To facilitate thedefinition, letI[ν/a] be the interpretation thatassigns the individuala to the variable ν and is otherwiseexactly likeI. Then we have:
- An atomic sentence⌈πτ1...τn⌉(of ℒ) istrueI if and only if
- n = 0 (i.e., π is a sentence letter) and the extensionof π is the truth value TRUE; or
- n = 1 andaτ1 is in theextension of π; or
- n > 1 and ⟨aτ1,...,aτn⟩ is in theextension of π.
- A negation⌈¬ψ⌉ istrueI if and only if ψ is nottrueI.
- A material conditional⌈ψ →θ⌉ is trueI iff, if ψ istrueI, then θ is trueI.
- A universally quantified sentence⌈∀νψ⌉ istrueI if and only if, for all individualsa∈D, ψ is trueI[ν/a].[4]
Clauses for the other standard Boolean operators and the existentialquantifier under their usual definitions follow straightaway fromthese clauses. In particular, where
| ∃νφ =¬∀ν¬φ |
it follows that:
- An existentially quantified sentence⌈∃νψ⌉ is istrueI if and only if, for some individuala∈D, ψ is trueI[ν/a].
It is easy to verify that, in each of the above cases, replacing onecoextensional term, predicate, or sentence for another has no effecton the truth values rendered by the above clauses, thus guaranteeingthe validity of the classical substitutivity principles and, hence,the extensionality of first-order logic with a Tarskian semantics.
From Tarskian to Possible World Semantics. The truthconditional clauses for the three logical operators directly reflectthe meanings of the natural language expressions they symbolize:‘¬’ meansnot; ‘→’ meansif...then; ‘∀’ meansall. It iseasy to see, however, that we cannot expect to add an equally simpleclause for sentences containing an operator that symbolizes necessity.For a Tarskian interpretationfixes the domain ofquantification and the extensions of all the predicates. Prettyclearly, however, to capture necessity and possibility, one must beable to consider alternative “possible” domains ofquantification and alternative “possible” extensions forpredicates as well. For, intuitively, under different circumstances,fewer, more, or other things might have existed and things thatactually exist might, in those circumstances, have had very differentproperties. (6), for example, is false because John could have hadnon-mammalian pets: a canary, say, or a turtle, or, undervery different circumstances, a dragon. A bit more formallyput: Both the domain of quantification and the extension of thepredicate ‘P’ could, in some sense or other, havebeen different.
Possible world semantics, of course, uses the concept of a possibleworld to give substance to the idea of alternative extensions andalternative domains of quantification. (Possible world semantics canbe traced most clearly back to the work of Carnap (1947), its basicdevelopment culminating in the work of Hintikka (1957, 1961), Bayart(1958, 1959), and Kripke (1959, 1963a,1963b).[5]) Similar to Tarskian semantics, a possible world interpretationM of a modal language ℒ specifies a nonempty setD, although thought of now as the set of “possibleindividuals” ofM. Also as in Tarskian semantics,M assigns each term τ of ℒ a referentaτ inD.[6] Additionally however,M specifies a setW, the set of“possible worlds” ofM, one of which is designatedits “actual world”, and each worldw inW isassigned its own domain of quantification,d(w) ⊆D, intuitively, the set of individuals that exist inw.[7] To capture the idea of both the actual and possible extensions of apredicate,M assigns to eachn-place predicate π afunctionMπ — theintension ofπ — that, for each possible worldw, returns theextensionMπ(w) of πatw: a truth value, ifn = 0; a set ofindividuals, ifn = 1; and a set ofn-tuples ofindividuals, ifn > 1.[8] We can thus rigorously define a “possible extension” of apredicate π to be any of itsw-extensionsMπ(w), for any worldw.
The Tarskian truth conditions above are now generalized byrelativizing them to worlds as follows: for any possible worldw (theworld of evaluation):
- An atomic sentence⌈πτ1...τn⌉(of ℒ) istrueMatw ifand only if:
- n = 0 and thew-extension of π is the truthvalue TRUE; or
- n = 1 andaτ1 is in thew-extension of π; or
- n > 1 and⟨aτ1,...,aτn⟩ is in thew-extension of π.
- A negation⌈¬ψ⌉ istrueM atw if and only ψ is nottrueM inw.
- A materialconditional⌈ψ→θ⌉ istrueM atw iff, if ψ istrueM atw, then θ istrueM atw.
- A quantified sentence⌈∀νψ⌉ istrueM atw if and only if, for allindividualsa that exist inw, ψ istrueM[ν/a].
And to these, of course, is added the critical modal case thatexplicitly interprets the modal operator to be a quantifier overworlds, as we'd initially anticipated informally in our principleNec:
- A necessitation⌈◻ψ⌉is trueM atw if and only if, for allpossible worldsu ofM, ψ is trueMatu.[9]
A sentence φ isfalseM atw justin case it is not trueM atw, and φ issaid to betrueM just in case φ istrueM at the actual world ofM.
On the assumption that there is a (nonempty) set of all possibleworlds and a set of all possible individuals, we can define“objective” notions of truth at a world and of truthsimpliciter, that is, notions that are not simply relative toformal, mathematical interpretations but, rather, correspond toobjective reality in all its modal glory. Let ℒ be a modallanguage whose names and predicates represent those in some fragmentof ordinary language (as in our examples (5) and (6) above). Say thatM is the “intended” interpretation of ℒ if(i) its setW of “possible worlds” is in fact theset of all possible worlds, (ii) its designated “actualworld” is in fact the actual world, (iii) its setD of“possible individuals” is in fact the set of all possibleindividuals, and (iv) the referents assigned to the names of ℒand the intensions assigned to the predicates of ℒ are the onesthey in fact have. Then, whereM is the intended interpretationof ℒ, we can say that a sentence φ of ℒ istrueat a possible worldw just in case φ istrueM atw, and that φ istruejust in case it is trueM at the actual world.(Falsity atw and falsity,simpliciter, are definedaccordingly.) Under the assumption in question, then, the modal clauseabove takes on pretty much the exact form of our informal principleNec.
Call the abovebasic possible world semantics. Spelling out thetruth conditions for (6) (relative to the intended interpretation ofits language), basic possible world semantics tells us that (6) istrue if and only if
| For all possible worldsw,‘∀x(Px →Mx)’ is true atw. |
And by unpacking (8) in terms of the quantificational, materialconditional, and atomic clauses above we have that (6) is true if andonly if
| For all possible worldsw, and for all possibleindividualsa that exist inw, ifa is in thew-extension of ‘P’ thena is in thew-extension of ‘M’. |
Since we are evaluating (6) with regard to the intended interpretationof its language, thew-extension of ‘P’ thatis returned by its intension, for any worldw, is the (perhapsempty) set of John's pets inw and that of‘M’ is the set of mammals inw. Hence, ifw is a world where John has a pet canary — COBOL, say— COBOL is in thew-extension of ‘P’but not that of ‘M’ , i.e.,‘∀x(Px →Mx)’ is false atw and, hence, by the truth condition (9), (6) is false at theactual world — that is, (6) is falsesimpliciter, as itshould be.
Note that interpreting modal operators as quantifiers over possibleworlds provides a nice theoretical justification for the usualdefinition of the possibility operator in terms of necessity,specifically:
| ⌈◇φ⌉ =⌈¬◻¬φ⌉. |
That is, a sentence is possible just in case its negation isn'tnecessary. Since, semantically speaking, the necessity operator isliterally a universal quantifier, the definition correspondsexactly to the definition(7) of the existential quantifier. For, unpacking the right side ofdefinition (10) according to the negation and necessitation clausesabove (and invoking the definitions of truth and truth at a worldsimpliciter), we have:
| ⌈◇φ⌉ is true iff itis not the case that, for all possible worldsw, φ is nottrue atw. |
Clearly, however, if it is not the case that φ fails to be true atall possible worlds, then it must be true at some world; hence:
| ⌈◇φ⌉ is true iff,for some possible worldw, φ is true atw. |
And that corresponds exactly to our intuitive truth conditionPoss above. Thus, spelling out the negation‘¬□∀x(Px →Mx)’of our false sentence(6) above in accordance with definition (10) (and the standard definitionof conjunction ∧), we have:
| Possibly, one of John's pets is not a mammal:◇∃x(Px ∧ ¬Mx), |
for which (12) and the possible world truth conditions for quantified,Boolean, and atomic sentences yield the correct truth condition:
| There is a possible worldw and an individualaexisting inw that is in thew-extension of‘P’ but not that of ‘M’, |
that is, less stuffily, there is a possible world in which, amongJohn's pets, at least one is not a mammal.
Summary: Intensionality and Possible Worlds. Analyzed in termsof possible world semantics, then, the general failure of classicalsubstitutivity principles in modal logic is due, not to an irreduciblyintensional element in the meanings of the modal operators, but ratherto a sort of mismatch between the surface syntax of those operatorsand their semantics: syntactically, they are unary sentence operatorslike negation; but semantically, they are, quite literally,quantifiers. Their syntactic similarity to negation suggests that,like negation, the truth values of⌈□φ⌉ and⌈◇φ⌉, insofar as they aredeterminable at all, must be determined by the truth value of φ.That they are not (in general) so determined leads to the distinctivesubstitutivity failures noted above. The possible worlds analysis ofthe modal operators as quantifiers over worlds reveals that the unarysyntactic form of the modal operators obscures a semantically relevantparameter. When the modal operators are interpreted as quantifiers,this parameter becomes explicit and the reason underlying the failureof extensionality in modal logic becomes clear: That the truth valuesof⌈□φ⌉ and⌈◇φ⌉ are not in generaldetermined by the truth value of φ at the world of evaluation is,semantically speaking, nothing more than the fact that the truthvalues of ‘∀xFx’ and‘∃xFx’ are not in general determined by thetruth value of ‘Fx’, for any particular value of‘x’. Possible world semantics, therefore,explains the intensionality of modal logic by revealing thatthe syntax of the modal operators prevents an adequate expression ofthe meanings of the sentences in which they occur. Spelled out aspossible world truth conditions, those meanings can be expressed in awholly extensional fashion.(For a more formal exposition of this point, see the supplemental articleThe Extensionality of Possible World Semantics.)
1.3 Two Applications: The Analysis of Intensions and theDe Re /De Dicto Distinction
As noted, the focus of the present article is on the metaphysics ofpossible worlds rather than applications. Of course, the semantics ofmodal languages is itself an application, but one that is of singularimportance, both for historical reasons and because most applicationsare in fact themselves applications of (often extended or modifiedversions of) the semantical apparatus. Two particularly importantexamples are the analysis of intensions and a concomitant explicationof thede re/de dicto distinction.[10]
The Analysis of Intensions. As much a barrier to the acceptanceof modal logic as intensionality itself was the need to appeal tointensionsper se — properties, relations,propositions, and the like — in semantical explanations.Intensional entities have of course featured prominently in thehistory of philosophy since Plato and, in particular, have playednatural explanatory roles in the analysis ofintentional attitudes likebelief andmental content. For all their prominence and importance, however, the nature of theseentities has often been obscure and controversial and, indeed, as aconsequence, they were easily dismissed as ill-understood andmetaphysically suspect “creatures of darkness” (Quine1956, 180) by the naturalistically oriented philosophers of the early-to mid-20th century. It is a virtue of possible world semantics thatit yields rigorousdefinitions for intensional entities. Morespecifically, as described above, possible world semantics assigns toeachn-place predicate π a certain functionIπ — π's intension — that, foreach possible worldw, returns the extensionIπ(w) of π atw. We can definean intensionper se, independent of any language, to be anysuch function on worlds. More specifically:
- Aproposition is any function from worlds to truthvalues.
- Aproperty is any function from worlds to sets ofindividuals.
- Ann-place relation (n > 1) is anyfunction from worlds to sets ofn-tuples of individuals.
The adequacy of this analysis is a matter of lively debate thatfocuses chiefly upon whether or not intensions, so defined, are too“coarse-grained” to serve their intended purposes. (See,e.g., Stalnaker 1987 and 2012 for a strong defense of the analysis.)However, Lewis (1986, §1.5) argues that, even if the aboveanalysis fails for certain purposes, it does not follow thatintensions cannot be analyzed in terms of possible worlds, but onlythat more subtle constructions might be required. This reply appearsto side-step the objections from granularity while preserving thegreat advantage of the possible worlds analysis of intensions, viz.,the rigorous definability of these philosophically significantnotions.
TheDe Re /De Dicto Distinction. A particularlyrich application of the possible world analysis of intensions concernsthe analysis of the venerable distinction betweende re andde dicto modality.[11] Among the strongest modal intuitions is that the possession of aproperty has a modal character — that things exemplify, or failto exemplify, some propertiesnecessarily, oressentially, and others onlyaccidentally. Thus, forexample, intuitively, John's dog Algol is a pet accidentally; underless fortunate circumstances, she might have been, say, a stray thatno one ever adopted. But she is a dog essentially; she couldn't havebeen a flower, a musical performance, a crocodile or any other kind ofthing.
Spelling out this understanding in terms of worlds and the precedinganalysis of intensions, we can say that an individuala has apropertyF essentially ifa hasF in every worldin which it exists, that is, if, for all worldsw in whicha exists,a ∈F(w). Likewise,a hasF accidentally ifa hasF in theactual world @ but lacks it in some other world, that is, ifa∈F(@) but, for some worldw in whichaexists,a ∉F(w). Thus, let‘G’ and ‘T’ symbolize ‘isa dog’ and ‘is someone's pet’, respectively; then,where ‘E!x’ is short for‘∃y(x=y)’ (and, hence,expresses thatx exists), we have:
| Algol is a dog essentially: □(E!a →Ga) |
| Algol is a pet accidentally:Ta ∧ ◇(E!a∧ ¬Ta) |
More generally, sentences like (15) and (16) in which properties areascribed to a specific individual in a modal context — signaledformally by the occurrence of a name or the free occurrence of avariable in the scope of a modal operator — are said to exhibitmodalityde re[12] (modalityof the thing). Modal sentences that do not, like
| Necessarily, all dogs are mammals:□∀x(Gx →Mx) |
are said to exhibit modalityde dicto (roughly, modalityoftheproposition). Possibleworld semantics provides an illuminating analysis of the keydifference between the two: The truth conditions for both modalitiesinvolve a commitment to possible worlds; however, the truth conditionsfor sentences exhibiting modalityde re involve in addition acommitment to the meaningfulness oftransworld identity, the thesis that, necessarily, every individual (typically, at anyrate) exists and exemplifies (often very different) properties in manydifferent possible worlds. More specifically, basic possible worldsemantics yields intuitively correct truth values for sentences of thelatter sort by (i) permitting world domains to overlap and (ii)assigning intensions to predicates, thereby, in effect, relativizingpredicate extensions to worlds. In this way, one and the sameindividual can be in the extension of a given predicate at all worldsin which they exist, at some such worlds only, or at none at all. (Forfurther discussion, see the entry onessential vs. accidental properties.)
2. Three Philosophical Conceptions of Possible Worlds
The power and appeal of basic possible world semantics is undeniable.In addition to providing a clear, extensional formal semantics for aformerly somewhat opaque, intensional notion, cashing possibility astruth in some possible world and necessity as truth in every suchworld seems to tap into very deep intuitions about the nature ofmodality and the meaning of our modal discourse. Unfortunately, thesemantics leaves the most interesting — and difficult —philosophical questions largely unanswered. Two arise with particularforce:
| QW | What, exactly, is a possible world? |
And, givenQW:
| QE | What is it for something to exist in a possible world? |
In this section we will concern ourselves with, broadly speaking, thethree most prominent philosophical approaches to these questions.[13]
2.1 Concretism
Recall the informal picture that we began with: a world is, so to say,the “limit” of a series of increasingly more inclusivesituations. Fleshed out philosophical accounts of this informal ideagenerally spring from rather different intuitions about what one takesthe “situations” in the informal picture to be. Aparticularly powerful intuition is that situations are simplystructured collections of physical objects: the immediate situation ofour initial example above, for instance, consists of, among otherthings, the objects in Anne's office — notably Anne herself, herdesk and her computer, with her seated at the former and typing on thelatter — and at least some of the things in the next room— notably, her husband and the phone he is talking on. On thisview, for one situations to include anotherr is simplyforr to be a (perhaps rather complex and distributed) physicalpart ofs. The actual world, then, as the limit of a series ofincreasingly more inclusive situations in this sense, is simply theentire physical universe: all the things that are some spatiotemporaldistance from the objects in some arbitrary initial situation,structured as they in fact are; and other possible worlds are thingsof exactly the same sort. Call this theconcretist intuition,as possible worlds are understood to be concrete physical situationsof a special sort.
2.1.1 Concrete Worlds and Existence Therein
The originator and, by far, the best known proponent of concretism isDavid Lewis. For Lewis and, as noted, concretists generally, the actual world isthe concrete physical universe as it is, stretched out in space-time.As he rather poetically expresses it (1986, 1):
The world we live in is a very inclusive thing....There is nothing sofar away from us as not to be part of our world. Anything at anydistance is to be included. Likewise the world is inclusive in time.No long-gone ancient Romans, no long-gone pterodactyls, no long-goneprimordial clouds of plasma are too far in the past, nor are the deaddark stars too far in the future, to be part of this sameworld....[N]othing is so alien in kind as not to be part of our world,provided only that it does exist at some distance and direction fromhere, or at some time before or after or simultaneous with now.
The actual world provides us with our most salient example of what apossible world is. But, for the concretist, other possible worlds areno different in kind from the actual world (ibid., 2):
There are countless other worlds, other very inclusive things. Ourworld consists of us and all our surroundings, however, remote in timeand space; just as it is one big thing having lesser things as parts,so likewise do other worlds have lesser other-worldly things as parts.
It is clear that spatiotemporal relations play a critical role inLewis's conception. However, it is important to note that Lewisunderstands such relations in a very broad and flexible way so as toallow, in particular, for the possibility of spirits and otherentities that are typically thought of as non-spatial; so long as theyare located in time, Lewis writes, “that is good enough”(ibid., 73). So with this caveat, let us say that that anobjecta isconnected if any two of its parts bearsome spatiotemporal relation to each other,[14] and thata ismaximal if none of its parts isspatiotemporally related to anything that is not also one of itsparts. Then we have the following concretist answers to our questions:
| AW1 | w is a possible world =w is a maximal connected object.[15] |
And, hence, to exist in a world is simply to be a part of it:
| AE1 | Individuala exists in worldw =a is a part ofw. |
It follows fromAW1 (and reasonable assumptions) that distinctworlds do not overlap, spatiotemporally; that no spatiotemporal partof one world is part of another.[16] Moreover, givenLewis's counterfactual analysis of causation, it follows from this that objects in distinct worlds bear no causalrelations to one another; nothing that occurs in one world has anycausal impact on anything that occurs in any other world.
2.1.2 Actuality
Critically, for Lewis, worlds and their denizens do not differ in themanner in which they exist. The actual world does not enjoy akind of privileged existence that sets it apart from other worlds.Rather, what makes the actual world actual is simply that it isour world, the world that we happen to inhabit. Other worldsand their inhabitants exist just as robustly as we do, and inprecisely the same sense; all worlds and all of their denizens areequallyreal.[17] A significant semantic corollary of this thesis for Lewis is that theword ‘actual’ in the phrase ‘the actual world’does not indicate any specialproperty of the actual world thatdistinguishes it from all other worlds; likewise, an assertion of theform ‘a is actual’ does not indicate any specialproperty of the individuala that distinguishes it from theobjects existing in other worlds. Rather, ‘actual’ issimply anindexical whose extension is determined by thecontext of utterance. Thus, the referent of ‘the actualworld’ in a given utterance is simply the world of the speaker,just as the referent of an utterance of ‘the presentmoment’ is the moment of the utterance; likewise, an utteranceof the form ‘a is actual’ indicates only thata shares the same world as the speaker. The speaker therebyascribes no special property toa but, essentially, expressesno more than when she utters ‘a ishere’,understood in the broadest possible sense. By the same token, when wespeak of non-actualpossibilia — Lewis's preferred labelfor the denizens of possible worlds — we simply pick out thoseobjects that arenot here in the broadest sense. In the mouthof an other-worldly metaphysician, we here are all among thenon-actualpossibilia of which she speaks in her lectures onde re modality.
2.1.3 Modal Reductionism, Counterparts, and the Analysis of Intensions
Modal Reductionism and Counterparts. Lewis parted waysdramatically with his mentorW. V. O. Quine on modality. Quine (1960, §41) stands in a long line ofphilosophers dating back at least toDavid Hume who are skeptical, at best, of the idea that modality is an objectivefeature of reality and, consequently, who question whether modalassertions in general can be objectively true or false, or evencoherent. Lewis, by contrast, wholly embraces the objectivity ofmodality and the coherence of our modal discourse. What he denies,however, is that modality is a fundamentallyirreduciblefeature of the world. Lewis, that is, is amodalreductionist. For Lewis, modal notions are not primitive. Rather,truth conditions for modal sentences can be given in terms of worldsand their parts; and worlds themselves, Lewis claims, are definedentirely in non-modal terms. The earliest presentation of Lewis'stheory of modality (Lewis 1968) — reflecting Quine'smethod of regimentation — offers, rather than a possible world semantics, a scheme fortranslating sentences in the language of modal predicate logicinto sentences of ordinary first-order logic in which the modaloperators are replaced by explicit quantifiers over worlds.[18] The mature account of Lewis 1986 is much more semantic inorientation: it avoids any talk of translation and offers instead a(somewhat informal) account of concretist possible world truthconditions for a variety of modal assertions. Nonetheless, it isuseful to express the logical forms of these truth conditionsexplicitly in terms of worlds, existence in a world (in the sense ofAE1, of course), and thecounterpart relation, whichwill be discussed shortly:
| Wx: | x is aworld | |
| Ixy: | xexists in worldy | |
| Cxy: | x is acounterpart ofy |
For sentences like(17) involving onlyde dicto modalities, Lewis's truth conditionsare similar in form to the truth conditions generated by the modalclauses of basic possible world semantics; specifically, for (17):
| For every worldw, every individualx inwthat is a dog is a mammal: ∀w(Ww →∀x(Ixw → (Gx →Mx))). |
As in possible world semantics, the modal operators‘□’ and ‘◇’ “turninto” quantifiers over worlds in concretist truth conditions(1986, 5). Also as in possible world semantics, a quantifier (ineffect) ranging over individuals that occurs in the scope of aquantifier (in effect) ranging over worlds —‘∀x’ and ‘∀w’,respectively, in (18) — is, for each valuew of the boundworld variable, restricted to the objects existing inw.However, unlike possible world semantics, predicates are not to bethought of as having different extensions at different worlds. Rather,for Lewis, each (n-place) predicate has a single extension thatcan contain (n-tuples of) objects across many different worlds— intuitively, all of the objects that have the property (orn-tuples of objects that stand in the relation) expressed bythe predicate across all possible worlds. Thus, in particular, thepredicate ‘G’ picks out, not just this-worldly dogsbut other-worldly canines as well. Likewise, the pet predicate‘T’ picks out both actual and other-worldly pets.Such a move is not feasible in basic possible world semantics, whichis designed for a metaphysics in which one and the same individual canexemplify a given property in some worlds in which they exist but notothers. Hence, a typical predicate will be true of an individual withrespect to some worlds and false of it with respect to others. But,for Lewis, as we've seen, distinct possible worlds do not overlap and,hence, objects are worldbound, thereby eliminating the need torelativize predicate extensions to worlds.
However, this very feature of Lewis's account — worldboundedness— might appear to threaten its coherence. For example, sinceAlgol is in fact a pet, given worldboundedness and the definitionAE1 of existence in a worldw, we have:
| There is no worldw such that Algol exists inwand fails to be someone's pet: ¬∃w(Iaw ∧¬Ta), |
But, according to Lewis's analysis, the modal operators‘□’ and ‘◇’, semantically, arequantifiers over worlds. Hence, (19) might appear to be exactly theconcretist truth condition for the denial of (the right conjunct of) (16), i.e., it might appear that, on Lewis's analysis, Algol is not a petaccidentally but essentially; likewise, more generally, any individualand any intuitively accidental property of that individual.
In fact, Lewis whole-heartedly accepts that things have accidentalproperties and, indeed, would accept that(16) is robustly true. His explanation involves one of the mostinteresting and provocative elements of his theory: the doctrine ofcounterparts. Roughly, an objecty in a worldw2 is a counterpart of an objectx inw1 ify resemblesx and nothing elseinw2 resemblesx more thany.[19] Each object is thus its own (not necessarily unique) counterpart inthe world it inhabits but will typically differ in important ways fromits other-wordly counterparts. A typical other-worldly counterpart ofAlgol, for example, might resemble her very closely up to some pointin her history — a point, say, after which she continued to liveout her life as a stray instead of being brought home by our kindlydog-lover John. Hence, sentences makingde re assertions aboutwhatAlgol might have done or whatshe could or couldnot have been are unpacked, semantically, as sentences about hercounterparts in other possible worlds. Thus, when we analyze(16) accordingly, we have the entirely unproblematic concretist truthcondition:
| Algol is a pet, but there is a world in which exists acounterpart of hers that is not: Ta ∧ ∃w(Ww ∧∃x(Ixw ∧Cxa ∧ ¬Tx)). |
Ascriptions of essential properties, as in (15), are likewise unpacked in terms of counterparts: to say that Algol isa dog essentially is to say that
| All of Algol's counterparts in any world are dogs: ∀w(Ww → ∀x((Ixw ∧Cxa) →Gx)). |
The Analysis of Intensions. Lewis's possible world truthconditions are expressed in classical non-modal logic and, hence, theyare to be interpreted by means of standard Tarskian semantics. Thus,n-place predicates π are assigned extensionsEπ — in particular, for 1-place predicates,sets of individuals — as their semantic values, as described inthe exposition in§1.2 above. However, given worldboundedness and the fact that predicateextensions are drawn not simply from the actual world but from allpossible worlds, these extensions are able to serve asintensions in Lewis's theory. As in basic possible worldsemantics, intensional entities in general can be defined in terms ofthe basic ontology of the theory independent of the linguistic rolesthey can play as the intensions of predicates. And because individualsare worldbound, Lewis is able to simplify the definitions given in§1.3 by defining intensions as sets rather than functions:
- Aproposition is any set of worlds.
- Aproperty is any set of individuals.
- Ann-place relation (n > 1) is any setofn-tuples of individuals.[20]
Thus, on this analysis, a propositionp istrue in aworldw just in casew ∈p and an individuala has a propertyP just in casea ∈P. (Note that propositions are thus simply properties of worldson these definitions.)a hasPaccidentallyjust in casea ∈P butb ∉Pfor some other-worldly counterpart ofb ofa; anda hasPessentially ifb ∈Pfor every counterpartb ofa.
In Lewis's theory of modality, then, modal operators are understoodsemantically to be quantifiers over concrete worlds, predicates denoteintensions understood as sets of (n-tuples of) parts of thoseworlds, and sentences involvingde re modalities are understoodin terms of counterparts. To the extent that these notions are free ofmodality, Lewis has arguably reduced modal notions to non-modal.
2.1.4 Plenitude and Recombination
That Lewis's truth conditions for modal statements are themselves freeof modality and, hence, that his theory counts as a genuine reductionof modal notions to non-modal is not terribly controversial (albeitnot undisputed — see Lycan 1991, 224–27; Divers and Melia2002, 22–24). Significantly more controversial, and perhaps farmore critical to the project, is whether or not his account iscomplete, that is, whether or not, for all modal statementsφ, (i) if φ is intuitively true, then its Lewisian truthcondition holds (ii) if φ is intuitively false, then its Lewisiantruth condition fails.[21] The challenge to Lewis, then, is that his account can be consideredsuccessful only if it is complete in this sense.
The chief question Lewis faces in this regard is whether there areenough worlds to do the job. The truth condition (20) for the intuitively true (16) says that there exists a possible world in which a counterpart ofAlgol is no one's pet. By virtue of what in Lewis's theory does such aworld exist? The ideal answer for Lewis would be that some principlein his theory guarantees aplenitude of worlds, a maximallyabundant array of worlds that leaves “no gaps in logical space;no vacancies where a world might have been, but isn't” (Lewis1986, 86). From this it would follow that the worlds required by theconcretist truth condition for any intuitive modal truth exist. Towardthis end, Lewis initially considers the evocative principle:
| Ways | Absolutely every way that a world could be is a way that someworld is. |
Since, in particular, a world satisfying (20) seems quite obviously to be a way a world could be, byWayssuch a world exists. But there is a fatal flaw here: Lewis himself(1973, 84) identifiesways that a world could be with worldsthemselves. So understood,Ways collapses into the trivialitythat every world is identical to some world.[22]
Lewis finds a replacement forWays in a principle ofrecombination whereby “patching together parts ofdifferent possible worlds yields another possible world” (1986,87–88). The principle has two aspects. The first is theprinciple that “anything can coexist with anything”. For“if there could be a dragon, and there could be aunicorn,” Lewis writes, “but there couldn't be a dragonand a unicorn side by side, that would be ... a failure ofplenitude” (ibid., 88). Given that individuals areworldbound, however, the principle is expressed more rigorously (andmore generally) in terms of other-worldlyduplicates:
| R1 | For any (finite or infinite) number of objectsa1,a2, ..., there is a worldcontaining any number of duplicates of each of those objects in anyspatiotemporal arrangement (size and shape permitting). |
The second aspect of the principle expresses “the Humean denialof necessary connections” (ibid., 87), that is, the ideathat anything canfail to coexist with anything else. For“if there could be a talking head contiguous to the rest of aliving human body, but there couldn't be a talking head separate fromthe rest of a human body, that too would be a failure ofplenitude” (ibid). To express this a bit more rigorously,say that objectsa1,a2, ..., areindependent of objectsb1,b2, ..., if no sum of any parts of the former areparts or duplicates of any sum of any parts of the latter and viceversa; then we have:
| R2 | For any worldw any (finite or infinite number of)objectsa1,a2, ..., inwand any objectsb1,b2, ..., inw that are independent ofa1,a2, ..., there is a world containing duplicates ofa1,a2, ..., and no duplicates ofb1,b2, ... . |
Worlds that satisfy the concretist truth conditions for workadaypossibilities like (16) are easily conceived as consisting of duplicates of relevant parts ofthe actual world — suitably organized to retain their actualproperties, or not, as needed. Hence, the existence of such worldsdoes indeed appear to follow from the existence of the actual world byrecombination. Worlds containing talking donkeys, exotic speciesresulting from a wholly different evolutionary history, worlds withsilicon-based life forms, and so on present a bigger challenge to theview. Nonetheless, it is not entirely implausible to think such worldsexist given suitable duplication and reorganization of microphysical objects.[23]
Whether recombination completely captures our modal intuitionsregarding plenitude is still a matter of some dispute.[24] However, even if it doesn't, it is less than clear whether thiscounts against the success of Lewis's reductionist project. For, as arealist about worlds, Lewis does not seem to be under any obligationto “derive” plenitude from more fundamental principles.Hence, there is no obvious reason why he cannot respond to charges ofincompleteness by saying that it is simply a presupposition of histheory that logical space has no gaps, that there are always enoughworlds to satisfy the concretist truth condition for any intuitivemodal truth.[25] So understood, the role of recombination for a realist about worldslike Lewis is something like the role of such axioms as powerset andreplacement for a realist about sets: given some sets, theseprinciples provide us with a detailed — but always less thancomplete — characterization of what further sets there are.Their role, therefore, is to give us insight into the richness anddiversity of set theoretic space, not a complete mechanism for provingwhich particular sets do or do not exist. Likewise recombinationvis-à-vis worlds and logical space.
2.1.5 A Brief Assessment of Concretism
Lewis's theory is particularly commendable for its strikingoriginality and ingenuity and for the simple and straightforwardanswersAW1 andAE1 that it provides to our twoquestionsQW andQE above. Furthermore, because worldsare (plausibly) defined entirely in nonmodal terms, the truthconditions provided by Lewis's translation scheme themselves appear tobe free of any implicit modality. Hence, unlike many other popularaccounts of possible worlds (notably, the abstractionist accountsdiscussed in the following section), Lewis's promises to provide agenuineanalysis of the modal operators.
Perhaps the biggest — if not the most philosophicallysophisticated — challenge to Lewis's theory is “theincredulous stare”, i.e., less colorfully put, the fact that itsontology is wildly at variance with common sense. Lewis faces thisobjection head on: His theory of worlds, he acknowledges,“does disagree, to an extreme extent, with firm commonsense opinion about what there is” (1986, 133). However, Lewisargues that no other theory explains so much so economically. Withworlds in one's philosophical toolkit, one is able to provide elegantexplanations of a wide variety of metaphysical, semantical, andintentional phenomena. As high as the intuitive cost is, Lewis (135)concludes, the existence of worlds “ought to be accepted astrue. The theoretical benefits are worth it.”
Additional discussion of, and objections to, concretism can be foundin the supplemental documentFurther Problems for Concretism.
2.2 Abstractionism
A rather different set of intuitions about situations is that they areabstract entities of a certain sort: They arestatesorconditions, of varying detail and complexity, that aconcrete world could be in — they areways that things,as a whole, could be.[26] Thus, returning to our original example, one very simple way thingscould be is for our philosopher Anne to be in her office. We can nowimagine, as in our example, further detail being successively added tothat description to yield more complex ways things could be: Anneworking at her desk in her office; music being in the background; herhusband being on the phone in the next room; her neighbor mowing thelawn next door; and so on. Roughly speaking, then, a possible worldfor an abstractionist is thelimit of such a“process” of consistently extending and adding detail tosome initial state of the world; it is atotal way thingscould be, a consistent state of the world that settles everypossibility; a consistent state to which no further detail could beadded without rendering it inconsistent.
2.2.1 Abstract Possible Worlds and Existence Therein
To give the notion of a state, or condition, of the world a littlemore metaphysical substance, abstractionists typically appeal to moretraditional ontological categories. Thus, for example, that thingscould be in the simple state described above might be spelled out inone of the following ways:
- Thepropositionthat Anne is in her office and at herdesk is possibly true.
- Theset of propositions {that Anne is in heroffice,that Anne is at her desk} is such that, possibly,all of its members are true.
- Thepropertybeing such that Anne is in her officeand at her desk is possibly exemplified (by “things as awhole”).
Possible worlds are then defined as special cases of the type ofentity in question that are in some relevant sensetotal.Adams (1974), for example, defines possible worlds to be consistentsets of propositions that are total in the sense of containing, forevery propositionp, eitherp or its negation; Fine(1977), fleshing out ideas of Prior, defines a possible world to be aconsistent propositionw that is total in the sense that, forevery propositionp,w entails eitherp or itsnegation. For purposes here, however, we will sketch the fundamentalsof the abstractionist view in terms ofstates of affairs,following the basic features of the account developed by Plantinga(1974, 1976), an account that, in the literature, frequently serves asa particularly trenchant abstractionist counterpoint to Lewis's concretism.[27]
States of affairs (SOAs) are abstract, intensional entities typicallysignified by sentential gerundives like “Algol's being John'spet” and “There being more than ten solar planets”.Importantly, SOAs constitute a primitive ontological category for theabstractionist; they are not defined in terms of possible worlds inthe manner that propositions are in§1.3. Just as some propositions are true and others are not, some SOAs areactual and others are not.[28] Note, then, that to say an SOA is non-actual isnot to saythat it does not actuallyexist. It is simply to say that itis not, in fact, a condition, or state, that the concrete world isactually in. However, because ‘____ is actual’ is oftenused simply to mean ‘____ exists’, there is considerablepotential for confusion here. So, henceforth, to express that an SOAis actual we will usually say that itobtains.
An SOA is said to bepossible (necessary,impossible) insofar as it is possible (necessary, impossible)that it obtain. One SOAs is said toinclude anothert if, necessarily,s obtains only ift does;sprecludest if, necessarily,s obtainsonly ift doesn't. So, for example,Algol's being John'spet includesAlgol's being someone's pet and precludesthere being no pets. Thus, on the abstractionist'sunderstanding of a situation as a state or condition of the physicalworld rather than a concrete, structured piece of it, the inclusion ofone situation in another is a purelylogical relation, not amereological one. Finally, say that an SOAs istotal if, for everySOAt,s either includes or precludest.(Abstractionists often use ‘maximal’ instead of‘total’, but we have already introduced this term in thecontext of concretism.) Abstractionist possible worlds are nowdefinable straightaway:
| AW2 | w is a possible world =w is an SOA that is bothpossible and total.[29] |
It is easy to see that this definition covers the more intuitivecharacterizations of abstract possible worlds above: they areconsistent — i.e., possible — states of the world thatsettle every possibility, consistent states to which no further detailcould be added without rendering them inconsistent. Note also that,for the abstractionist, as for the concretist, the actual world is nodifferent in kind from any other possible world; all possible worldsexist, and in precisely the same sense as the actual world. The actualworld is simply the total possible SOA that, in fact, obtains. Andnon-actual worlds are simply those total possible SOAs that do not.
What of existence in such worlds? As we've seen, on Lewis's account,to exist in a concrete worldw is literally to existinw, that is, within the spatiotemporal boundaries ofw. Clearly, because SOAs are abstract, individuals cannot existin abstractionist worlds in anything like the same literal,mereological sense. Accordingly, the abstractionist defines existencein a world simply to be a special case of the inclusion relation:
| AE2 | Individualaexists in possible worldw=w includesa's existing. |
Unlike concretism, then, abstractionism does not entail thatindividuals are worldbound; there is no inconsistency whatever in theidea that many distinct worlds can include the existence of one andthe same individual. Indeed, typically, abstractionists are staunchlycommitted to transworld identity and hold that most any givenindividual exists in many possible worlds and, moreover, thatcontingent individuals, at least, can exemplify very differentproperties from world to world. Abstractionists, therefore, have noneed to appeal to counterparts to understandde re modalitiesand can therefore accept the truth conditions for such modalitiesgiven by basic possible world semantics (spelled out, of course, interms of their definitionsAW2 andAE2). In particular,they can take the standard possible world truth condition for, e.g.,the right conjunct of (16) at face value: ‘◇(E!a ∧ ¬Ta)’is true on the abstractionist's approach if and only if there is aworld in which Algol herself, rather than some counterpart of hers,exists but fails to be anyone's pet.
2.2.2 Irreducible Modality and Intensional Entities
It is important to note that the possible worlds of abstractionism donot yield a reductive analysis of modality. The reason for this isclear: abstract possible worlds are defined in irreducibly modal terms— a possible world is an SOA that (among other things)possibly obtains; or a set of propositions such that it ispossible that all of its members are true; or a property thatispossibly exemplified; and so on. Hence, unpacked in termsof the abstractionist's definitions, the possible world truthconditions for modal propositions are themselves irreducibly modal.For example, when we unpack Plantinga's definition of a possible worldin the semantic clause for sentences of the form⌈◻ψ⌉ in order to derivethe truth condition for(17), ‘□∀x(Gx →Mx)’, weend up with this:
| For all SOAsw, if (i)possibly,w obtainsand (ii) for all SOAss, either (a)necessarily,w obtains only ifs does or (b)necessarily,w obtains only ifs doesn't, then,‘∀x(Gx →Mx)’ is true atw. |
If we now unpack the modal operators in (22) using the correspondingtruth conditional clauses of standard possible world semantics, theresult will contain further world quantifiers. And spelling out thoseworld quantifiers in turn using Plantinga’s definition willre-introduce those same modal operators yet again.
More generally, and a bit more exactly, put: As noted above, thelogical framework of basic possible world semantics is classicalpredicate logic. The logical framework of abstractionism is modalpredicate logic. Hence, if possible world semantics is supplementedwith abstractionist definitions of possible worlds, then the logicalframework of possible world semantics becomes modal predicate logic aswell and, as a consequence, the extensionality of the semantics islost once again. (This point is expressed somewhat more formally inthe supplemental documentThe Intensionality of Abstractionist Possible World Semantics.) Since, as noted above, the central motivation for possible worldsemantics was to deliver an extensional semantics for modal languages,any motivation for abstractionism as a semantic theory is arguably undermined.[30]
However, it is not entirely clear that this observation constitutes anobjection to abstractionism. For abstractionists can argue that thegoal of their analysis is the converse of the reductionist's goal: Thereductionist wants to understand modality in terms of worlds; theabstractionist, by contrast, wants to understand worlds in terms ofmodality. That is, abstractionists can argue that we begin with aprimitive notion of modality and, typically upon a certain amount ofphilosophical reflection, we subsequently discover an intimateconnection to the notion of a possible world, as revealed in theprinciplesNec andPoss. The analysis that abstractionists provide is designed to make thisconnection explicit, ideally, in such a way thatNec andPoss fall out as theorems of their theory (see, e.g., Plantinga1985 and Menzel and Zalta 2014).
Hand in glove with the irreducible nature of modality is the nature ofintensional entities. Concretists define intensional entities in termsof worlds, as described in§2.1.3. Abstractionists, by contrast, define worlds in terms of intensionalentities. This divergence in their choice of ontological primitivesreflects, not only their differing stances toward modality, but alsoan important methodological difference with regard to metaphysicalinquiry. The concretist is far more pragmatic; notions ofproperty,relation,proposition, and thelike play certain roles in our theorizing and are subject to a“jumble of conflictingdesiderata” (Lewis 1986,54). Within a given theory, any entities that can play those rolesfruitfully for the purposes at hand are justifiably identified withthose notions — regardless of how well they comport withpre-theoretic intuitions. Thus, Lewis finds it to be a strength of hisposition that he is able to adopt the set theoretic definitions in§2.1.3. By contrast, at least some abstractionists —Plantinga (1987) perhaps most notably — believe that we haveintuitive, pre-theoretic knowledge of intensional entities thatprecludes their being identified with set theoretic constructions ofany sort.[31] (See Stalnaker 1976 for a particularly illuminating discussion of thecontrast between concretism and abstractionism with respect to thetreatment intensional entities.)
2.2.3 Actuality and Actualism
As was noted in§2.1.2, for the concretist, there is no special property of the actual world—actuality — that distinguishes it, in anyabsolute sense, from all of the others; it is simply the world thatwe inhabit. For abstractionists, however, actualityis a special property that distinguishes exactly one possibleworld from all others — the actual world is the only world thathappens toobtain; it is the one and only way things could bethat is the way things as a whole, in fact,are. However, formost abstractionists, the distinctiveness of the actual world does notlie simply in its actuality but in its ontological comprehensiveness:the actual world encompasses all that there is. In a word: mostabstractionists areactualists.
Actualism is the thesis that everything that there is, everything that hasbeing in any sense, is actual. In terms of possible worlds:Everything that exists in any world exists in the actual world.[32] Possibilism, by contrast, is the denial of actualism; it is thethesis that there aremere possibilia, i.e., things that arenot actual, things that exist in other possible worlds but fail toexist in the actual world. Concretists are obviously not actualists(on their understanding of ‘actual’, at any rate).[33] Indeed, for the concretist, since individuals are worldbound,everything that exists in any nonactual possible world is distinctfrom everything in the actual world. However, although possibilism andabstractionism are entirely compatible — Zalta (1983), forexample, embraces both positions — abstractioniststendto be actualists. The reason for this is clear: Basic possible worldsemantics appears to be committed to possibilism and abstractionismpromises a way of avoiding that commitment.
The specter of possibilism first arises with regard tonon-actual possible worlds, which would seem by definition tobe prime examples of merepossibilia. However, we have justseen that the abstractionist can avoid this apparent commitment topossibilism by defining possible worlds to be SOAs of a certain sort.So defined, non-actual worlds, i.e., worlds that fail to obtain, canstill actually exist. Hence, the commitment of basic possible worldsemantics to non-actual worlds does not in itself threaten theactualist's ontological scruples.
However, the specter of possibilism is not so easily exorcised. Fornon-actual worlds are not the only, or even the most compelling,examples of merepossibilia that seem to emerge out of basicpossible world semantics. For instance, it is quite reasonable tothink that evolution could have taken a very different course (or, ifyou like, that God could have made very different creative choices)and that there could have been individuals — call themExotics — that are biologically very different from allactually existing individuals; so different, in fact, that no actuallyexisting thing could possibly have been an Exotic. According to basicpossible world semantics, the sentence ‘There could have beenExotics’ or, more formally,
| ◇∃xEx |
is true just in case there is a world in which‘∃xEx’ is true, i.e., when all is said anddone, just in case:
| There is a possible worldw and an individualainw such thata is an Exotic inw, |
which, a bit less formally, is simply to say that
| Some individual is an Exotic in some possible world. |
However, since no actually existing thing could have been an Exotic,anything that is an Exotic in some possible world cannot be among thethings that exist in the actual world. Thus, the truth conditions thatbasic possible world semantics assigns to some of our intuitive modalbeliefs appear to entail that there are non-actual individuals as wellas non-actual possible worlds. Defining possible worlds as SOAsprovided a way for the actualist to embrace non-actual worlds withoutcompromising her actualism. But how is the actualist to understand theapparent commitment to non-actualindividuals in such truthconditions as (25)?
Answers that have been given to this question represent a rather deepdivide between actualist abstractionists. On the one hand,“trace” actualists introduce actually existing entitiesinto their ontologies that can play the role of merepossibiliain (25) and its like. Trace actualists come in two varieties:new actualists andhaecceitists. New actualists likeLinsky and Zalta (1996) and Williamson (1998, 2000, 2013) argue that,in fact, all individuals are actually existing, necessary beings butnot all of them are necessarilyconcrete. Some concreteindividuals — those traditionally(mis-)categorizedas contingent beings — areonly contingently concrete. Likewise, some non-concrete individuals— those, like possible Exotics, traditionally(mis-)categorizedas contingently non-actual merepossibilia — are only contingently non-concrete.[34]
This novel take on modal metaphysics allows the new actualist toreinterpret possible world semantics so as to avoid possibilism.Notably, the domaind(w) of a worldw isunderstood not as the set of things that exist inw — forall individuals exist in all worlds — but the set of things thatareconcrete inw.[35] Hence, for the new actualist, the correct truth condition for (23) is:
| There is a possible worldw and an individualathat is (i) concrete inw and (ii) an Exotic inw. |
On the other hand, haecceitists like Plantinga introduce specialproperties — haecceities — to similar ends. The haecceityof an individuala is the property of beingthat veryindividual, the propertybeinga. A property is ahaecceity, then, just in case it is possible that it is thehaecceity of some individual.[36] It is a necessary truth that everything has a haecceity. Moreimportantly, for haecceitists, haecceities are necessary beings. Thus,not only is it the case that, had any particular individualafailed to exist, its haecceityha would still haveexisted, it is also the case that, for any “merelypossible” individuala, there is an actually existinghaecceity that would have beena's haecceity hadaexisted. More generally (and more carefully) put: Necessarily, for anyindividuala, (i)a has a haecceityh and (ii)necessarily,h exists.
Like the new actualists, then, the metaphysics of the haecceitistsenables them to systematically reinterpret possible world semantics insuch a way that the truth conditions of modal discourse are expressedsolely in term of actually existing entities of some sort rather thanactual and non-actual individuals. More specifically, for thehaecceitist, the domaind(w) of a worldw istaken to be the set of haecceities that areexemplified inw, that is, the set of haecceitiesh such thatwincludesh's being exemplified. Likewise, thew-extension of a (1-place) predicate π is taken to be aset of haecceities — intuitively, those haecceitiesthat are coexemplified inw with the property expressed byπ. So reinterpreted, the truth condition for (23) is:
| There is a possible worldw and a haecceityhthat is (i) exemplified inw and (ii) coexemplified with thepropertybeing an Exotic inw. |
By contrast, “no-trace”, orstrict, actualistslike Prior (1957), Adams (1981), and Fitch (1996) hew closely to theintuition that, had a contingent individuala failed to exist,there would have been absolutely no trace, no metaphysical vestige, ofa — neithera itself in some non-concrete statenor any abstract proxy fora. Hence, unlike trace actualism,there are no such vestiges in the actual world of objects that are notactual but only could have been. The logical consequences for no-traceactualists, however, appear to be severe; at the least they cannotprovide a standardcompositional semantics for modal languages, according to which (roughly) themeaning of a sentence is determined by its logical form and themeanings of its semantically significant constituents. In particular,if there is nothing to play the role of a “possibleExotic”, nothing that is, or represents, an Exotic in some otherpossible world — a merepossibile, a contingentlynon-concrete individual, an unexemplified haecceity — then thestrict actualist cannot provide standard, compositional truthconditions for quantified propositions like (23) that yield the intuitively correct truth value. For, understoodcompositionally, (23) is true if and only if ‘∃xEx’ is true atsome worldw. And that, in turn, is true atw if andonly if ‘Ex’ is true atw for some value of‘x’. But, as just noted, for the strict actualist,there is no such value of ‘x’. Hence, for thestrict actualist, ‘Ex’ is false atw for allvalues of ‘x’ and, hence, (23) is false as well. (These issues are explored in much greater detailin the entry on thepossibilism-actualism debate.)
2.2.4 A Brief Assessment of Abstractionism
Like concretism, abstractionism provides a reasonably clear andintuitive account of what worlds are and what it is to exist in them,albeit from a decidedly different perspective. Although, as noted in§2.2.2, the fact that modality is a primitive in abstractionist definitionsof possible worlds arguably compromises its ability to providesemantically illuminating truth conditions for the modal operators,those definitions can be taken to illuminate the connection betweenour basic modality concepts and the evocative notion of a possibleworld that serves as such a powerful conceptual tool for constructingphilosophical arguments and for analyzing and developing solutions tophilosophical problems. In this regard, particularly noteworthy are:Plantinga's (1974) influential work onthe ontological argument and the free will defense againstthe problem of evil; Adams' (1974, 1981) work onactualism and actuality; and Stalnaker's (1968, 1987) work oncounterfactual conditionals andmental content.
A number of important objections have been voiced in regard toabstractionism. Some of these are addressed in the documentProblems with Abstractionism.
2.3 Combinatorialism
As its name might suggest, our third approach —combinatorialism — takes possible worlds to berecombinations, or rearrangements, of certain metaphysical simples.Both the nature of simples and the nature of recombination vary fromtheory to theory. Quine (1968) and Cresswell (1972), for example,suggest taking simples to be space-time points (modeled, perhaps, astriples of real numbers) and worlds themselves to be arbitrary sets ofsuch points, each set thought of intuitively as a way that mattercould be distributed throughout space-time. (A worldw, soconstrued, then, isactual just in case a space-time pointp is a member ofw if and only ifp is occupiedby matter.) Alternatively, some philosophers define states a worldcould be in, and possible worlds themselves, simply to be maximallyconsistent sets of sentences[37] in an expressively rich language —“recombinations”, certainly, of the sentences of thelanguage. (Lewis refers to this view aslinguistic ersatzism.[38]) However, the predominant version of combinatorialism finds itsorigins in Russell's (1918/1919) theory oflogical atomism and Wittgenstein's (1921, 1922, 1974) short but enormouslyinfluentialTractatus Logico-Philosophicus. A suggestive paper by Skyrms (1981) spelling out some of the ideas intheTractatus, in turn, inspired a rich and sophisticatedaccount that is developed and defended in great detail in an importantseries of books and articles by D. M. Armstrong (1978a, 1978b, 1986a,1989, 1997, 2004b, 2004c). In this section, we present a somewhatsimplified version of combinatorialism that draws primarily uponArmstrong's work. Unless otherwise noted, this is what we shall meanby ‘combinatorialism’ for the remainder.
2.3.1 The Basic Ontology of Combinatorialism
Wittgenstein famously asserted that the world is the totality offacts, not of things (ibid., §1.1). Thecombinatorialist spells out Wittgenstein's aphorism explicitly interms of an ontology of objects (a.k.a., particulars), universals(a.k.a., properties and relations), and facts. Facts are either atomicor molecular. Every atomic fact —Sachverhalt, in thelanguage of theTractatus — is “constituted”by ann-place relation (= property, forn=1) andn objects thatstand in, orexemplify, thatrelation. Thus, for example, suppose that John is 1.8 meters tall.Then, in addition to John and the propertybeing 1.8 meterstall, there is for the combinatorialist the atomic fact of John'sexemplifying that property. More generally, atomic facts existaccording to the following principle:
| AF | Objectsa1, ...,anexemplifyn-place relationR iff there is the facta1, ..., an's exemplifying R([R,a1,...,an], forshort). |
Say that theai are theconstituentobjects of the fact in question andR itsconstituentuniversal, and thatR and theaiallexist in[R,a1,...,an].
A fact ismonadic if its constituent universal is a property.Amolecular factf is a conjunction of atomic facts.Its constituent objects and universals are exactly those of itsconjuncts and an entity exists inf just in case it exists inone of its conjuncts. (For simplicity, we stipulate that an atomicfact has (only) itself as a conjunct and, hence, is“trivially” molecular.) One factfincludesanotherg if every conjunct ofg is a conjunct off. (Note, importantly, that inclusion, so defined, is quitedifferent from the homonymous notion defined in the discussion ofabstractionism above — most notably, combinatorial inclusion isnot amodal notion.) For purposes below, say that an objecta is abare particular in a molecular factf ifthere is no monadic conjunct off of whicha is theconstituent object, no conjunct of the forma exemplifies F,for some propertyF.a is abare particular ifit is bare in every molecular fact. Intuitively, of course, a bareparticular is an unpropertied object.
There is no upper bound on the “size” of a molecular factand no restriction on which atomic facts can form a conjunction; forany atomic facts at all, there is a molecular fact whose conjuncts areexactly those facts. As a first cut, then, we can spell outWittgenstein's characterization of the (actual) world as the totalityof facts by defining the world to be the largest molecular fact, themolecular fact that includes all of the atomic facts.[39]
Although objects and universals are typically included along withfacts in the basic ontology of combinatorialism, facts are typicallyconsidered more fundamental. Indeed, taking his queue from theTractarian thesis that the world consists of facts, not things,Armstrong (1986a, 577) argues that facts alone are ontologically basicand that objects and universals are simply “aspects of,abstractions from” facts. Accordingly, he calls the objectconstituent of a fact of the form [P,a] a“thin” particular, an object “considered inabstraction from all its [intrinsic] properties” (1993, 433);and whereN is the conjunction of “all the non-relationalproperties of that particular (which would presumably includeP), the atomic facta's exemplifying N itself is thecorresponding “thick” particular ” (ibid.,434 — we will occasionally use italics to distinguish a thinparticulara from the corresponding thick particulara).Though not all combinatorialists of every stripe buy into Armstrong's“factualist” metaphysics (Bricker 2006), they do generallyagree that facts are more fundamental, at least to the extent thatboth the notion of a bare particular, i.e., an object exemplifying noproperties, and that of an unexemplified property are consideredincoherent; insofar as they exist at all, the existence of bothparticulars and universals depends on their “occurring” insome fact or other. Whatever their exact ontological status, it is animportant combinatorialist thesis that exactlywhat objectsand universals exist is ultimately a matter for natural science, notmetaphysics, to decide.
Objects can be either simple or complex. An object issimple ifit has no proper parts, andcomplex otherwise. Like objects,universals too divide into simple and complex. A universal is simpleif it has no other universal as a constituent, and complex otherwise.Complex universals accordingly come in two varieties: conjunctive— the constituents of which are simply its conjuncts — andstructural. A structural universalU is one that is exemplifiedby a complex objectO, and its constituents are universals(distinct fromU) exemplified by simple parts ofO thatare relevant toO's being an instance ofU.[40] It is important to note that, for Armstrong, the constituencyrelation is not the mereological parthood relation. Rather, complexuniversals (hence also complex facts of which they are constituents)enjoy a “non-mereological mode of composition” (1997,119–123) that, in particular, allows for a richer conception oftheir structure.[41] (An assumption of our simplified account here will be that both theproper part of relation and the constituency relation arewell-founded. It follows that (i) there is nogunk, i.e., that every complex object is composed, ultimately, entirely ofsimples and (ii) complex universals — hence the complex facts inwhich they are exemplified — are ultimately“grounded” in simple facts, i.e., that they cannot beinfinitely decomposed into further complex universals/facts.[42])
To illustrate the basic idea: in Figure 1, the left-hand diagramdepicts a water moleculeW comprising an oxygen atomoand two hydrogen atomsh1 andh2.For the combinatorialist, “thick” particulars like themolecule itself as well as its constituent atoms are themselves facts:o is the fact [O,o] in which the universaloxygen (O) is exemplified by a thin particularo;[43] likewiseh1 andh2.W inturn comprises those monadic facts and the relational facts[B,o,h1],[B,o,h2] wherein the covalent bondingrelationB holds between the oxygen atom and the two hydrogenatoms. The structural universalWater itself, then, shares thisstructure — it is, so to say, anisomorph consisting ofthe monadic universalsO andH and the binary relationB, structured as indicated in the right-hand diagram of Figure 1.[44]

Figure 1: A Water MoleculeW and the Structural UniversalWater
2.3.2 States of Affairs and Recombination
It should be clear fromprincipleAF that all atomic factshold; that is, all of them reflectactual exemplification relations. Obviously, however, possibilityencompasses more than what is actual, that is, there arepossible facts as well as actual facts; the world'suniversals might have been exemplified by its objects verydifferently. If they had — if the world's objects and universalshad combined in a very different way — there would have been avery different set of atomic facts and, hence, a very different world.
To spell out the idea of a possible fact, the combinatorialistintroduces the more general notion of an atomic(combinatorial)state of affairs, that is, an entity that simply has theform of an atomic fact —n objects exemplifyingann-place relation — but without any requirement thatthe exemplification relation in question actually holds between them.More exactly:
| AS | For any objectsa1, ...,an and anyn-place relationR,there is an atomic (combinatorial) state of affairsa1, ...,an's exemplifyingR (again,[R,a1,...,an], forshort). |
Thus, even if the two hydrogen atomsh1 andh2 in a water molecule do not in fact stand in thecovalent bonding relationB, there is nonetheless the(non-factual) state of affairs[B,h1,h2].
Combinatorialism takes facts to be literal, structured parts of thephysical world. This suggests that a non-factual state of affairs— a merelypossible fact — must be part of amerely possible physical world. This idea is at odds with the strong,scientifically-grounded form of actualism that typically motivatescombinatorialism. Two options are available: The combinatorialist canfollow the (actualist) abstractionists and define states of affairs tobe philosophical or mathematical constructs consisting only of actualobjects, properties, relations, and facts. For example, the state ofaffairs[R,a1,...,an] cansimply be identified with the orderedn-tuple⟨R,a1,...,an⟩.So long as the combinatorialist is willing to adopt the additionalmetaphysical or set theoretic machinery, this sort of approach offersa way of introducing non-factual states of affairs that does notinvolve any untoward ontological commitments to merely possibleentities. Alternatively, following Armstrong (1989, 46–51; 1997,172–4), the combinatorialist can refuse to grant non-factualstates of affairs any genuine ontological status and adopt a form of modal fictionalism that nonetheless permits one to speakas if such states ofaffairs exist. The exposition to follow will remain largely neutralbetween these options.
Constituency for states of affairs is understood as for facts.Additionally, analogous to molecular facts, there are molecular statesof affairs — conjunctions of atomic states of affairs. Inclusionbetween states of affairs is understood exactly as it is between factsand being abare particular in a molecular state of affairss is understood as for facts:a is a bare particular ins if there is no monadic conjunct ofs of the forma exemplifies F. The notion of recombination is nowdefinable straightaway:
| s is arecombination of a molecular state ofaffairsf =s is a molecular state of affairs whose constituent objects andconstituent universals are exactly those off.s is anon-trivial recombination off if it does not includethe same states of affairs asf. |
Very roughly then, apossible world will be a certain sort ofrecombination of (some portion of) theactual world, themolecular fact that includes all of the atomic facts. This idea willbe refined in the following sections.
2.3.3 Structural States of Affairs and Supervenience
Say that a state of affairs isstructural if it is atomic andits constituent universal is structural or it is molecular andincludes a structural state of affairs; and say that it issimple otherwise. The difference between structural and simpleuniversals and states of affairs is particularly significant withregard to the important concept ofsupervenience (Armstrong1989, Ch 8).[45] Entity or entitiesS supervene on entity or entitiesRif and only if the existence ofR necessitates that ofS(ibid., 103). (Necessitation here is, of course, ultimately tobe spelled out in terms of combinatorial possible worlds.)Non-structural states of affairs supervene directly on their atomic conjuncts.[46] However, things are not in general quite so straightforward forstructural states of affairs. For, although structural states ofaffairs are ultimately constituted entirely by simple states ofaffairs, unlike non-structural states of affairs, structural states ofaffairs typically supervene on more than the totality of theirconstituents. For, in many cases, whether or not a structural factexists depends not only on the existence of its constituent facts butalso on theabsence of certain others (Armstrong 1997, 34ff).For example, as noted in our example above, our water moleculeW comprises two further facts in which two hydrogen atomsh1 andh2 both stand in thecovalent binding relation with an oxygen atomo. However, ifo were to bind with a further hydrogen atomh3, then, despite the fact that the constituentfacts ofW would still hold,W would not be water; therewould be no such fact asW's being water.[47] Rather,W would exist only as a complex part of a hydroniumion; the new binding [B,o,h3] would,so to say, “spoil” the instantiation ofWater.Thus, more generally, whether or not a structural state of affairsS exists in a possible world typically requires something overand above its constituent states of affairs being “weldedtogether” in the right sort of way (Armstrong, 1997, 36); itrequires also that there be no relevant “spoilers” forS.[48] Armstrong draws directly on the initial passages of theTractatus[49] for the necessary apparatus: a structural state of affairsSin any possible worldw, supervenes, not simply on itsconstituent atomic states of affairs but on a certainhigher-order state of affairsTw,namely, the state of affairs that the (first-order) atomic states ofaffairs ofw areall the (first-order) atomic states ofaffairs and, hence, thatw includes no spoilers forS. Armstrong (ibid., 35, 134–5, 196–201)callsTw thetotality state of affairs forthe atomic states of affairs ofw.[50]
2.3.4 Combinatorial Possible Worlds and Existence Therein
The idea of possibility being rooted in arbitrary recombinations ofthe actual world, rearrangements of its objects and universals, isintuitively appealing. Clearly, however, not just any suchrecombination can count as a possible world. Some states of affairsare intuitively impossible — [being an elephant,e], wheree is an individual electron, say — andsome pairs of states of affairs, while individually possible, are notcompossible — the states of affairs [having 1kgmass,a] and [having 2kg mass,a] for a givenobjecta, or, for a given mereological summ of simples,the states of affairs [being a baboon,m] and [beinga hoolock,m]. But nothing that has been said rules out theexistence of recombinations of the actual world — rearrangementsof its objects and universals — that include such states ofaffairs. Obviously, however, such recombinations cannot be thought torepresent genuinely possible worlds. Of course, like theabstractionist, the combinatorialist could simply stipulate as part ofthe definition that all legitimate recombinations must be genuinelypossible states of affairs of a certain sort, genuinelypossible recombinations. But this will not do. For, likeconcretism, combinatorialism purports to be areductiveaccount of modality, an account of possible worlds that does notdepend ultimately on modal notions (see Armstrong 1989, 33).[51]
Here the distinction between simple and structural states of affairstogether with the combinatorialist's strong notion of superveniencecome to the fore. For, given that structural facts supervene on simplefacts and the actual totality factT@, the actualworld can be defined more parsimoniously as the molecular fact thatincludes all thesimple atomic facts and the totality factT@. And at the level of simples, there are nolimitations whatever on recombination (Wittgenstein 1921,2.062-2.063); hence, any recombination of simple objects anduniversals is by definition considered possible. Thus Armstrong(1986a, 579):
The simple individuals, properties, and relations may be combined inall ways to yield possible [simple] atomic states of affairs,provided only that the form of atomic facts is respected. That is thecombinatorial idea.
Worlds, in particular, can be defined as special cases of suchrecombinations, together with appropriate totality facts. To statethis, we need a condition that ensures the existence of a uniqueactual world:
| States of affairss andt are identical iff theyinclude exactly the same states of affairs. |
Given this, we have:
| The (combinatorial) actual world =the fact @ that includes exactly allthe simple atomic facts and the totality state of affairsT@ for the conjunction of those facts. |
| AW3 | w is a (combinatorial) possible world =w is a recombination of thesimple atomic facts of the actual world conjoined with the totalityfactTw for that recombination.[52] |
Armstrong's ontological commitments are notoriously rather slipperybut, givenAW3, a reasonably complete notion of existence in aworld is forthcoming. First, let us note that, for Armstrong, the“combinatorial idea” yields a substantial metaphysicalthesis, as well, viz., theontological free lunch (1986,12ff), i.e., the thesis that “[w]hat supervenes is no additionof being”; that “whatever supervenes ... is not somethingontologically additional to the subvenient entity or entities.”Hence, for Armstrong, it appears thatsimple states ofaffairs and their constituents exist most fundamentally and that theexistence of more complex entities is in a certain sensederivative. Thus:
| Entitya existsfundamentally in(combinatorial) possible worldw =(i)a is a simple state ofaffairs thatw includes or (ii)a is a constituent orconjunct of an entity that exists fundamentally inw. |
Given this, existence in a world generally — both fundamentaland derivative — both for simples and (first-order[53]) non-simples alike, is definable as follows:
| AE3 | Entitya exists in (combinatorial) possible worldw = either (i)a exists fundamentally inw or (ii)a superveneson entities that exist inw. |
Semantics receives rather short shrift in Armstrong's version ofcombinatorialism — at least, semantics in the model theoreticsense of§1.2 — but, as it has played an important role in our discussion ofconcretism and abstractionism, we note briefly how the ontology ofcombinatorialism might be taken to populate a possible worldinterpretation of the language of modal predicate logic. Specifically,we can take the range of the modal operators — understood,semantically, as quantifiers — to be all of the combinatorialpossible worlds in the sense ofAW3. The domaind(w) of each worldw is the set of all simple andcomplex objects that exist inw according toAE3 and thew-extensionIπ(w) of a predicateπ expressing a simple or complex universalR is the set ofalln-tuples, ⟨a1, ...,an⟩ such that the atomic fact[R,a1,...,an] existsinw.
2.3.5 Analytic and Emergent Modalities; Essential Properties
There are, then, for the combinatorialist no intrinsically modalphenomena; there are just all of the various worlds that exist onunrestricted combinatorial grounds alone. Ultimately, all genuinepossibilities, simple or not, are just states of affairs that exist inthese combinatorial worlds in the sense ofAE3. However, it isnot immediately as clear how to understand many intuitivenecessities/impossibilities involving complexstructural universals, for example, the impossibilities noted in theprevious section, viz., that something simultaneously have a mass ofboth 1kg and 2kg or simultaneously be both a baboon and a hoolock.Likewise, it is not entirely clear how combinatorialism accounts forintuitive facts about essential properties, such as that our watermoleculeW is essentially water or that Algol is essentially adog. Combinatorialists argue that such modal facts can nevertheless beexplained in terms that require no appeal to primitive modal featuresof the world (Armstrong 2004b, 15).
Analytic Modalities. Armstrong argues that manyintuitive modal facts — notably, the impossibility of an objectexemplifying more than one determinate of the same determinable— can be understood ultimately as logical, or analytic,modalities that are grounded in meaning rather than any primitivemodal features of reality. For example, intuitively it is impossiblethat an object simultaneously exemplify the structural propertieshaving 2kg mass andhaving 1kg mass. The combinatorialreason for this (cf. Armstrong 1989, 79) is that, for an objecta to exemplify the former property is simply for there to be adivision ofa into two wholly distinct parts, both of whichexemplify the latter property. Moreover, this division into parts isentirely arbitrary, that is, forany parta1ofa exemplifyinghaving 1kg mass, there is a (unique)parta2 ofa wholly distinct froma1 that also exemplifies that property. It followsthat, if our 2kg objecta itselfalso exemplifieshaving 1kg mass, then, asa is a part of itself, theremust be a 1kg part ofa that is wholly distinct froma.And that is analytically false, false “solely by virtue of themeaning we attach to” the word ‘part’ (ibid., 80).[54]
Emergent Modalities. Combinatorialism purports toexplain a further class of intuitive modal facts as features thatsimply “emerge” from facts about structural properties.[55] The discussion of structural states of affairs and supervenienceabove provides an example. Let us suppose the actual worldw1 includes our water moleculeW from Figure1 plus a further hydrogen atomh3. In this world,onlyh1 andh2 bind too.Hence, this world includes the state of affairsW's being waterbut not the state of affairsI's being hydronium in whicho,h1,h2, andh3 are so bonded as to constitute a hydronium ionI. Conversely, however, given the unrestricted nature ofrecombination, there is a worldw2 that includesW structured as it actually is inw1 butwhich also includes the spoiler[B,o,h3] — whereo andh3 bond — and, hence, the structural state ofaffairsI's being hydronium. Thus, the absence of[B,o,h3] inw1enables the emergence ofW's being water and precludesI'sbeing hydronium whilst its presence inw2enables the emergence of the latter but precludes the former. As aconsequence, it is impossible that the states of affairsW's beingwater andI's being hydronium coexist.[56]
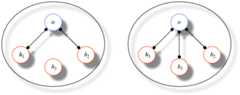
Figure 2:W's being water and (given a bond betweenoandh3)I's being hydronium
Although more dramatic, large-scale examples of incompatible states ofaffairs — such as a thing's being simultaneously both a baboonand a hoolock — might be vastly more complex, there is noobvious reason why their impossibility could not have the same sort ofcombinatorial explanation.
Essential Properties. It follows from theunrestricted nature of recombination that, for any simple objecta and simple universalP,a recombines withP in some worlds and fails to recombine withP inothers. Generalizing from this fact, it follows that no simple or sumof simples has any simple universal or conjunction of simpleuniversals essentially. It also follows that no such object has anystructural property essentially. For assumeo is such an objectand that it exemplifies a structural propertyP. SincePis structural, it supervenes on some set of simple states of affairs.But by the nature of recombination, there are combinatorial worlds inwhich those states of affairs do not exist and, hence, in whichP doesn't buto — being a simple or a sum ofsimples — does.
Thick particulars like our water moleculeW don't fare muchbetter because of the possibility of spoilers. For Armstrong (1997,35),W is simply the conjunction of its constituent states ofaffairs. As we've just seen, however, in the presence of spoilers,that conjunction would exist — hence,W would exist— without beingWater. Hence, it would seem that at leastsome properties that, intuitively, are essential to their bearers turnout not to be for the combinatorialist. The problem is compounded bythe fact that some intuitively non-essential properties of some thickparticulars are arguably essential for the combinatorialist. The shapeproperties of a thick particularA, for example, would seem tobe a function of its constituent states of affairs. Moreover, theexemplification of such properties are not obviously subject tospoilers the way that natural kind properties likeWater are.Hence, asA is identical to the conjunction of its constituentstates of affairs, it would seem that it will have the same shape inany world in which it exists, i.e., it will have that shapeessentially.
That said, combinatorialism can arguably provide a reasonably robustanalysis of intuitions about the essential properties of ordinarythick particulars like dogs or persons. Such objects can be taken tobe temporal successions of sums of simples and each sum in thesuccession as its temporal parts. Sums in the same rough temporalneighborhood are composed of roughly the same simples and arestructured in roughly the same way. Similarities between such objectsacross worlds in turn determine counterpart relations. FollowingLewis, the essential properties of such objects can then be identifiedwith those properties exemplified by (all of the temporal parts of)all of its counterparts in every world in which it exists (Armstrong1997, 99–103, 169).[57]
2.3.6 Fewer Things and Other Things: Modified Combinatorialism
Since a possible world is a recombination of the actual world andevery recombination includes states of affairs involving every simpleindividual and every simple universal, byAE3, every simpleentity exists in every world. Hence, there could not have been fewerof them; nor could there have been simples other than the ones thereactually are. In this section, we address this issue and the issue ofcontingent existence generally in combinatorialism.
Fewer things. Combinatorialism as it stands has noproblem accounting for the general intuition that there could havebeen fewer things. We have already noted in§2.3.3 and again in§2.3.5 how our water moleculeW, as such, might not have existed.More generally, given the unrestricted nature of recombination, foranya involving a structural factS, there arerecombinations of the actual world wherein either (a) some of therelations amonga's constituents that are critical toS's structure fail to be exemplified by those constituents, or(b) there are further states of affairs included by thoserecombinations that act as spoilers forS. Consequently, thecombinatorialist seems to have no difficulty explaining how theremight have been fewer water molecules, humans, etc.
Intuitively, however, there isn't anything in the idea of a simplethat suggests that simples are necessary beings — especially if,as combinatorialists generally agree, simples are physical things ofsome sort and simple universals are properties of, and relationsamong, those things. For there is nothing in the nature of a simpleobject to suggest that any given simple had to have existed. Likewise,there is nothing in the nature of a simple universal to suggest it hadto have been exemplified and, hence, on the combinatorialist's ownconception of universals, that it had to exist. Otherwise put, assimples exist only insofar as they are constituents of facts, thereseems no reason why there couldn't have been a very small number offacts, indeed, just a single simple, atomic, monadic fact and, hence,a lone simple object and a lone simple universal.
In fact, however,AW3 can be easily modified to accommodatethese intuitions without doing any serious violence tocombinatorialist intuitions. Specifically, the combinatorialist canadmit “contracted” worlds in which fewer simples exist byallowing any recombination ofany simple fact — thatis, equivalently, by allowing any state of affairs — to count asa possible world:
| AW3′ | w is a (combinatorial) possible world =w is a recombination of somesimple factf conjoined with the totality state of affairsTw for that recombination. |
AE3 requires no modification, as it was defined with sufficientgenerality above. UnderAW3′, however,AE3 entailsthat all entities alike — objects and universals, simple andstructural — are contingent and, indeed, that every simpleobject is the sole constituent of some combinatorial possible world.
Other things. Intuitively, not only could there havebeen fewer things, there could have been more things or, moregenerally, thingsother than those that actually exist. Asabove, combinatorialism as it stands seems able to account for manyinstances of this intuition: Figure 2 illustrates how a non-actualhydronium ionI might exist in another world. Likewise, thereseems no reason to deny, e.g., that there are rearrangementswof the actual world's simples wherein exist all of the human beingsthat actually exist (at, say, 0000GMT 1 January 2013) and more besidesthat are composed of simples that, in fact, constitute things otherthan human beings (Armstrong 1997, 165).[58] Combinatorialism also seems able to account for the possibility ofconjunctive and structural universals that are simply rearrangementsof actual simples. It is not implausible to think that suchrecombinations can give rise to, say, exotic biological kinds thathave no actual instances (Armstrong 1989, 55–56). Thus, inparticular, combinatorialism seems quite able to provide the truthcondition (24) for (23) and, hence, can account for some possibilities involving“missing” universals that, intuitively, ought to bepossible.
However, it is far from clear that such possibilities exhaust themodal intuition that other things could have existed. Notably,intuitively, there could have been differentsimpleuniversals distinct from any that actually exist — differentfundamental properties of simples, for example. Likewise for simpleobjects. Either way, there seems to be nothing in the idea of a simpleobject or simple universal that suggests there couldn't have beensimples other than, or in addition to, the simples there are in fact.ButAW3′ does not allow for this; the simples of everypossible world are a subset of the actual simples and there is noobvious way of modifying the principle to accommodate the intuition.Nor is there any obvious way of modifying the principle to accommodatethe intuition in question.[59]
The combinatorialist could of course abandon actualism and includemerely possible simples into her ontology. Again, she could follow thenew actualists and draw a division between actually concrete andnon-actual, possibly concrete simples; or she could introducePlantinga-style haecceities to go proxy for merely possible simples.But all of these options would be badly out of step with the strong,naturalist motivations for combinatorialism: There is but the onephysical world comprising all of the facts; recombinations of (atleast some of) those facts — arbitrary rearrangements of theirsimple objects and universals — determine the possible worlds.Merepossibilia, merely possible non-concretia, andnon-qualitative haecceities have no real place in that picture.
The “purest” option for the combinatorialist is simply tobrazen it out and argue that the actual simples are, in fact, all thesimples there could be (Armstrong 1989, 54ff; Driggers 2011,56–61). A more robust option suggested by Skyrms (1981) makessome headway against the problem by introducing an“outer”, or “second-grade” realm ofpossibility, but at the cost of moving beyond the basic intuitions ofcombinatorialism (Armstrong 1989, 60; 1997, 165–167). Finally,Sider (2005, 681) suggests that combinatorialists who (like Armstrong)are modal fictionalists can deal with the problem of missing entitiessimply by appealing to yet more fictionalism: As the combinatorialistfictionalready includes non-actual states of affairs withactually existing constituents, there seems no reason not to extendthe fiction to include non-actual states of affairs whose constituentsinclude non-actual particulars and universals. Fictionalism itself,however, leaves the combinatorialist with the deep problems detailedby Kim (1986), Lycan (1993), and Rosen (1993).[60]
2.3.7 A Brief Assessment of Combinatorialism
As with concretism and abstractionism, combinatorialism providesreasonably clear definitions of possible worlds and existence in aworld and is noteworthy for its attempt to avoid what might be thoughtof as the metaphysical excesses of the two competing views. Incontrast to concretism, combinatorialism is staunchly actualist:instead of an infinity of alternative physical universes, each withits own unique inhabitants existing as robustly as the inhabitants ofthe actual world, the worlds of combinatorialism are simplyrearrangements of the universals and particulars of the actual world;and commitment even to them might be avoided if some version offictionalism is tenable. Likewise, in contrast to abstractionism'srather rich and unrestrained ontology of SOAs, combinatorialism'sstates of affairs are comparatively modest. Moreover, in contrast tonearly all versions of abstractionism, combinatorialism shares withconcretism the virtue of a reductive theory of modality: Modalstatements, ultimately, are true or false in virtue of how thingsstand with respect to worlds that are themselves defined in non-modalterms.
Combinatorialism's ontological modesty, however, is also a weakness.For, unlike, the two competing approaches, there are modal intuitionsthat the combinatorialist is not easily able to account for, notably,the intuition that there could have been other things. Additionaldifficulties are discussed in the supplemental documentFurther Problems for Combinatorialism.
Bibliography
- Adams, R., 1974. ‘Theories of Actuality’,Noûs, 8: 211–31; reprinted in Loux (1979):190–209
- –––, 1981. ‘Actualism and Thisness’,Synthese, 49: 3–41
- Armstrong, D. M., 1978a,Universals and Scientific Realism,Volume I: Nominalism and Realism, Cambridge: Cambridge UniversityPress.
- –––, 1978b,Universals and ScientificRealism, Volume II: A Theory of Universals, Cambridge: CambridgeUniversity Press.
- –––, 1986a, ‘The Nature ofPossibility’,The Canadian Journal of Philosophy, 16(4):575–594.
- –––, 1986b. ‘In Defense of StructuralUniversals’,Australasian Journal of Philosophy, 64(1):85–88.
- –––, 1989.A Combinatorial Theory ofPossibility, New York: Cambridge University Press.
- –––, 1993. ‘A World of States ofAffairs’, in J. Tomberlin (ed.),PhilosophicalPerspectives, 7: 429–440.
- –––, 1997.A World of States of Affairs,New York: Cambridge University Press.
- –––, 2004a. ‘Theorie Combinatoire Revue etCorrigée’, in J-M. Monnoyer (Ed.)La Structure duMond: Objets, Propriétés, États et Choses,Paris: Vrin, 185–198.
- –––, 2004b. ‘CombinatorialismRevisited’, translation (with minor corrections) of Armstrong2004a, URL =http://eprints.nottingham.ac.uk/716/, ISBN: 2-7116-1627-4.
- –––, 2004c.Truth and Truthmakers,Cambridge: Cambridge University Press.
- –––, 2009. ‘Reply to Keller,’, inMonnoyer 2007, 157–162.
- Barcan, R., 1946. ‘A Functional Calculus of First OrderBased on Strict Implication’,Journal of Symbolic Logic,11: 1–16.
- Bayart, A., 1958, ‘La correction de la logique modale dupremier et second ordre S5’,Logique et Analyse, 1:28–44. Translated in Cresswell forthcoming.
- –––, 1959, ‘Quasi-adéquation de lalogique modale de second ordre S5 et adéquation de la logiquemodale de premier ordre S5’,Logique et Analyse, 2:99–121.
- Beall, J., 2000. ‘A Neglected Response to the Grimresult’,Analysis, 60(1): 38–41.
- Bigelow, J. and R. Pargetter, 1987. ‘Beyond the BlankStare’,Theoria, 53: 97–114.
- Bradley, R., 1989. ‘Possibility and Combinatorialism:Wittgenstein Versus Armstrong’,Canadian Journal ofPhilosophy, 19(1): 15–41.
- Bricker, P., 1980. ‘Prudence’,Journal ofPhilosophy, 77(7): 381–401.
- –––, 1987. ‘Reducing Possible Worlds toLanguage’,Philosophical Studies, 52(3):331–355.
- –––, 1996. ‘Isolation and Unification: TheRealist Analysis of Possible Worlds’,PhilosophicalStudies, 84(2/3): 225–238.
- –––, 2001. ‘Island Universes and theAnalysis of Modality’, in G. Preyer, F. Siebelt (eds.),Reality and Humean Supervenience: Essays on the Philosophy of DavidLewis, Rowman and Littlefield.
- –––, 2006. ‘The Relation Between Generaland Particular: Supervenience vs. Entailment’, in D. Zimmerman(ed.),Oxford Papers in Metaphysics, vol. 3, Oxford: OxfordUniversity Press, 251–287.
- –––, 2008. ‘Concrete PossibleWorlds’, in T. Sider, J. Hawthorne, and D. Zimmerman (eds.),Contemporary Debates in Metaphysics Blackwell Publishing,111–134.
- Bringsjord, S., 1985. ‘Are There Set Theoretic PossibleWorlds?’,Analysis, 45(1): 64.
- Bueno, O., C. Menzel, and E. Zalta, 2014. ‘Worlds andPropositions Set Free’,Erkenntnis, 79:797–820.
- Carnap, R., 1947.Meaning and Necessity. Chicago: TheUniversity of Chicago Press.
- Chihara, C., 1998.The Worlds of Possibility, Oxford:Clarendon Press
- Copeland, B. J., 2002. ‘The Genesis of Possible WorldsSemantics’,Journal of Philosophical Logic, 31:99–137.
- –––, 2006. ‘Meredith, Prior, and theHistory of Possible Worlds Semantics’,Synthese, 150(3):373–397.
- Cresswell, M. J., 1972. ‘The World is Everything that is theCase’,Journal of Philosophy, 50: 1–13. Reprintedin Loux (1979), 129–145.
- –––, 1973.Logics and Languages, London,Methuen.
- –––, 1985a.Structured Meanings: TheSemantics of Propositional Attitudes, Bradford Books/MITPress.
- –––, 1985b.Adverbial Modification.Dordrecht, Reidel.
- –––, 1988.Semantical Essays: PossibleWorldsand Their Rivals. Dordrecht, Kluwer Academic Publishers.
- –––, 1990.Entities and Indices.Dordrecht, Kluwer.
- –––, 1994.Language in the World.Cambridge: Cambridge University Press.
- –––, 1996.Semantic Indexicality.Dordrecht: Kluwer.
- –––, 2004. ‘Adequacy Conditions forCounterpart Theory’,Australasian Journal of Philosophy,82(1): 28–41.
- –––, 2015. ‘Arnould Bayart's ModalCompleteness Theorems — Translated with an Introduction andCommentary’,Logique et Analyse, 229: 89–142.
- Darby G., and D. Watson, 2010. ‘Lewis's Principle ofRecombination: Reply to Efird and Stoneham’,Dialectica,64(3): 435–445.
- Davies, M., 1981.Meaning, Quantification, Necessity: Themes inPhilosophical Logic, London: Routledge and Kegan Paul.
- DeRosset, L., 2009a. ‘Possible Worlds I: ModalRealism’,Philosophy Compass, 4(6): 998–1008.
- –––, 2009b. ‘Possible Worlds II:Non-reductive Theories of Possible Worlds’,PhilosophyCompass, 4(6): 1009–1021.
- Divers, J., 2002.Possible Worlds, London: Routledge.
- Divers, J. and J. Melia, 2002. ‘The Analytic Limit ofGenuine Modal Realism’,Mind, 111(441): 15–36.
- Driggers, R. K., 2011. ‘M-Combinatorialism and the Semanticsof SQML’, M.A. Thesis, Texas A&M University. URL =http://hdl.handle.net/1969.1/ETD-TAMU-2011-05-9484
- Eddon, M., 2007. ‘Armstrong on Quantities andResemblance’,Philosophical Studies, 136(3):385–404.
- Efird, D. and T. Stoneham, 2008. ‘What is the Principle ofRecombination?’,Dialectica, 62(4): 483–494.
- Egan, A., 2004. ‘Second-order predication and theMetaphysics of Properties’,Australasian Journal ofPhilosophy, 82(1): 48–66.
- Etchemendy, J., 1990.The Concept of Logical Consequence,Cambridge, MA: Harvard University Press. (Reissued by Stanford: CSLIPublications, 1999.)
- Feldman, F., 1971. ‘Counterparts’,Journal ofPhilosophy, 68: 406–9.
- Fara, D. G., 2009. ‘Dear Haecceitism’,Erkenntnis, 70: 285–297.
- Fara, M. and T. Williamson, 2005. ‘Counterparts andActuality’,Mind, 114(453): 1–30.
- Fine, K., 1977. ‘Postscript’, in Prior 1977,116–161.
- –––, 1978. ‘Model Theory for Modal Logics:Part I — TheDe Re/De Dicto Distinction’,Journal of Philosophical Logic, 7: 125–56.
- Forbes, G., 1985.The Metaphysics of Modality, Oxford:Clarendon Press.
- –––, 1982. ‘Canonical CounterpartTheory’,Analysis, 42(1): 33–37.
- Fitch, G. W., 1996, ‘In Defense of AristotelianActualism’,Philosophical Perspectives, 10:53–71.
- Forrest, P. and D. M. Armstrong, 1984. ‘An Argument againstDavid Lewis's Theory of Possible Worlds’,AustralasianJournal of Philosophy, 62: 164–168.
- Garson, J., 2006.Modal Logic for Philosophers. New York:Cambridge University Press.
- Goldblatt, R., 2003. “Mathematical Modal Logic: A View ofits Evolution”, in D. M. Gabbay and J. Woods (eds.),Handbookof the History of Logic, Vol. 7: Logic and the Modalities in theTwentieth Century. Amsterdam: Elsevier, pp. 1–98.
- Grim, P., 1986. ‘On Sets and Worlds: A Reply toMenzel’,Analysis, 46(4): 186–191.
- Hazen, A., 1979. ‘Counterpart Theoretic Semantic for Modallogic’,Journal of Philosophy, 76: 319–338.
- Hunter, G. and W. Seager, 1981. ‘The Discreet Charm ofCounterpart Theory’,Analysis, 41(2): 73–76.
- Heil, J., 2007. ‘The Legacy of Linguisticism’,Australasian Journal of Philosophy, 84(2): 233–244.
- Hintikka, J., 1957. ‘Modality as referentialmultiplicity’,Ajatus, 20: 49–64.
- –––, 1961. ‘Modality andQuantification’,Theoria, 27: 119–28.
- Hughes, G. and Cresswell, M., 1968.An Introduction to ModalLogic, London: Methuen.
- Jager, T., 1982. ‘An Actualist Semantics for QuantifiedModal Logic’,Notre Dame Journal of Formal Logic, 23(3)(July): 335–49.
- Kanger, S., 1957.Provability in Logic, Stockholm: Almqvistand Wiksell.
- Kaplan, D., 1975. ‘How to Russell a Frege-Church’,Journal of Philosophy, 72: 716–29; reprinted in Loux(1979), pp. 210–24.
- Kaplan, D., 1979. ‘Transworld Heir Lines’, in Loux(1979), pp. 88–109.
- –––, 1995. ‘A Problem in Possible WorldSemantics’, in W. Sinnott-Armstrong, D. Raffman, and N. Asher(eds.),Modality, Morality and Belief: Essays in Honor of RuthBarcan Marcus, Cambridge: Cambridge University Press,41–52.
- Keller, P., 2007. ‘A World of Truthmakers’, inMonnoyer 2007, 105–156.
- –––, 2009. ‘Review of D. M. Armstrong,Truth and Truthmakers’,Mind, 118(472):1101–1105.
- Kemeny, J. G., 1956a. ‘A New Approach to Semantics —Part I’,The Journal of Symbolic Logic, 21(1):1–27.
- –––, 1956b. ‘A New Approach to Semantics— Part II’,The Journal of Symbolic Logic, 21(2):149–161.
- Kim, J., 1986. ‘Possible Worlds and Armstrong'sCombinatorialism’,Canadian Journal of Philosophy, 16(4):595–612.
- Kripke, S., 1959. ‘A Completeness Theorem in ModalLogic’,Journal of Symbolic Logic, 24(1):1–14.
- –––, 1963a. ‘Semantical Analysis of ModalLogic I: Normal Modal Propositional Calculi’,Zeitschriftfür Mathematische Logik und Grundlagen der Mathematik, 9:67–96.
- –––, 1963b. ‘Semantical Considerations onModal Logic’,Acta Philosophica Fennica, 16:83–94.
- –––, 1972. ‘Naming and Necessity’,Cambridge, Massachusetts: Harvard, 1980.
- Lewis, D., 1968. ‘Counterpart Theory and Quantified ModalLogic’,Journal of Philosophy, 65: 113–126.
- –––, 1970. ‘General Semantics’,Synthese, 22: 18–67.
- –––, 1973.Counterfactuals, Cambridge,Massachussetts: Harvard University Press.
- –––, 1986.On The Plurality of Worlds,Oxford: Blackwell.
- –––, 1986a. ‘Against StructuralUniversals’,Australasian Journal of Philosophy, 64(1):25–46.
- –––, 1991.Parts of Classes, Oxford:Basil Blackwell Ltd.
- –––, 1992, ‘Critical Notice: Armstrong, D.M.,A Combinatorial Theory of Possibility’,Australasian Journal of Philosophy, 70(2): 211–224.
- Lewis, C. I. and C. H. Langford, 1932.Symbolic Logic, NewYork: The Appleton-Century Company; reprinted in paperback by NewYork: Dover Publications, 1951.
- Linsky, B. and E. Zalta, 1994. ‘In Defense of the SimplestQuantified Modal Logic’, in J. Tomberlin (ed.),PhilosophicalPerspectives, 8: 431–458.
- –––, 1996. ‘In Defense of the ContingentlyConcrete’,Philosophical Studies, 84:283–294.
- Loux, M. (ed.), 1979.The Possible and the Actual, Ithaca:Cornell.
- Lycan, W., 1988. ‘On the Plurality of Worlds by DavidLewis’,The Journal of Philosophy, 85(1):42–47.
- –––, 1991. ‘Two — No, Three —Concepts of Possible Worlds’,Proceedings of the AristotelianSociety, New Series, 91: 215–227.
- –––, 1993. ‘Armstrong's New CombinatorialTheory of Modality’, in J. Bacon, K. Campbell, and L. Reinhardt(eds.),Ontology, Causality, and Mind: Essays in Honour of D. M.Armstrong, Cambridge: Cambridge University Press, 3–22.
- Maddy, P., 1980. ‘Perception and MathematicalIntuition’,The Philosophical Review, 89(2):163–196.
- Mates, B., 1968. ‘Leibniz on Possible Worlds’, in B.van Rootselaar and J. F. Staal (eds.),Logic, Methodology andPhilosophy of Science, vol. 3, Amsterdam: North-Holland PublishingCompany, 507–29; reprinted in H. Frankfurt (ed.),Leibniz, Notre Dame: University of Notre Dame Press (1972),335–364.
- Marcus, R., 1986. ‘Possibilia and Possible Worlds’,Grazer Philosophische Studien, 25/26 (1985/1986):107–33.
- McDaniel, K., 2006. ‘Modal Realisms”,PhilosophicalPerspectives, 20: 303–331.
- McNamara, P., 1993. ‘Does the Actual World ActuallyExist?’,Philosophical Studies, 69: 59–81.
- Menzel, C., 1986. ‘On Set Theoretic Possible Worlds’,Analysis, 46(2): 68–72.
- –––, 1989. ‘On an Unsound Proof of theExistence of Possible Worlds’,Notre Dame Journal of FormalLogic, 30(4): 598–603.
- –––, 1990. ‘Actualism, OntologicalCommitment, and Possible Worlds Semantics’,Synthese, 85:355–89.
- –––, 1991. ‘The True Modal Logic’,Journal of Philosophical Logic, 20: 331–374.
- –––, 2012. ‘Sets and Worlds Again’,Analysis, 72(2): 304–309.
- Menzel, C., and E. Zalta, 2014, ‘The Fundamental Theorem ofWorld Theory’,Journal of Philosophical Logic, 43(2):333–363.
- Meredith, C. and A. Prior, 1956. ‘Interpretations ofDifferent Modal Logics in the “Property Calculus”’,in Copeland, B. (ed.) 1996,Logic and Reality: Essays on the Legacyof Arthur Prior, Oxford: Clarendon Press.
- Merricks, T., 2003. ‘The End of Counterpart Theory ’,The Journal of Philosophy, 100(10): 521–549.
- Merrill, G., 1978. ‘Formalization, Possible Worlds and theFoundations of Modal Logic’,Erkenntnis, 12:305–327.
- Monnoyer, J. (ed.), 2007.Metaphysics and Truthmakers,Frankfurt am Main: Ontos Verlag.
- Montague, R., 1974.Formal Philosophy, New Haven, CT: YaleUniversity Press
- Moreland, J. P., 2011. ‘Exemplification and ConstituentRealism: A Clarification and Modest Defense’,Axiomathes,online. doi:10.1007/s10516-011-9148-x
- Nolan, D., 1996. ‘Recombination Unbound’,Philosophical Studies, 84(2/3): 239–262.
- Nortmann, U., 2002. ‘The Logic of Necessity in Aristotle: AnOutline of Approaches to the Modal Syllogistic, Together with aGeneral Account ofde dicto- andde re-Necessity’,History and Philosophy of Logic, 23: 253–265.
- Novakofski, J. M. S. Brewer, N. Mateus-Pinilla, J. Killefer, andR. H. McCusker, 2005. ‘Prion Biology Relevant to BovineSpongiform Encephalopathy’,Journal of Animal Science,83(6): 1455–1476. doi:10.2527/2005.8361455x
- Pickavance, T., 2014. ‘Bare Particulars andExemplification’,American Philosophical Quarterly,51(2): 95–108.
- Plantinga, A., 1974.The Nature of Necessity, Oxford:Oxford University Press.
- –––, 1976. ‘Actualism and PossibleWorlds’,Theoria, 42: 139–60; reprinted in Loux(1979): 253–73.
- –––, 1985. ‘Replies’, inAlvinPlantinga, J. Tomberlin and P. van Inwagen (eds.), Dordrecht: D.Reidel: 313–96.
- –––, 1987. ‘Two Concepts of Modality:Realism and Modal Reductionism’, in J. Tomberlin (ed.),Philosophical Perspectives, 1: 189–231.
- Pollock, J., 1985. ‘Plantinga on Possible Worlds’, inAlvin Plantinga, J. Tomberlin and P. van Inwagen (eds.),Dordrecht: D. Reidel, pp. 121–44.
- Prior, A. N., 1952. ‘Modalityde dicto and modalityde re,Theoria, 18(3): 174–180.
- –––, 1977.Worlds, Times, and Selves,Amherst: University of Massachusetts Press.
- –––, 1956. ‘Modality and Quantification inS5’,Journal of Symbolic Logic, 21: 60–2.
- Pruss, A., 2001. ‘The Cardinality Objection to David Lewis'sModal Realism’,Philosophical Studies, 104:169–178.
- Quine, W. V. O., 1948. ‘On What There Is’, inFroma Logical Point of View, New York: Harper, 1953, 1–19.
- –––, 1953. ‘Three Grades of ModalInvolvement’,Proceedings of the XIth International Congressof Philosophy, 14: 65–81.
- –––, 1956. ‘Quantifiers and PropositionalAttitudes’,The Journal of Philosophy, 53:177–187.
- –––, 1960.Word and Object, Cambridge,MA: MIT Press.
- –––, 1968. ‘Propositional Objects’,Critica: Revista Hispanoamericana de Filosofia, 2(5):3–29. Reprinted in W. V. Quine, 1977,OntologicalRelativity, Columbia University Press: 139–160.
- Rosen, G., 1993. ‘A Problem for Fictionalism about PossibleWorlds’,Analysis, 53(2): 71–81.
- Roy, T., 1995. ‘In Defense of Linguistic Ersatzism’,Philosophical Studies, 80(3): 217–242.
- Russell, B., 1918/1919. ‘The Philosophy of LogicalAtomism’,The Monist, 28: 495–527; 29: 32–63,190–222, 345–380. Reprinted in Russell 1956, 177–281and published in book form as Russell 1985.
- –––, 1956.Logic and Knowledge, London:Allen and Unwin.
- –––, 1985.The Philosophy of LogicalAtomism, with an introduction by D. Pears, London: Routledge.
- Salmon, N., 1988. ‘Review ofOn the Plurality ofWorlds,Philosophical Review, 97(2): 237–244.
- Shalkowski, S., 1994. ‘The Ontological Ground of the AlethicModality’,The Philosophical Review, 103(4):669–688.
- Schneider, S., 2001. ‘Alien Individuals, Alien Universals,and Armstrong's Combinatorial Theory of Possibility’,TheSouthern Journal of Philosophy, 39: 575–593.
- Sider, T., 2002. ‘The Ersatz Pluriverse’,Journalof Philosophy, 99(6): 279–315.
- –––, 2005. ‘Another Look at Armstrong'sCombinatorialism’,Noûs, 39(4): 679–695.
- Skyrms, B., 1981. ‘Tractarian Nominalism’,Philosophical Studies, 40(2): 199–206.
- Stalnaker, R., 1968. ‘A Theory of Conditionals’ inStudies in Logical Theory,American PhilosophicalQuarterly Monograph Series, 2. Oxford: Blackwell, pp.98–112.
- –––, 1976. ‘Possible Worlds’,Noûs, 10(1): 65–75.
- –––, 1987.Inquiry, Boston: BradfordBooks, MIT Press.
- –––, 2012.Mere Possibilities: MetaphysicalFoundations of Modal Semantics, Princeton: Princeton UniversityPress.
- Tarski, A., 1933. ‘The concept of truth in the languages ofthe deductive sciences’ (Polish),Prace Towarzystwa NaukowegoWarszawskiego, Wydzial III Nauk Matematyczno-Fizycznych, 34,Warsaw; expanded English translation in Tarski (1983),152–278.
- –––, 1944. ‘The semantic conception oftruth’,Philosophy and Phenomenological Research, 4:13–47.
- –––, 1983.Logic, Semantics, Metamathematics,papers from 1923 to 1938, edited by John Corcoran. Indianapolis:Hackett Publishing Company.
- Tomberlin, J., and van Inwagen, P. (eds.), 1985.Profiles:Alvin Plantinga, Dordrecht: D. Reidel, pp. 121–44.
- van Inwagen, P., 1986. ‘Two Concepts of PossibleWorlds’, inMidwest Studies in Philosophy, XI, P. French,T. Uehling, and H. Wettstein (eds.), Minneapolis: University ofMinnesota Press, 185–213.
- –––, 2008. ‘McGinn on Existence’,The Philosophical Quarterly, 58(20): 36–58.
- Washington, C., 1998. ‘Use/Mention Distinction andQuotation’, inRoutledge Encyclopedia of Philosophy, vol.9, W. Craig (ed.), London and New York: Routledge.
- Williamson, T., 1998. ‘Bare Possibilia’,Erkenntnis, 48: 257–273.
- –––, 2000. ‘The Necessary Framework ofObjects’,Topoi, 19: 201–208.
- –––, 2013.Modal Logic as Metaphysics.Oxford: Oxford University Press.
- Wittgenstein, L., 1921. ‘Logisch-PhilosophischeAbhandlung’, with a forward by Bertrand Russell,Annalen derNaturphilosophie, 14, published by Wilhelm Ostwald, Leipzig:Verlag Unesma: 185–262. Also available online in HTML, PDF, andePub formats in a side-by-side presentation with the translationsWittgenstein (1922) and Wittgenstein (1974) athttp://people.umass.edu/klement/tlp/.
- –––, 1922.TractatusLogico-Philosophicus, trans. of Wittgenstein (1921) by C. K.Ogden, Routledge & Kegan Paul.
- –––, 1974.TractatusLogico-Philosophicus, revised edition, trans. of Wittgenstein(1921) by D. F. Pears and B. F. McGuinness, New York and London:Routledge & Kegan Paul.
- Yagisawa, T., 2010.Worlds and Individuals, Possible andOtherwise, Oxford: Oxford University Press.
- Zalta, E., 1983.Abstract Objects: An Introduction to AxiomaticMetaphysics, Dordrecht: D. Reidel.
- –––, 1993. ‘Twenty-Five Basic Theorems inSituation and World Theory’,Journal of PhilosophicalLogic, 22(4): 385–428.
Academic Tools
How to cite this entry. Preview the PDF version of this entry at theFriends of the SEP Society. Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entryatPhilPapers, with links to its database.
Other Internet Resources
- Browse papers by related topics at Phil Papers:
- actualism and possibilism
- counterpart theory
- essentialism andde re modality
- essentialism and quantified modal logic
- modal ersatzism (roughly what is referred to as abstractionism in this entry)
- modal fictionalism
- modal realism (referred to as "concretism" in this entry)
- possible worlds
- possible world semantics
- Theories of modality
- modal primitivism
- universals
Related Entries
essential vs. accidental properties |identity: transworld |Lewis, David: metaphysics |logic, history of: modal logic |logic: classical |logic: intensional |logic: modal |modality: epistemology of |natural kinds |possibilism-actualism debate |possible objects |Prior, Arthur |rigid designators |states of affairs
Acknowledgments
The author wishes to express his deep gratitude to Phillip Bricker andMax Cresswell for extensive comments on several drafts of this entryand for numerous illuminating discussions of its content and relatedtopics. The entry is vastly better for their generous input. Errorsand other infelicities that remain are of course the soleresponsibility of the author. A great deal of this entry was writtenwith the support of the Alexander von Humboldt Foundation while theauthor was a Visiting Fellow at the Munich Center for MathematicalPhilosophy in 2011–12. Thanks are due to the Center's director,Professor Hannes Leitgeb, for making the author's stay at thisremarkable venue possible. Finally, the author would like to expresshis thanks to the SEP Editors for their extraordinary patience indealing with the very tardy author of a badly-needed entry.
About
Mirror Sites
View this site from another server:
The Stanford Encyclopedia of Philosophy iscopyright © 2025 byThe Metaphysics Research Lab, Department of Philosophy, Stanford University
Library of Congress Catalog Data: ISSN 1095-5054


