KR101440680B1 - Homomorphic Encryption and Decryption Method using Chinese Remainder Theorem and apparatus using the same - Google Patents

Abstract

Translated fromKorean

평문(p)으로부터 모듈러(M)를 연산하는 단계, 상기 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 단계, 및 랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c)을 생성하는 단계를 포함하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법이 개시된다.(M) from the plaintext (p), randomizing the modulus (M) by adding an error (E), and applying a Chinese restorative (CRT) to the randomized modular And generating a ciphertext (c) based on the rest of the theorem.

Description

Translated fromKorean

중국인 나머지 정리에 기반한 준동형 암복호화 방법 및 이를 이용한 장치{Homomorphic Encryption and Decryption Method using Chinese Remainder Theorem and apparatus using the same}[0001] The present invention relates to a quasi-dynamic encryption / decryption method based on the Chinese restorative scheme and a device using the same.

본 발명은 중국인 나머지 정리에 기반한 준동형 암복호화 방법 및 이를 이용한 장치에 관한 것이다.The present invention relates to a quasi-static encryption / decryption method based on the Chinese rest theorem and an apparatus using the same.

준동형 암호화 기술은 암호화된 상태에서 곱셈이나 덧셈이 가능하도록 하는 암호화 기술로서, 여러 분야에서 활용이 기대되고 있다. 예를 들면, 프라이버시를 보호할 필요가 있는 경우, 준동형 암호화 기술은 복호화를 할 필요없이 암호화된 상태에서 처리가 가능하므로, 유용할 수 있다.The perturbed encryption technology is an encryption technology that enables multiplication or addition in an encrypted state and is expected to be used in various fields. For example, if privacy needs to be protected, the perturbed encryption technique can be useful because it can be processed in an encrypted state without having to decrypt it.

2009년 완전 준동형 암호화 기술을 제시된 뒤로 완전 준동형 암호에 대한 연구가 활발하게 이루어지고 있으며, 특히, 정수 기반 완전 준동형 암호화 기술은 횟수에 제한 없이 암호문간의 더하기와 곱하기 연산을 지원할 수 있는 기술이다. 하지만, 이러한 기술은 공개키의 크기가 지나치게 클 뿐만 아니라 암호화에 많은 시간이 걸린다고 하는 단점이 있다.Full-fledged-type encryption is being actively researched since full-fledged encryption technology was presented in 2009, and in particular, integer-based full-fledged encryption is a technique that can support addition and multiplication between ciphertexts without limitation . However, this technique has a disadvantage that not only the size of the public key is excessively large but also the encryption takes a long time.

또한, 종래 다른 완전 준동형 암호화 기술들은, 안전하지 못하거나 충분한 횟수만큼 덧셈이나 곱셈을 지원하지 못하는 단점이 있다.In addition, other fully-perturbed cryptographic techniques have the disadvantage that they are unsafe or do not support addition or multiplication a sufficient number of times.

본 발명의 일 실시예에 따르면, 안전하고, 덧셈 및 곱셈의 횟수가 수용가능하고, 평문의 크기에 제한이 없고 속도와 저장 용량이 효율적인, 중국인 나머지 정리에 기반한 준동형 암복호화 방법이 제공될 수 있다.According to an embodiment of the present invention, there can be provided a quasi-static encryption / decryption method based on Chinese restitution, which is secure, accommodates the number of additions and multiplications, has no restriction on the size of plain texts, and is efficient in speed and storage capacity have.

본 발명의 다른 실시예에 따르면, 안전하고, 덧셈 및 곱셈의 횟수가 수용가능하고, 평문의 크기에 제한이 없고 속도와 저장 용량이 효율적인, 중국인 나머지 정리에 기반한 준동형 암호화 장치 또는 복호화 장치가 제공될 수 있다.According to another embodiment of the present invention, there is provided a cantilever type encryption device or decryption device based on the Chinese rest theorem that is safe, accommodates the number of times of addition and multiplication, has no restriction on the size of the plain text, and is efficient in speed and storage capacity .

본 발명의 다른 실시예에 따르면, 안전하고, 덧셈 및 곱셈의 횟수가 수용가능하고, 평문의 크기에 제한이 없고 속도와 저장 용량이 효율적인, 중국인 나머지 정리에 기반한 준동형 암호화 또는 복호화 방법을 실행하기 위한 프로그램을 기록한 컴퓨터로 판독 가능한 기록 매체가 제공될 수 있다.According to another embodiment of the present invention, there is provided a method for performing a perceptual encryption or decryption method based on the Chinese remaining theorem, which is safe, acceptable for the number of additions and multiplications, A computer-readable recording medium on which a program for recording a program can be provided.

본 발명의 일 실시예에 따르면, 평문(p)으로부터 모듈러(M)를 연산하는 단계; 상기 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 단계; 및 랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c)을 생성하는 단계;를 포함하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법이 제공될 수 있다.According to one embodiment of the present invention, there is provided a method for processing a data stream, comprising: computing a modulus M from a plaintext p; Adding the error (E) to the modulator (M) and randomizing the modulus (M); And generating a ciphertext (c) by applying a Chinese restorative (CRT) to the randomized moduler (A).

본 발명의 다른 실시예에 따르면, 평문(p)으로부터 모듈러(M)를 연산하는 모듈러 연산부; 상기 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 랜덤화부; 및 랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c)을 생성하는 CRT 연산부;를 포함하는 중국인 나머지 정리에 기반한 준동형 암호화 장치가 제공될 수 있다.According to another embodiment of the present invention, a modular arithmetic unit for calculating a modulo M from a plain text p; A randomizer for randomizing the modulo M with an error E; And a CRT operation unit for applying the Chinese remaining theorem (CRT) to the randomized moduler (A) to generate the encryption statement (c).

본 발명의 다른 실시예에 따르면, 암호화문(c)을 복호화하는 복호화부;를 포함하며, 상기 복호화부는, 수학식 M = (c mod S) mod Q에 의해 모듈러를 계산하고,According to another embodiment of the present invention, there is provided a decoding apparatus for decoding a ciphertext (c), the decoding unit calculating a modulus by the following equation: M = (c mod S) mod Q,

수학식 p = CRT_Q(M) 에 의해 중국인 나머지 정리(CRT)를 적용하여 평문(p)을 생성하며, 상기 암호화문(c)는, 제13항 내지 제15항 중 어느 하나의 항에 의해 암호화된 암호화문 인것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 복호화 장치가 제공될 수 있다.(C) is generated by applying the Chinese Residual Theorem (CRT) by the formula p = CRT_Q (M) to generate a plaintext (p) It is possible to provide a perceptual decryption apparatus based on the Chinese rest theorem characterized by being an encrypted encryption statement.

본 발명의 실시예에 따른 방법을 실행하기 위한 프로그램을 기록한 것을 특징으로 하는 컴퓨터로 판독 가능한 기록 매체가 제공될 수 있다.A computer-readable recording medium having a program recorded thereon for executing the method according to the embodiment of the present invention can be provided.

본 발명의 하나 이상의 실시예에 따르면, 안전한 레벨까지 암호화가 가능하며, 암호화된 상태에서 덧셈 및 곱셈의 횟수가 현실적으로 수용가능한 횟수까지 지원이 될 수 있다. 또한, 암호화를 할 평문의 크기에 제한이 없고 속도와 저장 용량이 효율적일 수 있다.According to one or more embodiments of the present invention, it is possible to encrypt up to a secure level and support up to the number of times the addition and multiplication can be actually accepted in the encrypted state. Also, there is no limit on the size of the plain text to be encrypted, and the speed and storage capacity can be efficient.

도 1은 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치를 설명하기 위한 도면이고,
도 2는 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치에 사용되는 용어 및 파라미터들을 정의한 도면이고,
도 3은 도 1의 실시예에 의해 암호화된 암호화문을 복호화하는 복호화 장치를 설명하기 위한 도면이고,
도 4는 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치에 의해 암호화된 암호화문의 덧셈 및 곱셈을 설명하기 위한 도면이고,
도 5는 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치 및/또는 복호화 장치가 적용되는 컴퓨터 시스템을 설명하기 위한 도면이고,
도 6은 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 방법을 설명하기 위한 도면이고,
도 7은 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 복호화 방법을 설명하기 위한 도면이고,
도 8은 본 발명의 다른 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치를 설명하기 위한 도면이고, 그리고
도 9는 도 8의 실시예에 의해 암호화된 암호화문을 복호화하는 복호화 장치를 설명하기 위한 도면이다.FIG. 1 is a view for explaining a perceptual type encryption apparatus based on the Chinese rest theorem according to an embodiment of the present invention, and FIG.
FIG. 2 is a diagram illustrating terms and parameters used in a perceptual type encryption apparatus based on the Chinese rest theorem according to an embodiment of the present invention,
FIG. 3 is a view for explaining a decryption apparatus for decrypting an encrypted statement encrypted by the embodiment of FIG. 1,
FIG. 4 is a diagram for explaining addition and multiplication of an encryption inquiry encrypted by a perceptual type encryption device based on the Chinese rest theorem according to an embodiment of the present invention,
5 is a diagram for explaining a computer system to which a cantilever type encryption apparatus and / or a decryption apparatus based on the Chinese rest theorem according to an embodiment of the present invention is applied,
FIG. 6 is a diagram for explaining a perceptual type encryption method based on the Chinese rest theorem according to an embodiment of the present invention, and FIG.
FIG. 7 is a view for explaining a quasi-static decoding method based on the Chinese rest theorem according to an embodiment of the present invention, and FIG.
8 is a view for explaining a perceptual type encryption device based on the Chinese rest theorem according to another embodiment of the present invention, and
9 is a diagram for explaining a decryption apparatus for decrypting an encrypted statement encrypted by the embodiment of FIG.

이상의 본 발명의 목적들, 다른 목적들, 특징들 및 이점들은 첨부된 도면과 관련된 이하의 바람직한 실시예들을 통해서 쉽게 이해될 것이다. 그러나 본 발명은 여기서 설명되는 실시예들에 한정되지 않고 다른 형태로 구체화될 수도 있다. 오히려, 여기서 소개되는 실시예들은 개시된 내용이 철저하고 완전해질 수 있도록 그리고 당업자에게 본 발명의 사상이 충분히 전달될 수 있도록 하기 위해 제공되는 것이다. 본 명세서에서, 어떤 구성요소가 다른 구성요소 상에 있다고 언급되는 경우에 그것은 다른 구성요소 상에 직접 형성될 수 있거나 또는 그들 사이에 제 3의 구성요소가 개재될 수도 있다는 것을 의미한다.BRIEF DESCRIPTION OF THE DRAWINGS The above and other objects, features, and advantages of the present invention will become more readily apparent from the following description of preferred embodiments with reference to the accompanying drawings. However, the present invention is not limited to the embodiments described herein but may be embodied in other forms. Rather, the embodiments disclosed herein are provided so that the disclosure can be thorough and complete, and will fully convey the scope of the invention to those skilled in the art. In this specification, when an element is referred to as being on another element, it may be directly formed on another element, or a third element may be interposed therebetween.

본 명세서에서 사용된 용어는 실시예들을 설명하기 위한 것이며 본 발명을 제한하고자 하는 것은 아니다. 본 명세서에서, 단수형은 문구에서 특별히 언급하지 않는 한 복수형도 포함한다. 명세서에서 사용되는 '포함한다(comprises)' 및/또는 '포함하는(comprising)'은 언급된 구성요소는 하나 이상의 다른 구성요소의 존재 또는 추가를 배제하지 않는다.The terminology used herein is for the purpose of illustrating embodiments and is not intended to be limiting of the present invention. In the present specification, the singular form includes plural forms unless otherwise specified in the specification. The terms "comprises" and / or "comprising" used in the specification do not exclude the presence or addition of one or more other elements.

이하, 도면을 참조하여 본 발명을 상세히 설명하도록 한다. 아래의 특정 실시예들을 기술하는데 있어서, 여러 가지의 특정적인 내용들은 발명을 더 구체적으로 설명하고 이해를 돕기 위해 작성되었다. 하지만 본 발명을 이해할 수 있을 정도로 이 분야의 지식을 갖고 있는 독자는 이러한 여러 가지의 특정적인 내용들이 없어도 사용될 수 있다는 것을 인지할 수 있다. 어떤 경우에는, 발명을 기술하는 데 있어서 흔히 알려졌으면서 발명과 크게 관련 없는 부분들은 본 발명을 설명하는 데 있어 별 이유 없이 혼돈이 오는 것을 막기 위해 기술하지 않음을 미리 언급해 둔다.Hereinafter, the present invention will be described in detail with reference to the drawings. In describing the specific embodiments below, various specific details have been set forth in order to explain the invention in greater detail and to assist in understanding it. However, it will be appreciated by those skilled in the art that the present invention may be understood by those skilled in the art without departing from such specific details. In some instances, it should be noted that portions of the invention that are not commonly known in the description of the invention and are not significantly related to the invention do not describe confusing reasons for explaining the present invention.

도 1은 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치를 설명하기 위한 도면이고, 도 2는 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치에 사용되는 용어 및 파라미터들을 정의한 도면이다.FIG. 1 is a view for explaining a cantilever type encryption device based on the Chinese rest theorem according to an embodiment of the present invention. FIG. 2 is a block diagram of a cantilever type encryption device based on the Chinese rest theorem according to an embodiment of the present invention. ≪ / RTI >

이들 도면을 참조하여, 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치(이하, '준동형 암호화 장치'라고 함)를 설명하기로 한다.Referring to these drawings, a cantilever type encryption device based on the Chinese rest theorem according to an embodiment of the present invention (hereinafter referred to as a "cantilever type encryption device") will be described.

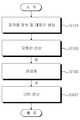
본 발명의 일 실시예에 따른 준동형 암호화 장치는, 평문(p)으로부터 모듈러(M)를 연산하는 모듈러 연산부(10), 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 랜덤화부(20), 및 랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c)을 생성하는 CRT 연산부(30)를 포함할 수 있다.The cantilever type encryption apparatus according to an embodiment of the present invention includes amodular operation unit 10 for calculating a modulo M from a plain text p, arandomization unit 10 for randomizing the modulo M with anerror E 20, and aCRT operation unit 30 for applying the Chinese remaining theorem (CRT) to the randomized moduler A to generate an encryption statement (c).

모듈러 연산부(10)는 다음의 수학식 1에 의해서, 평문(p)으로부터 모듈러(modular)(M)를 계산한다.The modulararithmetic unit 10 calculates a modular (M) from the plain text p by the following equation (1).

<수학식 1>&Quot; (1) &quot;

M= p mod QM = p mod Q

여기서, Q = {q_i｜ 1≤i≤k, i와 k는 양의 정수} = {q₁,q₂, ... , q_k}이고, q_i는 서로 소인 양의 정수이며, q_i는 d 비트의 길이를 가질 수 있다.Where q = {q_i |₁ | i k, i and k are positive integers} = {q₁ , q₂ , ..., q_k }, q_i is a positive integer of a positive integer, and q_i can have a length of d bits.

수학식 1에 의거하여, 모듈러 연산부(10)는 M = {m_i｜ 1≤i≤k, i와 k는 양의 정수} = {m₁, m₂, ... , m_k} 값을 출력한다.On the basis of the equation (1), the modulararithmetic unit 10 is M = | {a m_i 1≤i≤k, i and k is a positive_{integer} = {m 1, m 2} , ..., m k} value Output.

모듈러 연산부(10)는, 평문(p)의 사이즈를 크게 하는 동작을 수행하는 것으로서, 일 예에 따르면, 평문(p)의 사이즈를 k배 만큼 크게 할 수 있다.Themodular operation unit 10 performs an operation of increasing the size of the plain text p, and according to an example, the size of the plain text p can be increased by k times.

랜덤화부(20)는, 다음의 수학식 2에 의해서, 모듈러 연산부(10)에 의해 출력되는 M에 에러를 부여하여 랜덤화하는 동작을 수행한다.The randomizingunit 20 performs an operation of giving an error to the M output from themodular operation unit 10 and randomizing it by the following equation (2).

<수학식 2>&Quot; (2) &quot;

A = M + E·QA = M + E Q

여기서, E= {e_i｜ 1≤i≤k, i와 k는 양의 정수} = {e₁, e₂, ... , e_k}이고, e_i는 λ비트를 가질 수 있다. 한편, λ는 ρ = 2 ·λ 에 의해 정의될 수 있고, 여기서, ρ는 시큐어리티 파라미터이다.Here, E = {e_i |₁ | i k, i and k are positive integers} = {e₁ , e₂ , ..., e_k }, and e_i can have a lambda bit. On the other hand,? Can be defined by? = 2?, Where? Is a security parameter.

본 발명의 일 실시예에 따르면, 에러 e_i는 랜덤하게 선택된 것일 수 있다.According to one embodiment of the present invention, the error e_i may be randomly selected.

랜덤화부(20)는, 랜덤하게 선택한 에러값을 더하여 평문(p)을 숨기기 위한 동작을 수행하는 것이다. 본 실시예에서는, 랜덤하게 선택한 에러값을 E와 곱하였지만, 후술하는 대체 실시예(도 8과 도 9의 실시예를 참조)에서는 랜덤하게 선택한 에러값을 M과 곱할 수 있다.Therandomizer 20 adds an error value selected at random and performs an operation for hiding the plain text p. In the present embodiment, the randomly selected error value is multiplied by E, but an error value selected at random can be multiplied by M in an alternative embodiment (see embodiments of FIGS. 8 and 9) to be described later.

CRT 연산부(30)는, 다음의 수학식 3에 의해, 랜덤화부(20)에 의해 출력되는 랜덤화된 모듈러에 대하여 CRT(Chinese Remainder Theorem: CRT)을 적용하여 암호화문(c)을 출력한다.TheCRT calculation unit 30 applies a CRT (CRT) to the randomized moduler output by therandomization unit 20 according to the following equation (3) to output the encryption statement (c).

<수학식 3>&Quot; (3) &quot;

c = CRT_S(A)c = CRT_S (A)

CRT는 중국인의 나머지 정리를 적용하는 연산자이고, S= {s_i｜ 1≤i≤k, i와 k는 양의 정수} 로서 키(Key)이며, k는 키의 갯수를 나타낸다. 본 발명의 실시예에 따르면, 여기서 키(Key)는 비밀키일 수 있다.The CRT is an operator that applies the rest of the Chinese theorem, S = {s_i | 1 ≤ i ≤ k, i and k are positive integers}, and k is the number of keys. According to an embodiment of the present invention, the key may be a secret key.

CRT는, 예를 들면, s_1, s_2, ..., s_k가 서로 소인 정수라고 하고, b = s_1· s_2· s_3· ... s_k 라고 하면, 이때 임의의 수열 a_1, a_2, ..., a_k 대하여 c=a_k (mod s_k) 가 되는 c가 mod s 로 유일하게 존재한다는 정리이다.For example, if the s_1, s_2,..., S_k are constants of a small number, and b = s_1 · s_2 · s_3 · · · s_k, Theorem that c is a mod s with c = a_k (mod s_k) for a_k.

c에 대한 연립 합동식은 다음과 같이 기재될 수 있다.The algebraic equations for c can be written as:

c = a_1 (mod s_1)c = a_1 (mod s_1)

c = a_2 (mod s_2)c = a_2 (mod s_2)

..

..

..

c = a_k (mod s_k)
c = a_k (mod s_k)

상기 수식 CRT_S(A)에서, A는 나머지에 해당하고 S는 제수(나누는 수)에 해당하며, 수식 CRT_S(A)의 해 c 는 상기 연립 합동식을 만족하는 값이 된다.In the above formula CRT_S (A), A corresponds to the remainder, S corresponds to the divisor (division number), and the solution c of the formula CRT_S (A) satisfies the alliance joint expression.

S는 비밀키로서, {q₁· s₁, q₂·s₂, ..., q_k·s_k}가 서로 소인 집합이 되도록 소수 s₁, s₂, ..., s_k가 선택될 수 있다.S is a secret key and prime numbers s₁ , s₂ , ..., s_k are selected so that {q₁ · s₁ , q₂ · s₂ , ..., q_k · s_k } .

CRT 연산부(30)는, 비밀키 S = {s₁, s₂, ..., s_k}를 적용하여 연산하기 때문에, 비밀키를 모르는 공격자로부터는 안전한 암호화 동작을 수행한다. 본 실시예는, EACDP(Error-free Approximate Greatest Common Divisor Problem)가 안전하기만 하면, 안전한 암호 시스템이라고 할 수 있다.The CRTarithmetic unit 30 performs a secure encryption operation from an attacker who does not know the secret key because the secret key S = {s₁ , s₂ , ..., s_k } is calculated. This embodiment can be said to be a secure cryptographic system as long as the EACDP (Error-free Approximation Greatest Common Divisor Problem) is secure.

한편, 상술한 모듈러 연산부(10), 랜덤화부(20), 및 CRT 연산부(30)는 각각 Q, E, S와 같은 값들을 입력값으로 이용하며, 이들 값들은 d, k, λ, η, 및 ρ와 같은 파라미터들과 도 2의 (b)에 나타낸 수식으로서 정의될 수 있다.The moduloarithmetic unit 10, therandomizer 20 and the CRTarithmetic unit 30 use values such as Q, E, and S as input values, respectively, and these values are d, k, And &lt; RTI ID = 0.0 &gt; p, &lt; / RTI &gt;

본 발명의 일 실시예에 따르면, 위 파라미터들은 예를 들면, T 번 곱셈을 한다고 가정하면, 수학식 4를 만족하도록, λ , d, 및 η 가 정의될 수 있을 것이다.According to an embodiment of the present invention, assuming that the above parameters are, for example, multiplied by T times,?, D, and? May be defined so as to satisfy equation (4).

<수학식 4>&Quot; (4) &quot;

(T+1)·(2·λ + d) 〈 η(T + 1) · (2 · λ + d) <η

다만, 수학식 4는 예시적인 것으로서 본원 발명이 수학식 4에 의해서만 한정되는 것이 아님을 본 발명이 속하는 기술분야에서 통상의 지식을 가진 자(이하, '당업자')라면 이해할 수 있을 것이다.It should be understood, however, that Equation (4) is an example and that the present invention is not limited only to Equation (4), and that those skilled in the art will be able to understand the present invention.

도시하지는 않았지만, 본 발명의 대체적 실시예에 따른 준동형 암호화 장치는, 파라미터 선택부를 더 포함할 수 있다. 파라미터 선택부는, 예를 들면, 위 파라미터들 d, k, λ, η, 및 ρ와 Q 및 E를 선택할 수 있다.Although not shown, the perceptual encryption apparatus according to the alternative embodiment of the present invention may further include a parameter selection unit. The parameter selection unit can select, for example, the above parameters d, k, lambda, eta, and p and Q and E.

일반적으로, λ가 커지면 안전성이 높아지므로, 본원 명세서에는 λ를 종종 시큐어리티 파라미터라고 부르기로 한다.Generally, as? Increases, safety becomes high. Therefore, in the present specification,? Is sometimes referred to as a security parameter.

또한, 도시하지는 않았지만, 본 발명의 대체적 실시예에 따른 준동형 암호화 장치는, 비밀 키 생성부를 더 포함할 수 있다. 비밀 키 생성부는, 예를 들면, {q₁· s₁, q₂·s₂, ..., q_k·s_k}가 서로 소인 집합이 되도록 소수 s₁, s₂, ..., s_k 를 선택할 수 있다.Also, although not shown, the perceptual-type encryption apparatus according to the alternative embodiment of the present invention may further include a secret-key generation unit. Secret key generation unit,_{e.g., {q 1 · s 1,} q 2 · s 2, ..., q k · s k} is prime_{s 1, s 2, ...,} s such that each set of postmarks_k can be selected.

도 3은 도 1의 실시예에 의해 암호화된 암호화문을 복호화하는 복호화 장치를 설명하기 위한 도면이다.3 is a diagram for explaining a decryption apparatus for decrypting an encrypted statement encrypted by the embodiment of FIG.

도 3을 참조하면, 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 복호화 장치는, 도 1을 참조하여 설명한 암호화 장치에 의해 암호화된 암호화문을 복호화하는 복호화부를 포함할 수 있다.Referring to FIG. 3, the restructuring based on the Chinese restorative scheme according to an embodiment of the present invention may include a decryption unit for decrypting an encrypted statement encrypted by the encryption apparatus described with reference to FIG.

본 발명의 일 실시예에 따르면 복호화부는, 다음의 수학식 5에 의해서, 모듈러를 계산하는 제2 모듈러 연산부(40)를 포함할 수 있다.According to an embodiment of the present invention, the decoding unit may include a second modulararithmetic unit 40 for calculating a moduler by the following equation (5).

<수학식 5>&Quot; (5) &quot;

M = (c mod S) mod QM = (c mod S) mod Q

여기서, C는 도 1을 참조하여 설명한 암호화 장치에 의해 암호화된 암호화 문이다.Here, C is an encryption statement encrypted by the encryption apparatus described with reference to FIG.

제2 모듈러 연산부(40)는 도 3에 도시된 바와 같이 암호화문(c), 비밀키(S), 및 Q를 입력받아서, 모듈러 M을 출력할 수 있다.The second modulararithmetic unit 40 can receive the encryption key c, the secret key S and Q as shown in FIG.

복호화부는, 또한, 다음의 수학식 6에 의해서, CRT 연산을 수행하는 제2 CRT 연산부(50)를 더 포함할 수 있다.The decoding unit may further include a secondCRT arithmetic unit 50 for performing a CRT operation according to Equation (6).

<수학식 6>&Quot; (6) &quot;

p = CRT_Q(M)p = CRT_Q (M)

제2 CRT 연산부(50)는, 도 3에 도시된 바와 같이, 제2 모듈러 연산부(40)가 출력하는 모듈러에 중국인 나머지 정리(CRT)를 적용하여 평문(p)을 생성할 수 있다.The secondCRT arithmetic unit 50 may generate the plain text p by applying the remaining Chinese theorem (CRT) to the moduler output by the second modulararithmetic unit 40, as shown in FIG.

이상 도 3을 참조하여 설명한 복호화부는, 도 1을 참조하여 설명한 암호화 장치에 포함되도록 구성되거나, 또는 도 1을 참조하여 설명한 암호화 장치와는 무관하게 독립된 장치(예를 들면, 모바일 기기, 데스크 탑, 서버 등)에 포함되도록 구성될 수 있다.The decryption unit described with reference to FIG. 3 may be configured to be included in the encryption apparatus described with reference to FIG. 1, or may be configured to include an independent apparatus (for example, a mobile apparatus, a desktop, Server, etc.).

도 4는 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치에 의해 암호화된 암호화문의 덧셈 및 곱셈을 설명하기 위한 도면이다.FIG. 4 is a diagram for explaining addition and multiplication of an encryption inquiry encrypted by a perceptual type encryption device based on the Chinese rest theorem according to an embodiment of the present invention. FIG.

도 4(a)를 참조하면, 본 발명의 일 실시예에 따른 준동형 암호화 장치는, 도 1을 참조하여 설명한 암호화 장치에 의해 암호화된 암호화문 c1과 c2를, 다음의 수학식 7에 의해서 덧셈 연산하는 덧셈 연산부(60)를 더 포함할 수 있다.Referring to FIG. 4A, the perceptual type encryption apparatus according to an embodiment of the present invention includes encryption statements c1 and c2 encrypted by the encryption apparatus described with reference to FIG. 1 by the following equation (7) And anadder 60 for calculating an adder.

<수학식 7>&Quot; (7) &quot;

(c1+c2) mod N(c1 + c2) mod N

여기서 N은 도 2에 나타낸 바와 같이 수학식

에 의해 정의된다.Where N is an integer,

Lt; / RTI &gt;

도 4(b)를 참조하면, 본 발명의 일 실시예에 따른 준동형 암호화 장치는, 도 1을 참조하여 설명한 암호화 장치에 의해 암호화된 암호화문 c1과 c2를, 다음의 수학식 8에 의해서 곱셈 연산하는 곱셈 연산부(70)를 더 포함할 수 있다.Referring to FIG. 4 (b), the cantilever type encrypting apparatus according to an embodiment of the present invention includes encrypting c1 and c2 encrypted by the encrypting apparatus described with reference to FIG. 1 using the following equation (8) And amultiplication operation unit 70 for operating the multiplication operation unit.

<수학식 8>&Quot; (8) &quot;

(c1×c2) mod N(c1 x c2) mod N

도 4(a) 또는 도 4(b)에 도시된 바와 같은 수학식에 따른 연산동작을 수행하는 덧셈 연산부 및/또는 곱셈 연산부는, 도 1을 참조하여 설명한 암호화 장치에 포함되도록 구성되거나, 또는 도 3을 참조하여 설명한 복호화 장치에 포함되도록 구성되거나, 또는 도 1 또는 도 3에서 설명한 장치들과는 무관하게 독립된 장치에 포함되도록 구성될 수 있다.The addition operation unit and / or the multiplication operation unit for performing the arithmetic operation according to the equation shown in FIG. 4 (a) or 4 (b) may be configured to be included in the encryption apparatus described with reference to FIG. 1, 3, or may be configured to be included in an independent apparatus regardless of the apparatuses described in Fig. 1 or Fig.

도 5는 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치 및/또는 복호화 장치가 적용되는 컴퓨터 시스템을 설명하기 위한 도면이다.5 is a diagram illustrating a computer system to which a cantilever type encryption device and / or a decryption device based on the Chinese rest theorem according to an embodiment of the present invention is applied.

도 1 내지 도 4를 참조하여 설명한 본 발명의 실시예들과, 도 6 이하를 참조하여 설명할 본원 발명의 실시예들은, 예를 들면 도 5에 도시된 컴퓨터 시스템에 구현될 수 있다.Embodiments of the present invention described with reference to Figs. 1 to 4 and embodiments of the present invention to be described with reference to Fig. 6 and the following can be implemented in the computer system shown in Fig. 5, for example.

도 5의 컴퓨터 시스템은 스마트 폰이나 PDA와 같은 모바일 기기, 데스크 탑 PC, 타블렛 PC, 또는 서버와 같은 컴퓨터 시스템 중의 어느 하나일 수 있으나, 이들 컴퓨터 시스템에만 한정되는 것이 아니다.The computer system of FIG. 5 may be any one of a mobile device such as a smart phone or PDA, a desktop PC, a tablet PC, or a computer system such as a server, but is not limited to these computer systems.

도 5의 컴퓨터 시스템에는, 도 1 과 도 2 를 참조하여 설명한 본 발명의 암호화 장치나, 도 6 과 도 8을 참조하여 설명한 암호화 방법이 구현될 수 있다.In the computer system of Fig. 5, the encryption apparatus of the present invention described with reference to Figs. 1 and 2 or the encryption method described with reference to Figs. 6 and 8 can be implemented.

다르게는, 도 5의 컴퓨터 시스템에는, 도 3을 참조하여 설명한 본 발명의 복호화 장치나, 도 9를 참조하여 설명한 암호화 방법이 구현될 수 있다.Alternatively, the decryption apparatus of the present invention described with reference to Fig. 3 or the encryption method described with reference to Fig. 9 can be implemented in the computer system of Fig.

또한, 도 5의 컴퓨터 시스템에는, 상술한 본원 발명에 따른 암호화 장치 및 복호화 장치, 및 그 방법들이 모두 구현될 수도 있다.Further, in the computer system of Fig. 5, both the encryption apparatus and the decryption apparatus according to the present invention described above, and the methods may be implemented.

또한, 도 5의 컴퓨터 시스템에는, 도 4를 참조하여 설명한 덧셈 또는 곱셈 동작을 수행하는 연산부가 구현될 수도 있다.The computer system of FIG. 5 may also be implemented with an arithmetic unit that performs the addition or multiplication operation described with reference to FIG.

도 5를 참조하면, 컴퓨터 시스템(100)은, 프로그램 로직(101), 프로세서(103), 저장부(105), 및 메모리(107)를 포함할 수 있다.5, thecomputer system 100 may includeprogram logic 101, aprocessor 103, a storage 105, and amemory 107. [

프로그램 로직(101)은, 컴퓨터에서 실행가능한 코드(Code)의 형태로 구현될 수 있으며, 저장부(105)에 저장되어 있다가 프로세서(103)의 제어하에 메모리(107)에 로딩되어 동작할 수 있다.Theprogram logic 101 may be implemented in the form of a code executable on a computer and may be stored in the storage unit 105 and loaded into thememory 107 under the control of theprocessor 103 for operation have.

예를 들면, 프로그램 로직(101)은, 도 1을 참조하여 설명한 모듈러 연산부(10), 랜덤화부(20), 및 CRT 연산부(30)의 동작을 수행하는 코드(code)를 포함할 수 있으며, 이러한 코드는 메모리(107)에 로딩되어 동작할 수 있다.For example, theprogram logic 101 may include a code for performing operations of themodular operation unit 10, therandomization unit 20, and theCRT operation unit 30 described with reference to Fig. 1, These codes may be loaded into thememory 107 and operated.

다른 예를 들면, 프로그램 로직(101)은, 도 3을 참조하여 설명한 제2모듈러 연산부(40), 및 제2 CRT 연산부(50)의 동작을 수행하는 코드(code)를 포함할 수 있다.For example, theprogram logic 101 may include a code for performing operations of the secondmodular operation unit 40 and the secondCRT operation unit 50 described with reference to FIG.

또 다른 예를 들면, 프로그램 로직(101)은, 도 4를 참조하여 설명한 곱셈 및 덧셈 연산을 수행하는 코드(code)를 포함할 수 있다.As another example, theprogram logic 101 may include code for performing the multiplication and addition operations described with reference to FIG.

다른 예를 들면, 프로그램 로직(101)은, 도 6 및/또는 도 7 동작을 수행하는 코드(code)를 포함할 수 있다.As another example, theprogram logic 101 may include code for performing the operations of Figures 6 and / or 7.

또 다른 예를 들면, 프로그램 로직(101)은, 도 8 및/또는 도 9의 동작을 수행하는 코드(code)를 포함할 수 있다.As another example, theprogram logic 101 may include code for performing the operations of FIG. 8 and / or FIG.

다른 예를 들면, 프로그램 로직(101)은, 파라미터 선택부(미도시)나 비밀키 생성부(미도시)의 동작을 수행하는 코드를 포함할 수 있다.As another example, theprogram logic 101 may include code for performing operations of a parameter selection unit (not shown) and a secret key generation unit (not shown).

이상 설명한 실시예는, 도 1, 도 3, 도 4, 도 6 내지 도 9를 참조하여 설명한 실시예들이 모두 컴퓨터에서 실행가능한 프로그램의 코드로 구현되는 예를 설명하였지만, 상술한 구성요소들 중 적어도 일부는 하드웨어 로직으로도 구현이 가능할 것이다. 예를 들면, 모듈러 연산부(10), 랜덤화부(20), 또는 CRT 연산부(30)는 하드웨어 로직으로도 구현이 가능할 것이다. 다른 구성요소들도 마찬가지로 하드웨어 로직으로도 구현이 가능하다.Although the embodiments described above have been described by way of examples in which all of the embodiments described with reference to Figs. 1, 3, 4, and 6 to 9 are implemented by the code of a program executable in a computer, at least one of the above- Some will be implemented with hardware logic as well. For example, themodular operation unit 10, therandomization unit 20, or theCRT operation unit 30 may be implemented with hardware logic. Other components can be implemented in hardware logic as well.

도 6은 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 방법을 설명하기 위한 도면이다.FIG. 6 is a view for explaining a perceptual encryption method based on Chinese restitution according to an embodiment of the present invention. Referring to FIG.

발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 방법(이하, '본 준동형 암호화 방법'이라고 함)을 도 6을 참조하여 설명하되, 도 5의 컴퓨터 시스템(100)에 적용한 것을 예로 들어서 설명하기로 한다.(Hereinafter referred to as a "base perturbed type encryption method") based on the Chinese rest theorem according to an embodiment of the present invention will be described with reference to FIG. 6 and applied to thecomputer system 100 of FIG. 5 as an example I will explain it.

프로그램 로직(101)은, 메모리(107)에 로딩되어 프로세서(103)의 제어하에, 공개용 정보 및 대칭키(비밀키) 생성 동작을 수행한다(S101). 여기서, 공개용 정보는 도 2에 도시된 정보들 중 적어도 일부이며, 대칭키는 S일 수 있다.Theprogram logic 101 is loaded into thememory 107 and performs operations for generating public information and a symmetric key (secret key) under the control of the processor 103 (S101). Here, the public information is at least a part of the information shown in FIG. 2, and the symmetric key may be S.

이후, 프로그램 로직(101)은, 메모리(107)에 로딩되어 프로세서(103)의 제어하에, 모듈러 연산 동작을 수행한다(S103). 여기서, 모듈러 연산 동작은, 예를 들면, 상술한 수학식 1에 의한 연산 동작일 수 있다.Then, theprogram logic 101 is loaded into thememory 107 and performs a modular operation operation under the control of the processor 103 (S103). Here, the moduler operation may be, for example, the operation of Equation (1).

프로그램 로직(101)은, 메모리(107)에 로딩되어 프로세서(103)의 제어하에, 랜덤화 동작을 수행한다(S105). 여기서, 랜덤화 동작은, 예를 들면, 상술한 수학식 2에 의한 연산 동작일 수 있다.Theprogram logic 101 is loaded into thememory 107 and performs a randomizing operation under the control of the processor 103 (S105). Here, the randomizing operation may be an arithmetic operation according to the above-described equation (2), for example.

프로그램 로직(101)은, 메모리(107)에 로딩되어 프로세서(103)의 제어하에, CRT 연산 동작을 수행한다(S107). 여기서, CRT 연산 동작은, 예를 들면, 상술한 수학식 3에 의한 연산 동작일 수 있다. S107의 동작이 완료되면 암호화문(c)가 출력되며, 후술할 도 7에서의 모듈러 연산(S201)의 입력이 될 수 있다.Theprogram logic 101 is loaded into thememory 107 and performs a CRT operation under the control of the processor 103 (S107). Here, the CRT calculation operation may be, for example, a calculation operation according to the above-described equation (3). When the operation of S107 is completed, the encryption statement (c) is output and can be input to the modular operation (S201) in FIG. 7 to be described later.

도 7은 본 발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 복호화 방법을 설명하기 위한 도면이다.FIG. 7 is a view for explaining a quasi-static decoding method based on the Chinese rest theorem according to an embodiment of the present invention.

발명의 일 실시예에 따른 중국인 나머지 정리에 기반한 준동형 복호화 방법(이하, '본 준동형 암호화 방법'이라고 함)을 도 7을 참조하여 설명하되, 도 5의 컴퓨터 시스템(100)에 적용한 것을 예로 들어서 설명하기로 한다.A quasi-dynamic decoding method based on Chinese restitution according to an embodiment of the present invention (hereinafter referred to as a "baseline-type encryption method") will be described with reference to FIG. 7 and applied to thecomputer system 100 of FIG. 5 as an example I will explain it.

프로그램 로직(101)은, 메모리(107)에 로딩되어 프로세서(103)의 제어하에, 모듈러 연산 동작을 수행한다(S201). 여기서, 모듈러 연산 동작은,, 예를 들면, 상술한 수학식 5에 의한 연산 동작일 수 있다.Theprogram logic 101 is loaded into thememory 107 and performs a modular operation operation under the control of the processor 103 (S201). Here, the modular operation operation may be, for example, the operation operation according to the above-described expression (5).

이후, 프로그램 로직(101)은, 메모리(107)에 로딩되어 프로세서(103)의 제어하에, CRT 연산 동작을 수행한다(S203). 여기서, CRT 연산 동작은, 예를 들면, 상술한 수학식 6에 의한 연산 동작일 수 있다.Thereafter, theprogram logic 101 is loaded into thememory 107 and performs a CRT operation operation under the control of the processor 103 (S203). Here, the CRT calculation operation may be, for example, a calculation operation according to the above-described expression (6).

도 8은 본 발명의 다른 실시예에 따른 중국인 나머지 정리에 기반한 준동형 암호화 장치를 설명하기 위한 도면이다.FIG. 8 is a view for explaining a perceptual type encryption apparatus based on the Chinese rest theorem according to another embodiment of the present invention. FIG.

도 8을 참조하면, 도 1의 실시예의 대체 실시예로서, 도 1의 랜덤화부(20)는 수학식 2에 의한 동작 대신에, 다음의 수학식 9에 의한 랜덤화 동작을 수행할 수 있다.Referring to FIG. 8, as an alternative embodiment of the embodiment of FIG. 1, therandomizer 20 of FIG. 1 may perform a randomization operation according to Equation (9) instead of the operation of Equation (2).

<수학식 9>&Quot; (9) &quot;

A' = E·M + Q
A '= E.m + Q

수학식 2의 결과물과 구별하기 위해서, 수학식 9의 결과물은 A'로서 표기하였으며, A'는 CRT 연산부(30)의 입력이 되며, A'는 CRT 연산부(30)에 의해서 암호화문 c'로서 출력된다. A 'is an input of theCRT operation unit 30, and A' is an encrypted text c 'by theCRT operation unit 30 as a result of Equation (9) .

도 9는 도 8의 실시예에 의해 암호화된 암호화문을 복호화하는 복호화 장치를 설명하기 위한 도면이다.9 is a diagram for explaining a decryption apparatus for decrypting an encrypted statement encrypted by the embodiment of FIG.

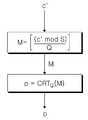
도 9를 참조하면, 도 3의 실시예의 대체 실시예로서, 도 3의 제2 모듈러 연산부(40)는 수학식 5 대신에, 다음의 수학식 10에 의한 모듈러 연산 동작을 수행할 수 있다.Referring to FIG. 9, as an alternative embodiment of the embodiment of FIG. 3, the second modulararithmetic unit 40 of FIG. 3 may perform a modular arithmetic operation according to Equation (10) instead of Equation (5).

<수학식 10>&Quot; (10) &quot;

M =[(c mod S)/Q ］M = [(c mod S) / Q]

여기서, [ ]는 가우스 기호로서 소수점 이하의 값을 버리는 것이다.
Here, [] is a Gaussian symbol to discard a value less than a decimal point.

이후, CRT 연산부 동작은 전술한 도 3의 실시예의 동작과 동일하므로, 생략하기로 한다.Hereinafter, the operation of the CRT operation unit is the same as the operation of the embodiment of FIG. 3 described above, and therefore will not be described.

상기와 같이 본 발명은 비록 한정된 실시예와 도면에 의해 설명되었으나, 본 발명은 상기의 실시예에 한정되는 것은 아니며, 본 발명이 속하는 분야에서 통상의 지식을 가진 자라면 이러한 기재로부터 다양한 수정 및 변형이 가능하다. 그러므로, 본 발명의 범위는 설명된 실시예에 국한되어 정해져서는 아니 되며, 후술하는 특허청구범위뿐 아니라 이 특허청구범위와 균등한 것들에 의해 정해져야 한다.While the present invention has been described with reference to the particular embodiments and drawings, it is to be understood that the invention is not limited to the disclosed embodiments, but, on the contrary, is intended to cover various modifications and equivalent arrangements included within the spirit and scope of the appended claims. This is possible. Therefore, the scope of the present invention should not be limited to the described embodiments, but should be determined by the equivalents of the claims, as well as the claims.

10: 모듈러 연산부20: 랜덤화부
30: CRT 연산부
60: 덧셈 연산부70: 곱셈 연산부
100; 컴퓨터 시스템101: 프로그램 로직
103: 프로세서107: 메모리
109: 저장부10: modular operation unit 20: randomization unit
30: CRT operation unit
60: addition operation unit 70: multiplication operation unit
100; Computer system 101: Program logic
103: Processor 107: Memory
109:

Claims (20)

Translated fromKorean

프로세서 및 메모리를 구비한 컴퓨터에서 수행되는 중국인 나머지 정리에 기반한 준동형 암복호화 방법에 있어서,
평문(p)으로부터 모듈러(M)를 연산하는 단계;
상기 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 단계; 및
랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c)을 생성하는 단계;를 포함하되,
상기 모듈러(M)를 연산하는 단계는,
수학식 M = p mod Q
에 의해 연산하는 단계이며, 여기서, Q = {q_i｜ 1≤i≤k, i와 k는 양의 정수} = {q₁,q₂, ... , q_k}이고, q_i는 서로 소인 양의 정수이며
상기 랜덤화하는 단계는,
수학식 A = M + E·Q
에 의해 연산하는 단계이며, 여기서, E= {e_i｜ 1≤i≤k, i와 k는 양의 정수}인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.A quasi-static encryption / decryption method based on Chinese rest theorem performed in a computer having a processor and a memory,
Computing modular (M) from plaintext (p);
Adding the error (E) to the modulator (M) and randomizing the modulus (M); And
Applying a Chinese restorative (CRT) to the randomized modular (A) to generate an encryption statement (c)
The step of calculating the modulus (M)
Equation M = p mod Q
Where q = {q_i |₁ | i k, i and k are positive integers} = {q₁ , q₂ , ..., q_k }, and q_i are positive integers
Wherein the randomizing comprises:
Equation A = M + E Q
And the step of computing by, where, E = | homomorphism decryption method based on the Chinese Remainder Theorem, characterized in that {e_i 1≤i≤k, i and k is a positive integer}.삭제delete삭제delete제1항에 있어서,
상기 암호화문을 생성하는 단계는,
수학식 c = CRT_S(A)
에 의해 연산하는 단계이며, 여기서 CRT는 중국인의 나머지 정리이고, S= s_i｜ 1≤i≤k, i와 k는 양의 정수} 로서 키(Key)인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.The method according to claim 1,
Wherein the step of generating the encryption statement comprises:
The equation c = CRT_S (A)
, Wherein the CRT is the remaining theorem of the Chinese, and S = s_i |₁ | i k, where i and k are positive integers} A method for perpetual cancer encryption.제4항에 있어서,
상기 q_i의 길이는 d 이고,
상기 e_i의 길이는 2·λ이고,
상기 λ는 에러의 크기를 정의하기 위한 시큐어리티 파라미터이고,
상기 k는 상기 키(Key)의 갯수를 정의하는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.5. The method of claim 4,
The length of q_i is d,
The length of e_i is 2 · λ,
Is the security parameter for defining the magnitude of the error,
Wherein the k defines the number of the keys.제5항에 있어서,
수학식 (T+1)·(2·λ + d) 〈 η 를 만족하도록, λ , d, 및 η 가 정의되며,
여기서, T는 곱셈의 횟수를 의미하며, η는 Si의 길이인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.6. The method of claim 5,
Λ, d, and η are defined so as to satisfy the following equation (T + 1) · (2 · λ + d) <η,
Where T is the number of multiplications and η is the length of the Si.제1항에 있어서,
상기 중국인 나머지 정리에 기반한 준동형 암복호화 방법은,
평문(p2)으로부터 모듈러(M)를 연산하는 단계("제2 연산단계"라고 함);
상기 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 단계("제2 랜덤화단계"라고 함);
에러(E)가 부가되어 랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c2)을 생성하는 단계("제2 암호화문 생성단계"라고 함); 및
수학식 (c1+c2) mod N
에 의해 상기 c1과 상기 c2의 덧셈을 수행하는 단계;를 더 포함하며,
상기 c1은 상기 평문(p)으로부터, 상기 모듈러를 연산하는 단계, 상기 랜덤화하는 단계, 및 상기 암호화문을 생성하는 단계를 순차적으로 수행하여 생성된 암호화문이고, 상기 c2는, 제2 연산단계, 제2 랜덤화단계, 및 상기 제2암호화문 생성단계의 수행결과 생성된 암호화문이며, N은 다음 수학식

에 의해 정의되는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.The method according to claim 1,
According to the Chinese restorative-based quasi-
Calculating the modulus M from the plaintext p2 (referred to as "second calculation step");
Adding the error E to the modulator M to randomize it (referred to as "second randomization step");
(Referred to as "second encryption statement generation step") by applying the Chinese restitution (CRT) to the randomized modular A with the addition of an error (E) to generate an encryption statement c2; And
(C1 + c2) mod N
And performing the addition of the c1 and the c2 by the adder,
Wherein c1 is an encryption statement generated by sequentially executing the moduler calculation, the randomization, and the encryption statement from the plaintext (p), and c2 is a second operation step , A second randomization step, and an encryption statement generated as a result of performing the second encryption statement generation step,

Wherein the method is defined by the Chinese restorative.제7항에 있어서,
수학식 (c1×c2) mod N
에 의해 상기 c1과 상기 c2의 곱셈을 수행하는 단계;를 더 포함하는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.8. The method of claim 7,
(C1 x c2) mod N
And performing a multiplication of the c1 and the c2 by the second residual theorem.제1항에 있어서,
상기 랜덤화하는 단계는,
수학식 A = E·M + Q
에 의해 연산하는 단계이며, 여기서, E= {e_i｜ 1≤i≤k, i와 k는 양의 정수}인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.The method according to claim 1,
Wherein the randomizing comprises:
Equation A = E M + Q
And the step of computing by, where, E = | homomorphism decryption method based on the Chinese Remainder Theorem, characterized in that {e_i 1≤i≤k, i and k is a positive integer}.제4항에 있어서,
상기 암호화문(c)를 복호화하는 단계;를 더 포함하며,
상기 복호화하는 단계는,
수학식 M = (c mod S) mod Q
에 의해 모듈러를 계산하는 단계; 및
수학식 p = CRT_Q(M)
에 의해 중국인 나머지 정리(CRT)를 적용하여 평문(p)을 생성하는 단계;를 포함하는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암복호화 방법.5. The method of claim 4,
And decrypting the encryption statement (c)
Wherein the step of decrypting comprises:
M = (c mod S) mod Q
&Lt; / RTI &gt; And
The equation p = CRT_Q (M)
And generating a plaintext (p) by applying a Chinese restitution (CRT) to the plaintext (p).평문(p)으로부터 모듈러(M)를 연산하는 모듈러 연산부;
상기 모듈러(M)에 에러(E)를 부가하여 랜덤화하는 랜덤화부; 및
랜덤화된 모듈러(A)에 대하여 중국인 나머지 정리(CRT)를 적용하여 암호화문(c)을 생성하는 CRT 연산부;를 포함하며,
상기 모듈러 연산부는,
수학식 M = p mod Q
에 의해 연산하며, 여기서, Q = {q_i｜ 1≤i≤k, i와 k는 양의 정수} = {q₁,q₂, ... , q_k}이고, q_i는 서로 소인 양의 정수이며,
상기 랜덤화부는,
수학식 A = M + E·Q
에 의해 연산하며, 여기서, E= {e_i｜ 1≤i≤k, i와 k는 양의 정수}인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암호화 장치.A modular operation unit for calculating a modulo M from the plain text p;
A randomizer for randomizing the modulo M with an error E; And
And a CRT operation unit for applying the Chinese remaining theorem (CRT) to the randomized moduler (A) to generate an encryption statement (c)
Wherein the modular arithmetic unit comprises:
Equation M = p mod Q
Where q = {q_i |₁ | i k, i and k are positive integers} = {q₁ , q₂ , ..., q_k }, and q_i are positive integers,
The randomizer,
Equation A = M + E Q
, Where E = {e_i |₁ | i k, where i and k are positive integers}.삭제delete삭제delete제11항에 있어서,
상기 CRT 연산부는,
수학식 c = CRT_S(A)
에 의해 연산하며, 여기서 CRT는 중국인의 나머지 정리이고, S= s_i｜ 1≤i≤k, i와 k는 양의 정수} 로서 키(Key)이고,
상기 q_i의 길이는 d 이고, 상기 e_i의 길이는 2·λ이고,
상기 λ는 에러의 크기를 정의하기 위한 시큐어리티 파라미터이고,
상기 k는 상기 키(Key)의 갯수를 정의하는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암호화 장치.12. The method of claim 11,
The CRT operation unit,
The equation c = CRT_S (A)
Where CRT is the rest of the Chinese theorem, S = s_i |₁ | i k, i and k are positive integers}
The length of q_i is d, the length of e_i is 2 · lambda,
Is the security parameter for defining the magnitude of the error,
And the k defines a number of the keys.제14항에 있어서,
수학식 (T+1)·(2·λ + d) 〈 η 를 만족하도록, λ , d, 및 η 가 정의되며,
여기서, T는 곱셈의 횟수를 의미하며, η는 Si의 길이인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암호화 장치.15. The method of claim 14,
Λ, d, and η are defined so as to satisfy the following equation (T + 1) · (2 · λ + d) <η,
Where T denotes the number of times of multiplication, and? Is the length of Si.제11항에 있어서,
상기 평문(p)으로부터, 상기 모듈러 연산부, 상기 랜덤화부, 및 상기 CRT 연산부의 순차적 동작에 의해 생성된 암호화문이 c1라고 하고,
평문(p2)으로부터, 상기 모듈러 연산부, 상기 랜덤화부, 및 상기 CRT 연산부의 순차적 동작에 의해 생성된 암호화문이 c2라고 할 때,
수학식 (c1+c2) mod N
에 의해 c1과 c2의 덧셈이 수행될 수 있으며, 여기서 N은 다음 수학식

에 의해 정의되는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암호화 장치.12. The method of claim 11,
The encrypted statement generated by the sequential operation of the modular operation unit, the randomization unit, and the CRT operation unit from the plain text p is c1,
And the encrypted statement generated by the sequential operation of the modular operation unit, the randomization unit, and the CRT operation unit from the plain text p2 is c2,
(C1 + c2) mod N
Lt; RTI ID = 0.0 &gt; c1 &lt; / RTI &gt; and c2 may be performed by &lt;

Wherein the encryption key is defined by the Chinese restorative.제16항에 있어서,
수학식 (c1×c2) mod N
에 의해 곱셈이 수행될 수 있는 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암호화 장치.17. The method of claim 16,
(C1 x c2) mod N
And the multiplication can be performed by the Chinese restorative.제11항에 있어서,
상기 랜덤화부는,
수학식 A = E·M + Q
에 의해 연산하며, 여기서, E= {e_i｜ 1≤i≤k, i와 k는 양의 정수}인 것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 암호화 장치.12. The method of claim 11,
The randomizer,
Equation A = E M + Q
, Where E = {e_i |₁ | i k, where i and k are positive integers}.암호화문(c)을 복호화하는 복호화부;를 포함하며,
상기 복호화부는
수학식 M = (c mod S) mod Q
에 의해 모듈러를 계산하고,
수학식 p = CRT_Q(M)
에 의해 중국인 나머지 정리(CRT)를 적용하여 평문(p)을 생성하며,
상기 암호화문(c)는, 제11항, 제14항, 및 제15항 중 어느 하나의 항에 의해 암호화된 암호화문 인것을 특징으로 하는 중국인 나머지 정리에 기반한 준동형 복호화 장치.And a decryption unit for decrypting the encryption statement (c)
The decoding unit
M = (c mod S) mod Q
Lt; RTI ID = 0.0 &gt; modulo &lt;
The equation p = CRT_Q (M)
(P) by applying the Chinese Residual Theorem (CRT)
Wherein the encryption statement (c) is an encryption statement encrypted by any one of claims 11, 14, and 15.제1항 및, 제4항 내지 제10항 중 어느 한 항의 방법을 실행하기 위한 프로그램을 기록한 것을 특징으로 하는 컴퓨터로 판독 가능한 기록 매체.A computer-readable recording medium having recorded thereon a program for executing the method according to any one of claims 1 to 10.

Images