JP2004287333A - Distributed computing apparatus and distributed computing system - Google Patents

Abstract

<P>PROBLEM TO BE SOLVED: To provide a distributed computing apparatus and a distributed computing system realizing reduction of the amount of arithmetic operations in distributed computing. <P>SOLUTION: The distributed computing apparatus is provided with a distributed computing section 305-i which performs distributed computing by using distributed information generated from n pieces of secret information by a (L, k, n) ramp threshold secret sharing scheme. When the member ID possessed by the distributed computing apparatus is set to m<SB>p</SB>(p≤n) and the distributed information used by the distributed computing section 305-i for distributed computing is set to Y<SB>p</SB>, the distributed information is the information generated as follows. When a value X on an extension field GF(q<SP>L</SP>) which is obtained by extending a finite field GF(q) by L-th order and whose generator is α is represented as X=ΣX<SB>j</SB>α<SP>j</SP>; 0≤j≤L-1, a polynomial h<SB>x</SB>(x) on a (k-1)th order finite field GF(q) which satisfies h<SB>x</SB>(I<SB>j</SB>)=X<SB>j</SB>; 0≤j≤L-1 is generated. The information is generated by computing, from this polynomial h<SB>x</SB>(x), by computing the value on the finite field GF(q) wherein Y<SB>p</SB>=h<SB>x</SB>(m<SB>p</SB>). <P>COPYRIGHT: (C)2005,JPO&NCIPI

Description

Translated fromJapanese

【０００１】
【発明の属する技術分野】
本発明は、例えば、複数の分散計算装置が保持する秘密情報から生成された分散情報を用いる分散計算方法を実施する分散計算システム、及び、この分散計算システムの一部を構成する分散計算装置に関するものである。
【０００２】
【従来の技術】
現在、暗号の技術分野では、マルチパーティ・プロトコルと呼ばれる、分散計算方法が実現されている。ここで、一般的なマルチパーティ・プロトコルについて説明する。今、ｎ人のメンバ（ｎ個の演算装置としてもよい）より構成されるネットワークがあるとして、メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）を持つそれぞれのメンバが、他のメンバには知られたくない秘密情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）を保持しているものとする。ある関数ｆが与えられたときに、各メンバは各自の秘密情報Ｘ_ｉを秘密にしたまま、その関数Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）を計算して、求めるべき値Ｚを算出しようとする。なお、関数ｆは、例えば、すべての秘密情報Ｘ_ｉを足し合わせる関数Ｚ＝Ｘ_１＋Ｘ_２＋…＋Ｘ_ｎであったり、すべての秘密情報Ｘ_ｉのうち最大の値を出力する関数Ｚ＝ｍａｘ｛Ｘ_１，Ｘ_２，…，Ｘ_ｎ｝であったりする。
【０００３】
このように、各メンバが、ネットワーク上で、各自の秘密情報Ｘ_ｉ自体を一切漏らさないで、お互いになんらかの通信を行い、最終的に値Ｚを計算し得る機能を実現するプロトコルを、関数ｆに関するマルチパーティ・プロトコルと呼ぶ。上記機能は、関数ｆの計算を行う信頼できる第三者のセンターを設け、各メンバが各自の秘密情報をこのセンターへ秘密に送信することにより実現できるが、ここでは、そのようなセンターがない場合を説明する。
【０００４】
図２は、マルチパーティ・プロトコルの概念説明図である。図２の例においては、メンバ（参加者）人数を３人とし、それぞれのメンバＩＤ（ＩＤ情報）をＡ，Ｂ，Ｃとし、それぞれが保持する秘密情報をＸ_Ａ，Ｘ_Ｂ，Ｘ_Ｃとする。メンバＩＤ＿Ａ，Ｂ，Ｃ、及び、秘密情報Ｘ_Ａ，Ｘ_Ｂ，Ｘ_Ｃなどの値は、ある有限体ＧＦ（ｑ）（ｑは、素数又は素数のべき乗の値）上の値とし、マルチパーティ・プロトコルで分散計算しようとする関数ｆ（Ｘ_Ａ，Ｘ_Ｂ，Ｘ_Ｃ）内の演算（加算及び乗算）は、有限体ＧＦ（ｑ）上の演算とする。以降、特に断りがない限り、演算は、有限体ＧＦ（ｑ）上で行うものとする。
【０００５】
関数ｆ（Ｘ_Ａ，Ｘ_Ｂ，Ｘ_Ｃ）のマルチパーティ・プロトコルによる分散計算を行う際に、まず、各メンバは、自分の保持する秘密情報を（ｋ，ｎ）しきい値秘密分散法で分散する（図２に符号▲１▼で示される処理）。（ｋ，ｎ）しきい値秘密分散法は、情報Ｘをｎ個に分散させ、そのｎ個の分散情報のうちｋ個（ｋ≦ｎ）の分散情報が集まれば、情報Ｘを復元することができ、ｋ−１個以下の分散情報しか集まらないときには、情報Ｘについてなんら知ることができない、といった秘密分散法である。図２の場合には、ｎは３であり、ｋは２又は３である。
【０００６】
次に、各メンバは、自分の秘密情報を分散した分散情報をそれぞれ他のメンバに配布する（図２に符号▲２▼で示される処理）。これらの分散情報を配布する際には、どの２人のメンバ間にも、その２人のメンバ以外には通信内容を秘密とすることができる秘密通信路が確立されているものとする。次に、それら配布された分散情報を用いて、関数ｆ（Ｘ_Ａ，Ｘ_Ｂ，Ｘ_Ｃ）で定められる計算方法で、各メンバが分散計算を行う（図２に符号▲３▼で示される処理）。この分散計算の際には、各メンバ同士が情報交換を行うこともある。この各メンバが保持する分散計算の計算結果Ｚ’_Ａ，Ｚ’_Ｂ，Ｚ’_Ｃはそれぞれ、最終的な計算結果Ｚ＝ｆ（Ｘ_Ａ，Ｘ_Ｂ，Ｘ_Ｃ）を秘密分散した分散情報となっている。したがって、最終的に、各メンバが持っている分散計算の計算結果Ｚ’_Ａ，Ｚ’_Ｂ，Ｚ’_Ｃを集め、（ｋ，ｎ）しきい値秘密分散法の秘密再構成を行うと、最終的な計算結果Ｚを得ることができる（図２の符号▲４▼で示される処理）。
【０００７】
次に、図２に示されるマルチパーティ・プロトコルを、ｎ人のメンバに拡張した場合について説明する。各メンバのメンバＩＤをｍ_ｉ（ｉ＝１，２，…，ｎ）、メンバＩＤがｍ_ｉであるメンバの保持する秘密情報をＸ_ｉ（ｉ＝１，２，…，ｎ）とする。各メンバは、各自が保持する秘密情報を（ｋ，ｎ）しきい値秘密分散法で分散する。ここでの（ｋ，ｎ）しきい値秘密分散法は、Ｓｈａｍｉｒ法（シャミア法：Ｓｈａｍｉｒ’ｓ ｍｅｔｈｏｄ）（例えば、非特許文献１参照）を用いるものとする。
【０００８】
メンバＩＤがｍ_ｉであるメンバは、次式（１）のようなｋ−１次多項式ｈ_ｘｉ（ｘ）を生成し、この式を用いて秘密情報を分散する。
【数７】

上記式（１）において、Ｒ_ｘｉ，１，Ｒ_ｘｉ，２，…，Ｒ_{ｘｉ，ｋ−１}は、メンバＩＤがｍ_ｉであるメンバが決める乱数であり、有限体ＧＦ（ｑ）上の値からｋ−１個選択されたものである。
【０００９】
メンバＩＤがｍ_ｉであるメンバで計算され、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎ）であるメンバに配布される分散情報を、Ｙ_ｉ，ｐと表わす場合に、分散情報Ｙ_ｉ，ｐは、上記式（１）の関数を用いて、次式（２）のように計算することができる。
【数８】

【００１０】
各メンバが他のメンバから分散情報を受け取ると、結果として、メンバＩＤがｍ_ｉであるメンバは、ｎ個の分散情報Ｙ_１，ｉ，Ｙ_２，ｉ，…，Ｙ_ｎ，ｉを保持することになる。これら各メンバが保持する分散情報Ｙ_１，ｉ，Ｙ_２，ｉ，…，Ｙ_ｎ，ｉを用いて、すなわち、各メンバが協力して、所望の分散計算Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）を行う。
【００１１】
ここでは、各メンバが行う分散計算として、分散加算の場合と分散乗算の場合を説明する。上記式（１）に示されるような多項式を用いて、秘密情報Ａ及びＢを秘密分散させ、メンバＩＤがｍ_ｉであるメンバが、分散情報ａ_ｉ及びｂ_ｉを既に持っている状態を考える。この場合、秘密情報Ａ及びＢと分散情報ａ_ｉ及びｂ_ｉとの関係は、次式（３）及び（４）のようになる。
【数９】

ここで、Ｒ_Ａ，ｊ（ｊ＝１，２，…，ｋ−１）及びＲ_Ｂ，ｊ（ｊ＝１，２，…，ｋ−１）は乱数である。
【００１２】
各メンバが分散情報ａ_ｉ及びｂ_ｉから計算を行って、秘密情報Ｃ（＝Ａ＋Ｂ）を秘密分散させた値ｃ_ｉをメンバＩＤがｍ_ｉであるメンバが持つようにする計算処理を「分散加算」と呼ぶ。また、各メンバが分散情報ａ_ｉ及びｂ_ｉから計算を行って、秘密情報Ｃ（＝Ａ×Ｂ）を秘密分散させた値ｃ_ｉをメンバＩＤがｍ_ｉであるメンバが持つようにする計算処理を「分散乗算」と呼ぶ。さらに、ある定数Ｄと秘密情報Ａとの乗算結果Ｃ（＝Ｄ×Ａ）を秘密分散させた値ｃ_ｉをメンバＩＤがｍ_ｉであるメンバが持つようにする計算処理を「分散定数乗算」と呼ぶ。上記のような、任意の分散情報の分散加算、分散定数乗算、及び、分散乗算が可能になると、加算、定数乗算、及び、乗算を含む任意の関数Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）は、分散計算が可能となる。以降では、上記式（１）のような多項式により秘密情報Ａ及びＢを秘密分散させ、各メンバが、分散情報ａ_ｉ及びｂ_ｉを既に持っている状態を考え、各メンバが分散情報ａ_ｉ及びｂ_ｉから計算を行って、Ｃ＝ｆ（Ａ，Ｂ）を秘密分散させた値ｃ_ｉを求める処理を説明する。
【００１３】
まず、マルチパーティ・プロトコルにおける分散加算（加算計算）を次式（５）を用いて説明する。
Ｃ＝ｆ（Ａ，Ｂ）＝Ａ＋Ｂ …（５）
メンバＩＤがｍ_ｉであるメンバは、すでに秘密情報Ａ及びＢの分散情報ａ_ｉ及びｂ_ｉを持っているものとする。これら分散情報ａ_ｉ及びｂ_ｉは、任意のメンバの秘密情報の分散情報（Ｙ_１，ｉ，Ｙ_２，ｉ，…，Ｙ_ｎ，ｉ）のいずれかでもよいし、分散計算した途中結果の値でもよい。分散加算においては、分散情報同士の足し算を行うことで、計算結果Ｃの分散情報ｃ_ｉ（ｉ＝１，２，…，ｎ）を得ることができる。例えば、メンバＩＤがｍ_ｉであるメンバは、次式（６）のような計算を行い、計算結果ｃ_ｉを得る。
ｃ_ｉ＝ａ_ｉ＋ｂ_ｉ …（６）
【００１４】
次に、マルチパーティ・プロトコルにおける分散定数乗算（定数乗算計算）を次式（７）を用いて説明する。
Ｃ＝ｆ（Ａ）＝Ｄ×Ａ …（７）
ここで、Ｄは、有限体ＧＦ（ｑ）上の定数であり、どのメンバにも既知な値とする。例えば、メンバＩＤがｍ_ｉであるメンバは、次式（８）のような計算を行い、計算結果ｃ_ｉを得る。
ｃ_ｉ＝Ｄ×ａ_ｉ …（８）
【００１５】
次に、マルチパーティ・プロトコルにおける分散乗算（乗算計算）を次式（９）を用いて説明する。
Ｃ＝ｆ（Ａ，Ｂ）＝Ａ×Ｂ …（９）
分散乗算においては、次の２通りの方法があり、ここでの説明では、それらの方式をそれぞれ方式▲１▼、方式▲２▼と記述することにする。方式▲１▼では、各メンバは、次のようなステップＳ１０１〜Ｓ１０３を行う。ここでは、メンバＩＤがｍ_ｉであるメンバが実行する処理を記述する。ステップＳ１０１において、分散情報同士の乗算ｃ_ｉ，ｉ＝ａ_ｉ×ｂ_ｉを行う。
【００１６】
次のステップＳ１０２において、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの。）である他のメンバの値との乗算ａ_ｉ×ｂ_ｐ及びａ_ｐ×ｂ_ｉの結果に相当するものが得られるように通信及び計算処理をする。すなわち、次式（１０）となるような、メンバＩＤがｍ_ｉであるメンバが乗算結果ｃ_ｉ，ｐを持つことができ、メンバＩＤがｍ_ｐであるメンバが乗算結果ｃ_ｐ，ｉを持つことができるように、計算と通信を行う。
ａ_ｉ×ｂ_ｐ＋ａ_ｐ×ｂ_ｉ＝ｃ_ｉ，ｐ＋ｃ_ｐ，ｉ …（１０）
このように、他のメンバとの情報のやりとりを行うことにより、他のメンバの値との乗算ａ_ｉ×ｂ_ｐ及びａ_ｐ×ｂ_ｉの結果に相当する式（１０）が得られるようにするが、他のメンバの値ａ_ｐ及びｂ_ｐが分からないように、また、自分の値ａ_ｉ及びｂ_ｉが、他のメンバに分からないように、紛失通信を行う。「紛失通信」とは、送信側が、Ｍ個の情報を符号化（暗号化）して送信するが、受信側においては、そのうち一つしか受け取る（意味のあるように復号が可能となる）ことができず、また、送信側においては、受信側がどの情報を受け取った（意味のあるように復号が可能となった）かを知ることができない通信方法をいう。
【００１７】
次の、ステップＳ１０３においては、ステップＳ１０２の結果に、メンバＩＤから計算される係数ｒ_ｐを乗算して足し合わせることにより、次式（１１）及び（１２）で示される、乗算結果Ｃの分散情報ｃ_ｉ（ｉ＝１，２，…，ｎ）を得る。
【数１０】

【００１８】
また、方式▲２▼では、各メンバは、次のようなステップＳ２０１〜Ｓ２０５を行う。ここでは、メンバＩＤがｍ_ｉであるメンバが実行する処理を記述する。ステップＳ２０１において、分散情報同士の乗算ｃ’_ｉ＝ａ_ｉ×ｂ_ｉを行う。
【００１９】
次のステップＳ２０２において、ステップＳ２０１で求めたｃ’_ｉを（ｋ’，ｎ）しきい値秘密分散法を用いて分散し、分散情報ｃ’_ｉ，ｐ（ｐ＝１，２，…，ｎでｐ≠ｉであるもの）をメンバＩＤがｍ_ｐである他のメンバへ配布する。また、他のメンバから、分散情報ｃ’_ｐ，ｉ（ｐ＝１，２，…，ｎでｐ≠ｉであるもの）を受け取る。
【００２０】
次のステップＳ２０３において、Ｃ’_ｉ＝（ｃ’_１，ｉ、ｃ’_２，ｉ、…、ｃ’_ｎ，ｉ）に変換行列ＥＰＥ^−１を掛け合わせることにより、Ｄ_ｉ＝（ｄ_１，ｉ、ｄ_２，ｉ、…、ｄ_ｎ，ｉ）に変換する。行列Ｅは、メンバＩＤから計算される行列であり、
Ｅ＝（ｅ_ｉｊ）＝（ｍ_ｉ^ｊ−１） （ｉ，ｊ＝１、２、…、ｎ）
となるようなｎ×ｎ行列であり、その逆行列をＥ^−１とする。また、行列Ｐは、次式のようにベクトルのｋ＋１番目以降の値を０とするような変換を行うｎ×ｎ行列である。
Ｐ（ｘ_１、ｘ_２、…、ｘ_ｎ）^ｔ
＝（ｘ_１、ｘ_２、…、ｘ_ｋ、０、…、０） …（８０）
【００２１】
次のステップＳ２０４において、ステップＳ２０３で求めたｄ_ｐ，ｉ（ｐ＝１，２，…，ｎでｐ≠ｉであるもの）を、メンバＩＤがｍ_ｐである他のメンバへ配布する。また、他のメンバから、計算結果ｄ_ｉ，ｐ（ｐ＝１，２，…，ｎでｐ≠ｉであるもの）を受け取る。
【００２２】
次のステップＳ２０５において、ステップＳ２０３、Ｓ２０４で得たｄ_ｉ，ｐ（ｐ＝１，２，…，ｎ）を分散情報として、（ｋ’、ｎ）しきい値秘密分散法の秘密再構成を行うことにより、乗算結果Ｃの分散情報ｃ_ｉ（ｉ＝１、２、…、ｎ）を得る。
【００２３】
このように分散乗算においては、分散加算の場合のように簡単には計算できないが、紛失通信を用いると計算可能となる。上記のように、各メンバ同士が秘密通信、紛失通信を行って計算処理をすると、入力値を公開せずに、与えられた関数ｆ（加算と乗算で構成される関数）の計算を行うことができる。
【００２４】
Ｓｈａｍｉｒ法に代表される通常の（ｋ，ｎ）しきい値秘密分散法においては、秘密情報をｎ個の分散情報に符号化し、ｋ（≦ｎ）個以上の分散情報が集まれば、もとの秘密情報を復元することができるが、ｋ−１個以下であると、その秘密情報については全く知ることができないという性質を、多項式補間を用いることにより実現している。
【００２５】
具体的には、次式（１３）のようなｋ−１次多項式ｈ_Ｓ（ｘ）を用いてもとの秘密情報を分散する。
【数１１】

ここで、Ｓは、もとの秘密情報であり、Ｒ_Ｓ，１，Ｒ_Ｓ，２，…，Ｒ_{Ｓ，ｋ−１}は、分配者が決める乱数である。
【００２６】
分配するｎ人の各メンバには、メンバＩＤとして、ｍ_１，ｍ_２，…，ｍ_ｎが付与されているものとし、メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）に対する分散情報Ｓ_ｉは、上記式（１３）を用いて、次式（１４）のように計算することができる。
【数１２】

【００２７】
ここでは、メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）、秘密情報Ｓ、分散情報Ｓ_ｉ（ｉ＝１，２，…，ｎ）、乱数Ｒ_Ｓ，１，Ｒ_Ｓ，２，…，Ｒ_{Ｓ，ｋ−１}などの値は、それぞれ、ある有限体ＧＦ（ｑ）（ｑは、素数又は素数のべき乗の値）上の値とし、演算（加算及び乗算）は、それぞれ、有限体ＧＦ（ｑ）上の演算とする。また、上記式（１３）より、次式（１５）という関係式が成り立つ。
ｈ_Ｓ（０）＝Ｓ …（１５）
【００２８】
もとの秘密情報Ｓを、各メンバに配布した分散情報から再構成する場合には、分散情報を分配したメンバのうち、ｔ人（ｋ≦ｔ）を集めてきて、そのメンバＩＤと分散情報を持ち寄り、次式（１６）及び（１７）で計算することで達成できる。
【数１３】

ここで、ｍ’_１，ｍ’_２，…，ｍ’_ｔは、集まったメンバのメンバＩＤであり、Ｓ’_１，Ｓ’_２，…，Ｓ’_ｔは、集まったメンバが保持する分散情報である。
【００２９】
このＳｈａｍｉｒ法に代表される通常の（ｋ，ｎ）しきい値秘密分散法においては、もとの秘密情報Ｓとその分散情報Ｓ_ｉ（ｉ＝１，２，…，ｎ）は、ともに有限体ＧＦ（ｑ）上の値であり、分散情報Ｓ_ｉ（ｉ＝１，２，…，ｎ）の情報量は、もとの秘密情報Ｓの情報量よりも小さくすることができない性質がある。
【００３０】
【非特許文献１】
岡本龍明他、「現代暗号」（産業図書）、第２１４−２１６ページ及び第２２７−２３６ページ
【非特許文献２】
ジー・アール・ブラクレイ及びキャサリン・メドウズ、「セキュリティ・オブ・ランプ・スキームズ」、プロスィージャ・オブ・クリプト’８８、レクチャー・ノーツ・イン・コンピュータ・サイエンス４０３、スプリンガー・ベルラグ、、第２４２−２６８ページ、１９９０年（Ｇ．Ｒ．ＢＬＡＫＬＥＹ ＡＮＤ ＣＡＴＨＥＲＩＮＥ ＭＥＡＤＯＷＳ，“ＳＥＣＵＲＩＴＹ ＯＦ ＲＡＭＰ ＳＣＨＥＭＥＳ”， ＰＲＯＣ． ＯＦ ＣＲＹＰＴＯ ’８８， ＬＥＣＴＵＲＥ ＮＯＴＥＳ ＩＮ ＣＯＭＰＵＴＥＲ ＳＣＩＥＮＣＥ ４０３， ＳＰＲＩＮＧＥＲ−ＶＥＲＬＡＧ， ｐｐ． ２４２−２６８ （１９９０）
【００３１】
【発明が解決しようとする課題】
しかしながら、上記した従来のマルチパーティ・プロトコルによる分散計算においては、通常の（ｋ，ｎ）しきい値秘密分散法を用いて、それぞれの秘密情報の秘密分散を行っているため、各メンバにおける分散計算においては、その秘密情報と同じ情報量、すなわち、同じ大きさの有限体上における演算を行う必要がある。このため、秘密情報をｎ人に分散して演算しているにもかかわらず、メンバそれぞれの分散演算処理における、演算量、演算回路に必要な回路規模、演算に必要な記憶容量、演算時間等の演算コストを下げることができないといった問題があった。
【００３２】
そこで、本発明は上記したような従来技術の課題を解決するためになされたものであり、その目的は、分散計算における演算量を低減することができる分散計算装置及び分散計算システムを提供することである。
【００３３】
【課題を解決するための手段】
本発明に係る分散計算装置は、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により１又は複数個（通常は２個以上であるが、１個の場合も有りうる。）の秘密情報から生成された分散情報を用いて、分散計算する分散計算手段を有し、この分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、上記分散計算手段が分散計算に用いる分散情報をＹ_ｐとしたときに、上記分散情報は、有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαである拡大体ＧＦ（ｑ^Ｌ）上の値を次式Ｘ＝ΣＸ_ｊα^ｊ；０≦ｊ≦Ｌ−１を満たすＸとするときに、次式ｈ_Ｘ（Ｉ_ｊ）＝Ｘ_ｊ；０≦ｊ≦Ｌ−１を満たすｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成し、上記多項式ｈ_Ｘ（ｘ）から、Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）なる有限体ＧＦ（ｑ）上の値を計算することによって生成された情報であることを特徴としている。
【００３４】
また、本発明に係る他の分散計算装置は、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により、秘密情報から分散情報を生成する秘密分散計算手段を有し、上記秘密分散計算手段が、上記分散情報が配布される他の分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、メンバＩＤがｍ_ｐである上記分散情報をＹ_ｐとし、有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαである拡大体ＧＦ（ｑ^Ｌ）上の値を次式Ｘ＝ΣＸ_ｊα^ｊ；０≦ｊ≦Ｌ−１を満たすＸとするときに、次式ｈ_Ｘ（Ｉ_ｊ）＝Ｘ_ｊ；０≦ｊ≦Ｌ−１を満たすｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成する多項式生成手段と、上記多項式ｈ_Ｘ（ｘ）から、Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）なる有限体ＧＦ（ｑ）上の値を計算することによって生成する分散情報生成手段とを有することを特徴としている。
【００３５】
また、本発明に係る他の分散計算装置は、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により１又は複数個（通常は２個以上であるが、１個の場合も有りうる。）の秘密情報から生成された分散情報を用いて、分散計算する分散計算手段を有し、この分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、上記分散計算手段が分散計算に用いる分散情報をＹ_ｐとしたときに、上記分散情報は、
有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαで生成多項式がｇ（ｘ）である拡大体ＧＦ（ｑ^Ｌ）上の値を次式
Ｘ＝ΣＸ_ｊ α^ｊ；０≦ｊ≦Ｌ−１
で表されるＸとし、Ｒ_Ｘ，ｊ（０≦ｊ≦ｋ−Ｌ−１）を乱数とするときに、次式
【数１４】

で表されるｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成し、
上記多項式ｈ_Ｘ（ｘ）から、
Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）
なる有限体ＧＦ（ｑ）上の値を計算することによって生成された情報であることを特徴としている。
【００３６】
また、本発明に係る他の分散計算装置は、ランプ型（Ｌ、ｋ、ｎ）しきい値秘密分散法により、秘密情報から分散情報を生成する秘密分散計算手段を有し、上記秘密分散計算手段が、上記分散情報が配布される補記あの分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、メンバＩＤがｍ_ｐである上記分散情報をＹ_ｐとし、有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαで生成多項式がｇ（ｘ）である拡大体ＧＦ（ｑ^Ｌ）上の値を次式
Ｘ＝ΣＸ_ｊ α^ｊ；０≦ｊ≦Ｌ−１
で表されるＸとし、Ｒ_Ｘ，ｊ（０≦ｊ≦ｋ−Ｌ−１）を乱数とするときに、次式
【数１５】

で表されるｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成する多項式生成手段と、上記多項式ｈ_Ｘ（ｘ）から、Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）なる有限体ＧＦ（ｑ）上の値を計算することによって生成する分散情報生成手段とを有することを特徴としている。
【００３７】
【発明の実施の形態】
本発明においては、従来技術のマルチパーティ・プロトコルによる分散計算において用いていた、Ｓｈａｍｉｒ法に代表される通常の（ｋ，ｎ）しきい値秘密分散法に代えて、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いる。それにより、各メンバに必要な演算は、もとの秘密情報の有限体の大きさよりも小さい有限体上で行うことができ、演算コストを下げることができる。
【００３８】
先ず、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法について説明する。Ｓｈａｍｉｒ法に代表される通常の（ｋ，ｎ）しきい値秘密分散法は、ｎ個の分散情報の内のｋ−１個の分散情報しか集まらない場合には、その分散情報のもとの秘密情報については、全く知ることができない方法である。これに対し、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法は、あるパラメータＬ（１≦Ｌ≦ｋ≦ｎ）を導入し、各分散情報Ｓ_ｉ（ｉ＝１，２，…，ｎ）の情報量を、もとの秘密情報Ｓの１／Ｌに減らすことにより、ｎ個の分散情報の内のｋ−ｄ（１≦ｄ≦Ｌ−１）個の分散情報が集まったときには、ｋ個の分散情報が集まっていなくても、もとの秘密情報についての何らかの情報が漏れる性質を持つ。
【００３９】
Ｓｈａｍｉｒ法をランプ型に拡張した方式は、例えば、上記非特許文献２に記載されている。その方式においては、まず、もとの秘密情報Ｓは、次式（１８）で示されるようなベクトル値とする。
Ｓ＝（Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１） …（１８）
また、Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１はそれぞれ、有限体ＧＦ（ｑ）上の値とし、Ｒ_Ｓ２，０，Ｒ_Ｓ２，１，…，Ｒ_{Ｓ２，ｋ−Ｌ−１}はそれぞれ、分配者が決める乱数で有限体ＧＦ（ｑ）上の値である。また、予め、Ｉ_０，Ｉ_１，…，Ｉ_ｋ−１のｋ個の有限体ＧＦ（ｑ）上の値を決めておく。そして、次式（１９）及び（２０）のようなｋ−１次多項式ｈ_Ｓ２（ｘ）を用いて秘密情報を秘密分散する。
【００４０】
【数１６】

【００４１】
分散情報が配布されるｎ人の各メンバには、メンバＩＤとして、ｍ_１，ｍ_２，…，ｍ_ｎが付与されているものとし、メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）に対する分散情報Ｘ_ｉは、次式（２１）のように計算する。
Ｘ_ｉ＝ｈ_Ｓ２（ｍ_ｉ） …（２１）
【００４２】
ここでは、演算（加算及び乗算）は、それぞれ、有限体ＧＦ（ｑ）上の演算とする。したがって、分散情報Ｘ_ｉは、有限体ＧＦ（ｑ）上の値である。以降、特に断りがない限り、演算は、有限体ＧＦ（ｑ）上で行うものとする。また、上記式（１９）より、次式（２２）の関係式が成り立つ。
ｈ_Ｓ２（Ｉ_０）＝Ｓ_０
ｈ_Ｓ２（Ｉ_１）＝Ｓ_１
…
ｈ_Ｓ２（Ｉ_Ｌ−１）＝Ｓ_Ｌ−１ …（２２）
【００４３】
各メンバに配布した分散情報Ｘ_ｉから、もとの秘密情報Ｓ＝（Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１）を再構成する場合には、分散情報を分配したメンバのうち、ｋ人以上のｔ人（ｋ≦ｔ）のメンバを集めてきて、そのメンバＩＤと分散情報を持ち寄り、次式（２３）及び（２４）で計算すると、もとの秘密情報Ｓ＝（Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１）を求めることができる。なお、次式（２３）及び（２４）において、ｍ’_１，ｍ’_２，…，ｍ’_ｔは、集まったメンバのメンバＩＤであり、Ｘ’_１，Ｘ’_２，…，Ｘ’_ｔは、メンバＩＤがｍ’_１，ｍ’_２，…，ｍ’_ｔであるメンバの保持する分散情報である。
【００４４】
【数１７】

【００４５】
【数１８】

【００４６】
このランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法においては、もとの秘密情報Ｓ＝（Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１）は、その分散情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）のＬ倍の情報量を持つことができる。すなわち、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法には、分散情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）の情報量を、もとの秘密情報Ｓの情報量の１／Ｌとすることができる性質がある。
【００４７】
≪第１の実施形態≫
［第１の実施形態の構成］
本発明の第１の実施形態においては、ｎ人のメンバ（ｎ個の分散計算装置としてもよい）が、それぞれ秘密情報を持ち、それらの秘密情報を引数とした関数ｆの計算結果を求めるため、分散計算を行う場合を説明する。ｎ人のメンバには、メンバを識別するための情報であるメンバＩＤとして、ｍ_１，ｍ_２，…，ｍ_ｎが割り当てられている。メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）は、それぞれ有限体ＧＦ（ｑ）（ｑは、素数又は素数のべき乗）上の値である。
【００４８】
また、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバは、秘密情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）を持っているものとする。ここで、メンバが保持する秘密情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）は、有限体ＧＦ（ｑ）のＬ次拡大体ＧＦ（ｑ^Ｌ）上の値であり、有限体ＧＦ（ｑ）上の値Ｘ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}で表すことができる。有限体ＧＦ（ｑ）をＬ次拡大して拡大体ＧＦ（ｑ^Ｌ）を生成したときの生成多項式（既約多項式）をｇ（ｘ）とし、ｇ（ｘ）＝０の解の一つをαとすると、秘密情報Ｘ_ｉは、次式（２５）で記述することができる。
Ｘ_ｉ＝Ｘ_ｉ，０＋Ｘ_ｉ，１α＋…＋Ｘ_{ｉ，Ｌ−１}α^Ｌ−１ …（２５）
また、秘密情報Ｘ_ｉは、ベクトル表現を用いて、次式（２６）のように記述することができる。
Ｘ_ｉ＝（Ｘ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}） …（２６）
【００４９】
図１は、第１の実施形態に係る分散計算方法を実施する構成（分散計算システム）を示すブロック図である。第１の実施形態においては、加算のみから構成されている関数を用いた分散計算を行う。図１に示されるように、第１の実施形態の分散計算方法（マルチパーティ・プロトコル）を実施する構成は、ｎ個（２≦ｎ）の分散処理部（分散計算装置）１０１−ｉ（ｉ＝１，２，…，ｎ）と、秘密再構成計算部１０２と、個々の分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）の秘密通信路１０３とを有する。各分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）は、メンバＩＤがｍ_ｉであるメンバが担当する演算を実行する。ｎ個の分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）からの出力が、秘密再構成計算部１０２への入力となる。
【００５０】
分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）（分散処理部の全体を示す場合には、符号１０１を用いる。）は、各メンバが分散計算する部分である。分散処理部１０１は、図２に符号▲１▼で示される秘密情報の分散を行ったり、図２に符号▲３▼で示される分散計算を行う。各分散処理部１０１−ｉ（ｉ＝１、２，…，ｎ）は、他の分散処理部１０１−ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）と秘密通信路１０３で接続されている。この秘密通信路１０３は、通信している２人のメンバ以外には通信内容を秘密とすることができるような通信路である。また、各分散処理部１０１−ｉ（ｉ＝１、２，…，ｎ）からの出力は、秘密再構成計算部１０２へ入力される。
【００５１】
秘密再構成計算部１０２は、各メンバの分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）からの出力を受け取り、受け取ったｎ個の値を、ｎ個の分散情報としたときの秘密の再構成を行う計算をし、その再構成されたもとの秘密を出力する。秘密再構成計算部１０２に入力されるｎ個の分散情報は、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法で分散されている情報である。
【００５２】
図３は、図１の秘密再構成計算部１０２の構成を示すブロック図である。図３に示されるように、秘密再構成計算部１０２は、線形結合部２０１を有する。線形結合部２０１は、秘密再構成計算部１０２への入力を受け取り、メンバＩＤ＿ｍ_ｉから計算される係数を用いて、それらの入力の線形結合計算を行い、その計算結果を出力する。線形結合部２０１からの出力が、秘密再構成計算部１０２の出力となる。ここで、各メンバの分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）から出力される値（すなわち、秘密再構成計算部１０２へ入力される値）をＺ’_ｉ（ｉ＝１，２，…，ｎ）とし、メンバＩＤ＿ｍ_ｉから計算される係数をｒ_０，ｉ，ｒ_１，ｉ，…，ｒ_{Ｌ−１，ｉ}（ｉ＝１，２，…，ｎ）とする。このとき、秘密再構成計算部１０２は、次式（２７）及び（２８）の計算を行い、その結果Ｚ＝（Ｚ_０，Ｚ_１，…，Ｚ_Ｌ−１）を出力する。
【００５３】
【数１９】

【００５４】
【数２０】

【００５５】
上記式（２７）及び（２８）における各演算は、有限体ＧＦ（ｑ）上で行う。なお、以降の説明においては、断りがない限り、演算は、有限体ＧＦ（ｑ）上で行うものとする。
【００５６】
各メンバの分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）における処理は、各メンバがそれぞれ他のメンバにはその処理の内容が分からないように行う。秘密再構成計算部１０２における処理は、処理を統合するセンター（すなわち、センターが管理する演算装置）のようなものが行ってもよいし、集まったメンバのうち、だれか１人、又は、複数人（すなわち、集まったメンバのいずれかが管理する演算装置）で行ってもよい。ただし、計算結果Ｚを必要としているメンバが行うのが望ましい。
【００５７】
図４は、図１の分散処理部１０１−ｉ（ｉ＝１，２，…，ｎ）の構成を示すブロック図である。図４に示されるように、分散処理部１０１−ｉは、秘密情報記憶部３０１−ｉと、秘密分散計算部３０２−ｉと、送信部３０３−ｉと、受信部３０４−ｉと、分散計算部３０５−ｉとを有する。秘密情報記憶部３０１−ｉからの出力が秘密分散計算部３０２−ｉへ入力され、秘密分散計算部３０２−ｉからの出力が送信部３０３−ｉ及び分散計算部３０５−ｉへ入力される。送信部３０３−ｉは、秘密通信路１０３へ情報を送信する。また、秘密通信路１０３から受け取る情報は、受信部３０４−ｉへ入力され、受信部３０４−ｉからの出力が分散計算部３０５−ｉへ入力される。分散計算部３０５−ｉからの出力が、分散処理部１０１−ｉの出力となる。
【００５８】
秘密情報記憶部３０１−ｉは、メンバＩＤがｍ_ｉであるメンバが保持する秘密情報Ｘ_ｉを保持しており、この秘密情報Ｘ_ｉを秘密分散計算部３０２−ｉへ出力する。メンバが保持する秘密情報（すなわち、秘密情報記憶部３０１−ｉに保持されている秘密情報）Ｘ_ｉは有限体ＧＦ（ｑ）のＬ次拡大体ＧＦ（ｑ^Ｌ）上の値であり、生成元α及び有限体ＧＦ（ｑ）上の値Ｘ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}を用いて、次式のように記述することができる。
Ｘ_ｉ＝Ｘ_ｉ，０＋Ｘ_ｉ，１α＋…＋Ｘ_{ｉ，Ｌ−１}α^Ｌ−１
【００５９】
秘密分散計算部３０２−ｉへは、メンバＩＤがｍ_ｉであるメンバが保持する秘密情報Ｘ_ｉが入力される。秘密分散計算部３０２−ｉは、入力された秘密情報Ｘ_ｉをランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法（Ｌ≦ｋ≦ｎ）を用いて分散し、送信部３０３−ｉ、及び、秘密通信路１０３を経由して他のメンバに配布する。メンバが保持する秘密情報Ｘ_ｉは拡大体ＧＦ（ｑ^Ｌ）上の値である。秘密分散計算部３０２−ｉで生成される分散情報をＹ_ｉ，ｐ（ｐ＝１，２，…，ｎ）とすると、自分自身に対する分散情報Ｙ_ｉ，ｉは、分散計算部３０５−ｉへ出力され、その他の分散情報Ｙ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）は送信部３０３−ｉへ出力される。メンバが保持する秘密情報Ｘ_ｉは拡大体ＧＦ（ｑ^Ｌ）上の値であり、その分散情報Ｙ_ｉ，ｐは、その有限体ＧＦ（ｑ）上の値である。
【００６０】
送信部３０３−ｉは、秘密分散計算部３０２−ｉからの出力Ｙ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を受け取り、それを秘密通信路１０３を通して他の各メンバ（メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）であるメンバ）に送信する。なお、Ｙ_ｉ，ｐは、メンバＩＤがｍ_ｉであるメンバからメンバＩＤがｍ_ｐであるメンバに送信される分散情報である。
【００６１】
受信部３０４−ｉは、他の各メンバの送信部３０３−ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）から送信される情報Ｙ_ｐ，ｉ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を受け取り、それを分散計算部３０５−ｉへ出力する。なお、Ｙ_ｐ，ｉは、メンバＩＤがｍ_ｐであるメンバからメンバＩＤがｍ_ｉであるメンバに送信される分散情報である。
【００６２】
分散計算部３０５−ｉは、秘密分散計算部３０２−ｉから、秘密情報Ｘ_ｉの分散情報であるＹ_ｉ，ｉを受け取る。さらに、受信部３０４−ｉから、他のメンバから配布された、秘密情報Ｘ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）の分散情報Ｙ_１，ｉ，Ｙ_２，ｉ，…，Ｙ_ｎ，ｉ（分散情報Ｙ_ｉ，ｉ以外のもの）を受け取る。分散計算部３０５−ｉは、受け取ったｎ個の分散情報Ｙ_ｐ，ｉ（ｐ＝１，２，…，ｎ）を用いて分散計算を行い、求めるべき計算結果（最終の計算結果）Ｚの分散情報（中間の計算結果）Ｚ’_ｉを出力する。
【００６３】
分散計算部３０５−ｉは、関数Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）に従った演算をするために、一つ若しくは複数の分散加算部を有する。例えば、
Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝Ｘ_１＋Ｘ_２＋…＋Ｘ_ｎ
（すなわち、秘密情報の総和）を計算させようとする場合には、分散計算部３０５−ｉは、図６に示されるような構成（ｎ−１個の分散加算部５０１−１，５０１−２，…，５０１−（ｎ−１）からなる）になる。また、
Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝Ｘ_Ｍ＋Ｘ_Ｎ
（すなわち、ある特定の秘密情報の和）を計算させようとする場合には、分散計算部３０５−ｉは、図７に示されるような構成（１個の分散加算部６０１からなる）になる。
【００６４】
図５は、第１の実施形態における秘密分散計算部３０２−ｉ（ｉ＝１，２，…，ｎ）の構成を示すブロック図である。図５に示されるように、秘密分散計算部３０２−ｉは、多項式生成部４０１−ｉと、分散情報生成部４０２−ｉとを有する。また、多項式生成部４０１−ｉは、乱数生成部４０３−ｉと、（ｋ−１）次多項式生成部４０４−ｉとを有する。秘密分散計算部３０２−ｉへの入力は、多項式生成部４０１−ｉへ入力され、多項式生成部４０１−ｉからの出力が、分散情報生成部４０２−ｉへ入力される。分散情報生成部４０２−ｉからの出力が、秘密分散計算部３０２−ｉからの出力となる。また、多項式生成部４０１−ｉへの入力は、（ｋ−１）次多項式生成部４０４−ｉへ入力され、乱数生成部４０３−ｉからの出力も（ｋ−１）次多項式生成部４０４−ｉへ入力される。（ｋ−１）次多項式生成部４０４−ｉからの出力が、多項式生成部４０１−ｉからの出力となる。
【００６５】
多項式生成部４０１−ｉは、Ｌ個の有限体ＧＦ（ｑ）上の値Ｘ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}を受け取り、それらの値から、次式（２９）を満たすｋ−１次多項式ｈ_Ｘｉ（ｘ）を生成し、その生成した多項式ｈ_Ｘｉ（ｘ）を表現する情報を出力する。
ｈ_Ｘｉ（Ｉ_０）＝Ｘ_ｉ，０
ｈ_Ｘｉ（Ｉ_１）＝Ｘ_ｉ，１
…
ｈ_Ｘｉ（Ｉ_Ｌ−１）＝Ｘ_{ｉ，Ｌ−１} …（２９）
ただし、Ｉ_０，Ｉ_１，…，Ｉ_Ｌ−１は、メンバＩＤと重複しない値で、予め決められている有限体ＧＦ（ｑ）上の値とする。
【００６６】
分散情報生成部４０２−ｉは、多項式ｈ_Ｘｉ（ｘ）を受け取り、次式（３０）で示す有限体ＧＦ（ｑ）上のｎ個の値Ｙ_ｉ，ｐ（ｐ＝１，２，…，ｎ）を生成して出力する。
Ｙ_ｉ，ｐ＝ｈ_Ｘｉ（ｍ_ｐ） …（３０）
ここで、ｐ＝１，２，…，ｎであり、Ｙ_ｉ，ｐは、メンバＩＤがｍ_ｉであるメンバからメンバＩＤがｍ_ｐであるメンバに対して配布される分散情報を示す。
【００６７】
乱数生成部４０３−ｉは、有限体ＧＦ（ｑ）上のｋ−Ｌ個の乱数Ｒ_Ｘｉ，０，Ｒ_Ｘｉ，１，…，Ｒ_{Ｘｉ，ｋ−Ｌ−１}を生成して出力する。
【００６８】
（ｋ−１）次多項式生成部４０４−ｉは、秘密分散計算部３０２−ｉへの入力であるメンバが保持する秘密情報Ｘ_ｉ、及び、乱数生成部４０３−ｉからの乱数Ｒ_Ｘｉ，０，Ｒ_Ｘｉ，１，…，Ｒ_{Ｘｉ，ｋ−Ｌ−１}を受け取り、次式（３１）及び（３２）で示されるようなｋ−１次多項式ｈ_Ｘ（ｘ）を生成し、その生成した多項式ｈ_Ｘ（ｘ）を表現する情報を出力する。
【００６９】
【数２１】

【００７０】
なお、メンバが保持する秘密情報Ｘ_ｉは拡大体ＧＦ（ｑ^Ｌ）上の値であり、前述したように、生成元α及び有限体ＧＦ（ｑ）上の値Ｘ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}を用いて
Ｘ_ｉ＝Ｘ_ｉ，０＋Ｘ_ｉ，１α＋…＋Ｘ_{ｉ，Ｌ−１}α^Ｌ−１
の形で記述することができる。また、上記式（３１）及び（３２）は、メンバＩＤがｍ_ｉであるメンバの（ｋ−１）次多項式生成部４０４−ｉが生成する多項式ｈ_Ｘ（ｘ）である。
【００７１】
図８は、図６又は図７の分散加算部５０１又は６０１の構成を示すブロック図である。図８を用いて、分散計算部３０５−ｉの構成要素となる、分散加算部５０１又は６０１の構成を説明する。図８に示されるように、分散加算部５０１又は６０１は、加算部７０１を有する。加算部７０１は、２つの入力（有限体ＧＦ（ｑ）上の値）を受け取り、それらの有限体ＧＦ（ｑ）上の加算をした値を出力する。入力値をａ及びｂとすると、その出力ｃは、次式（３３）のようになる。
ｃ＝ａ＋ｂ …（３３）
上記式（３３）は、有限体ＧＦ（ｑ）上の演算（加算）である。
【００７２】
分散情報ａ及びｂは、それぞれ、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成式（上記式（２７）及び（２８））を行うと、拡大体ＧＦ（ｑ^Ｌ）上の値
Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）
Ｂ＝（Ｂ_０，Ｂ_１，…，Ｂ_Ｌ−１）
になる。ここで、Ａ_０，Ａ_１，…，Ａ_Ｌ−１，Ｂ_０，Ｂ_１，…，Ｂ_Ｌ−１はそれぞれ、有限体ＧＦ（ｑ）上の値である。分散加算部５０１又は６０１から出力される分散情報ｃは、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行うと、
Ｃ＝Ａ＋Ｂ …（３４）
となる拡大体ＧＦ（ｑ^Ｌ）上の値Ｃ＝（Ｃ_０，Ｃ_１，…，Ｃ_Ｌ−１）となる。ここで、Ｃ_０，Ｃ_１，…，Ｃ_Ｌ−１はそれぞれ、有限体ＧＦ（ｑ）上の値である。上記式（３４）は、拡大体ＧＦ（ｑ^Ｌ）上の演算（加算）である。
【００７３】
［第１の実施形態の動作］
図９は、第１の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を示すフローチャートである。分散計算を行うための各メンバはｎ人であり、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバは、秘密情報Ｘ_ｉを持っている。メンバＩＤ＿ｍ_ｉは有限体ＧＦ（ｑ）上の値であり、秘密情報Ｘ_ｉは拡大体ＧＦ（ｑ^Ｌ）上の値である。また、メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）は、メンバ全員に公開されている。分散計算に用いる有限体ＧＦ（ｑ）、ランプ型秘密分散法のパラメータＬ、有限体ＧＦ（ｑ）から拡大体ＧＦ（ｑ^Ｌ）へ拡大するのに用いる既約多項式ｇ（ｘ）、その生成元α、及び、分散計算させたい関数ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）は、予め決められているものとする。関数ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）は、拡大体ＧＦ（ｑ^Ｌ）上の演算で、第１の実施形態においては、拡大体ＧＦ（ｑ^Ｌ）上の加算（例えば、Ｘ_Ａ＋Ｘ_Ｂ）のみで構成されているものとする。
【００７４】
図９に示されるように、まず、各メンバが保持する秘密情報を、ランプ型（Ｌ，ｋ，ｈ）秘密分散法を用いて分散し、他のメンバに配布する（ステップＳ８０１）。ステップＳ８０１は、図４の秘密分散計算部３０２−ｉにおける動作を示しており、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバの保持する秘密情報Ｘ_ｉから、上記式（３０）を用いて、分散情報Ｙ_ｉ，ｐ（ｐ＝１，２，…，ｎ）を計算し、メンバＩＤがｍ_ｐであるメンバに対して配布する。
【００７５】
次に、各メンバは、自分自身の秘密情報の分散情報、及び、他のメンバから配布された分散情報を用いて、関数ｆの分散計算を行う（ステップＳ８０２）。ステップＳ８０２は、図４の分散計算部３０５−ｉにおける動作を示しており、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、関数ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）で指示される通りの分散計算を行う。例えば、
ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝Ｘ_Ａ＋Ｘ_Ｂ
である場合には、メンバＩＤがｍ_ｉであるメンバは、配布された結果自分が保持する分散情報Ｙ_Ａ，ｉ及びＹ_Ｂ，ｉから、次の分散加算計算
Ｚ’_ｉ＝Ｙ_Ａ，ｉ＋Ｙ_Ｂ，ｉ
を実行する。この分散加算計算の計算結果（中間の計算結果）Ｚ’_ｉは、拡大体ＧＦ（ｑ^Ｌ）上の計算結果（最終の計算結果）Ｚ（ここで、Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝Ｘ_Ａ＋Ｘ_Ｂである。）の分散情報（すなわち、ランプ型（Ｌ，ｋ，ｎ）秘密分散法で分散された分散情報）となっている。
【００７６】
次の、ステップＳ８０３において、各メンバが計算した計算結果Ｚ’_ｉから、関数ｆの計算結果Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）を、ランプ型（Ｌ，ｋ，ｎ）秘密分散法に基づいて秘密再構成する。ステップＳ８０３は、図１の秘密再構成計算部１０２における動作を示しており、メンバＩＤがｍ_ｉであるメンバがステップＳ８０２で計算した結果Ｚ’_ｉ（ｉ＝１，２，…，ｎ）から、上記式（２７）を用いて計算し、関数ｆの計算結果Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）を得ることができる。
【００７７】
図１０は、分散加算における動作を示すフローチャートである。例えば、拡大体ＧＦ（ｑ^Ｌ）上の値Ａ及びＢの加算を行う場合を考える。図１０に示されるように、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、自身が保持する情報Ａ及びＢの分散情報ａ_ｉ及びｂ_ｉより、その和ｃ_ｉ＝ａ_ｉ＋ｂ_ｉを計算して出力する（ステップＳ９０１）。
【００７８】
［第１の実施形態の効果］
以上に説明したように、第１の実施形態によれば、関数ｆ（ただし、関数ｆは、加算のみの関数）に対するマルチパーティ・プロトコル（各メンバの保持する秘密情報を公開しないまま、各メンバが分散計算を行うことにより、関数ｆの計算結果を得るプロトコル）において、関数ｆにおける拡大体ＧＦ（ｑ^Ｌ）上の計算を、各メンバの分散演算処理においては、その拡大体よりも小さな有限体ＧＦ（ｑ）上の計算のみを行うことで、達成することができる。このため、メンバそれぞれの分散演算処理における、演算量、演算回路に必要な回路規模、演算に必要な記憶容量、演算時間等の演算コストを削減することができる。
【００７９】
≪第２の実施形態≫
第１の実施形態においては、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いた、マルチパーティ・プロトコルによる分散計算の、分散加算方法について説明したが、第２の実施形態においては、マルチパーティ・プロトコルによる分散計算の、分散定数乗算方法を説明する。第１の実施形態と同様に、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いていることから、従来のマルチパーティ・プロトコルによる分散計算と比較すると、各メンバに必要な演算は、もとの秘密情報の有限体の大きさよりも小さい有限体上で行うことができ、演算コストを下げることができる。
【００８０】
［第２の実施形態の構成］
第１の実施形態と同様に、第２の実施形態においては、ｎ人のメンバ（ｎ個の分散計算装置でもよい）が、それぞれ秘密情報を持ち、それらの秘密情報を引数とした関数ｆの計算結果を求めるため、分散計算を行う場合を説明する。ｎ人のメンバには、メンバＩＤとして、ｍ_１，ｍ_２，…，ｍ_ｎが割り当てられている。メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）は、それぞれ有限体ＧＦ（ｑ）（ｑは素数又は素数のべき乗）上の値である。
【００８１】
また、メンバＩＤがｍ_ｉであるメンバは、秘密情報Ｘ_ｉを持っているものとする。ここで、メンバが保持する秘密情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）は、有限体ＧＦ（ｑ）のＬ次拡大体ＧＦ（ｑ^Ｌ）上の値であり、有限体ＧＦ（ｑ）上の値Ｘ_ｉ，０，Ｘ_ｉ，１，…、Ｘ_{ｉ，Ｌ−１}で表すことができる。有限体ＧＦ（ｑ）をＬ次拡大して拡大体ＧＦ（ｑ^Ｌ）を生成したときの生成多項式（既約多項式）をｇ（ｘ）とし、生成元をαとする。
【００８２】
第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）は、第１の実施形態のものと同様に、図１のようになる。第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）が第１の実施形態のものと異なる点は、分散処理部１０１−ｉの構成及び動作である。
【００８３】
図１１は、第２の実施形態における分散処理部（分散計算装置）１０１−ｉ（ｉ＝１，２，…，ｎ）の構成を示すブロック図である。図１１に示されるように、第２の実施形態における分散処理部１０１−ｉは、秘密情報記憶部１００１−ｉと、秘密分散計算部１００２−ｉと、送信部１００３−ｉと、受信部１００４−ｉと、分散計算部１００５−ｉとを有する。秘密情報記憶部１００１−ｉからの出力が秘密分散計算部１００２−ｉへ入力され、秘密分散計算部１００２−ｉからの出力が送信部１００３−ｉ及び分散計算部１００５−ｉへ入力される。送信部１００３−ｉは、秘密通信路１０３へ情報を送信する。また、秘密通信路１０３から受け取る情報は、受信部１００４−ｉへ入力され、受信部１００４−ｉからの出力が分散計算部１００５−ｉへ入力される。分散計算部１００５−ｉからの出力が、第２の実施形態における分散処理部１０１−ｉの出力となる。
【００８４】
第２の実施形態における秘密情報記憶部１００１−ｉ、秘密分散計算部１００２−ｉ、送信部１００３−ｉ、及び受信部１００４−ｉは、第１の実施形態における秘密情報記憶部３０１−ｉ、秘密分散計算部３０２−ｉ、送信部３０３−ｉ、及び受信部３０４−ｉと、構成及び動作が同じである。しかし、第２の実施形態における分散計算部１００５−ｉは、第１の実施形態における分散計算部３０５−ｉと、構成及び動作が異なる。
【００８５】
第２の実施形態における分散計算部１００５−ｉは、分散加算に加えて、分散定数乗算を行うので、秘密通信路１０３を介して他のメンバの分散処理部１０１−ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）との通信を行う手段を有している。分散計算部１００５−ｉは、秘密分散計算部１００２−ｉから、秘密情報Ｘ_ｉの分散情報Ｙ_ｉ，ｉを受け取る。さらに、受信部１００４−ｉから、他のメンバから配布された、秘密情報Ｘ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）の分散情報Ｙ_１，ｉ，Ｙ_２，ｉ，…，Ｙ_ｎ，ｉを受け取る。これらｎ個の分散情報Ｙ_ｐ，ｉ（ｐ＝１，２，…ｎ）を用いて分散計算を行い、計算結果（最終の計算結果）Ｚの分散情報（中間の計算結果）Ｚ’_ｉを出力する。分散計算部１００５−ｉは、関数Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）に従って、一つ若しくは複数の分散定数乗算部と０以上若しくは複数の分散加算部とを有する。例えば、
Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝ｔ_１Ｘ_１＋ｔ_２Ｘ_２＋…＋ｔ_ｎＸ_ｎ
（秘密情報の線形結合計算）を計算させようとする場合には、分散計算部１００５−ｉは、図１２に示されるような構成（ｎ個の分散定数乗算部１１０１（１１０１−１，１１０１−２，…，１１０１−ｎ）と、ｎ−１個の分散加算部１１０２（１１０２−１，１１０２−２，…，１１０２−（ｎ−１））からなる）になる。
【００８６】
図１３は、図１２の分散定数乗算部１１０１の構成を示すブロック図である。図１３を用いて、分散計算部１００５−ｉの構成要素となる、分散定数乗算部１１０１の構成を説明する。図１３に示されるように、分散定数乗算部１１０１は、拡大体乗算部１２０１と、秘密分散計算部１２０２と、送信部１２０３と、受信部１２０４と、加算部１２０５とを有する。拡大体乗算部１２０１は、分散定数乗算部１１０１への入力を受け取る。拡大体乗算部１２０１からの出力は秘密分散計算部１２０２へ入力され、秘密分散計算部１２０２からの出力が送信部１２０３及び加算部１２０５へ入力される。送信部１２０３は、秘密通信路１０３へ情報を送信する。また、秘密通信路１０３から受け取る情報は、受信部１２０４へ入力され、受信部１２０４からの出力が加算部１２０５へ入力される。加算部１２０５からの出力が、分散定数乗算部１１０１の出力となる。
【００８７】
分散定数乗算部１１０１は、２つの入力（有限体ＧＦ（ｑ）上の値及び拡大体ＧＦ（ｑ^Ｌ）上の定数）を受け取る。ここで、拡大体ＧＦ（ｑ^Ｌ）上の値
Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）
及び、拡大体ＧＦ（ｑ^Ｌ）上の定数
Ｄ＝（Ｄ_０，Ｄ_１，…，Ｄ_Ｌ−１）
の乗算Ｃ＝Ｄ×Ａを分散計算する場合を考える。ここで、Ａ_０，Ａ_１，…，Ａ_Ｌ−１，Ｄ_０，Ｄ_１，…，Ｄ_Ｌ−１はそれぞれ、有限体ＧＦ（ｑ）上の値である。このとき、分散定数乗算部１１０１への入力は、値Ａの（メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバの保持する）分散情報ａ_ｉ及び拡大体ＧＦ（ｑ^Ｌ）上の定数Ｄである。以降、分散定数乗算部１１０１は、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバの分散計算部１００５−ｉに含まれているものとして説明する。
【００８８】
拡大体乗算部１２０１は、分散定数乗算部１１０１への入力である、分散情報ａ_ｉ及び拡大体ＧＦ（ｑ^Ｌ）上の定数Ｄ＝（Ｄ_０，Ｄ_１，…，Ｄ_Ｌ−１）を受け取り、まず、次式（３５）で示される２Ｌ−１個の値Ｅ’_ｉ，０，Ｅ’_ｉ，１，…，Ｅ’_{ｉ，２（Ｌ−１）}を計算する。
【００８９】
【数２２】

ここで、ｒ_ｊ，ｉ（ｊ＝０，１，…，Ｌ−１）は、上記式（２８）で表される、メンバＩＤから計算される係数である。
【００９０】
一方、拡大体ＧＦ（ｑ^Ｌ）上における乗算を可能とするために、下記の式（３７）で示す有限体ＧＦ（ｑ）上の値ｇ_ｊ，ｈ（ｊ＝０，１，…，Ｌ−１； ｈ＝０，１，…，Ｌ−１）は、拡大体演算用に予め計算し保持しておくようにしておく。拡大体ＧＦ（ｑ^Ｌ）を生成するときの生成多項式ｇ（ｘ）を下記の式（３６）で示す。
【００９１】
【数２３】

【００９２】
【数２４】

【００９３】
これら保持しておいたｇ_ｊ，ｈ（ｊ＝０，１，…，Ｌ−１； ｈ＝０，１，…，Ｌ−１）、はじめに計算した上記式（３５）のＥ’_ｉ，ｈ（ｈ＝０，１，…，Ｌ−１）、及び、上記式（２８）で表されるメンバＩＤから計算される係数ｒ_ｊ，ｉ（ｊ＝０，１，…，Ｌ−１）を用いて、次式（３８）を計算する。
【００９４】
【数２５】

【００９５】
ここで、Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）は、拡大体乗算部１２０１からの出力である。拡大体乗算部１２０１からの出力Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）は、秘密分散計算部１２０２へ入力される。
【００９６】
例えば、Ｌ＝２、ｇ（ｘ）＝ｘ^２＋ｘ＋１の場合には、上記式（３７）から、ｇ_ｊ，ｈ（ｊ＝０，１，…，Ｌ−１； ｈ＝０，１，…，Ｌ−１）は、
ｇ_０，０＝１
ｇ_０，１＝１
ｇ_１，０＝−１
ｇ_１，１＝−１ …（３９）
となり、拡大体乗算部１００１（メンバＩＤがｍ_ｉであるメンバのもの）は、下記の式（４０）によりＥ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１）を計算し、出力する。
【００９７】
【数２６】

【００９８】
秘密分散計算部１２０２は、拡大体乗算部１２０１からの出力Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を受け取る。この拡大体乗算部１２０１からの出力Ｅ_ｉは、拡大体ＧＦ（ｑ^Ｌ）上の値である。秘密分散計算部１２０２は、受け取った値Ｅ_ｉを、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法（ｋ≦ｎ）を用いて分散し、送信部１２０３、及び、秘密通信路１０３を経由して他のメンバに配布する。秘密分散計算部１２０２は、図５に示される秘密分散計算部３０２−ｉと同様な構成をしており、入力される値が秘密情報Ｘ_ｉ＝（Ｘ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}）に代えて、値Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）が入力される。このとき、（ｋ−１）次多項式生成部４０４−ｉで生成される多項式は、次式（４１）になる。
【００９９】
【数２７】

【０１００】
ここで、Ｈ_ｊ（ｘ）は上記式（３２）のものである。同様に、分散情報生成部４０２−ｉで生成される、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎ）であるメンバに対して配布する分散情報Ｆ_ｉ，ｐは、上記式（４１）を用いて、次式（４２）で算出する。
Ｆ_ｉ，ｐ＝ｈ_Ｅｉ（ｍ_ｐ） …（４２）
分散情報Ｆ_ｉ，ｐは、その有限体ＧＦ（ｑ）上の値である。
【０１０１】
自分自身に対する分散情報Ｆ_ｉ，ｉは、加算部１２０５へ出力し、その他の分散情報Ｆ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を送信部１２０３及び秘密通信路１０３を経由して各メンバに配布する。
【０１０２】
送信部１２０３は、秘密分散計算部１２０２からの出力Ｆ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を受け取り、それを秘密通信路１０３を通して他の各メンバに送信する。
【０１０３】
受信部１２０４は、他の各メンバ（メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）であるメンバ）の送信部１２０３から送信される情報Ｆ_ｐ，ｉ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を受け取り、それを加算部１２０５へ出力する。
【０１０４】
送信部１２０３及び受信部１２０４は、他のメンバの分散処理部１０１−ｐとの送受信する機能を持っており、分散処理部１０１−ｉにおける送信部１００３−ｉ及び受信部１００４−ｉと共通化した構成にしてもよい。
【０１０５】
加算部１２０５は、秘密分散計算部１２０２からの出力Ｆ_ｉ，ｉを受け取る。さらに、加算部１２０５は、受信部１２０４から、他のメンバの秘密分散計算部１２０２からの出力Ｆ_１，ｉ，Ｆ_２，ｉ，…，Ｆ_ｎ，ｉを受け取る。これらｎ個の分散情報Ｆ_ｐ，ｉ（ｐ＝１，２，…，ｎ）を、次式（４３）のようにすべて加算（有限体ＧＦ（ｑ）上の加算）し、その計算結果ｃ_ｉを出力する。
ｃ_ｉ＝Ｆ_１，ｉ＋Ｆ_２，ｉ＋…＋Ｆ_ｎ，ｉ …（４３）
【０１０６】
この加算部１２０５からの出力ｃ_ｉが、分散定数乗算部１１０１の出力となる。分散定数乗算部１１０１への入力を分散情報ａ_ｉ（ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行うと、拡大体ＧＦ（ｑ^Ｌ）上の値Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）になる）、及び、定数Ｄ＝（Ｄ_０，Ｄ_１，…，Ｄ_Ｌ−１）とすると、そのとき分散定数乗算部１１０１から出力される分散情報ｃ_ｉは、メンバでランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成行うと、
Ｃ＝Ｄ×Ａ …（４４）
となる拡大体ＧＦ（ｑ^Ｌ）上の値Ｃ＝（Ｃ_０，Ｃ_１，…，Ｃ_Ｌ−１）となる。ここで、Ｃ_０，Ｃ_１，…，Ｃ_Ｌ−１は、有限体ＧＦ（ｑ）上の値である。また、上記式（４４）は、拡大体ＧＦ（ｑ^Ｌ）上の演算（乗算）である。
【０１０７】
［第２の実施形態の動作］
図１４は、第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を示すフローチャートである。図１４に示されるように、第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作は、上記した第１の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作と類似している。しかし、第１の実施形態のステップＳ８０２（図９）において分散加算のみしか行わなかったが、第２の実施形態のステップＳ１３０２（図１４）おいては、分散定数乗算をも行う点が相違する。
【０１０８】
図１４を用いて、第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を説明する。なお、第１の実施形態と異なるステップＳ１３０２のみを説明する。図１４に示されるように、ステップＳ１３０２においては、各メンバは、自分自身の秘密情報の分散情報、及び、他のメンバから配布された分散情報を用いて、関数ｆの分散計算を行う。ステップＳ１３０２は、図１１の分散計算部１００５−ｉにおける動作を示しており、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、関数ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）で指示される通りの分散計算を行う。この関数ｆは、第１の実施形態においては、加算のみしか扱わなかったが、第２の実施形態においては、定数乗算も扱う。例えば、ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝ｔ_ＡＸ_Ａ＋ｔ_ＢＸ_Ｂ
（ｔ_Ａ，ｔ_Ｂは、拡大体ＧＦ（ｑ^Ｌ）上の定数）である場合には、メンバＩＤがｍ_ｉであるメンバは、配布された結果自分が保持する分散情報Ｙ_Ａ，ｉ及びＹ_Ｂ，ｉから、ｔ_Ａ及びＹ_Ａ，ｉを入力とする分散定数乗算計算（分散定数乗算部１１０１の動作）、及び、ｔ_Ｂ及びＹ_Ｂ，ｉを入力とする分散定数乗算計算（分散定数乗算部１１０１の動作）を行って、その２つの出力の加算を行って計算結果（中間の計算結果）Ｚ’_ｉを求める。その計算結果Ｚ’_ｉは、拡大体ＧＦ（ｑ^Ｌ）上の計算結果（最終の計算結果）
Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝ｔ_ＡＸ_Ａ＋ｔ_ＢＸ_Ｂ
の分散情報（すなわち、ランプ型（Ｌ，ｋ，ｎ）秘密分散法で分散された分散情報）となっている。
【０１０９】
図１５は、第２の実施形態における分散定数乗算の動作を示すフローチャートである。例えば、拡大体ＧＦ（ｑ^Ｌ）上の値Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）、及び、定数Ｄ＝（Ｄ_０，Ｄ_１，…，Ｄ_Ｌ−１）の乗算を行う場合を考える。
【０１１０】
まず、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、自身が保持する情報Ａの分散情報ａ_ｉ、及び、定数Ｄより、上記式（３８）を用いて、Ｅ_ｉ＝（Ｅ_ｉ，０、Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を求める（ステップＳ１４０１）。ステップＳ１４０１は、図１３の拡大体乗算部１２０１における動作を表している。
【０１１１】
次に、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、ステップＳ１４０１で計算した値Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）をランプ型（Ｌ，ｋ，ｎ）秘密分散法を用いて分散情報Ｆ_ｉ，ｐ（ｐ＝１，２，…，ｎ）を作り、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）である他のメンバに分散情報Ｆ_ｉ，ｐを配布する（ステップＳ１４０２）。ステップＳ１４０２は、図１３の秘密分散計算部１２０２及び送信部１２０３における動作を示している。
【０１１２】
次に、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、ステップＳ１４０２の動作により受け取った分散情報Ｆ_ｐ，ｉ（ｐ＝１，２，…，ｎ）をすべて加算し（上記式（４３））、値ｃ_ｉを求めて出力する（ステップＳ１４０３）。ステップＳ１４０３は、図１３の受信部１２０４及び加算部１２０５における動作を示している。
【０１１３】
［第２の実施形態の効果］
以上に説明したように、第２の実施形態によれば、第１の実施形態と同様に、関数ｆ（ただし、関数ｆは、加算及び定数乗算のみからなる関数）に対するマルチパーティ・プロトコル（各メンバの保持する秘密情報を公開しないまま、各メンバが分散計算を行うことにより、関数ｆの計算結果を得るプロトコル）において、関数ｆにおける拡大体ＧＦ（ｑ^Ｌ）上の計算を、各メンバの分散演算処理においては、その拡大体よりも小さな有限体ＧＦ（ｑ）上の計算のみを行うことで、達成することができる。このため、メンバそれぞれの分散演算処理における、演算量、演算回路に必要な回路規模、演算に必要な記憶容量、演算時間等の演算コストを削減することができる。
【０１１４】
また、第１の実施形態とは異なり、第２の実施形態においては、分散加算計算だけでなく、分散定数乗算計算も可能となる。
【０１１５】
≪第３の実施形態≫
第１の実施形態においては、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いた、マルチパーティ・プロトコルによる分散計算の、分散加算方法についてついて説明したが、第３の実施形態においては、マルチパーティ・プロトコルによる分散計算の、分散乗算方法を説明する。第１及び第２の実施形態と同様に、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いていることから、従来のマルチパーティ・プロトコルによる分散計算と比較すると、各メンバに必要な演算は、もとの秘密情報の有限体の大きさよりも小さい有限体上で行うことができ、演算コストを下げることができる。
【０１１６】
［第３の実施形態の構成］
第１及び第２の実施形態と同様に、第３の実施形態においては、ｎ人のメンバ（ｎ個の分散計算装置でもよい）が、それぞれ秘密情報を持ち、それらの秘密情報を引数とした関数ｆの計算結果を求めるため、分散計算を行う場合を説明する。ｎ人のメンバには、メンバＩＤとして、ｍ_１，ｍ_２，…，ｍ_ｎが割り当てられている。メンバＩＤ＿ｍ_ｉ（ｉ＝１，２，…，ｎ）は、それぞれ有限体ＧＦ（ｑ）（ｑは、素数又は素数のべき乗）上の値である。
【０１１７】
また、メンバＩＤがｍ_ｉであるメンバは、秘密情報Ｘ_ｉを持っているものとする。ここで、メンバが保持する秘密情報Ｘ_ｉ（ｉ＝１，２，…，ｎ）は、有限体ＧＦ（ｑ）のＬ次拡大体ＧＦ（ｑ^Ｌ）上の値であり、有限体ＧＦ（ｑ）上の値であるＸ_ｉ，０，Ｘ_ｉ，１，…，Ｘ_{ｉ，Ｌ−１}で表すことができる。有限体ＧＦ（ｑ）をＬ次拡大して拡大体ＧＦ（ｑ^Ｌ）を生成したときの生成多項式（既約多項式）をｇ（ｘ）とし、生成元をαとする。
【０１１８】
第３の実施形態に係る分散計算方法を実施する構成（分散計算システム）は、第１及び第２の実施形態のものと同様に、図１のようになる。第３の実施形態に係る分散計算方法を実施する構成（分散計算システム）が第１の実施形態のものと異なる点は、分散処理部１０１−ｉの構成及び動作である。
【０１１９】
第３の実施形態における分散処理部（分散計算装置）１０１−ｉ（ｉ＝１，２，…，ｎ）の構成は、第２の実施形態のものと同様に図１１のようになる。第３の実施形態における分散処理部１０１−ｉが、第２の実施形態のものと異なる点は、分散計算部１００５−ｉの構成及び動作である。
【０１２０】
第３の実施形態における分散計算部１００５−ｉは、分散加算（第１の実施形態）及び分散定数乗算（第２の実施形態）に加えて、分散乗算を行うので、第２の実施形態のものと同様に、秘密通信路１０３を介して他のメンバの分散処理部１０１−ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）との通信を行う手段を有している。分散計算部１００５−ｉは、秘密分散計算部１００２−ｉから、秘密情報Ｘ_ｉの分散情報Ｙ_ｉ，ｉを受け取る。さらに、受信部１００４−ｉから、他のメンバから配布された、秘密情報Ｘ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）の分散情報Ｙ_１，ｉ，Ｙ_２，ｉ，…，Ｙ_ｎ，ｉを受け取る。これらｎ個の分散情報Ｙ_ｐ，ｉ（ｐ＝１，２，…，ｎ）を用いて、分散計算を行い、計算結果（最終の計算結果）Ｚの分散情報（中間の計算結果）Ｚ’_ｉを出力する。分散計算部１００５−ｉは、関数Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）に従って、一つ若しくは複数の分散乗算部、０以上若しくは複数の分散加算部、及び、０以上若しくは複数の分散定数乗算部からなる。例えば、
Ｚ＝ｆ（Ｘ_１、Ｘ_２，…，Ｘ_ｎ）
＝（ｔ_１Ｘ_１＋ｔ_２Ｘ_２＋…＋ｔ_ｎＸ_ｎ）×Ｘ_Ｍ
（秘密情報の線形結合計算とメンバＩＤがｍ_Ｍであるメンバの保持する秘密情報との乗算）を計算させようとする場合には、分散計算部１００５−ｉは、図１６のような構成（ｎ個の分散定数乗算部１５０１、ｎ−１個の分散加算部１５０２、１個の分散乗算部１５０３からなる）になる。また、
Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝Ｘ_Ｍ×Ｘ_Ｎ
（メンバＩＤがｍ_Ｍ、ｍ_Ｎであるメンバの保持する秘密情報同士の乗算）を計算させようとする場合には、分散計算部１００５−ｉは、図１７のような構成（１個の分散乗算部１６０１からなる）になる。
【０１２１】
図１８は、図１６の分散乗算部１５０３又は図１７の分散乗算部１６０１の構成を示すブロック図である。図１８を用いて、第３の実施形態における分散計算部１００５−ｉの構成要素となる、分散乗算部１５０３，１６０１の構成を説明する。図１８に示されるように、分散乗算部１５０３，１６０１は、乗算部１７０１と、紛失通信計算部１７０２と、分散情報計算部１７０３と、秘密分散計算部１７０４と、送信部１７０５と、受信部１７０６と、加算部１７０７とを有する。分散乗算部１５０３，１６０１への入力は、乗算部１７０１、及び、紛失通信計算部１７０２へ入力される。乗算部１７０１は、分散乗算部１５０３，１６０１への入力を受け取り、分散情報計算部１７０３へ出力する。また、紛失通信計算部１７０２は、分散乗算部１５０３，１６０１への入力を受け取り、分散情報計算部１７０３へ出力する。分散情報計算部１７０３は、乗算部１７０１、及び、紛失通信計算部１７０２からの出力を受け取り、分散情報計算部１７０３からの出力が秘密分散計算部１７０４へ入力される。秘密分散計算部１７０４からの出力は送信部１７０５及び加算部１７０７へ入力される。送信部１７０５は、秘密通信路１０３へ情報を送信する。また、秘密通信路１０３から受け取る情報は、受信部１７０６へ入力され、受信部１７０６からの出力が加算部１７０７へ入力される。加算部１７０７からの出力が、分散乗算部１５０３，１６０１の出力となる。
【０１２２】
分散乗算部１５０３，１６０１は、２つの入力（有限体ＧＦ（ｑ）上の値）を受け取る。拡大体ＧＦ（ｑ^Ｌ）上の値Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）、及び、Ｂ＝（Ｂ_０，Ｂ_１，…，Ｂ_Ｌ−１）の乗算Ｃ＝Ａ×Ｂを分散計算しようとする場合を考える。ここで、Ａ_０，Ａ_１，…，Ａ_Ｌ−１，Ｂ_０，Ｂ_１，…，Ｂ_Ｌ−１は、有限体ＧＦ（ｑ）上の値である。このとき、分散乗算部１５０３，１６０１への入力は、値Ａ及びＢの（メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバの保持する）分散情報ａ_ｉ及びｂ_ｉである。分散情報ａ_ｉ及びｂ_ｉは、有限体ＧＦ（ｑ）上の値である。以降、分散乗算部１５０３，１６０１は、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバの分散計算部１００５−ｉに含まれるものとして説明する。乗算部１７０１は、分散乗算部１５０３，１６０１への入力である分散情報ａ_ｉ及びｂ_ｉを受け取り、それらの乗算ｃ’_ｉ＝ａ_ｉ×ｂ_ｉ（有限体ＧＦ（ｑ）上の乗算）を行い、乗算結果ｃ’_ｉを、分散情報計算部１７０３へ出力する。
【０１２３】
紛失通信計算部１７０２は、分散乗算部１５０３，１６０１への入力ａ_ｉ及びｂ_ｉを受け取り、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）である他のメンバの紛失通信計算部１７０２への入力値との乗算、すなわち、ａ_ｉ×ｂ_ｐ及びａ_ｐ×ｂ_ｉの結果に相当するもの（乗算結果そのものではない）が得られるように通信及び計算処理をする。すなわち、
ａ_ｉ×ｂ_ｐ＝ｄ_ｉ，ｐ，＋ｄ_ｐ，ｉ …（４５）
ａ_ｐ×ｂ_ｉ＝ｅ_ｉ，ｐ，＋ｅ_ｐ，ｉ …（４６）
となるような、ｄ_ｉ，ｐ及びｅ_ｉ，ｐをメンバＩＤがｍ_ｉであるメンバが保持することができ、ｄ_ｐ，ｉ及びｅ_ｐ，ｉをメンバＩＤがｍ_ｐであるメンバが、それぞれ保持することができるように、計算及び通信を行う。紛失通信計算部１７０２は、それぞれｎ−１個の値ｄ_ｉ，ｐ（ｐ＝１，２，…ｎであり、ｐ≠ｉであるもの）及びｅ_ｉ，ｐ（ｐ＝１，２，…ｎであり、ｐ≠ｉであるもの）を算出し、分散情報計算部１７０３へ出力する。
【０１２４】
分散情報計算部１７０３は、乗算部１７０１からの出力ｃ’_ｉと、紛失通信計算部１７０２からの出力ｄ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）及びｅ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を受け取り、それらを用いて、まず、次式（４７）により、値Ｇ_ｕ，ｖ（ｕ＝１，２，…，Ｌ−１；ｖ＝１，２，…，Ｌ−１）を計算する。
【０１２５】
【数２８】

【０１２６】
ただし、上記式（４７）において、ｒ_ｕ，ｉ（ｕ＝０，１，…，Ｌ−１）は、上記式（２８）で表される、メンバＩＤから計算される係数である。
【０１２７】
次に、次式（４８）のような２Ｌ−１個の値Ｅ’_ｉ，０，Ｅ’_ｉ，１，…，Ｅ’_{ｉ，２（Ｌ−１）}を計算する。
【数２９】

【０１２８】
次に、次式（４９）により、分散情報計算部１７０３からの出力Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を計算する。
【数３０】

【０１２９】
ただし、ｇ_ｊ，ｈ（ｊ＝０，１，…，Ｌ−１； ｈ＝０，１，…，Ｌ−１）は、上記式（３７）で表される、拡大体ＧＦ（ｑ^Ｌ）の生成多項式ｇ（ｘ）の係数から計算される値である。分散情報計算部１７０３からの出力Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）は、秘密分散計算部１７０４へ入力される。
【０１３０】
例えば、Ｌ＝２、ｇ（ｘ）＝ｘ^２＋ｘ＋１の場合には、出力Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１）は、次式（５０）により、計算される。
【数３１】

【０１３１】
第３の実施形態における秘密分散計算部１７０４、送信部１７０５、受信部１７０６、及び、加算部１７０７は、分散定数乗算部１１０１（第２の実施形態）の秘密分散計算部１２０２、送信部１２０３、受信部１２０４、及び、加算部１２０５とそれぞれ同様なものである。
【０１３２】
秘密分散計算部１７０４からの出力Ｆ_ｉ，ｉ（秘密分散計算部１７０４へ入力されるＥ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）の自分自身への分散情報）は、加算部１７０７へ出力され、さらに、秘密分散計算部１７０４からの出力Ｆ_ｉ，ｐ（秘密分散計算部１７０４へ入力されるＥ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）のメンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）であるメンバへの分散情報）は送信部１７０５へ出力される。
【０１３３】
送信部１７０５は、秘密分散計算部１７０４からの出力を秘密通信路１０３を通して他のメンバの受信部１７０６へ送信する。また、受信部１７０６は、他のメンバの送信部１７０５から出力Ｆ_ｐ，ｉ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を秘密通信路１０３を通して受信し、その受信した値を加算部１７０７へ出力する。加算部１７０７は、秘密分散計算部１７０４からの出力Ｆ_ｉ，ｉ、及び、受信部１７０６からの出力Ｆ_ｐ，ｉ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を受け取り、それらの加算を行い、その計算結果ｃ_ｉを出力する。加算部１７０７からの出力が、分散乗算部１５０３，１６０１からの出力となる。送信部１７０５及び受信部１７０６は、他のメンバの分散処理部１０１−ｐとの送受信する機能を持っており、分散処理部１０１−ｉにおける送信部１００３−ｉ及び受信部１００４−ｉと共通化した構成にしてもよい。
【０１３４】
図１９は、図１８の紛失通信計算部１７０２の構成を示すブロック図である。図１９を用いて、紛失通信計算部１７０２の構成を説明する。紛失通信計算部１７０２は、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）であるメンバの分散計算部１００５−ｉに含まれるものとして説明する。
【０１３５】
図１９に示されるように、紛失通信計算部１７０２は、ｉ−１個の通信計算受信部１８０１−ｐ（ｐ＝１，２，…，ｉ−１）と、ｉ−１個の通信計算受信部１８０２−ｐ（ｐ＝１，２，…，ｉ−１）、ｎ−ｉ個の通信計算送信部１８０３−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）と、ｎ−ｉ個の通信計算送信部１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）とを有する。紛失通信計算部１７０２へ入力される２つの入力のうち、一つは、通信算受信部１８０１−ｐ（ｐ＝１，２，…，ｉ−１）及び通信計算送信部１８０３−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）へ、他の一つは、通信計算受信部１８０２−ｐ（ｐ＝１，２，…，ｉ−１）及び通信算送信部１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）へ入力される。通信計算受信部１８０１−ｐ，１８０２−ｐ（ｐ＝１，２，…，ｉ−１）、及び、通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）からの出力が、紛失通信計算部１７０２からの出力となる。通信計算受信部１８０１−ｐ，１８０２−ｐ（ｐ＝１，２，…，ｉ−１）、及び通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）は、秘密通信路１０３を通して、他のメンバとの情報のやりとりを行うことにより、前述の通り、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）である他のメンバの値との乗算、すなわち、ａ_ｉ×ｂ_ｐ及びａ_ｐ×ｂ_ｉの結果に相当するもの（乗算結果そのものではない）が得られるようにするが、他のメンバの値ａ_ｐ及びｂ_ｐが分からないように、また、自分の値ａ_ｉ及びｂ_ｉが、他のメンバに分からないように、紛失通信というものを行う。前述した通り、紛失通信とは、送信側が、Ｍ個の情報を符号化（暗号化）して送信するが、受信側においては、そのうち一つしか受け取る（意味のあるように復号が可能となる）ことができず、また、送信側においては、受信側がどの情報を受け取った（意味のあるように復号が可能となった）かを知ることができない通信方法をいうことにする。この実施形態においては、法ｑのもとでの離散対数を計算することが困難であることを利用して、紛失通信を構成する。
【０１３６】
通信計算受信部１８０１−ｐ，１８０２−ｐ（ｐ＝１，２，…，ｉ−１）、及び、通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）は、ｉの値によって、通信計算受信部又は通信計算送信部を持たなかったりする。例えば、ｉ＝１の場合には、通信計算受信部を持たず、２×（ｎ−１）個の通信計算送信部を持つ。また、ｉ＝ｎの場合には、通信計算送信部を持たず、２×（ｎ−１）個の通信計算受信部を持つことになる。また、他のメンバとの送受信の関係は、メンバＩＤがｍ_ｉであるメンバの通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）からは、それぞれ、秘密通信路１０３を通して、メンバＩＤがｍ_ｐであるメンバの通信計算受信部１８０１−ｉ，１８０２−ｉのそれぞれへ情報が渡される。図２０及び図２１で詳細を説明する。
【０１３７】
図２０は、図１９の通信計算受信部１８０１−ｐ，１８０２−ｐ（ｐ＝１，２，…，ｉ−１）の構成を示すブロック図である。図２０を用いて、通信計算受信部１８０１−ｐ，１８０２−ｐ（ｐ＝１，２，…，ｉ−１）の構成を説明する。図２０に示されるように、通信計算受信部１８０１−ｐ，１８０２−ｐ（ｐ＝１，２，…，ｉ−１）は、インデックス計算送信部１９０１と、受信復元部１９０２とを有する。通信計算受信部１８０１−ｐは、紛失通信計算部１７０２への２つの入力のうち一つの入力を受け取り、通信計算受信部１８０２−ｐは、他の一つの入力を受け取る。ここでは、通信計算受信部１８０１−ｐへの入力をａ_ｉとし、通信計算受信部１８０２−ｐへの入力をｂ_ｉとする。通信計算受信部１８０１−ｐと１８０２−ｐは、内部的に同じ構造なので、ここでは、通信計算受信部１８０１−ｐについて説明し、通信算受信部１８０２−ｐに相当する説明は、括弧〔 〕内に記述する。通信計算受信部１８０１−ｐ 〔１８０２−ｐ〕 への入力は、インデックス計算送信部１９０１へ入力される。インデックス計算送信部１９０１からの出力は、受信復元部１９０２へ入力される。受信復元部１９０２からの出力が通信計算受信部１８０１−ｐ 〔１８０２−ｐ〕 からの出力となる。
【０１３８】
インデックス計算送信部１９０１は、通信計算受信部１８０１−ｐ 〔１８０２−ｐ〕 への入力ａ_ｉ 〔ｂ_ｉ〕 を受け取り、次式（５１）で示す計算を施して、ａ’_ｉ，ｐ 〔ｂ’_ｉ，ｐ〕 を計算し、秘密通信路１０３を通して、メンバＩＤがｍ_ｐであるメンバへ送信する（ｐ＝１，２，…，ｉ−１）。
【数３２】

【０１３９】
上記式（５１）において、ｈ及びｇは、有限体ＧＦ（ｑ）の２つの生成元とし、ｒＡ_ｉ，ｐ 〔ｒＢ_ｉ，ｐ〕 は、乱数として有限体ＧＦ（ｑ）上の値を選ぶ。また、インデックス計算送信部１９０１は、上記式（５１）で用いた乱数ｒＡ_ｉ，ｐ 〔ｒＢ_ｉ，ｐ〕 を受信復元部１９０２へ出力する。
【０１４０】
受信復元部１９０２は、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｉ−１）であるメンバからｑ個（ｑは有限体ＧＦ（ｑ）の要素数）の情報を受け取り、ａ_ｉ番目の情報ｄ’_ｉ，ｐ 〔ｂ_ｉ番目の情報ｅ’_ｉ，ｐ〕 を、次式（５２）で計算することにより、目的とする値ｄ_ｉ，ｐ 〔ｅ_ｉ，ｐ〕 を計算する。受信復元部１９０２は、それ以外の受け取った情報は、メンバＩＤがｍ_ｉであるメンバにとっては、乱数に見える。
【０１４１】
【数３３】

【０１４２】
値ｄ’_ｉ，ｐ 〔ｅ’_ｉ，ｐ〕 は、２つの情報ｄ’_{１，ｉ，ｐ}及びｄ’_{２，ｉ，ｐ}〔ｅ’１，ｊ，ｐ及びｅ’_{２，ｉ，ｐ}〕 から成っているものとする。計算される値ｄ_ｉ，ｐ 〔ｅ_ｉ，ｐ〕 が、受信復元部１９０２の出力となり、通信計算受信部１８０１−ｐ 〔１８０２−ｐ〕 からの出力となる。
【０１４３】
図２１は、図１９の通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）の構成を示すブロック図である。図２１を用いて、通信計算送信部１８０３−ｐ，１８０４−ｐの構成を説明する。図２１に示されるように、通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）は、乱数生成部２００１と、有限体要素生成部２００２と、乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）とを有する。
【０１４４】
通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｔ）への入力は、乱数生成部２００１及び有限体要素生成部２００２からの出力とともに、乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）へ入力される。乱数生成部２００１からの出力が、通信計算送信部１８０３−ｐ，１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）からの出力となる。通信計算送信部１８０３−ｐは、紛失通信計算部１７０２の２つの入力のうち一つの入力を受け取り、通信計算送信部１８０４−ｐは、他の一つの入力を受け取る。ここでは、通信計算送信部１８０３−ｐへの入力をａ_ｉ、通信計算送信部１８０４−ｐへの入力をｂ_ｉとおく。通信計算送信部１８０３−ｐ，１８０４−ｐは、内部的に同じ構造なので、ここでは、通信計算送信部１８０３−ｐについて説明し、通信計算送信部１８０４−ｐに相当する説明は、括弧〔 〕内に記述する。
【０１４５】
図２１に示される乱数生成部２００１は、有限体ＧＦ（ｑ）上の値の乱数を生成して出力する。乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）へは、同じ乱数が出力される。乱数生成部２００１からの出力が通信計算送信部１８０３−ｐ 〔１８０４−ｐ〕 （ｐ＝ｉ＋１，ｉ＋２，…，ｎ）からの出力となる。
【０１４６】
図２１に示される有限体要素生成部２００２は、有限体ＧＦ（ｑ）上の値を０，１，…，ｑ−１と、順次生成し、それぞれ、乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）へ出力する。すなわち、乗数計算送信部２００３−１へは０を、乗数計算送信部２００３−２へは１を、乗数計算送信部２００３−ｊへはｊ−１を、乗数計算送信部２００３−ｑへはｑ−１を、出力する。
【０１４７】
図２１に示される乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）は、通信計算送信部１８０３−ｐ 〔１８０４−ｐ〕 （ｐ＝ｉ＋１，ｉ＋２，…，ｎ）から入力される値ａ_ｉ 〔ｂ_ｉ〕 、乱数生成部２００１から乱数を、有限体要素生成部２００２から対応する有限体要素ａ−１を、秘密通信路１０３を通してメンバＩＤがｍ_ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）であるメンバからの情報（他のメンバの通信計算受信部１８０１−ｉ 〔１８０２−ｉ〕 のインデックス計算送信部１９０１から出力）ａ’_ｐ，ｉ 〔ｂ’_ｐ，ｉ〕 を、受け取り、それらの入力から計算をして、計算結果を出力する。乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）からの出力、合計ｑ個の出力は、秘密通信１０３を通して、ａの値の小さい順に、メンバＩＤがｍ_ｐ（ｐ＝ｉ＋１、ｉ＋２，…，ｎ）であるメンバへ送信する。今、乱数生成部２００１からの出力をｄ_ｉ，ｐ 〔ｅ_ｉ，ｐ〕 とする。また、秘密通信路１０３を通して受信する値を、ａ’_ｐ，ｉ（通信計算送信部１８０３−ｐに相当） 〔ｂ’_ｐ，ｉ（通信計算送信部１８０４−ｐに相当）〕とする。有限体要素生成部２００２から乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）へは、ａ−１が入力される。乗数計算送信部２００３−ａ（ａ＝１，２，…，ｑ）は、次式（５３）〜（５５）の計算を行い、ｄ’_{ｐ，ｉ，ａ} 〔ｅ’_{ｐ，ｉ，ａ}〕 をそれぞれ計算し（ｄ’_{ｐ，ｉ，ａ}〔ｅ’_{ｐ，ｉ，ａ}〕 は式（５２）の説明で述べたように２つの値からなる）、秘密通信路１０３を通してナンバＩＤがｍ_ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）であるメンバへ、ａ＝１，２，…，ｑの順に送信する。
【０１４８】
【数３４】

【０１４９】
ここで、ｋＡ_ａ 〔ｋＢ_ａ（ａ＝１，２，…，ｑ）〕 は、それぞれ、ｑ個の有限体ＧＦ（ｑ）上の値の乱数である。これらの出力ｄ’_{ｐ，ｉ，ａ}又はｅ’_{ｐ，ｉ，ａ}を秘密通信路１０３を通して、メンバＩＤがｍ_ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）であるメンバの通信計算受信部１８０１−ｉ 〔通信計算受信部１８０２−ｉ〕 が受け取ると、受け取ったメンバは、ａ＝ａ_ｐ 〔ｂ_ｐ〕 に相当するａ番目の情報ｄ’_ｐ，ｉ＝ｄ’_{ｐ，ｉ，ａ}〔ｅ’_ｐ，ｉ＝ｅ’_{ｐ，ｉ，ａ}〕 を式（５２）で復号することができる（それ以外の受け取った情報は、メンバＩＤがｍ_ｐであるメンバにとっては、乱数に見える）。
【０１５０】
図２１で示される乱数生成部２００１からの出力ｄ_ｉ，ｐ 〔ｅ_ｉ，ｐ〕 が通信計算送信部１８０３−ｐ 〔１８０４−ｐ〕 （ｐ＝ｉ＋１，ｉ＋２，…，ｎ）からの出力となる。
【０１５１】
図１８のような構成の分散乗算部１５０３，１６０１への入力を分散情報ａ_ｉ及びｂ_ｉ（ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行うと、それぞれ、拡大体ＧＦ（ｑ^Ｌ）上の値Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）及びＢ＝（Ｂ_０，Ｂ_１，…，Ｂ_Ｌ−１）になる）とすると、そのとき分散乗算部１５０３，１６０１から出力される分散情報ｃ_ｉは、メンバでランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成行うと、
Ｃ＝Ａ×Ｂ …（５６）
となる拡大体ＧＦ（ｑ^Ｌ）上の値Ｃ＝（Ｃ_０，Ｃ_１，…，Ｃ_Ｌ−１）となる。ここで、Ｃ_０，Ｃ_１，…，Ｃ_Ｌ−１は、有限体ＧＦ（ｑ）上の値である。式（５６）は、拡大体ＧＦ（ｑ^Ｌ）上の演算（乗算）である。
【０１５２】
［第３の実施形態の動作］
図２２は、第３の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を示すフローチャートである。第３の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作は、図２２に示されるように、上記した第１及び第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作と類似している。しかし、第１の実施形態のステップＳ８０２（図９）において分散加算のみ、第２の実施形態のステップＳ１３０２（図１４）においては分散加算と分散定数乗算のみしか行わなかったが、第３の実施形態のステップＳ２１０２（図２２）おいては、分散乗算をも行う点が相違する。
【０１５３】
図２２を用いて、第３の実施形態の分散計算法を実施する構成（分散計算システム）の動作を説明する。なお、第１及び第２の実施形態と異なるステップＳ２１０２のみを説明する。図２２に示されるように、ステップＳ２１０２においては、各メンバは、自分自身の秘密情報の分散情報、及び、他のメンバから配布された分散情報を用いて、関数ｆの分散計算を行う。ステップＳ２１０２は、図１１の分散計算部１００５−ｉにおける動作を示しており、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、関数ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）で指示される通りの分散計算を行う。この関数ｆは、第１の実施形態においては加算のみ、第２の実施形態においては、加算と定数乗算しか扱わなかったが、第３の実施形態においては、乗算も取り扱う。例えば、
ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝（ｔ_ＡＸ_Ａ＋ｔ_ＢＸ_Ｂ）×Ｘ_Ｃ
（ｔ_Ａ及びｔ_Ｂは、拡大体ＧＦ（ｑ^Ｌ）上の定数）である場合には、メンバＩＤがｍ_ｉであるメンバは、配布された結果自分が保持する分散情報Ｙ_Ａ，ｉ、Ｙ_Ｂ，ｉ、及び、Ｙ_ｃ，ｉから、ｔ_Ａ及びＹ_Ａ，ｉを入力とする分散定数乗算計算（分散定数乗算部１１０１の動作）、ｔ_Ｂ及びＹ_Ｂ，ｉを入力とする分散定数乗算計算（分散定数乗算部１１０１の動作）を行って、その２つの出力の分散加算（分散加算部５０１，６０１の動作）を行い、さらに、その加算結果とＹ_ｃ，ｉとの分散乗算計算（分散乗算部１５０３，１６０１の動作）を行ってＺ’_ｉを求める。その計算結果Ｚ’_ｉは、拡大体ＧＦ（ｑ^Ｌ）上の計算結果
Ｚ＝ｆ（Ｘ_１，Ｘ_２，…，Ｘ_ｎ）＝（ｔ_ＡＸ_Ａ＋ｔ_ＢＸ_Ｂ）×Ｘ_Ｃ
の（ランプ型（Ｌ，ｋ，ｎ）秘密分散法で分散された）分散情報となっている。
【０１５４】
図２３は、第３の実施形態における分散乗算における動作を示すフローチャートである。例えば、拡大体ＧＦ（ｑ^Ｌ）上の値Ａ＝（Ａ_０，Ａ_１，…，Ａ_Ｌ−１）、Ｂ＝（Ｂ_０、Ｂ_１，…，Ｂ_Ｌ−１）の乗算を行う場合を考える。まず、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、自身が保持する値Ａ及びＢの分散情報ａ_ｉ及びｂ_ｉより、その積ｃ’_ｉ＝ａ_ｉ×ｂ_ｉ、及び、紛失通信を用いて、上記式（４５）及び（４６）にあるような値ｄ_ｉ，ｐ及びｅ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を求める（ステップＳ２２０１）。ステップＳ２２０１は、図１８における乗算部１７０１（値ｃ’_ｉを求める）、及び、紛失通信計算部１７０２（値ｄ_ｉ，ｐ及びｅ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）を求める）における動作を表している。
【０１５５】
次に、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、ステップＳ２２０１で計算した値ｃ’_ｉ及びｄ_ｉ，ｐ，ｅ_ｉ，ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）から、式（４９）を用いて、Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を求める（ステップＳ２２０２）。ステップＳ２２０２は、図１８の分散情報計算部１７０３における動作を示している。
【０１５６】
次に、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、ステップＳ２２０２で計算した値Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）をランプ型（Ｌ，ｋ，ｎ）秘密分散法を用いて分散情報Ｆ_ｉ，ｐ（ｐ＝１，２，…，ｎ）を作り、メンバＩＤがｍ_ｐ（ｐ＝１，２，…，ｎであり、ｐ≠ｉであるもの）である他のメンバに分散情報Ｆ_ｉ，ｐを配布する（ステップＳ２２０３）。ステップＳ２２０３は、図１８の秘密分散計算部１７０４及び送信部１７０５における動作を示している。
【０１５７】
次に、メンバＩＤがｍ_ｉ（ｉ＝１，２，…，ｎ）である各メンバは、ステップＳ２２０３の動作により受け取った分散情報Ｆ_ｉ，ｐ（ｐ＝１，２，…，ｎ）をすべて加算し（上記式（４３））、値ｃ_ｉを求めて出力する（ステップＳ２２０４）。ステップＳ２２０４は、図１８の受信部１７０６及び加算部１７０７における動作を示している。
【０１５８】
［第３の実施形態の効果］
以上に説明したように、第３の実施形態によれば、第１及び第２の実施形態と同様に、関数ｆ（ただし、関数ｆは、加算、定数乗算、及び、乗算からなる関数）に対するマルチパーティ・プロトコル（各メンバの保持する秘密情報を公開しないまま、各メンバが分散計算を行うことにより、関数ｆの計算結果を得るプロトコル）において、関数ｆにおける拡大体ＧＦ（ｑ^Ｌ）上の計算を、各メンバの分散演算処理においては、その拡大体よりも小さな有限体ＧＦ（ｑ）上の計算のみを行うことで、達成することができる。このため、メンバそれぞれの分散演算処理における、演算量、演算回路に必要な回路規模、演算に必要な記憶容量、演算時間等の演算コストを削減することができる。
【０１５９】
また、第１及び第２の実施形態とは異なり、第３の実施形態においては、分散加算計算、分散定数乗算計算だけでなく、分散乗算計算も可能となる。
【０１６０】
なお、第１〜第３の実施形態においての「メンバ」は、必ずしも１人の人間である必要はなく、秘密情報を保持し、計算手段（分散秘密再構成計算部）を構成要素として持つ装置とすることもできる。すなわち、１人の人間が、上記装置を複数個持って処理を進めることができる。この場合には、１人の人間が、複数のメンバとなる。また、１台の上記装置を複数の人間が管理して処理を進めることもできる。この場合は、複数の人間が、１人のメンバとなる。
【０１６１】
≪第４の実施形態≫
第１〜３の実施形態において、各メンバにおける分散計算部３０５−ｉ、又は、１００５−ｉにおける分散計算に用いる分散情報は、必ずしもメンバの保有する秘密Ｘ_ｉの分散情報でなくとも分散計算は可能である。すなわち、外部（センタのようなものを仮定してもよい）から、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法で分散された分散情報を、目的とする関数ｆの計算に必要な分だけいくつか（メンバの数ｎよりも多くてもよい）与えられ、それを用いて分散計算するような分散処理部を構成することが可能である。そのような分散処理部を用いた分散計算方法を実施する構成（分散計算システム）の構成を図２４に示し、その分散処理部（分散計算装置）の構成を図２５（ａ）及び（ｂ）に示す。
【０１６２】
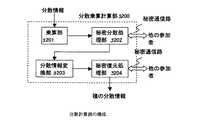
図２４に示されるように、第４の実施形態の秘密計算方法を実施する構成（分散計算システム）は、秘密分散送信部２３０１と、ｎ個の分散処理部２３０２−ｉ（ｉ＝１，２，…，ｎ）と、秘密再構成計算部２３０３とを有する。
【０１６３】
秘密分散送信部２３０１は、関数ｆへ入力する拡大体ＧＦ（ｑ^Ｌ）上の値の、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法で分散した分散情報を求め、各分散処理部２３０２−ｉ（ｉ＝１，２，…，ｎ）へ出力する。例えば、Ｄ＝ｆ（Ａ，Ｂ，Ｃ）（Ａ，Ｂ，Ｃ，Ｄは、拡大体ＧＦ（ｑ^Ｌ）上の値）を分散計算させる場合には、秘密分散送信部２３０１は、Ａ，Ｂ，Ｃをランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法で分散し、その分散情報ａ_ｉ，ｂ_ｉ，ｃ_ｉ（ｉ＝１，２，…，ｎ）を、各分散処理部２３０２−ｉへ出力する。
【０１６４】
図２５（ａ）及び（ｂ）に示されるように、各分散処理部２３０２−ｉは、秘密分散送信部２３０１からの出力を受信する分散情報受信部２４０６−ｉを持ち、その分散情報受信部２４０６−ｉで受信した分散情報を分散計算部２４０５−ｉへ出力する。
【０１６５】
分散計算部２４０５−ｉは、所望の関数ｆに、定数乗算及び乗算が含まれている場合には、他の分散処理部２３０２−ｉと秘密通信を行う秘密通信路１０３が備わっており、分散情報受信部２４０６−ｉから受け取った値、及び、受信部２４０４−ｉから受け取った値（図２５（ａ）の場合）を用いて、関数ｆの分散計算を行う。分散計算部２４０５−ｉの構成は、第１〜第３の実施形態のものと同様であり、分散計算結果を出力する。この分散計算部２４０５−ｉからの出力は、秘密再構成計算部２３０３へ入力される。秘密情報記憶部２４０１−ｉ、秘密分散計算部２４０２−ｉ、送信部２４０３−ｉ、及び、受信部２４０４−ｉは、第１〜第３の実施形態のものと同様である。また、分散情報受信部２４０６−ｉは、受信部２４０４−ｉと同等な機能を持つため、分散情報受信部２４０６−ｉの機能を受信部２４０４−ｉに持たせ、受信機能を一つのみ持つ構成とすることも可能である。
【０１６６】
図２４に示される秘密再構成計算部２３０３は、第１〜第３の実施形態の秘密再構成計算部と同様なものであり、最終的な関数ｆの計算結果を出力する。第１〜第３の実施形態のものと同様に、秘密再構成計算部２３０３における処理は、処理を統合するセンターのようなものが行ってもよいし、集まったメンバのうち、だれか１人、又は、複数人で行ってもよい。ただし、計算結果Ｚを必要としているメンバが行うのが望ましい。また、最終的な秘密再構成の処理（秘密再構成計算部２３０３の動作）は、誰か１以上の複数のメンバの分散処理部が行ってもよいので、そのような構成の分散処理部の構成を、図２６及び図２７（ａ）及び（ｂ）に示す。これは、第１〜第３の実施形態の分散処理部、及び、図２５（ａ）及び（ｂ）に示す分散処理部に、秘密再構成計算部が追加された形になる。図２６及び図２７（ａ）及び（ｂ）の構成においては、分散処理部自身で最終的な計算結果Ｚを再構成することができるので、分散計算部２５０５−ｉからの出力Ｚ’_ｉは、必要に応じて、分散処理部から外への出力として、出力するか否かを選択することができる。そのため、図２６及び図２７（ａ）及び（ｂ）においては、分散計算部２５０５−ｉからの出力を、破線の矢印で描いている。図２６及び図２７（ａ）及び（ｂ）の構成を持つ分散処理部が１以上の複数個含まれていれば、図１及び図２４の構成を持つ分散計算システムにおける、秘密再構成計算部１０２及び２３０３を備えなくても、最終の計算結果Ｚを得ることが可能となる。
【０１６７】
また、第２の実施形態において、図１３の拡大体乗算部１２０１の構成の説明において、式（３５）でＥ’_ｉ，０，Ｅ’_ｉ，１，…，Ｅ’_{ｉ，２（Ｌ−１）}を計算した後、式（３８）のＥ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を計算するようにしていたが、Ｌ＝２等の例を挙げている通り、式（４０）のように、Ｅ’_ｉ，０，Ｅ’_ｉ，１，…，Ｅ’_{ｉ，２（Ｌ−１）}を求めずに、直接Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を求めるようにしてもよい。
【０１６８】
また、同様に、第３の実施形態において、図１８の分散情報計算部１７０３の構成の説明で、式（４７）でＧ_ｕ，ｖ（ｕ＝０，１，２，…，Ｌ−１； ｖ＝０，１，２，…，Ｌ−１）、さらに、式（４８）でＥ’_ｉ，０，Ｅ’_ｉ，１，…，Ｅ’_{ｉ，２（Ｌ−１）}を計算した後、式（４９）のＥ_ｉ＝（Ｅ_ｉ，０、Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を計算するようにしていたが、Ｌ＝２の例を挙げている通り、式（５０）のようにＧ_ｕ，ｖ（ｕ＝０，１，２，…，Ｌ−１； ｖ＝０，１，２，…，Ｌ−１）、及び、Ｅ’_ｉ，０，Ｅ’_ｉ，１，…，Ｅ’_{ｉ，２（Ｌ−１）}を求めずに、直接Ｅ_ｉ＝（Ｅ_ｉ，０，Ｅ_ｉ，１，…，Ｅ_{ｉ，Ｌ−１}）を求めるようにしてもよい。
【０１６９】
第３の実施形態における、紛失通信計算部１７０２において、▲１▼通信計算受信部１８０１−ｐ（ｐ＝１，２，…，ｉ−１）を通信計算送信部に置き換え、さらに、通信計算送信部１８０３−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）を通信計算受信部に置き換えた構成、又は、▲２▼通信計算受信部１８０２−ｐ（ｐ＝１，２，…，ｉ−１）を通信計算送信部に置き換え、さらに、通信計算送信部１８０４−ｐ（ｐ＝ｉ＋１，ｉ＋２，…，ｎ）を通信計算受信部に置き換えた構成、又は、▲３▼通信計算受信部をすべて通信計算送信部に、さらに、通信計算送信部をすべて通信計算受信部に置き換えた構成、などの構成でも、同じ動作や効果を得ることができる。
【０１７０】
第３の実施形態における、紛失通信計算部１７０２において、通信計算送信部１８０１−ｐ（又は１８０２−ｐ）と通信計算受信部１８０３−ｊ（又は１８０４−ｊ）との間の秘密通信路１０３における情報のやり取りは、式（５１）や式（５３）〜（５５）のように、暗号化されたような情報、すなわち、法ｑのもとにおける離散対数を計算することが困難であること利用して送りたい情報を隠蔽している情報なので、とくに秘密に通信しなくても、メンバの秘密情報や分散計算の途中結果などが露呈されることはない。式（５１）においては、送りたい情報ａ_ｉ（又はｂ_ｉ）を有限体ＧＦ（ｑ）の生成元ｈのべき数として隠蔽し、式（５３）〜（５５）で得られる情報から得るべき必要な情報ａ_ｉ（ａ−１）−ｄ_ｉ，ｐ（又はｂ_ｉ（ａ−１）−ｅ_ｉ，ｐ）は、式（５１）で用いた乱数ｒＡ_ｐ，ｉ（又はｒＢ_ｐ，ｉ）を知らないと算出できないようになっている。したがって、上記における通信においては、秘密通信路ではなく、放送型の通信路や盗聴される可能性のある通信路で通信してもよい。
【０１７１】
≪第５の実施形態≫
本発明の第５〜第７の実施形態に係る分散計算においては、第１〜第４の実施形態と同様に、従来用いられている（ｋ，ｎ）しきい値秘密分散法に代えて、ランプ型秘密分散法（すなわち、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法）を用いる。以下の説明においては、秘密情報や乱数などの変数はすべてある有限体ＧＦ（ｑ）上の元であるとする。第１〜第４の実施形態では、しきい値ｋと分散情報の個数ｎとの間にはｋ≦ｎと言う関係が成り立っていたが、第５〜第７の実施形態では、２ｋ−１≦ｎという関係が成り立っているものとする。
【０１７２】
第１〜第４の実施形態においては、式（１９）のようなｋ−１次多項式を利用して分散情報を計算していたが、第５〜第７の実施形態においては、次式（５７）のような（ｋ−１）次多項式を利用して分散情報を計算する。
【数３５】

【０１７３】
ここで、Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１はそれぞれ、秘密情報であり、Ｒ_０，…，Ｒ_{ｋ−Ｌ−１}はそれぞれ、ランダムな値である。また、ｇ（ｘ）は、Ｌ次の既約多項式であり、第１〜第４の実施形態における、式（３６）の生成多項式ｇ（ｘ）に相当するものである。この既約多項式は予め与えられるものとする。メンバＩＤ（すなわち、ＩＤ情報）ｗ_ｉをもっているメンバ（すなわち、参加者）に渡す分散情報はｆ（ｗ_ｉ）となる。各メンバが持っているメンバＩＤ＿ｗ_ｉは公開されているものとする。第１〜第４の実施形態では、メンバＩＤをｍ_ｉ（ｉ＝１，２，…，ｎ）と表記していたが、第５〜第７の実施形態では、メンバＩＤをｗ_ｉ（ｉ＝０，１，…，ｎ−１）と表記し、メンバＩＤがｗ_ｉであるメンバのことを、メンバＰ_ｉと呼ぶことにする。
【０１７４】
第５〜第７の実施形態においては、秘密情報（Ｓ_０，…，Ｓ_Ｌ−１）を既約多項式ｇ（ｘ）を利用して有限体ＧＦ（ｑ）のＬ次拡大体ＧＦ（ｑ^Ｌ）の値として扱う。つまり、方程式ｇ（ｘ）＝０の解をαとしたときに、
Ｓ＝Ｓ_Ｌ−１α^Ｌ−１＋…＋Ｓ_１α＋Ｓ_０
と表す。これより、秘密情報に関する計算は、有限体ＧＦ（ｑ^Ｌ）上の演算で表すことができ、これはｇ（ｘ）を法とする多項式の加算や乗算で実現することができる。
【０１７５】
メンバＩＤがｗ_ｉであるメンバＰ_ｉ（ｉ＝０，…，ｎ−１）に、それぞれｆ（ｗ_ｉ）を分散情報として渡す。このときの分散情報のサイズは、秘密情報の１／Ｌとなっている。秘密情報の復元は、（ｋ，ｎ）しきい値法と同様に、多項式を復元し、さらにその後、ｍｏｄ ｇ（ｘ）を計算する。
【０１７６】
［第５の実施形態の構成］
以下、第５の実施形態においてはランプ型秘密分散を利用した分散計算について説明する。特に、分散計算の具体例として、分散加算を行うものとする。この点から、第５の実施形態は、上記第１の実施形態と類似した内容となるが、分散情報の生成方法が異なる。
【０１７７】
第５の実施形態は、秘密分散及び秘密復元（再構成）、また分散計算を行うシステムについて説明する。特に、分散計算の具体例として、分散加算を行うものとする。以下、分散計算において、秘密情報をＡ＝（Ａ_０，…，Ａ_Ｌ−１）及びＢ＝（Ｂ_０，…，Ｂ_Ｌ−１）とする。そして、メンバＩＤがｗ_ｊであるメンバがもつ分散情報は、次式（５８）を用いて、それぞれａ（ｗ_ｊ）及びｂ（ｗ_ｊ）とする。
【数３６】

【０１７８】
このとき、分散情報の和を表す多項式は次式（５９）のようになる。
【数３７】

【０１７９】
これより、次式（６０）が得られる。
【数３８】

【０１８０】
この式に、ｘ＝αを代入すると、右辺は拡大体ＧＦ（ｑ^Ｌ）における加算を表している。したがって、
ｃ_ｊ＝ａ（ｗ_ｊ）＋ｂ（ｗ_ｊ）
は秘密情報Ａ及びＢの和である値Ｃ（＝Ａ＋Ｂ）の分散情報を表している。したがって、分散加算においては、メンバＰ_ｊは、持っている分散情報の和を計算すればよい。
【０１８１】
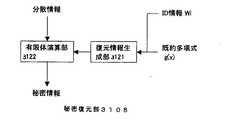
第５の実施形態に係る分散計算システムの構成は、図１、又は、図２４にある、第１〜第４の実施形態に係る分散計算システムと同様なものになる。第５の実施形態は、第１〜第４の実施形態とは、分散情報を生成するランプ型秘密分散法が異なることから、それぞれの構成要素、秘密分散送信部２３０１、分散処理部１０１，２３０２、及び秘密再構成計算部１０２，２３０３の内部の構成や動作が異なる。図２８は、第５の実施形態に係る分散計算装置（図１、図２４の分散計算処理部１０１，２３０２に相当する）の構成を示すブロック図である。図２８に示されるように、第５の実施形態に係る分散計算装置は、秘密分散部分３００１と、分散計算部分３００２と、秘密復元部分３００３と、秘密通信路１０３とを有する。図２８に示される秘密分散部分３００１は、秘密分散部３１０１と、送信部３１０２とを有する。また、図２８に示される分散計算部分３００２は、受信部３１０３と、記憶部３１０４と、分散計算部３１０５と、送信部３１０６とを有する。さらに、図２８に示される秘密復元部分３００３は、受信部３１０７と、秘密復元部３１０８とを有する。分散計算装置は、秘密分散部分３００１、分散計算部分３００２、及び、秘密復元部分３００３のうち、いずれか１つ又は２つしか持たない場合もありうる（後の図３１〜図３３で説明する）。
【０１８２】
秘密分散部３１０１は、秘密情報についてランプ型秘密分散を実行して分散情報を計算する。送信部３１０２は、他のメンバとそれぞれ秘密通信路１０３でつながっており、一対一の秘密通信を行う。そして、計算結果を他のメンバに配布する。その結果、各メンバは分散情報を得る。
【０１８３】
受信部３１０３は、他のメンバ若しくはメンバとは別に設けられたセンターから上記分散情報を受け取る。この結果、メンバは分散情報を保持する。記憶部３１０４は、秘密分散で得られた分散情報及び分散計算の結果を保持する。分散計算部３１０５は、記憶部３１０４で保持されている分散情報について計算を行う。そして、秘密情報についての任意の演算結果の分散情報を得る。
【０１８４】
第５の実施形態においては、分散計算部３１０５は、秘密情報の和の分散情報を求める場合について示す。一般に、分散計算部３１０５は、第５の実施形態で示す分散加算、後述する第６の実施形態で示す分散乗算、及び、後述する第７の実施形態で示す分散定数乗算の組み合わせで構成される。送信部３１０６は、分散計算の結果を配布する。ここで、送信部３１０６についても、秘密通信路１０３を介して、分散情報の配布を行う。ここで、受信部３１０３、記憶部３１０４、分散計算部３１０５、送信部３１０６は、各メンバが持っている。
【０１８５】
受信部３１０７は、他のメンバから分散計算結果を受け取る。秘密復元部３１０８は、全てのメンバから受け取った分散情報を用いて秘密情報の復元（再構成）をする。送信部３１０２と送信部３１０６、及び受信部３１０３と受信部３１０７は、メンバが同時に持つ際は、共通化した構成にしてもよい。
【０１８６】
図２９は、図２８の秘密分散部３１０１の構成を示すブロック図である。図２９に示されるように、秘密分散部３１０１は、乱数生成部３１１１と、有限体演算部３１１２とを有する。乱数生成部３１０１は、秘密分散計算を行う際に利用する乱数を生成する。有限体演算部３１１２は、秘密情報、メンバのメンバＩＤ、上記生成された乱数、及び既約多項式から分散情報を生成する。
【０１８７】
図３０は、図２８の秘密復元部３１０８の構成を示すブロック図である。図３０に示されるように、秘密復元部３１０８は、復元情報生成部３１２１と、有限体演算部３１２２とを有する。復元情報生成部３１２１は、メンバＩＤ及び既約多項式から秘密復元に利用する情報を生成する。有限体演算部３１２２は、上記生成した情報及び分散情報から秘密情報の復元計算を行う。
【０１８８】
図２８に示される秘密分散部分３００１は、秘密分散を行う部分である。図２８に示される分散計算部分３００２は、分散情報を受け取って、分散計算を実行する部分である。図２８に示される秘密復元部分３００３は、最後に、分散計算結果を集めて、もとの秘密情報の計算結果を復元する部分である。図２８に示される秘密分散部分３００１である秘密分散部３１０１及び送信部３１０２は、各メンバが持っていてもよいし、メンバとは独立したセンターが持っていてもよい。図２８に示される秘密復元部分３００３である受信部３１０７及び秘密復元部３１０８は、少なくとも１人のメンバが持っていてもよいし、メンバとは独立したセンターが行ってもよい。
【０１８９】
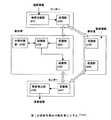
以下、メンバが保持する秘密情報について分散計算を行い、計算結果をメンバが得る場合についての分散計算システムの構成を図３１に示す。「参加者」で示しているブロックが、各メンバの分散計算装置であり、図では２つしか描かれていないが、実際にはｎ個存在する。各参加者はそれぞれ、秘密分散部分３００１、分散計算部分３００２、及び、秘密復元部分３００３を有している。また、メンバが保持する秘密情報についての分散計算を行い、センターが計算結果を得る場合についての分散計算システムの構成を図３２に示す。図３２は、図１の分散計算システムと同様な構成図である。「参加者」で示しているブロックが、各メンバの分散計算装置であり、図では２つしか描かれていないが、実際にはｎ個存在する。また、「センター」で示しているブロックが、最終的に計算結果を復元する部分であり、図１の秘密再構成計算部１０２に相当する部分である。各参加者はそれぞれ、秘密分散部分３００１、及び、分散計算部分３００２を有している。また、センターが持っている秘密情報についての分散計算を行い、センターが計算結果を得る場合についての分散計算システムの構成を図３３に示す。図３３は、図２４の分散計算システムと同様な構成図である。「参加者」で示しているブロックは、各メンバの分散計算装置であり、図では２つしか描かれていないが、実際にはｎ個存在する。また、上部の「センター」で示しているブロック（秘密分散部３１０１、及び、送信部３１０２からなる部分）は、秘密情報を分散する部分であり、図２４の秘密分散送信部２３０１に相当する部分である。また、下部の「センター」で示しているブロック（秘密復元部３１０８、及び、受信部３１０７からなる部分）は、最終的に計算結果を復元する部分であり、図２４の秘密再構成計算部２３０３に相当する部分である。各参加者はそれぞれ、分散計算部分３００２を有している。
【０１９０】
［第５の実施形態の動作］
第５の実施形態においては、ランプ型秘密分散法を利用した分散計算について手順を示す。分散計算の具体例として、各メンバが保持する秘密情報から秘密分散を行って分散情報を得て、分散情報から元の秘密情報の和を求める手順を示す。
【０１９１】
最初に秘密分散における動作を示す。秘密情報をＳ＝（Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１）とする。秘密情報Ｓ＝（Ｓ_０，Ｓ_１，…，Ｓ_Ｌ−１）及びランダムに生成した値Ｒ_０，…，Ｒ_{ｋ−Ｌ−１}と、次式（６１）
【数３９】

のような多項式を用いて、次式（６２）に示される、メンバＰ_ｊ向けの分散情報ｓ_ｊを生成する。
【数４０】

【０１９２】
この計算は、次のようなｎ×ｎ行列
Ｅ＝（ｅ_ｉｊ）
ｅ_ｉｊ＝ｗ_ｉ^ｊ（ｉ＝０，…，ｎ−１； ｊ＝０，…，ｎ−１）
を用いて、
（ｓ_０，…，ｓ_ｎ−１）^ｔ
＝Ｅ（ｆ_０，ｆ_１，…，ｆ_ｋ−１，０，…，０）^ｔ
のように表すことができる。そして、分散情報ｓ_ｊをメンバＰ_ｊに渡す。
【０１９３】
秘密復元のために集まった分散情報をｔ個（ｔ≧ｋ）とする。まず、秘密復元の各メンバＰ’_ｊから分散情報ｓ’_ｊ及び各メンバのメンバＩＤ ｗ’_ｊ（ｊ＝０，…，ｔ−１）を受け取っておく。そして、次式（６３）の連立方程式から、多項式の係数ｆ_０，ｆ_１，…，ｆ_ｋ−１を求める。
ｓ’_ｊ＝ｆ_ｋ−１ｗ’_ｊ^ｋ−１＋…＋ｆ_１ｗ’_ｊ＋ｆ_０ …（６３）
ここで、ｊ＝０，…，ｔ−１である。
【０１９４】
そして、得られた多項式について、既約多項式ｇ（ｘ）による剰余（次式（６４）を計算する。
【数４１】

得られた多項式の係数が復元された秘密情報にあたる。
【０１９５】
この計算は、以下に示すような行列を利用した計算と等価である。既約多項式ｇ（ｘ）を法とする多項式の剰余算を表す行列をＧとしておく。そして、メンバのメンバＩＤ＿ｗ’_ｉから、ｔ×ｔ行列
Ｅ’＝（ｅ’_ｉｊ）
ｅ’_ｉｊ＝ｗ’_ｉ^ｊ（ｉ＝０，…，ｔ−１； ｊ＝０，…，ｔ−１）を生成する。行列Ｇ、及び、行列Ｅ’の逆行列Ｅ’^−１より、行列Ｒ＝ＧＥ’^−１＝（ｒ_ｉｊ）を計算する。このようにして得られたｒ_ｉｊを用いて、次式（６５）の計算を実行する。
【数４２】

その結果得られるＳ_０，…，Ｓ_Ｌ−１が復元された秘密情報である。
【０１９６】
ここで、行列Ｇの生成方法について説明する。行列Ｇは、（ｔ−１）次多項式
ｈ（ｘ）＝ｈ_ｔ−１ｘ^ｔ−１＋…＋ｈ_１ｘ＋ｈ_０
を既約多項式
ｇ（ｘ）＝ｘ^Ｌ＋…＋ｇ_１ｘ＋ｇ_０
で割った余りである、次式（６６）
【数４３】

より、次式（６７）のようにして行列Ｇを得る。
【０１９７】
【数４４】

【０１９８】
例えば、ＧＦ（３１）、ｔ＝１６、既約多項式ｇ（ｘ）＝ｘ^３＋ｘ＋３の場合において、行列Ｇを計算した結果は以下のようになる。１５次多項式（式（６８）を以下のように定義する。
【数４５】

【０１９９】
既約多項式ｇ（ｘ）を法とした剰余算の結果は次式（６９）のようになる。
【数４６】

【０２００】
これより、行列Ｇは次式（７０）のようになる。
【数４７】

【０２０１】
次に、分散計算における動作を説明する。第５の実施形態においては具体例として分散加算について説明する。メンバＰ_ｊは秘密情報Ａ及びＢの分散情報ａ_ｊ及びｂ_ｊを持っているものとする。分散加算においては、各メンバが保持する分散情報の和を計算すればよい。つまり、各メンバが保持する秘密情報の和Ａ＋Ｂの分散情報を求めるためには、メンバＰ_ｊは分散情報の和ａ_ｊ＋ｂ_ｊを計算すればよい。
【０２０２】
［第５の実施形態の効果］
以上に説明したように、各メンバの行う演算は、もとの秘密情報が定義される有限体（上記説明においてはＬ次拡大体）より小さな有限体で行うことができる。これより、各メンバはより少ない計算資源で秘密情報に関する加算を実行することが可能となる。
【０２０３】
≪第６の実施形態≫
本発明の第６の実施形態においては、具体例として分散乗算散について説明する。秘密情報をＡ＝（Ａ_０，…，Ａ_Ｌ−１）及びＢ＝（Ｂ_０，…，Ｂ_Ｌ−１）とする。分散情報は以下の多項式（式（７１））から計算する。
【数４８】

【０２０４】
このとき、分散情報の積を表す多項式は次式（７２）のようになる。
【数４９】

【０２０５】
これより、次式（７３）が成り立つ。
【数５０】

【０２０６】
これに、ｘ＝αを代入すると、これは拡大体ＧＦ（ｑ^Ｌ）上における乗算となっている。したがって、ａ（ｗ_ｉ）ｂ（ｗ_ｉ）は、２（ｋ−１）次多項式による値ＡＢの分散情報を表している。ただし、従来と同様に、秘密情報を変えないように、多項式の次数を下げる変換操作（ＢＰＢ^−１）Ｃ＝Ｄが必要となる（従来技術の説明の分散乗算（方式▲２▼）におけるステップＳ２０３の処理に相当し、Ｃ＝（ａ（ｗ_０）ｂ（ｗ_０），ａ（ｗ_１）ｂ（ｗ_１），…，ａ（ｗ_ｎ−１）ｂ（ｗ_ｎ−１））である）。従来のＳｈａｍｉｒ法による（ｋ，ｎ）しきい値秘密分散法においては、秘密情報は多項式の定数項であった。したがって、行列Ｐは単にｋ次以上の項の係数を０とする演算（式（８０）を満たす行列Ｐ）でよい。
Ｐ（ｘ_１、ｘ_２、…、ｘ_ｎ）^ｔ
＝（ｘ_１、ｘ_２、…、ｘ_ｋ、０、…、０） …（８０）
【０２０７】
一方、ランプ型秘密分散法においては、秘密情報は式（６１）の多項式ｆ（ｘ）の
Ｓ_Ｌ−１ｘ^Ｌ−１＋…＋Ｓ_１ｘ＋Ｓ_０
の部分、つまりｇ（ｘ）で割った余りである。これより、行列Ｐは、ｍｏｄ ｇ（ｘ）において合同となるように多項式の次数を２（ｋ−１）次から（ｋ−１）次に下げる演算とすればよい。
【０２０８】
［第６の実施形態の構成］
第６の実施形態においては、第５の実施形態における分散計算について、秘密情報の積を計算する分散乗算を実現する装置について示す。しかし、同じように秘密情報の積を計算する分散乗算を実現する第３の実施形態とは、分散情報の生成方法が異なる（第３の実施形態では、式（１９）にあるようなｋ−１次多項式から分散情報を生成し、第６の実施形態では、式（５７）にあるようなｋ−１次多項式から分散情報を生成する）ことから、構成や動作は、全く異なったものとなっている。第６の実施形態においては、ある秘密情報Ａ，Ｂについての分散情報（ａ_０，…，ａ_ｎ−１），（ｂ_０，…，ｂ_ｎ−１）が与えられており、分散情報（ａ_０，…，ａ_ｎ−１），（ｂ_０，…，ｂ_ｎ−１）から秘密情報の積Ｄ（＝ＡＢ）の分散情報（ｄ_０，…，ｄ_ｎ−１）を計算する。
【０２０９】
図３４は、分散乗算を行う場合における、分散計算部の構成を示すブロック図である。図３４に示されるように、分散乗算計算部３２００は、乗算部３２０１と、秘密分散処理部３２０２と、分散情報変換部３２０３と、秘密復元処理部３２０４とを有する。乗算部３２０１においては、メンバが保持する分散情報の積を計算する。秘密分散処理部３２０２においては、乗算部で計算した値について秘密分散を行う。ここでは、ランプ型秘密分散法ではなく、（ｋ，ｎ）しきい値秘密分散を用いて分散情報を生成する（このときのしきい値は、秘密分散部３１０１におけるランプ型（Ｌ，ｋ，ｎ）秘密分散法におけるしきい値ｋとは異なる値ｋ’（ｋ’≦ｎ）でもよい）。分散情報変換部３２０３においては、秘密分散処理部３２０２で得られた第２の分散情報について、変換を行う。秘密復元処理部３２０４においては、分散情報変換部３２０３で計算した結果について秘密復元処理を行う。乗算結果を他のメンバと交換し、その結果得られた分散情報を復元する。ここでは、秘密分散処理部３２０２と同様に、（ｋ，ｎ）しきい値法を用いて秘密復元の計算を行う（このときのしきい値は、秘密分散処理部３２０２におけるしきい値と同じ値を用いる）。
【０２１０】
［第６の実施形態の動作］
第６の実施形態においては、分散計算によって、秘密情報Ａ，Ｂの分散情報ａ_ｉ（ｉ＝０，…，ｎ−１）及びｂ_ｉ（ｉ＝０，…，ｎ−１）から、秘密情報の積ＡＢの分散情報を計算する手順を示す。分散乗算においては、各メンバの保持する分散情報の積を変換しなければならない。そして、変換の際にはメンバ間で分散情報に関するやり取りが必要である。
【０２１１】
処理の手順は図３５のようになる。ここで、メンバＰ_ｊ（ｊ＝０，…，ｎ−１）は、各メンバのメンバＩＤ＿ｗ_ｉ（ｉ＝０，…，ｎ−１）及び、分散情報ａ_ｊ及びｂ_ｊを受け取っているものとする。以下においては、便宜上行列を利用して説明する。
【０２１２】
図３５に示されるように、ステップ１において、メンバＰ_ｉは分散情報の積ｃ_ｉ＝ａ_ｉｂ_ｉを計算する。この分散情報の積ｃ_ｉは秘密情報Ａ及びＢの積ＡＢの分散情報となるが、秘密分散を行う多項式の次数が２（ｋ−１）であり、都合が悪い。そこで、以下のステップにおいては、秘密分散、配布（ステップ２、３）、変換処理（ステップ４）、計算結果の分散情報の交換、及び、計算結果の復元（ステップ５、６）の処理を行うことによって、得られた分散情報を、しきい値がｋとなるように変換を行う。
【０２１３】
ステップ２において、メンバＰ_ｉは分散情報の積ｃ_ｉについて秘密分散を行う。ここにおける秘密分散は（ｋ’，ｎ）しきい値法（ｋ’≦ｎ）を利用する。メンバＰ_ｉは、分散情報の積ｃ_ｉ及び乱数からランダムなｋ’−１次の多項式（式（７４））を生成し、分散情報ｃ_ｉ，ｊ（ｊ＝０，…，ｎ−１）を計算する。
【数５１】

ここで、Ｒ_ｉ，ｍ（ｍ＝１，…，ｋ’−１）はメンバＰ_ｉがランダムに生成する数値である。
【０２１４】
これは、次のようなｎ×ｎ行列Ｅ＝（ｅ_ｉｊ）を用いて、次式（７５）のように表すことができる。
【数５２】

【０２１５】
ステップ３において、他のメンバと通信を行って、分散情報ｃ_ｉ，ｊを交換する。メンバＰ_ｉは、上記計算した（ｃ_ｉ，０，…，ｃ_{ｉ，ｎ−１}）について、ｃ_ｉ，ｊ（ｊ＝０，…，ｎ−１であり、ｊ≠ｉであるもの）を、メンバＰ_ｊに配布する。この結果、メンバＰ_ｊは（ｃ_０，ｊ，…，ｃ_{ｎ−１，ｊ}）を受け取る。
【０２１６】
ステップ４において、Ｐ_ｊはＣ_ｊ＝（ｃ_０，ｊ，…，ｃ_{ｎ−１，ｊ}）（２（ｋ−１）次多項式由来）を、Ｄ_ｊ＝（ｄ_０，ｊ，…，ｄ_{ｎ−１，ｊ}）（（ｋ−１）次多項式由来）に変換する。変換は、例えば、以下のように生成される行列Ｐ及び行列Ｅを用いた際の、Ｄ_ｊ＝（ＥＰＥ^−１）Ｃ_ｊと等価な計算である。つまり、ＥＰＥ^−１＝（ｐ_ｉｊ）について、ｄ_ｉｊ＝Σ_ｋ ｐ_ｉｋｃ_ｋｊ（ｉ＝０，…，ｎ−１）を計算する。
【０２１７】
ここで、行列Ｐは、秘密分散における多項式を２（ｋ−１）次から（ｋ−１）次に下げるような変換であり、ｍｏｄ ｇ（ｘ）において合同となるように多項式の次数を下げる演算である。図３６に、変換行列Ｐの生成方法の一例を示す。そして、具体的に、ＧＦ（３１）、ｋ＝８（これは、秘密分散部３１０１におけるランプ型秘密分散のしきい値である）、ｎ＝１６、既約多項式ｇ（ｘ）＝ｘ^３＋ｘ＋３の場合において、行列Ｐを計算した結果は以下のようになる。１４次（２（ｋ−１）次に相当）多項式を次式（７６）のように定義する。
【数５３】

【０２１８】
上記演算の結果、７次に次数を下げたｍｏｄ ｇ（ｘ）において合同な多項式は次式（７７）のようになる。
【数５４】

【０２１９】
これより、行列Ｐは次式（７８）のようになる。
【０２２０】
【数５５】

【０２２１】
ステップ５において、他のメンバと通信を行って、情報ｄ_ｉ，ｊを交換する。メンバＰ_ｊは情報ｄ_ｉ，ｊ（ｉ＝０，…，ｎ−１； ｉ≠ｊ）をＰ_ｉに配布する。この結果、メンバＰ_ｉは（ｄ_ｉ，０，…，ｄ_{ｉ，ｎ−１}）を受け取る。
【０２２２】
ステップ６において、メンバＰ_ｉは秘密復元の計算を行う。メンバＰ_ｉは（ｄ_ｉ，０，…，ｄ_{ｉ，ｎ−１}）から情報Ａ，Ｂの積ＡＢの分散情報であるｄ_ｉを式（７９）により計算する。ここでの復元操作は（ｋ’，ｎ）しきい値法における秘密復元を行う。
【数５６】

【０２２３】
以上の計算を行うことで、しきい値がｋであるような、秘密情報の積ＡＢの分散情報ｄ_ｉを得ることができる。
【０２２４】
［第６の実施形態の効果］
以上に説明したように、各メンバの行う演算は、もとの秘密情報が定義される有限体（上記説明においてはＬ次拡大体）より小さな有限体で行うことができる。これより、第５の実施形態の加算に加えて、乗算についても同様に、各メンバはより少ない計算資源で実行することが可能となる。
【０２２５】
≪第７の実施形態≫
［第７の実施形態の構成］
本発明の第７の実施形態においては、メンバ間で共有している定数Ｃと、秘密情報Ｓとの定数倍ＣＳの分散情報を計算する。しかし、同じように秘密情報の定数の積を計算する分散定数乗算を実現する第２の実施形態とは、分散情報の生成方法が異なる（第２の実施形態では、式（１９）にあるようなｋ−１次多項式から分散情報を生成し、第７の実施形態では、式（５７）にあるようなｋ−１次多項式から分散情報を生成する）ことから、構成や動作は、全く異なったものとなっている。（ｋ，ｎ）しきい値法を利用した定数倍については、自分の保持する分散情報を定数倍することで得られるが、本発明においては、定数は拡大体ＧＦ（ｑ^Ｌ）の元となりうる。このとき、定数倍の結果の分散情報が基礎体の元となるように分散計算を行う必要がある。
【０２２６】
第７の実施形態の分散定数乗算を行う場合における、分散計算部の構成を示すブロック図は、図３７のようになる。図３７において、分散定数算乗算部は、分散乗算装置３２００（図３４）及び定数情報生成部３３０１とを有する。定数情報生成部３３０１は、拡大体ＧＦ（ｑ^Ｌ）で定義された、メンバ間で共通の定数とメンバＩＤから定数の分散情報を生成する。そして、分散乗算装置は、秘密情報Ｓの分散情報と、上記定数情報生成部３３０１で生成された定数Ｃの分散情報との積を分散乗算計算部３２００で計算する。
【０２２７】
［第７の実施形態の動作］
秘密情報Ｓに対する、メンバＰ_ｊの保持する分散情報をｓ_ｊとする。拡大体ＧＦ（ｑ^Ｌ）で表される定数Ｃ＝（Ｃ_０，…，Ｃ_Ｌ−１）から、以下のようにして情報ｃ_ｊを計算する。
ｃ_ｊ＝Ｃ_０＋Ｃ_１ｗ_ｊ＋…＋Ｃ_Ｌ−１ｗ_ｊ^Ｌ−１
定数Ｃはメンバ間で共有しているので、メンバＰ_ｊは、自分の持つべき情報ｃ_ｊを生成することができる。
【０２２８】
以下、分散乗算と同様の手順によって、情報ｃ_ｊと分散情報ｓ_ｊとをもとに、定数乗算ＣＳの分散情報を計算することができる。
【０２２９】
このとき、次数の変換は（ｋ＋Ｌ−２）次から（ｋ−１）次への変換となるので、図３６における行列Ｐの生成において、２（ｋ−１）の部分をｋ＋Ｌ−２と置き換えた図３８のようになる。この分散乗算における行列Ｐにおける非ゼロ部分をより少なくすることができ、演算量を少なくすることができる。
【０２３０】
［第７の実施形態の効果］
以上に説明したように、第５及び第６の実施形態の加算及び乗算に加えて、メンバ間で共有している、拡大体ＧＦ（ｑ^Ｌ）で表される定数についての定数倍についても同様に、各メンバはより少ない計算資源で実行することが可能となる。
【０２３１】
【発明の効果】
以上に説明したように、本発明によれば、関数ｆにおける拡大体ＧＦ（ｑ^Ｌ）上の計算を、各メンバの分散演算処理においては、その拡大体ＧＦ（ｑ^Ｌ）よりも小さな有限体ＧＦ（ｑ）上の計算のみを行うことで、達成することができるので、メンバそれぞれの分散演算処理における、演算量、演算回路に必要な回路規模、演算に必要な記憶容量、演算時間等の演算コストを削減することができるという効果がある。
【図面の簡単な説明】
【図１】本発明の第１の実施形態に係る分散計算方法を実施する構成（分散計算システム）を示すブロック図である。
【図２】マルチパーティ・プロトコルの概念説明図である。
【図３】図１の秘密再構成計算部の構成を示すブロック図である。
【図４】図１の分散処理部（分散計算装置）の構成を示すブロック図である。
【図５】図４の秘密分散計算部の構成を示すブロック図である。
【図６】図４の分散計算部の例（その１）の構成を示すブロック図である。
【図７】図４の分散計算部の例（その２）の構成を示すブロック図である。
【図８】図６又は図７の分散加算部の構成を示すブロック図である。
【図９】本発明の第１の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を示すフローチャートである。
【図１０】本発明の第１の実施形態おける分散加算の動作を示すフローチャートである。
【図１１】本発明の第２の実施形態に係る分散処理部（分散計算装置）の構成を示すブロック図である。
【図１２】図１１の分散計算部の構成を示すブロック図である。
【図１３】図１２の分散定数乗算部の構成を示すブロック図である。
【図１４】本発明の第２の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を示すフローチャートである。
【図１５】本発明の第２の実施形態における分散定数乗算の動作を示すフローチャートである。
【図１６】本発明の第３の実施形態における分散計算部（その１）の構成を示すブロック図である。
【図１７】本発明の第３の実施形態における分散計算部（その２）の構成を示すブロック図である。
【図１８】図１６及び図１７の分散乗算部の構成を示すブロック図である。
【図１９】図１８の紛失通信計算部の構成を示すブロック図である。
【図２０】図１９の通信計算受信部の構成を示すブロック図である。
【図２１】図１９の通信計算送信部の構成を示すブロック図である。
【図２２】本発明の第３の実施形態に係る分散計算方法を実施する構成（分散計算システム）の動作を示すフローチャートである。
【図２３】本発明の第３の実施形態における分散乗算の動作を示すフローチャートである。
【図２４】本発明の第４の実施形態に係る分散計算方法を実施する構成（分散計算システム）を示すブロック図である。
【図２５】（ａ）及び（ｂ）のそれぞれは、図２４の分散処理部（分散計算装置）の構成を示すブロック図である。
【図２６】図２５の分散処理部（分散計算装置）の変形例（その１）の構成を示すブロック図である。
【図２７】（ａ）及び（ｂ）のそれぞれは、図２５の分散処理部（分散計算装置）の変形例（その２）の構成を示すブロック図である。
【図２８】本発明の第５の実施形態に係る分散計算装置の構成を示すブロック図である。
【図２９】図２８の秘密分散部の構成を示すブロック図である。
【図３０】図２８の秘密復元部の構成を示すブロック図である。
【図３１】本発明の第５の実施形態に係る分散計算システム（その１）の構成を示すブロック図である。
【図３２】本発明の第５の実施形態に係る分散計算システム（その２）の構成を示すブロック図である。
【図３３】本発明の第５の実施形態に係る分散計算システム（その３）の構成を示すブロック図である。
【図３４】第５〜第７の実施形態の分散計算部が分散乗算を行う場合の構成を示すブロック図である。
【図３５】第５〜第７の実施形態の分散計算部が分散乗算を行う場合の処理手順を示すフローチャートである。
【図３６】第５〜第７の実施形態における変換行列の生成手順の説明図である。
【図３７】本発明の第７の実施形態における分散定数乗算部の構成を示すブロック図である。
【図３８】第７の実施形態における変換行列の生成手順の説明図である。
【符号の説明】
１０１（１０１−１，…，１０１−ｎ） 分散処理部（分散計算装置）、
１０２ 秘密再構成計算部、
１０３ 秘密通信路、
２０１ 線形結合部、
３０１−ｉ 秘密情報記憶部、
３０２−ｉ 秘密分散計算部、
３０３−ｉ 送信部、
３０４−ｉ 受信部、
３０５−ｉ 分散計算部、
４０１−ｉ 多項式生成部、
４０２−ｉ 分散情報生成部、
４０３−ｉ 乱数生成部、
４０４−ｉ （ｋ−１）次多項式生成部、
５０１−１，…，５０１−（ｎ−１） 分散加算部、
６０１ 分散加算部、
７０１ 加算部、
１００１−ｉ 秘密情報記憶部、
１００２−ｉ 秘密分散計算部、
１００３−ｉ 送信部、
１００４−ｉ 受信部、
１００５−ｉ 分散計算部、
１１０１−１，…，１１０１−ｎ 分散定数乗算部、
１１０２−１，…，１１０２−（ｎ−１） 分散加算部、
１２０１ 拡大体乗算部、
１２０２ 秘密分散計算部、
１２０３ 送信部、
１２０４ 受信部、
１２０５ 加算部、
１５０１−１，…，１５０１−ｎ 分散定数乗算部、
１５０２−１，…，１５０２−（ｎ−１） 分散加算部、
１５０３ 分散乗算部、
１６０１ 分散乗算部、
１７０１ 乗算部、
１７０２ 紛失通信計算部、
１７０３ 分散情報計算部、
１７０４ 秘密分散計算部、
１７０５ 送信部、
１７０６ 受信部、
１７０７ 加算部、
１８０１−１，…，１８０１−（ｉ−１） 通信計算受信部、
１８０２−１，…，１８０２−（ｉ−１） 通信計算受信部、
１８０３−（ｉ＋１），…，１８０３−ｎ 通信計算送信部、
１８０４−（ｉ＋１），…，１８０４−ｎ 通信計算送信部、
１９０１ インデックス計算送信部、
１９０２ 受信復元部、
２００１ 乱数生成部、
２００２ 有限体要素生成部、
２００３−１，…，２００３−ｑ 乗数計算送信部、
２３０１ 秘密分散送信部、
２３０２（２３０２−１，…，２３０２−ｎ） 分散処理部（分散計算装置）、
２３０３ 秘密再構成計算部、
２４０１−ｉ 秘密情報記憶部、
２４０２−ｉ 秘密分散計算部、
２４０３−ｉ 送信部、
２４０４−ｉ 受信部、
２４０５−ｉ 分散計算部、
２４０６−ｉ 分散情報受信部、
２５０１−ｉ 秘密情報記憶部、
２５０２−ｉ 秘密分散計算部、
２５０３−ｉ 送信部、
２５０４−ｉ 受信部、
２５０５−ｉ 分散計算部、
２５０６−ｉ 分散情報受信部、
２５０７−ｉ 秘密再構成計算部、
３１０１ 秘密分散部、
３１０２ 送信部、
３１０３ 受信部、
３１０４ 記憶部、
３１０５ 分散計算部、
３１０６ 送信部、
３１０７ 受信部、
３１０８ 秘密復元部、
３１１１ 乱数生成部、
３１１２ 有限体演算部、
３１２１ 復元情報生成部、
３１２２ 有限体演算部、
３２００ 分散乗算計算部、
３２０１ 乗算部、
３２０２ 秘密分散処理部、
３２０３ 分散情報変換部、
３２０４ 秘密復元処理部、
３３０１ 定数情報生成部、
Ｘ_ｉ 分散計算装置が保持する秘密情報、
Ｙ_ｉ，ｊ 秘密情報Ｘ_ｉから生成された分散情報、
Ｚ’_ｉ 分散情報Ｙ_ｉ，ｊから生成された情報（秘密Ｚの分散情報）、
Ｚ もとの秘密、
ｈ_Ｘｉ（ｘ） 分散計算装置が生成する多項式、
ｍ_１，ｍ_２，…，ｍ_ｎ メンバＩＤ。[0001]
TECHNICAL FIELD OF THE INVENTION
The present invention relates to, for example, a distributed computing system that implements a distributed computing method using shared information generated from secret information held by a plurality of distributed computing devices, and a distributed computing device that constitutes a part of the distributed computing system. Things.
[0002]
[Prior art]
At present, in the technical field of cryptography, a distributed calculation method called a multi-party protocol has been realized. Here, a general multi-party protocol will be described. Now, assuming that there is a network composed of n members (or n arithmetic units), member ID_m_iEach member having (i = 1, 2,..., N) has secret information X that the other members do not want to know._i(I = 1, 2,..., N). When a certain function f is given, each member has its own secret information X_iIs kept secret, the function Z = f (X₁, X₂, ..., X_n) To calculate the value Z to be obtained. The function f is, for example, all secret information X_iFunction Z = X₁+ X₂+ ... + X_nOr all confidential information X_iOutput the largest value of the following: Z = max ｛X₁, X₂, ..., X_nOr｝.
[0003]
In this way, each member can transmit his / her own secret information X on the network._iA protocol that realizes a function of performing some kind of communication with each other without leaking itself and finally calculating the value Z is called a multi-party protocol related to the function f. The above function can be realized by providing a reliable third-party center for calculating the function f and each member secretly transmitting their own secret information to this center, but here, there is no such center. The case will be described.
[0004]
FIG. 2 is a conceptual explanatory diagram of the multi-party protocol. In the example of FIG. 2, the number of members (participants) is three, the member IDs (ID information) are A, B, and C, and the secret information held by each is X._A, X_B, X_CAnd Member ID_A, B, C, and secret information X_A, X_B, X_CAre values on a certain finite field GF (q) (q is a prime number or a power of a prime number), and a function f (X_A, X_B, X_CThe operations in () (addition and multiplication) are operations on a finite field GF (q). Hereinafter, unless otherwise specified, the calculation is performed on the finite field GF (q).
[0005]
Function f (X_A, X_B, X_C), First, each member distributes secret information held by itself using the (k, n) threshold secret sharing method (in FIG. 2, reference numeral {circle around (1)}). Processing shown). In the (k, n) threshold secret sharing scheme, information X is distributed into n pieces of information, and if k pieces of (k ≦ n) pieces of shared information among the n pieces of shared information are collected, the information X is restored. , And when only k-1 or less pieces of shared information are collected, no information X can be known. In the case of FIG. 2, n is 3, and k is 2 or 3.
[0006]
Next, each member distributes shared information obtained by distributing its own secret information to other members (processing indicated by reference numeral {circle around (2)} in FIG. 2). When distributing these pieces of shared information, it is assumed that a secret communication channel is established between any two members that can keep communication contents secret except for the two members. Next, the function f (X_A, X_B, X_C), Each member performs distributed calculation (processing indicated byreference numeral 3 in FIG. 2). At the time of this distributed calculation, each member may exchange information. The calculation result Z 'of the distributed calculation held by each member_A, Z '_B, Z '_CAre the final calculation results Z = f (X_A, X_B, X_C) Is shared information. Therefore, finally, the calculation result Z 'of the distributed calculation held by each member_A, Z '_B, Z '_CAre collected and the secret reconstruction of the (k, n) threshold secret sharing scheme is performed, a final calculation result Z can be obtained (the process indicated byreference numeral 4 in FIG. 2).
[0007]
Next, a case where the multi-party protocol shown in FIG. 2 is extended to n members will be described. The member ID of each member is m_i(I = 1, 2,..., N), and the member ID is m_iX is the secret information held by the member_i(I = 1, 2,..., N). Each member distributes the secret information held by each member by a (k, n) threshold secret sharing scheme. Here, the (k, n) threshold secret sharing scheme uses the Shamir method (Shamir's method) (for example, see Non-Patent Document 1).
[0008]
Member ID is m_iIs a k−1 degree polynomial h as in the following equation (1)._xi(X) is generated, and the secret information is distributed using this equation.
(Equation 7)

In the above formula (1), R_{xi, 1}, R_{xi, 2}, ..., R_{xi, k-1}Means that the member ID is m_iIs a random number determined by a member, and is selected from (k−1) values from values on a finite field GF (q).
[0009]
Member ID is m_iAnd the member ID is m_p(P = 1, 2,..., N)_{i, p}, The shared information Y_{i, p}Can be calculated as in the following equation (2) using the function of the above equation (1).
(Equation 8)

[0010]
When each member receives the shared information from the other members, as a result, the member ID becomes m_iIs n pieces of shared information Y_{1, i}, Y_{2, i}, ..., Y_{n, i}Will be held. Distributed information Y held by each of these members_{1, i}, Y_{2, i}, ..., Y_{n, i}, Ie, each member cooperates to obtain a desired distributed calculation Z = f (X₁, X₂, ..., X_n)I do.
[0011]
Here, the case of the variance addition and the case of the variance multiplication are described as the variance calculation performed by each member. Secret information A and B are secretly shared using a polynomial as shown in the above equation (1), and the member ID is m_iIs the shared information a_iAnd b_iConsider that you already have In this case, secret information A and B and shared information a_iAnd b_iIs as shown in the following equations (3) and (4).
(Equation 9)

Where R_{A, j}(J = 1, 2,..., K-1) and R_{B, j}(J = 1, 2,..., K-1) are random numbers.
[0012]
Each member shares information a_iAnd b_iFrom the secret c (= A + B)_iIs the member ID is m_iThe calculation process that a member has is referred to as “dispersion addition”. Also, each member shares the shared information a._iAnd b_iFrom the secret information C (= A × B)_iIs the member ID is m_iThe calculation process that a member has is called "dispersion multiplication". Further, a value c obtained by secretly sharing a result C (= D × A) of multiplication of a certain constant D and secret information A_iIs the member ID is m_iThe calculation process that a member has is called “dispersion constant multiplication”. As described above, when variance addition, variance constant multiplication, and variance multiplication of arbitrary variance information are enabled, any function Z = f (X₁, X₂, ..., X_n) Enables distributed calculation. Hereafter, secret information A and B are secretly shared by a polynomial such as the above equation (1), and each member performs shared information a._iAnd b_iEach member has shared information a._iAnd b_iIs calculated from C = f (A, B), a value c in which secret sharing is performed._iThe following describes the processing for obtaining.
[0013]
First, the distributed addition (addition calculation) in the multi-party protocol will be described using the following equation (5).
C = f (A, B) = A + B (5)
Member ID is m_iIs already sharing information a of secret information A and B_iAnd b_iIt is assumed that you have These shared information a_iAnd b_iIs the shared information (Y_{1, i}, Y_{2, i}, ..., Y_{n, i}) May be used, or the value of the intermediate result of the dispersion calculation may be used. In the variance addition, by performing addition of the pieces of shared information, the shared information c of the calculation result C is obtained._i(I = 1, 2,..., N) can be obtained. For example, if the member ID is m_iIs calculated as in the following equation (6), and the calculation result c_iGet.
c_i= A_i+ B_i    … (6)
[0014]
Next, the dispersion constant multiplication (constant multiplication calculation) in the multi-party protocol will be described using the following equation (7).
C = f (A) = D × A (7)
Here, D is a constant on the finite field GF (q), and is a value known to all members. For example, if the member ID is m_iCalculates the following equation (8) and calculates the result c_iGet.
c_i= D × a_i    … (8)
[0015]
Next, distributed multiplication (multiplication calculation) in the multi-party protocol will be described using the following equation (9).
C = f (A, B) = A × B (9)
There are the following two methods in the variance multiplication, and in this description, these methods will be described as a method (1) and a method (2), respectively. In the method (1), each member performs the following steps S101 to S103. Here, the member ID is m_iDescribes the process performed by a member. In step S101, multiplication c between pieces of shared information is performed._{i, i}= A_i× b_iI do.
[0016]
In the next step S102, the member ID is m_p(P = 1, 2,..., N and p ≠ i) multiplication a with the value of another member_i× b_pAnd a_p× b_iCommunication and calculation processing are performed so as to obtain a result equivalent to the result of (1). That is, the member ID is m such that the following equation (10) is obtained._iIs the multiplication result c_{i, p}And the member ID is m_pIs the multiplication result c_{p, i}Perform calculations and communications so that you can have
a_i× b_p+ A_p× b_i= C_{i, p}+ C_{p, i}    … (10)
In this way, by exchanging information with other members, multiplication a with the values of other members a_i× b_pAnd a_p× b_iTo obtain the expression (10) corresponding to the result of_pAnd b_pSo that you don't know_iAnd b_iHowever, it performs oblivious transfer so that other members do not know. "Lost communication" means that the transmitting side encodes (encrypts) and transmits M pieces of information, but the receiving side receives only one of them (they can be decoded in a meaningful way). This is a communication method in which the transmitting side cannot know which information the receiving side has received (the decoding has become meaningful) on the transmitting side.
[0017]
In the next step S103, a coefficient r calculated from the member ID is added to the result of step S102._pAre multiplied by each other, and the shared information c of the multiplication result C represented by the following equations (11) and (12) is obtained._i(I = 1, 2,..., N).
(Equation 10)

[0018]
In the method (2), each member performs the following steps S201 to S205. Here, the member ID is m_iDescribes the process performed by a member. In step S201, multiplication c 'between shared information items_i= A_i× b_iI do.
[0019]
In the next step S202, c ′ obtained in step S201_iIs distributed using the (k ′, n) threshold secret sharing scheme, and the shared information c ′_{i, p}(P = 1, 2,..., N and p ≠ i) and the member ID is m_pDistribute to other members. Also, from another member, the shared information c '_{p, i}(P = 1, 2,..., N and p ≠ i) are received.
[0020]
In the next step S203, C '_i= (C '_{1, i}, C '_{2, i}, ..., c '_{n, i}) To the transformation matrix EPE^-1By multiplying_i= (D_{1, i}, D_{2, i}, ..., d_{n, i}). The matrix E is a matrix calculated from the member ID,
E = (e_ij) = (M_i^j-1) (I, j = 1, 2,..., N)
An n × n matrix such that^-1And Further, the matrix P is an n × n matrix that performs a conversion such that values of the (k + 1) th and subsequent vectors of the vector are set to 0 as in the following equation.
P (x₁, X₂, ..., x_n)^t
= (X₁, X₂, ..., x_k, 0, ..., 0) ... (80)
[0021]
In the next step S204, d obtained in step S203_{p, i}(P = 1, 2,..., N and p ≠ i) and the member ID is m_pDistribute to other members. Also, from other members, the calculation result d_{i, p}(P = 1, 2,..., N and p ≠ i) are received.
[0022]
In the next step S205, d obtained in steps S203 and S204_{i, p}By using (p = 1, 2,..., N) as shared information and performing secret reconstruction of (k ′, n) threshold secret sharing, shared information c of the multiplication result C is obtained._i(I = 1, 2,..., N).
[0023]
As described above, in the distributed multiplication, the calculation cannot be performed easily as in the case of the dispersion addition, but can be calculated by using the oblivious transfer. As described above, when each member performs secret communication and lost communication and performs calculation processing, calculation of a given function f (function composed of addition and multiplication) is performed without disclosing input values. Can be.
[0024]
In a normal (k, n) threshold secret sharing scheme represented by the Shamir method, secret information is encoded into n pieces of shared information, and if k (≦ n) or more pieces of shared information are collected, the original Can be restored, but if k-1 or less, the secret information cannot be known at all. This is realized by using polynomial interpolation.
[0025]
Specifically, a k-1 order polynomial h such as the following equation (13)_SThe original secret information is distributed using (x).
(Equation 11)

Here, S is the original secret information, and R_{S, 1}, R_{S, 2}, ..., R_{S, k-1}Is a random number determined by the distributor.
[0026]
Each of the n members to be distributed has a member ID of m₁, M₂, ..., m_nIs assigned, and the member ID_m_iShared information S for (i = 1, 2,..., N)_iCan be calculated as in the following equation (14) using the above equation (13).
(Equation 12)

[0027]
Here, member ID_m_i(I = 1, 2,..., N), secret information S, shared information S_i(I = 1, 2,..., N), random number R_{S, 1}, R_{S, 2}, ..., R_{S, k-1}Are values on a certain finite field GF (q) (q is a prime number or a power of a prime number), and operations (addition and multiplication) are operations on the finite field GF (q), respectively. And From the above equation (13), the following equation (15) holds.
h_S(0) = S (15)
[0028]
When reconstructing the original secret information S from the shared information distributed to each member, t members (k ≦ t) are collected from the members to which the shared information is distributed, and the member ID and the shared information are collected. Can be achieved by calculating by the following equations (16) and (17).
(Equation 13)

Where m '₁, M '₂, ..., m '_tIs the member ID of the gathered members, and S '₁, S '₂, ..., S '_tIs shared information held by the gathered members.
[0029]
In a normal (k, n) threshold secret sharing scheme represented by the Shamir scheme, the original secret information S and its shared information S_i(I = 1, 2,..., N) are values on the finite field GF (q), and the shared information S_iThe information amount of (i = 1, 2,..., N) has a property that it cannot be made smaller than the information amount of the original secret information S.
[0030]
[Non-patent document 1]
Tatsuaki Okamoto et al., "Modern Cryptography" (Sangyo Tosho), pp. 214-216 and 227-236.
[Non-patent document 2]
G. Brackley and Catherine Meadows, "Security of Lamp Schemes", Procedures of Crypt '88, Lecture Notes in Computer Science 403, Springer Berlag, pp. 242-268, 1990 (GR BLAKLEY AND CATHERINE MEADOWS, "SECURITY OF RAMP SCHEMES", PROC. OF CRYPTO '88, LECTURE NOTES IN COMPUTER SCIENCE 403, SPRING2P.
[0031]
[Problems to be solved by the invention]
However, in the above-described shared calculation using the conventional multi-party protocol, the secret sharing of each piece of secret information is performed using the ordinary (k, n) threshold secret sharing method. In the calculation, it is necessary to perform an operation on a finite field having the same information amount as the secret information, that is, the same size. Therefore, despite the secret information being distributed among n persons, the amount of computation, the circuit scale required for the computation circuit, the storage capacity required for computation, the computation time, etc., in the distributed computation processing of each member. However, there is a problem that the operation cost cannot be reduced.
[0032]
Therefore, the present invention has been made to solve the above-described problems of the related art, and an object of the present invention is to provide a distributed computing device and a distributed computing system that can reduce the amount of computation in distributed computation. It is.
[0033]
[Means for Solving the Problems]
The distributed computing device according to the present invention employs a ramp type (L, k, n) threshold secret sharing scheme, in which one or more (usually two or more, but there may be only one) secrets. The distributed computing device has distributed computing means for performing distributed computation using the distributed information generated from the information._p(P ≦ n), and the shared information used for the shared calculation by the shared calculation means is Y_p, The variance information is an extended field obtained by expanding the finite field GF (q) by L-order, and an extended field GF (q^L) Is calculated by the following equation: X = ΣX_jα^jWhen X satisfies 0 ≦ j ≦ L−1, the following expression h_X(I_j) = X_jA polynomial h on a k-1 order finite field GF (q) satisfying 0 ≦ j ≦ L-1_X(X), and the above polynomial h_XFrom (x), Y_p= H_X(M_p) Which is information generated by calculating a value on a finite field GF (q).
[0034]
Further, another sharing calculation apparatus according to the present invention includes secret sharing calculation means for generating shared information from secret information by a ramp type (L, k, n) threshold secret sharing method. Means that the member ID held by another distributed computing device to which the distributed information is distributed is m_p(P ≦ n) and the member ID is m_pThe above shared information is expressed as Y_pAnd an extended field GF (q) whose creator is α in an extended field obtained by expanding the finite field GF (q) by L order^L) Is calculated by the following equation: X = ΣX_jα^jWhen X satisfies 0 ≦ j ≦ L−1, the following expression h_X(I_j) = X_jA polynomial h on a k-1 order finite field GF (q) satisfying 0 ≦ j ≦ L-1_XPolynomial generating means for generating (x), and the polynomial h_XFrom (x), Y_p= H_X(M_pAnd a shared information generation means for generating a value by calculating a value on the finite field GF (q).
[0035]
Further, another distributed computing device according to the present invention employs a ramp type (L, k, n) threshold secret sharing scheme, and one or more (usually two or more, but may be one). ) Has distributed calculation means for performing distributed calculation using the shared information generated from the secret information._p(P ≦ n), and the shared information used for the shared calculation by the shared calculation means is Y_pAnd the above-mentioned shared information is
An extended field obtained by expanding the finite field GF (q) by L-th order, with the generator α and the generator polynomial g (x)^L)
X = ΣX_j  α^j0 ≦ j ≦ L-1
X represented by_{X, j}When (0 ≦ j ≦ k−L−1) is a random number,
[Equation 14]

A polynomial h on a k-1 order finite field GF (q) represented by_X(X), and
The above polynomial h_XFrom (x),
Y_p= H_X(M_p)
It is characterized by being information generated by calculating a value on a finite field GF (q).
[0036]
Further, another sharing calculation apparatus according to the present invention includes secret sharing calculation means for generating shared information from secret information by a ramp-type (L, k, n) threshold secret sharing method. Means that the member ID held by the distributed computing device to which the distributed information is distributed is m_p(P ≦ n) and the member ID is m_pThe above shared information is expressed as Y_pAnd an extended field obtained by expanding the finite field GF (q) by L-th order, the generator being α and the generating polynomial g (x) being an extended field GF (q^L)
X = ΣX_j  α^j0 ≦ j ≦ L-1
X represented by_{X, j}When (0 ≦ j ≦ k−L−1) is a random number,
[Equation 15]

A polynomial h on a k-1 order finite field GF (q) represented by_XPolynomial generating means for generating (x), and the polynomial h_XFrom (x), Y_p= H_X(M_pAnd a shared information generation means for generating a value by calculating a value on the finite field GF (q).
[0037]
BEST MODE FOR CARRYING OUT THE INVENTION
In the present invention, instead of the ordinary (k, n) threshold secret sharing method represented by the Shamir method, which has been used in the distributed calculation by the conventional multi-party protocol, a ramp type (L, k, n) Use a threshold secret sharing scheme. Thereby, the operation necessary for each member can be performed on a finite field smaller than the finite field of the original secret information, and the operation cost can be reduced.
[0038]
First, a ramp-type (L, k, n) threshold secret sharing scheme will be described. In a normal (k, n) threshold secret sharing scheme represented by the Shamir method, when only k-1 pieces of shared information among n pieces of shared information are collected, the original of the shared information is used. This is a method that cannot be known at all about confidential information. On the other hand, the ramp type (L, k, n) threshold secret sharing scheme introduces a certain parameter L (1 ≦ L ≦ k ≦ n) and sets each shared information S_iBy reducing the information amount of (i = 1, 2,..., N) to 1 / L of the original secret information S, k−d (1 ≦ d ≦ L−1) of the n pieces of shared information When the pieces of shared information are collected, some information about the original secret information is leaked even if k pieces of shared information are not collected.
[0039]
A method in which the Shamir method is extended to a lamp type is described in, for example,Non-Patent Document 2 described above. In that method, first, the original secret information S is set to a vector value represented by the following equation (18).
S = (S₀, S₁, ..., S_L-1)… (18)
Also, S₀, S₁, ..., S_L-1Are values on the finite field GF (q), and R_S2,0, R_S2,1, ..., R_{S2, k-L-1}Are random numbers determined by the distributor and are values on the finite field GF (q). In addition, I₀, I₁, ..., I_k-1Are determined on the k finite fields GF (q). Then, a k-1 order polynomial h such as the following equations (19) and (20)_S2Secret information is secretly shared using (x).
[0040]
(Equation 16)

[0041]
Each of the n members to whom the shared information is distributed has a member ID of m₁, M₂, ..., m_nIs assigned, and the member ID_m_iShared information X for (i = 1, 2,..., N)_iIs calculated as in the following equation (21).
X_i= H_S2(M_i…… (21)
[0042]
Here, the operations (addition and multiplication) are each operations on a finite field GF (q). Therefore, the shared information X_iIs a value on the finite field GF (q). Hereinafter, unless otherwise specified, the calculation is performed on the finite field GF (q). From the above equation (19), the following relational equation (22) holds.
h_S2(I₀) = S₀
h_S2(I₁) = S₁
…
h_S2(I_L-1) = S_L-1        … (22)
[0043]
Distributed information X distributed to each member_iFrom the original secret information S = (S₀, S₁, ..., S_L-1)), Among the members to which the shared information has been distributed, k or more t members (k ≦ t) are gathered, the member IDs and the shared information are brought, and the following equation (23) is obtained. And (24), the original secret information S = (S₀, S₁, ..., S_L-1). In the following equations (23) and (24), m ′₁, M '₂, ..., m '_tIs the member ID of the gathered members, X '₁, X '₂, ..., X '_tMeans that the member ID is m '₁, M '₂, ..., m '_tIs the shared information held by the member.
[0044]
[Equation 17]

[0045]
(Equation 18)

[0046]
In this ramp type (L, k, n) threshold secret sharing scheme, the original secret information S = (S₀, S₁, ..., S_L-1) Is the distributed information X_iIt is possible to have L times the information amount of (i = 1, 2,..., N). That is, in the ramp type (L, k, n) threshold secret sharing scheme, the shared information X_iThere is a property that the information amount of (i = 1, 2,..., N) can be 1 / L of the information amount of the original secret information S.
[0047]
<< 1st Embodiment >>
[Configuration of First Embodiment]
In the first embodiment of the present invention, n members (or n distributed computing devices) each have secret information, and obtain a calculation result of a function f using the secret information as an argument. The case where the distributed calculation is performed will be described. The n members have m as a member ID which is information for identifying the members.₁, M₂, ..., m_nIs assigned. Member ID_m_i(I = 1, 2,..., N) are values on a finite field GF (q) (q is a prime number or a power of a prime number).
[0048]
Also, if the member ID is m_i(I = 1, 2,..., N) are members of the secret information X_i(I = 1, 2,..., N). Here, the secret information X held by the member_i(I = 1, 2,..., N) is an L-order extension field GF (q) of the finite field GF (q).^L) On the finite field GF (q)_{i, 0}, X_{i, 1}, ..., X_{i, L-1}Can be represented by The finite field GF (q) is L-order expanded to an expanded field GF (q^L) Is generated as g (x) and one of the solutions of g (x) = 0 is α, the secret information X_iCan be described by the following equation (25).
X_i= X_{i, 0}+ X_{i, 1}α + ... + X_{i, L-1}α^L-1    … (25)
Also, secret information X_iCan be described as the following equation (26) using a vector expression.
X_i= (X_{i, 0}, X_{i, 1}, ..., X_{i, L-1})… (26)
[0049]
FIG. 1 is a block diagram showing a configuration (distributed computing system) for implementing the distributed computing method according to the first embodiment. In the first embodiment, variance calculation is performed using a function consisting only of addition. As shown in FIG. 1, the configuration for implementing the distributed calculation method (multi-party protocol) of the first embodiment includes n (2 ≦ n) distributed processing units (distributed calculation devices) 101-i (i = 1, 2,..., N), a secret reconstruction calculation unit 102, and asecret communication channel 103 of each distributed processing unit 101-i (i = 1, 2,..., N). Each distributed processing unit 101-i (i = 1, 2,..., N) has a member ID m_iExecute the operation assigned to the member. Outputs from the n distributed processing units 101-i (i = 1, 2,..., n) are input to the secret reconstruction calculation unit 102.
[0050]
The distributed processing unit 101-i (i = 1, 2,..., N) (the reference numeral 101 is used to indicate the entire distributed processing unit) is a part where each member performs distributed calculation. The distribution processing unit 101 performs distribution of secret information indicated byreference numeral 1 in FIG. 2 and performs distribution calculation indicated byreference numeral 3 in FIG. Each distributed processing unit 101-i (i = 1, 2,..., N) is secret from another distributed processing unit 101-p (where p = 1, 2,..., N and p ≠ i). They are connected by acommunication path 103. Thesecret communication channel 103 is a communication channel that can keep the communication contents secret except for the two communicating members. The output from each of the distributed processing units 101-i (i = 1, 2,..., N) is input to the secret reconstruction calculation unit 102.
[0051]
The secret reconstruction calculation unit 102 receives the output from the distribution processing unit 101-i (i = 1, 2,..., N) of each member, and uses the received n values as n pieces of shared information. To perform the reconstruction of the secret, and output the reconstructed original secret. The n pieces of shared information input to the secret reconstruction calculation unit 102 are information that is shared by a ramp (L, k, n) threshold secret sharing method.
[0052]
FIG. 3 is a block diagram showing a configuration of the secret reconstruction calculation unit 102 of FIG. As shown in FIG. 3, the secret reconstruction calculation unit 102 includes a linear combination unit 201. The linear combination unit 201 receives the input to the secret reconstruction calculation unit 102, and receives the member ID_m_i, A linear combination calculation of those inputs is performed by using the coefficient calculated from, and the calculation result is output. The output from the linear combination unit 201 is the output of the secret reconstruction calculation unit 102. Here, the value output from the distributed processing unit 101-i (i = 1, 2,..., N) of each member (that is, the value input to the secret reconstruction calculation unit 102) is Z ′._i(I = 1, 2,..., N) and member ID_m_iThe coefficient calculated from_{0, i}, R_{1, i}, ..., r_{L-1, i}(I = 1, 2,..., N). At this time, the secret reconstruction calculation unit 102 calculates the following equations (27) and (28), and as a result, Z = (Z₀, Z₁, ..., Z_L-1) Is output.
[0053]
[Equation 19]

[0054]
(Equation 20)

[0055]
Each operation in the above equations (27) and (28) is performed on a finite field GF (q). In the following description, unless otherwise specified, the calculation is performed on a finite field GF (q).
[0056]
The processing in the distributed processing unit 101-i (i = 1, 2,..., N) of each member is performed such that each member does not know the contents of the processing by the other members. The processing in the secret reconstruction calculation unit 102 may be performed by a center that integrates the processing (that is, an arithmetic unit managed by the center), or one or more of the members gathered. It may be performed by a person (that is, an arithmetic device managed by one of the gathered members). However, it is desirable that the member who needs the calculation result Z perform the calculation.
[0057]
FIG. 4 is a block diagram showing a configuration of the distributed processing unit 101-i (i = 1, 2,..., N) of FIG. As shown in FIG. 4, the distribution processing unit 101-i includes a secret information storage unit 301-i, a secret distribution calculation unit 302-i, a transmission unit 303-i, a reception unit 304-i, and a distribution calculation unit. Unit 305-i. The output from the secret information storage unit 301-i is input to the secret sharing calculation unit 302-i, and the output from the secret sharing calculation unit 302-i is input to the transmission unit 303-i and the sharing calculation unit 305-i. The transmission unit 303-i transmits information to thesecret communication channel 103. The information received from thesecret channel 103 is input to the receiving unit 304-i, and the output from the receiving unit 304-i is input to the distribution calculation unit 305-i. The output from the distribution calculation unit 305-i is the output of the distribution processing unit 101-i.
[0058]
The secret information storage unit 301-i stores the member ID m_iSecret information X held by the member_iAnd this secret information X_iIs output to the secret sharing calculation unit 302-i. Secret information held by the member (that is, secret information held in secret information storage unit 301-i) X_iIs the L-order extension GF (q) of the finite field GF (q)^L) And the value X on the generator α and the finite field GF (q)_{i, 0}, X_{i, 1}, ..., X_{i, L-1}And can be described as:
X_i= X_{i, 0}+ X_{i, 1}α + ... + X_{i, L-1}α^L-1
[0059]
The member ID is m to the secret sharing calculation unit 302-i._iSecret information X held by the member_iIs entered. The secret sharing calculation unit 302-i receives the input secret information X_iIs distributed using a ramp-type (L, k, n) threshold secret sharing scheme (L ≦ k ≦ n), and distributed to other members via the transmitting unit 303-i and thesecret channel 103. I do. Secret information X held by members_iIs the extended field GF (q^L) The above value. The shared information generated by secret sharing calculation section 302-i is Y_{i, p}(P = 1, 2,..., N), the shared information Y for itself_{i, i}Is output to the variance calculation unit 305-i, and the other variance information Y_{i, p}(P = 1, 2,..., N and p ≠ i) are output to the transmission unit 303-i. Secret information X held by members_iIs the extended field GF (q^L) Is the above value, and the distributed information Y_{i, p}Is a value on the finite field GF (q).
[0060]
The transmission unit 303-i outputs the output Y from the secret sharing calculation unit 302-i._{i, p}(P = 1, 2,..., N and p ≠ i), and passes it through thesecret communication channel 103 to each of the other members (member ID is m_p(Where p = 1, 2,..., N and p ≠ i). Note that Y_{i, p}Means that the member ID is m_iMember ID is m from member_pIs the shared information transmitted to the member.
[0061]
The receiving unit 304-i transmits information Y transmitted from the transmitting units 303-p (p = 1, 2,..., N and p ≠ i) of each of the other members._{p, i}(P = 1, 2,..., N, and p ≠ i), and outputs it to the distribution calculation unit 305-i. Note that Y_{p, i}Means that the member ID is m_pMember ID is m from member_iIs the shared information transmitted to the member.
[0062]
The sharing calculation unit 305-i sends the secret information X from the secret sharing calculation unit 302-i._iY, which is the shared information of_{i, i}Receive. Further, the receiving unit 304-i distributes the secret information X distributed from another member._p(P = 1, 2,..., N and p ≠ i) shared information Y_{1, i}, Y_{2, i}, ..., Y_{n, i}(Shared information Y_{i, i}Except). The distribution calculation unit 305-i receives the n pieces of received distribution information Y_{p, i}(P = 1, 2,..., N) is used to perform a dispersion calculation, and the calculation result (final calculation result) Z to be obtained (intermediate calculation result) Z ′_iIs output.
[0063]
The variance calculation unit 305-i calculates the function Z = f (X₁, X₂, ..., X_nIn order to perform the operation according to (1), one or a plurality of variance adding units are provided. For example,
Z = f (X₁, X₂, ..., X_n) = X₁+ X₂+ ... + X_n
(Ie, the sum of the secret information), the variance calculation unit 305-i has the configuration (n-1 variance addition units 501-1 and 501-2) as shown in FIG. , ..., 501- (n-1)). Also,
Z = f (X₁, X₂, ..., X_n) = X_M+ X_N
In the case of calculating the sum of a specific piece of secret information, the variance calculator 305-i has a configuration (consisting of one variance adder 601) as shown in FIG. .
[0064]
FIG. 5 is a block diagram illustrating a configuration of the secret sharing calculation unit 302-i (i = 1, 2,..., N) in the first embodiment. As shown in FIG. 5, the secret sharing calculation unit 302-i includes a polynomial expression generation unit 401-i and a shared information generation unit 402-i. Further, the polynomial generating section 401-i includes a random number generating section 403-i and a (k-1) -th order polynomial generating section 404-i. The input to the secret sharing calculation unit 302-i is input to the polynomial expression generation unit 401-i, and the output from the polynomial expression generation unit 401-i is input to the shared information generation unit 402-i. The output from the shared information generation unit 402-i is the output from the secret sharing calculation unit 302-i. Also, the input to the polynomial generation unit 401-i is input to the (k-1) -order polynomial generation unit 404-i, and the output from the random number generation unit 403-i is also the (k-1) -order polynomial generation unit 404-i. Input to i. The output from the (k-1) -order polynomial generator 404-i is the output from the polynomial generator 401-i.
[0065]
The polynomial generation unit 401-i calculates the value X on the L finite fields GF (q)._{i, 0}, X_{i, 1}, ..., X_{i, L-1}, And from those values, a k-1 order polynomial h satisfying the following equation (29)_Xi(X), and the generated polynomial h_XiOutput information representing (x).
h_Xi(I₀) = X_{i, 0}
h_Xi(I₁) = X_{i, 1}
…
h_Xi(I_L-1) = X_{i, L-1}    … (29)
Where I₀, I₁, ..., I_L-1Is a value that does not overlap with the member ID, and is a value on a predetermined finite field GF (q).
[0066]
The shared information generation unit 402-i calculates the polynomial h_Xi(X), and n values Y on a finite field GF (q) expressed by the following equation (30)_{i, p}(P = 1, 2,..., N) are generated and output.
Y_{i, p}= H_Xi(M_p…… (30)
Here, p = 1, 2,..., N and Y_{i, p}Means that the member ID is m_iMember ID is m from member_pShows the distributed information distributed to the member.
[0067]
The random number generation unit 403-i generates KL random numbers R on the finite field GF (q)._{Xi, 0}, R_{Xi, 1}, ..., R_{Xi, k-L-1}Is generated and output.
[0068]
(K-1) The degree polynomial generating unit 404-i outputs the secret information X held by the member which is the input to the secret sharing calculating unit 302-i._i, And the random number R from the random number generation unit 403-i_{Xi, 0}, R_{Xi, 1}, ..., R_{Xi, k-L-1}And a k-1 order polynomial h as shown in the following equations (31) and (32)_X(X), and the generated polynomial h_XOutput information representing (x).
[0069]
(Equation 21)

[0070]
The secret information X held by the member_iIs the extended field GF (q^L) And the value X on the generator α and the finite field GF (q) as described above._{i, 0}, X_{i, 1}, ..., X_{i, L-1}Using
X_i= X_{i, 0}+ X_{i, 1}α + ... + X_{i, L-1}α^L-1
Can be described in the form Further, the above equations (31) and (32) indicate that the member ID is m_iThe polynomial h generated by the (k-1) -order polynomial generator 404-i of the member_X(X).
[0071]
FIG. 8 is a block diagram showing the configuration of thevariance adder 501 or 601 in FIG. 6 or FIG. The configuration of thevariance addition unit 501 or 601 which is a component of the variance calculation unit 305-i will be described with reference to FIG. As illustrated in FIG. 8, thevariance adding unit 501 or 601 includes an adding unit 701. The adding unit 701 receives two inputs (values on the finite field GF (q)) and outputs a value obtained by adding the values on the finite field GF (q). Assuming that the input values are a and b, the output c is as shown in the following equation (33).
c = a + b (33)
The above equation (33) is an operation (addition) on the finite field GF (q).
[0072]
When shared secrets a and b are subjected to a secret reconstruction formula (the above formulas (27) and (28)) of the ramp type (L, k, n) threshold secret sharing scheme, respectively, the extended field GF (q^L) Value above
A = (A₀, A₁, ..., A_L-1)
B = (B₀, B₁, ..., B_L-1)
become. Where A₀, A₁, ..., A_L-1, B₀, B₁, ..., B_L-1Are values on the finite field GF (q). The shared information c output from the sharedadder 501 or 601 is obtained by performing secret reconstruction of the ramp type (L, k, n) threshold secret sharing scheme.
C = A + B (34)
The expanded field GF (q^L) Value C = (C₀, C₁, ..., C_L-1). Where C₀, C₁, ..., C_L-1Are values on the finite field GF (q). The above equation (34) can be expressed as^L) Is the above operation (addition).
[0073]
[Operation of First Embodiment]
FIG. 9 is a flowchart illustrating the operation of the configuration (distributed calculation system) that executes the distributed calculation method according to the first embodiment. Each member for performing the distributed calculation is n, and the member ID is m._i(I = 1, 2,..., N) are members of the secret information X_ihave. Member ID_m_iIs a value on the finite field GF (q), and the secret information X_iIs the extended field GF (q^L) The above value. Also, member ID_m_i(I = 1, 2,..., N) is open to all members. From the finite field GF (q) used for the distributed calculation, the parameter L of the ramp-type secret sharing scheme, and the finite field GF (q) to the expanded field GF (q^L), An irreducible polynomial g (x), its generator α, and a function f (X₁, X₂, ..., X_n) Is predetermined. Function f (X₁, X₂, ..., X_n) Is the extended field GF (q^L), In the first embodiment, the extended field GF (q^L) (Eg, X_A+ X_B) Alone.
[0074]
As shown in FIG. 9, first, secret information held by each member is distributed using a ramp-type (L, k, h) secret sharing method and distributed to other members (step S801). Step S801 shows the operation in the secret sharing calculation unit 302-i of FIG._i(I = 1, 2,..., N) secret information X held by each member_iFrom the above, using the above equation (30), the shared information Y_{i, p}(P = 1, 2,..., N) and the member ID is m_pDistribute to members.
[0075]
Next, each member performs the sharing calculation of the function f using the sharing information of its own secret information and the sharing information distributed from other members (step S802). Step S802 shows the operation in the distribution calculation unit 305-i in FIG. 4, and the member ID is m_iEach member of (i = 1, 2,..., N) has a function f (X₁, X₂, ..., X_nThe variance calculation is performed as specified in ()). For example,
f (X₁, X₂, ..., X_n) = X_A+ X_B
If the member ID is m_iIs the distributed information Y held by the member as a result of the distribution._{A, i}And Y_{B, i}From the following variance addition calculation
Z '_i= Y_{A, i}+ Y_{B, i}
Execute Calculation result (intermediate calculation result) Z ′ of the dispersion addition calculation_iIs the extended field GF (q^L) Above (final calculation result) Z (where Z = f (X₁, X₂, ..., X_n) = X_A+ X_BIt is. ) (That is, shared information distributed by the ramp type (L, k, n) secret sharing method).
[0076]
In the next step S803, a calculation result Z 'calculated by each member_iFrom the calculation result of the function f, Z = f (X₁, X₂, ..., X_n) Is secretly reconstructed based on a ramp-type (L, k, n) secret sharing scheme. Step S803 shows the operation in the secret reconstruction calculation unit 102 of FIG. 1, and the member ID is m_iIs the result Z 'calculated by the member in step S802._i(I = 1, 2,..., N), using the above equation (27), and calculating the function f by Z = f (X₁, X₂, ..., X_n) Can be obtained.
[0077]
FIG. 10 is a flowchart showing the operation in the variance addition. For example, the extension field GF (q^L) Consider the case where the above values A and B are added. As shown in FIG. 10, the member ID is m_iEach member of (i = 1, 2,..., N) has the shared information a of the information A and B held by itself._iAnd b_iFrom the sum c_i= A_i+ B_iIs calculated and output (step S901).
[0078]
[Effects of First Embodiment]
As described above, according to the first embodiment, the multi-party protocol for the function f (where the function f is a function of addition only) (without disclosing the secret information held by each member) Performs a variance calculation, thereby obtaining a calculation result of the function f) in the extension field GF (q^LThe above calculation can be achieved by performing only the calculation on the finite field GF (q) smaller than the extension field in the distributed operation processing of each member. For this reason, in the distributed operation processing of each member, the operation cost such as the amount of operation, the circuit scale required for the operation circuit, the storage capacity required for the operation, and the operation time can be reduced.
[0079]
<< 2nd Embodiment >>
In the first embodiment, the distributed addition method of the distributed calculation by the multi-party protocol using the ramp type (L, k, n) threshold secret sharing method has been described. Describes a method of multiplying a distributed constant in distributed calculation by a multi-party protocol. Similar to the first embodiment, since a ramp-type (L, k, n) threshold secret sharing scheme is used, the operations required for each member are different from those of the conventional multi-party protocol. Can be performed on a finite field smaller than the size of the finite field of the original secret information, and the calculation cost can be reduced.
[0080]
[Configuration of Second Embodiment]
As in the first embodiment, in the second embodiment, n members (or may be n distributed computing devices) each have secret information, and the function f of the function f using the secret information as an argument. A case in which dispersion calculation is performed to obtain a calculation result will be described. For n members, the member ID is m₁, M₂, ..., m_nIs assigned. Member ID_m_i(I = 1, 2,..., N) are values on a finite field GF (q) (q is a prime number or a power of a prime number).
[0081]
Also, if the member ID is m_iIs secret information X_iIt is assumed that you have Here, the secret information X held by the member_i(I = 1, 2,..., N) is an L-order extension field GF (q) of the finite field GF (q).^L) On the finite field GF (q)_{i, 0}, X_{i, 1}, ..., X_{i, L-1}Can be represented by The finite field GF (q) is L-order expanded to an expanded field GF (q^L) Is generated as g (x), and the generator is α.
[0082]
The configuration (distributed computing system) for implementing the distributed computing method according to the second embodiment is as shown in FIG. 1, as in the first embodiment. The configuration (distributed calculation system) for implementing the distributed calculation method according to the second embodiment is different from that of the first embodiment in the configuration and operation of the distributed processing unit 101-i.
[0083]
FIG. 11 is a block diagram illustrating a configuration of a distributed processing unit (distributed computing device) 101-i (i = 1, 2,..., N) in the second embodiment. As shown in FIG. 11, the sharing processing unit 101-i in the second embodiment includes a secret information storage unit 1001-i, a secret sharing calculation unit 1002-i, a transmitting unit 1003-i, and areceiving unit 1004. -I and a distributed calculation unit 1005-i. The output from the secret information storage unit 1001-i is input to the secret sharing calculation unit 1002-i, and the output from the secret sharing calculation unit 1002-i is input to the transmission unit 1003-i and the sharing calculation unit 1005-i. The transmitting unit 1003-i transmits information to thesecret communication channel 103. Information received from thesecret channel 103 is input to the receiving unit 1004-i, and an output from the receiving unit 1004-i is input to the distribution calculation unit 1005-i. The output from the distribution calculation unit 1005-i is the output of the distribution processing unit 101-i in the second embodiment.
[0084]
The secret information storage unit 1001-i, the secret sharing calculation unit 1002-i, the transmission unit 1003-i, and the reception unit 1004-i in the second embodiment are the same as the secret information storage unit 301-i in the first embodiment. The configuration and operation are the same as those of the secret sharing calculation unit 302-i, the transmission unit 303-i, and the reception unit 304-i. However, the variance calculation unit 1005-i according to the second embodiment is different in configuration and operation from the variance calculation unit 305-i according to the first embodiment.
[0085]
Since the share calculation unit 1005-i in the second embodiment performs share constant multiplication in addition to share addition, the share processing units 101-p (p = 1, 2) of the other members via thesecret communication path 103. ,..., N and p ≠ i). The sharing calculation unit 1005-i sends the secret information X from the secret sharing calculation unit 1002-i._iInformation Y of_{i, i}Receive. Further, the secret information X distributed from another member from the receiving unit 1004-i._p(P = 1, 2,..., N and p ≠ i) shared information Y_{1, i}, Y_{2, i}, ..., Y_{n, i}Receive. These n pieces of shared information Y_{p, i}(P = 1, 2,..., N), and performs variance calculation._iIs output. The variance calculation unit 1005-i calculates the function Z = f (X₁, X₂, ..., X_n), One or more dispersion constant multiplying units and zero or more dispersion adding units. For example,
Z = f (X₁, X₂, ..., X_n) = T₁X₁+ T₂X₂+ ... + t_nX_n
To calculate (linear combination calculation of secret information), the variance calculation unit 1005-i has a configuration (n number of variance constant multiplication units 1101 (1101-1, 1101- , 1101-n) and n-1 variance addition units 1102 (consisting of 1102-1, 1102-2, ..., 1102- (n-1)).
[0086]
FIG. 13 is a block diagram showing a configuration of the dispersion constant multiplication unit 1101 in FIG. The configuration of the dispersion constant multiplication unit 1101, which is a component of the dispersion calculation unit 1005-i, will be described with reference to FIG. As illustrated in FIG. 13, the sharing constant multiplication unit 1101 includes an extension field multiplication unit 1201, a secret sharing calculation unit 1202, a transmission unit 1203, a reception unit 1204, and anaddition unit 1205. The extension field multiplication unit 1201 receives an input to the dispersion constant multiplication unit 1101. The output from the extension field multiplication unit 1201 is input to the secret sharing calculation unit 1202, and the output from the secret sharing calculation unit 1202 is input to the transmission unit 1203 and theaddition unit 1205. The transmission unit 1203 transmits information to thesecret communication channel 103. Information received from thesecret channel 103 is input to the receiving unit 1204, and an output from the receiving unit 1204 is input to the addingunit 1205. The output from the addingunit 1205 is the output of the dispersion constant multiplying unit 1101.
[0087]
The dispersion constant multiplication unit 1101 receives two inputs (a value on a finite field GF (q) and an extended field GF (q^L) Above). Here, the expanded field GF (q^L) Value above
A = (A₀, A₁, ..., A_L-1)
And the extended field GF (q^L) Constant on
D = (D₀, D₁, ..., D_L-1)
Of the multiplication C = D × A is calculated. Where A₀, A₁, ..., A_L-1, D₀, D₁, ..., D_L-1Are values on the finite field GF (q). At this time, the input to the dispersion constant multiplication unit 1101 is (value of the member A is m_i(Retained by members with i = 1, 2,..., N) shared information a_iAnd the extended field GF (q^L) Is the constant D above. Thereafter, the dispersion constant multiplication unit 1101 determines that the member ID is m_iThe description will be made assuming that the member of (i = 1, 2,..., N) is included in the distributed calculation unit 1005-i.
[0088]
The expansion field multiplying unit 1201 is an input to the dispersion constant multiplying unit 1101,_iAnd the extended field GF (q^L) On the constant D = (D₀, D₁, ..., D_L-1), And 2L-1 values E ′ represented by the following equation (35)_{i, 0}, E '_{i, 1}, ..., E '_{i, 2 (L-1)}Is calculated.
[0089]
(Equation 22)

Where r_{j, i}(J = 0, 1,..., L−1) are coefficients calculated from the member ID, which are expressed by the above equation (28).
[0090]
On the other hand, the expanded field GF (q^L)), The value g on the finite field GF (q) shown in the following equation (37)_{j, h}(J = 0, 1,..., L-1; h = 0, 1,..., L-1) are calculated and stored in advance for the enlarged field operation. Expanded field GF (q^L) Is generated by the following equation (36).
[0091]
(Equation 23)

[0092]
[Equation 24]

[0093]
G_{j, h}(J = 0, 1,..., L−1; h = 0, 1,..., L−1), and E ′ of the above equation (35) calculated first_{i, h}(H = 0, 1,..., L−1) and a coefficient r calculated from the member ID represented by the above equation (28)_{j, i}The following equation (38) is calculated using (j = 0, 1,..., L−1).
[0094]
(Equation 25)

[0095]
Where E_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is an output from the extension field multiplication unit 1201. Output E from expansion field multiplication unit 1201_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is input to the secret sharing calculation unit 1202.
[0096]
For example, L = 2, g (x) = x²In the case of + x + 1, from the above equation (37), g_{j, h}(J = 0,1, ..., L-1; h = 0,1, ..., L-1)
g_0,0= 1
g_0,1= 1
g_1,0= -1
g_1,1= -1 (39)
And the extension field multiplication unit 1001 (member ID is m_i) Is given by the following equation (40)._i= (E_{i, 0}, E_{i, 1}) Is calculated and output.
[0097]
(Equation 26)

[0098]
The secret sharing calculation unit 1202 calculates the output E from the extension field multiplication unit 1201._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}Receive). The output E from the expansion field multiplication unit 1201_iIs the extended field GF (q^L) The above value. The secret sharing calculation unit 1202 calculates the received value E_iIs distributed using a ramp-type (L, k, n) threshold secret sharing scheme (k ≦ n), and is distributed to other members via the transmitting unit 1203 and thesecret communication channel 103. Secret sharing calculation section 1202 has a configuration similar to that of secret sharing calculation section 302-i shown in FIG._i= (X_{i, 0}, X_{i, 1}, ..., X_{i, L-1}) Instead of the value E_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is entered. At this time, the polynomial generated by the (k-1) -order polynomial generation unit 404-i is as follows (41).
[0099]
[Equation 27]

[0100]
Where H_j(X) is of the above formula (32). Similarly, the member ID generated by the shared information generation unit 402-i is m_p(P = 1, 2,..., N) distributed information F distributed to members_{i, p}Is calculated by the following equation (42) using the above equation (41).
F_{i, p}= H_Ei(M_p)… (42)
Distributed information F_{i, p}Is a value on the finite field GF (q).
[0101]
Distributed information F for itself_{i, i}Is output to theaddition unit 1205, and the other shared information F_{i, p}(P = 1, 2,..., N and p ≠ i) are distributed to each member via the transmission unit 1203 and thesecret communication channel 103.
[0102]
The transmission unit 1203 outputs the output F from the secret sharing calculation unit 1202._{i, p}(P = 1, 2,..., N and p ≠ i), and transmits it to the other members through thesecret communication channel 103.
[0103]
The receiving unit 1204 checks each of the other members (member ID is m_p(A member where p = 1, 2,..., N and p ≠ i))_{p, i}(P = 1, 2,..., N and p ≠ i), and outputs it to the addingsection 1205.
[0104]
The transmitting unit 1203 and the receiving unit 1204 have a function of transmitting and receiving to and from the distributed processing unit 101-p of another member, and are shared with the transmitting unit 1003-i and the receiving unit 1004-i in the distributed processing unit 101-i. A configuration may be adopted.
[0105]
Theaddition unit 1205 calculates the output F from the secret sharing calculation unit 1202._{i, i}Receive. Further, theaddition unit 1205 receives the output F from the secret sharing calculation unit 1202 of another member from the reception unit 1204._{1, i}, F_{2, i}, ..., F_{n, i}Receive. These n pieces of shared information F_{p, i}(P = 1, 2,..., N) are all added (addition on a finite field GF (q)) as in the following equation (43), and the calculation result c_iIs output.
c_i= F_{1, i}+ F_{2, i}+ ... + F_{n, i}    … (43)
[0106]
Output c from thisadder 1205_iIs the output of the dispersion constant multiplication unit 1101. The input to the dispersion constant multiplication unit 1101 is_i(When the secret reconstruction of the ramp type (L, k, n) threshold secret sharing scheme is performed, the extended field GF (q^L) Value A = (A₀, A₁, ..., A_L-1)) And a constant D = (D₀, D₁, ..., D_L-1), The dispersion information c output from the dispersion constant multiplication unit 1101 at that time._iIs the secret reconstruction of the ramp type (L, k, n) threshold secret sharing scheme by the members,
C = D × A (44)
The expanded field GF (q^L) Value C = (C₀, C₁, ..., C_L-1). Where C₀, C₁, ..., C_L-1Is a value on the finite field GF (q). In addition, the above equation (44) gives an expanded field GF (q^L) Is the above operation (multiplication).
[0107]
[Operation of Second Embodiment]
FIG. 14 is a flowchart illustrating the operation of a configuration (distributed calculation system) that executes the distributed calculation method according to the second embodiment. As shown in FIG. 14, the operation of the configuration (distributed calculation system) for implementing the distributed calculation method according to the second embodiment is the same as the configuration (distributed calculation) for executing the distributed calculation method according to the first embodiment described above. System). However, only the variance addition is performed in step S802 (FIG. 9) of the first embodiment, but the difference is that the dispersion constant multiplication is also performed in step S1302 (FIG. 14) of the second embodiment. .
[0108]
The operation of the configuration (distributed computing system) that implements the distributed computing method according to the second embodiment will be described with reference to FIG. Only the step S1302 different from the first embodiment will be described. As shown in FIG. 14, in step S1302, each member performs the sharing calculation of the function f using the sharing information of its own secret information and the sharing information distributed from other members. Step S1302 shows the operation in the distribution calculation unit 1005-i of FIG. 11, and the member ID is m_iEach member of (i = 1, 2,..., N) has a function f (X₁, X₂, ..., X_nThe variance calculation is performed as specified in ()). This function f handles only addition in the first embodiment, but also handles constant multiplication in the second embodiment. For example, f (X₁, X₂, ..., X_n) = T_AX_A+ T_BX_B
(T_A, T_BIs the extended field GF (q^L), The member ID is m_iIs the distributed information Y held by the member as a result of the distribution._{A, i}And Y_{B, i}From t_AAnd Y_{A, i}Multiplication calculation (operation of the dispersion constant multiplication unit 1101) with t as an input, and t_BAnd Y_{B, i}Is performed (operation of the dispersion constant multiplication unit 1101), and the two outputs are added to obtain a calculation result (intermediate calculation result) Z ′_iAsk for. The calculation result Z '_iIs the extended field GF (q^L) Above calculation result (final calculation result)
Z = f (X₁, X₂, ..., X_n) = T_AX_A+ T_BX_B
(That is, shared information distributed by the ramp-type (L, k, n) secret sharing method).
[0109]
FIG. 15 is a flowchart showing the operation of the dispersion constant multiplication in the second embodiment. For example, the extension field GF (q^L) Value A = (A₀, A₁, ..., A_L-1) And a constant D = (D₀, D₁, ..., D_L-1) Is performed.
[0110]
First, if the member ID is m_iEach member of (i = 1, 2,..., N) has the shared information a of the information A held by itself._i, And the constant D, using the above equation (38),_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is obtained (step S1401). Step S1401 represents the operation of the enlarged field multiplication unit 1201 in FIG.
[0111]
Next, if the member ID is m_iEach member of (i = 1, 2,..., N) has the value E calculated in step S1401._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) To the shared information F using a ramp type (L, k, n) secret sharing scheme._{i, p}(P = 1, 2, ..., n) and the member ID is m_p(P = 1, 2,..., N and p ≠ i) shared information F_{i, p}Is distributed (step S1402). Step S1402 shows the operation of the secret sharing calculation unit 1202 and the transmission unit 1203 of FIG.
[0112]
Next, if the member ID is m_iEach member of (i = 1, 2,..., N) receives the shared information F received by the operation of step S1402._{p, i}(P = 1, 2,..., N) are all added (the above equation (43)), and the value c_iIs obtained and output (step S1403). Step S1403 shows the operation of the receiving unit 1204 and the addingunit 1205 in FIG.
[0113]
[Effect of Second Embodiment]
As described above, according to the second embodiment, as in the first embodiment, the multi-party protocol (each function is a function consisting of only addition and constant multiplication) for each function f In a protocol that obtains the calculation result of the function f by performing a distributed calculation by each member without disclosing the secret information held by the member, the extension field GF (q^LThe above calculation can be achieved by performing only the calculation on the finite field GF (q) smaller than the extension field in the distributed operation processing of each member. For this reason, in the distributed operation processing of each member, the operation cost such as the amount of operation, the circuit scale required for the operation circuit, the storage capacity required for the operation, and the operation time can be reduced.
[0114]
Further, unlike the first embodiment, the second embodiment allows not only the variance addition calculation but also the variance constant multiplication calculation.
[0115]
<< 3rd Embodiment >>
In the first embodiment, the distributed addition method of the distributed calculation by the multi-party protocol using the ramp type (L, k, n) threshold secret sharing method has been described. In the following, a distributed multiplication method of distributed calculation by a multi-party protocol will be described. As in the first and second embodiments, a ramp-type (L, k, n) threshold secret sharing scheme is used. The necessary operation can be performed on a finite field smaller than the size of the finite field of the original secret information, and the operation cost can be reduced.
[0116]
[Configuration of Third Embodiment]
As in the first and second embodiments, in the third embodiment, n members (or n distributed computing devices) each have secret information, and the secret information is used as an argument. A case where a variance calculation is performed to obtain a calculation result of the function f will be described. For n members, the member ID is m₁, M₂, ..., m_nIs assigned. Member ID_m_i(I = 1, 2,..., N) are values on a finite field GF (q) (q is a prime number or a power of a prime number).
[0117]
Also, if the member ID is m_iIs secret information X_iIt is assumed that you have Here, the secret information X held by the member_i(I = 1, 2,..., N) is an L-order extension field GF (q) of the finite field GF (q).^L) And X on the finite field GF (q)_{i, 0}, X_{i, 1}, ..., X_{i, L-1}Can be represented by The finite field GF (q) is L-order expanded to an expanded field GF (q^L) Is generated as g (x), and the generator is α.
[0118]
The configuration (distributed computing system) for implementing the distributed computing method according to the third embodiment is as shown in FIG. 1, as in the first and second embodiments. The configuration (distributed calculation system) that implements the distributed calculation method according to the third embodiment differs from that of the first embodiment in the configuration and operation of the distributed processing unit 101-i.
[0119]
The configuration of the distributed processing unit (distributed computing device) 101-i (i = 1, 2,..., N) in the third embodiment is as shown in FIG. 11 as in the second embodiment. The difference between the distributed processing unit 101-i in the third embodiment and that in the second embodiment is the configuration and operation of the distributed calculation unit 1005-i.
[0120]
The variance calculation unit 1005-i in the third embodiment performs variance multiplication in addition to variance addition (first embodiment) and variance constant multiplication (second embodiment). In the same manner as the above, there is a means for communicating with the distributed processing unit 101-p (where p = 1, 2,..., N and p ≠ i) via thesecret communication channel 103. are doing. The sharing calculation unit 1005-i sends the secret information X from the secret sharing calculation unit 1002-i._iInformation Y of_{i, i}Receive. Further, the secret information X distributed from another member from the receiving unit 1004-i._p(P = 1, 2,..., N and p ≠ i) shared information Y_{1, i}, Y_{2, i}, ..., Y_{n, i}Receive. These n pieces of shared information Y_{p, i}Using (p = 1, 2,..., N), the variance calculation is performed, and the variance information (intermediate calculation result) Z ′ of the calculation result (final calculation result) Z_iIs output. The variance calculation unit 1005-i calculates the function Z = f (X₁, X₂, ..., X_n), One or a plurality of variance multipliers, zero or more variance adders, and zero or more variance constant multipliers. For example,
Z = f (X₁, X₂, ..., X_n)
= (T₁X₁+ T₂X₂+ ... + t_nX_n) × X_M
(Linear combination calculation of secret information and member ID is m_MWhen multiplication by the secret information held by the member is performed, the distribution calculation unit 1005-i has the configuration shown in FIG. 16 (n distribution constant multiplication units 1501, n−1 And a variance multiplication unit 1503). Also,
Z = f (X₁, X₂, ..., X_n) = X_M× X_N
(Member ID is m_M, M_NIn order to calculate the secret information held by a member (multiplication between secret information), the distribution calculation unit 1005-i has a configuration (consisting of one distribution multiplication unit 1601) as shown in FIG.
[0121]
FIG. 18 is a block diagram showing a configuration of the variance multiplier 1503 in FIG. 16 or the variance multiplier 1601 in FIG. The configuration of the variance multipliers 1503 and 1601, which are the components of the variance calculator 1005-i in the third embodiment, will be described with reference to FIG. As shown in FIG. 18, distributed multiplication units 1503 and 1601 include amultiplication unit 1701, an oblivioustransfer calculation unit 1702, a sharedinformation calculation unit 1703, a secret distribution calculation unit 1704, atransmission unit 1705, and areception unit 1706. And an adder 1707. Inputs to distributed multiplication units 1503 and 1601 are input tomultiplication unit 1701 and oblivioustransfer calculation unit 1702. Themultiplication unit 1701 receives an input to the distribution multiplication units 1503 and 1601, and outputs the input to the distributioninformation calculation unit 1703. Further, oblivioustransfer calculation section 1702 receives inputs to distributed multiplication sections 1503 and 1601, and outputs the input to distributedinformation calculation section 1703. The sharedinformation calculation unit 1703 receives the outputs from themultiplication unit 1701 and the oblivioustransfer calculation unit 1702, and the output from the sharedinformation calculation unit 1703 is input to the secret sharing calculation unit 1704. The output from secret sharing calculation section 1704 is input totransmission section 1705 and addition section 1707. Thetransmission unit 1705 transmits information to thesecret communication channel 103. Information received from thesecret channel 103 is input to thereceiving unit 1706, and an output from the receivingunit 1706 is input to the adding unit 1707. The output from the adder 1707 is the output of the variance multipliers 1503 and 1601.
[0122]
The variance multipliers 1503 and 1601 receive two inputs (values on a finite field GF (q)). Expanded field GF (q^L) Value A = (A₀, A₁, ..., A_L-1) And B = (B₀, B₁, ..., B_L-1) Is assumed to be subjected to distributed calculation of C = A × B. Where A₀, A₁, ..., A_L-1, B₀, B₁, ..., B_L-1Is a value on the finite field GF (q). At this time, the inputs to the variance multipliers 1503 and 1601 are the values A and B (member ID is m_i(Retained by members with i = 1, 2,..., N) shared information a_iAnd b_iIt is. Distributed information a_iAnd b_iIs a value on the finite field GF (q). Thereafter, the distributed multiplication units 1503 and 1601 determine that the member ID is m_iThe description will be made assuming that the member of which is (i = 1, 2,..., N) is included in the distributed calculation unit 1005-i. Themultiplication unit 1701 receives the shared information a which is an input to the distributed multiplication units 1503 and 1601._iAnd b_iAnd their multiplication c ′_i= A_i× b_i(Multiplication on a finite field GF (q)), and the multiplication result c ′_iIs output to the sharedinformation calculation unit 1703.
[0123]
Theoblivious transfer calculator 1702 calculates the input a to the distributed multipliers 1503 and 1601._iAnd b_iAnd the member ID is m_{p (}p = 1, 2,..., n and p ≠ i) multiplied by the input value to theoblivious transfer calculator 1702, ie, a_i× b_pAnd a_p× b_iThe communication and calculation processing are performed so as to obtain a result equivalent to the result (not the result of multiplication itself). That is,
a_i× b_p= D_{i, p}, + D_{p, i}    … (45)
a_p× b_i= E_{i, p}, + E_{p, i}    … (46)
D_{i, p}And e_{i, p}Is the member ID is m_iD can hold d_{p, i}And e_{p, i}Is the member ID is m_pPerform calculation and communication so that each member can hold the respective members. The oblivioustransfer calculation unit 1702 calculates n-1 values d_{i, p}(P = 1, 2,... N and p ≠ i) and e_{i, p}(Where p = 1, 2,..., N and p） i) are calculated and output to the sharedinformation calculation unit 1703.
[0124]
The sharedinformation calculation unit 1703 calculates the output c ′ from the multiplication unit 1701._iAnd the output d from the lost communication calculation unit 1702_{i, p}(P = 1, 2,..., N and p ≠ i) and e_{i, p}(P = 1, 2,..., N and p ≠ i), and using them, first, the value G is calculated by the following equation (47)._{u, v}(U = 1, 2,..., L−1; v = 1, 2,..., L−1).
[0125]
[Equation 28]

[0126]
However, in the above equation (47), r_{u, i}(U = 0, 1,..., L−1) is a coefficient calculated from the member ID and represented by the above equation (28).
[0127]
Next, 2L-1 values E ′ as in the following equation (48)_{i, 0}, E '_{i, 1}, ..., E '_{i, 2 (L-1)}Is calculated.
(Equation 29)

[0128]
Next, the output E from the sharedinformation calculation unit 1703 is calculated by the following equation (49)._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is calculated.
[Equation 30]

[0129]
Where g_{j, h}(J = 0, 1,..., L−1; h = 0, 1,..., L−1) is an extended field GF (q^L) Is a value calculated from the coefficient of the generator polynomial g (x). Output E from sharedinformation calculation section 1703_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is input to the secret sharing calculation unit 1704.
[0130]
For example, L = 2, g (x) = x²+ X + 1, the output E_i= (E_{i, 0}, E_{i, 1}) Is calculated by the following equation (50).
[Equation 31]

[0131]
The secret sharing calculation unit 1704, thetransmitting unit 1705, the receivingunit 1706, and the adding unit 1707 according to the third embodiment include the secret sharing calculating unit 1202, the transmitting unit 1203, and the secret sharing unit 1101 (the second embodiment). It is the same as the receiving unit 1204 and the addingunit 1205, respectively.
[0132]
Output F from secret sharing calculation section 1704_{i, i}(E input to secret sharing calculation section 1704_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is output to the adding unit 1707, and further, the output F from the secret sharing calculating unit 1704 is output._{i, p}(E = (E input to secret sharing calculation section 1704)_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is m_p(P = 1, 2,..., N and p ≠ i), and the shared information is output to thetransmitting unit 1705.
[0133]
Thetransmitting unit 1705 transmits the output from the secret sharing calculation unit 1704 to thereceiving unit 1706 of another member through thesecret communication channel 103. The receivingunit 1706 outputs the output F from thetransmitting unit 1705 of another member._{p, i}(Where p = 1, 2,..., N and p ≠ i) are received through thesecret communication channel 103, and the received value is output to the adder 1707. The addition unit 1707 outputs the output F from the secret sharing calculation unit 1704._{i, i}, And the output F from the receiving unit 1706_{p, i}(Where p = 1, 2,..., N and p ≠ i), add them, and calculate the result c_iIs output. The output from the adder 1707 is the output from the variance multipliers 1503 and 1601. Thetransmitting unit 1705 and thereceiving unit 1706 have a function of transmitting and receiving to and from the distributed processing unit 101-p of another member, and are shared with the transmitting unit 1003-i and the receiving unit 1004-i in the distributed processing unit 101-i. A configuration may be adopted.
[0134]
FIG. 19 is a block diagram showing the configuration of theoblivious transfer calculator 1702 in FIG. The configuration of theoblivious transfer calculator 1702 will be described with reference to FIG. The oblivioustransfer calculating section 1702 determines that the member ID is m_iThe description will be made assuming that the member of which is (i = 1, 2,..., N) is included in the distributed calculation unit 1005-i.
[0135]
As shown in FIG. 19, theoblivious transfer calculator 1702 includes i-1 communication calculation receivers 1801-p (p = 1, 2,..., I-1) and i-1 communication calculation receivers Unit 1802-p (p = 1, 2,..., I-1), ni communication calculation transmitting units 1803-p (p = i + 1, i + 2,..., N) and ni communication calculation And a transmission unit 1804-p (p = i + 1, i + 2,..., N). One of the two inputs to the lostcommunication calculation unit 1702 is a communication calculation reception unit 1801-p (p = 1, 2,..., I-1) and a communication calculation transmission unit 1803-p (p = i + 1, i + 2,..., n) and the other one is a communication calculation receiving unit 1802-p (p = 1, 2,..., i-1) and a communication calculation transmitting unit 1804-p (p = i + 1, i + 2). ,..., N). From the communication calculation receiving units 1801-p, 1802-p (p = 1, 2,..., I-1) and the communication calculation transmitting units 1803-p, 1804-p (p = i + 1, i + 2,..., N) Is the output from theoblivious transfer calculator 1702. The communication calculation receiving units 1801-p and 1802-p (p = 1, 2,..., I−1) and the communication calculation transmitting units 1803-p and 1804-p (p = i + 1, i + 2,. By exchanging information with other members through thesecret communication channel 103, as described above, the member ID becomes m_p(P = 1, 2,..., N and p ≠ i) multiplied by the value of another member, ie, a_i× b_pAnd a_p× b_iIs obtained (not the multiplication result itself), but the value a of the other member is_pAnd b_pSo that you don't know_iAnd b_iHowever, it performs what is called oblivious transfer so that other members do not know. As described above, the oblivious transfer means that the transmitting side encodes (encrypts) M pieces of information and transmits it, but the receiving side receives only one of them (they can be decoded in a meaningful manner). ), And a communication method in which the transmitting side cannot know what information the receiving side has received (the decoding has become meaningful). In this embodiment, oblivious transfer is configured by utilizing the difficulty of calculating a discrete logarithm under the modulus q.
[0136]
The communication calculation receiving units 1801-p and 1802-p (p = 1, 2,..., I−1) and the communication calculation transmitting units 1803-p and 1804-p (p = i + 1, i + 2,. , I, or may not have a communication calculation receiving unit or a communication calculation transmitting unit. For example, when i = 1, there is no communication calculation receiving unit, and there are 2 × (n−1) communication calculation transmitting units. When i = n, the communication calculation transmitting unit is not provided, and 2 × (n−1) communication calculation receiving units are provided. Also, the relationship of transmission and reception with other members is as follows._iFrom the communication calculation transmission units 1803-p and 1804-p (p = i + 1, i + 2,..., N) of the member through thesecret communication path 103, respectively._pIs passed to each of the communication calculation receiving units 1801-i and 1802-i of the member. Details will be described with reference to FIGS.
[0137]
FIG. 20 is a block diagram showing a configuration of the communication calculation receiving units 1801-p and 1802-p (p = 1, 2,..., I-1) in FIG. The configuration of the communication calculation receiving units 1801-p and 1802-p (p = 1, 2,..., I-1) will be described with reference to FIG. As shown in FIG. 20, the communication calculation receiving units 1801-p and 1802-p (p = 1, 2,..., I-1) include an indexcalculation transmitting unit 1901 and areception restoring unit 1902. The communication calculation receiving unit 1801-p receives one of the two inputs to the lostcommunication calculating unit 1702, and the communication calculation receiving unit 1802-p receives the other input. Here, the input to the communication calculation receiving unit 1801-p is a_iAnd the input to the communication calculation receiving unit 1802-p is b_iAnd Since the communication calculation receiving units 1801-p and 1802-p have the same internal structure, the communication calculation receiving unit 1801-p will be described here, and the description corresponding to the communication calculation receiving unit 1802-p will be described in parentheses []. Describe within. The input to the communication calculation receiving unit 1801-p [1802-p] is input to the indexcalculation transmitting unit 1901. The output from indexcalculation transmitting section 1901 is input toreception restoring section 1902. The output from thereception restoring unit 1902 is the output from the communication calculation receiving unit 1801-p [1802-p].
[0138]
The indexcalculation transmitting unit 1901 receives the input a from the communication calculation receiving unit 1801-p [1802-p]._i  [B_i], And is subjected to a calculation represented by the following equation (51) to obtain a ′_{i, p}  [B '_{i, p}Is calculated through thesecret channel 103 and the member ID is m_p(P = 1, 2,..., I−1).
(Equation 32)

[0139]
In the above equation (51), h and g are two generators of the finite field GF (q), and rA_{i, p}  [RB_{i, p}] Selects a value on a finite field GF (q) as a random number. Also, the indexcalculation transmitting unit 1901 calculates the random number rA used in the above equation (51)._{i, p}  [RB_{i, p}Is output to thereception restoring section 1902.
[0140]
Thereception restoring unit 1902 checks that the member ID is m_pQ information (q is the number of elements of the finite field GF (q)) is received from the member (p = 1, 2,..., I−1), and a_iTh information d '_{i, p}  [B_iTh information e '_{i, p}Is calculated by the following equation (52) to obtain the target value d._{i, p}  [E_{i, p}] Is calculated. Thereception restoring unit 1902 determines that the other received information indicates that the member ID is m_iFor members who are, it looks like a random number.
[0141]
[Equation 33]

[0142]
Value d '_{i, p}  [E '_{i, p}] Is two pieces of information d ′_{1, i, p}And d '_{2, i, p}[E'1, j, p and e '_{2, i, p}] The calculated value d_{i, p}  [E_{i, p}] Is the output of thereception restoring unit 1902 and is the output from the communication calculation receiving unit 1801-p [1802-p].
[0143]
FIG. 21 is a block diagram illustrating a configuration of the communication calculation transmission units 1803-p and 1804-p (p = i + 1, i + 2,..., N) in FIG. The configuration of the communication calculation transmission units 1803-p and 1804-p will be described with reference to FIG. As shown in FIG. 21, the communication calculation transmitting units 1803-p and 1804-p (p = i + 1, i + 2,..., N) include a randomnumber generation unit 2001, a finite fieldelement generation unit 2002, and a multiplier calculation transmission unit. 2003-a (a = 1, 2,..., Q).
[0144]
The inputs to the communication calculation transmission units 1803-p and 1804-p (p = i + 1, i + 2,..., T) are output from the randomnumber generation unit 2001 and the finite fieldelement generation unit 2002, as well as the multiplier calculation transmission unit 2003-a. (A = 1, 2,..., Q). The output from the randomnumber generation unit 2001 is the output from the communication calculation transmission units 1803-p and 1804-p (p = i + 1, i + 2,..., N). The communication calculation transmission unit 1803-p receives one of the two inputs of the lostcommunication calculation unit 1702, and the communication calculation transmission unit 1804-p receives the other input. Here, the input to the communication calculation transmitting unit 1803-p is a_i, The input to the communication calculation transmitting unit 1804-p is b_ifar. Since the communication calculation transmission units 1803-p and 1804-p have the same internal structure, the communication calculation transmission unit 1803-p will be described here, and the description corresponding to the communication calculation transmission unit 1804-p will be described in parentheses []. Describe within.
[0145]
The randomnumber generation unit 2001 illustrated in FIG. 21 generates and outputs a random number having a value on a finite field GF (q). The same random number is output to the multiplier calculation transmitting unit 2003-a (a = 1, 2,..., Q). The output from the randomnumber generation unit 2001 is the output from the communication calculation transmission unit 1803-p [1804-p] (p = i + 1, i + 2,..., N).
[0146]
The finite fieldelement generation unit 2002 shown in FIG. 21 sequentially generates values on the finite field GF (q) as 0, 1,..., Q−1, and respectively calculates the multiplier calculation transmission unit 2003-a (a = 1, 2,..., Q). That is, 0 is set to the multiplier calculation transmitting unit 2003-1, 1 is set to the multiplier calculating transmitting unit 2003-2, j-1 is set to the multiplier calculating transmitting unit 2003-j, and q is set to the multiplier calculating transmitting unit 2003-q. -1 is output.
[0147]
Multiplier calculation transmitting section 2003-a (a = 1, 2,..., Q) shown in FIG. 21 receives input from communication calculation transmitting section 1803-p [1804-p] (p = i + 1, i + 2,. Value a_i  [B_i], The random number from the randomnumber generation unit 2001, the corresponding finite field element a-1 from the finite fieldelement generation unit 2002, and the member ID m_p(P = i + 1, i + 2,..., N) Information from the member (output from the indexcalculation transmission unit 1901 of the communication calculation reception units 1801-i [1802-i] of the other members) a ′_{p, i}  [B '_{p, i}], Calculate from those inputs, and output the calculation result. The outputs from the multiplier calculation transmitting unit 2003-a (a = 1, 2,..., Q), that is, q outputs in total, have the member ID m_p(P = i + 1, i + 2,..., N). Now, let the output from the randomnumber generation unit 2001 be d_{i, p}  [E_{i, p}]. Also, the value received through thesecret channel 103 is a '_{p, i}(Corresponding to the communication calculation transmitting unit 1803-p) [b '_{p, i}(Corresponding to the communication calculation transmitting unit 1804-p)]. A-1 is input from the finite fieldelement generation unit 2002 to the multiplier calculation transmission unit 2003-a (a = 1, 2,..., Q). The multiplier calculation transmitting section 2003-a (a = 1, 2,..., Q) calculates the following equations (53) to (55), and obtains d ′._{p, i, a}  [E '_{p, i, a}] Respectively (d '_{p, i, a}[E '_{p, i, a}] Is composed of two values as described in the description of the equation (52)._p(P = i + 1, i + 2,..., N) are transmitted in the order of a = 1, 2,.
[0148]
[Equation 34]

[0149]
Where kA_a  [KB_a(A = 1, 2,..., Q)] are random numbers of values on q finite fields GF (q), respectively. These outputs d '_{p, i, a}Or e '_{p, i, a}Through thesecret communication channel 103 and the member ID is m_pWhen the communication calculation receiving unit 1801-i [communication calculation receiving unit 1802-i] of the member whose (p = i + 1, i + 2,..., N) receives the received member, a = a_p  [B_pA'd information d 'corresponding to_{p, i}= D '_{p, i, a}[E '_{p, i}= E '_{p, i, a}] Can be decoded by Expression (52) (other received information is that the member ID is m_pFor members who are, it looks like a random number.)
[0150]
Output d from randomnumber generation section 2001 shown in FIG._{i, p}  [E_{i, p}] Is the output from the communication calculation transmitting unit 1803-p [1804-p] (p = i + 1, i + 2,..., N).
[0151]
The input to the distributed multiplication units 1503 and 1601 having the configuration shown in FIG._iAnd b_i(When the secret reconstruction of the ramp type (L, k, n) threshold secret sharing scheme is performed, each of the extended fields GF (q^L) Value A = (A₀, A₁, ..., A_L-1) And B = (B₀, B₁, ..., B_L-1)), The shared information c output from the shared multiplication units 1503 and 1601 at that time._iIs the secret reconstruction of the ramp type (L, k, n) threshold secret sharing scheme by the members,
C = A × B (56)
The expanded field GF (q^L) Value C = (C₀, C₁, ..., C_L-1). Where C₀, C₁, ..., C_L-1Is a value on the finite field GF (q). Equation (56) is given by the extended field GF (q^L) Is the above operation (multiplication).
[0152]
[Operation of Third Embodiment]
FIG. 22 is a flowchart illustrating the operation of a configuration (distributed calculation system) that executes the distributed calculation method according to the third embodiment. The operation of the configuration (distributed calculation system) that implements the distributed calculation method according to the third embodiment is, as shown in FIG. 22, configured to execute the distributed calculation method according to the above-described first and second embodiments. (Distributed computing system). However, only variance addition is performed in step S802 (FIG. 9) of the first embodiment, and only variance addition and dispersion constant multiplication are performed in step S1302 (FIG. 14) of the second embodiment. The difference is that variance multiplication is also performed in step S2102 (FIG. 22) of the embodiment.
[0153]
The operation of the configuration (distributed computing system) that implements the distributed computing method of the third embodiment will be described with reference to FIG. Only the step S2102 different from the first and second embodiments will be described. As shown in FIG. 22, in step S2102, each member performs the sharing calculation of the function f using the sharing information of its own secret information and the sharing information distributed from other members. Step S2102 shows the operation in the distribution calculation unit 1005-i of FIG. 11, and the member ID is m_iEach member of (i = 1, 2,..., N) has a function f (X₁, X₂, ..., X_nThe variance calculation is performed as specified in ()). This function f handles only addition in the first embodiment and only addition and constant multiplication in the second embodiment, but also handles multiplication in the third embodiment. For example,
f (X₁, X₂, ..., X_n) = (T_AX_A+ T_BX_B) × X_C
(T_AAnd t_BIs the extended field GF (q^L), The member ID is m_iIs the distributed information Y held by the member as a result of the distribution._{A, i}, Y_{B, i}, And Y_{c, i}From t_AAnd Y_{A, i}Constant multiplication calculation (operation of the dispersion constant multiplication unit 1101) with t_BAnd Y_{B, i}Is performed (operation of the dispersion constant multiplication unit 1101), and variance addition of the two outputs is performed (operation of the dispersion addition units 501 and 601)._{c, i}Multiplication calculation (operations of the multiplication units 1503 and 1601) with Z ′_iAsk for. The calculation result Z '_iIs the extended field GF (q^L) Calculation result above
Z = f (X₁, X₂, ..., X_n) = (T_AX_A+ T_BX_B) × X_C
(Distributed by a ramp-type (L, k, n) secret sharing scheme).
[0154]
FIG. 23 is a flowchart showing the operation in the distributed multiplication in the third embodiment. For example, the extension field GF (q^L) Value A = (A₀, A₁, ..., A_L-1), B = (B₀, B₁, ..., B_L-1) Is performed. First, if the member ID is m_iEach member having (i = 1, 2,..., N) has shared information a of values A and B held by itself._iAnd b_iFrom the product c '_i= A_i× b_i, And the value of d as in equations (45) and (46) using oblivious transfer_{i, p}And e_{i, p}(Where p = 1, 2,..., N and p ≠ i) are obtained (step S2201). Step S2201 is performed by multiplying unit 1701 (value c 'in FIG. 18)._iIs obtained), and the oblivious transfer calculator 1702 (value d)_{i, p}And e_{i, p}(Where p = 1, 2,..., N and p ≠ i) is obtained.
[0155]
Next, if the member ID is m_iEach member with (i = 1, 2,..., N) has the value c ′ calculated in step S2201._iAnd d_{i, p}, E_{i, p}(Where p = 1, 2,..., N and p ≠ i), Eq._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is obtained (step S2202). Step S2202 shows the operation of the sharedinformation calculation unit 1703 in FIG.
[0156]
Next, if the member ID is m_iEach member of (i = 1, 2,..., N) has the value E calculated in step S2202._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) To the shared information F using a ramp type (L, k, n) secret sharing scheme._{i, p}(P = 1, 2, ..., n) and the member ID is m_p(P = 1, 2,..., N and p ≠ i) shared information F_{i, p}Is distributed (step S2203). Step S2203 shows the operation in the secret sharing calculation unit 1704 and thetransmission unit 1705 in FIG.
[0157]
Next, if the member ID is m_i(I = 1, 2,..., N) are members of the shared information F received by the operation of step S2203._{i, p}(P = 1, 2,..., N) are all added (the above equation (43)), and the value c_iIs obtained and output (step S2204). Step S2204 shows the operation of thereceiving unit 1706 and the adding unit 1707 of FIG.
[0158]
[Effects of Third Embodiment]
As described above, according to the third embodiment, similarly to the first and second embodiments, the function f (where the function f is a function composed of addition, constant multiplication, and multiplication) is used. In a multi-party protocol (a protocol that obtains the calculation result of a function f by performing a distributed calculation by each member without disclosing secret information held by each member), an extension field GF (q^LThe above calculation can be achieved by performing only the calculation on the finite field GF (q) smaller than the extension field in the distributed operation processing of each member. For this reason, in the distributed operation processing of each member, the operation cost such as the amount of operation, the circuit scale required for the operation circuit, the storage capacity required for the operation, and the operation time can be reduced.
[0159]
Further, unlike the first and second embodiments, the third embodiment enables not only the variance addition calculation and the variance constant multiplication calculation but also the variance multiplication calculation.
[0160]
The “member” in the first to third embodiments does not necessarily need to be a single person, but holds secret information and has a calculation unit (distributed secret reconstruction calculation unit) as a component. It can also be. That is, one person can proceed with the process by holding a plurality of the above devices. In this case, one person becomes a plurality of members. Further, a single device can be managed by a plurality of persons and the processing can be advanced. In this case, a plurality of persons become one member.
[0161]
<< 4th Embodiment >>
In the first to third embodiments, the shared information used for the shared calculation in the shared calculation unit 305-i or 1005-i in each member is not necessarily the secret X held by the member._iEven if it is not the shared information, the shared calculation can be performed. That is, shared information distributed from outside (it may be assumed to be a center) by a ramp-type (L, k, n) threshold secret sharing method is necessary for calculating a target function f. It is possible to provide a distributed processing unit that is given some (may be larger than the number n of members) and uses it to perform distributed calculation. FIG. 24 shows the configuration of a distributed calculation method (distributed calculation system) using such a distributed processing unit, and FIGS. 25A and 25B show the configuration of the distributed processing unit (distributed calculation device). Shown in
[0162]
As shown in FIG. 24, the configuration (distributed calculation system) that implements the secret calculation method according to the fourth embodiment includes a secret sharedtransmission unit 2301 and n shared processing units 2302-i (i = 1, 2). ,..., N) and a secret reconstruction calculation unit 2303.
[0163]
The secretsharing transmission unit 2301 outputs the extension field GF (q^L), And obtains shared information distributed by a ramp-type (L, k, n) threshold secret sharing scheme, and outputs the obtained shared information to each shared processing unit 2302-i (i = 1, 2,..., N). . For example, D = f (A, B, C) (A, B, C, D is an extended field GF (q^L), The secretsharing transmission unit 2301 shares A, B, and C with the ramp type (L, k, n) threshold secret sharing method, and obtains the shared information a._i, B_i, C_i(I = 1, 2,..., N) are output to the respective distributed processing units 2302-i.
[0164]
As shown in FIGS. 25A and 25B, each of the shared processing units 2302-i has a shared information receiving unit 2406-i that receives the output from the secretsharing transmitting unit 2301, and the shared information receiving unit The shared information received in 2406-i is output to the shared calculation unit 2405-i.
[0165]
When the desired function f includes constant multiplication and multiplication, the distribution calculation unit 2405-i includes thesecret communication channel 103 that performs secret communication with another distribution processing unit 2302-i. The variance calculation of the function f is performed using the value received from the information receiving unit 2406-i and the value received from the receiving unit 2404-i (in the case of FIG. 25A). The configuration of the variance calculator 2405-i is the same as that of the first to third embodiments, and outputs a variance calculation result. The output from the sharing calculation unit 2405-i is input to the secret reconstruction calculation unit 2303. A secret information storage unit 2401-i, a secret sharing calculation unit 2402-i, a transmission unit 2403-i, and a reception unit 2404-i are the same as those in the first to third embodiments. Also, since the shared information receiving unit 2406-i has a function equivalent to the receiving unit 2404-i, the function of the shared information receiving unit 2406-i is given to the receiving unit 2404-i, and only one receiving function is provided. A configuration is also possible.
[0166]
The secret reconstruction calculation unit 2303 shown in FIG. 24 is the same as the secret reconstruction calculation unit of the first to third embodiments, and outputs the final calculation result of the function f. As in the first to third embodiments, the processing in the secret reconstruction calculation unit 2303 may be performed by a center that integrates the processing, or one of the gathered members may be used. Or, it may be performed by a plurality of persons. However, it is desirable that the member who needs the calculation result Z perform the calculation. Further, the final secret reconstruction processing (operation of the secret reconstruction calculation unit 2303) may be performed by a distributed processing unit of one or more members, and therefore, the configuration of the distributed processing unit having such a configuration. Are shown in FIGS. 26 and 27 (a) and (b). This is a form in which a secret reconstruction calculation unit is added to the distribution processing units of the first to third embodiments and the distribution processing units shown in FIGS. 25A and 25B. In the configurations of FIGS. 26 and 27 (a) and (b), since the final calculation result Z can be reconstructed by the distribution processing unit itself, the output Z 'from the distribution calculation unit 2505-i is output._iCan select whether or not to output as output to the outside from the distributed processing unit as necessary. Therefore, in FIG. 26 and FIGS. 27A and 27B, the output from the variance calculation unit 2505-i is depicted by a dashed arrow. If one or more distributed processing units having the configurations shown in FIGS. 26 and 27 (a) and (b) are included, the secret reconstruction calculation unit in the distributed computing system having the configurations shown in FIGS. It is possible to obtain the final calculation result Z without the provision of 102 and 2303.
[0167]
In the second embodiment, in the description of the configuration of the extended field multiplication unit 1201 in FIG._{i, 0}, E '_{i, 1}, ..., E '_{i, 2 (L-1)}Is calculated, then E in equation (38) is calculated._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is calculated, but as in the example of L = 2, E ′ is calculated as in equation (40)._{i, 0}, E '_{i, 1}, ..., E '_{i, 2 (L-1)}E directly without seeking_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) May be obtained.
[0168]
Similarly, in the third embodiment, in the description of the configuration of the sharedinformation calculation unit 1703 in FIG._{u, v}(U = 0, 1, 2,..., L-1; v = 0, 1, 2,..., L-1)._{i, 0}, E '_{i, 1}, ..., E '_{i, 2 (L-1)}Is calculated, then E in equation (49) is calculated._i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) Is calculated, but as in the example of L = 2, G is calculated as in equation (50)._{u, v}(U = 0, 1, 2,..., L−1; v = 0, 1, 2,..., L−1) and E ′_{i, 0}, E '_{i, 1}, ..., E '_{i, 2 (L-1)}E directly without seeking_i= (E_{i, 0}, E_{i, 1}, ..., E_{i, L-1}) May be obtained.
[0169]
In the lostcommunication calculation unit 1702 in the third embodiment, (1) the communication calculation reception unit 1801-p (p = 1, 2,..., I-1) is replaced with a communication calculation transmission unit, and further, the communication calculation transmission is performed. A configuration in which the unit 1803-p (p = i + 1, i + 2,..., N) is replaced with a communication calculation receiving unit, or (2) a communication calculation receiving unit 1802-p (p = 1, 2,..., I-1) Is replaced by a communication calculation transmitting unit, and further, the communication calculation transmitting unit 1804-p (p = i + 1, i + 2,..., N) is replaced by a communication calculation receiving unit. The same operation and effect can be obtained by a configuration in which the calculation transmission unit is further replaced with a communication calculation reception unit.
[0170]
In the lostcommunication calculation unit 1702 in the third embodiment, thesecret communication path 103 between the communication calculation transmission unit 1801-p (or 1802-p) and the communication calculation reception unit 1803-j (or 1804-j) is used. As for the exchange of information, it is difficult to calculate the encrypted information, that is, the discrete logarithm under the modulo q, as shown in Expressions (51) and (53) to (55). Since it is information that conceals the information that the user wants to send, secret information of members and intermediate results of the distributed calculation will not be revealed even if communication is not performed in secret. In equation (51), the information a_i(Or b_i) Is hidden as a power number of the generator h of the finite field GF (q), and necessary information a to be obtained from the information obtained by Expressions (53) to (55)_i(A-1) -d_{i, p}(Or b_i(A-1) -e_{i, p}) Is the random number rA used in equation (51)._{p, i}(Or rB_{p, i}) Can not be calculated without knowing. Therefore, in the above communication, the communication may be performed not on the secret communication path but on a broadcast-type communication path or a communication path that may be eavesdropped.
[0171]
<< 5th Embodiment >>
In the sharing calculation according to the fifth to seventh embodiments of the present invention, similarly to the first to fourth embodiments, instead of the conventionally used (k, n) threshold secret sharing method, A ramp-type secret sharing scheme (ie, a ramp-type (L, k, n) threshold secret sharing scheme) is used. In the following description, it is assumed that variables such as secret information and random numbers are all elements on a certain finite field GF (q). In the first to fourth embodiments, the relationship of k ≦ n is established between the threshold value k and the number n of pieces of shared information. However, in the fifth to seventh embodiments, 2k−1 It is assumed that a relationship of ≦ n is established.
[0172]
In the first to fourth embodiments, the shared information is calculated using the (k-1) -th order polynomial as in Expression (19). In the fifth to seventh embodiments, the following expression ( The shared information is calculated using a (k-1) -order polynomial such as 57).
(Equation 35)

[0173]
Where S₀, S₁, ..., S_L-1Are secret information, and R₀, ..., R_k-L-1Are random values, respectively. Further, g (x) is an L-order irreducible polynomial, and corresponds to the generator polynomial g (x) of Expression (36) in the first to fourth embodiments. This irreducible polynomial is given in advance. Member ID (that is, ID information) w_iThe distributed information to be passed to the member having the_i). Member ID_w which each member has_iShall be public. In the first to fourth embodiments, the member ID is m_i(I = 1, 2,..., N), but in the fifth to seventh embodiments, the member ID is set to w._i(I = 0, 1,..., N-1) and the member ID is w_iIs a member P_iI will call it.
[0174]
In the fifth to seventh embodiments, the secret information (S₀, ..., S_L-1) Using an irreducible polynomial g (x) to an L-order extension field GF (q) of a finite field GF (q)^L). That is, when the solution of the equation g (x) = 0 is α,
S = S_L-1α^L-1+ ... + S₁α + S₀
It expresses. From this, the calculation regarding the secret information is performed by the finite field GF (q^L)), Which can be realized by addition or multiplication of polynomials modulo g (x).
[0175]
Member ID is w_iMember P_i(I = 0,..., N−1), respectively, f (w_i) As distributed information. The size of the shared information at this time is 1 / L of the secret information. Restoration of secret information restores a polynomial, and then calculates mod g (x), as in the (k, n) threshold method.
[0176]
[Configuration of Fifth Embodiment]
In the following, in the fifth embodiment, a description will be given of a sharing calculation using a ramp-type secret sharing. In particular, it is assumed that variance addition is performed as a specific example of variance calculation. From this point, the fifth embodiment has contents similar to those of the first embodiment, but differs in a method of generating shared information.
[0177]
In the fifth embodiment, a system that performs secret sharing and secret restoration (reconstruction), and shared calculation will be described. In particular, it is assumed that variance addition is performed as a specific example of variance calculation. Hereinafter, in the distributed calculation, the secret information is expressed as A = (A₀, ..., A_L-1) And B = (B₀, ..., B_L-1). And the member ID is w_jThe shared information possessed by the member is represented by a (w_j) And b (w_j).
[Equation 36]

[0178]
At this time, the polynomial representing the sum of the shared information is as shown in the following equation (59).
(37)

[0179]
From this, the following equation (60) is obtained.
[Equation 38]

[0180]
By substituting x = α into this equation, the right side becomes an extended field GF (q^L) Represents the addition. Therefore,
c_j= A (w_j) + B (w_j)
Represents shared information of a value C (= A + B) which is a sum of secret information A and B. Therefore, in the variance addition, the member P_jSuffices to calculate the sum of the pieces of shared information.
[0181]
The configuration of the distributed computing system according to the fifth embodiment is the same as the distributed computing system according to the first to fourth embodiments shown in FIG. 1 or FIG. The fifth embodiment is different from the first to fourth embodiments in that a ramp-type secret sharing scheme for generating shared information is different. Therefore, the respective components, a secretsharing transmission unit 2301, and sharingprocessing units 101 and 2302 are provided. , And secret reconstruction calculators 102 and 2303 are different. FIG. 28 is a block diagram illustrating a configuration of a distributed calculation device (corresponding to the distributedcalculation processing units 101 and 2302 in FIGS. 1 and 24) according to the fifth embodiment. As shown in FIG. 28, the shared computing device according to the fifth embodiment includes asecret sharing part 3001, a sharingcalculation part 3002, asecret restoration part 3003, and asecret communication channel 103. Thesecret sharing part 3001 illustrated in FIG. 28 includes a secret sharing unit 3101 and atransmission unit 3102. Also, thevariance calculation unit 3002 illustrated in FIG. 28 includes areception unit 3103, astorage unit 3104, a variance calculation unit 3105, and atransmission unit 3106. Further, thesecret restoration section 3003 shown in FIG. 28 includes areceiving section 3107 and asecret restoration section 3108. The shared computing device may have only one or two of thesecret sharing part 3001, the sharedcalculation part 3002, and the secret restoration part 3003 (described later with reference to FIGS. 31 to 33). .
[0182]
The secret sharing unit 3101 performs ramp-type secret sharing on the secret information to calculate the shared information. Thetransmitting unit 3102 is connected to the other members via thesecret communication channel 103, and performs one-to-one secret communication. Then, the calculation result is distributed to other members. As a result, each member obtains shared information.
[0183]
The receivingunit 3103 receives the shared information from another member or a center provided separately from the member. As a result, the member holds the shared information. Thestorage unit 3104 holds the shared information obtained by the secret sharing and the result of the shared calculation. The variance calculation unit 3105 calculates the variance information held in thestorage unit 3104. Then, shared information of an arbitrary calculation result of the secret information is obtained.
[0184]
In the fifth embodiment, a case will be described in which the share calculation unit 3105 obtains share information of the sum of secret information. In general, the variance calculator 3105 is configured by a combination of variance addition shown in the fifth embodiment, variance multiplication shown in a sixth embodiment described later, and variance constant multiplication shown in a seventh embodiment described later. . Thetransmitting unit 3106 distributes the result of the distributed calculation. Here, thetransmission unit 3106 also distributes shared information via thesecret communication channel 103. Here, each of the members has thereception unit 3103, thestorage unit 3104, the distribution calculation unit 3105, and thetransmission unit 3106.
[0185]
The receivingunit 3107 receives the result of the distribution calculation from another member. Thesecret restoring unit 3108 restores (reconstructs) secret information using the shared information received from all members. Thetransmitting unit 3102 and thetransmitting unit 3106 and thereceiving unit 3103 and thereceiving unit 3107 may have a common configuration when the members have the same.
[0186]
FIG. 29 is a block diagram showing a configuration of secret sharing section 3101 of FIG. As shown in FIG. 29, the secret sharing unit 3101 has a randomnumber generation unit 3111 and a finitefield operation unit 3112. The random number generation unit 3101 generates a random number used when performing secret sharing calculation. The finitefield operation unit 3112 generates shared information from the secret information, the member ID of the member, the generated random number, and the irreducible polynomial.
[0187]
FIG. 30 is a block diagram showing a configuration of thesecret restoration unit 3108 of FIG. As shown in FIG. 30, thesecret restoration unit 3108 includes a restoration information generation unit 3121 and a finitefield operation unit 3122. The restoration information generation unit 3121 generates information used for secret restoration from the member ID and the irreducible polynomial. The finitefield operation unit 3122 performs restoration calculation of secret information from the generated information and the shared information.
[0188]
Asecret sharing part 3001 shown in FIG. 28 is a part for performing secret sharing. Thedistribution calculation part 3002 illustrated in FIG. 28 is a part that receives the distribution information and executes the distribution calculation. 28. Finally, thesecret restoring part 3003 shown in FIG. 28 is a part that collects the distribution calculation results and restores the calculation result of the original secret information. Each member may have the secret sharing unit 3101 and thetransmission unit 3102, which are thesecret sharing unit 3001 shown in FIG. 28, or a center independent of the members. The receivingunit 3107 and thesecret restoring unit 3108, which are thesecret restoring units 3003 shown in FIG. 28, may be owned by at least one member, or may be performed by a center independent of the members.
[0189]
In the following, FIG. 31 shows the configuration of a distributed computing system in a case where a distributed calculation is performed on secret information held by a member and the calculation result is obtained by the member. The block indicated by "participant" is the distributed computing device of each member, and although only two are illustrated in the figure, there are actually n units. Each participant has asecret sharing part 3001, a sharingcalculation part 3002, and asecret restoring part 3003. FIG. 32 shows the configuration of a distributed computing system in a case where a member performs a distributed calculation on secret information held by the member and the center obtains a result of the calculation. FIG. 32 is a configuration diagram similar to that of the distributed computing system of FIG. The block indicated by "participant" is the distributed computing device of each member, and although only two are illustrated in the figure, there are actually n units. The block indicated by "center" is a part for finally restoring the calculation result, and is a part corresponding to the secret reconstruction calculation unit 102 in FIG. Each participant has asecret sharing part 3001 and a sharingcalculation part 3002. FIG. 33 shows the configuration of a distributed calculation system in a case where the center performs secret calculation on secret information held by the center and obtains a calculation result. FIG. 33 is a configuration diagram similar to the distributed computing system of FIG. The block indicated by "participant" is a distributed computing device of each member, and although only two are shown in the figure, there are actually n blocks. 24. The block indicated by the upper "center" (the portion including the secret sharing unit 3101 and the transmitting unit 3102) is a portion for distributing secret information, and corresponds to the secretsharing transmitting unit 2301 in FIG. It is. Further, the block indicated by the lower part “center” (a part composed of thesecret restoration part 3108 and the reception part 3107) is a part for restoring the calculation result finally, and the secret reconstruction calculation part 2303 in FIG. Is the part corresponding to. Each participant has a distributedcalculation portion 3002.
[0190]
[Operation of Fifth Embodiment]
In the fifth embodiment, a procedure for sharing calculation using a ramp-type secret sharing scheme will be described. As a specific example of the sharing calculation, a procedure will be described in which secret sharing is performed from secret information held by each member to obtain shared information, and the sum of the original secret information is obtained from the shared information.
[0191]
First, the operation in secret sharing will be described. S = (S₀, S₁, ..., S_L-1). Secret information S = (S₀, S₁, ..., S_L-1) And a randomly generated value R₀, ..., R_k-L-1And the following equation (61)
[Equation 39]

The member P shown in the following equation (62) using a polynomial such as_jInformation s for_jGenerate
(Equation 40)

[0192]
This calculation is an n × n matrix such as
E = (e_ij)
e_ij= W_i^j(I = 0, ..., n-1; j = 0, ..., n-1)
Using,
(S₀, ..., s_n-1)^t
= E (f₀, F₁, ..., f_k-1, 0, ..., 0)^t
Can be expressed as Then, the shared information s_jIs the member P_jPass to.
[0193]
It is assumed that t pieces of shared information collected for secret restoration (t ≧ k). First, each member P 'of the secret restoration_jFrom the shared information s'_jAnd the member ID w 'of each member_j(J = 0,..., T−1) is received. Then, from the simultaneous equation of the following equation (63), the coefficient f of the polynomial is calculated.₀, F₁, ..., f_k-1Ask for.
s'_j= F_k-1w '_j  ^k-1+ ... + f₁w '_j+ F₀    … (63)
Here, j = 0,..., T−1.
[0194]
Then, for the obtained polynomial, the remainder (the following equation (64)) is calculated by the irreducible polynomial g (x).
(Equation 41)

The obtained coefficients of the polynomial correspond to the restored secret information.
[0195]
This calculation is equivalent to a calculation using a matrix as shown below. Let G be the matrix representing the remainder of the polynomial modulo the irreducible polynomial g (x). And the member ID_w 'of the member_iFrom the t × t matrix
E '= (e'_ij)
e '_ij= W '_i^j(I = 0, ..., t-1; j = 0, ..., t-1). Matrix G and inverse matrix E 'of matrix E'^-1From the matrix R = GE ′^-1= (R_ij) Is calculated. The r thus obtained_ijIs used to calculate the following equation (65).
(Equation 42)

The resulting S₀, ..., S_L-1Is the restored secret information.
[0196]
Here, a method of generating the matrix G will be described. The matrix G is a (t-1) degree polynomial
h (x) = h_t-1x^t-1+ ... + h₁x + h₀
To the irreducible polynomial
g (x) = x^L+ ... + g₁x + g₀
The following equation (66) is the remainder when divided by
[Equation 43]

Thus, a matrix G is obtained as in the following equation (67).
[0197]
[Equation 44]

[0198]
For example, GF (31), t = 16, irreducible polynomial g (x) = x³In the case of + x + 3, the result of calculating the matrix G is as follows. A 15th-order polynomial (Equation (68) is defined as follows.
[Equation 45]

[0199]
The result of the remainder calculation modulo the irreducible polynomial g (x) is as shown in the following equation (69).
[Equation 46]

[0200]
Thus, the matrix G is as shown in the following equation (70).
[Equation 47]

[0201]
Next, the operation in the distributed calculation will be described. In the fifth embodiment, variance addition will be described as a specific example. Member P_jIs the shared information a of the secret information A and B_jAnd b_jIt is assumed that you have In the distributed addition, the sum of the shared information held by each member may be calculated. That is, in order to obtain the shared information of the sum A + B of the secret information held by each member, the member P_jIs the sum of shared information a_j+ B_jCan be calculated.
[0202]
[Effects of Fifth Embodiment]
As described above, the operation performed by each member can be performed in a finite field smaller than the finite field in which the original secret information is defined (in the above description, an L-order expanded field). As a result, each member can execute the addition regarding the secret information with less computational resources.
[0203]
<< Sixth Embodiment >>
In the sixth embodiment of the present invention, variance multiplication and dispersion will be described as a specific example. A = (A₀, ..., A_L-1) And B = (B₀, ..., B_L-1). The shared information is calculated from the following polynomial (Equation (71)).
[Equation 48]

[0204]
At this time, the polynomial representing the product of the shared information is as shown in the following equation (72).
[Equation 49]

[0205]
Thus, the following equation (73) holds.
[Equation 50]

[0206]
Substituting x = α into this, this gives the extension field GF (q^L) Above. Therefore, a (w_i) B (w_i) Represents the variance information of the value AB by the 2 (k-1) -order polynomial. However, as in the conventional case, a conversion operation (BPB) that lowers the degree of the polynomial so as not to change the secret information^-1) C = D is required (corresponding to the process of step S203 in the variance multiplication (method {circle around (2)) described in the related art), and C = (a (w₀) B (w₀), A (w₁) B (w₁), ..., a (w_n-1) B (w_n-1))). In the conventional (k, n) threshold secret sharing scheme based on the Shamir method, the secret information is a constant term of a polynomial. Therefore, the matrix P may be simply an operation of setting the coefficient of the k-th or higher-order term to 0 (matrix P that satisfies Expression (80)).
P (x₁, X₂, ..., x_n)^t
= (X₁, X₂, ..., x_k, 0, ..., 0) ... (80)
[0207]
On the other hand, in the ramp-type secret sharing scheme, the secret information is expressed by the polynomial f (x) of the equation (61).
S_L-1x^L-1+ ... + S₁x + S₀
, That is, the remainder when divided by g (x). Thus, the matrix P may be an operation of lowering the degree of the polynomial from 2 (k-1) to (k-1) so as to be congruent in mod g (x).
[0208]
[Configuration of Sixth Embodiment]
In the sixth embodiment, an apparatus for realizing distributed multiplication for calculating the product of secret information will be described with respect to the distributed calculation in the fifth embodiment. However, the method of generating shared information is different from that of the third embodiment that implements distributed multiplication for calculating the product of secret information in the same manner (in the third embodiment, k− Since the shared information is generated from the first-order polynomial, and in the sixth embodiment, the shared information is generated from the (k−1) -order polynomial as shown in Expression (57), the configuration and operation are completely different. Has become. In the sixth embodiment, the shared information (a₀, ..., a_n-1), (B₀, ..., b_n-1) Is given, and the shared information (a₀, ..., a_n-1), (B₀, ..., b_n-1) To the shared information (d) of the product D (= AB) of the secret information.₀, ..., d_n-1) Is calculated.
[0209]
FIG. 34 is a block diagram illustrating a configuration of a variance calculation unit when performing variance multiplication. As shown in FIG. 34, the shared multiplication calculation unit 3200 includes amultiplication unit 3201, a secret sharing processing unit 3202, a shared information conversion unit 3203, and a secret restoration processing unit 3204. Themultiplication unit 3201 calculates a product of the pieces of shared information held by the members. The secret sharing processing unit 3202 performs secret sharing on the value calculated by the multiplication unit. Here, the shared information is generated using the (k, n) threshold secret sharing instead of the ramp secret sharing method (the threshold at this time is the ramp type (L, k, n) A value k ′ (k ′ ≦ n) different from the threshold value k in the secret sharing scheme may be used). The shared information converting unit 3203 performs conversion on the second shared information obtained by the secret sharing processing unit 3202. The secret restoration processing unit 3204 performs a secret restoration process on the result calculated by the shared information conversion unit 3203. The result of the multiplication is exchanged with another member, and the resulting shared information is restored. Here, similarly to the secret sharing processing unit 3202, the calculation of the secret restoration is performed using the (k, n) threshold method (the threshold at this time is the same as the threshold value in the secret sharing processing unit 3202). Value).
[0210]
[Operation of Sixth Embodiment]
In the sixth embodiment, the shared information a of the secret information A and B is obtained by the shared calculation._i(I = 0,..., N-1) and b_iThe procedure of calculating the shared information of the product AB of the secret information from (i = 0,..., N−1) will be described. In distributed multiplication, the product of the shared information held by each member must be converted. At the time of conversion, it is necessary to exchange shared information between members.
[0211]
The processing procedure is as shown in FIG. Here, member P_j(J = 0,..., N-1) is the member ID_w of each member._i(I = 0,..., N−1) and shared information a_jAnd b_jAssume that you have received In the following, description will be made using a matrix for convenience.
[0212]
As shown in FIG. 35, instep 1, the member P_iIs the product of the shared information c_i= A_ib_iIs calculated. The product c of this shared information_iIs the shared information of the product AB of the secret information A and B, but the degree of the polynomial for performing the secret sharing is 2 (k-1), which is inconvenient. Therefore, in the following steps, processing of secret sharing, distribution (steps 2 and 3), conversion processing (step 4), exchange of shared information of calculation results, and restoration of calculation results (steps 5 and 6) are performed. Thus, the obtained shared information is converted so that the threshold value becomes k.
[0213]
Instep 2, member P_iIs the product of the shared information c_iFor secret sharing. The secret sharing here uses the (k ', n) threshold method (k'≤n). Member P_iIs the product of the shared information c_iAnd a random k'-1 order polynomial (Equation (74)) is generated from the random number and the shared information c._{i, j}(J = 0,..., N−1) is calculated.
(Equation 51)

Where R_{i, m}(M = 1,..., K′−1) is the member P_iIs a numerical value that is randomly generated.
[0214]
This results in an n × n matrix E = (e_ij) Can be expressed as in the following equation (75).
(Equation 52)

[0215]
Instep 3, communication with other members is performed to obtain the shared information c._{i, j}Exchange. Member P_iIs calculated above (c_{i, 0}, ..., c_{i, n-1}) For c_{i, j}(J = 0,..., N−1 and j ≠ i) are assigned to the member P_jDistribute to As a result, member P_jIs (c_{0, j}, ..., c_{n-1, j}Receive).
[0216]
Instep 4, P_jIs C_j= (C_{0, j}, ..., c_{n-1, j}) (Derived from the 2 (k-1) -order polynomial)_j= (D_{0, j}, ..., d_{n-1, j}) (Derived from the (k−1) -order polynomial). The conversion is performed, for example, by using a matrix P and a matrix E generated as follows._j= (EPE^-1) C_jThis is a calculation equivalent to That is, EPE^-1= (P_ij) For d_ij= Σ_k  p_ikc_kj(I = 0,..., N−1) is calculated.
[0217]
Here, the matrix P is a transformation that reduces the polynomial in the secret sharing from the 2 (k−1) th order to the (k−1) th order, and lowers the degree of the polynomial so as to be congruent in mod g (x). It is an operation. FIG. 36 shows an example of a method of generating the transformation matrix P. Then, specifically, GF (31), k = 8 (this is the threshold value of the ramp-type secret sharing in secret sharing section 3101), n = 16, irreducible polynomial g (x) = x³In the case of + x + 3, the result of calculating the matrix P is as follows. A 14th-order (corresponding to 2 (k-1) th-order) polynomial is defined as in the following equation (76).
(Equation 53)

[0218]
As a result of the above operation, a congruent polynomial in mod g (x) with the order reduced to the seventh order is as the following expression (77).
(Equation 54)

[0219]
Thus, the matrix P is as shown in the following equation (78).
[0220]
[Equation 55]

[0221]
Instep 5, the communication with other members is performed, and information d_{i, j}Exchange. Member P_jIs information d_{i, j}(I = 0, ..., n-1; i−１j) is P_iDistribute to As a result, member P_iIs (d_{i, 0}, ..., d_{i, n-1}Receive).
[0222]
Instep 6, member P_iPerforms a secret recovery calculation. Member P_iIs (d_{i, 0}, ..., d_{i, n-1}) To d which is the shared information of the product AB of the information A and B_iIs calculated by equation (79). The restoring operation here performs a secret restoring by the (k ', n) threshold method.
[Equation 56]

[0223]
By performing the above calculation, the shared information d of the product AB of the secret information such that the threshold value is k_iCan be obtained.
[0224]
[Effects of Sixth Embodiment]
As described above, the operation performed by each member can be performed in a finite field smaller than the finite field in which the original secret information is defined (in the above description, an L-order expanded field). As a result, in addition to the addition in the fifth embodiment, the multiplication can be similarly performed by each member with less computational resources.
[0225]
<< Seventh embodiment >>
[Configuration of Seventh Embodiment]
In the seventh embodiment of the present invention, the shared information of the constant C shared by the members and the constant times CS of the secret information S is calculated. However, the method of generating the shared information is different from that of the second embodiment that implements the shared constant multiplication of calculating the product of the constants of the secret information in the same manner (in the second embodiment, the expression (19) , The shared information is generated from the k-1 order polynomial in the seventh embodiment, and the shared information is generated from the k-1 order polynomial in Expression (57) in the seventh embodiment. It has become. The constant multiplication using the (k, n) threshold method can be obtained by multiplying the shared information held by itself by a constant, but in the present invention, the constant is an extended field GF (q^L). At this time, it is necessary to perform the dispersion calculation so that the dispersion information obtained as a result of the constant times becomes the basis of the base field.
[0226]
FIG. 37 is a block diagram illustrating the configuration of the variance calculator when performing the variance constant multiplication according to the seventh embodiment. In FIG. 37, the dispersion constant arithmetic and multiplication unit includes a dispersion multiplication device 3200 (FIG. 34) and a constant information generation unit 3301. The constant information generation unit 3301 calculates the extension field GF (q^LThe shared information of the constants is generated from the constants and the member IDs common to the members defined in ()). In the distributed multiplication device, the distributed multiplication calculation unit 3200 calculates the product of the shared information of the secret information S and the shared information of the constant C generated by the constant information generation unit 3301.
[0227]
[Operation of Seventh Embodiment]
Member P for secret information S_jThe shared information held by s_jAnd Expanded field GF (q^L) Constant C = (C₀, ..., C_L-1) From the information c as follows:_jIs calculated.
c_j= C₀+ C₁w_j+ ... + C_L-1w_j^L-1
Since the constant C is shared between members, the member P_jIs the information c to have_jCan be generated.
[0228]
Hereinafter, information c is obtained by the same procedure as the variance multiplication._jAnd shared information s_j, The dispersion information of the constant multiplication CS can be calculated.
[0229]
At this time, since the degree conversion is a conversion from the (k + L-2) order to the (k-1) order, the 2 (k-1) part is replaced with k + L-2 in the generation of the matrix P in FIG. FIG. The non-zero portion in the matrix P in this distributed multiplication can be further reduced, and the amount of calculation can be reduced.
[0230]
[Effects of Seventh Embodiment]
As described above, in addition to the addition and multiplication of the fifth and sixth embodiments, the extension field GF (q^LSimilarly, each member can be executed with less computational resources with respect to a constant multiple of the constant represented by ()).
[0231]
【The invention's effect】
As described above, according to the present invention, the extension field GF (q^L) In the distributed arithmetic processing of each member, the extended field GF (q^L) Can be achieved by performing only calculations on a finite field GF (q) smaller than), the amount of calculation, the circuit scale required for the calculation circuit, and the storage required for calculation in the distributed calculation processing of each member. There is an effect that calculation costs such as capacity and calculation time can be reduced.
[Brief description of the drawings]
FIG. 1 is a block diagram showing a configuration (distributed computing system) for implementing a distributed computing method according to a first embodiment of the present invention.
FIG. 2 is a conceptual explanatory diagram of a multi-party protocol.
FIG. 3 is a block diagram illustrating a configuration of a secret reconstruction calculation unit in FIG. 1;
FIG. 4 is a block diagram illustrating a configuration of a distributed processing unit (distributed calculation device) in FIG. 1;
FIG. 5 is a block diagram illustrating a configuration of a secret sharing calculation unit in FIG. 4;
FIG. 6 is a block diagram illustrating a configuration of an example (part 1) of a dispersion calculation unit in FIG. 4;
FIG. 7 is a block diagram illustrating a configuration of an example (part 2) of the dispersion calculation unit in FIG. 4;
FIG. 8 is a block diagram illustrating a configuration of a variance adding unit in FIG. 6 or FIG. 7;
FIG. 9 is a flowchart illustrating an operation of a configuration (distributed calculation system) that executes the distributed calculation method according to the first embodiment of the present invention.
FIG. 10 is a flowchart showing an operation of variance addition in the first embodiment of the present invention.
FIG. 11 is a block diagram illustrating a configuration of a distributed processing unit (distributed computing device) according to a second embodiment of the present invention.
FIG. 12 is a block diagram illustrating a configuration of a dispersion calculation unit in FIG. 11;
13 is a block diagram illustrating a configuration of a dispersion constant multiplication unit in FIG.
FIG. 14 is a flowchart illustrating an operation of a configuration (distributed calculation system) that executes a distributed calculation method according to the second embodiment of the present invention.
FIG. 15 is a flowchart illustrating an operation of multiplication of a dispersion constant according to the second embodiment of the present invention.
FIG. 16 is a block diagram illustrating a configuration of a distributed calculation unit (part 1) according to the third embodiment of this invention.
FIG. 17 is a block diagram illustrating a configuration of a distributed calculation unit (part 2) according to the third embodiment of this invention.
FIG. 18 is a block diagram illustrating a configuration of a distributed multiplication unit in FIGS. 16 and 17;
FIG. 19 is a block diagram showing a configuration of an oblivious transfer calculator of FIG. 18;
20 is a block diagram illustrating a configuration of a communication calculation receiving unit in FIG.
FIG. 21 is a block diagram illustrating a configuration of a communication calculation transmitting unit in FIG. 19;
FIG. 22 is a flowchart illustrating an operation of a configuration (distributed calculation system) that implements a distributed calculation method according to the third embodiment of the present invention.
FIG. 23 is a flowchart illustrating an operation of distributed multiplication according to the third embodiment of the present invention.
FIG. 24 is a block diagram showing a configuration (distributed computing system) for implementing a distributed computing method according to a fourth embodiment of the present invention.
FIGS. 25A and 25B are block diagrams each showing a configuration of a distributed processing unit (distributed computing device) of FIG. 24;
FIG. 26 is a block diagram illustrating a configuration of a modified example (1) of the distributed processing unit (distributed computing device) of FIG. 25;
FIGS. 27A and 27B are block diagrams each showing a configuration of a modification (No. 2) of the distributed processing unit (distributed computing device) of FIG. 25;
FIG. 28 is a block diagram illustrating a configuration of a distributed computing device according to a fifth embodiment of the present invention.
FIG. 29 is a block diagram illustrating a configuration of a secret sharing unit in FIG. 28;
FIG. 30 is a block diagram illustrating a configuration of a secret restoration unit in FIG. 28;
FIG. 31 is a block diagram illustrating a configuration of a distributed computing system (part 1) according to a fifth embodiment of the present invention.
FIG. 32 is a block diagram illustrating a configuration of a distributed computing system (part 2) according to the fifth embodiment of the present invention.
FIG. 33 is a block diagram illustrating a configuration of a distributed computing system (part 3) according to the fifth embodiment of the present invention.
FIG. 34 is a block diagram illustrating a configuration in which the variance calculation units of the fifth to seventh embodiments perform variance multiplication.
FIG. 35 is a flowchart illustrating a processing procedure when the variance calculators of the fifth to seventh embodiments perform variance multiplication.
FIG. 36 is an explanatory diagram of a conversion matrix generation procedure in the fifth to seventh embodiments.
FIG. 37 is a block diagram illustrating a configuration of a dispersion constant multiplication unit according to a seventh embodiment of the present invention.
FIG. 38 is an explanatory diagram of a procedure for generating a transformation matrix according to the seventh embodiment.
[Explanation of symbols]
101 (101-1,..., 101-n) distributed processing unit (distributed computing device)
102 secret reconstruction calculator,
103 secret channel,
201 linear combination,
301-i secret information storage unit,
302-i secret sharing calculation unit,
303-i transmission unit,
304-i receiving unit,
305-i distributed calculation unit,
401-i polynomial generator,
402-i shared information generation unit,
403-i random number generation unit,
404-i (k-1) degree polynomial generation unit,
.., 501- (n−1) variance addition unit,
601 variance adder,
701 adder,
1001-i secret information storage unit,
1002-i secret sharing calculation unit,
1003-i transmitting unit,
1004-i receiving unit,
1005-i distributed calculation unit,
1101-1,..., 1101-n
1102-1, ..., 1102- (n-1) variance addition unit,
1201 enlargement field multiplication unit,
1202 secret sharing calculation unit,
1203 transmission unit,
1204 receiver,
1205 adder,
1501-1,..., 1501-n dispersion constant multiplication unit
1502-1, ..., 1502- (n-1) variance addition unit,
1503 Distributed multiplication unit,
1601 distributed multiplication unit,
1701 Multiplication unit,
1702 oblivious transfer calculator,
1703 shared information calculation unit,
1704 Secret sharing calculation unit,
1705 transmission unit,
1706 receiver,
1707 adder,
1801-1,..., 1801- (i-1) communication calculation receiving unit;
1802-1, ..., 1802- (i-1) communication calculation receiving unit,
1803- (i + 1), ..., 1803-n communication calculation transmitting unit,
1804- (i + 1), ..., 1804-n communication calculation transmitting unit,
1901 index calculation transmitting section,
1902 reception restoration unit,
2001 random number generator,
2002 Finite field element generator,
2003-1,..., 2003-q Multiplier calculation transmitting unit,
2301 Secret sharing transmission unit,
2302 (2302-1, ..., 2302-n) distributed processing unit (distributed computing device),
2303 secret reconstruction calculator,
2401-i secret information storage unit,
2402-i secret sharing calculation unit,
2403-i transmitting unit,
2404-i receiver,
2405-i distributed calculation unit,
2406-i shared information receiving unit,
2501-i secret information storage unit,
2502-i secret sharing calculation unit,
2503-i transmitting unit,
2504-i receiving unit,
2505-i distributed calculation unit,
2506-i distributed information receiving unit,
2507-i secret reconstruction calculation unit,
3101 secret sharing unit,
3102 transmitting section,
3103 receiver,
3104 storage unit,
3105 distributed calculation unit,
3106 transmitting unit,
3107 receiver,
3108 Secret restoration unit,
3111 random number generation unit,
3112 Finite field operation unit,
3121 restoration information generation unit,
3122 Finite field operation unit,
3200 distributed multiplication calculation unit,
3201 multiplication unit,
3202 secret sharing processing unit,
3203 shared information conversion unit,
3204 secret restoration processing unit,
3301 constant information generation unit,
X_i  Secret information held by the distributed computing device,
Y_{i, j}  Secret information X_iDistributed information generated from
Z '_i  Distributed information Y_{i, j}(Shared information of secret Z) generated from
Z The original secret,
h_Xi(X) a polynomial generated by the distributed computing device,
m₁, M₂, ..., m_n  Member ID.

Claims (30)

Translated fromJapanese

分散計算を行う分散計算装置であって、
ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により１又は複数個の秘密情報から生成された分散情報を用いて、分散計算する分散計算手段を有し、
この分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、上記分散計算手段が分散計算に用いる分散情報をＹ_ｐとしたときに、上記分散情報は、
有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαである拡大体ＧＦ（ｑ^Ｌ）上の値を次式
Ｘ＝ΣＸ_ｊα^ｊ；０≦ｊ≦Ｌ−１
で表されるＸとするときに、次式
ｈ_Ｘ（Ｉ_ｊ）＝Ｘ_ｊ；０≦ｊ≦Ｌ−１
を満たすｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成し、
上記多項式ｈ_Ｘ（ｘ）から、
Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）
なる有限体ＧＦ（ｑ）上の値を計算することによって生成された情報である
ことを特徴とする分散計算装置。A distributed computing device that performs distributed computation,
A shared calculation means for performing shared calculation using shared information generated from one or more pieces of secret information by a ramp type (L, k, n) threshold secret sharing method;
Assuming that the member ID held by the distributed computing device is m_p (p ≦ n) and the shared information used for the shared calculation by the shared calculating means is Y_p , the shared information is
A value on an extension field GF (q^L ) whose origin is α in an extension field in which the finite field GF (q) is L-order-extended is expressed by the following equation: X = ΣX_j α^j ; 0 ≦ j ≦ L−1
When the in represented by X, the following equation_{h X (I j) = X} j; 0 ≦ j ≦ L-1
It generates a k-1 order finite GF (q) on the polynomial_h X (x) satisfying,
From the above polynomial h_x (x),
_{Y p = h X (m p} )
A distributed computing apparatus characterized in that the information is information generated by calculating a value on a finite field GF (q).ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いて秘密情報から生成された分散情報を受信する分散情報受信手段をさらに有し、
上記分散計算手段が分散計算に用いる分散情報が、上記分散情報受信手段で受信された分散情報を含む
ことを特徴とする請求項１に記載の分散計算装置。A shared information receiving means for receiving shared information generated from secret information by using a ramp type (L, k, n) threshold secret sharing method;
The distributed computing device according to claim 1, wherein the distributed information used by the distributed calculating means for the distributed calculation includes the distributed information received by the distributed information receiving means.分散計算を行う分散計算装置であって、
ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により、秘密情報から分散情報を生成する秘密分散計算手段を有し、
上記秘密分散計算手段が、
上記分散情報が配布される他の分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、メンバＩＤがｍ_ｐである上記分散情報をＹ_ｐとし、有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαである拡大体ＧＦ（ｑ^Ｌ）上の値を次式
Ｘ＝ΣＸ_ｊα^ｊ；０≦ｊ≦Ｌ−１
で表されるＸとするときに、次式
ｈ_Ｘ（Ｉ_ｊ）＝Ｘ_ｊ；０≦ｊ≦Ｌ−１
を満たすｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成する多項式生成手段と、
上記多項式ｈ_Ｘ（ｘ）から、
Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）
なる有限体ＧＦ（ｑ）上の値を計算することによって生成する分散情報生成手段とを有する
ことを特徴とする分散計算装置。A distributed computing device that performs distributed computation,
A secret sharing calculation means for generating shared information from secret information by a ramp type (L, k, n) threshold secret sharing method;
The secret sharing calculation means,
The member ID to other distributed computing system in which the shared information is distributed to hold a m_{p (p} ≦ n), the distributed information member ID is m_p and Y_p, the finite field GF a (q) L The value on the extension field GF (q^L ) whose generator is α in the next extension field is expressed by the following equation: X = ΣX_j α^j ; 0 ≦ j ≦ L−1
When the in represented by X, the following equation_{h X (I j) = X} j; 0 ≦ j ≦ L-1
A polynomial generation means for generating a k-1 order finite GF (q) on the polynomial_h X (x) satisfying,
From the above polynomial h_x (x),
_{Y p = h X (m p} )
And a shared information generating means for generating by calculating a value on a finite field GF (q).上記秘密情報を保持する秘密情報記憶手段をさらに有することを特徴とする請求項３に記載の分散計算装置。4. The distributed computing apparatus according to claim 3, further comprising secret information storage means for holding the secret information.上記秘密分散計算手段で生成された分散情報を他の分散計算装置へ送信する送信手段をさらに有することを特徴とする請求項３又は４のいずれかに記載の分散計算装置。5. The shared computing device according to claim 3, further comprising a transmitting unit that transmits the shared information generated by the secret sharing calculating unit to another shared computing device.他の分散計算装置からの分散情報を受信する受信手段をさらに有することを特徴とする請求項３から５までのいずれかに記載の分散計算装置。The distributed computing device according to any one of claims 3 to 5, further comprising a receiving unit that receives distributed information from another distributed computing device.上記秘密分散計算手段で生成したこの分散計算装置自身に対する分散情報、及び、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により他の分散計算装置で生成され上記受信手段で受信された分散情報を用いて、分散計算する分散計算手段をさらに有することを特徴とする請求項６に記載の分散計算装置。The shared information generated by the secret sharing calculation means for the sharing calculation apparatus itself, and generated by another sharing calculation apparatus by the ramp type (L, k, n) threshold secret sharing method and received by the receiving means. The distributed computing device according to claim 6, further comprising a distributed computing unit that performs distributed computation using the distributed information.上記分散計算手段の計算結果、及び、他の分散計算装置の分散計算手段からの計算結果Ｚ’_ｉから、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行って、拡大体ＧＦ（ｑ^Ｌ）上の値
Ｚ＝ΣＺ_ｊα^ｊ（ｊは、０≦ｊ≦Ｌ−１である整数）を得る秘密再構成手段をさらに有し、
上記秘密再構成手段は、次式

のような線形結合を行う線形結合手段を有する
ことを特徴とする請求項１、２、７のいずれかに記載の分散計算装置。The secret reconstruction of the ramp type (L, k, n) threshold secret sharing method is performed from the calculation result of the above-mentioned sharing calculation means and the calculation result Z ′_i from the sharing calculation means of another sharing calculation apparatus. , Further comprising a secret reconstruction means for obtaining a value Z = ΣZ_j α^j (j is an integer satisfying 0 ≦ j ≦ L−1) on the extension field GF (q^L ),
The secret reconstruction means is expressed by the following equation

8. The distributed computing apparatus according to claim 1, further comprising a linear combination means for performing a linear combination as described above.上記分散計算手段が、
有限体ＧＦ（ｑ）をＬ次拡大した拡大体ＧＦ（ｑ^Ｌ）上の２つの値であるＡ及びＢの加算の分散加算を実行する場合に、この分散計算装置自身が保持する上記Ａ及びＢに対する分散情報の加算を行う加算手段を有する
ことを特徴とする請求項１、２、７のいずれかに記載の分散計算装置。The variance calculation means,
When performing variance addition of two values A and B on an extension field GF (q^L ) obtained by expanding the finite field GF (q) by L-order, the variance calculation apparatus itself holds the above A and 8. The distributed computing apparatus according to claim 1, further comprising an adding unit for adding shared information to B.上記分散計算手段で、有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαである拡大体ＧＦ（ｑ^Ｌ）上の定数Ｄと、拡大体ＧＦ（ｑ^Ｌ）上の値Ａとの乗算の分散定数乗算をする場合には、
この分散計算装置自身が保持する値Ａに対する分散情報ａ_ｉ、定数Ｄ、及び、メンバＩＤを用いて、拡大体ＧＦ（ｑ^Ｌ）上の乗算
Ｃ＝Ｄ×ａ_ｉ＝ΣＣ_ｊα^ｊ；０≦ｊ≦Ｌ−１
となるＣ_ｊの分散情報であるＥ_ｉ，ｊ（０≦ｊ≦Ｌ−１）を求める拡大体乗算手段と、
上記拡大体乗算手段の計算結果であるＥ_ｉ，ｊを、さらにランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法で分散して分散情報であるＦ_ｉ，ｐを生成する第２の秘密分散計算手段と、
上記第２の秘密分散計算手段で生成した分散情報であるＦ_ｉ，ｐを送信する第２の送信手段と、
他の分散計算装置の第２の送信手段から分散情報であるＦ_ｐ，ｉを受信する第２の受信手段と、
上記第２の秘密分散計算手段から生成したこの分散計算装置自身に対する分散情報であるＦ_ｉ，ｉ、及び、その第２の受信手段で受信した分散情報であるＦ_ｐ，ｉをすべて加算する第２の加算手段と、
を有することを特徴とする請求項１、２、７のいずれかに記載の分散計算装置。A constant D on an extension field GF (q^L ) whose origin is α in an extension field obtained by expanding the finite field GF (q) by L-order by the variance calculation means, and a value A on the extension field GF (q^L ) When multiplying by the dispersion constant multiplication with
Using the shared information a_i , the constant D, and the member ID for the value A held by the shared computing device itself, multiplication C = D × a_i = ΣC_j α^j ; 0 on the extended field GF (q^L ); ≤j≤L-1
Expanding field multiplying means for obtaining E_{i, j} (0 ≦ j ≦ L−1) which is shared information of C_j ,
_{Ei, j} , which is the calculation result of the expansion field multiplying means, is further distributed by a ramp-type (L, k, n) threshold secret sharing method to generate_{Fi, p} , which is shared information. Secret sharing calculation means,
Second transmitting means for transmitting the shared information_{Fi, p} generated by the second secret sharing calculating means;
Second receiving means for receiving the shared information_{Fp, i} from the second transmitting means of another distributed computing device;
The sum of all of the shared information F_{i, i} generated by the second secret sharing calculation means for the shared calculation apparatus itself and the shared information F_{p, i} received by the second receiving means are added. Means for adding 2;
8. The distributed computing device according to claim 1, wherein the distributed computing device comprises:上記分散計算手段で、有限体ＧＦ（ｑ）を生成多項式
ｇ（ｘ）＝Σｇ_ｉｘ^ｉ；０≦ｉ≦Ｌ
を用いてＬ次拡大した拡大体で生成元がαである、拡大体ＧＦ（ｑ^Ｌ）上の値Ａ及びＢの乗算
Ｃ＝ＡＢ＝ΣＣ_ｊα^ｊ；０≦ｊ≦Ｌ−１
の分散乗算をする場合には、
この分散計算装置自身が保持する値Ａ及びＢに対する分散情報ａ_ｉ及びｂ_ｉの有限体ＧＦ（ｑ）上の乗算
ｃ_ｉ＝ａ_ｉ×ｂ_ｉ
を行う乗算手段と、
他の分散計算装置の分散情報記憶手段に保持されている値Ａ及びＢの分散情報であるａ_ｐ及びｂ_ｐの積ａ_ｉ×ｂ_ｐ及びａ_ｐ×ｂ_ｉの分割情報であるｄ_ｉ，ｐ及びｅ_ｉ，ｐを紛失通信を用いて求める紛失通信計算手段と、
上記乗算手段の乗算結果であるｃ_ｉ、その紛失通信計算手段の計算結果であるｄ_ｉ，ｐ及びｅ_ｉ，ｐ、メンバＩＤ、及び、生成多項式の係数であるｇ_ｉを用いて、Ｃの各次数の係数であるＣ_ｊの分散情報であるＥ_ｉ，ｊ（０≦ｊ≦Ｌ−１）を求める分散情報計算手段と、
上記分散情報計算手段の計算結果であるＥ_ｉ，ｊを、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法で分散して分散情報であるＦ_ｉ，ｐを生成する第３の秘密分散手段と、
上記第３の秘密分散手段で生成した分散情報であるＦ_ｉ，ｐを送信する第３の送信手段と、
他の分散計算装置の第３の送信手段から分散情報であるＦ_ｐ，ｉを受信する第３の受信手段と、
上記第３の秘密分散手段から生成したこの装置自身に対する分散情報であるＦ_ｉ，ｉ、及び、その第３の受信手段で受信した分散情報であるＦ_ｐ，ｉをすべて加算する第３の加算手段と
を有することを特徴とする請求項１、２、７のいずれかに記載の分散計算装置。The variance calculation means generates a finite field GF (q) as a generator polynomial g (x) = Σg_i xⁱ ; 0 ≦ i ≦ L
Is a multiplication of the values A and B on the extension field GF (q^L ) in the extension field L-extended using L = C = AB = ΣC_j α^j ; 0 ≦ j ≦ L−1
When performing the variance multiplication of
Multiplication c_i = a_i × b_i on finite field GF (q) of shared information a_i and b_i for values A and B held by the distributed calculation device itself
Multiplying means for performing
A division information of the product a_i × b_p and a_p × b_i of a_p and b_p is the variance value information A and B are held in the shared information memory means other distributed computing devices d_{i, p} and e_i, and oblivious calculating means which calculates using oblivious to_p,
Using c_i which is the multiplication result of the multiplication means, di_{, p} and e_{i, p} which are the calculation results of the oblivious transfer calculation means, the member ID, and g_i which is the coefficient of the generator polynomial, Shared information calculating means for obtaining E_{i, j} (0 ≦ j ≦ L−1) as shared information of C_j which is a coefficient of each order;
A third secret that generates_{Ei, j,} which is the shared information, by distributing_{Ei, j} , which is the calculation result of the shared information calculation means_, using a ramp-type (L, k, n) threshold secret sharing method. Dispersal means;
Third transmission means for transmitting the shared information_{Fi, p} generated by the third secret sharing means,
Third receiving means for receiving the shared information_{Fp, i} from third transmitting means of another distributed computing device;
A third addition for adding all of the shared information F_{i, i} generated by the third secret sharing unit for the device itself and the shared information F_{p, i} received by the third receiving unit. 8. The distributed computing apparatus according to claim 1, further comprising: means.上記秘密分散計算手段における上記多項式生成手段は、
有限体ＧＦ（ｑ）上のｋ−Ｌ個の乱数であるＲ_Ｘ，ｊ（０≦ｊ≦ｋ−Ｌ−１）を生成する乱数生成手段と、
上記乱数であるＲ_Ｘ，ｊ、及び、予め決められたｋ個の有限体ＧＦ（ｑ）上の値であるＩ_ｊ（０≦ｊ≦ｋ−１）を用いて、

のような式で表される多項式を生成するｋ−１次多項式生成手段と
を有することを特徴とする請求項３から７までのいずれかに記載の分散計算装置。The polynomial generation means in the secret sharing calculation means,
Random number generation means for generating KL random numbers R_{X, j} (0 ≦ j ≦ kL-1) on the finite field GF (q);
Using R_{X, j as} the random number and I_j (0 ≦ j ≦ k−1) which is a value on a predetermined k finite fields GF (q),

The k-th order polynomial generating means for generating a polynomial represented by the following expression: and a distributed computing apparatus according to any one of claims 3 to 7.上記請求項１から１２までのいずれかに記載の分散計算装置と同じ構成を持つ複数個の分散計算装置と、
上記複数個の分散計算装置から出力される計算結果を受け取って、受け取った計算結果から、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行う秘密再構成装置と
を有することを特徴とする分散計算システム。A plurality of distributed computing devices having the same configuration as the distributed computing device according to any one of claims 1 to 12,
A secret reconstruction device that receives calculation results output from the plurality of distributed calculation devices and performs secret reconstruction of a ramp type (L, k, n) threshold secret sharing method from the received calculation results; A distributed computing system characterized by having.上記請求項１から１２までのいずれかに記載の分散計算装置と同じ構成を持つ複数個の分散計算装置を有し、
上記複数個の分散計算装置のうち、少なくとも１以上は、
他の分散計算装置の分散計算手段からの計算結果を受け取り、この装置自身の分散計算手段の計算結果と、他の分散計算装置の分散計算手段から受け取った計算結果から、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行って、拡大体ＧＦ（ｑ^Ｌ）上の値
Ｚ＝ΣＺ_ｊα^ｊ；０≦ｊ≦Ｌ−１
を得る秘密再構成手段を有する
ことを特徴とする分散計算システム。A plurality of distributed computing devices having the same configuration as the distributed computing device according to any one of claims 1 to 12,
Among the plurality of distributed computing devices, at least one or more
Receiving the calculation result from the dispersion calculation means of another distributed calculation device, and calculating the ramp type (L, k) , N) perform a secret reconstruction of the threshold secret sharing scheme to obtain a value Z = {Z_j α^j ; 0 ≦ j ≦ L−1 on the extended field GF (q^L )
And a secret reconstructing means for obtaining the following.ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いて、分散計算に用いる分散情報を生成する秘密分散計算装置をさらに有し、
分散計算手段を持つ上記分散計算装置のうちすべては、その秘密分散計算装置からの分散情報を受信する分散情報受信手段を有する
ことを特徴とする請求項１３又は１４のいずれかに記載の分散計算システム。A secret sharing calculation device that generates shared information used for sharing calculation by using a ramp type (L, k, n) threshold secret sharing method;
15. The distributed computing device according to claim 13, wherein all of the distributed computing devices having the distributed computing device include distributed information receiving means for receiving the distributed information from the secret distributed computing device. system.分散計算を行う分散計算装置であって、
ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により１又は複数個の秘密情報から生成された分散情報を用いて、分散計算する分散計算手段を有し、
この分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、上記分散計算手段が分散計算に用いる分散情報をＹ_ｐとしたときに、上記分散情報は、
有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαで生成多項式がｇ（ｘ）である拡大体ＧＦ（ｑ^Ｌ）上の値を次式
Ｘ＝ΣＸ_ｊ α^ｊ；０≦ｊ≦Ｌ−１
で表されるＸとし、Ｒ_Ｘ，ｊ（０≦ｊ≦ｋ−Ｌ−１）を乱数とするときに、次式

で表されるｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成し、
上記多項式ｈ_Ｘ（ｘ）から、
Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）
なる有限体ＧＦ（ｑ）上の値を計算することによって生成された情報である
ことを特徴とする分散計算装置。A distributed computing device that performs distributed computation,
A shared calculation means for performing shared calculation using shared information generated from one or more pieces of secret information by a ramp type (L, k, n) threshold secret sharing method;
Assuming that the member ID held by the distributed computing device is m_p (p ≦ n) and the shared information used for the shared calculation by the shared calculating means is Y_p , the shared information is
A value on an extension field GF (q^L ) in which a generator is α and a generator polynomial is g (x) in an extension field in which the finite field GF (q) is L-order-extended is represented by the following equation X = ΣX_j α^j ; j ≦ L-1
And R_{X, j} (0 ≦ j ≦ kL−1) as a random number,

It generates in represented by k-1 order finite GF (q) on the polynomial_h X (x),
From the above polynomial h_x (x),
_{Y p = h X (m p} )
A distributed computing apparatus characterized in that the information is information generated by calculating a value on a finite field GF (q).ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いて秘密情報から生成された分散情報を受信する分散情報受信手段をさらに有し、
上記分散計算手段が分散計算に用いる分散情報が、上記分散情報受信手段で受信された分散情報を含む
ことを特徴とする請求項１６に記載の分散計算装置。A shared information receiving means for receiving shared information generated from secret information by using a ramp type (L, k, n) threshold secret sharing method;
17. The distributed computing apparatus according to claim 16, wherein the shared information used by the shared calculating means for the shared calculation includes the shared information received by the shared information receiving means.分散計算を行う分散計算装置であって、ランプ型（Ｌ、ｋ、ｎ）しきい値秘密分散法により、秘密情報から分散情報を生成する秘密分散計算手段を有し、
上記秘密分散計算手段が、
上記分散情報が配布される補記あの分散計算装置が保持するメンバＩＤをｍ_ｐ（ｐ≦ｎ）とし、メンバＩＤがｍ_ｐである上記分散情報をＹ_ｐとし、有限体ＧＦ（ｑ）をＬ次拡大した拡大体で生成元がαで生成多項式がｇ（ｘ）である拡大体ＧＦ（ｑ^Ｌ）上の値を次式
Ｘ＝ΣＸ_ｊ α^ｊ；０≦ｊ≦Ｌ−１
で表されるＸとし、Ｒ_Ｘ，ｊ（０≦ｊ≦ｋ−Ｌ−１）を乱数とするときに、次式

で表されるｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｘ（ｘ）を生成する多項式生成手段と、
上記多項式ｈ_Ｘ（ｘ）から、
Ｙ_ｐ＝ｈ_Ｘ（ｍ_ｐ）
なる有限体ＧＦ（ｑ）上の値を計算することによって生成する分散情報生成手段とを有する
ことを特徴とする分散計算装置。A shared calculation device for performing shared calculation, comprising secret sharing calculation means for generating shared information from secret information by a ramp-type (L, k, n) threshold secret sharing method,
The secret sharing calculation means,
The member ID held by the distributed computing device to which the shared information is distributed is m_p (p ≦ n), the shared information whose member ID is m_p is Y_p , and the finite field GF (q) is L A value on an extension field GF (q^L ) in which the generator is α and the generator polynomial is g (x) in the next extension field is expressed by the following equation: X = ΣX_j α^j ; 0 ≦ j ≦ L−1
And R_{X, j} (0 ≦ j ≦ kL−1) as a random number,

A polynomial generating means for generating in represented by k-1 order finite GF (q) on the polynomial_h X (x),
From the above polynomial h_x (x),
_{Y p = h X (m p} )
And a shared information generating means for generating by calculating a value on a finite field GF (q).上記秘密情報を保持する秘密情報記憶手段をさらに有することを特徴とする請求項１８に記載の分散計算装置。19. The distributed computing apparatus according to claim 18, further comprising secret information storage means for holding the secret information.上記秘密分散計算手段で生成された分散情報を他の分散計算装置へ送信する送信手段をさらに有することを特徴とする請求項１８又は１９のいずれかに記載の分散計算装置。20. The shared computing device according to claim 18, further comprising a transmitting unit that transmits the shared information generated by the secret sharing calculating unit to another shared computing device.他の分散計算装置からの分散情報を受信する受信手段をさらに有することを特徴とする請求項１８から２０までのいずれかに記載の分散計算装置。21. The distributed computing device according to claim 18, further comprising receiving means for receiving shared information from another distributed computing device.上記秘密分散計算手段で生成したこの分散計算装置自身に対する分散情報、及び、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法により他の分散計算装置で生成され上記受信手段で受信された分散情報を用いて、分散計算する分散計算手段をさらに有する特徴とする請求項２１に記載の分散計算装置。The shared information generated by the secret sharing calculation means for the sharing calculation apparatus itself, and generated by another sharing calculation apparatus by the ramp type (L, k, n) threshold secret sharing method and received by the receiving means. 22. The distributed computing device according to claim 21, further comprising distributed computing means for performing distributed computation using the distributed information.上記分散計算手段の計算結果、及び、他の分散計算装置の分散計算手段からの計算結果Ｚ’_ｉから、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行って、拡大体ＧＦ（ｑ^Ｌ）上の値
Ｚ＝ΣＺ_ｊ α_ｊ（ｊは、０≦ｊ≦Ｌ−１である整数）
を得る秘密再構成手段をさらに有し、
上記秘密再構成手段は、メンバＩＤより生成した行列
Ｅ＝（ｅ_ｊｉ）、ｅ_ｊｉ＝ｍ_ｊ^ｉ−１（ｉ、ｊ＝１，２，…，ｎ）
の逆行列Ｅ^−１と、ｔ次の多項式の係数を表すベクトルに対して、拡大体ＧＦ（ｑ^Ｌ）の生成多項式ｇ（ｘ）の剰余を与えるような行列Ｇより、次式のような行列
Ｇ Ｅ^−１＝（ｒ_ｊｉ）
を満たすｒ_ｊｉを計算する復元情報生成手段と、
その復元情報生成手段で生成したｒ_ｊｉ、及び、Ｚ’_ｉから、

のような計算を行う有限体演算手段と、
を有することを特徴とする請求項１６、１７、２２のいずれかに記載の分散計算装置。The secret reconstruction of the ramp type (L, k, n) threshold secret sharing method is performed from the calculation result of the above-mentioned sharing calculation means and the calculation result Z ′_i from the sharing calculation means of another sharing calculation apparatus. , The value Z on the extension field GF (q^L ) Z = ΣZ_j α_j (j is an integer satisfying 0 ≦ j ≦ L−1)
Further comprising secret reconstruction means for obtaining
The secret reconstruction means,_the matrix_E generated from the member^{_{ID = (e ji), e}} ji = m j i-1 (i, j = 1,2, ..., n)
And a matrix G that gives the remainder of the generator polynomial g (x) of the extended field GF (q^L ) for the inverse matrix E⁻¹ of Matrix G E^-1 = (r_ji )
Restoration information generating means for calculating r_ji that satisfies
From r_ji and Z ′_i generated by the restoration information generating means,

Finite field operation means for performing calculations such as
23. The distributed computing device according to claim 16, wherein the distributed computing device comprises:上記分散計算手段が、
有限体ＧＦ（ｑ）をＬ次拡大した拡大体ＧＦ（ｑ^Ｌ）上の２つの値であるＡ及びＢの加算の分散加算を実行する場合に、この分散計算装置自身が保持する上記Ａ及びＢに対する分散情報の加算を行う加算手段を有する
ことを特徴とする請求項１６、１７、２２のいずれかに記載の分散計算装置。The variance calculation means,
When performing variance addition of two values A and B on an extension field GF (q^L ) obtained by expanding the finite field GF (q) by L-order, the above-described A and 23. The distributed computing device according to claim 16, further comprising an adding unit for adding shared information to B.上記分散計算手段で、有限体ＧＦ（ｑ）をＬ次拡大した拡大体ＧＦ（ｑ^Ｌ）上の値Ａ及びＢの乗算の分散乗算をする場合には、
この分散計算装置自身が保持する値Ａ及びＢに対する分散情報ａ_ｉ及びｂ_ｉの有限体ＧＦ（ｑ）上の乗算
ｃ_ｉ＝ａ_ｉ×ｂ_ｉ
を行う乗算手段と、
上記乗算手段の結果であるｃ_ｉを、さらに（ｋ’，ｎ）しきい値秘密分散法で分散して分散情報であるｃ_ｉ，ｐを生成する第２の秘密分散計算手段と、
上記第２の秘密分散計算手段で生成した分散情報であるｃ_ｉ，ｐを送信する第２の送信手段と、
他の分散計算装置の第２の送信手段からの分散情報であるｃ_ｐ，ｉを受信する第２の受信手段と、
第２の秘密分散計算手段から生成したこの分散計算装置自身に対する分散情報であるｃ_ｉ，ｉ、及び、その第２の受信手段で受信した分散情報であるｃ_ｐ，ｉを、しきい値がｋで、同じ秘密情報を復元するような分散情報に変換する中間情報変換手段と、
その中間情報変換手段の計算結果を送信する第３の送信手段と、
他の分散装置の第３の送信手段からの計算結果を受信する第３の受信手段と、
その中間情報変換手段のこの分散計算装置自身に対する計算結果と、第３の受信手段で受信した計算結果を（ｋ’，ｎ）しきい値秘密分散法の秘密再構成を行う秘密復元処理手段と、
を有することを特徴とする請求項１６、１７、２２のいずれかに記載の分散計算装置。When the variance calculation means performs variance multiplication of the multiplication of the values A and B on an extension field GF (q^L ) obtained by expanding the finite field GF (q) by L-order,
Multiplication c_i = a_i × b_i on finite field GF (q) of shared information a_i and b_i for values A and B held by the distributed calculation device itself
Multiplying means for performing
The c_i is the result of the multiplication means, c_i, and a second secret distribution calculation means for generating a_p a further (k ', n) distributed to the distributed information in threshold secret sharing scheme,
Second transmitting means for transmitting the shared information ci_{, p} generated by the second secret sharing calculating means,
A second receiving unit that receives_{cp, i} that is shared information from a second transmitting unit of another distributed computing device;
The threshold value of the shared information ci_{, i} generated by the second secret sharing calculation means for the shared calculation apparatus itself and the shared information_{cp, i} received by the second receiving means are set as threshold values. k, an intermediate information conversion means for converting the same secret information into shared information for restoring the same secret information;
Third transmission means for transmitting the calculation result of the intermediate information conversion means,
A third receiving unit that receives a calculation result from the third transmitting unit of another distributed device;
Secret recovery processing means for performing the secret reconstruction of the (k ', n) threshold secret sharing method by calculating the calculation result of the intermediate information conversion means for the sharing calculation apparatus itself and the calculation result received by the third receiving means; ,
23. The distributed computing device according to claim 16, wherein the distributed computing device comprises:上記中間情報変換手段は、
メンバＩＤから生成される、秘密分散に利用される第１の行列と、
ランダムな２（ｋ−１）次多項式を初期値とする多項式
ｈ（ｘ）＝Σｈ_ｊ ｘ^ｊ；０≦ｊ≦２（ｋ−１）
と、
拡大体ＧＦ（ｑＬ）の生成多項式ｇ（ｘ）を多項式ｈ（ｘ）の最高次数の係数倍した多項式と、の差分多項式を計算することを繰り返すことを、次数が（ｋ−１）次になるまで続け、得られた（ｋ−１）次多項式の係数を元の多項式の係数ｈ_ｊの線形結合で表すという方法で生成した第２の行列と、
メンバＩＤから生成される、秘密復元に利用される第３の行列と、
の３つの行列の積で表される変換行列により変換する
ことを特徴とする請求項２５に記載の分散計算装置。The intermediate information conversion means,
A first matrix used for secret sharing, generated from the member ID,
Polynomial h (x) = Σh_j x^j with a random 2 (k−1) order polynomial as an initial value; 0 ≦ j ≦ 2 (k−1)
When,
Repeating the calculation of the difference polynomial between the generator polynomial g (x) of the extension field GF (qL) and the polynomial multiplied by the coefficient of the highest order of the polynomial h (x), the order is (k−1) A second matrix generated in such a way that the obtained coefficients of the (k−1) -order polynomial are represented by a linear combination of coefficients h_j of the original polynomial;
A third matrix used for secret recovery, generated from the member ID;
26. The distributed computing apparatus according to claim 25, wherein the transformation is performed by a transformation matrix represented by a product of three matrices.上記分散計算手段で、
有限体ＧＦ（ｑ）をＬ次拡大した拡大体ＧＦ（ｑ^Ｌ）上の定数Ｄが、次式
Ｄ＝ΣＤ_ｊ α^ｊ；０≦ｊ≦Ｌ−１
で表されるとし、この定数Ｄと、拡大体ＧＦ（ｑ^Ｌ）上の値Ａとの乗算の分散定数乗算をする場合には、
あらかじめ決められた値Ｒ_Ｄ，ｊ（０≦ｊ≦ｋ−Ｌ−１）を用いて、次式

で表されるｋ−１次の有限体ＧＦ（ｑ）上の多項式ｈ_Ｄ（ｘ）を生成し、
上記多項式ｈ_Ｄ（ｘ）から、
ｄ_ｉ＝ｈ_Ｄ（ｍ_ｉ）
なる有限体ＧＦ（ｑ）上の値を計算することによって、この分散計算装置自身に対する定数Ｄの分散情報ｄ_ｉを生成する定数情報生成手段と、
その定数情報生成手段で生成した分散情報ｄ_ｉとこの分散計算装置自身が保持する値Ａに対する分散情報ａ_ｉを用いた分散乗算を実行する分散乗算手段と、
を有することを特徴とする請求項１６、１７、２２のいずれかに記載の分散計算装置。In the above dispersion calculation means,
A constant D on an extension field GF (q^L ) obtained by expanding the finite field GF (q) into the L-th order is represented by the following equation: D = ΣD_j α^j ;
When the constant D is multiplied by the dispersion constant of the multiplication of the constant A and the value A on the extension field GF (q^L ),
Using a predetermined value R_{D, j} (0 ≦ j ≦ kL−1), the following equation

Generate a polynomial h_D (x) on a k-1 order finite field GF (q) represented by
From the above polynomial h_D (x),
d_i = h_D (m_i )
By calculating the values on the finite field GF (q) comprising, a constant information generating means for generating shared information d_i constant D for the distributed computing system itself,
A dispersion multiplying means for performing a distributed multiplier using distributed information a_i with respect to the value A of distributed computing apparatus itself of the distributed information d_i Toko generated in the constant information generating means is held,
23. The distributed computing device according to claim 16, wherein the distributed computing device comprises:上記請求項１６から２７までのいずれかに記載の分散計算装置と同じ構成を持つ複数個の分散計算装置と、
上記複数個の分散計算装置から出力される計算結果を受け取って、受け取った計算結果から、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行う秘密再構成装置と
を有することを特徴とする分散計算システム。A plurality of distributed computing devices having the same configuration as the distributed computing device according to any one of claims 16 to 27;
A secret reconstruction device that receives calculation results output from the plurality of distributed calculation devices and performs secret reconstruction of a ramp type (L, k, n) threshold secret sharing method from the received calculation results; A distributed computing system characterized by having.上記請求項１６から２７までのいずれかに記載の分散計算装置と同じ構成を持つ複数個の分散計算装置を有し、
上記複数個の分散計算装置のうち、少なくとも１以上は、
他の分散計算装置の分散計算手段からの計算結果を受け取り、この装置自身の分散計算手段の計算結果と、他の分散計算装置の分散計算手段から受け取った計算結果から、ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法の秘密再構成を行って、拡大体ＧＦ（ｑ^Ｌ）上の値
Ｚ＝ΣＺ_ｊ α^ｊ；０≦ｊ≦Ｌ−１
を得る秘密再構成手段を有する
ことを特徴とする分散計算システム。A plurality of distributed computing devices having the same configuration as the distributed computing device according to any one of claims 16 to 27,
Among the plurality of distributed computing devices, at least one or more
Receiving the calculation result from the dispersion calculation means of another distributed calculation device, and calculating the ramp type (L, k) , N) perform a secret reconstruction of the threshold secret sharing scheme to obtain a value Z = {Z_j α^j ; 0 ≦ j ≦ L−1 on the extended field GF (q^L )
And a secret reconstructing means for obtaining the following.ランプ型（Ｌ，ｋ，ｎ）しきい値秘密分散法を用いて、分散計算に用いる分散情報を生成する秘密分散計算装置をさらに有し、
分散計算手段を持つ上記分散計算装置のうちすべては、その秘密分散計算装置からの分散情報を受信する分散情報受信手段を有する
ことを特徴とする請求項２８又は２９のいずれかに記載の分散計算システム。A secret sharing calculation device that generates shared information used for sharing calculation by using a ramp type (L, k, n) threshold secret sharing method;
30. The distributed computing device according to claim 28, wherein all of the distributed computing devices having the distributed computing device include distributed information receiving means for receiving the distributed information from the secret distributed computing device. system.

Images