CN116330267A - A control method based on singular point calculation of industrial robot wrist - Google Patents

Abstract

The invention belongs to the field of industrial robot control, and particularly relates to a control method based on calculation of wrist singular points of an industrial robot. The method comprises the steps of establishing a kinematic model, solving kinematic positive solutions, solving a velocity jacobian matrix, decoupling the jacobian matrix and analyzing wrist singular deformation. The method comprises the steps of obtaining a kinematic forward solution through connecting rod transformation of a kinematic model, obtaining a velocity jacobian matrix of each joint, decoupling the velocity jacobian matrix into a block matrix according to the translation velocity and the rotation velocity of the joint, obtaining a determinant result after decoupling treatment, wherein when the determinant is zero, the corresponding velocity is a singular point of a wrist joint of a robot mechanical arm, and after the singular point is obtained through calculation, avoiding the singular point in the control of the robot mechanical arm, so that the problem that the singular point influences the operation stability of the robot mechanical arm is solved.

Description

Translated fromChinese

一种基于工业机器人腕部奇异点计算的控制方法A control method based on singular point calculation of industrial robot wrist

技术领域technical field

本发明属于工业机器人控制领域，具体的，为一种基于工业机器人腕部奇异点计算的控制方法。The invention belongs to the field of industrial robot control, in particular, it is a control method based on the singular point calculation of the industrial robot wrist.

背景技术Background technique

工业机器人可以对多个运动轴，包括方向、位置和工作流程进行编程。工业机器人通常包括具有多个轴的机器人臂以及可编程控制器(控制装置)，控制器在运行中控制或调整工业机器人的运动过程。Industrial robots can program multiple axes of motion, including orientation, position, and workflow. An industrial robot usually includes a robot arm with multiple axes and a programmable controller (control device), which controls or adjusts the motion process of the industrial robot during operation.

运动学奇异是机械结构不可避免的固有特性。其不仅限制了机器人真正运行空间，当机器人运动到奇异点时，其雅可比矩阵不存在逆解，从而使关节跟踪速度和加速度无穷大，形成冲击进而将造成工业机器人稳定性变差，跟踪能力下降等问题，这些不足严重影响机器人的运动性能。Kinematic singularity is an unavoidable inherent property of mechanical structures. It not only limits the real running space of the robot, but when the robot moves to a singular point, its Jacobian matrix does not have an inverse solution, so that the joint tracking speed and acceleration are infinite, forming an impact, which will cause the stability of the industrial robot to deteriorate and the tracking ability to decline These problems seriously affect the motion performance of the robot.

针对机器人运动学奇异位形问题，提出一种计算六轴机器人腕部奇异位形的方法。通过计算出机器人处于奇异位形时各关节的状态，使机器人远离奇异位形，提高工业机器人性能。Aiming at the singularity problem of robot kinematics, a method for calculating the singularity of the wrist of a six-axis robot is proposed. By calculating the state of each joint when the robot is in a singular configuration, the robot is kept away from the singular configuration and the performance of the industrial robot is improved.

发明内容Contents of the invention

本发明提供了一种基于计算工业机器人奇异位形的控制方法，可以克服机器人在奇异位形时稳定性差的缺陷。The invention provides a control method based on calculating the singular configuration of an industrial robot, which can overcome the defect of poor stability of the robot in the singular configuration.

为实现上述目的，本发明采用如下技术方案，To achieve the above object, the present invention adopts the following technical solutions,

一种基于工业机器人腕部奇异点计算的控制方法，包括以下步骤：A control method based on the singular point calculation of the wrist of an industrial robot, comprising the following steps:

步骤一：定义基坐标系和机器人机械臂关节坐标系，且保证机器人关节坐标系与基坐标系方向相同，根据机器人运动参数，建立机器人运动学模型；Step 1: Define the base coordinate system and the robot arm joint coordinate system, and ensure that the robot joint coordinate system is in the same direction as the base coordinate system, and establish a robot kinematics model according to the robot motion parameters;

步骤二：根据机器人机械臂运动学模型的连杆变换，求取机器人运动学正解；Step 2: According to the connecting rod transformation of the robot arm kinematics model, obtain the positive solution of the robot kinematics;

步骤三：求解机器人机械臂的速度雅可比矩阵，得到包括机器人关节平动速度和转动速度的速度雅可比矩阵；Step 3: Solve the velocity Jacobian matrix of the robot arm to obtain the velocity Jacobian matrix including the translational velocity and rotational velocity of the robot joints;

步骤四：对求取的速度雅可比矩阵进行解耦运算，将该矩阵按照平动速度和转动速度分为多个矩阵；Step 4: Decoupling the obtained velocity Jacobian matrix, and dividing the matrix into multiple matrices according to the translational velocity and rotational velocity;

步骤五：根据解耦后的速度雅可比矩阵，计算整个雅可比矩阵的行列式结果，在行列式结果为零时，则为机器人机械臂的奇异点；Step 5: Calculate the determinant result of the entire Jacobian matrix according to the decoupled velocity Jacobian matrix. When the determinant result is zero, it is the singular point of the robot arm;

步骤六：在得到机器人机械臂的奇异点后，根据绕开奇异点的轨迹对机器人机械臂的控制。Step 6: After obtaining the singular point of the robot arm, control the robot arm according to the trajectory that bypasses the singular point.

所述对机器人进行运动学模型的连杆变换，其变换矩阵为：The connecting rod transformation of the kinematics model is carried out to the robot, and its transformation matrix is:

并计算机器人运动学正解，计算公式和结果为：And calculate the positive solution of robot kinematics, the calculation formula and result are:

其中：in:

n_x＝-s₅(s₁s₄+c₄(c₁c₂s₃+c₁c₃s₂))-c₅(c₁s₂s₃-c₁c₂c₃)n_x ＝-s₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-c₅ (c₁ s₂ s₃ -c₁ c₂ c₃ )

n_y＝s₅(c₁s₄-c₄(c₂s₁s₃+c₃s₁s₂))-c₅(s₁s₂s₃-c₂c₃s₁)n_y ＝s₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-c₅ (s₁ s₂ s₃ -c₂ c₃ s₁ )

n_z＝-s₂₃c₅-c₂₃c₄s₅n_z ＝-s₂₃ c₅ -c₂₃ c₄ s₅

o_x＝s₆(c₅(s₁s₄+c₄(c₁c₂s₃+c₁c₃s₂))-s₅(c₁s₂s₃-c₁c₂c₃))-c₆(c₄s₁-s₄(c₁c₂s₃+c₁c₃s₂))o_x ＝s₆ (c₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-s₅ (c₁ s₂ s₃ -c₁ c₂ c₃ ) )-c₆ (c₄ s₁ -s₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))

o_y＝c₆(c₁c₄+s₄(c₂s₁s₃+c₃s₁s₂))-s₆(c₅(c₁s₄-c₄(c₂s₁s₃+c₃s₁s₂))+s₅(s₁s₂s₃-c₂c₃s₁))o_y ＝c₆ (c₁ c₄ +s₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-s₆ (c₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))+s₅ (s₁ s₂ s₃ -c₂ c₃ s₁ ))

o_z＝c₂₃c₆s₄-s₆(s₂₃s₅-c₂₃c₄c₅)o_z ＝c₂₃ c₆ s₄ -s₆ (s₂₃ s₅ -c₂₃ c₄ c₅ )

a_x＝s₆(c₄s₁-s₄(c₁c₂s₃+c₁c₃s₂))+c₆(c₅(s₁s₄+c₄(c₁c₂s₃+c₁c₃s₂))-s₅(c₁s₂s₃-c₁c₂c₃))a_x ＝s₆ (c₄ s₁ -s₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))+c₆ (c₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-s₅ (c₁ s₂ s₃ -c₁ c₂ c₃ ))

a_y＝-s₆(c₁c₄+s₄(c₂s₁s₃+c₃s₁s₂))-c₆(c₅(c₁s₄-c₄(c₂s₁s₃+c₃s₁s₂))+s₅(s₁s₂s₃-c₂c₃s₁))a_y ＝-s₆ (c₁ c₄ +s₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-c₆ (c₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))+s₅ (s₁ s₂ s₃ -c₂ c₃ s₁ ))

a_z＝-c₆(s₂₃s₅-c₂₃c₄c₅)-c₂₃s₄s₆a_z ＝-c₆ (s₂₃ s₅ -c₂₃ c₄ c₅ )-c₂₃ s₄ s₆

P_x＝c₁(L₁+L₄c₂₃+L₃s₂₃+L₂s₂)P_x ＝c₁ (L₁ +L₄ c₂₃ +L₃ s₂₃ +L₂ s₂ )

P_y＝s₁(L₁+L₄c₂₃+L₃s₂₃+L₂s₂)P_y ＝s₁ (L₁ +L₄ c₂₃ +L₃ s₂₃ +L₂ s₂ )

P_z＝L₃c₂₃-L₄s₂₃+L₂c₂P_z ＝L₃ c₂₃ -L₄ s₂₃ +L₂ c₂

其中,c₁-c₆,s₁-s₆依次表示机器人各关节变量θ₁-θ₆的正弦值和余弦值，c₂₃，s₂₃分别表示关节变量θ₂和θ₃之和的正弦值和余弦值；L₁表示机器人关节1和关节2之间连杆在水平方向上的长度，L₂表示机器人关节2和关节3之间连杆长度，L₃表示机器人关节3和关节4之间连杆在垂直方向上的长度，L₄表示机器人关节3和关节4之间连杆在水平方向上的长度；n_x-n_z，o_x-o_z，a_x-a_z表示组成旋转矩阵的三个单位向量，每个参数都是旋转矩阵的一部分；P_x，P_y，P_z表示机器人6轴原点坐标在机器人基坐标系下的表示。Among them, c₁ -c₆ , s₁ -s₆ represent the sine value and cosine value of each joint variable θ₁ -θ₆ of the robot in turn, c₂₃ , s₂₃ represent the sine value of the sum of joint variables θ₂ and θ₃ respectively and cosine value; L₁ represents the length of the connecting rod between joint 1 andjoint 2 of the robot in the horizontal direction, L₂ represents the length of the connecting rod betweenjoint 2 andjoint 3 of the robot, and L₃ represents the length of the connecting rod betweenjoint 3 andjoint 4 of the robot The length of the connecting rod in the vertical direction, L₄ represents the length of the connecting rod in the horizontal direction between therobot joint 3 andjoint 4; n_x -n_z , o_x -o_z , a_x -a_z represent the composition rotation matrix The three unit vectors of , each parameter is a part of the rotation matrix; P_x , P_y , P_z represent the representation of the robot's 6-axis origin coordinates in the robot's base coordinate system.

所述求解机器人的速度雅可比矩阵，包括如下步骤：The speed Jacobian matrix of the solution robot comprises the following steps:

步骤一：确定机械臂体速度、机械臂的速度雅可比矩阵关系，得到方程：Step 1: Determine the relationship between the body speed of the manipulator and the Jacobian matrix of the speed of the manipulator, and obtain the equation:

其中ξ为机械臂体速度，J为机械臂的速度雅可比矩阵，q为关节位置变量，

为q的导数，为关节速度向量，且：Where ξ is the velocity of the manipulator body, J is the velocity Jacobian matrix of the manipulator, q is the joint position variable,

is the derivative of q, is the joint velocity vector, and:

其中⁰v_n代表末端执行器的线速度，⁰ω_n代表末端执行器的角速度，J_v为雅可比矩阵的上半部分，定义关节速度向量

与⁰v_n的关系，J_ω为雅可比矩阵的下半部分，定义关节速度向量/>

与⁰ω_n的关系where⁰ v_n represents the linear velocity of the end effector,^0ω_n represents the angular velocity of the end effector, and J_v is the upper half of the Jacobian matrix, defining the joint velocity vector

Relation to⁰ v_n , J_ω is the lower half of the Jacobian matrix, defining the joint velocity vector />

Relationship with⁰ ω_n

步骤二：确定机械臂末端执行器的线速度，采用微分链式法则处理，计算方程为：Step 2: Determine the linear velocity of the end effector of the manipulator, and use the differential chain rule to process it. The calculation equation is:

其中

为机械臂末端执行器的线速度，q_i代表机器人第i个关节的位置变量，/>

代表导数，为关节速度向量in

is the linear velocity of the end effector of the manipulator, q_i represents the position variable of the i-th joint of the robot, />

Represents the derivative, which is the joint velocity vector

由此确定矩阵J_v的第i列结果为：Therefore, the i-th column of the matrix J_v is determined to be:

计算方程为：The calculation equation is:

其中

代表相对于坐标系0，第i个关节的轴方向的单位向量，/>

代表第i个关节坐标系原点坐标；in

Represents the unit vector of the axis direction of the i-th joint relative to the coordinate system 0, />

Represents the i-th joint coordinate system origin coordinates;

步骤三：确定机器人机械臂速度雅可比矩阵中的转动关节角速度矩阵，可得到矩阵第i列的角速度，为：Step 3: Determine the rotational joint angular velocity matrix in the robot arm velocity Jacobian matrix, and the angular velocity of the i-th column of the matrix can be obtained as:

其中J_ωi代表速度雅可比矩阵第i列的角速度向量矩阵，其中

代表相对于坐标系0，第i个关节的轴方向的单位向量。where J_ωi represents the angular velocity vector matrix of the i-th column of the velocity Jacobian matrix, where

A unit vector representing the axis direction of the i-th joint relative to coordinate system 0.

所述对机器人机械臂的速度雅可比矩阵做解耦处理，处理方式为按平动关节的平动速度和转动关节的转动速度分解速度雅可比矩阵，得到：The decoupling process is performed on the velocity Jacobian matrix of the robot arm, and the processing method is to decompose the velocity Jacobian matrix according to the translational velocity of the translational joint and the rotational velocity of the rotational joint, and obtain:

其中J_O为转动关节速度列向量矩阵，J_P为平动关节的速度列向量矩阵，J₁₁和J₂₂代表分块矩阵中的中间矩阵，定义J_O为：Among them, J_O is the velocity column vector matrix of the rotational joint, J_P is the velocity column vector matrix of the translational joint, J₁₁ and J₂₂ represent the intermediate matrix in the block matrix, and J_O is defined as:

由于关节4-6交于同一点o，因此可选择坐标系，使得o₄＝o₅＝o₆＝o₇＝o，其中o₄、o₅、o₆和o₇代表关节坐标系原点，则转动关节速度列向量矩阵可表示为：Since the joints 4-6 intersect at the same point o, the coordinate system can be selected such that o₄ =o₅ =o₆ =o₇ =o, where o₄ , o₅ , o₆ and o₇ represent the origin of the joint coordinate system, Then the rotational joint velocity column vector matrix can be expressed as:

其中

和/>

分别为机器人机械臂转动关节4～6的角速度向量。in

and />

are the angular velocity vectors of therotational joints 4 to 6 of the robot arm, respectively.

所述对机器人机械臂的速度雅可比矩阵做解耦处理，由于手腕轴线交于同一点o，因此解耦得到的矩阵J₁₂为零矩阵，即：The decoupling process is performed on the speed Jacobian matrix of the robotic arm of the robot. Since the wrist axis intersects at the same point o, the matrix_J12 obtained by decoupling is a zero matrix, namely:

所述计算整个雅可比矩阵的行列式结果，即：The result of calculating the determinant of the entire Jacobian matrix is:

detJ＝detJ₁₁detJ₂₂，detJ = detJ₁₁ detJ₂₂ ,

其中对于detJ₁₁、detJ₂₂中的一个为0，或者两者都为0时，矩阵J₁₁和J₂₂中对应的机器人机械臂关节平动速度和/或转动速度为奇异点。When one of detJ₁₁ and detJ₂₂ is 0, or both of them are 0, the corresponding translation velocity and/or rotation velocity of the joints of the robotic arm in the matrices J₁₁ and J₂₂ are singular points.

若矩阵J₁₁和J₂₂的行列式为0，则矩阵中的列向量线性相关。If the determinants of the matrices J₁₁ and J₂₂ are 0, the column vectors in the matrices are linearly related.

本发明具有以下有益效果和优点：The present invention has following beneficial effect and advantage:

1.可以解决工业机器人在运动中遇到腕部奇异点不能通过的问题，通过计算出机器人处于奇异位形时各关节的状态，使机器人远离奇异位形，提高工业机器人性能。1. It can solve the problem that the industrial robot cannot pass through the singular point of the wrist during the movement. By calculating the state of each joint when the robot is in the singular configuration, the robot can be kept away from the singular configuration and the performance of the industrial robot can be improved.

2.针对机器人运动学奇异位形问题，提出一种根据机器人正向运动学结合速度雅可比矩阵计算六轴机器人腕部奇异位形的方法。通过计算出机器人处于奇异位形时各关节的状态，使机器人远离奇异位形，提高工业机器人性能。2. Aiming at the singularity problem of robot kinematics, a method for calculating the singularity of the wrist of a six-axis robot is proposed based on the forward kinematics of the robot combined with the velocity Jacobian matrix. By calculating the state of each joint when the robot is in a singular configuration, the robot is kept away from the singular configuration and the performance of the industrial robot is improved.

附图说明Description of drawings

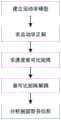
图1工业机器人奇异位形计算流程图；Fig. 1 Flowchart of singular configuration calculation of industrial robot;

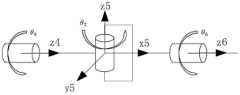
图2工业机器人运动学建模示意图；Fig. 2 Schematic diagram of industrial robot kinematics modeling;

图3工业机器腕部奇异位形示意图。Figure 3 Schematic diagram of the singular configuration of the wrist of an industrial machine.

具体实施方式Detailed ways

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。In order to make the object, technical solution and advantages of the present invention clearer, the present invention will be further described in detail below in conjunction with the accompanying drawings and embodiments. It should be understood that the specific embodiments described here are only used to explain the present invention, not to limit the present invention.

如图1所示，本发明包括如下步骤：As shown in Figure 1, the present invention comprises the following steps:

1.建立工业机器人的运动学模型1. Establish the kinematics model of the industrial robot

2.求解工业机器人运动学正解2. Solve the positive solution of industrial robot kinematics

3.求解工业机器人的速度雅可比矩阵3. Solve the speed Jacobian matrix of industrial robots

4.对雅可比矩阵进行解耦运算4. Decoupling the Jacobian matrix

5.求解工业机器人腕部奇异位形5. Solve the singular configuration of the wrist of an industrial robot

建立工业机器人的运动学模型，根据6轴工业机器人关节和连杆结构，建立机器人运动学模型。Establish the kinematics model of the industrial robot, and establish the kinematics model of the robot according to the joint and connecting rod structure of the 6-axis industrial robot.

所述机器人关节和连杆结构，关节坐标系定义如图2所示：The robot joint and connecting rod structure, the definition of the joint coordinate system is shown in Figure 2:

图中{1}、{2}、{3}、{4}、{5}、{6}代表各个关节处的坐标系，其坐标系方向均定义为与基坐标系相同。坐标系{i}(i＝1，2，3)的原点定义为机器人i轴轴心和i+1轴轴心公垂线与机器人i轴轴心的交点，腕关节坐标系{4}、{5}、{6}原点定义为机器人四轴轴心和五轴轴心交点。{1}, {2}, {3}, {4}, {5}, and {6} in the figure represent the coordinate systems at each joint, and the directions of the coordinate systems are defined to be the same as the base coordinate system. The origin of the coordinate system {i} (i=1, 2, 3) is defined as the intersection point of the common vertical line of the robot’s i-axis axis and the i+1 axis axis and the robot’s i-axis axis. The wrist joint coordinate system {4}, The origin of {5} and {6} is defined as the intersection point of the four-axis axis and the five-axis axis of the robot.

所述机器人运动学模型的连杆变换矩阵如下：The link transformation matrix of the robot kinematics model is as follows:

计算机器人运动学正解Computational Robot Kinematics Positive Solution

其中in

n_x＝-s₅(s₁s₄+c₄(c₁c₂s₃+c₁c₃s₂))-c₅(c₁s₂s₃-c₁c₂c₃)n_x ＝-s₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-c₅ (c₁ s₂ s₃ -c₁ c₂ c₃ )

n_y＝s₅(c₁s₄-c₄(c₂s₁s₃+c₃s₁s₂))-c₅(s₁s₂s₃-c₂c₃s₁)n_y ＝s₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-c₅ (s₁ s₂ s₃ -c₂ c₃ s₁ )

n_z＝-s₂₃c₅-c₂₃c₄s₅n_z ＝-s₂₃ c₅ -c₂₃ c₄ s₅

o_x＝s₆(c₅(s₁s₄+c₄(c₁c₂s₃+c₁c₃s₂))-s₅(c₁s₂s₃-c₁c₂c₃))-c₆(c₄s₁-s₄(c₁c₂s₃+c₁c₃s₂))o_x ＝s₆ (c₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-s₅ (c₁ s₂ s₃ -c₁ c₂ c₃ ) )-c₆ (c₄ s₁ -s₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))

o_y＝c₆(c₁c₄+s₄(c₂s₁s₃+c₃s₁s₂))-s₆(c₅(c₁s₄-c₄(c₂s₁s₃+c₃s₁s₂))+s₅(s₁s₂s₃-c₂c₃s₁))o_y ＝c₆ (c₁ c₄ +s₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-s₆ (c₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))+s₅ (s₁ s₂ s₃ -c₂ c₃ s₁ ))

o_z＝c₂₃c₆s₄-s₆(s₂₃s₅-c₂₃c₄c₅)o_z ＝c₂₃ c₆ s₄ -s₆ (s₂₃ s₅ -c₂₃ c₄ c₅ )

a_x＝s₆(c₄s₁-s₄(c₁c₂s₃+c₁c₃s₂))+c₆(c₅(s₁s₄+c₄(c₁c₂s₃+c₁c₃s₂))-s₅(c₁s₂s₃-c₁c₂c₃))a_x ＝s₆ (c₄ s₁ -s₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))+c₆ (c₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-s₅ (c₁ s₂ s₃ -c₁ c₂ c₃ ))

a_y＝-s₆(c₁c₄+s₄(c₂s₁s₃+c₃s₁s₂))-c₆(c₅(c₁s₄-c₄(c₂s₁s₃+c₃s₁s₂))+s₅(s₁s₂s₃-c₂c₃s₁))a_y ＝-s₆ (c₁ c₄ +s₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-c₆ (c₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))+s₅ (s₁ s₂ s₃ -c₂ c₃ s₁ ))

a_z＝-c₆(s₂₃s₅-c₂₃c₄c₅)-c₂₃s₄s₆a_z ＝-c₆ (s₂₃ s₅ -c₂₃ c₄ c₅ )-c₂₃ s₄ s₆

P_x＝c₁(L₁+L₄c₂₃+L₃s₂₃+L₂s₂)P_x ＝c₁ (L₁ +L₄ c₂₃ +L₃ s₂₃ +L₂ s₂ )

P_y＝s₁(L₁+L₄c₂₃+L₃s₂₃+L₂s₂)P_y ＝s₁ (L₁ +L₄ c₂₃ +L₃ s₂₃ +L₂ s₂ )

P_z＝L₃c₂₃-L₄s₂₃+L₂c₂P_z ＝L₃ c₂₃ -L₄ s₂₃ +L₂ c₂

求解工业机器人的速度雅可比矩阵，雅可比矩阵是关节速度空间，到笛卡尔速度空间的映射，其逆矩阵，就是笛卡尔速度空间，到关节速度空间的映射。雅可比矩阵是时变的线性映射。Solve the velocity Jacobian matrix of industrial robots. The Jacobian matrix is the mapping from the joint velocity space to the Cartesian velocity space, and its inverse matrix is the mapping from the Cartesian velocity space to the joint velocity space. The Jacobian matrix is a time-varying linear map.

其中，ξ和J由下式给出where ξ and J are given by

向量ξ被称为体速度，注意这个速度向量并非位置变量的倒数，这是由于角速度向量不是任何时变数量的倒数，矩阵J被称为机械臂的雅可比矩阵。J是一个6×n的矩阵，其中n是机器人中的连杆数量。The vector ξ is called the body velocity. Note that this velocity vector is not the reciprocal of the position variable. This is because the angular velocity vector is not the reciprocal of any time-varying quantity. The matrix J is called the Jacobian matrix of the manipulator. J is a 6×n matrix, where n is the number of links in the robot.

想要描述刚体的运动，需要6个变量，其中3个平移速度分量，3个旋转速度分量，想要确定这6个输出变量，至少需要6个输出，且雅可比矩阵的6个列向量必须线性无关，也就是说这个6个列向量可以张成一个6维的向量空间。To describe the motion of a rigid body, 6 variables are required, including 3 translational velocity components and 3 rotational velocity components. To determine these 6 output variables, at least 6 outputs are required, and the 6 column vectors of the Jacobian matrix must be Linearly independent, that is to say, the 6 column vectors can be stretched into a 6-dimensional vector space.

末端执行器的线速度是

使用微分的链式法则，有The linear velocity of the end effector is

Using the chain rule of differentiation, we have

因此，矩阵J_v的第i列(记为J_vi)可由下式给出：Therefore, the ith column of matrix J_v (denoted J_vi ) can be given by:

其中，矩阵的第i列J_vi为Among them, the i-th column J_vi of the matrix is

雅可比矩阵的下半部分为The lower half of the Jacobian matrix is

J_ω＝(J_ω1…J_ωn)J_ω ＝(J_ω1 …J_ωn )

其中，矩阵的第i列J_ωi为Among them, the i-th column J_ωi of the matrix is

当雅可比矩阵的行列式等于零,该方阵是奇异矩阵，此情况下雅可比矩阵的逆矩阵不存在，不能通过笛卡尔速度求出对应的关节速度，通过求解雅可比矩阵行列式为零的情况，可以确定机器人的奇异位形。When the determinant of the Jacobian matrix is equal to zero, the square matrix is a singular matrix. In this case, the inverse matrix of the Jacobian matrix does not exist, and the corresponding joint speed cannot be obtained through the Cartesian velocity. By solving the Jacobian matrix, the determinant is zero. situation, the singular configuration of the robot can be determined.

一般情况下，难以求解非线性方程detJ(q)＝0，但是对于装备有球形手腕的机械臂，可以对雅可比矩阵进行解耦，求解奇异点位置。In general, it is difficult to solve the nonlinear equation detJ(q)=0, but for a robotic arm equipped with a spherical wrist, the Jacobian matrix can be decoupled to solve for the singular point position.

通过解耦，可以分离出腕部奇异点的雅可比矩阵。By decoupling, the Jacobian of the wrist singularity can be isolated.

对于有球形手腕的6轴机器人，雅可比矩阵为6*6矩阵，当For a 6-axis robot with a spherical wrist, the Jacobian matrix is a 6*6 matrix, when

detJ(q)＝0detJ(q)=0

时，位形q为奇异点When , the configuration q is a singular point

若将雅可比矩阵分解成如下3*3的矩阵块If the Jacobian matrix is decomposed into the following 3*3 matrix blocks

最后三个关节总为转动关节The last three joints are always rotational joints

由于手腕轴线交于同一点o，若我们选择坐标系使得o₄＝o₅＝o₆＝o₇＝o，则Since the wrist axis intersects at the same point o, if we choose the coordinate system such that o₄ ＝o₅ ＝o₆ ＝o₇ ＝o, then

因此，雅可比矩阵有以下形式Therefore, the Jacobian matrix has the form

其行列式为Its determinant is

detJ＝detJ₁₁detJ₂₂detJ = detJ₁₁ detJ₂₂

手腕奇异点wrist singularity

因为

是表式机器人4，5，6轴方向的三维向量，其方向由连杆变换矩阵T的旋转算子部分决定。because

is the three-dimensional vector of the 4, 5, and 6-axis directions of the table robot, and its direction is determined by the rotation operator part of the linkage transformation matrix T.

其中

是3×3矩阵，是变换矩阵T的旋转算子部分in

is a 3×3 matrix, and is the rotation operator part of the transformation matrix T

根据运动学正解，可以计算According to the positive solution of kinematics, it can be calculated

其中

代表第i个关节变换矩阵T的旋转算子部分，以上公式中，/>

统一省略了左上角标0，/>

为轴方向在轴所在坐标系中的表示in

Represents the rotation operator part of the i-th joint transformation matrix T, in the above formula, />

Uniformly omit the upper left corner mark 0, />

is the representation of the axis direction in the coordinate system where the axis is located

J₂₂是一个3*3的方阵，当向量

线性相关时，球形手腕处于奇异位形，即当θ₅＝0或180°时，/>

处于同一条直线上，球形手腕处于奇异位形，如图3所示。并在此基础上绕开奇异点。J₂₂ is a 3*3 square matrix, when the vector

When linearly related, the spherical wrist is in a singular configuration, that is, when θ₅ =0 or 180°, />

On the same straight line, the spherical wrist is in a singular configuration, as shown in Figure 3. And on this basis, the singularity is bypassed.

Claims (7)

1. The control method based on the calculation of the wrist singular point of the industrial robot is characterized by comprising the following steps:

step one: defining a base coordinate system and a robot mechanical arm joint coordinate system, ensuring that the directions of the robot joint coordinate system and the base coordinate system are the same, and establishing a robot kinematic model according to robot motion parameters;

step two: according to the link transformation of the robot mechanical arm kinematic model, solving the robot kinematic positive solution;

step three: solving a speed jacobian matrix of the mechanical arm of the robot to obtain a speed jacobian matrix comprising the translation speed and the rotation speed of the joint of the robot;

step four: decoupling operation is carried out on the solved velocity jacobian matrix, and the matrix is divided into a plurality of matrixes according to the translation velocity and the rotation velocity;

step five: calculating a determinant result of the whole jacobian matrix according to the decoupled velocity jacobian matrix, and when the determinant result is zero, the singular point of the robot mechanical arm is obtained;

step six: after the singular points of the robot arm are obtained, the robot arm is controlled according to the track of the singular points.

2. The control method based on industrial robot wrist singular point calculation according to claim 1, characterized in that:

the connecting rod transformation for the robot kinematic model is characterized in that the transformation matrix is as follows:

and calculating the kinematic forward solution of the robot, wherein the calculation formula and the result are as follows:

wherein:

n_x ＝-s₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-c₅ (c₁ s₂ s₃ -c₁ c₂ c₃ )

n_y ＝s₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-c₅ (s₁ s₂ s₃ -c₂ c₃ s₁ )

n_z ＝-s₂₃ c₅ -c₂₃ c₄ s₅

o_x ＝s₆ (c₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-s₅ (c₁ s₂ s₃ -c₁ c₂ c₃ ))-c₆ (c₄ s₁ -s₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))

o_y ＝c₆ (c₁ c₄ +s₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-s₆ (c₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))+s₅ (s₁ s₂ s₃ -c₂ c₃ s₁ ))

o_z ＝c₂₃ c₆ s₄ -s₆ (s₂₃ s₅ -c₂₃ c₄ c₅ )

a_x ＝s₆ (c₄ s₁ -s₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))+c₆ (c₅ (s₁ s₄ +c₄ (c₁ c₂ s₃ +c₁ c₃ s₂ ))-s₅ (c₁ s₂ s₃ -c₁ c₂ c₃ ))

a_y ＝-s₆ (c₁ c₄ +s₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))-c₆ (c₅ (c₁ s₄ -c₄ (c₂ s₁ s₃ +c₃ s₁ s₂ ))+s₅ (s₁ s₂ s₃ -c₂ c₃ s₁ ))

a_z ＝-c₆ (s₂₃ s₅ -c₂₃ c₄ c₅ )-c₂₃ s₄ s₆

P_x ＝c₁ (L₁ +L₄ c₂₃ +L₃ s₂₃ +L₂ s₂ )

P_y ＝s₁ (L₁ +L₄ c₂₃ +L₃ s₂₃ +L₂ s₂ )

P_z ＝L₃ c₂₃ -L₄ s₂₃ +L₂ c₂

wherein c₁ -c₆ ,s₁ -s₆ Sequentially representing the joint variable theta of the robot₁ -θ₆ Sine and cosine values of c₂₃ ，s₂₃ Respectively represent the joint variable theta₂ And theta₃ Sine and cosine values of the sum; l (L)₁ Represents the length of the connecting rod between the robot joint 1 and the joint 2 in the horizontal direction, L₂ Indicating the length of the link between the robot joint 2 and the joint 3, L₃ Represents the length of the link between the robot joint 3 and the joint 4 in the vertical direction, L₄ Representing the length of the link between the robot joint 3 and the joint 4 in the horizontal direction; n is n_x -n_z ，o_x -o_z ，a_x -a_z Representing three unit vectors constituting a rotation matrix, each parameter being a part of the rotation matrix; p (P)_x ，P_y ，P_z The representation of the origin coordinates of the robot 6 axis in the robot base coordinate system is shown.

3. Control based on industrial robot wrist singular point calculation according to claim 1Process for producing, P_y The method is characterized in that:

the method for solving the velocity jacobian matrix of the robot comprises the following steps:

step one: determining the relationship between the body speed of the mechanical arm and the jacobian matrix of the speed of the mechanical arm to obtain an equation:

wherein xi is the speed of the mechanical arm body, J is the jacobian matrix of the speed of the mechanical arm, q is the joint position variable,

the derivative of q, the joint velocity vector, and:

wherein the method comprises the steps of⁰ v_m Representing the linear velocity of the end effector,⁰ ω_n represents the angular velocity of the end effector, J_v For the upper half of the jacobian matrix, a joint velocity vector is defined

And (3) with⁰ v_n Relation of J_ω For the lower half of the jacobian matrix, a joint velocity vector is defined

And (3) with⁰ ω_n Relation of (2)

Step two: determining the linear speed of the mechanical arm end effector, adopting differential chain type rule processing, and calculating the equation as follows:

wherein the method comprises the steps of

Is the linear speed, q of the mechanical arm end effector_i Position variable representing the i-th joint of the robot, for example>

Representing the derivative, being the joint velocity vector

Thereby determining matrix J_v The i-th column of results is:

the calculation equation is:

wherein the method comprises the steps of

Representing the unit vector of the axial direction of the ith joint with respect to the coordinate system 0, +.>

Representing the origin coordinate of the ith joint coordinate system;

step three: determining a rotational joint angular velocity matrix in a robot arm velocity jacobian matrix to obtain an angular velocity of an ith column of the matrix, wherein the angular velocity is as follows:

wherein J_ωi An angular velocity vector matrix representing the ith column of the velocity jacobian matrix, wherein

Represents a unit vector in the axial direction of the ith joint with respect to the coordinate system 0.

4. The control method based on industrial robot wrist singular point calculation according to claim 1, characterized in that:

the method comprises the steps of decoupling a speed jacobian matrix of a robot arm, wherein the speed jacobian matrix is decomposed according to the translation speed of a translation joint and the rotation speed of a rotation joint, and the speed jacobian matrix is obtained:

wherein J_O For a rotational joint velocity column vector matrix, J_P Velocity column vector matrix for translation joint, J₁₁ And J₂₂ Representing an intermediate matrix in the partitioned matrix, defining J_O The method comprises the following steps:

since the joints 4-6 intersect at the same point o, the coordinate system can be selected such that o₄ ＝o₅ ＝o₆ ＝o₇ O, where o₄ 、o₅ 、o₆ And o₇ Representing the origin of the joint coordinate system, the rotational joint velocity column vector matrix may be expressed as:

wherein the method comprises the steps of

And->

The angular velocity vectors of the robot arm rotating joints 4 to 6 are respectively.

5. The control method based on industrial robot wrist singular point calculation according to claim 4, characterized in that:

the velocity jacobian matrix of the robot arm is decoupled, and the wrist axis intersects with the same point o, so that the matrix J is obtained by decoupling₁₂ Zero matrix, i.e.:

。

6. the control method based on industrial robot wrist singular point calculation according to claim 1, characterized in that:

the determinant result of the entire jacobian matrix is calculated, namely:

detJ＝detJ₁₁ detJ₂₂ ，

wherein for detJ₁₁ 、detJ₂₂ When one of them is 0, or both are 0, matrix J₁₁ And J₂₂ The translation speed and/or the rotation speed of the corresponding robot mechanical arm joint are singular points.

7. The control method based on industrial robot wrist singular point calculation according to claim 6, characterized in that:

if matrix J₁₁ And J₂₂ Is 0, the column vectors in the matrix are linearly related.

Images