Movatterモバイル変換

[0]ホーム
URL:

CN116108763A - Method for predicting bubble collapse critical point of foaming material based on temperature - Google Patents

Method for predicting bubble collapse critical point of foaming material based on temperatureDownload PDF

Info

Publication number
CN116108763A
CN116108763ACN202310391747.3ACN202310391747ACN116108763ACN 116108763 ACN116108763 ACN 116108763ACN 202310391747 ACN202310391747 ACN 202310391747ACN 116108763 ACN116108763 ACN 116108763A
Authority
CN
China
Prior art keywords
bubble
power law
population
critical point
new
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Granted
Application number
CN202310391747.3A
Other languages
Chinese (zh)
Other versions
CN116108763B (en
Inventor
姚婷
刘佳斌
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Hunan University of Technology
Original Assignee
Hunan University of Technology
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Hunan University of TechnologyfiledCriticalHunan University of Technology
Priority to CN202310391747.3ApriorityCriticalpatent/CN116108763B/en
Publication of CN116108763ApublicationCriticalpatent/CN116108763A/en
Application grantedgrantedCritical
Publication of CN116108763BpublicationCriticalpatent/CN116108763B/en
Activelegal-statusCriticalCurrent
Anticipated expirationlegal-statusCritical

Links

Images

Classifications

Landscapes

Abstract

Translated fromChinese

本发明提供了一种基于温度的发泡材料气泡破裂临界点预测的方法，选择样本空间来预测未来时间范围内的气泡破裂临界点，获取发泡材料的气泡体积数据，并代入到对数周期幂律模型中；将温度变化的历史数据加入到对数周期幂律模型中，构建新对数周期幂律模型；采用多种群遗传算法估计新对数周期幂律模型中的全部非线性参数；采用最小二乘法求得新对数周期幂律模型中的全部线性参数；进行Lomb周期图分析，采用滑动窗口法根据所获得

Figure ZY_1
值预测最终区间。本发明得到了一个融合温度与气泡体积数据的预测发泡材料气泡破裂临界点模型，使预测更符合现实情况，提高了模型预测精确度。

Figure 202310391747

The invention provides a temperature-based method for predicting the critical point of bubble rupture in foaming materials, selects the sample space to predict the critical point of bubble rupture in the future time range, obtains the bubble volume data of the foaming material, and substitutes it into the logarithmic cycle In the power law model; add the historical data of temperature changes to the logarithmic periodic power law model to construct a new logarithmic periodic power law model; use a multi-population genetic algorithm to estimate all nonlinear parameters in the new logarithmic periodic power law model; All linear parameters in the new logarithmic periodic power law model are obtained by the least square method; Lomb periodogram analysis is carried out, and the sliding window method is used according to the obtained

Figure ZY_1
Value predicts the final interval. The invention obtains a model for predicting the critical point of bubble rupture of the foaming material combined with temperature and bubble volume data, which makes the prediction more in line with the actual situation and improves the prediction accuracy of the model.

Figure 202310391747

Description

Translated fromChinese
基于温度的发泡材料气泡破裂临界点预测的方法A method for predicting the critical point of bubble rupture in foaming materials based on temperature

技术领域Technical Field

本发明涉及发泡材料技术领域，特别涉及一种基于温度的发泡材料气泡破裂临界点预测的方法。The invention relates to the technical field of foaming materials, and in particular to a method for predicting a critical point of bubble rupture of a foaming material based on temperature.

背景技术Background Art

通过物理或化学的方式在聚合物材料内部引入大量的微细气泡，将聚合物的特性和小气泡的特性优化组合于一体，显著提高材料性能或赋予原聚合物所不具有的崭新特性，这已成为当前聚合物材料开发应用的重要方向之一，相比于普通塑料制品，这种结构具有许多优异的性能，如重量小、强度高、韧性好、尺寸稳定等，因此微孔聚合物材料也被喻为21 世纪新型材料。尽管发泡材料具有上述诸多优点，但由于传统发泡的工艺条件以及发泡剂的选择存在局限性，使得发泡材料的泡孔尺寸偏大且分布不均匀，这些大而不均匀的气泡在较大应力作用下容易成为裂纹源，使材料的机械性能下降。Introducing a large number of fine bubbles into polymer materials by physical or chemical means, optimizing the combination of polymer properties and small bubble properties, significantly improving material performance or giving new properties that the original polymer does not have, has become one of the important directions for the development and application of polymer materials. Compared with ordinary plastic products, this structure has many excellent properties, such as light weight, high strength, good toughness, dimensional stability, etc. Therefore, microporous polymer materials are also known as new materials in the 21st century. Although foaming materials have many advantages mentioned above, due to the limitations of traditional foaming process conditions and the selection of foaming agents, the pore size of foaming materials is large and unevenly distributed. These large and uneven bubbles are easy to become crack sources under large stress, which reduces the mechanical properties of the material.

公开号为CN114818519A的中国专利申请公开了一种预测发泡材料气泡破裂的方法、系统及计算机可读介质，方法包括：选择一个样本空间来预测未来时间范围内的气泡破裂临界点；将选择的样本空间进一步划分为多个子区间；对于每个子区间，采用粒子群优化算法（PSO）拟合对数周期幂律（LPPL）模型中的参数，确立LPPL模型，并获得临界点；针对每个子区间的LPPL模型拟合结果，运用Lomb周期图验证LPPL模型拟合的曲线和临界点是否有效，由Lomb周期图验证的转折点为气泡破裂临界点。该方法可以比较准确、提前预测气泡破裂，从而控制发泡材料气泡破裂的过程，有效提高发泡材料的机械性能。The Chinese patent application with publication number CN114818519A discloses a method, system and computer-readable medium for predicting bubble rupture of foaming materials, the method comprising: selecting a sample space to predict the critical point of bubble rupture within a future time range; further dividing the selected sample space into multiple sub-intervals; for each sub-interval, using the particle swarm optimization algorithm (PSO) to fit the parameters in the logarithmic periodic power law (LPPL) model, establishing the LPPL model, and obtaining the critical point; for the LPPL model fitting results of each sub-interval, using the Lomb periodogram to verify whether the curve and critical point fitted by the LPPL model are valid, and the turning point verified by the Lomb periodogram is the critical point of bubble rupture. This method can predict bubble rupture more accurately and in advance, thereby controlling the process of bubble rupture of foaming materials and effectively improving the mechanical properties of foaming materials.

温度是影响发泡材料气泡尺寸和分布的主要因素之一，它对聚合物熔体的表面张力，气体在聚合物熔体中的溶解度以及扩散系数等都有影响。通过将温度作为外生变量加入到气泡体积预测中，研究气泡破裂临近区间，对提高发泡材料的机械性能具有重要的现实意义，而上述方案并未将温度因素考虑其中。Temperature is one of the main factors affecting the size and distribution of bubbles in foaming materials. It affects the surface tension of polymer melts, the solubility of gases in polymer melts, and the diffusion coefficient. By adding temperature as an exogenous variable to the prediction of bubble volume, studying the interval near bubble rupture has important practical significance for improving the mechanical properties of foaming materials, while the above scheme does not take temperature factors into consideration.

发明内容Summary of the invention

本发明的目的是：针对上述背景技术中存在的不足，提供一种气泡破裂临界点预测的方法，将温度加入到对数周期幂律模型中，构建新对数周期幂律模型(XLPPL)，并用多种群遗传算法来估计新对数周期幂律模型中的非线性参数，最后以区间预测代替点预测，提高气泡破裂预测精确度。The purpose of the present invention is to provide a method for predicting the critical point of bubble burst in response to the shortcomings of the above-mentioned background technology, add temperature to the logarithmic periodic power law model, construct a new logarithmic periodic power law model (XLPPL), and use a multi-population genetic algorithm to estimate the nonlinear parameters in the new logarithmic periodic power law model, and finally replace the point prediction with interval prediction to improve the accuracy of bubble burst prediction.

为了达到上述目的，本发明提供了一种基于温度的发泡材料气泡破裂临界点预测的方法，包括如下步骤：In order to achieve the above object, the present invention provides a method for predicting the critical point of bubble rupture of a foaming material based on temperature, comprising the following steps:

S1，选择样本空间来预测未来时间范围内的气泡破裂临界点，通过提取气泡的面积、当量直径、几何中心、速度、加速度特征参数获取发泡材料的气泡体积数据，并代入到对数周期幂律模型中；S1, select sample space to predict the critical point of bubble rupture in the future time range, obtain the bubble volume data of the foaming material by extracting the bubble area, equivalent diameter, geometric center, velocity, and acceleration characteristic parameters, and substitute them into the logarithmic periodic power law model;

S2，将温度变化的历史数据加入到对数周期幂律模型中，构建新对数周期幂律模型；S2, adding the historical data of temperature change into the logarithmic periodic power law model to construct a new logarithmic periodic power law model;

S3，采用多种群遗传算法估计新对数周期幂律模型中的全部非线性参数；S3, using a multi-population genetic algorithm to estimate all nonlinear parameters in the new log-periodic power law model;

其中，发泡材料气泡破裂的对数周期幂律模型的形式如下：Among them, the logarithmic periodic power law model of bubble collapse of foaming materials is as follows:

Figure SMS_1
；
Figure SMS_1
;

其中，

Figure SMS_6
为所求的气泡破裂点临界点的气泡体积，
Figure SMS_9
为气泡测量的初始时间，
Figure SMS_12
为气泡破裂的临界点时间，即气泡临近破裂的时间；
Figure SMS_10
为气泡加速度；
Figure SMS_13
为对数周期振动频率，
Figure SMS_8
为相位，
Figure SMS_16
都是振幅，
Figure SMS_5
对应于气泡的体积初始值，
Figure SMS_17
对应于气泡速度，
Figure SMS_2
为气泡增长前后的直径差；
Figure SMS_11
表示达到气泡临近破裂的时间
Figure SMS_3
时，
Figure SMS_14
可能达到的值，且
Figure SMS_7
，
Figure SMS_15
代表着向上的加速，
Figure SMS_4
刻画了气泡体积序列的超指数特征，而
Figure SMS_18
描述了气泡体积的周期型震荡；in,
Figure SMS_6
is the bubble volume at the critical point of bubble collapse,
Figure SMS_9
is the initial time of bubble measurement,
Figure SMS_12
is the critical point time of bubble rupture, that is, the time when the bubble is about to rupture;
Figure SMS_10
is the bubble acceleration;
Figure SMS_13
is the logarithmic periodic vibration frequency,
Figure SMS_8
is the phase,
Figure SMS_16
are all amplitudes,
Figure SMS_5
Corresponding to the initial value of the volume of the bubble,
Figure SMS_17
corresponds to the bubble velocity,
Figure SMS_2
is the diameter difference before and after the bubble grows;
Figure SMS_11
Indicates the time when the bubble is about to burst
Figure SMS_3
hour,
Figure SMS_14
possible values, and
Figure SMS_7
,
Figure SMS_15
Represents upward acceleration.
Figure SMS_4
It describes the super-exponential characteristics of the bubble volume series, and
Figure SMS_18
Describes the periodic oscillation of the bubble volume;

设定

Figure SMS_19
，
Figure SMS_20
及
Figure SMS_21
，对数周期幂律模型简写为以下形式：set up
Figure SMS_19
,
Figure SMS_20
and
Figure SMS_21
, the log-periodic power law model can be simplified as follows:

Figure SMS_22
；
Figure SMS_22
;

其中，

Figure SMS_23
，在对数周期幂律模型中添加温度变化的历史数据，新对数周期幂律模型简写为以下模式：in,
Figure SMS_23
, adding the historical data of temperature changes to the logarithmic periodic power law model, the new logarithmic periodic power law model is abbreviated as follows:

Figure SMS_24
；
Figure SMS_24
;

其中，

Figure SMS_25
，
Figure SMS_26
也为振幅且为线性参数，
Figure SMS_27
是温度变化的历史数据；in,
Figure SMS_25
,
Figure SMS_26
is also the amplitude and is a linear parameter,
Figure SMS_27
It is the historical data of temperature change;

S4，采用最小二乘法求得新对数周期幂律模型中的全部线性参数；S4, using the least squares method to obtain all linear parameters in the new log-periodic power law model;

S5，进行Lomb周期图分析，以对新对数周期幂律模型获得的

Figure SMS_28
值进行统计检验，通过Lomb周期图统计验证的转折点是XLPPL模型的气泡破裂点；S5, Lomb periodogram analysis was performed to obtain the new logarithmic periodic power law model
Figure SMS_28
The values were statistically tested, and the turning point statistically verified by the Lomb periodogram was the bubble bursting point of the XLPPL model;

S6，采用滑动窗口法根据所获得

Figure SMS_29
值预测最终区间。S6, using the sliding window method according to the obtained
Figure SMS_29
The final interval of value prediction.

进一步地，S3具体包括如下子步骤：Furthermore, S3 specifically includes the following sub-steps:

S31，随机生成U个初始种群，每个种群中随机产生W个染色体，这些染色体个体构成了一个种群，每个染色体表示由对数周期幂律模型的全部非线性参数组成的可行解；S31, randomly generate U initial populations, randomly generate W chromosomes in each population, these chromosome individuals constitute a population, and each chromosome represents a feasible solution composed of all nonlinear parameters of the logarithmic periodic power law model;

S32，计算适应度，适应度代表个体在此环境中生存的可能性，适应度越大表示此个体被遗传到下一代的几率越大；S32, calculate the fitness, which represents the possibility of an individual surviving in this environment. The greater the fitness, the greater the probability that the individual will be inherited to the next generation;

S33，选择挑选出本代本种群中的最优个体；S33, select the best individual in this generation and this population;

S34，在此代种群中个体基因交叉获得新的个体，得到新一代种群，新一代种群中的个体按概率遗传了父代中部分的基因片段，保留了父代的部分特性；S34, in this generation of population, the genes of individuals are crossed to obtain new individuals, and a new generation of population is obtained. The individuals in the new generation of population inherit part of the gene fragments of the parent generation according to probability, and retain some characteristics of the parent generation;

S35，通过预设的基因突变概率随机改变个体上某个基因片段，获得新的个体；S35, randomly changing a gene fragment on an individual through a preset gene mutation probability to obtain a new individual;

S36，将进化生成的子代种群重插入父代种群中；S36, reinserting the evolved offspring population into the parent population;

S37，移民，将独立的多个种群联合成一个统一的整体；S37, immigration, uniting separate populations into a unified whole;

S38，迭代计算并判断，输出最终染色体，获得优化的全部非线性参数。S38, iteratively calculate and judge, output the final chromosome, and obtain all optimized nonlinear parameters.

进一步地，S32中多种群遗传算法通过计算

Figure SMS_30
时刻的气泡体积
Figure SMS_31
与新对数周期幂律模型拟合结果之间的残差平方和评估每个染色体的适应度值：Furthermore, the multi-population genetic algorithm in S32 calculates
Figure SMS_30
Bubble volume at time
Figure SMS_31
The fitness value of each chromosome is evaluated by the residual sum of squares between the results of fitting the new logarithmic periodic power law model:

Figure SMS_32
其中，
Figure SMS_33
代表第
Figure SMS_34
个群体中第
Figure SMS_35
条染色体的残差平方和；
Figure SMS_36
，
Figure SMS_37
，
Figure SMS_32
in,
Figure SMS_33
Representative
Figure SMS_34
In the group
Figure SMS_35
The residual sum of squares of chromosomes;
Figure SMS_36
,
Figure SMS_37
,

Figure SMS_38
对应第
Figure SMS_39
个种群的第
Figure SMS_40
条染色体。
Figure SMS_38
Corresponding to
Figure SMS_39
The first
Figure SMS_40
Chromosomes.

进一步地，S37中用第

Figure SMS_41
个种群中适应度值最小
Figure SMS_42
的染色体代替第u+1个种群中适应度值最大
Figure SMS_43
的染色体，以将独立的多个种群联合成一个统一的整体。Further, in S37,
Figure SMS_41
The fitness value is the smallest among the populations
Figure SMS_42
The chromosome with the largest fitness value in the u+1th population is replaced by
Figure SMS_43
chromosomes to unite multiple independent populations into a unified whole.

进一步地，S38中如果新种群的最小适应度值

Figure SMS_44
小于上一次迭代过程中该种群的最小适应度值，则更新记录；否则，该种群的原始记录保持不变；如果所有种群的最小适应度值都没有发生改变，或者达到迭代次数上限，那么计算终止，最后一次迭代结束之后所有种群的最小适应度值及其相应染色体是多种群遗传算法的输出。Furthermore, in S38, if the minimum fitness value of the new population
Figure SMS_44
If the minimum fitness value of the population is less than the minimum fitness value of the population in the previous iteration, the record is updated; otherwise, the original record of the population remains unchanged; if the minimum fitness value of all populations has not changed, or the upper limit of the number of iterations is reached, the calculation is terminated. After the last iteration, the minimum fitness value of all populations and their corresponding chromosomes are the output of the multi-population genetic algorithm.

进一步地，S4中Furthermore, in S4

Figure SMS_45
；
Figure SMS_45
;

Figure SMS_46
；
Figure SMS_46
;

Figure SMS_47
；
Figure SMS_47
;

其中，

Figure SMS_48
，
Figure SMS_49
为时间单位，
Figure SMS_50
为总时间单位，新对数周期幂律模型中的全部线性参数使用以下等式计算所得：in,
Figure SMS_48
,
Figure SMS_49
is the time unit,
Figure SMS_50
is the total time unit, and all linear parameters in the new log-periodic power law model are calculated using the following equations:

Figure SMS_51
。
Figure SMS_51
.

进一步地，S5中运用Lomb周期图测试多种群遗传算法得到的新对数周期幂律模型模型的周期性频率

Figure SMS_52
和
Figure SMS_53
是否是持续的，以确定该模型拟合的曲线和临界点是否有效；Furthermore, the Lomb periodogram is used in S5 to test the periodic frequency of the new logarithmic periodic power law model obtained by the multi-population genetic algorithm.
Figure SMS_52
and
Figure SMS_53
Is it continuous, to determine whether the curve and critical point fitted by the model are valid;

Lomb周期图首先预设频率序列

Figure SMS_54
，其中，
Figure SMS_55
是预先给定频率序列的长度；对于给定的频率f，功率谱密度
Figure SMS_56
通过Lomb周期图分析计算如下：The Lomb periodogram first presets the frequency sequence
Figure SMS_54
,in,
Figure SMS_55
is the length of the pre-given frequency sequence; for a given frequency f, the power spectral density
Figure SMS_56
The calculation is performed through Lomb periodogram analysis as follows:

Figure SMS_57
；
Figure SMS_57
;

其中，

Figure SMS_58
，表示对数体积的周期型震荡，
Figure SMS_59
表示为
Figure SMS_60
的均值，时间偏移
Figure SMS_61
计算为：in,
Figure SMS_58
, represents the periodic oscillation of the logarithmic volume,
Figure SMS_59
Expressed as
Figure SMS_60
The mean of the time offset
Figure SMS_61
Calculated as:

Figure SMS_62
；
Figure SMS_62
;

然后从生成的

Figure SMS_63
、即功率谱密度序列中删除无效值，如果
Figure SMS_64
系列中没有有效值，则Lomb周期图拒绝原假设，XLPPL对临界点的计算无效。Then from the generated
Figure SMS_63
, that is, invalid values are deleted from the power spectrum density sequence. If
Figure SMS_64
If there are no valid values in the series, the Lomb periodogram rejects the null hypothesis and XLPPL's calculation of critical points is invalid.

进一步地，无效值包括以下情况：Furthermore, invalid values include the following:

Figure SMS_65
对应的频率是由随机序列引起的；给定的统计显著性水平下，
Figure SMS_66
小于由
Figure SMS_67
计算的临界值，其中
Figure SMS_68
表示给定的统计显著性水平
Figure SMS_69
下测定的临界值。
Figure SMS_65
The corresponding frequencies are caused by random sequences; at a given statistical significance level,
Figure SMS_66
Less than
Figure SMS_67
Calculate the critical value, where
Figure SMS_68
Indicates a given level of statistical significance
Figure SMS_69
The critical value determined below.

进一步地，S6中在预设窗口大小的数组或字符串上执行要求，滑动表示窗口按照预设方向移动，窗口大小是固定的或者变动的，数组是由

Figure SMS_70
值组成的
Figure SMS_71
，窗口大小为常数
Figure SMS_72
，窗口由
Figure SMS_73
开始，不断向后滑动，当窗口达到
Figure SMS_74
时停止，然后选择包含
Figure SMS_75
值最多的窗口作为最终预测区间。Further, in S6, the requirement is executed on an array or string of a preset window size, sliding means that the window moves in a preset direction, the window size is fixed or variable, and the array is composed of
Figure SMS_70
Values
Figure SMS_71
, the window size is a constant
Figure SMS_72
, the window consists of
Figure SMS_73
Start, keep sliding back, when the window reaches
Figure SMS_74
Stop when the
Figure SMS_75
The window with the most values is taken as the final prediction interval.

本发明的上述方案有如下的有益效果：The above scheme of the present invention has the following beneficial effects:

本发明提供的基于温度的发泡材料气泡破裂临界点预测的方法，将温度加入到LPPL模型中，得到一个融合温度与气泡体积数据的预测发泡材料气泡破裂临近点模型，使得该预测方法更符合现实情况，同时采用多种群遗传算法求非线性参数，进一步提高了模型的预测精确度；另外，采取了一种以区间估计替代点估计的方法，能有效克服点估计存在的随机性和分散性问题。The method for predicting the critical point of bubble rupture of foaming materials based on temperature provided by the present invention adds temperature into the LPPL model to obtain a model for predicting the near point of bubble rupture of foaming materials that integrates temperature and bubble volume data, so that the prediction method is more in line with the actual situation. At the same time, a multi-population genetic algorithm is used to calculate nonlinear parameters, which further improves the prediction accuracy of the model. In addition, a method of replacing point estimation with interval estimation is adopted, which can effectively overcome the randomness and dispersion problems existing in point estimation.

本发明的其它有益效果将在随后的具体实施方式部分予以详细说明。Other beneficial effects of the present invention will be described in detail in the subsequent specific implementation section.

附图说明BRIEF DESCRIPTION OF THE DRAWINGS

图1为本发明的步骤流程框架图；FIG. 1 is a flowchart of the steps of the present invention;

图2为本发明的多种群遗传算法流程框架图；FIG2 is a flowchart of a multi-population genetic algorithm of the present invention;

图3为本发明的滑动窗口法示例图；FIG3 is an example diagram of the sliding window method of the present invention;

图4为本发明的Lomb周期图验证气泡破裂临界区间；FIG4 is a Lomb period diagram of the present invention to verify the critical interval of bubble burst;

图5为本发明的气泡破裂预测区间内振荡的Lomb周期图。FIG. 5 is a Lomb period diagram of oscillations within the bubble burst prediction interval of the present invention.

具体实施方式DETAILED DESCRIPTION

以下通过特定的具体实例说明本公开的实施方式，本领域技术人员可由本说明书所揭露的内容轻易地了解本公开的其他优点与功效。显然，所描述的实施例仅仅是本公开一部分实施例，而不是全部的实施例。本公开还可以通过另外不同的具体实施方式加以实施或应用，本说明书中的各项细节也可以基于不同观点与应用，在没有背离本公开的精神下进行各种修饰或改变。需说明的是，在不冲突的情况下，以下实施例及实施例中的特征可以相互组合。基于本公开中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本公开保护的范围。The following describes the embodiments of the present disclosure through specific examples, and those skilled in the art can easily understand other advantages and effects of the present disclosure from the contents disclosed in this specification. Obviously, the described embodiments are only a part of the embodiments of the present disclosure, rather than all of the embodiments. The present disclosure can also be implemented or applied through other different specific embodiments, and the details in this specification can also be modified or changed in various ways based on different viewpoints and applications without departing from the spirit of the present disclosure. It should be noted that the following embodiments and features in the embodiments can be combined with each other without conflict. Based on the embodiments in the present disclosure, all other embodiments obtained by ordinary technicians in the field without making creative work are within the scope of protection of the present disclosure.

需要说明的是，下文描述在所附权利要求书的范围内的实施例的各种方面。应显而易见，本文中所描述的方面可体现于广泛多种形式中，且本文中所描述的任何特定结构及/或功能仅为说明性的。基于本公开，所属领域的技术人员应了解，本文中所描述的一个方面可与任何其它方面独立地实施，且可以各种方式组合这些方面中的两者或两者以上。举例来说，可使用本文中所阐述的任何数目个方面来实施设备及/或实践方法。另外，可使用除了本文中所阐述的方面中的一或多者之外的其它结构及/或功能性实施此设备及/或实践此方法。It should be noted that various aspects of the embodiments within the scope of the appended claims are described below. It should be apparent that the aspects described herein may be embodied in a wide variety of forms, and any specific structure and/or function described herein is merely illustrative. Based on the present disclosure, it should be understood by those skilled in the art that an aspect described herein may be implemented independently of any other aspect, and two or more of these aspects may be combined in various ways. For example, any number of aspects described herein may be used to implement the device and/or practice the method. In addition, other structures and/or functionalities other than one or more of the aspects described herein may be used to implement this device and/or practice this method.

还需要说明的是，以下实施例中所提供的图示仅以示意方式说明本公开的基本构想，图式中仅显示与本公开中有关的组件而非按照实际实施时的组件数目、形状及尺寸绘制，其实际实施时各组件的型态、数量及比例可为一种随意的改变，且其组件布局型态也可能更为复杂。另外，在以下描述中，提供具体细节是为了便于透彻理解实例。然而，所属领域的技术人员将理解，可在没有这些特定细节的情况下实践所述方面。It should also be noted that the illustrations provided in the following embodiments are only schematic illustrations of the basic concept of the present disclosure. The drawings only show components related to the present disclosure rather than being drawn according to the number, shape and size of components in actual implementation. The type, quantity and proportion of each component in actual implementation may be changed at will, and the component layout type may also be more complicated. In addition, in the following description, specific details are provided to facilitate a thorough understanding of the examples. However, those skilled in the art will understand that the aspects described can be practiced without these specific details.

如图1所示，本发明的实施例提供了一种基于温度的发泡材料气泡破裂临界点预测的方法，具体包括如下步骤：As shown in FIG1 , an embodiment of the present invention provides a method for predicting the critical point of bubble rupture of a foaming material based on temperature, which specifically includes the following steps:

S1，选择样本空间来预测未来时间范围内的气泡破裂临界点，通过提取气泡的面积、当量直径、几何中心、速度、加速度特征参数获取发泡材料的气泡体积数据，并将该数据代入到对数周期幂律（LPPL）模型中。S1, select the sample space to predict the critical point of bubble rupture in the future time range, obtain the bubble volume data of the foaming material by extracting the area, equivalent diameter, geometric center, velocity, and acceleration characteristic parameters of the bubble, and substitute the data into the logarithmic periodic power law (LPPL) model.

需要说明的是，样本空间的数据使用的是气泡体积，气泡体积的具体获取方法与背景技术中的公开文献一致，此处不再赘述。It should be noted that the data of the sample space uses the bubble volume, and the specific method for obtaining the bubble volume is consistent with the public literature in the background technology, which will not be repeated here.

S2，将温度变化的历史数据加入到对数周期幂律（LPPL）模型中，构建新对数周期幂律（XLPPL）模型。S2, the historical data of temperature change are added to the logarithmic periodic power law (LPPL) model to construct a new logarithmic periodic power law (XLPPL) model.

其中，发泡材料气泡破裂的对数周期幂律模型的形式如下：Among them, the logarithmic periodic power law model of bubble collapse of foaming materials is as follows:

Figure SMS_76
；
Figure SMS_76
;

其中，

Figure SMS_81
就是所求的气泡破裂点临界点的气泡体积，
Figure SMS_79
为气泡测量的初始时间，
Figure SMS_91
为气泡破裂的临界点时间，即气泡临近破裂的时间；
Figure SMS_80
为气泡加速度；
Figure SMS_90
为对数周期振动频率，
Figure SMS_82
为相位，
Figure SMS_87
都是振幅，
Figure SMS_83
对应于气泡的体积初始值，
Figure SMS_86
对应于气泡速度，
Figure SMS_77
为气泡增长前后的直径差。其中，
Figure SMS_93
表示达到气泡临近破裂的时间
Figure SMS_85
时，
Figure SMS_92
可能达到的值，且
Figure SMS_84
，
Figure SMS_88
代表着向上的加速，
Figure SMS_78
刻画了气泡体积序列的超指数特征，而
Figure SMS_89
描述了气泡体积的周期型震荡。in,
Figure SMS_81
is the bubble volume at the critical point of bubble rupture,
Figure SMS_79
is the initial time of bubble measurement,
Figure SMS_91
is the critical point time of bubble rupture, that is, the time when the bubble is about to rupture;
Figure SMS_80
is the bubble acceleration;
Figure SMS_90
is the logarithmic periodic vibration frequency,
Figure SMS_82
is the phase,
Figure SMS_87
are all amplitudes,
Figure SMS_83
Corresponding to the initial value of the volume of the bubble,
Figure SMS_86
corresponds to the bubble velocity,
Figure SMS_77
is the diameter difference before and after the bubble grows.
Figure SMS_93
Indicates the time when the bubble is about to burst
Figure SMS_85
hour,
Figure SMS_92
possible values, and
Figure SMS_84
,
Figure SMS_88
Represents upward acceleration.
Figure SMS_78
It describes the super-exponential characteristics of the bubble volume series, and
Figure SMS_89
Describes the periodic oscillations of the bubble volume.

在实际的拟合中，设定

Figure SMS_94
，
Figure SMS_95
及
Figure SMS_96
。该模型还可以简写为以下形式：In the actual fitting, we set
Figure SMS_94
,
Figure SMS_95
and
Figure SMS_96
The model can also be simplified as follows:

Figure SMS_97
；
Figure SMS_97
;

其中，

Figure SMS_98
，在LPPL模型中添加温度变化的历史数据，XLPPL模型可以简写为以下模式：in,
Figure SMS_98
, adding the historical data of temperature changes to the LPPL model, the XLPPL model can be simplified as follows:

Figure SMS_99
；
Figure SMS_99
;

其中，

Figure SMS_100
，
Figure SMS_101
与
Figure SMS_102
一样都是振幅且为线性参数，
Figure SMS_103
是温度变化的历史数据。in,
Figure SMS_100
,
Figure SMS_101
and
Figure SMS_102
They are both amplitude and linear parameters.
Figure SMS_103
It is the historical data of temperature change.

S3，采用多种群遗传算法（MPGA）估计XLPPL模型中的4个非线性参数。S3, Multi-population genetic algorithm (MPGA) is used to estimate the four nonlinear parameters in the XLPPL model.

同时如图2所示，S3具体包括如下步骤：As shown in FIG. 2 , S3 specifically includes the following steps:

S31，随机生成

Figure SMS_104
个初始种群。S31, randomly generated
Figure SMS_104
An initial population.

其中，每个种群中随机产生

Figure SMS_105
个染色体，这
Figure SMS_106
个染色体个体构成了一个种群，每个染色体表示由对数周期幂律模型的四个非线性参数组成的可行解。Among them, each population randomly generates
Figure SMS_105
Chromosomes, this
Figure SMS_106
The chromosome individuals constitute a population, and each chromosome represents a feasible solution consisting of four nonlinear parameters of the log-periodic power law model.

S32，计算适应度。S32, calculate fitness.

其中，适应度代表了个体在此环境中生存的可能性，一个个体的适应度越大，此个体被遗传到下一代的几率越大。多种群遗传算法通过计算

Figure SMS_107
时刻的气泡体积
Figure SMS_108
与XLPPL模型拟合结果之间的残差平方和(RSS)评估每个染色体（即四个非线性参数）的适应度值：Among them, fitness represents the possibility of an individual surviving in this environment. The greater the fitness of an individual, the greater the probability that the individual will be inherited to the next generation.
Figure SMS_107
Bubble volume at time
Figure SMS_108
The residual sum of squares (RSS) between the XLPPL model fitting results evaluates the fitness value of each chromosome (ie, four nonlinear parameters):

Figure SMS_111
其中，
Figure SMS_114
代表第
Figure SMS_116
个群体中第
Figure SMS_110
条染色体的残差平方和(RSS)；
Figure SMS_113
，
Figure SMS_115
，
Figure SMS_117
对应第
Figure SMS_109
种群的第
Figure SMS_112
条染色体。
Figure SMS_111
in,
Figure SMS_114
Representative
Figure SMS_116
In the group
Figure SMS_110
The residual sum of squares (RSS) of each chromosome;
Figure SMS_113
,
Figure SMS_115
,
Figure SMS_117
Corresponding to
Figure SMS_109
The population
Figure SMS_112
Chromosomes.

S33，选择挑选出本代本种群中的最优个体，使他们有较大概率被遗传到下一代中。S33, select the best individuals in this generation and this population so that they have a greater probability of being inherited to the next generation.

S34，在此代种群中个体基因交叉获得新的个体，从而得到新一代种群，新一代种群中的个体按概率遗传了父代中一部分的基因片段，保留了父代一部分特性。S34, in this generation of population, individual genes cross to obtain new individuals, thus obtaining a new generation of population. The individuals in the new generation of population inherit part of the gene fragments from the parent generation according to probability, and retain part of the characteristics of the parent generation.

S35，通过以一定的基因突变概率随机改变一个个体上某个基因片段，获得新的个体。在遗传算法中可以通过变异参数的设定，让基因片段突变概率增大，发生的位置增多。S35, by randomly changing a gene fragment on an individual with a certain gene mutation probability, a new individual is obtained. In the genetic algorithm, the mutation probability of the gene fragment can be increased and the number of locations where it occurs can be increased by setting the mutation parameters.

S36，将进化生成的子代种群重插入父代种群中，其插入原则可以选择为均匀随机插入，也可以选择基于个体适应度插入，基于个体适应度插入可以实现保留精英个体到下一代的效果。S36, reinsert the evolved offspring population into the parent population. The insertion principle can be selected as uniform random insertion or insertion based on individual fitness. Insertion based on individual fitness can achieve the effect of retaining elite individuals to the next generation.

S37，移民。S37, immigration.

用第

Figure SMS_118
个种群中适应度值最小
Figure SMS_119
的染色体代替第u+1个种群中适应度值最大
Figure SMS_120
的染色体，以将独立的多个种群联合成一个统一的整体。Use
Figure SMS_118
The fitness value is the smallest among the populations
Figure SMS_119
The chromosome with the largest fitness value in the u+1th population is replaced by
Figure SMS_120
chromosomes to unite multiple independent populations into a unified whole.

S38，如果新种群的最小适应度值

Figure SMS_121
小于上一次迭代过程的相应记录(即上一次迭代过程中该种群的最小适应度值)，则更新记录；否则，该种群的原始记录保持不变。所有种群最小适应度值
Figure SMS_122
和相应染色体的记录也采用相同的方式进行处理。如果所有种群的最小适应度值都没有发生改变，或者达到迭代次数上限，那么算法终止，最后一次迭代结束之后所有种群的最小适应度值及其相应染色体
Figure SMS_123
是多种群遗传算法的输出。多种群遗传算法优化非线性参数
Figure SMS_124
的具体流程如图2所示。S38, if the minimum fitness value of the new population
Figure SMS_121
If the value is less than the corresponding record of the previous iteration (i.e. the minimum fitness value of the population in the previous iteration), the record is updated; otherwise, the original record of the population remains unchanged.
Figure SMS_122
The records of the corresponding chromosomes are processed in the same way. If the minimum fitness value of all populations does not change, or the upper limit of the number of iterations is reached, the algorithm terminates. After the last iteration, the minimum fitness value of all populations and their corresponding chromosomes are
Figure SMS_123
is the output of the multi-population genetic algorithm. Multi-population genetic algorithm optimizes nonlinear parameters
Figure SMS_124
The specific process is shown in Figure 2.

S4，采用最小二乘法求得XLPPL模型中的4个线性参数。S4, the four linear parameters in the XLPPL model are obtained using the least squares method.

Figure SMS_125
；
Figure SMS_125
;

Figure SMS_126
；
Figure SMS_126
;

Figure SMS_127
；
Figure SMS_127
;

其中，

Figure SMS_128
，
Figure SMS_129
为时间单位，
Figure SMS_130
为总时间单位，则线性参数可使用以下等式计算所得：in,
Figure SMS_128
,
Figure SMS_129
is the time unit,
Figure SMS_130
is the total time unit, the linear parameter can be calculated using the following equation:

Figure SMS_131
Figure SMS_131

S5，进行Lomb周期图分析，以对XLPPL模型获得的

Figure SMS_132
值进行统计检验，经过Lomb周期图分析统计验证的转折点被认为是XLPPL模型的气泡破裂点。S5, Lomb periodogram analysis was performed to analyze the
Figure SMS_132
The values were statistically tested, and the turning points statistically verified by Lomb periodogram analysis were considered to be the bubble bursting points of the XLPPL model.

运用Lomb周期图测试多种群遗传算法得到的XLPPL模型的周期性频率

Figure SMS_133
和
Figure SMS_134
是否是持续的，以确定该模型拟合的曲线和临界点是否有效。Using Lomb periodogram to test the periodic frequency of XLPPL model obtained by multi-population genetic algorithm
Figure SMS_133
and
Figure SMS_134
Whether it is continuous to determine whether the curve and critical point fitted by the model are valid.

Lomb周期图首先预设频率序列

Figure SMS_135
，其中，
Figure SMS_136
是预先给定频率序列的长度；对于给定的频率
Figure SMS_137
，功率谱密度
Figure SMS_138
可通过Lomb周期图分析计算如下：The Lomb periodogram first presets the frequency sequence
Figure SMS_135
,in,
Figure SMS_136
is the length of a given frequency sequence; for a given frequency
Figure SMS_137
, power spectral density
Figure SMS_138
The calculation can be done through Lomb periodogram analysis as follows:

Figure SMS_139
；
Figure SMS_139
;

其中，

Figure SMS_140
，表示对数体积的周期型震荡，
Figure SMS_141
表示为
Figure SMS_142
的均值，时间偏移
Figure SMS_143
计算为：in,
Figure SMS_140
, represents the periodic oscillation of the logarithmic volume,
Figure SMS_141
Expressed as
Figure SMS_142
The mean of the time offset
Figure SMS_143
Calculated as:

Figure SMS_144
；
Figure SMS_144
;

然后从生成的

Figure SMS_145
、即功率谱密度序列中删除无效值，如果
Figure SMS_146
系列中没有有效值，则Lomb周期图拒绝原假设，XLPPL对临界点的计算无效。Then from the generated
Figure SMS_145
, that is, invalid values are deleted from the power spectrum density sequence. If
Figure SMS_146
If there are no valid values in the series, the Lomb periodogram rejects the null hypothesis and XLPPL's calculation of critical points is invalid.

其中，无效值包括以下情况：Invalid values include the following:

Figure SMS_147
对应的频率是由随机序列引起的；给定的统计显著性水平下，
Figure SMS_148
小于由
Figure SMS_149
计算的临界值，其中
Figure SMS_150
表示给定的统计显著性水平
Figure SMS_151
下测定的临界值。
Figure SMS_147
The corresponding frequencies are caused by random sequences; at a given statistical significance level,
Figure SMS_148
Less than
Figure SMS_149
Calculate the critical value, where
Figure SMS_150
Indicates a given level of statistical significance
Figure SMS_151
The critical value determined below.

由Lomb周期图分析统计验证的临界点被认为是发泡材料气泡破裂临界点。The critical point statistically verified by Lomb periodogram analysis is considered to be the critical point of bubble rupture of the foaming material.

S6，采用滑动窗口法根据所获得

Figure SMS_152
值预测最终区间。S6, using the sliding window method according to the obtained
Figure SMS_152
The final interval of value prediction.

Lomb周期图分析后所获得的临界点并不是一个而是多个，滑动窗口法便是建立在多个临界点上，从第一个临界点开始，窗口向后移动，直到有一个

Figure SMS_153
值减15位置，选择窗口内
Figure SMS_154
值最多的区间为最终预测区间。The critical points obtained after Lomb periodogram analysis are not one but multiple. The sliding window method is based on multiple critical points. Starting from the first critical point, the window moves backward until there is one.
Figure SMS_153
Value minus 15, select the window
Figure SMS_154
The interval with the most values is the final prediction interval.

同时如图3所示，滑动窗口法指的是在给特定窗口大小的数组或字符串上执行要求的操作，其中滑动指的是该窗口是按照一定方向移动，窗口大小可以是固定的，也可以是变动的。在该方法中数组是由

Figure SMS_155
值组成的
Figure SMS_156
，窗口大小为15，窗口由
Figure SMS_157
开始，不断向后滑动，当窗口达到
Figure SMS_158
时停止，然后选择包含
Figure SMS_159
值最多的窗口为最终预测区间。以图3为例，在该图中窗口大小为15，由于最后一个窗口包含的
Figure SMS_160
值最多，所以选择最后一个窗口为预测区间。As shown in Figure 3, the sliding window method refers to performing the required operation on an array or string of a specific window size, where sliding means that the window moves in a certain direction, and the window size can be fixed or variable. In this method, the array is composed of
Figure SMS_155
Values
Figure SMS_156
, the window size is 15, and the window consists of
Figure SMS_157
Start, keep sliding back, when the window reaches
Figure SMS_158
Stop when the
Figure SMS_159
The window with the most values is the final prediction interval. Taking Figure 3 as an example, the window size in this figure is 15.
Figure SMS_160
The last window has the most values, so the last window is selected as the prediction interval.

最终，根据气泡破裂临界点确定气泡破裂区间，获得最有可能的气泡破裂区间，以此进行优化提高发泡材料的机械性能。Finally, the bubble rupture interval is determined according to the critical point of bubble rupture, and the most likely bubble rupture interval is obtained, so as to optimize and improve the mechanical properties of the foaming material.

以下通过具体案例进一步说明本方法的效果，选用的是聚合物微孔发泡材料，是特指泡孔尺寸小于100μm，孔密度大于1.0×106个/cm3的聚合物多孔发泡材料。主要关注的一个过程是希望在气泡消失之前（即模具被填充之前）检查流场的行为和气泡的形状。特别是，提前知道气泡消失点的位置可能很重要，以防止模具中出现不需要的气泡。当气泡接近破裂点时，观察气泡在生长运动过程中的尺寸变化，发现气泡在孔口生长过程中由于受到表面张力作用而呈半球形，随着气体不断注入，气泡向上拉伸，颈部开始向内凹陷，最终体积胀大到一定值后脱离孔口。气泡在上升过程中速度呈现出先增大后趋于稳定的现象，同时气泡由起始的圆球形发展为椭球形，纵横比明显减小。气泡急剧增大的生长过程的变化对应于临界行为，是对数周期震荡和幂律增长的典型特征。The following is a specific example to further illustrate the effect of this method. The polymer microporous foam material is selected, which specifically refers to a polymer porous foam material with a pore size of less than 100μm and a pore density of more than 1.0×106/cm3 . One of the main concerns is to check the behavior of the flow field and the shape of the bubble before the bubble disappears (that is, before the mold is filled). In particular, it may be important to know the location of the bubble vanishing point in advance to prevent the appearance of unwanted bubbles in the mold. When the bubble approaches the rupture point, the size change of the bubble during the growth movement is observed. It is found that the bubble is hemispherical due to the surface tension during the growth process of the orifice. As the gas is continuously injected, the bubble stretches upward, the neck begins to sink inward, and finally the volume expands to a certain value and then leaves the orifice. The speed of the bubble increases first and then stabilizes during the rising process. At the same time, the bubble develops from the initial spherical shape to an ellipsoidal shape, and the aspect ratio is significantly reduced. The change in the growth process of the bubble's rapid growth corresponds to the critical behavior, which is a typical feature of logarithmic periodic oscillation and power law growth.

随着温度的不断提高，发泡塑料制品的内部会形成气泡，分别记录不同直径气泡的面积、当量直径、速度等特征参数，并记录制品内温度的变化情况。As the temperature continues to rise, bubbles will form inside the foamed plastic product. The characteristic parameters such as the area, equivalent diameter, and speed of bubbles of different diameters are recorded separately, and the temperature changes inside the product are recorded.

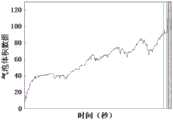
将温度变化的历史数据加入到LPPL模型中，构建XLPPL模型，采用MPGA算法估计XLPPL模型中的非线性参数，不断对比新种群与上一次记录种群的最小适应度，当新种群的最小适应度小于上一次记录种群的最小适应度时更新记录，当所有种群的最小适应度不再更新或达到迭代上限时，MPGA算法终止，得到4个非线性参数。将4个非线性参数代入XLPPL模型，采用最小二乘法估计XLPPL模型中的4个线性参数，然后通过Lomb周期图分析统计验证得到发泡材料气泡破裂临界点，运用滑动窗口算法根据气泡破裂临界点求得气泡破裂临界区间。气泡破裂临界区间如图4所示，数据模拟出来的各参数的具体数值分别为

Figure SMS_163
Figure SMS_164
，
Figure SMS_166
，
Figure SMS_162
，
Figure SMS_165
，
Figure SMS_167
，
Figure SMS_168
，
Figure SMS_161
，因此最终预测区间为[305,320]秒。The historical data of temperature changes are added to the LPPL model to construct the XLPPL model. The MPGA algorithm is used to estimate the nonlinear parameters in the XLPPL model. The minimum fitness of the new population is continuously compared with the minimum fitness of the last recorded population. When the minimum fitness of the new population is less than the minimum fitness of the last recorded population, the record is updated. When the minimum fitness of all populations is no longer updated or reaches the iteration limit, the MPGA algorithm terminates and four nonlinear parameters are obtained. Substitute the four nonlinear parameters into the XLPPL model, use the least squares method to estimate the four linear parameters in the XLPPL model, and then analyze and statistically verify the critical point of bubble rupture of the foaming material through Lomb periodogram analysis. The sliding window algorithm is used to obtain the critical interval of bubble rupture based on the critical point of bubble rupture. The critical interval of bubble rupture is shown in Figure 4. The specific values of each parameter simulated by the data are:
Figure SMS_163
Figure SMS_164
,
Figure SMS_166
,
Figure SMS_162
,
Figure SMS_165
,
Figure SMS_167
,
Figure SMS_168
,
Figure SMS_161
, so the final prediction interval is [305,320] seconds.

气泡破裂的最终崩溃点是对数周期振荡的高潮，从图5中可以看到在该预测区间内振荡的Lomb周期图有非常显著的频率峰值，峰值代表着大气泡破裂发生前的小气泡挤压活动异常明显，即将发生大的破裂。通过该方法，可以提前获知可能的气泡破裂临界点并采取措施避免，提高发泡材料的机械性能。The final collapse point of bubble rupture is the climax of logarithmic periodic oscillation. From Figure 5, we can see that the Lomb periodic diagram oscillating in the prediction interval has a very significant frequency peak. The peak represents that the small bubble extrusion activity before the large bubble rupture is abnormally obvious, and a large rupture is about to occur. Through this method, the possible critical point of bubble rupture can be known in advance and measures can be taken to avoid it, thereby improving the mechanical properties of the foamed material.

以上所述是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明所述原理的前提下，还可以作出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。The above is a preferred embodiment of the present invention. It should be pointed out that for ordinary technicians in this technical field, several improvements and modifications can be made without departing from the principles of the present invention. These improvements and modifications should also be regarded as the scope of protection of the present invention.

Claims (9)

Translated fromChinese
1.一种基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，包括如下步骤：1. A method for predicting the critical point of bubble rupture of a foaming material based on temperature, characterized in that it comprises the following steps:S1，选择样本空间来预测未来时间范围内的气泡破裂临界点，通过提取气泡的面积、当量直径、几何中心、速度、加速度特征参数获取发泡材料的气泡体积数据，并代入到对数周期幂律模型中；S1, select sample space to predict the critical point of bubble rupture in the future time range, obtain the bubble volume data of the foaming material by extracting the bubble area, equivalent diameter, geometric center, velocity, and acceleration characteristic parameters, and substitute them into the logarithmic periodic power law model;S2，将温度变化的历史数据加入到对数周期幂律模型中，构建新对数周期幂律模型；S2, adding the historical data of temperature change into the logarithmic periodic power law model to construct a new logarithmic periodic power law model;S3，采用多种群遗传算法估计新对数周期幂律模型中的全部非线性参数；S3, using a multi-population genetic algorithm to estimate all nonlinear parameters in the new log-periodic power law model;其中，发泡材料气泡破裂的对数周期幂律模型的形式如下：Among them, the logarithmic periodic power law model of bubble collapse of foaming materials is as follows:
Figure QLYQS_1
；
Figure QLYQS_1
;其中，
Figure QLYQS_3
为所求的气泡破裂点临界点的气泡体积，
Figure QLYQS_7
为气泡测量的初始时间，
Figure QLYQS_10
为气泡破裂的临界点时间，即气泡临近破裂的时间；
Figure QLYQS_4
为气泡加速度；
Figure QLYQS_6
为对数周期振动频率，
Figure QLYQS_9
为相位，
Figure QLYQS_11
都是振幅，
Figure QLYQS_2
对应于气泡的体积初始值，
Figure QLYQS_5
对应于气泡速度，
Figure QLYQS_8
为气泡增长前后的直径差；in,
Figure QLYQS_3
is the bubble volume at the critical point of bubble collapse,
Figure QLYQS_7
is the initial time of bubble measurement,
Figure QLYQS_10
is the critical point time of bubble rupture, that is, the time when the bubble is about to rupture;
Figure QLYQS_4
is the bubble acceleration;
Figure QLYQS_6
is the logarithmic periodic vibration frequency,
Figure QLYQS_9
is the phase,
Figure QLYQS_11
are all amplitudes,
Figure QLYQS_2
Corresponding to the initial value of the volume of the bubble,
Figure QLYQS_5
corresponds to the bubble velocity,
Figure QLYQS_8
is the diameter difference before and after the bubble grows;设定
Figure QLYQS_12
，
Figure QLYQS_13
及
Figure QLYQS_14
，对数周期幂律模型简写为以下形式：set up
Figure QLYQS_12
,
Figure QLYQS_13
and
Figure QLYQS_14
, the log-periodic power law model can be simplified as follows:
Figure QLYQS_15
；
Figure QLYQS_15
;其中，
Figure QLYQS_16
，在对数周期幂律模型中添加温度变化的历史数据，新对数周期幂律模型简写为以下模式：in,
Figure QLYQS_16
, adding the historical data of temperature changes to the logarithmic periodic power law model, the new logarithmic periodic power law model is abbreviated as follows:
Figure QLYQS_17
；
Figure QLYQS_17
;其中，
Figure QLYQS_18
，
Figure QLYQS_19
为振幅且为线性参数，
Figure QLYQS_20
是温度变化的历史数据；in,
Figure QLYQS_18
,
Figure QLYQS_19
is the amplitude and is a linear parameter,
Figure QLYQS_20
It is the historical data of temperature change;S4，采用最小二乘法求得新对数周期幂律模型中的全部线性参数；S4, using the least squares method to obtain all linear parameters in the new log-periodic power law model;S5，进行Lomb周期图分析，以对新对数周期幂律模型获得的
Figure QLYQS_21
值进行统计检验，通过Lomb周期图统计验证的转折点是新对数周期幂律模型的气泡破裂点；S5, Lomb periodogram analysis was performed to obtain the new logarithmic periodic power law model
Figure QLYQS_21
The values were statistically tested, and the turning point verified by Lomb periodogram statistics is the bubble bursting point of the new logarithmic periodic power law model;S6，采用滑动窗口法根据所获得
Figure QLYQS_22
值预测最终区间。S6, using the sliding window method according to the obtained
Figure QLYQS_22
The final interval of value prediction.2.根据权利要求1所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S3具体包括如下子步骤：2. The method for predicting the critical point of bubble rupture of a foaming material based on temperature according to claim 1, characterized in that S3 specifically comprises the following sub-steps:S31，随机生成
Figure QLYQS_23
个初始种群，每个种群中随机产生
Figure QLYQS_24
个染色体，这些染色体个体构成了一个种群，每个染色体表示由对数周期幂律模型的全部非线性参数组成的可行解；S31, randomly generated
Figure QLYQS_23
Initial populations, each of which is randomly generated
Figure QLYQS_24
chromosomes, these chromosome individuals constitute a population, and each chromosome represents a feasible solution consisting of all nonlinear parameters of the log-periodic power law model;S32，计算适应度，适应度代表个体在此环境中生存的可能性，适应度越大表示此个体被遗传到下一代的几率越大；S32, calculate the fitness, which represents the possibility of an individual surviving in this environment. The greater the fitness, the greater the probability that the individual will be inherited to the next generation;S33，挑选出本代本种群中的最优个体；S33, select the best individual in this generation and this population;S34，在此代种群中个体基因交叉获得新的个体，得到新一代种群，新一代种群中的个体按概率遗传了父代中部分的基因片段，保留了父代的部分特性；S34, in this generation of population, the genes of individuals are crossed to obtain new individuals, and a new generation of population is obtained. The individuals in the new generation of population inherit part of the gene fragments of the parent generation according to probability, and retain some characteristics of the parent generation;S35，通过预设的基因突变概率随机改变个体上某个基因片段，获得新的个体；S35, randomly changing a gene fragment on an individual through a preset gene mutation probability to obtain a new individual;S36，将进化生成的子代种群重插入父代种群中；S36, reinserting the evolved offspring population into the parent population;S37，移民，将独立的多个种群联合成一个统一的整体；S37, immigration, uniting separate populations into a unified whole;S38，迭代计算并判断，输出最终染色体，获得优化的全部非线性参数。S38, iteratively calculate and judge, output the final chromosome, and obtain all optimized nonlinear parameters.3.根据权利要求2所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S32中多种群遗传算法通过计算
Figure QLYQS_25
时刻的气泡体积
Figure QLYQS_26
与新对数周期幂律模型拟合结果之间的残差平方和评估每个染色体的适应度值：3. The method for predicting the critical point of bubble burst of a foaming material based on temperature according to claim 2, characterized in that the multi-population genetic algorithm in S32 calculates
Figure QLYQS_25
Bubble volume at time
Figure QLYQS_26
The fitness value of each chromosome is evaluated by the residual sum of squares between the results of fitting the new logarithmic periodic power law model:
Figure QLYQS_27
其中，
Figure QLYQS_28
代表第
Figure QLYQS_29
个群体中第
Figure QLYQS_30
条染色体的残差平方和；
Figure QLYQS_31
，
Figure QLYQS_32
，
Figure QLYQS_27
in,
Figure QLYQS_28
Representative
Figure QLYQS_29
In the group
Figure QLYQS_30
The residual sum of squares of chromosomes;
Figure QLYQS_31
,
Figure QLYQS_32
,
Figure QLYQS_33
对应第
Figure QLYQS_34
个种群的第
Figure QLYQS_35
条染色体。
Figure QLYQS_33
Corresponding to
Figure QLYQS_34
The first
Figure QLYQS_35
Chromosomes.4.根据权利要求3所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S37中用第
Figure QLYQS_36
个种群中适应度值最小
Figure QLYQS_37
的染色体代替第
Figure QLYQS_38
个种群中适应度值最大
Figure QLYQS_39
的染色体，以将独立的多个种群联合成一个统一的整体。4. The method for predicting the critical point of bubble collapse of a foaming material based on temperature according to claim 3, characterized in that in S37,
Figure QLYQS_36
The fitness value is the smallest among the populations
Figure QLYQS_37
Chromosomes replace
Figure QLYQS_38
The fitness value is the largest in the population
Figure QLYQS_39
chromosomes to unite multiple independent populations into a unified whole.5.根据权利要求4所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S38中如果新种群的最小适应度值
Figure QLYQS_40
小于上一次迭代过程中该种群的最小适应度值，则更新记录；否则，该种群的原始记录保持不变；如果所有种群的最小适应度值都没有发生改变，或者达到迭代次数上限，那么计算终止，最后一次迭代结束之后所有种群的最小适应度值及其相应染色体是多种群遗传算法的输出。5. The method for predicting the critical point of bubble burst of a foaming material based on temperature according to claim 4, characterized in that in S38, if the minimum fitness value of the new population is
Figure QLYQS_40
If the minimum fitness value of the population is less than the minimum fitness value of the population in the previous iteration, the record is updated; otherwise, the original record of the population remains unchanged; if the minimum fitness value of all populations has not changed, or the upper limit of the number of iterations is reached, the calculation is terminated. After the last iteration, the minimum fitness value of all populations and their corresponding chromosomes are the output of the multi-population genetic algorithm.6.根据权利要求5所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S4中6. The method for predicting the critical point of bubble rupture of a foaming material based on temperature according to claim 5, characterized in that in S4
Figure QLYQS_41
；
Figure QLYQS_41
;
Figure QLYQS_42
；
Figure QLYQS_42
;
Figure QLYQS_43
；
Figure QLYQS_43
;其中，
Figure QLYQS_44
，
Figure QLYQS_45
为时间单位，
Figure QLYQS_46
为总时间单位，新对数周期幂律模型中的全部线性参数使用以下等式计算求得：in,
Figure QLYQS_44
,
Figure QLYQS_45
is the time unit,
Figure QLYQS_46
is the total time unit, and all linear parameters in the new logarithmic periodic power law model are calculated using the following equations:
Figure QLYQS_47
。
Figure QLYQS_47
.7.根据权利要求6所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S5中运用Lomb周期图测试多种群遗传算法得到的新对数周期幂律模型模型的周期性频率
Figure QLYQS_48
和
Figure QLYQS_49
是否是持续的，以确定该模型拟合的曲线和临界点是否有效；7. The method for predicting the critical point of bubble rupture of a foaming material based on temperature according to claim 6, characterized in that the periodic frequency of the new logarithmic periodic power law model obtained by the multi-population genetic algorithm is tested by using the Lomb periodogram in S5
Figure QLYQS_48
and
Figure QLYQS_49
Is it continuous, to determine whether the curve and critical point fitted by the model are valid;Lomb周期图首先预设频率序列
Figure QLYQS_50
，其中，N是预先给定频率序列的长度；对于给定的频率
Figure QLYQS_51
，功率谱密度
Figure QLYQS_52
通过Lomb周期图分析计算如下：The Lomb periodogram first presets the frequency sequence
Figure QLYQS_50
, where N is the length of the pre-given frequency sequence; for a given frequency
Figure QLYQS_51
, power spectral density
Figure QLYQS_52
The calculation is performed through Lomb periodogram analysis as follows:
Figure QLYQS_53
其中，
Figure QLYQS_54
，表示对数体积的周期型震荡，
Figure QLYQS_55
表示为
Figure QLYQS_56
的均值，时间偏移
Figure QLYQS_57
计算为：
Figure QLYQS_53
in,
Figure QLYQS_54
, represents the periodic oscillation of the logarithmic volume,
Figure QLYQS_55
Expressed as
Figure QLYQS_56
The mean value, time offset
Figure QLYQS_57
Calculated as:
Figure QLYQS_58
；
Figure QLYQS_58
;然后从生成的
Figure QLYQS_59
中删除无效值，如果
Figure QLYQS_60
系列中没有有效值，则Lomb周期图拒绝原假设，新对数周期幂律模型对临界点的计算无效，
Figure QLYQS_61
为功率谱密度序列。Then from the generated
Figure QLYQS_59
Remove invalid values if
Figure QLYQS_60
If there is no valid value in the series, the Lomb periodogram rejects the null hypothesis, and the new logarithmic periodic power law model is invalid for the calculation of critical points.
Figure QLYQS_61
is the power spectral density sequence.8.根据权利要求7所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，无效值包括以下情况：8. The method for predicting the critical point of bubble rupture of a foaming material based on temperature according to claim 7, wherein the invalid value includes the following situations:
Figure QLYQS_62
对应的频率是由随机序列引起的；给定的统计显著性水平下，
Figure QLYQS_63
小于由
Figure QLYQS_64
计算的临界值，其中
Figure QLYQS_65
表示给定的统计显著性水平
Figure QLYQS_66
下测定的临界值。
Figure QLYQS_62
The corresponding frequencies are caused by random sequences; at a given statistical significance level,
Figure QLYQS_63
Less than
Figure QLYQS_64
Calculate the critical value, where
Figure QLYQS_65
Indicates a given level of statistical significance
Figure QLYQS_66
The critical value determined below.9.根据权利要求1所述的基于温度的发泡材料气泡破裂临界点预测的方法，其特征在于，S6中在预设窗口大小的数组或字符串上执行要求，滑动表示窗口按照预设方向移动，数组是由
Figure QLYQS_67
值组成的
Figure QLYQS_68
，窗口大小为常数F，窗口由
Figure QLYQS_69
开始，不断向后滑动，当窗口达到
Figure QLYQS_70
时停止，然后选择包含
Figure QLYQS_71
值最多的窗口作为最终预测区间。9. The method for predicting the critical point of bubble rupture of a foaming material based on temperature according to claim 1, characterized in that in S6, the requirement is executed on an array or a string of a preset window size, the sliding indicates that the window moves in a preset direction, and the array is composed of
Figure QLYQS_67
Values
Figure QLYQS_68
, the window size is a constant F, and the window is
Figure QLYQS_69
Start, keep sliding back, when the window reaches
Figure QLYQS_70
Stop when the
Figure QLYQS_71
The window with the most values is taken as the final prediction interval.
CN202310391747.3A2023-04-132023-04-13Method for predicting bubble collapse critical point of foaming material based on temperatureActiveCN116108763B (en)

Priority Applications (1)

Application NumberPriority DateFiling DateTitle
CN202310391747.3ACN116108763B (en)2023-04-132023-04-13Method for predicting bubble collapse critical point of foaming material based on temperature

Applications Claiming Priority (1)

Application NumberPriority DateFiling DateTitle
CN202310391747.3ACN116108763B (en)2023-04-132023-04-13Method for predicting bubble collapse critical point of foaming material based on temperature

Publications (2)

Publication NumberPublication Date
CN116108763Atrue CN116108763A (en)2023-05-12
CN116108763B CN116108763B (en)2023-06-27

Family

ID=86261953

Family Applications (1)

Application NumberTitlePriority DateFiling Date
CN202310391747.3AActiveCN116108763B (en)2023-04-132023-04-13Method for predicting bubble collapse critical point of foaming material based on temperature

Country Status (1)

CountryLink
CN (1)CN116108763B (en)

Citations (7)

* Cited by examiner, † Cited by third party
Publication numberPriority datePublication dateAssigneeTitle
CN103282417A (en)*2011-01-072013-09-04埃克森美孚化学专利公司Foamable thermoplastic reactor blends and foam article therefrom
CN106584742A (en)*2016-12-232017-04-26齐鲁工业大学Method for preparing foaming buffer packing material
US20170305040A1 (en)*2016-04-262017-10-26Gn Hearing A/SCustom elastomeric earmold with secondary material infusion
CN108345956A (en)*2017-12-062018-07-31太原理工大学Time series data logarithm period power law prediction technique based on SAX representations
WO2020063690A1 (en)*2018-09-252020-04-02新智数字科技有限公司Electrical power system prediction method and apparatus
CN114555316A (en)*2019-10-182022-05-27马特利艾斯有限责任公司 Method for making a product of a multi-gradient foamed polymer material
CN114818519A (en)*2022-06-302022-07-29湖南工商大学Method, system and computer readable medium for predicting bubble collapse of foamed material

Patent Citations (7)

* Cited by examiner, † Cited by third party
Publication numberPriority datePublication dateAssigneeTitle
CN103282417A (en)*2011-01-072013-09-04埃克森美孚化学专利公司Foamable thermoplastic reactor blends and foam article therefrom
US20170305040A1 (en)*2016-04-262017-10-26Gn Hearing A/SCustom elastomeric earmold with secondary material infusion
CN106584742A (en)*2016-12-232017-04-26齐鲁工业大学Method for preparing foaming buffer packing material
CN108345956A (en)*2017-12-062018-07-31太原理工大学Time series data logarithm period power law prediction technique based on SAX representations
WO2020063690A1 (en)*2018-09-252020-04-02新智数字科技有限公司Electrical power system prediction method and apparatus
CN114555316A (en)*2019-10-182022-05-27马特利艾斯有限责任公司 Method for making a product of a multi-gradient foamed polymer material
CN114818519A (en)*2022-06-302022-07-29湖南工商大学Method, system and computer readable medium for predicting bubble collapse of foamed material

Non-Patent Citations (1)

* Cited by examiner, † Cited by third party
Title
姚婷等: "润滑油抗泡沫添加剂", 《化工时刊》, vol. 29, no. 11*

Also Published As

Publication numberPublication date
CN116108763B (en)2023-06-27

Similar Documents

PublicationPublication DateTitle
CN112703720B (en)Default filter setting system and method for device control applications
CN108564235B (en)A kind of improved FOA-BPNN exit time prediction technique
CN115276177A (en)Energy storage battery charging and discharging power control method and device and battery control system
CN102938869B (en)Before utilizing, resonant cavity realizes the method for little back cavity micro speaker system LF-response
CN116108763A (en)Method for predicting bubble collapse critical point of foaming material based on temperature
CN111950167A (en) A kind of polylactic acid composite material model construction and performance prediction method
CN117574690B (en)Biochar preparation analysis method based on negative carbon emission and related device
CN115228511A (en)Rapid temperature change method of ultralow temperature test box
CN107038306A (en)A kind of optimal Latin hypercube experimental design method based on self-adapted genetic algorithm
Chang et al.Numerical analysis of circular straight mufflers equipped with three chambers at high-order-modes
CN108170947B (en)Method for acquiring novel lattice structure based on firefly algorithm
Sotta et al.Monte Carlo simulation of a grafted polymer chain confined in a tube
CN118350293B (en) Design method and device of superstructure
CN119648081A (en) A production and distribution optimization method based on improved genetic algorithm
CN114818519B (en) Method, system and computer readable medium for predicting bubble collapse of foamed materials
CN117494405A (en) An improved gradient descent hydrological model parameter optimization method
CN117034500A (en)Method, system, equipment and storage medium for designing multidimensional resonant cavity type sound absorber
CN116361711A (en) Vehicle carbon dioxide real-time emission prediction method, device, equipment and storage medium
CN114329702B (en)High-stability method and device for calibrating and designing reaction spectrum based on improved differential evolution algorithm
Jiang et al.Optimization of process parameters for biological 3D printing forming based on BP neural network and genetic algorithm
CN103136390B (en)A kind of parameter optimization method of metamaterial modular construction and device
Pilát et al.General tuning of weights in MOEA/D
CN103164554A (en)Method for determining metamaterial unit structure
CN112084596A (en) An intelligent recommendation system and recommendation method for structural parameters of laminates
Aguirre et al.Adaptive∈-ranking on MNK-Landscapes

Legal Events

DateCodeTitleDescription
PB01Publication
PB01Publication
SE01Entry into force of request for substantive examination
SE01Entry into force of request for substantive examination
GR01Patent grant
GR01Patent grant
[8]ページ先頭
©2009-2025 Movatter.jp