CN114741657A - Fixed time algebraic parameter estimation algorithm of Chua circuit system - Google Patents

Abstract

The invention discloses a fixed time algebraic parameter estimation algorithm of a Chua circuit system, which is used for predicting and outputting a fixed time algebraic parameter based on a constructed fixed time algebraic parameter estimation algorithm; constructing a fixed time algebraic parameter estimation algorithm: establishing a nonlinear mathematical model according to the Chua circuit system; determining a kernel function by using a Volterra integral operator; determining the stability of the fixed time; and constructing and obtaining a fixed time algebraic parameter estimation algorithm according to the kernel function and the nonlinear mathematical model. The invention can realize the accurate estimation of the parameters in the fixed time which does not depend on the initial value of the system under the condition that only the output signal is known; by skillfully selecting the kernel function in the Volterra integral operator, the influence of the initial value of the system can be effectively eliminated, and the calculation of the output derivative of the Chua circuit system is avoided; different from the traditional adaptive parameter estimation algorithm, the algebraic parameter estimation algorithm provided by the invention can realize the rapid and accurate estimation of parameters.

Description

Translated fromChinese

Chua电路系统的固定时间代数参数估计算法A Fixed-Time Algebraic Parameter Estimation Algorithm for Chua Circuit Systems

技术领域technical field

本发明涉及Chua电路系统的固定时间代数参数估计算法，属于Chua电路系统参数估计技术领域。The invention relates to a fixed-time algebraic parameter estimation algorithm of a Chua circuit system, and belongs to the technical field of parameter estimation of a Chua circuit system.

背景技术Background technique

混沌现象作为微分动力系统中十分重要的非线性动力学现象,因其在安全通信、激光系统、电子化学和神经生理学等领域的应用,受到学者们的广泛关注。自混沌学的发展逐渐步入正轨以来,人们一直尝试用肉眼可见的方法去观察混沌这一令人捉摸不透的动力学现象。由此,电学中非线性电路的研究逐渐进入人们的眼球,同时成为揭开分支与混沌机理过程中的重要研究课题。关于非线性电路中混沌现象的研究有三十年以上的历史,在研究者们的不懈努力下,许多以混沌机理研究为目的的电路被构造出来。同时,研究者们还对一部分实用电路中产生的混沌现象进行了密切研究。Chaos, as a very important nonlinear dynamical phenomenon in differential dynamical systems, has received extensive attention from scholars due to its applications in secure communications, laser systems, electronic chemistry and neurophysiology. Since the development of chaos theory has been on the right track, people have been trying to observe the elusive dynamic phenomenon of chaos with the naked eye. As a result, the study of nonlinear circuits in electricity has gradually entered people's attention, and has become an important research topic in the process of uncovering the mechanism of branching and chaos. The research on the chaotic phenomenon in nonlinear circuits has a history of more than 30 years. With the unremitting efforts of researchers, many circuits have been constructed for the purpose of studying the chaotic mechanism. At the same time, researchers have also closely studied the chaotic phenomenon generated in some practical circuits.

1983年,加利福尼亚大学的Leon Chua教授设计出了第一个可以通过实验模拟混沌现象发生的Chua电路。这是一个具有里程碑意义的设计,它开辟了混沌行为应用于现实世界的新道路。Chua电路是一个可以产生双涡卷混沌的三阶自治电路,通过赋予一个分段线性负电阻不同形式的参数组合,从而产生尤为丰富的分支与混沌行为。Chua电路是能引起混沌现象出现的自治电路中构造最为简单的一个,任何在三阶自治系统中产生的混沌现象,都可以通过Chua电路系统模拟展现出来。Shilnikov定理中对Chua系统产生的混沌形态做出了严格证明，基于此,人们得以通过电路这一形式来对分支和混沌的各种机理进行观察和研究。因此对于Chua电路的研究引起了很多研究者的兴趣,Chua系统也逐渐成为了混沌现象研究中的标准模型。In 1983, Professor Leon Chua of the University of California designed the first Chua circuit that can simulate the occurrence of chaotic phenomena experimentally. This is a landmark design that opens up new avenues for chaotic behavior to be applied to the real world. Chua circuit is a third-order autonomous circuit that can generate double scroll chaos. By giving a piecewise linear negative resistance different forms of parameter combinations, it can produce particularly rich branching and chaotic behaviors. The Chua circuit is the simplest one of the autonomous circuits that can cause chaotic phenomena. Any chaotic phenomenon generated in the third-order autonomous system can be simulated by the Chua circuit system. Shilnikov's theorem has made a strict proof of the chaotic form generated by Chua system. Based on this, people can observe and study various mechanisms of branching and chaos in the form of circuits. Therefore, the study of Chua circuit has aroused the interest of many researchers, and the Chua system has gradually become the standard model in the study of chaotic phenomena.

最初的关于Chua电路系统的研究需要假设系统的参数是精确已知的。考虑到在实际的电路设计中,由于受到元器件老化、不确定干扰以及测量成本等各种内部外部因素的影响,电路中的某些参数往往很难精确或直接获取。因此,如何解决具有未知参数的Chua电路系统的参数估计问题就变得尤为重要,当系统仅有部分状态变量可用时,问题将变得更加困难。为了解决这一问题,学者们提出了各种各样不同的方法,如基于延迟嵌入的方法和基于控制理论的方法等。其中基于控制理论的方法可以通过观测器设计和系统辨识等方法从隐藏变量中估计未知参数,从而得到越来越广泛的应用。Initial studies of Chua's circuit system assumed that the parameters of the system were precisely known. Considering that in the actual circuit design, due to the influence of various internal and external factors such as component aging, uncertain interference and measurement cost, some parameters in the circuit are often difficult to obtain accurately or directly. Therefore, how to solve the parameter estimation problem of the Chua circuit system with unknown parameters becomes particularly important, and the problem becomes more difficult when only part of the state variables of the system are available. In order to solve this problem, scholars have proposed a variety of different methods, such as methods based on delayed embedding and methods based on control theory. Among them, the methods based on control theory can estimate unknown parameters from hidden variables through methods such as observer design and system identification, which are more and more widely used.

估计参数的收敛速度是在参数估计的过程中非常关键的一个性能指标,前文中所涉及的文献大多仅能实现参数的渐近估计。渐近估计仅能保证参数的估计误差在时间趋向于无穷时趋向于零,因此无法得到更快的估计速度。从时间优化的角度来看，使估计误差有限时间收敛的估计方法才是时间最优的估计算法。此外,有限时间估计算法通常带有分数幂项,使得有限时间参数估计和传统的渐近估计相比,往往具有更好的鲁棒性和抗扰动性。正是由于有限时间参数估计的诸多优点,关于混沌系统的有限时间参数估计研究受到越来越多研究者的关注,并取得了许多积极的成果。The convergence speed of the estimated parameters is a very critical performance index in the process of parameter estimation, and most of the literatures involved in the above can only realize the asymptotic estimation of the parameters. Asymptotic estimation can only guarantee that the estimation error of the parameter tends to zero when the time tends to infinity, so it cannot obtain a faster estimation speed. From the point of view of time optimization, the estimation method that makes the estimation error converge in limited time is the time-optimized estimation algorithm. In addition, the finite-time estimation algorithm usually has fractional power terms, which makes the finite-time parameter estimation have better robustness and anti-disturbance than the traditional asymptotic estimation. Because of the many advantages of finite-time parameter estimation, the research on finite-time parameter estimation of chaotic systems has been paid more and more attention by researchers, and many positive results have been achieved.

不管是传统的渐近参数估计算法还是近年来被广泛研究的有限时间估计算法,其收敛时间都是依赖于参数的初始估计误差的,并随初始估计误差的增大而增大。为了克服这一缺陷,有关文献提出了固定时间稳定性的概念。固定时间稳定性在保留了有限时间稳定收敛速度快、收敛精度高等诸多优点的同时,还具有收敛时间不依赖初始值的优良特性,因此成为国内外的研究热点。近年来,混沌系统的固定时间同步和固定时间控制等问题被大量研究,但关于混沌系统的固定时间参数估计问题的研究却鲜有报道。Whether it is the traditional asymptotic parameter estimation algorithm or the finite-time estimation algorithm that has been widely studied in recent years, the convergence time depends on the initial estimation error of the parameters, and increases with the increase of the initial estimation error. In order to overcome this defect, the related literature proposes the concept of fixed time stability. Fixed-time stability retains the advantages of fast convergence speed and high convergence accuracy of finite-time stability, and also has the excellent characteristic that the convergence time does not depend on the initial value, so it has become a research hotspot at home and abroad. In recent years, fixed-time synchronization and fixed-time control of chaotic systems have been studied a lot, but the research on fixed-time parameter estimation of chaotic systems is rarely reported.

发明内容SUMMARY OF THE INVENTION

本发明所要解决的技术问题是克服现有技术的缺陷，提供基于Volterra积分算子的Chua电路系统的固定时间代数参数估计算法，该算法能够做到在仅有输出信号已知的情况下,在不依赖于系统初始值的固定时间内实现对参数的精确估计；通过在Volterra积分算子中巧妙的选取核函数,本发明能够有效消除系统初始值的影响,同时避免了对Chua电路系统输出导数的计算；此外，不同于传统的自适应参数估计算法，本发明提出的代数参数估计算法能够实现参数的快速、准确估计。The technical problem to be solved by the present invention is to overcome the defects of the prior art, and to provide a fixed-time algebraic parameter estimation algorithm of the Chua circuit system based on the Volterra integral operator, which can achieve a Accurate estimation of parameters is realized in a fixed time independent of the initial value of the system; by cleverly selecting the kernel function in the Volterra integral operator, the present invention can effectively eliminate the influence of the initial value of the system, and avoid the output derivative of the Chua circuit system. In addition, different from the traditional self-adaptive parameter estimation algorithm, the algebraic parameter estimation algorithm proposed by the present invention can realize fast and accurate estimation of parameters.

为达到上述目的，本发明提供Chua电路系统的固定时间代数参数估计算法，包括：In order to achieve the above object, the present invention provides a fixed-time algebraic parameter estimation algorithm of the Chua circuit system, including:

基于构建的固定时间代数参数估计算法，预测输出固定时间代数参数；Based on the constructed fixed-time algebraic parameter estimation algorithm, predict and output fixed-time algebraic parameters;

构建固定时间代数参数估计算法，通过以下步骤实现：Construct a fixed-time algebraic parameter estimation algorithm, implemented through the following steps:

根据Chua电路系统，建立非线性数学模型；According to the Chua circuit system, establish a nonlinear mathematical model;

利用Volterra积分算子，确定核函数K(t,τ)；Use the Volterra integral operator to determine the kernel function K(t,τ);

确定固定时间稳定性；determine fixed time stability;

根据核函数K(t,τ)和非线性数学模型，构建获得固定时间代数参数估计算法。According to the kernel function K(t,τ) and the nonlinear mathematical model, a fixed-time algebraic parameter estimation algorithm is constructed.

优先地，根据Chua电路系统，构建简化非线性模型，并建立无量纲非线性数学模型，包括：Chua电路系统的简化非线性模型的表达式为：Preferentially, according to the Chua circuit system, a simplified nonlinear model is constructed, and a dimensionless nonlinear mathematical model is established, including: the expression of the simplified nonlinear model of the Chua circuit system is:

式中，R为线性电阻，

是电容器C₁的电压，

是电容器C₂的电压，i_l是通过电感L的电流；

是关于电容器电压的函数，

表达式为：where R is the linear resistance,

is the voltage across capacitor_C1 ,

is the voltage across capacitor C2 and_{i lis} the current through inductor L;

is a function of capacitor voltage,

The expression is:

公式(2)中m₀，m₁和B_p为二极管的三个固定常数；In formula (2), m₀ , m₁ and B_p are three fixed constants of the diode;

利用无量纲形式，构建非线性数学模型；Use dimensionless form to construct nonlinear mathematical model;

非线性数学模型的表达式为：The expression of the nonlinear mathematical model is:

式中，f(x₁)＝ax₁+b(|x₁+1|-|x₁-1|) (4)，In the formula, f(x₁ )=ax₁ +b(|x₁ +1|-|x₁ -1|) (4),

式中，y₁和y₂表示公式(3)的输出；m₀、m₁和B_p为Chua二极管的三个固定常数，

是电容C₁的电压，

是电容C₂的电压，i_l是通过电感L的电流。In the formula, y₁ and y₂ represent the output of formula (3); m₀ , m₁ and B_p are the three fixed constants of the Chua diode,

is the voltage across capacitor_C1 ,

is the voltage across capacitor C2 and_{i lis} the current through inductor L.

优先地，利用Volterra积分算子，确定核函数K(t,τ)，包括：Preferentially, using the Volterra integral operator, determine the kernel function K(t,τ), including:

定义

为R_≥0到R的希尔伯特空间内的局部平方可积函数，R表示实数，R_≥0表示非负实数，局部平方可积函数f(t)经过Volterra积分算子进行映射定义：definition

is a local square integrable function in the Hilbert space from R_{≥ 0} to R, R represents a real number, R_{≥ 0} represents a non-negative real number, and the local square integrable function f(t) is defined by the Volterra integral operator mapping:

式中，K(·,·)：R×R→R希尔伯特-施密特核函数；In the formula, K(·,·): R×R→R Hilbert-Schmidt kernel function;

基于莱布尼兹微分规则，[V_Kf](t)由如下微分方程产生：Based on Leibniz's differential rule, [V_K f](t) is generated by the following differential equation:

式中，K(t,t)为核函数，ξ₀为预设的初始值常数；In the formula, K(t, t) is the kernel function, and ξ₀ is the preset initial value constant;

定义f⁽ⁱ⁾(t),i∈Z₊为f(t)的i阶导数，Z₊为正整数，则[V_Kf⁽ⁱ⁾](t)展开为：Define f⁽ⁱ⁾ (t), i∈Z₊ is the i-order derivative of f(t), and Z₊ is a positive integer, then [V_K f⁽ⁱ⁾ ](t) is expanded as:

式中，K⁽ⁱ⁾(·,·)表示K(·,·)关于第二个变量的i阶导数；In the formula, K⁽ⁱ⁾ (·,·) represents the i-order derivative of K(·,·) with respect to the second variable;

核函数K(t,τ)的选取决定了Volterra积分算子的映射[V_Kf](t)效果，选取的核函数为：

The selection of the kernel function K(t,τ) determines the mapping [V_K f](t) effect of the Volterra integral operator, and the selected kernel function is:

公式(9)中，ω_h，ω＞0均为预设的参数；In formula (9), ω_h , ω>0 are all preset parameters;

公式(9)展开得到：Equation (9) is expanded to get:

其中f_p(τ),p＝0,1,2满足：Where f_p (τ), p = 0, 1, 2 satisfy:

式中，q＝{0,1,2}；In the formula, q={0,1,2};

基于公式(11)，计算获得

Based on formula (11), the calculation is obtained

基于公式(10)和公式(12)，得到核函数关于的导数：Based on formula (10) and formula (12), the derivative of the kernel function with respect to:

得到对于

有：get for

Have:

K⁽ⁱ⁾(t,t)＝0,K⁽ⁱ⁾(t,0)＝0(14)。K⁽ⁱ⁾ (t,t)=0, K⁽ⁱ⁾ (t,0)=0(14).

优先地，确定固定时间稳定性，包括：Preferentially, determine fixed-time stability, including:

Chua电路系统为：The Chua circuit system is:

式中，f(0)＝0,x(t)∈Rⁿ,f(x(t)):Rⁿ→Rⁿ为定义域n维空间Rⁿ到值域n维空间Rⁿ中的一个连续函数，x₀＝x(t₀)表示Chua电路系统的初始值，t₀表示初始时刻；In the formula, f(0)=0, x(t)∈Rⁿ , f(x(t)): Rⁿ →Rⁿ is one of the definition domain n-dimensional space Rⁿ to the value domain n-dimensional space Rⁿ Continuous function, x₀ =x(t₀ ) represents the initial value of the Chua circuit system, and t₀ represents the initial moment;

将公式(15)的解记为x(t,x₀)；Denote the solution of formula (15) as x(t,x₀ );

若存在一个不依赖于Chua电路系统初始值x₀的固定时间T，使得对任意初始状态x₀，有

成立，则判定Chua电路系统的平衡点x＝0是全局固定时间稳定的。If there is a fixed time T that does not depend on the initial value x₀ of the Chua circuit system, such that for any initial state x₀ , we have

If it is established, it is determined that the balance point x=0 of the Chua circuit system is stable in the global fixed time.

优先地，在构建固定时间代数参数估计算法之前，对Chua电路系统做如下处理：Preferentially, before constructing a fixed-time algebraic parameter estimation algorithm, the Chua circuit system is processed as follows:

将公式(3)变换为关于Chua电路系统输出及其导数形式：Transform equation (3) into the form of the output of the Chua circuit system and its derivative:

其中，y₃＝|y₁+1|-|y₁-1|，where y₃ =|y₁ +1|-|y₁ -1|,

参数θ₁，θ₂和θ₃满足：The parameters θ₁ , θ₂ and θ₃ satisfy:

θ₁＝-β(1+a),θ₂＝β,θ₃＝-bβ (17)；θ₁ =-β(1+a), θ₂ =β, θ₃ =-bβ (17);

将对β,a,b,γ的估计转变为对θ₁,θ₂,θ₃,γ的估计；Convert the estimates of β, a, b, γ into estimates of θ₁ , θ₂ , θ₃ , γ;

对公式(16)两边同时进行积分算子V_K运算：Perform the integral operator V_K operation on both sides of formula (16) at the same time:

式中，y₁(t),y₂(t)为公式(3)的输出；In the formula, y₁ (t), y₂ (t) is the output of formula (3);

将公式(14)带入公式(18)，得到：Substituting equation (14) into equation (18), we get:

将公式(19)带入公式(18)，得到：Substituting equation (19) into equation (18), we get:

基于公式(20)，设计参数估计器；Based on formula (20), design a parameter estimator;

对

构造微分方程：right

Construct the differential equation:

其中，

由公式(13)获得；in,

Obtained by formula (13);

若核函数K(t,τ)满足公式(9)，则

对

成立；If the kernel function K(t,τ) satisfies formula (9), then

right

established;

由微分方程得到

因此公式(20)改写成：obtained from the differential equation

Therefore formula (20) is rewritten as:

其中，in,

其中，v₁(t)和v₂(t)满足持续可激励假设。Among them, v₁ (t) and v₂ (t) satisfy the continuous stimuli hypothesis.

优先地，在构建固定时间代数参数估计算法之前，设定如下持续可激励假设：Preferentially, before building a fixed-time algebraic parameter estimation algorithm, set the following persistent motivating assumptions:

假设1：函数v₁(t)和v₂(t)满足持续可激励条件,存在常数r＞0,T₀＞0使得如下不等式对

成立:Assumption 1: The functions v₁ (t) and v₂ (t) satisfy the continuous excitation condition, and there are constants r > 0 and T₀ > 0 such that the following inequalities

Established:

式中，I_3×3为3×3的单位矩阵；In the formula, I_3×3 is a 3×3 unit matrix;

对公式(23)分别左乘v₁^T(t)和v₂(t)，得到：Left-multiplying v₁^T (t) and v₂ (t) to formula (23), respectively, yields:

其中in

对于公式(26)两边同时进行积分算子

运算，其中K_g＝e^-g(t-τ),g＞0，得到：For both sides of equation (26), the integral operator is performed simultaneously

Operation, where K_g =e^-g(t-τ) , g>0, we get:

其中，

in,

Chua电路系统产生变量s_1,f(t)、s_2,f(t)、v_1,f(t)和v_2,f(t)：The Chua circuitry produces variables s_1,f (t), s_2,f (t), v_1,f (t) and v_2,f (t):

优先地，根据核函数K(t,τ)和非线性数学模型，构建获得固定时间代数参数估计算法，包括：固定时间代数参数估计算法的表达式为：Preferentially, according to the kernel function K(t,τ) and the nonlinear mathematical model, a fixed-time algebraic parameter estimation algorithm is constructed and obtained, including: the expression of the fixed-time algebraic parameter estimation algorithm is:

参数ε，g满足：

Parameters ε, g satisfy:

其中，

表示参数

的上一个值，

表示参数

的上一个值，min{eig(v_1,f(t))}和min{eig(v_2,f(t))}分别表示v_1,f(t)和v_2,f(t)特征值最小值。in,

Indicates parameters

the previous value of ,

Indicates parameters

The previous value of , min{eig(v1_,f (t))} and min{eig(v2_,f (t))} denote v1_,f (t) and v2_,f (t) features respectively value minimum.

一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，其特征在于，所述处理器执行所述程序时实现上述任一项所述方法的步骤。An electronic device includes a memory, a processor, and a computer program stored in the memory and executable on the processor, wherein the processor implements the steps of any one of the methods described above when the processor executes the program.

一种计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现上述任一项所述方法的步骤。A computer-readable storage medium on which a computer program is stored, and when the computer program is executed by a processor, implements the steps of any one of the above-mentioned methods.

本发明所达到的有益效果：Beneficial effects achieved by the present invention:

1、首先,和已有的基于渐近收敛和有限时间收敛的参数估计策略相比较,本发明所提出的固定时间参数估计算法在保证了收敛速度快和收敛精度高的同时,还具有收敛时间不依赖于初始估计误差的特点；1. First, compared with the existing parameter estimation strategies based on asymptotic convergence and finite-time convergence, the fixed-time parameter estimation algorithm proposed in the present invention not only ensures fast convergence speed and high convergence accuracy, but also has a convergence time. Does not depend on the characteristics of the initial estimation error;

2、此外,本发明所使用的Volterra积分算子,能够有效消除系统初始值的影响,同时避免对系统输出导数的计算,使得所提算法只需用到系统的输出信息,因此能够有效减少传感器的使用,从而有效降低算法的实现成本；2. In addition, the Volterra integral operator used in the present invention can effectively eliminate the influence of the initial value of the system, and at the same time avoid the calculation of the output derivative of the system, so that the proposed algorithm only needs to use the output information of the system, so it can effectively reduce the number of sensors. It can effectively reduce the implementation cost of the algorithm;

3、最后,在现有的文献中,为了得到足够多的方程来消去未知变量的影响,需要选取几个不同的核函数，而本发明所提算法除了能实现固定时间参数估计外,只需要选取一个核函数,从而使得算法复杂度大大降低。3. Finally, in the existing literature, in order to obtain enough equations to eliminate the influence of unknown variables, it is necessary to select several different kernel functions. In addition to realizing fixed-time parameter estimation, the algorithm proposed in the present invention only needs to A kernel function is selected, which greatly reduces the complexity of the algorithm.

附图说明Description of drawings

图1为本发明的Chua电路系统的原理图；1 is a schematic diagram of the Chua circuit system of the present invention;

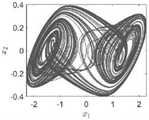
图2为本发明的Chua电路系统的混沌吸引子三维图；2 is a three-dimensional diagram of a chaotic attractor of the Chua circuit system of the present invention;

图3为本发明的Chua电路系统在x₁Ox₂平面上投影的混沌吸引子图；Fig. 3 is the chaotic attractor diagram of the Chua circuit system of the present invention projected on the x₁ Ox₂ plane;

图4为本发明的Chua电路系统在x₂Ox₃平面上投影的混沌吸引子图；Fig. 4 is the chaotic attractor diagram of the Chua circuit system of the present invention projected on the x₂ Ox₃ plane;

图5为本发明的Chua电路系统在x₁Ox₃平面上投影的混沌吸引子图；Fig. 5 is the chaotic attractor diagram of the Chua circuit system of the present invention projected on the x₁ Ox₃ plane;

图6为本发明在自适应初始值

下β真实值和估计值曲线图；Fig. 6 is the adaptive initial value of the present invention

Lower β true value and estimated value curve;

图7为本发明在自适应初始值

下γ真实值和估计值曲线图；Fig. 7 is the adaptive initial value of the present invention

Lower γ true value and estimated value curve;

图8为本发明在自适应初始值

下a真实值和估计值曲线图；Fig. 8 is the adaptive initial value of the present invention

Below a graph of true and estimated values;

图9为本发明在自适应初始值

下b真实值和估计值曲线图；Fig. 9 is the adaptive initial value of the present invention

Lower b true value and estimated value curve;

图10为本发明在自适应初始值

下β真实值和估计值曲线图；Fig. 10 shows the adaptive initial value of the present invention

Lower β true value and estimated value curve;

图11为本发明在自适应初始值

下γ真实值和估计值曲线图；Fig. 11 is the adaptive initial value of the present invention

Lower γ true value and estimated value curve;

图12为本发明在自适应初始值

下a真实值和估计值曲线图；Fig. 12 is the adaptive initial value of the present invention

Below a graph of true and estimated values;

图13为本发明在自适应初始值

下n真实值和估计值曲线图；Fig. 13 shows the adaptive initial value of the present invention

Lower n real value and estimated value curve;

图14为本发明的流程图。Figure 14 is a flow chart of the present invention.

具体实施方式Detailed ways

以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。The following examples are only used to illustrate the technical solutions of the present invention more clearly, and cannot be used to limit the protection scope of the present invention.

实施例一Example 1

Chua电路系统的固定时间代数参数估计算法，包括以下步骤：A fixed-time algebraic parameter estimation algorithm for the Chua circuit system, including the following steps:

步骤1、根据Chua电路系统建立非线性数学模型；Step 1. Establish a nonlinear mathematical model according to the Chua circuit system;

步骤2、利用Volterra积分算子，确定核函数K(t,τ)；Step 2. Use the Volterra integral operator to determine the kernel function K(t, τ);

步骤3、根据核函数K(t,τ)和非线性数学模型，确定固定时间稳定性，构建固定时间代数参数估计算法；Step 3, according to the kernel function K(t, τ) and the nonlinear mathematical model, determine the fixed-time stability, and construct a fixed-time algebraic parameter estimation algorithm;

基于构建的固定时间代数参数估计算法，预测输出固定时间代数参数。Based on the constructed fixed-time algebraic parameter estimation algorithm, the fixed-time algebraic parameters are predicted and output.

步骤1包括：Step 1 includes:

Chua电路系统包括三个储能元件(一个电感L和两个电容C₁、C₂)、一个线性电阻R和一个称为Chua二极管的非线性电阻器,Chua电路系统简化非线性数学模型如下：The Chua circuit system includes three energy storage elements (an inductor L and two capacitors C₁ , C₂ ), a linear resistor R and a nonlinear resistor called a Chua diode. The simplified nonlinear mathematical model of the Chua circuit system is as follows:

公式(1)中，R为线性电阻，

是C₁的电压，

是C₂的电压，i_l是通过电感L的电流；

是电压

的函数，用来表示通过非线性电阻的电流,该非线性函数

由如下的奇对称分段线性函数描述:In formula (1), R is the linear resistance,

is the voltage of_C1 ,

is the voltage of C₂ and i_l is the current through the inductor L;

is the voltage

A function of , used to represent the current through a nonlinear resistor, the nonlinear function

It is described by the following oddly symmetric piecewise linear function:

公式(2)中m₀，m₁和B_p为Chua二极管的三个固定常数；In formula (2), m₀ , m₁ and B_p are three fixed constants of Chua diode;

假设1：在实验过程中，面对变量多或者无法完全复原模型的情况下，可以通过无量纲化的方式，通过一个合适的变量替代，将一个涉及物理量的方程的部分或全部的单位移除，以求简化实验或者计算的目的。Assumption 1: During the experiment, when there are too many variables or the model cannot be completely restored, part or all of the units of an equation involving a physical quantity can be removed by a suitable variable substitution in a dimensionless way. , in order to simplify the experiment or calculation purpose.

公式(1)转化为无量纲形式:Equation (1) is transformed into dimensionless form:

公式(3)中，y₁和y₂表示Chua电路系统的输出；f(x₁)具体表示为公式(4)；β，γ，a，b，x₁，x₂，x₃具体表示公式(5)；In formula (3), y₁ and y₂ represent the output of the Chua circuit system; f(x₁ ) is specifically represented by formula (4); β, γ, a, b, x₁ , x₂ , and x₃ specifically represent the formula (5);

f(x₁)＝ax₁+b(|x₁+1|-|x₁-1|) (4)f(x₁ )=ax₁ +b(|x₁ +1|-|x₁ -1|) (4)

步骤2具体为：Step 2 is specifically:

定义

为R_≥0到R的希尔伯特空间内的局部平方可积函数，R表示实数，R_≥0表示非负实数，局部平方可积函数f(t)经过Volterra积分算子进行映射定义：definition

is a local square integrable function in the Hilbert space from R_{≥ 0} to R, R represents a real number, R_{≥ 0} represents a non-negative real number, and the local square integrable function f(t) is defined by the Volterra integral operator mapping:

公式(6)中K(·,·)：R×R→R希尔伯特-施密特核函数；K(·,·) in formula (6): R×R→R Hilbert-Schmidt kernel function;

对于公式(6)，用微分方程的形式能更好的进行实际计算，基于莱布尼兹微分规则，[V_Kf](t)由如下微分方程产生：For formula (6), the actual calculation can be better performed in the form of a differential equation. Based on Leibniz’s differential rule, [V_K f](t) is generated by the following differential equation:

式中，K(t,t)为核函数，ξ₀为预设的初始值常数；In the formula, K(t, t) is the kernel function, and ξ₀ is the preset initial value constant;

定义f⁽ⁱ⁾(t),i∈Z₊为f(t)的i阶导数，Z₊为正整数，则[V_Kf⁽ⁱ⁾](t)展开为：Define f⁽ⁱ⁾ (t), i∈Z₊ is the i-order derivative of f(t), and Z₊ is a positive integer, then [V_K f⁽ⁱ⁾ ](t) is expanded as:

其中K⁽ⁱ⁾(·,·)表示K(·,·)关于第二个变量的i阶导数；where K⁽ⁱ⁾ (·,·) represents the i-order derivative of K(·,·) with respect to the second variable;

核函数K(t,τ)的选取决定了Volterra积分算子的映射[V_Kf](t)效果，本发明选取核函数为：The selection of the kernel function K(t,τ) determines the mapping [V_K f](t) effect of the Volterra integral operator, and the kernel function selected in the present invention is:

公式(9)中ω_h，ω＞0均为预设的参数；In formula (9), ω_h and ω>0 are all preset parameters;

公式(9)展开得到：Equation (9) is expanded to get:

其中f_p(τ),p＝0,1,2满足：Where f_p (τ), p = 0, 1, 2 satisfy:

式中，q＝{0,1,2}；In the formula, q={0,1,2};

基于公式(11)，计算获得

Based on formula (11), the calculation is obtained

基于公式(10)和公式(12)，得到核函数关于的导数：Based on formula (10) and formula (12), the derivative of the kernel function with respect to:

基于公式(12)与公式(13)，得到对于

有：Based on formula (12) and formula (13), we get for

Have:

K⁽ⁱ⁾(t,t)＝0,K⁽ⁱ⁾(t,0)＝0 (14)。K⁽ⁱ⁾ (t,t)=0, K⁽ⁱ⁾ (t,0)=0 (14).

步骤3中确定固定时间稳定性，具体包括以下步骤：Instep 3, the fixed time stability is determined, which specifically includes the following steps:

性质1：考虑如下Chua电路系统：Property 1: Consider the following Chua circuit system:

其中f(0)＝0,x(t)∈Rⁿ,f(x(t)):Rⁿ→Rⁿ为定义域n维空间Rⁿ到值域n维空间Rⁿ中的一个连续函数，x₀＝x(t₀)表示Chua电路系统的初始值，t₀表示初始时刻，为一个定值；where f(0)=0, x(t)∈Rⁿ , f(x(t)): Rⁿ →Rⁿ is a continuous function from the definition domain n-dimensional space Rⁿ to the value domain n-dimensional space Rⁿ , x₀ =x(t₀ ) represents the initial value of the Chua circuit system, and t₀ represents the initial moment, which is a fixed value;

性质2：公式(15)解记为x(t,x₀)：如果存在一个不依赖于Chua电路系统初始值x₀的固定时间T，使得对任意初始状态x₀，有

成立，那么公式(15)的平衡点x＝0是全局固定时间稳定的。Property 2: Formula (15) can be solved as x(t, x₀ ): if there is a fixed time T that does not depend on the initial value x₀ of the Chua circuit system, such that for any initial state x₀ , there is

is established, then the equilibrium point x=0 of formula (15) is globally fixed time stable.

在构建固定时间代数参数估计算法之前，需要对Chua电路系统做如下处理：Before constructing a fixed-time algebraic parameter estimation algorithm, the Chua circuit system needs to be processed as follows:

为了方便参数估计器的设计，将公式(3)重新写成关于Chua电路系统输出及其导数形式：In order to facilitate the design of the parameter estimator, formula (3) is rewritten as the output of the Chua circuit system and its derivative form:

其中y₃＝|y₁+1|-|y₁-1|，参数θ₁，θ₂和θ₃满足：where y₃ =|y₁ +1|-|y₁ -1|, the parameters θ₁ , θ₂ and θ₃ satisfy:

θ₁＝-β(1+a),θ₂＝β,θ₃＝-bβ (17)θ₁ =-β(1+a), θ₂ =β, θ₃ =-bβ (17)

对β,a,b,γ的估计转变为对θ₁,θ₂,θ₃,γ的估计；The estimation of β, a, b, γ is transformed into the estimation of θ₁ , θ₂ , θ₃ , γ;

对公式(16)两边同时进行积分算子V_K运算：Perform the integral operator V_K operation on both sides of formula (16) at the same time:

公式(18)中，y₁(t),y₂(t)是已知的，但其导数

是未知的，因此

是未知的；将公式(18)展开，并将公式(14)带入公式(18)，得到：In formula (18), y₁ (t), y₂ (t) are known, but their derivatives

is unknown, so

is unknown; expanding Equation (18) and substituting Equation (14) into Equation (18) yields:

将公式(19)带入公式(18)，得到：Substituting equation (19) into equation (18), we get:

公式(20)中，除了参数θ₁,θ₂,θ₃,γ外，其他变量都是已知的，因此可以用来设计参数估计器。然而直接根据公式(6)去计算公式(20)中的Volterra积分算子映射非常繁琐，用微分方程对公式(20)中的所需变量进行计算，更方便实际。In formula (20), except the parameters θ₁ , θ₂ , θ₃ , γ, other variables are known, so they can be used to design the parameter estimator. However, it is very cumbersome to directly calculate the Volterra integral operator mapping in formula (20) according to formula (6), and it is more convenient and practical to use differential equations to calculate the required variables in formula (20).

性质1：对

构造微分方程：Property 1: Yes

Construct the differential equation:

其中

由公式(13)获得；若核函数K(t,τ)满足公式(9)，则

对

成立；in

Obtained by formula (13); if the kernel function K(t,τ) satisfies formula (9), then

right

established;

由性质1得到

因此公式(20)改写成：obtained fromproperty 1

Therefore formula (20) is rewritten as:

为了方便参数估计器设计，公式(22)重新写为：For the convenience of parameter estimator design, Equation (22) is rewritten as:

其中in

其中v₁(t)，v₂(t)满足持续可激励假设。where v₁ (t), v₂ (t) satisfy the continual motivating hypothesis.

在构建固定时间代数参数估计算法之前，设定如下持续可激励假设：Before building a fixed-time algebraic parameter estimation algorithm, the following persistent motivating assumptions are made:

假设1：函数v₁(t)和v₂(t)满足持续可激励条件,即存在常数r＞0,T₀＞0使得如下不等式对

成立:Assumption 1: The functions v₁ (t) and v₂ (t) satisfy the continuous excitation condition, that is, there are constants r > 0, T₀ > 0 such that the following inequalities

Established:

式中，I_3×3为3×3的单位矩阵；In the formula, I_3×3 is a 3×3 unit matrix;

根据假设1，公式(23)的两个等式中一个是向量形式，另一个是标量形式，因此对两式分别左乘v₁^T(t)和v₂(t)，得到：According toAssumption 1, one of the two equations of formula (23) is in vector form and the other is in scalar form, so the two equations are left-multiplied by v₁^T (t) and v₂ (t), respectively, to get:

其中in

对于公式(26)两边同时进行积分算子

运算，其中K_g＝e^-g(t-τ),g＞0，得到：For both sides of equation (26), the integral operator is performed simultaneously

Operation, where K_g =e^-g(t-τ) , g>0, we get:

其中

变量s_1,f(t)，s_2,f(t)，v_1,f(t)和v_2,f(t)由如下Chua电路系统产生：in

The variables s1_,f (t), s2_,f (t), v1_,f (t) and v2_,f (t) are generated by the following Chua circuit system:

步骤3中的固定时间代数参数估计算法具体为：The fixed-time algebraic parameter estimation algorithm instep 3 is specifically:

定理1：参数θ，γ的估计值

满足：Theorem 1: Estimation of parameters θ, γ

Satisfy:

其中

表示参数

的上一个值，

表示参数

的上一个值，其中各变量由公式(21)、(24)、(27)和(29)给出，min{eig(v_1,f(t))}和min{eig(v_2,f(t))}分别表示v_1,f(t)和v_2,f(t)特征值最小值。in

Indicates parameters

the previous value of ,

Indicates parameters

, where the variables are given by equations (21), (24), (27), and (29), min{eig(v_1,f (t))} and min{eig(v_2,f (t))} represent the minimum eigenvalues of v1_,f (t) and v2_,f (t), respectively.

若满足假设1，且参数ε，g满足Ifassumption 1 is satisfied, and the parameters ε, g satisfy

那么对于任意t≥T₀，都满足Then for any t≥T₀ , all satisfy

即

能够在固定时间T₀实现对参数θ，γ的估计。which is

The estimation of the parameters θ, γ can be achieved at a fixed time T₀ .

定理1的证明如下：The proof ofTheorem 1 is as follows:

由v_1,f(t)的定义以及假设1可得，当t≥T₀：From the definition of v_1,f (t) andassumption 1, when t ≥ T₀ :

同理可得：The same can be obtained:

由(33)和(34)可知当t≥T₀时v_1,f(t)和v_2,f(t)可逆，并满足From (33) and (34), it can be known that v_1,f (t) and v_2,f (t) are invertible when t≥T₀ , and satisfy

因此由公式(28)可知，当t≥T₀时，

成立，由此定理1得证。Therefore, according to formula (28), when t≥T₀ ,

is established, andtheorem 1 is proved.

实施例二Embodiment 2

Chua系统电路根据说明书附图1进行建模，参数选择为：The Chua system circuit is modeled according to Figure 1 of the specification, and the parameters are selected as:

x₁(0)＝-0.9,x₂(0)＝-0.15,x₃(0)＝1.47x₁ (0)=-0.9, x₂ (0)=-0.15, x₃ (0)=1.47

γ＝27,β＝15.6,a＝-5/7,b＝-3/14γ=27, β=15.6, a=-5/7, b=-3/14

系统的混沌吸引子及其在各坐标平面的投影如说明书附图2所示。固定时间代数参数估计算法按照定理1进行设计，参数选择按照说明书附表1所示。The chaotic attractor of the system and its projection on each coordinate plane are shown in Figure 2 of the description. The fixed-time algebraic parameter estimation algorithm is designed according toTheorem 1, and the parameter selection is shown in Table 1 of the specification.

表1Table 1

为了验证算法的固定时间收敛性，分别选取两个不同的自适应初始值：In order to verify the fixed-time convergence of the algorithm, two different adaptive initial values are selected respectively:

(C.1):

(C.1):

(C.2):

(C.2):

来进行算法的仿真验证。for the simulation verification of the algorithm.

当选取k＝10^-12,T₀＝0.6s，可以算出参数估计器的收敛时间T_max≈1.4s，选取自适应初始值

仿真结果如附图6-图9所示。由图6-图9可得，本发明提出算法能够在1.4秒内实现对系统参数的准确估计。当选取一个大的自适应初始值

仿真结果如附图10-图13所示，由附图10-图13可得，即使在大的初始状态下，本发明算法依然能够在1.4秒内实现对系统的准确估计，由此验证了算法的固定时间收敛性质。When k=10^-12 , T₀ =0.6s, the convergence time of the parameter estimator T_max ≈ 1.4s can be calculated, and the adaptive initial value is selected

The simulation results are shown in Figures 6-9. As can be seen from Fig. 6-Fig. 9, the algorithm proposed by the present invention can realize accurate estimation of system parameters within 1.4 seconds. When choosing a large adaptive initial value

The simulation results are shown in Figures 10-13, which can be obtained from Figures 10-13. Even in a large initial state, the algorithm of the present invention can still achieve accurate estimation of the system within 1.4 seconds, which verifies The fixed-time convergence properties of the algorithm.

本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。The present application is described with reference to flowchart illustrations and/or block diagrams of methods, apparatus (systems), and computer program products according to embodiments of the present application. It will be understood that each flow and/or block in the flowchart illustrations and/or block diagrams, and combinations of flows and/or blocks in the flowchart illustrations and/or block diagrams, can be implemented by computer program instructions. These computer program instructions may be provided to the processor of a general purpose computer, special purpose computer, embedded processor or other programmable data processing device to produce a machine such that the instructions executed by the processor of the computer or other programmable data processing device produce Means for implementing the functions specified in a flow or flow of a flowchart and/or a block or blocks of a block diagram.

这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。These computer program instructions may also be stored in a computer-readable memory capable of directing a computer or other programmable data processing apparatus to function in a particular manner, such that the instructions stored in the computer-readable memory result in an article of manufacture comprising instruction means, the instructions The apparatus implements the functions specified in the flow or flow of the flowcharts and/or the block or blocks of the block diagrams.

这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。These computer program instructions can also be loaded on a computer or other programmable data processing device to cause a series of operational steps to be performed on the computer or other programmable device to produce a computer-implemented process such that The instructions provide steps for implementing the functions specified in the flow or blocks of the flowcharts and/or the block or blocks of the block diagrams.

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变形，这些改进和变形也应视为本发明的保护范围。The above are only the preferred embodiments of the present invention. It should be pointed out that for those skilled in the art, without departing from the technical principle of the present invention, several improvements and modifications can also be made. These improvements and modifications It should also be regarded as the protection scope of the present invention.

Claims (9)

Translated fromChinese

1.Chua电路系统的固定时间代数参数估计算法，其特征在于，包括：1. The fixed time algebraic parameter estimation algorithm of Chua circuit system, is characterized in that, comprises:基于构建的固定时间代数参数估计算法，预测输出固定时间代数参数；Based on the constructed fixed-time algebraic parameter estimation algorithm, predict and output fixed-time algebraic parameters;构建固定时间代数参数估计算法，通过以下步骤实现：Construct a fixed-time algebraic parameter estimation algorithm, implemented through the following steps:根据Chua电路系统，建立非线性数学模型；According to the Chua circuit system, establish a nonlinear mathematical model;利用Volterra积分算子，确定核函数K(t,τ)；Use the Volterra integral operator to determine the kernel function K(t,τ);确定固定时间稳定性；determine fixed time stability;根据核函数K(t,τ)和非线性数学模型，构建获得固定时间代数参数估计算法。According to the kernel function K(t,τ) and the nonlinear mathematical model, a fixed-time algebraic parameter estimation algorithm is constructed.2.根据权利要求1所述的Chua电路系统的固定时间代数参数估计算法，其特征在于，2. The fixed-time algebraic parameter estimation algorithm of Chua circuit system according to claim 1, is characterized in that,根据Chua电路系统，构建简化非线性模型，并建立无量纲非线性数学模型，包括：According to the Chua circuit system, a simplified nonlinear model is constructed, and a dimensionless nonlinear mathematical model is established, including:Chua电路系统的简化非线性模型的表达式为：The expression for the simplified nonlinear model of the Chua circuit system is:

式中，R为线性电阻，

是电容器C₁的电压，

是电容器C₂的电压，i_l是通过电感L的电流；

是关于电容器电压的函数，

表达式为：where R is the linear resistance,

is the voltage across capacitor_C1 ,

is the voltage across capacitor C2 and_{i lis} the current through inductor L;

is a function of capacitor voltage,

The expression is:

公式(2)中m₀，m₁和B_p为二极管的三个固定常数；In formula (2), m₀ , m₁ and B_p are three fixed constants of the diode;利用无量纲形式，构建非线性数学模型；Use dimensionless form to construct nonlinear mathematical model;非线性数学模型的表达式为：The expression of the nonlinear mathematical model is:

式中，f(x₁)＝ax₁+b(|x₁+1|-|x₁-1|) (4)，In the formula, f(x₁ )=ax₁ +b(|x₁ +1|-|x₁ -1|) (4),

式中，y₁和y₂表示公式(3)的输出；m₀、m₁和B_p为Chua二极管的三个固定常数，

是电容C₁的电压，

是电容C₂的电压，i_l是通过电感L的电流。In the formula, y₁ and y₂ represent the output of formula (3); m₀ , m₁ and B_p are the three fixed constants of the Chua diode,

is the voltage across capacitor_C1 ,

is the voltage across capacitor C2 and_{i lis} the current through inductor L.3.根据权利要求2所述的Chua电路系统的固定时间代数参数估计算法，其特征在于，3. The fixed-time algebraic parameter estimation algorithm of Chua circuit system according to claim 2, is characterized in that,利用Volterra积分算子，确定核函数K(t,τ)，包括：Using the Volterra integral operator, determine the kernel function K(t,τ), including:定义

为R_≥0到R的希尔伯特空间内的局部平方可积函数，R表示实数，R_≥0表示非负实数，局部平方可积函数f(t)经过Volterra积分算子进行映射定义：definition

is a local square integrable function in the Hilbert space from R_{≥ 0} to R, R represents a real number, R_{≥ 0} represents a non-negative real number, and the local square integrable function f(t) is defined by the Volterra integral operator mapping:

式中，K(·,·)：R×R→R希尔伯特-施密特核函数；In the formula, K(·,·): R×R→R Hilbert-Schmidt kernel function;基于莱布尼兹微分规则，[V_Kf](t)由如下微分方程产生：Based on Leibniz's differential rule, [V_K f](t) is generated by the following differential equation:

式中，K(t,t)为核函数，ξ₀为预设的初始值常数；In the formula, K(t, t) is the kernel function, and ξ₀ is the preset initial value constant;定义f⁽ⁱ⁾(t),i∈Z₊为f(t)的i阶导数，Z₊为正整数，则[V_Kf⁽ⁱ⁾](t)展开为：Define f⁽ⁱ⁾ (t), i∈Z₊ is the i-order derivative of f(t), and Z₊ is a positive integer, then [V_K f⁽ⁱ⁾ ](t) is expanded as:

式中，K⁽ⁱ⁾(·,·)表示K(·,·)关于第二个变量的i阶导数；In the formula, K⁽ⁱ⁾ (·,·) represents the i-order derivative of K(·,·) with respect to the second variable;核函数K(t,τ)的选取决定了Volterra积分算子的映射[V_Kf](t)效果，选取的核函数为：The selection of the kernel function K(t,τ) determines the mapping [V_K f](t) effect of the Volterra integral operator, and the selected kernel function is:

公式(9)中，ω_h，ω＞0均为预设的参数；In formula (9), ω_h , ω>0 are all preset parameters;公式(9)展开得到：Equation (9) is expanded to get:

其中f_p(τ),p＝0,1,2满足：Where f_p (τ), p = 0, 1, 2 satisfy:

式中，q＝{0,1,2}；In the formula, q={0,1,2};基于公式(11)，计算获得

Based on formula (11), the calculation is obtained

基于公式(10)和公式(12)，得到核函数关于的导数：Based on formula (10) and formula (12), the derivative of the kernel function with respect to:

得到对于

有：get for

Have:K⁽ⁱ⁾(t,t)＝0,K⁽ⁱ⁾(t,0)＝0 (14)。K⁽ⁱ⁾ (t,t)=0, K⁽ⁱ⁾ (t,0)=0 (14).4.根据权利要求3所述的Chua电路系统的固定时间代数参数估计算法，其特征在于，4. The fixed-time algebraic parameter estimation algorithm of Chua circuit system according to claim 3, is characterized in that,确定固定时间稳定性，包括：Determine fixed-time stability, including:Chua电路系统为：The Chua circuit system is:

式中，f(0)＝0,x(t)∈Rⁿ,f(x(t)):Rⁿ→Rⁿ为定义域n维空间Rⁿ到值域n维空间Rⁿ中的一个连续函数，x₀＝x(t₀)表示Chua电路系统的初始值，t₀表示初始时刻；In the formula, f(0)=0, x(t)∈Rⁿ , f(x(t)): Rⁿ →Rⁿ is one of the definition domain n-dimensional space Rⁿ to the value domain n-dimensional space Rⁿ Continuous function, x₀ =x(t₀ ) represents the initial value of the Chua circuit system, and t₀ represents the initial moment;将公式(15)的解记为x(t,x₀)；Denote the solution of formula (15) as x(t,x₀ );若存在一个不依赖于Chua电路系统初始值x₀的固定时间T，使得对任意初始状态x₀，有

成立，则判定Chua电路系统的平衡点x＝0是全局固定时间稳定的。If there is a fixed time T that does not depend on the initial value x₀ of the Chua circuit system, such that for any initial state x₀ , we have

If it is established, it is determined that the balance point x=0 of the Chua circuit system is stable in the global fixed time.5.根据权利要求4所述的Chua电路系统的固定时间代数参数估计算法，其特征在于，5. The fixed-time algebraic parameter estimation algorithm of Chua circuit system according to claim 4, is characterized in that,在构建固定时间代数参数估计算法之前，对Chua电路系统做如下处理：Before constructing a fixed-time algebraic parameter estimation algorithm, the Chua circuit system is processed as follows:将公式(3)变换为关于Chua电路系统输出及其导数形式：Transform equation (3) into the form of the output of the Chua circuit system and its derivative:

其中，y₃＝|y₁+1|-|y₁-1|，where y₃ =|y₁ +1|-|y₁ -1|,参数θ₁，θ₂和θ₃满足：The parameters θ₁ , θ₂ and θ₃ satisfy:θ₁＝-β(1+a),θ₂＝β,θ₃＝-bβ (17)；θ₁ =-β(1+a), θ₂ =β, θ₃ =-bβ (17);将对β,a,b,γ的估计转变为对θ₁,θ₂,θ₃,γ的估计；Convert the estimates of β, a, b, γ into estimates of θ₁ , θ₂ , θ₃ , γ;对公式(16)两边同时进行积分算子V_K运算：Perform the integral operator V_K operation on both sides of formula (16) at the same time:

式中，y₁(t),y₂(t)为公式(3)的输出；In the formula, y₁ (t), y₂ (t) is the output of formula (3);将公式(14)带入公式(18)，得到：Substituting equation (14) into equation (18), we get:

将公式(19)带入公式(18)，得到：Substituting equation (19) into equation (18), we get:

基于公式(20)，设计参数估计器；Based on formula (20), design a parameter estimator;对

构造微分方程：right

Construct the differential equation:

其中，

由公式(13)获得；in,

Obtained by formula (13);若核函数K(t,τ)满足公式(9)，则

对

成立；If the kernel function K(t,τ) satisfies formula (9), then

right

established;由微分方程得到

因此公式(20)改写成：obtained from the differential equation

Therefore formula (20) is rewritten as:

其中，in,

其中，v₁(t)和v₂(t)满足持续可激励假设。Among them, v₁ (t) and v₂ (t) satisfy the continuous stimuli hypothesis.6.根据权利要求5所述的Chua电路系统的固定时间代数参数估计算法，其特征在于，6. The fixed time algebraic parameter estimation algorithm of Chua circuit system according to claim 5, is characterized in that,在构建固定时间代数参数估计算法之前，设定如下持续可激励假设：Before building a fixed-time algebraic parameter estimation algorithm, the following persistent motivating assumptions are made:假设1：函数v₁(t)和v₂(t)满足持续可激励条件,存在常数r＞0,T₀＞0使得如下不等式对

成立:Assumption 1: The functions v₁ (t) and v₂ (t) satisfy the continuous excitation condition, and there are constants r > 0 and T₀ > 0 such that the following inequalities

Established:

式中，I_3×3为3×3的单位矩阵；In the formula, I_3×3 is a 3×3 unit matrix;对公式(23)分别左乘v₁^T(t)和v₂(t)，得到：Left-multiplying v₁^T (t) and v₂ (t) to formula (23), respectively, yields:

其中in

对于公式(26)两边同时进行积分算子

运算，其中K_g＝e^-g(t-τ),g＞0，得到：For both sides of equation (26), the integral operator is performed simultaneously

Operation, where K_g =e^-g(t-τ) , g>0, we get:

其中，

in,

Chua电路系统产生变量s_1,f(t)、s_2,f(t)、v_1,f(t)和v_2,f(t)：The Chua circuitry produces variables s_1,f (t), s_2,f (t), v_1,f (t) and v_2,f (t):

7.根据权利要求6所述的Chua电路系统的固定时间代数参数估计算法，其特征在于，7. The fixed-time algebraic parameter estimation algorithm of Chua circuit system according to claim 6, is characterized in that,根据核函数K(t,τ)和非线性数学模型，构建获得固定时间代数参数估计算法，包括：According to the kernel function K(t,τ) and the nonlinear mathematical model, a fixed-time algebraic parameter estimation algorithm is constructed, including:固定时间代数参数估计算法的表达式为：The expression for the fixed-time algebraic parameter estimation algorithm is:

参数ε，g满足：

其中，

表示参数

的上一个值，

表示参数

的上一个值，min{eig(v_1,f(t))}和min{eig(v_2,f(t))}分别表示v_1,f(t)和v_2,f(t)特征值最小值。Parameters ε, g satisfy:

in,

Indicates parameters

the previous value of ,

Indicates parameters

The previous value of , min{eig(v1_,f (t))} and min{eig(v2_,f (t))} denote v1_,f (t) and v2_,f (t) features respectively value minimum.8.一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，其特征在于，所述处理器执行所述程序时实现权利要求1至7中任一项所述方法的步骤。8. An electronic device comprising a memory, a processor and a computer program stored on the memory and running on the processor, wherein the processor implements any one of claims 1 to 7 when the processor executes the program the steps of the method described in item.9.一种计算机可读存储介质，其上存储有计算机程序，其特征在于，该计算机程序被处理器执行时实现权利要求1至7中任一项所述方法的步骤。9. A computer-readable storage medium on which a computer program is stored, characterized in that, when the computer program is executed by a processor, the steps of the method according to any one of claims 1 to 7 are implemented.

Images