CN113723546A - Bearing fault detection method and system based on discrete hidden Markov model - Google Patents
Bearing fault detection method and system based on discrete hidden Markov modelDownload PDFInfo
- Publication number
- CN113723546A CN113723546ACN202111031722.XACN202111031722ACN113723546ACN 113723546 ACN113723546 ACN 113723546ACN 202111031722 ACN202111031722 ACN 202111031722ACN 113723546 ACN113723546 ACN 113723546A
- Authority
- CN
- China
- Prior art keywords
- hidden markov
- markov model
- discrete hidden
- bearing
- detected
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Granted
Links
Images
Classifications
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F18/00—Pattern recognition
- G06F18/20—Analysing
- G06F18/29—Graphical models, e.g. Bayesian networks
- G06F18/295—Markov models or related models, e.g. semi-Markov models; Markov random fields; Networks embedding Markov models
- G—PHYSICS
- G01—MEASURING; TESTING
- G01M—TESTING STATIC OR DYNAMIC BALANCE OF MACHINES OR STRUCTURES; TESTING OF STRUCTURES OR APPARATUS, NOT OTHERWISE PROVIDED FOR
- G01M13/00—Testing of machine parts
- G01M13/04—Bearings
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F18/00—Pattern recognition
- G06F18/20—Analysing
- G06F18/21—Design or setup of recognition systems or techniques; Extraction of features in feature space; Blind source separation
- G06F18/214—Generating training patterns; Bootstrap methods, e.g. bagging or boosting
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F18/00—Pattern recognition
- G06F18/20—Analysing
- G06F18/23—Clustering techniques
- G06F18/232—Non-hierarchical techniques
- G06F18/2321—Non-hierarchical techniques using statistics or function optimisation, e.g. modelling of probability density functions
- G06F18/23213—Non-hierarchical techniques using statistics or function optimisation, e.g. modelling of probability density functions with fixed number of clusters, e.g. K-means clustering
Landscapes
- Engineering & Computer Science (AREA)
- Data Mining & Analysis (AREA)
- Theoretical Computer Science (AREA)
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Bioinformatics & Cheminformatics (AREA)
- Artificial Intelligence (AREA)
- Bioinformatics & Computational Biology (AREA)
- Computer Vision & Pattern Recognition (AREA)
- Evolutionary Biology (AREA)
- Evolutionary Computation (AREA)
- General Engineering & Computer Science (AREA)
- Life Sciences & Earth Sciences (AREA)
- Probability & Statistics with Applications (AREA)
- Complex Calculations (AREA)
Abstract
Translated fromChineseDescription
Translated fromChinese技术领域technical field
本发明涉及故障检测技术领域,具体涉及一种基于离散隐马尔可夫模型的轴承故障检测方法和一种基于离散隐马尔可夫模型的轴承故障检测系统。The invention relates to the technical field of fault detection, in particular to a bearing fault detection method based on a discrete hidden Markov model and a bearing fault detection system based on a discrete hidden Markov model.
背景技术Background technique
机械设备和复杂机电系统的可靠性和安全性不仅对整个工业系统的高效运行起着至关重要的作用,而且对人身安全与环境保护也尤为关键。动态系统的故障侦测与诊断技术是提高系统的可靠性和降低事故风险的有效方法。随着HMM(Hidden Markov Model,隐马尔可夫模型)在各领域的成功应用以及工业界对可靠性和安全性的更高要求,HMM作为一种数据驱动的故障诊断方法受到越来越多关注。The reliability and safety of mechanical equipment and complex electromechanical systems not only play a vital role in the efficient operation of the entire industrial system, but are also critical to personal safety and environmental protection. The fault detection and diagnosis technology of dynamic system is an effective method to improve system reliability and reduce accident risk. With the successful application of HMM (Hidden Markov Model, Hidden Markov Model) in various fields and the industry's higher requirements for reliability and safety, HMM as a data-driven fault diagnosis method has received more and more attention .
目前,根据观测变量的表示方法HMM可分为离散HMM(离散隐马尔可夫模型)与连续HMM(连续隐马尔可夫模型)。但是,在DHMM的实际应用中有三个基本问题需要解决,即评估问题、解码问题以及学习问题,而学习问题是DHMM的三个基本问题中最难以未解决的问题。针对学习问题目前最广泛使用的是BW算法(Baum-Welch算法)和梯度算法,这两种算法虽然能给出DHMM参数的有效估计,但是,BW算法和梯度算法是局部优化方法,对初值有很强依赖性;此外,目前基于DHMM的故障诊断应用中,没有针对故障数据不足的实际情况。At present, HMM can be divided into discrete HMM (discrete hidden Markov model) and continuous HMM (continuous hidden Markov model) according to the representation method of observed variables. However, there are three basic problems to be solved in the practical application of DHMM, namely evaluation problem, decoding problem and learning problem, and the learning problem is the most difficult and unsolved problem among the three basic problems of DHMM. For learning problems, the BW algorithm (Baum-Welch algorithm) and the gradient algorithm are the most widely used. Although these two algorithms can provide effective estimates of the DHMM parameters, the BW algorithm and the gradient algorithm are local optimization methods. There is a strong dependence; in addition, in the current fault diagnosis application based on DHMM, there is no actual situation for insufficient fault data.
发明内容SUMMARY OF THE INVENTION
本发明旨在至少在一定程度上解决上述技术中的技术问题之一。为此,本发明的一个目的在于提出一种基于离散隐马尔可夫模型的轴承故障检测方法,能够降低对初值的依赖性,并能够提高搜索能力,从而能够提高离散隐马尔可夫模型参数学习的精度,并且能够保证故障检测的精度。The present invention aims to solve one of the technical problems in the above technologies at least to a certain extent. Therefore, an object of the present invention is to propose a bearing fault detection method based on the discrete hidden Markov model, which can reduce the dependence on the initial value and improve the search ability, thereby improving the parameters of the discrete hidden Markov model. The accuracy of learning can be guaranteed, and the accuracy of fault detection can be guaranteed.
本发明的第二个目的在于提出一种基于离散隐马尔可夫模型的轴承故障检测系统。The second purpose of the present invention is to propose a bearing fault detection system based on discrete hidden Markov model.
为达到上述目的,本发明第一方面实施例提出了一种基于离散隐马尔可夫模型的轴承故障检测方法,包括以下步骤:建立所述离散隐马尔可夫模型的优化算法;获取待检测轴承数据;对所述待检测轴承数据进行特征提取以得到所述待检测轴承不同故障类型的特征向量;确定所述离散隐马尔可夫模型的代码本以得到所述待检测轴承不同故障类型的观测序列;根据所述优化算法和所述待检测轴承不同故障类型的观测序列训练所述离散隐马尔可夫模型;根据所述待检测轴承不同故障类型的特征向量和训练后的所述离散隐马尔可夫模型对所述待检测轴承进行故障检测。In order to achieve the above object, the embodiment of the first aspect of the present invention proposes a bearing fault detection method based on a discrete hidden Markov model, which includes the following steps: establishing an optimization algorithm for the discrete hidden Markov model; obtaining a bearing to be detected data; perform feature extraction on the bearing data to be detected to obtain feature vectors of different fault types of the bearing to be detected; determine the codebook of the discrete hidden Markov model to obtain observations of different fault types of the bearing to be detected sequence; train the discrete hidden Markov model according to the optimization algorithm and the observation sequence of different fault types of the bearing to be detected; according to the feature vectors of the different fault types of the bearing to be detected and the trained discrete hidden Markov The Koff model performs fault detection on the bearing to be detected.
根据本发明实施例提出的基于离散隐马尔可夫模型的轴承故障检测方法,通过建立离散隐马尔可夫模型的优化算法,并对待检测轴承数据进行特征提取,以及确定离散隐马尔可夫模型的代码本,并根据述优化算法待检测轴承不同故障类型的观测序列训练离散隐马尔可夫模型,以根据待检测轴承不同故障类型的特征向量和训练后的离散隐马尔可夫模型对待检测轴承进行故障检测,由此,能够降低对初值的依赖性,并能够提高搜索能力,从而能够提高离散隐马尔可夫模型参数学习的精度,并且能够保证故障检测的精度。According to the bearing fault detection method based on the discrete hidden Markov model proposed in the embodiment of the present invention, the optimization algorithm of the discrete hidden Markov model is established, and the feature extraction of the bearing data to be detected is performed, and the value of the discrete hidden Markov model is determined. codebook, and train the discrete hidden Markov model according to the observation sequence of different fault types of the bearing to be detected by the optimization algorithm, so as to perform the detection of the bearing to be detected according to the eigenvectors of the different fault types of the bearing to be detected and the trained discrete hidden Markov model. In fault detection, the dependence on the initial value can be reduced, and the search ability can be improved, so that the accuracy of parameter learning of the discrete hidden Markov model can be improved, and the accuracy of fault detection can be guaranteed.
另外,根据本发明上述实施例提出的基于离散隐马尔可夫模型的轴承故障检测方法还可以具有如下附加的技术特征:In addition, the bearing fault detection method based on the discrete hidden Markov model proposed according to the above embodiments of the present invention may also have the following additional technical features:
进一步地,建立所述离散隐马尔可夫模型的优化算法,包括以下步骤:采用多个所述离散隐马尔可夫模型构建拓扑网格;采用正交设计量化法初始化所述拓扑网格;采用双策略竞争学习优化每个所述拓扑网格中的每个离散隐马尔可夫模型以得到第一序列拓扑网格;判断所述第一序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数;若是,则采用协同学习优化所述第一序列拓扑网格中的每个离散隐马尔可夫模型以得到第二序列拓扑网格;判断所述第二序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数;若是,则采用高斯变异优化所述第二序列拓扑网格中的每个离散隐马尔可夫模型以得到下一迭代的拓扑网格;确定所述下一迭代的拓扑网格中似然值最大的离散隐马尔可夫模型并对其执行自学习算法,直至得到的离散隐马尔可夫模型满足终止标准。Further, establishing an optimization algorithm for the discrete hidden Markov model, including the following steps: using a plurality of the discrete hidden Markov models to build a topology grid; using an orthogonal design quantization method to initialize the topology grid; using Dual-strategy competitive learning optimizes each discrete hidden Markov model in each of the topological grids to obtain a first sequence topological grid; judges each discrete hidden Markov model in the first sequence topological grid Whether the random real numbers uniformly distributed in the interval 0 to 1 are smaller than the parameters in the defined interval 0 to 1; if so, use collaborative learning to optimize each discrete hidden Markov model in the topological grid of the first sequence to obtain the second sequence Topological grid; determine whether the random real numbers of each discrete hidden Markov model in the second sequence topological grid uniformly distributed in the interval 0 to 1 are smaller than the parameters in the defined interval 0 to 1; if so, use Gaussian mutation optimization each discrete hidden Markov model in the second sequence of topological grids to obtain the topological grid of the next iteration; determine the discrete hidden Markov model with the largest likelihood value in the topological grid of the next iteration And perform self-learning algorithm on it until the obtained discrete hidden Markov model meets the termination criteria.
进一步地,对所述待检测轴承数据进行特征提取以得到所述待检测轴承不同故障类型的特征向量,包括以下步骤:采用Daubechies小波和小波包分解对所述待检测轴承数据进行特征提取以得到所述待检测轴承不同故障类型的特征向量。Further, performing feature extraction on the bearing data to be detected to obtain feature vectors of different fault types of the bearing to be detected, including the following steps: using Daubechies wavelet and wavelet packet decomposition to perform feature extraction on the bearing data to be detected to obtain The eigenvectors of different fault types of the bearing to be detected.
进一步地,确定所述离散隐马尔可夫模型的代码本以得到所述待检测轴承不同故障类型的观测序列,包括以下步骤:采用k-均值聚类算法确定所述离散隐马尔可夫模型的代码本,以得到所述待检测轴承不同故障类型的观测序列。Further, determining the codebook of the discrete hidden Markov model to obtain observation sequences of different fault types of the bearing to be detected includes the following steps: using a k-means clustering algorithm to determine the discrete hidden Markov model code book to obtain the observation sequence of different fault types of the bearing to be detected.
进一步地,根据所述优化算法和所述待检测轴承不同故障类型的观测序列训练所述离散隐马尔可夫模型,包括以下步骤:对所述待检测轴承不同故障类型的观测序列建立初始离散隐马尔可夫模型;采用所述优化算法训练所述初始离散隐马尔可夫模型直至产生所述观测序列的概率达到最大值。Further, training the discrete hidden Markov model according to the optimization algorithm and the observation sequences of different fault types of the bearing to be detected includes the following steps: establishing an initial discrete hidden Markov model for the observation sequences of the different fault types of the bearing to be detected; Markov model; using the optimization algorithm to train the initial discrete hidden Markov model until the probability of generating the observation sequence reaches a maximum value.
为达到上述目的,本发明第二方面实施例提出了一种基于离散隐马尔可夫模型的轴承故障检测系统。In order to achieve the above object, the embodiment of the second aspect of the present invention proposes a bearing fault detection system based on a discrete hidden Markov model.
基于离散隐马尔可夫模型的轴承故障检测系统,其特征在于,包括:构建模块,所述构建模块用于建立所述离散隐马尔可夫模型的优化算法;获取模块,所述获取模块用于获取待检测轴承数据;提取模块,所述提取模块用于对所述待检测轴承数据进行特征提取以得到所述待检测轴承不同故障类型的特征向量;第一处理模块,所述第一处理模块用于确定所述离散隐马尔可夫模型的代码本以得到所述待检测轴承不同故障类型的观测序列;第二处理模块,所述第二处理模块用于根据所述优化算法和所述待检测轴承不同故障类型的观测序列训练所述离散隐马尔可夫模型;第三处理模块,所述第三处理模块用于根据所述待检测轴承不同故障类型的特征向量和训练后的所述离散隐马尔可夫模型对所述待检测轴承进行故障检测。The bearing fault detection system based on the discrete hidden Markov model is characterized in that it includes: a building module, the building module is used to establish an optimization algorithm of the discrete hidden Markov model; an obtaining module, the obtaining module is used for Obtain the bearing data to be detected; an extraction module, which is used for feature extraction on the bearing data to be detected to obtain feature vectors of different fault types of the bearing to be detected; a first processing module, the first processing module A codebook for determining the discrete hidden Markov model to obtain observation sequences of different fault types of the bearing to be detected; a second processing module, the second processing module is configured to The discrete hidden Markov model is trained by the observation sequence for detecting different fault types of the bearing; the third processing module is used for the feature vector of the different fault types of the bearing to be detected and the trained discrete hidden Markov model. The hidden Markov model performs fault detection on the bearing to be detected.
根据本发明实施例提出的基于离散隐马尔可夫模型的轴承故障检测系统,通过构建模块建立离散隐马尔可夫模型的优化算法,并通过提取模块对待检测轴承数据进行特征提取,以及通过第一处理模块确定离散隐马尔可夫模型的代码本,并通过第二处理模块根据述优化算法待检测轴承不同故障类型的观测序列训练离散隐马尔可夫模型,以通过第三处理模块根据待检测轴承不同故障类型的特征向量和训练后的离散隐马尔可夫模型对待检测轴承进行故障检测,由此,能够降低对初值的依赖性,并能够提高搜索能力,从而能够提高离散隐马尔可夫模型参数学习的精度,并且能够保证故障检测的精度。According to the bearing fault detection system based on the discrete hidden Markov model proposed by the embodiment of the present invention, an optimization algorithm of the discrete hidden Markov model is established through the building module, and the feature extraction module is used to extract the bearing data to be detected, and the first The processing module determines the codebook of the discrete hidden Markov model, and trains the discrete hidden Markov model through the second processing module according to the observation sequence of different fault types of the bearing to be detected by the optimization algorithm, so as to pass the third processing module according to the bearing to be detected. The feature vectors of different fault types and the trained discrete hidden Markov model are used to detect the fault of the bearing to be detected, so that the dependence on the initial value can be reduced, and the search ability can be improved, so that the discrete hidden Markov model can be improved. The accuracy of parameter learning and the accuracy of fault detection can be guaranteed.
另外,根据本发明上述实施例提出的基于离散隐马尔可夫模型的轴承故障检测系统还可以具有如下附加的技术特征:In addition, the bearing fault detection system based on the discrete hidden Markov model proposed according to the above embodiments of the present invention may also have the following additional technical features:
进一步地,所述构建模块具体用于:采用多个所述离散隐马尔可夫模型构建拓扑网格;采用正交设计量化法初始化所述拓扑网格;采用双策略竞争学习优化每个所述拓扑网格中的每个离散隐马尔可夫模型以得到第一序列拓扑网格;判断所述第一序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数;若是,则采用协同学习优化所述第一序列拓扑网格中的每个离散隐马尔可夫模型以得到第二序列拓扑网格;判断所述第二序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数;若是,则采用高斯变异优化所述第二序列拓扑网格中的每个离散隐马尔可夫模型以得到下一迭代的拓扑网格;确定所述下一迭代的拓扑网格中似然值最大的离散隐马尔可夫模型并对其执行自学习算法,直至得到的离散隐马尔可夫模型满足终止标准。Further, the building module is specifically used for: constructing a topological grid by using a plurality of the discrete hidden Markov models; initializing the topological grid by using an orthogonal design quantization method; using dual-strategy competitive learning to optimize each of the Each discrete hidden Markov model in the topological grid is obtained to obtain a first sequence topological grid; it is judged that each discrete hidden Markov model in the first sequence topological grid is uniformly distributed in a random range from 0 to 1. Whether the real number is smaller than the parameters in the defined interval 0 to 1; if so, use collaborative learning to optimize each discrete hidden Markov model in the first sequence topological grid to obtain a second sequence topological grid; judge the second sequence topological grid Whether each discrete hidden Markov model in the sequence topology grid is uniformly distributed in the interval 0 to 1 is a random real number smaller than the parameter in the defined interval 0 to 1; if so, use Gaussian mutation to optimize the second sequence topology grid to obtain the topological grid of the next iteration; determine the discrete hidden Markov model with the largest likelihood value in the topological grid of the next iteration and perform a self-learning algorithm on it until The resulting discrete hidden Markov model satisfies the termination criteria.
进一步地,所述提取模块具体用于:采用Daubechies小波和小波包分解对所述待检测轴承数据进行特征提取以得到所述待检测轴承不同故障类型的特征向量。Further, the extraction module is specifically configured to: perform feature extraction on the bearing data to be detected by using Daubechies wavelet and wavelet packet decomposition to obtain feature vectors of different fault types of the bearing to be detected.
进一步地,所述第一处理模块具体用于:采用k-均值聚类算法确定所述离散隐马尔可夫模型的代码本,以得到所述待检测轴承不同故障类型的观测序列。Further, the first processing module is specifically configured to: adopt a k-means clustering algorithm to determine the codebook of the discrete hidden Markov model, so as to obtain observation sequences of different fault types of the bearing to be detected.
进一步地,所述第二处理模块具体用于:对所述待检测轴承不同故障类型的观测序列建立初始离散隐马尔可夫模型;采用所述优化算法训练所述初始离散隐马尔可夫模型直至产生所述观测序列的概率达到最大值。Further, the second processing module is specifically used to: establish an initial discrete hidden Markov model for the observation sequences of different fault types of the bearing to be detected; use the optimization algorithm to train the initial discrete hidden Markov model until The probability of producing the observation sequence reaches a maximum value.
附图说明Description of drawings
图1为本发明实施例的基于离散隐马尔可夫模型的轴承故障检测方法的流程图;FIG. 1 is a flowchart of a bearing fault detection method based on a discrete hidden Markov model according to an embodiment of the present invention;
图2为本发明一个实施例的建立离散隐马尔可夫模型的优化算法的流程图;2 is a flowchart of an optimization algorithm for establishing a discrete hidden Markov model according to an embodiment of the present invention;
图3为本发明一个实施例的离散隐马尔可夫模型优化算法与现有技术中BW算法的对比图;3 is a comparison diagram of a discrete hidden Markov model optimization algorithm according to an embodiment of the present invention and a BW algorithm in the prior art;
图4为本发明实施例的基于离散隐马尔可夫模型的轴承故障检测系统的方框示意图。FIG. 4 is a schematic block diagram of a bearing fault detection system based on a discrete hidden Markov model according to an embodiment of the present invention.
具体实施方式Detailed ways
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。The technical solutions in the embodiments of the present invention will be clearly and completely described below with reference to the accompanying drawings in the embodiments of the present invention. Obviously, the described embodiments are only a part of the embodiments of the present invention, but not all of the embodiments. Based on the embodiments of the present invention, all other embodiments obtained by those of ordinary skill in the art without creative efforts shall fall within the protection scope of the present invention.
图1为本发明实施例的基于离散隐马尔可夫模型的轴承故障检测方法的流程图。FIG. 1 is a flowchart of a bearing fault detection method based on a discrete hidden Markov model according to an embodiment of the present invention.
如图1所示,本发明实施例的基于离散隐马尔可夫模型的轴承故障检测方法,包括以下步骤:As shown in FIG. 1 , the bearing fault detection method based on the discrete hidden Markov model according to the embodiment of the present invention includes the following steps:
S1,建立离散隐马尔可夫模型的优化算法。S1, an optimization algorithm for establishing discrete hidden Markov models.
具体地,如图2所示,包括以下步骤:Specifically, as shown in Figure 2, the following steps are included:
S101,采用多个离散隐马尔可夫模型构建拓扑网格。S101, a topological mesh is constructed by using multiple discrete hidden Markov models.
更具体地,可采用多个离散隐马尔可夫模型构建拓扑网格G,并且该拓扑网格G的大小可为S×S。其中,每个离散隐马尔可夫模型可固定于拓扑网格G的设定位置,且可与邻域内的离散隐马尔可夫模型进行信息交互。通过利用多个离散隐马尔可夫模型构建拓扑网格G,能够在一定拓扑结构下充分挖掘极其有限的故障数据,以提高故障诊断系统的性能。More specifically, a topological grid G can be constructed by using a plurality of discrete hidden Markov models, and the size of the topological grid G can be S×S. Among them, each discrete hidden Markov model can be fixed at the set position of the topological grid G, and can exchange information with the discrete hidden Markov models in the neighborhood. By using multiple discrete hidden Markov models to build a topological grid G, the extremely limited fault data can be fully mined under a certain topology structure, so as to improve the performance of the fault diagnosis system.
为便于说明,下面将每个离散隐马尔可夫模型的参数集整体转换为一个K维向量,并可设在网格坐标(m,n)上的离散隐马尔可夫模型为Gmn=[z1,z2,…,zK](m,n=1,2,…,S),以及可设该离散隐马尔可夫模型的目标函数值为Obj(Gmn),此外还可设该离散隐马尔可夫模型构成的拓扑网格G,即设在网格坐标(m,n)上的离散隐马尔可夫模型Gmn的邻域为:For the convenience of explanation, the parameter set of each discrete hidden Markov model is converted into a K-dimensional vector as a whole, and the discrete hidden Markov model on the grid coordinates (m, n) can be set as Gmn =[ z1 , z2 ,...,zK ](m,n=1,2,...,S), and the objective function value of the discrete hidden Markov model can be set as Obj(Gmn ), and can also be set as The topological grid G constituted by the discrete hidden Markov model, that is, the neighborhood of the discrete hidden Markov model Gmn set on the grid coordinates (m, n) is:
其中,in,
进一步地,还可设Gt为第t次迭代后所得拓扑网格,并可设在Gt与Gt+1之间获得的拓扑网格依次为Gt+1/3和Gt+2/3。Bt是Gt的所有离散隐马尔可夫模型中目标函数值最小的模型,BTt是从G0直到Gt的所有离散隐马尔可夫模型中目标函数值最小的模型,PS、PC和PG是预定义的区间(0,1)内参数。Further, Gt can also be set as the topological mesh obtained after the t-th iteration, and the topological mesh obtained between Gt and Gt+1 can be set as Gt+1/3 and Gt+2 in turn./3 . Bt is the model with the smallest objective function value among all discrete hidden Markov models of Gt , BTt is the model with the smallest objective function value among all discrete hidden Markov models from G0 to Gt , PS , PC and PG are parameters within the predefined interval (0,1).
S102,采用正交设计量化法初始化拓扑网格。S102, the topological grid is initialized by using the orthogonal design quantization method.
更具体地,可定义zi为第i个因素,其量化域为[ci,di](其中,0≤ci≤di≤1),并可将[ci,di]量化为以下H(要求为奇数)个水平:More specifically, zi can be defined as thei -th factor, and its quantization domain is [ci ,di ] (where 0≤ci≤d i≤1 ), and [ci,d i] can be quantized for the following H (required odd) levels:
其中,j为变量。Among them, j is a variable.
进一步地,可采用排列法构建正交组LJ(HQ),其中J=Hl,Q=(Hl-1)/(H-1),l是满足的最小正整数。Further, an orthogonal group LJ (HQ ) can be constructed by the permutation method, where J=Hl , Q=(Hl -1)/(H-1), and l is satisfying The smallest positive integer of .
进一步地,可从正交组LJ(HQ)中随机选择K列得到LJ(HK),并可将得到的LJ(HK)应用于δi,j得到下列J个向量:Further, LJ (HK ) can be obtained by randomly selecting K columns from the orthogonal group LJ (HQ ), and the obtained LJ (HK ) can be applied to δi,j to obtain the following J vectors:
进一步地,还可从上述J个向量中随机选择S2个向量,并且每一个选择得到的向量还可经过标准化后恢复为λ=(π,A,B)的形式,从而可得到初始拓扑网格G0,同时可更新B0,且t←0。Further, S2 vectors can also be randomly selected from the above J vectors, and each selected vector can be restored to the form of λ=(π, A, B) after normalization, so that the initial topology network can be obtained. grid G0 , B0 can be updated at the same time, and t←0.
S103,采用双策略竞争学习优化每个拓扑网格中的每个离散隐马尔可夫模型以得到第一序列拓扑网格。S103, adopting dual-strategy competitive learning to optimize each discrete hidden Markov model in each topological grid to obtain a first sequence of topological grids.
更具体地,可对拓扑网格Gt中的每个离散隐马尔可夫模型执行双策略竞争学习,以得到第一序列拓扑网格Gt+1/3。More specifically, dual-policy competitive learning may be performed on each discrete hidden Markov model in the topological grid Gt to obtain a first sequence of topological grids Gt+1/3 .
举例而言,可先确定拓扑网格Gt中的每个离散隐马尔可夫模型,即Gij=[z1,z2,…,zK](i,j=1,2,…,S)的邻域中目标函数值最小的模型Mij=[α1,α2,…,αK],进而比较Gi,j与Mi,j的目标函数值。其中,若Gi,j的目标函数值小于Mi,j的目标函数值,则保留该离散隐马尔可夫模型;若Gi,j的目标函数值大于等于Mi,j的目标函数值,则采用Mi,j所生成的子模型Subij=[β1,β2,…,βK]取代该离散隐马尔可夫模型。、For example, each discrete hidden Markov model in the topological grid Gt can be determined first, that is, Gij =[z1 ,z2 ,...,zK ](i,j=1,2,..., The model with the smallest objective function value in the neighborhood of S) is Mij =[α1 ,α2 ,...,αK ], and then the objective function values of Gi,j and Mi,j are compared. Among them, if the objective function value of Gi,j is less than the objective function value of Mi,j , the discrete hidden Markov model is retained; if the objective function value of Gi,j is greater than or equal to the objective function value of Mi,j , the sub-model Subij =[β1 ,β2 ,...,βK ] generated by Mi,j is used to replace the discrete hidden Markov model. ,
进一步地,Mi,j可采用下面两种策略生成子模型:Further, Mi,j can use the following two strategies to generate sub-models:
策略一:Subij=[β1,β2,…,βK]由下式生成:Strategy 1: Subij = [β1 ,β2 ,...,βK ] is generated by the following formula:
其中,χ=αi+U(-1,1)×(αi-zi),U(-1,1)表示均匀分布于[-1,1]的随机实数。Wherein, χ=αi +U(-1,1)×(αi -zi ), U(-1,1) represents a random real number uniformly distributed in [-1,1].
策略二:Subij=[β1,β2,…,βK]由下式生成Strategy 2: Subij = [β1 ,β2 ,...,βK ] is generated by the following formula
其中,U(0,1)表示均匀分布于[0,1]的随机实数。Among them, U(0,1) represents a random real number uniformly distributed in [0,1].
此外需要说明的是,上述两种策略由概率PS确定,如果U(0,1)<PS,则执行策略一,否则执行策略二。In addition, it should be noted that the above two strategies are determined by the probability PS , if U(0,1)<PS ,
S104,判断第一序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数。S104: Determine whether the random real numbers of each discrete hidden Markov model uniformly distributed in the interval 0 to 1 in the topological grid of the first sequence are smaller than the parameters in the defined interval 0 to 1.
S105,若是,则采用协同学习优化第一序列拓扑网格中的每个离散隐马尔可夫模型以得到第二序列拓扑网格。S105, if yes, adopt collaborative learning to optimize each discrete hidden Markov model in the first sequence of topological grids to obtain a second sequence of topological grids.
更具体地,对于第一序列拓扑网格Gt+1/3中的每个离散隐马尔可夫模型,可判断U(0,1)<Pc是否成立,若成立,则可采用协同学习优化第一序列拓扑网格Gt+1/3中的每个离散隐马尔可夫模型以得到第二序列拓扑网格Gt+2/3。需要说明的是,协同学习的过程为:More specifically, for each discrete hidden Markov model in the first sequence topological grid Gt+1/3 , it can be judged whether U(0,1)<Pc holds, and if so, collaborative learning can be used. Each discrete hidden Markov model in the first sequence topological grid Gt+1/3 is optimized to obtain a second sequence topological grid Gt+2/3 . It should be noted that the process of collaborative learning is as follows:
首先,可设由Gij与Mij生成的搜索空间为First, the search space generated by Gij and Mij can be set as
其中,ε=[min(α1,z1),…,min(αK,zK)],whereε = [min(α1 ,z1 ),...,min(αK ,zK )],
进一步地,可将的第i维区域量化为以下F个水平:Further, it can be The i-th dimensional region of is quantized into the following F levels:
进一步地,可将变量z1,z2,…,zK分为V组,每组可看作一个因子,首先可随机产生V-1个整数ei(i=1,2,…,V-1),使其满足1<e1<e2<…<eV-1<K,接着可生成以下V个因子:Further, the variables z1 , z2 ,...,zK can be divided into V groups, and each group can be regarded as a factor. First, V-1 integers ei (i=1,2,...,V can be randomly generated -1), so that it satisfies 1<e1 <e2 <...<eV-1 <K, then the following V factors can be generated:
其中,第i个因子γi的F个水平定义为:where the F levels of theith factor γi are defined as:
其中,[η(i,1),η(i,2),…,η(i,F)]是对[ηi,1,ηi,2,…,ηi,F]各分量的随机重排且e0为0。where [η (i,1) ,η (i,2) ,…,η (i,F) ] is a random rearranged and e0 is 0.
进一步地,可参照步骤S102构建LU(FV)=[wij]U×V,并可应用LU(FV)产生下列U个模型:Further, LU (FV )=[wiij ]U×V can be constructed with reference to step S102, and LU (FV ) can be applied to generate the following U models:
进而可在这些模型中选择似然值最大的模型取代Gi,j。Then, among these models, the model with the largest likelihood value can be selected to replace Gi,j.
S106,判断第二序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数。S106: Determine whether the random real numbers of each discrete hidden Markov model uniformly distributed in the interval 0 to 1 in the topological grid of the second sequence are smaller than the parameters in the defined interval 0 to 1.
S107,若是,则采用高斯变异优化第二序列拓扑网格中的每个离散隐马尔可夫模型以得到下一迭代的拓扑网格。S107, if yes, optimize each discrete hidden Markov model in the second sequence of topological grids by using Gaussian mutation to obtain a topological grid of the next iteration.
更具体地,对于第二序列拓扑网格Gt+2/3中的每个离散隐马尔可夫模型,可判断U(0,1)<Pc是否成立,若成立,则可采用高斯变异优化第二序列拓扑网格Gt+2/3中的每个离散隐马尔可夫模型以得到下一迭代的拓扑网格Gt+1。需要说明的是,高斯变异的过程为:More specifically, for each discrete hidden Markov model in the second sequence topological grid Gt+2/3 , it can be judged whether U(0,1)<Pc holds, and if so, Gaussian variation can be used. Each discrete hidden Markov model in the second sequence of topological grids Gt+2/3 is optimized to obtain the topological grid Gt+1 of the next iteration. It should be noted that the process of Gaussian mutation is:
首先,可设t为迭代次数,并可设G(0,1/t)为高斯随机数产生器,由此,对于Gij=[z1,z2,…,zK],(i,j=1,2,…,S)的每个分量,即每个离散隐马尔可夫模型,可判断Um(0,1)≥1/K是否成立,若成立,则zm←zm+G(0,1/t),(m=1,2,…,K),其中,Um(0,1)是每个分量,即每个离散隐马尔可夫模型分别独立产生的随机数。由此,可采用新的离散隐马尔可夫模型取代原模型。First, t can be set as the number of iterations, and G(0, 1/t) can be set as a Gaussian random number generator, thus, for Gij =[z1 ,z2 ,...,zK ], (i, Each component of j=1,2,...,S), that is, each discrete hidden Markov model, can judge whether Um (0,1)≥1/K holds, and if so, then zm ←zm +G(0,1/t),(m=1,2,…,K), where Um (0,1) is a random number. Thus, a new discrete hidden Markov model can be used to replace the original model.
S108,确定下一迭代的拓扑网格中似然值最大的离散隐马尔可夫模型并对其执行自学习算法,直至得到的离散隐马尔可夫模型满足终止标准。S108: Determine the discrete hidden Markov model with the largest likelihood value in the topological grid of the next iteration, and perform a self-learning algorithm on it, until the obtained discrete hidden Markov model satisfies the termination criterion.
更具体地,可在下一迭代的拓扑网格Gt+1中确定似然值最大的离散隐马尔可夫模型,即Bt+1,并对其执行自学习算法。需要说明的是,自学习算法的过程为:More specifically, the discrete hidden Markov model with the largest likelihood value, ie, Bt+1 , can be determined in the topological grid Gt+1 of the next iteration, and a self-learning algorithm is performed on it. It should be noted that the process of the self-learning algorithm is:
首先,可将Bt+1记为Gij=[z1,z2,…,zK],由此可生成一个小规模的大小为S′×S′的初始拓扑网格sG0,并且该初始拓扑网格sG0中的离散隐马尔可夫模型,即sgkl(k,l=1,2,…,S′)为:First, we can denote Bt+1 as Gij= [z1 ,z2 , . The discrete hidden Markov model in the initial topological grid sG0 , that is, sgkl (k,l=1,2,...,S') is:
其中,的各元素为:in, The elements of are:
其中,σ是搜索半径。where σ is the search radius.
进一步地,生成初始拓扑网格sG0后,可设sGt为初始拓扑网格sG0经过t次迭代后所得网格,并可设sBTt是(sG0,sG1,…,sGt)的所有离散隐马尔可夫模型中目标函数值最小的模型,还可将拓扑网格sGt中目标函数值最小的离散隐马尔可夫模型记为sBt,此外,还可设sT是迭代终止准则、sPG是预定义的区间(0,1)内参数。Further, after the initial topological mesh sG0 is generated, sGt can be set as the mesh obtained after t iterations of the initial topological mesh sG0 , and sBTt can be set to be (sG0 ,sG1 ,...,sGt ) The model with thesmallest objective function value among all discrete hiddenMarkov models of Criterion,spG is a parameter within a predefined interval (0,1).
进一步地,可先对拓扑网格sGt中的每个离散隐马尔可夫模型执行双策略竞争学习中的策略二,得到拓扑网格sGt+1/2;进而可判断U(0,1)<sPG是否成立,若成立,则对拓扑网格sGt+1/2的每个模型执行高斯变异,得到拓扑网格sGt+1;最后可判断拓扑网格sGt+1中目标函数值最小的离散隐马尔可夫模型sBt+1的目标函数值是否大于sBTt,若是,则sBTt+1←sBt+1,若否,则sBTt+1←sBTt、sBt+1←sBTt。Further,
进一步地,可判断迭代次数t<sT是否成立,若成立,则t←t+1,继续执行上述步骤;若不成立,则以sBTt取代Gij并终止自学习过程。Further, it can be judged whether the number of iterations t<sT is established, if so, then t←t+1, and continue to perform the above steps; if not, replace Gij with sBTt and terminate the self-learning process.
下面将结合图3进一步说明本发明的离散隐马尔可夫模型优化算法的实用性。The practicability of the discrete hidden Markov model optimization algorithm of the present invention will be further described below with reference to FIG. 3 .
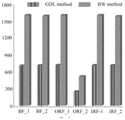
如图3所示,本发明离散隐马尔可夫模型优化算法,在获得1马力和2马力时的球体故障、外圈故障和内圈故障,即BF_1、BF_2,ORF_1、ORF_2,IRF_1、IRF_2的目标函数值时,其值明显小于现有技术中BW算法在1马力和2马力时的球体故障、外圈故障和内圈故障,即BF_1、BF_2,ORF_1、ORF_2,IRF_1、IRF_2获得的目标函数值,由此,可看出本发明离散隐马尔可夫模型优化算法能够克服现有技术中BW算法仅具有局部搜索能力且对初值有很强依赖性的缺点,从而能够提高离散隐马尔可夫模型参数学习的精度。As shown in Figure 3, the discrete hidden Markov model optimization algorithm of the present invention, when obtaining 1 horsepower and 2 horsepower, the sphere fault, outer ring fault and inner ring fault, namely BF_1, BF_2, ORF_1, ORF_2, IRF_1, IRF_2 The objective function value is significantly smaller than the sphere fault, outer ring fault and inner ring fault of the BW algorithm in the prior art at 1 horsepower and 2 horsepower, that is, the objective functions obtained by BF_1, BF_2, ORF_1, ORF_2, IRF_1, IRF_2 Therefore, it can be seen that the discrete hidden Markov model optimization algorithm of the present invention can overcome the shortcomings of the prior art that the BW algorithm only has local search ability and has a strong dependence on the initial value, thereby improving the discrete hidden Markov model. accuracy of model parameter learning.
S2,获取待检测轴承数据。S2, obtain the bearing data to be detected.
具体地,可通过轴承数据中心得到待检测轴承的数据。Specifically, the data of the bearing to be tested can be obtained through the bearing data center.
S3,对待检测轴承数据进行特征提取以得到待检测轴承不同故障类型的特征向量。S3, perform feature extraction on the bearing data to be detected to obtain feature vectors of different fault types of the bearing to be detected.
具体地,可采用Daubechies小波和小波包分解对待检测轴承数据进行特征提取以得到待检测轴承不同故障类型的特征向量,例如可采用db4和3个分解水平的小包分解对待检测轴承正常状况、以及每种故障状况的数据进行特征提取。Specifically, Daubechies wavelet and wavelet packet decomposition can be used to perform feature extraction on the bearing data to be detected to obtain feature vectors of different fault types of the bearing to be detected. Feature extraction is performed on the data of various fault conditions.
S4,确定离散隐马尔可夫模型的代码本以得到待检测轴承不同故障类型的观测序列。S4, determine the codebook of the discrete hidden Markov model to obtain observation sequences of different fault types of the bearing to be detected.
具体地,可采用k-均值聚类算法确定离散隐马尔可夫模型的代码本,以得到待检测轴承不同故障类型的观测序列,例如观测序列O=o1o2…oT。Specifically, the k-means clustering algorithm can be used to determine the codebook of the discrete hidden Markov model, so as to obtain the observation sequence of different fault types of the bearing to be detected, for example, the observation sequence O=o1 o2 ... oT .
S5,根据优化算法和待检测轴承不同故障类型的观测序列训练离散隐马尔可夫模型。S5, the discrete hidden Markov model is trained according to the optimization algorithm and the observation sequences of different fault types of the bearing to be detected.
具体地,可对待检测轴承不同故障类型的观测序列建立初始离散隐马尔可夫模型,并可采用优化算法训练初始离散隐马尔可夫模型直至产生观测序列的概率达到最大值,例如观测序列O=o1o2…oT的概率P(O|λ)达到最大,其中,λ=(A,B,π)为训练后的离散隐马尔可夫模型。Specifically, an initial discrete hidden Markov model can be established for the observation sequences of different fault types of the bearing to be detected, and an optimization algorithm can be used to train the initial discrete hidden Markov model until the probability of generating the observation sequence reaches the maximum value, for example, the observation sequence O= The probability P(O|λ) of o1 o2 ... oT reaches the maximum, where λ=(A, B, π) is the trained discrete hidden Markov model.
S6,根据待检测轴承不同故障类型的特征向量和训练后的离散隐马尔可夫模型对待检测轴承进行故障检测。S6, according to the feature vectors of different fault types of the bearing to be detected and the trained discrete hidden Markov model, the fault detection of the bearing to be detected is performed.
具体地,可将待检测轴承不同故障类型的特征向量输入训练后的离散隐马尔可夫模型,然后可采用量化指标:CP=logP(ot|o1o2…ot-1,λ),从而可根据最高的CP值来选择相应的故障类型作为最终的诊断决策。Specifically, the feature vectors of different fault types of the bearing to be detected can be input into the trained discrete hidden Markov model, and then the quantitative index can be used: CP=logP(ot |o1 o2 ...ot-1 , λ) , so that the corresponding fault type can be selected as the final diagnosis decision according to the highest CP value.
下面将结合表1和表2进一步说明本发明的基于离散隐马尔可夫模型的轴承故障检测方法的实用性。The practicability of the bearing fault detection method based on the discrete hidden Markov model of the present invention will be further described below with reference to Table 1 and Table 2.
如表1所示,通过本发明的基于离散隐马尔可夫模型的轴承故障检测方法对轴承的球体故障、外圈故障和内圈故障进行检测时,其训练运行状况和测试运行状况分别为1772rpm,1hp和1750rpm,2hp,其控制极限为2.0577,故障检测率均为100%;进一步如表2所示,在对轴承的球体故障、外圈故障和内圈故障进行测试时,即通过475、477、475测试样本分别对对轴承的球体故障、外圈故障和内圈故障进行测试时,其故障定位准确率分别为100%、98.95%、99.79%,由此,可看出本发明的基于离散隐马尔可夫模型的轴承故障检测方法具有较高的故障检测准确率和定位精度。As shown in Table 1, when the ball fault, outer ring fault and inner ring fault of the bearing are detected by the bearing fault detection method based on the discrete hidden Markov model of the present invention, the training operating conditions and the testing operating conditions are respectively 1772 rpm , 1hp and 1750rpm, 2hp, its control limit is 2.0577, and the fault detection rate is 100%; further as shown in Table 2, when testing the ball fault, outer ring fault and inner ring fault of the bearing, it passed 475, When the 477 and 475 test samples respectively test the ball fault, outer ring fault and inner ring fault of the bearing, the fault location accuracy rates are 100%, 98.95% and 99.79% respectively. The bearing fault detection method based on discrete hidden Markov model has high fault detection accuracy and positioning accuracy.
表1Table 1
表2Table 2
根据本发明实施例提出的基于离散隐马尔可夫模型的轴承故障检测方法,通过建立离散隐马尔可夫模型的优化算法,并对待检测轴承数据进行特征提取,以及确定离散隐马尔可夫模型的代码本,并根据述优化算法待检测轴承不同故障类型的观测序列训练离散隐马尔可夫模型,以根据待检测轴承不同故障类型的特征向量和训练后的离散隐马尔可夫模型对待检测轴承进行故障检测,由此,能够降低对初值的依赖性,并能够提高搜索能力,从而能够提高离散隐马尔可夫模型参数学习的精度,并且能够保证故障检测的精度。According to the bearing fault detection method based on the discrete hidden Markov model proposed in the embodiment of the present invention, the optimization algorithm of the discrete hidden Markov model is established, and the feature extraction of the bearing data to be detected is performed, and the value of the discrete hidden Markov model is determined. codebook, and train the discrete hidden Markov model according to the observation sequence of different fault types of the bearing to be detected by the optimization algorithm, so as to perform the detection of the bearing to be detected according to the eigenvectors of the different fault types of the bearing to be detected and the trained discrete hidden Markov model. In fault detection, the dependence on the initial value can be reduced, and the search ability can be improved, so that the accuracy of parameter learning of the discrete hidden Markov model can be improved, and the accuracy of fault detection can be guaranteed.
对应上述实施例,本发明还提出了一种基于离散隐马尔可夫模型的轴承故障检测系统。Corresponding to the above embodiments, the present invention also proposes a bearing fault detection system based on discrete hidden Markov model.
如图4所示,本发明的基于离散隐马尔可夫模型的轴承故障检测系统,包括构建模块10、获取模块20、提取模块30、第一处理模块40、第二处理模块50、第三处理模块60。其中,所述构建模块10用于建立所述离散隐马尔可夫模型的优化算法;所述获取模块20用于获取待检测轴承数据;所述提取模块30用于对所述待检测轴承数据进行特征提取以得到所述待检测轴承不同故障类型的特征向量;所述第一处理模块40用于确定所述离散隐马尔可夫模型的代码本以得到所述待检测轴承不同故障类型的观测序列;所述第二处理模块50用于根据所述优化算法和所述待检测轴承不同故障类型的观测序列训练所述离散隐马尔可夫模型;所述第三处理模块60用于根据所述待检测轴承不同故障类型的特征向量和训练后的所述离散隐马尔可夫模型对所述待检测轴承进行故障检测。As shown in FIG. 4 , the bearing fault detection system based on the discrete hidden Markov model of the present invention includes a building module 10 , an acquisition module 20 , an extraction module 30 , a first processing module 40 , a second processing module 50 , and a third processing module module 60. Wherein, the building module 10 is used to establish the optimization algorithm of the discrete hidden Markov model; the acquisition module 20 is used to acquire the bearing data to be detected; Feature extraction to obtain feature vectors of different fault types of the bearing to be detected; the first processing module 40 is used to determine the codebook of the discrete hidden Markov model to obtain the observation sequence of different fault types of the bearing to be detected The second processing module 50 is used to train the discrete hidden Markov model according to the optimization algorithm and the observation sequence of different fault types of the bearing to be detected; the third processing module 60 is used to train the discrete hidden Markov model according to the The eigenvectors for detecting different fault types of the bearing and the trained discrete hidden Markov model are used to detect the fault of the bearing to be detected.
在本发明的一个实施例中,所述构建模块10具体用于:采用多个所述离散隐马尔可夫模型构建拓扑网格;采用正交设计量化法初始化所述拓扑网格;采用双策略竞争学习优化每个所述拓扑网格中的每个离散隐马尔可夫模型以得到第一序列拓扑网格;判断所述第一序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数;若是,则采用协同学习优化所述第一序列拓扑网格中的每个离散隐马尔可夫模型以得到第二序列拓扑网格;判断所述第二序列拓扑网格中的每个离散隐马尔可夫模型均匀分布在区间0到1的随机实数是否小于定义区间0到1内参数;若是,则采用高斯变异优化所述第二序列拓扑网格中的每个离散隐马尔可夫模型以得到下一迭代的拓扑网格;确定所述下一迭代的拓扑网格中似然值最大的离散隐马尔可夫模型并对其执行自学习算法,直至得到的离散隐马尔可夫模型满足终止标准。In an embodiment of the present invention, the building module 10 is specifically configured to: construct a topological grid by using a plurality of the discrete hidden Markov models; initialize the topological grid by using an orthogonal design quantization method; adopt a dual strategy Competitive learning optimizes each discrete hidden Markov model in each of the topological grids to obtain a first sequence topological grid; judging that each discrete hidden Markov model in the first sequence topological grid is uniformly distributed Whether the random real numbers in the interval 0 to 1 are smaller than the parameters in the defined interval 0 to 1; if so, use collaborative learning to optimize each discrete hidden Markov model in the first sequence topology grid to obtain the second sequence topology grid Grid; judge whether the random real numbers of each discrete hidden Markov model uniformly distributed in the interval 0 to 1 in the second sequence topological grid are smaller than the parameters in the defined interval 0 to 1; if so, use Gaussian mutation to optimize the described each discrete hidden Markov model in the second sequence of topological grids to obtain the topological grid of the next iteration; determine the discrete hidden Markov model with the largest likelihood value in the topological grid of the next iteration It executes a self-learning algorithm until the resulting discrete hidden Markov model satisfies the termination criteria.
更具体地,构建模块10可采用多个离散隐马尔可夫模型构建拓扑网格G,并且该拓扑网格G的大小可为S×S。其中,每个离散隐马尔可夫模型可固定于拓扑网格G的设定位置,且可与邻域内的离散隐马尔可夫模型进行信息交互。通过利用多个离散隐马尔可夫模型构建拓扑网格G,能够在一定拓扑结构下充分挖掘极其有限的故障数据,以提高故障诊断系统的性能。More specifically, the building module 10 can use a plurality of discrete hidden Markov models to build a topological grid G, and the size of the topological grid G can be S×S. Among them, each discrete hidden Markov model can be fixed at the set position of the topological grid G, and can exchange information with the discrete hidden Markov models in the neighborhood. By using multiple discrete hidden Markov models to build a topological grid G, the extremely limited fault data can be fully mined under a certain topology structure, so as to improve the performance of the fault diagnosis system.
为便于说明,下面将每个离散隐马尔可夫模型的参数集整体转换为一个K维向量,并可设在网格坐标(m,n)上的离散隐马尔可夫模型为Gmn=[z1,z2,…,zK](m,n=1,2,…,S),以及可设该离散隐马尔可夫模型的目标函数值为Obj(Gmn),此外还可设该离散隐马尔可夫模型构成的拓扑网格G,即设在网格坐标(m,n)上的离散隐马尔可夫模型Gmn的邻域为:For the convenience of explanation, the parameter set of each discrete hidden Markov model is converted into a K-dimensional vector as a whole, and the discrete hidden Markov model on the grid coordinates (m, n) can be set as Gmn =[ z1 , z2 ,...,zK ](m,n=1,2,...,S), and the objective function value of the discrete hidden Markov model can be set as Obj(Gmn ), and can also be set as The topological grid G constituted by the discrete hidden Markov model, that is, the neighborhood of the discrete hidden Markov model Gmn set on the grid coordinates (m, n) is:
其中,in,
进一步地,还可设Gt为第t次迭代后所得拓扑网格,并可设在Gt与Gt+1之间获得的拓扑网格依次为Gt+1/3和Gt+2/3。Bt是Gt的所有离散隐马尔可夫模型中目标函数值最小的模型,BTt是从G0直到Gt的所有离散隐马尔可夫模型中目标函数值最小的模型,PS、PC和PG是预定义的区间(0,1)内参数。Further, Gt can also be set as the topological mesh obtained after the t-th iteration, and the topological mesh obtained between Gt and Gt+1 can be set as Gt+1/3 and Gt+2 in turn./3 . Bt is the model with the smallest objective function value among all discrete hidden Markov models of Gt , BTt is the model with the smallest objective function value among all discrete hidden Markov models from G0 to Gt , PS , PC and PG are parameters within the predefined interval (0,1).
更具体地,构建模块10可定义zi为第i个因素,其量化域为[ci,di](其中,0≤ci≤di≤1),并可将[ci,di]量化为以下H(要求为奇数)个水平:More specifically, the building block 10 can definezi as the ith factor whose quantization domain is [ci ,d i] (wherein 0≤ci≤d i≤1 ), and can use [ci ,di ] is quantized to the following H (odd required) levels:
其中,j为变量。Among them, j is a variable.
进一步地,可采用排列法构建正交组LJ(HQ),其中J=Hl,Q=(Hl-1)/(H-1),l是满足的最小正整数。Further, an orthogonal group LJ (HQ ) can be constructed by the permutation method, where J=Hl , Q=(Hl -1)/(H-1), and l is satisfying The smallest positive integer of .
进一步地,可从正交组LJ(HQ)中随机选择K列得到LJ(HK),并可将得到的LJ(HK)应用于δi,j得到下列J个向量:Further, LJ (HK ) can be obtained by randomly selecting K columns from the orthogonal group LJ (HQ ), and the obtained LJ (HK ) can be applied to δi,j to obtain the following J vectors:
进一步地,还可从上述J个向量中随机选择S2个向量,并且每一个选择得到的向量还可经过标准化后恢复为λ=(π,A,B)的形式,从而可得到初始拓扑网格G0,同时可更新B0,且t←0。Further, S2 vectors can also be randomly selected from the above J vectors, and each selected vector can be restored to the form of λ=(π, A, B) after normalization, so that the initial topology network can be obtained. grid G0 , B0 can be updated at the same time, and t←0.
更具体地,构建模块10可对拓扑网格Gt中的每个离散隐马尔可夫模型执行双策略竞争学习,以得到第一序列拓扑网格Gt+1/3。More specifically, the building module 10 may perform dual-policy competitive learning on each discrete hidden Markov model in the topological grid Gt to obtain a first sequence of topological grids Gt+1/3 .
举例而言,可先确定拓扑网格Gt中的每个离散隐马尔可夫模型,即Gij=[z1,z2,…,zK](i,j=1,2,…,S)的邻域中目标函数值最小的模型Mij=[α1,α2,…,αK],进而比较Gi,j与Mi,j的目标函数值。其中,若Gi,j的目标函数值小于Mi,j的目标函数值,则保留该离散隐马尔可夫模型;若Gi,j的目标函数值大于等于Mi,j的目标函数值,则采用Mi,j所生成的子模型Subij=[β1,β2,…,βK]取代该离散隐马尔可夫模型。、For example, each discrete hidden Markov model in the topological grid Gt can be determined first, that is, Gij =[z1 ,z2 ,...,zK ](i,j=1,2,..., The model with the smallest objective function value in the neighborhood of S) is Mij =[α1 ,α2 ,...,αK ], and then the objective function values of Gi,j and Mi,j are compared. Among them, if the objective function value of Gi,j is less than the objective function value of Mi,j , the discrete hidden Markov model is retained; if the objective function value of Gi,j is greater than or equal to the objective function value of Mi,j , the sub-model Subij =[β1 ,β2 ,...,βK ] generated by Mi,j is used to replace the discrete hidden Markov model. ,
进一步地,Mi,j可采用下面两种策略生成子模型:Further, Mi,j can use the following two strategies to generate sub-models:
策略一:Subij=[β1,β2,…,βK]由下式生成:Strategy 1: Subij = [β1 ,β2 ,...,βK ] is generated by the following formula:
其中,χ=αi+U(-1,1)×(αi-zi),U(-1,1)表示均匀分布于[-1,1]的随机实数。Wherein, χ=αi +U(-1,1)×(αi -zi ), U(-1,1) represents a random real number uniformly distributed in [-1,1].
策略二:Subij=[β1,β2,…,βK]由下式生成Strategy 2: Subij = [β1 ,β2 ,...,βK ] is generated by the following formula
其中,U(0,1)表示均匀分布于[0,1]的随机实数。Among them, U(0,1) represents a random real number uniformly distributed in [0,1].
此外需要说明的是,上述两种策略由概率PS确定,如果U(0,1)<PS,则执行策略一,否则执行策略二。In addition, it should be noted that the above two strategies are determined by the probability PS , if U(0,1)<PS ,
更具体地,对于第一序列拓扑网格Gt+1/3中的每个离散隐马尔可夫模型,可判断U(0,1)<Pc是否成立,若成立,则可采用协同学习优化第一序列拓扑网格Gt+1/3中的每个离散隐马尔可夫模型以得到第二序列拓扑网格Gt+2/3。需要说明的是,协同学习的过程为:More specifically, for each discrete hidden Markov model in the first sequence topological grid Gt+1/3 , it can be judged whether U(0,1)<Pc holds, and if so, collaborative learning can be used. Each discrete hidden Markov model in the first sequence topological grid Gt+1/3 is optimized to obtain a second sequence topological grid Gt+2/3 . It should be noted that the process of collaborative learning is as follows:
首先,可设由Gij与Mij生成的搜索空间为First, the search space generated by Gij and Mij can be set as
其中,ε=[min(α1,z1),…,min(αK,zK)],whereε = [min(α1 ,z1 ),...,min(αK ,zK )],
进一步地,可将的第i维区域量化为以下F个水平:Further, it can be The i-th dimensional region of is quantized into the following F levels:
进一步地,可将变量z1,z2,…,zK分为V组,每组可看作一个因子,首先可随机产生V-1个整数ei(i=1,2,…,V-1),使其满足1<e1<e2<…<eV-1<K,接着可生成以下V个因子:Further, the variables z1 , z2 ,...,zK can be divided into V groups, and each group can be regarded as a factor. First, V-1 integers ei (i=1,2,...,V can be randomly generated -1), so that it satisfies 1<e1 <e2 <...<eV-1 <K, then the following V factors can be generated:
其中,第i个因子γi的F个水平定义为:where the F levels of theith factor γi are defined as:
其中,[η(i,1),η(i,2),…,η(i,F)]是对[ηi,1,ηi,2,…,ηi,F]各分量的随机重排且e0为0。where [η (i,1) ,η (i,2) ,…,η (i,F) ] is a random rearranged and e0 is 0.
进一步地,可参照步骤S102构建LU(FV)=[wij]U×V,并可应用LU(FV)产生下列U个模型:Further, LU (FV )=[wiij ]U×V can be constructed with reference to step S102, and LU (FV ) can be applied to generate the following U models:
进而可在这些模型中选择似然值最大的模型取代Gi,j。Then, among these models, the model with the largest likelihood value can be selected to replace Gi,j.
更具体地,对于第二序列拓扑网格Gt+2/3中的每个离散隐马尔可夫模型,可判断U(0,1)<Pc是否成立,若成立,则可采用高斯变异优化第二序列拓扑网格Gt+2/3中的每个离散隐马尔可夫模型以得到下一迭代的拓扑网格Gt+1。需要说明的是,高斯变异的过程为:More specifically, for each discrete hidden Markov model in the second sequence topological grid Gt+2/3 , it can be judged whether U(0,1)<Pc holds, and if so, Gaussian variation can be used. Each discrete hidden Markov model in the second sequence of topological grids Gt+2/3 is optimized to obtain the topological grid Gt+1 of the next iteration. It should be noted that the process of Gaussian mutation is:
首先,可设t为迭代次数,并可设G(0,1/t)为高斯随机数产生器,由此,对于Gij=[z1,z2,…,zK],(i,j=1,2,…,S)的每个分量,即每个离散隐马尔可夫模型,可判断Um(0,1)≥1/K是否成立,若成立,则zm←zm+G(0,1/t),(m=1,2,…,K),其中,Um(0,1)是每个分量,即每个离散隐马尔可夫模型分别独立产生的随机数。由此,可采用新的离散隐马尔可夫模型取代原模型。First, t can be set as the number of iterations, and G(0, 1/t) can be set as a Gaussian random number generator, thus, for Gij =[z1 ,z2 ,...,zK ], (i, Each component of j=1,2,...,S), that is, each discrete hidden Markov model, can judge whether Um (0,1)≥1/K holds, and if so, then zm ←zm +G(0,1/t),(m=1,2,…,K), where Um (0,1) is a random number. Thus, a new discrete hidden Markov model can be used to replace the original model.
更具体地,构建模块10可在下一迭代的拓扑网格Gt+1中确定似然值最大的离散隐马尔可夫模型,即Bt+1,并对其执行自学习算法。需要说明的是,自学习算法的过程为:More specifically, the building module 10 may determine the discrete hidden Markov model with the largest likelihood value in the topological grid Gt+1 of the next iteration, ie, Bt+1 , and perform a self-learning algorithm on it. It should be noted that the process of the self-learning algorithm is:
首先,可将Bt+1记为Gij=[z1,z2,…,zK],由此可生成一个小规模的大小为S′×S′的初始拓扑网格sG0,并且该初始拓扑网格sG0中的离散隐马尔可夫模型,即sgkl(k,l=1,2,…,S′)为:First, we can denote Bt+1 as Gij= [z1 ,z2 , . The discrete hidden Markov model in the initial topological grid sG0 , that is, sgkl (k, l=1,2,...,S') is:
其中,的各元素为:in, The elements of are:
其中,σ是搜索半径。where σ is the search radius.
进一步地,生成初始拓扑网格sG0后,可设sGt为初始拓扑网格sG0经过t次迭代后所得网格,并可设sBTt是(sG0,sG1,…,sGt)的所有离散隐马尔可夫模型中目标函数值最小的模型,还可将拓扑网格sGt中目标函数值最小的离散隐马尔可夫模型记为sBt,此外,还可设sT是迭代终止准则、sPG是预定义的区间(0,1)内参数。Further, after the initial topological mesh sG0 is generated, sGt can be set as the mesh obtained after t iterations of the initial topological mesh sG0 , and sBTt can be set to be (sG0 ,sG1 ,...,sGt ) The model with thesmallest objective function value among all discrete hiddenMarkov models of Criterion,spG is a parameter within a predefined interval (0,1).
进一步地,可先对拓扑网格sGt中的每个离散隐马尔可夫模型执行双策略竞争学习中的策略二,得到拓扑网格sGt+1/2;进而可判断U(0,1)<sPG是否成立,若成立,则对拓扑网格sGt+1/2的每个模型执行高斯变异,得到拓扑网格sGt+1;最后可判断拓扑网格sGt+1中目标函数值最小的离散隐马尔可夫模型sBt+1的目标函数值是否大于sBTt,若是,则sBTt+1←sBt+1,若否,则sBTt+1←sBTt、sBt+1←sBTt。Further,
进一步地,可判断迭代次数t<sT是否成立,若成立,则t←t+1,继续执行上述步骤;若不成立,则以sBTt取代Gij并终止自学习过程。Further, it can be judged whether the number of iterations t<sT is established, if so, then t←t+1, and continue to perform the above steps; if not, replace Gij with sBTt and terminate the self-learning process.
下面将结合图3进一步说明本发明的离散隐马尔可夫模型优化算法的实用性。The practicability of the discrete hidden Markov model optimization algorithm of the present invention will be further described below with reference to FIG. 3 .
如图3所示,本发明离散隐马尔可夫模型优化算法,在获得1马力和2马力时的球体故障、外圈故障和内圈故障,即BF_1、BF_2,ORF_1、ORF_2,IRF_1、IRF_2的目标函数值时,其值明显小于现有技术中BW算法在1马力和2马力时的球体故障、外圈故障和内圈故障,即BF_1、BF_2,ORF_1、ORF_2,IRF_1、IRF_2获得的目标函数值,由此,可看出本发明离散隐马尔可夫模型优化算法能够克服现有技术中BW算法仅具有局部搜索能力且对初值有很强依赖性的缺点,从而能够提高离散隐马尔可夫模型参数学习的精度。As shown in Figure 3, the discrete hidden Markov model optimization algorithm of the present invention, when obtaining 1 horsepower and 2 horsepower, the sphere fault, outer ring fault and inner ring fault, namely BF_1, BF_2, ORF_1, ORF_2, IRF_1, IRF_2 The objective function value is significantly smaller than the sphere fault, outer ring fault and inner ring fault of the BW algorithm in the prior art at 1 horsepower and 2 horsepower, that is, the objective functions obtained by BF_1, BF_2, ORF_1, ORF_2, IRF_1, IRF_2 Therefore, it can be seen that the discrete hidden Markov model optimization algorithm of the present invention can overcome the shortcomings of the prior art that the BW algorithm only has local search ability and has a strong dependence on the initial value, thereby improving the discrete hidden Markov model. accuracy of model parameter learning.
在本发明的一个实施例中,获取模块20可通过轴承数据中心得到待检测轴承的数据。In one embodiment of the present invention, the acquisition module 20 can acquire the data of the bearing to be detected through the bearing data center.
在本发明的一个实施例中,提取模块30可采用Daubechies小波和小波包分解对待检测轴承数据进行特征提取以得到待检测轴承不同故障类型的特征向量,例如可采用db4和3个分解水平的小包分解对待检测轴承正常状况、以及每种故障状况的数据进行特征提取。In an embodiment of the present invention, the extraction module 30 can use Daubechies wavelet and wavelet packet decomposition to perform feature extraction on the bearing data to be detected to obtain feature vectors of different fault types of the bearing to be detected, for example, db4 and 3 decomposition levels of small packets can be used The normal condition of the bearing to be detected and the data of each fault condition are decomposed to perform feature extraction.
在本发明的一个实施例中,第一处理模块40可采用k-均值聚类算法确定离散隐马尔可夫模型的代码本,以得到待检测轴承不同故障类型的观测序列,例如观测序列O=o1o2…oT。In an embodiment of the present invention, the first processing module 40 can use the k-means clustering algorithm to determine the codebook of the discrete hidden Markov model, so as to obtain the observation sequence of different fault types of the bearing to be detected, for example, the observation sequence O= o1 o2 …oT .
在本发明的一个实施例中,第二处理模块50可可对待检测轴承不同故障类型的观测序列建立初始离散隐马尔可夫模型,并可采用优化算法训练初始离散隐马尔可夫模型直至产生观测序列的概率达到最大值,例如观测序列O=o1o2…oT的概率P(O|λ)达到最大,其中,λ=(A,B,π)为训练后的离散隐马尔可夫模型。In an embodiment of the present invention, the second processing module 50 may establish an initial discrete hidden Markov model for observation sequences of different fault types of the bearing to be detected, and may use an optimization algorithm to train the initial discrete hidden Markov model until the observation sequence is generated The probability of reaching the maximum value, for example, the probability P(O|λ) of the observation sequence O=o1 o2 ... oT reaches the maximum value, where λ=(A, B, π) is the trained discrete hidden Markov model .
在本发明的一个实施例中,第三处理模块60可将待检测轴承不同故障类型的特征向量输入训练后的离散隐马尔可夫模型,然后可采用量化指标:CP=logP(ot|o1o2…ot-1,λ),从而可根据最高的CP值来选择相应的故障类型作为最终的诊断决策。In one embodiment of the present invention, the third processing module 60 can input the feature vectors of different fault types of the bearing to be detected into the trained discrete hidden Markov model, and then can use the quantitative index: CP=logP(ot |o1 o2 ... ot-1 , λ), so that the corresponding fault type can be selected as the final diagnosis decision according to the highest CP value.
下面将结合表1和表2进一步说明本发明的基于离散隐马尔可夫模型的轴承故障检测系统的实用性。The practicability of the bearing fault detection system based on the discrete hidden Markov model of the present invention will be further described below with reference to Table 1 and Table 2.
如表1所示,通过本发明的基于离散隐马尔可夫模型的轴承故障检测系统对轴承的球体故障、外圈故障和内圈故障进行检测时,其训练运行状况和测试运行状况分别为1772rpm,1hp和1750rpm,2hp,其控制极限为2.0577,故障检测率均为100%;进一步如表2所示,在对轴承的球体故障、外圈故障和内圈故障进行测试时,即通过475、477、475测试样本分别对对轴承的球体故障、外圈故障和内圈故障进行测试时,其故障定位准确率分别为100%、98.95%、99.79%,由此,可看出本发明的基于离散隐马尔可夫模型的轴承故障检测系统具有较高的故障检测准确率和定位精度。As shown in Table 1, when the ball fault, outer ring fault and inner ring fault of the bearing are detected by the bearing fault detection system based on the discrete hidden Markov model of the present invention, the training operating conditions and the testing operating conditions are respectively 1772 rpm , 1hp and 1750rpm, 2hp, its control limit is 2.0577, and the fault detection rate is 100%; further as shown in Table 2, when testing the ball fault, outer ring fault and inner ring fault of the bearing, it passed 475, When the 477 and 475 test samples respectively test the ball fault, outer ring fault and inner ring fault of the bearing, the fault location accuracy rates are 100%, 98.95% and 99.79% respectively. The bearing fault detection system based on discrete hidden Markov model has high fault detection accuracy and positioning accuracy.
表1Table 1
表2Table 2
根据本发明实施例提出的基于离散隐马尔可夫模型的轴承故障检测系统,通过构建模块建立离散隐马尔可夫模型的优化算法,并通过提取模块对待检测轴承数据进行特征提取,以及通过第一处理模块确定离散隐马尔可夫模型的代码本,并通过第二处理模块根据述优化算法待检测轴承不同故障类型的观测序列训练离散隐马尔可夫模型,以通过第三处理模块根据待检测轴承不同故障类型的特征向量和训练后的离散隐马尔可夫模型对待检测轴承进行故障检测,由此,能够降低对初值的依赖性,并能够提高搜索能力,从而能够提高离散隐马尔可夫模型参数学习的精度,并且能够保证故障检测的精度。According to the bearing fault detection system based on the discrete hidden Markov model proposed by the embodiment of the present invention, an optimization algorithm of the discrete hidden Markov model is established through the building module, and the feature extraction module is used to extract the bearing data to be detected, and the first The processing module determines the codebook of the discrete hidden Markov model, and trains the discrete hidden Markov model through the second processing module according to the observation sequence of different fault types of the bearing to be detected by the optimization algorithm, so as to pass the third processing module according to the bearing to be detected. The feature vectors of different fault types and the trained discrete hidden Markov model are used to detect the fault of the bearing to be detected, so that the dependence on the initial value can be reduced, and the search ability can be improved, so that the discrete hidden Markov model can be improved. The accuracy of parameter learning and the accuracy of fault detection can be guaranteed.
在本发明的描述中,术语“第一”、“第二”仅用于描述目的,而不能理解为指示或暗示相对重要性或者隐含指明所指示的技术特征的数量。由此,限定有“第一”、“第二”的特征可以明示或者隐含地包括一个或者更多个该特征。“多个”的含义是两个或两个以上,除非另有明确具体的限定。In the description of the present invention, the terms "first" and "second" are only used for the purpose of description, and cannot be understood as indicating or implying relative importance or implying the number of indicated technical features. Thus, a feature defined as "first" or "second" may expressly or implicitly include one or more of that feature. "Plurality" means two or more, unless expressly specifically limited otherwise.
在本发明中,除非另有明确的规定和限定,术语“安装”、“相连”、“连接”、“固定”等术语应做广义理解,例如,可以是固定连接,也可以是可拆卸连接,或成一体;可以是机械连接,也可以是电连接;可以是直接相连,也可以通过中间媒介间接相连,可以是两个元件内部的连通或两个元件的相互作用关系。对于本领域的普通技术人员而言,可以根据具体情况理解上述术语在本发明中的具体含义。In the present invention, unless otherwise expressly specified and limited, the terms "installed", "connected", "connected", "fixed" and other terms should be understood in a broad sense, for example, it may be a fixed connection or a detachable connection , or integrated; it can be a mechanical connection or an electrical connection; it can be a direct connection or an indirect connection through an intermediate medium, and it can be the internal connection of the two elements or the interaction relationship between the two elements. For those of ordinary skill in the art, the specific meanings of the above terms in the present invention can be understood according to specific situations.
在本发明中,除非另有明确的规定和限定,第一特征在第二特征“上”或“下”可以是第一和第二特征直接接触,或第一和第二特征通过中间媒介间接接触。而且,第一特征在第二特征“之上”、“上方”和“上面”可是第一特征在第二特征正上方或斜上方,或仅仅表示第一特征水平高度高于第二特征。第一特征在第二特征“之下”、“下方”和“下面”可以是第一特征在第二特征正下方或斜下方,或仅仅表示第一特征水平高度小于第二特征。In the present invention, unless otherwise expressly specified and limited, a first feature "on" or "under" a second feature may be in direct contact between the first and second features, or the first and second features indirectly through an intermediary touch. Also, the first feature being "above", "over" and "above" the second feature may mean that the first feature is directly above or obliquely above the second feature, or simply means that the first feature is level higher than the second feature. The first feature being "below", "below" and "below" the second feature may mean that the first feature is directly below or obliquely below the second feature, or simply means that the first feature has a lower level than the second feature.
在本说明书的描述中,参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中,对上述术语的示意性表述不必对相同的实施例或示例。而且,描述的具体特征、结构、材料或者特点可以在任一个或多个实施例或示例中以合适的方式结合。此外,在不相互矛盾的情况下,本领域的技术人员可以将本说明书中描述的不同实施例或示例以及不同实施例或示例的特征进行结合和组合。In the description of this specification, description with reference to the terms "one embodiment," "some embodiments," "example," "specific example," or "some examples", etc., mean specific features described in connection with the embodiment or example , structure, material or feature is included in at least one embodiment or example of the present invention. In this specification, schematic representations of the above terms are not necessarily to the same embodiment or example. Furthermore, the particular features, structures, materials or characteristics described may be combined in any suitable manner in any one or more embodiments or examples. Furthermore, those skilled in the art may combine and combine the different embodiments or examples described in this specification, as well as the features of the different embodiments or examples, without conflicting each other.
Claims (10)
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202111031722.XACN113723546B (en) | 2021-09-03 | 2021-09-03 | Bearing fault detection method and system based on discrete hidden Markov model |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202111031722.XACN113723546B (en) | 2021-09-03 | 2021-09-03 | Bearing fault detection method and system based on discrete hidden Markov model |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN113723546Atrue CN113723546A (en) | 2021-11-30 |
| CN113723546B CN113723546B (en) | 2023-12-22 |
Family
ID=78681430
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202111031722.XAActiveCN113723546B (en) | 2021-09-03 | 2021-09-03 | Bearing fault detection method and system based on discrete hidden Markov model |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN113723546B (en) |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN115452369A (en)* | 2022-08-30 | 2022-12-09 | 西安航天精密机电研究所 | Gyro motor bearing fault diagnosis method |
Citations (12)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20100310157A1 (en)* | 2009-06-05 | 2010-12-09 | Samsung Electronics Co., Ltd. | Apparatus and method for video sensor-based human activity and facial expression modeling and recognition |
| CN103778919A (en)* | 2014-01-21 | 2014-05-07 | 南京邮电大学 | Speech coding method based on compressed sensing and sparse representation |
| CN107102223A (en)* | 2017-03-29 | 2017-08-29 | 江苏大学 | NPC photovoltaic DC-to-AC converter method for diagnosing faults based on improved hidden Markov model GHMM |
| CN107274011A (en)* | 2017-06-05 | 2017-10-20 | 上海电力学院 | The equipment state recognition methods of comprehensive Markov model and probability net |
| CN107378641A (en)* | 2017-08-23 | 2017-11-24 | 东北电力大学 | A kind of Monitoring Tool Wear States in Turning based on characteristics of image and LLTSA algorithms |
| CN109142969A (en)* | 2018-07-20 | 2019-01-04 | 西南交通大学 | A kind of power transmission line fault phase selection based on Continuous Hidden Markov Model |
| WO2019019252A1 (en)* | 2017-07-28 | 2019-01-31 | 平安科技(深圳)有限公司 | Acoustic model training method, speech recognition method and apparatus, device and medium |
| US20200019153A1 (en)* | 2018-07-13 | 2020-01-16 | United States Of America, As Represented By The Secretary Of The Navy | Real-Time Automation for Monitor and Control of Electro-Mechanical System |
| CN110705581A (en)* | 2019-07-18 | 2020-01-17 | 浙江运达风电股份有限公司 | Pitch bearing fault identification method based on improved hidden Markov model |
| CN111740582A (en)* | 2020-03-13 | 2020-10-02 | 东南大学 | PFC fault detection method of wireless charging system based on improved HMM |
| CN112345249A (en)* | 2020-07-28 | 2021-02-09 | 江苏理工学院 | Rolling bearing fault diagnosis method based on optimized variational modal decomposition |
| CN113139251A (en)* | 2021-04-23 | 2021-07-20 | 桂林电子科技大学 | Variable working condition rolling bearing fault diagnosis method for optimizing theme correlation analysis |
- 2021
- 2021-09-03CNCN202111031722.XApatent/CN113723546B/enactiveActive
Patent Citations (12)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20100310157A1 (en)* | 2009-06-05 | 2010-12-09 | Samsung Electronics Co., Ltd. | Apparatus and method for video sensor-based human activity and facial expression modeling and recognition |
| CN103778919A (en)* | 2014-01-21 | 2014-05-07 | 南京邮电大学 | Speech coding method based on compressed sensing and sparse representation |
| CN107102223A (en)* | 2017-03-29 | 2017-08-29 | 江苏大学 | NPC photovoltaic DC-to-AC converter method for diagnosing faults based on improved hidden Markov model GHMM |
| CN107274011A (en)* | 2017-06-05 | 2017-10-20 | 上海电力学院 | The equipment state recognition methods of comprehensive Markov model and probability net |
| WO2019019252A1 (en)* | 2017-07-28 | 2019-01-31 | 平安科技(深圳)有限公司 | Acoustic model training method, speech recognition method and apparatus, device and medium |
| CN107378641A (en)* | 2017-08-23 | 2017-11-24 | 东北电力大学 | A kind of Monitoring Tool Wear States in Turning based on characteristics of image and LLTSA algorithms |
| US20200019153A1 (en)* | 2018-07-13 | 2020-01-16 | United States Of America, As Represented By The Secretary Of The Navy | Real-Time Automation for Monitor and Control of Electro-Mechanical System |
| CN109142969A (en)* | 2018-07-20 | 2019-01-04 | 西南交通大学 | A kind of power transmission line fault phase selection based on Continuous Hidden Markov Model |
| CN110705581A (en)* | 2019-07-18 | 2020-01-17 | 浙江运达风电股份有限公司 | Pitch bearing fault identification method based on improved hidden Markov model |
| CN111740582A (en)* | 2020-03-13 | 2020-10-02 | 东南大学 | PFC fault detection method of wireless charging system based on improved HMM |
| CN112345249A (en)* | 2020-07-28 | 2021-02-09 | 江苏理工学院 | Rolling bearing fault diagnosis method based on optimized variational modal decomposition |
| CN113139251A (en)* | 2021-04-23 | 2021-07-20 | 桂林电子科技大学 | Variable working condition rolling bearing fault diagnosis method for optimizing theme correlation analysis |
Non-Patent Citations (4)
| Title |
|---|
| JIAWEI LIU等: "A discrete hidden Markov model fault diagnosis strategy based on K-means clustering dedicated to PEM fuel cell systems of tramways", 《INTERNATIONAL JOURNAL OF HYDROGEN ENERGY》, vol. 43, no. 27, pages 12428 - 12441* |
| 毛明明 等: "基于L-M神经网络的齿轮故障诊断", 《计算机技术与发展》, vol. 21, no. 1, pages 210 - 213* |
| 赵钰: "基于隐马尔科夫模型的风电机组轴承状态诊断方法", 《中国优秀硕士学位论文全文数据库 工程科技Ⅱ辑》, no. 4, pages 042 - 251* |
| 饶雷 等: "基于CNN-SVM和特征融合的齿轮箱故障诊断", 《组合机床与自动化加工技术》, no. 8, pages 130 - 133* |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN115452369A (en)* | 2022-08-30 | 2022-12-09 | 西安航天精密机电研究所 | Gyro motor bearing fault diagnosis method |
Also Published As
| Publication number | Publication date |
|---|---|
| CN113723546B (en) | 2023-12-22 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN110347932B (en) | Cross-network user alignment method based on deep learning | |
| CN106897254B (en) | Network representation learning method | |
| Sarmadi | Investigation of machine learning methods for structural safety assessment under variability in data: Comparative studies and new approaches | |
| CN115879030B (en) | A method and system for classifying network attacks on distribution networks | |
| CN115184054B (en) | Mechanical equipment semi-supervised fault detection and analysis method, device, terminal and medium | |
| CN107832789B (en) | Feature weighting K nearest neighbor fault diagnosis method based on average influence value data transformation | |
| CN113449672A (en) | Remote sensing scene classification method and device based on bilinear twin framework | |
| CN111062036A (en) | Malware identification model construction, identification method, medium and equipment | |
| CN114528547B (en) | ICPS unsupervised online attack detection method and device based on community feature selection | |
| CN113392901A (en) | Confrontation sample detection method based on deep learning model neural pathway activation characteristics | |
| Zhang et al. | Occlusion-robust face recognition using iterative stacked denoising autoencoder | |
| CN115865458B (en) | Network attack behavior detection method, system and terminal based on LSTM and GAT algorithm | |
| Shen et al. | Evolving deep multiple kernel learning networks through genetic algorithms | |
| CN113723546A (en) | Bearing fault detection method and system based on discrete hidden Markov model | |
| CN113642624A (en) | Intelligent diagnosis method and device for mobile communication network failure | |
| CN116186581B (en) | Floor identification method and system based on graph pulse neural network | |
| CN117675375A (en) | An intrusion detection method based on improved spectral clustering variational autoencoder | |
| CN113822771B (en) | Deep learning-based low false detection rate electricity larceny detection method | |
| CN116680695A (en) | Feature topology fusion-based black box graph attack resistance method | |
| CN116415196A (en) | Data anomaly detection method, storage medium and terminal based on smart industry | |
| CN112529156B (en) | A multi-method hybrid selection input method for neural network testing based on clustering | |
| Liu et al. | Intrusion detection based on feature reduction and model pruning in electricity trading network | |
| CN120579152B (en) | Abnormal subgraph detection method based on asymmetric automatic encoder | |
| Yu et al. | Learning latent structures in network games via data-dependent gated-prior graph variational autoencoders | |
| Ozawa et al. | An incremental principal component analysis for chunk data |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |