CN113363963B - Optimized three-phase SAPF direct current side control method by improving sparrow search algorithm - Google Patents
Optimized three-phase SAPF direct current side control method by improving sparrow search algorithmDownload PDFInfo
- Publication number
- CN113363963B CN113363963BCN202110548777.1ACN202110548777ACN113363963BCN 113363963 BCN113363963 BCN 113363963BCN 202110548777 ACN202110548777 ACN 202110548777ACN 113363963 BCN113363963 BCN 113363963B
- Authority
- CN
- China
- Prior art keywords
- current
- sparrow
- population
- sparrows
- value
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
Images
Classifications
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02J—CIRCUIT ARRANGEMENTS OR SYSTEMS FOR SUPPLYING OR DISTRIBUTING ELECTRIC POWER; SYSTEMS FOR STORING ELECTRIC ENERGY
- H02J3/00—Circuit arrangements for AC mains or AC distribution networks
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06N—COMPUTING ARRANGEMENTS BASED ON SPECIFIC COMPUTATIONAL MODELS
- G06N3/00—Computing arrangements based on biological models
- G06N3/004—Artificial life, i.e. computing arrangements simulating life
- G06N3/006—Artificial life, i.e. computing arrangements simulating life based on simulated virtual individual or collective life forms, e.g. social simulations or particle swarm optimisation [PSO]
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02J—CIRCUIT ARRANGEMENTS OR SYSTEMS FOR SUPPLYING OR DISTRIBUTING ELECTRIC POWER; SYSTEMS FOR STORING ELECTRIC ENERGY
- H02J3/00—Circuit arrangements for AC mains or AC distribution networks
- H02J3/01—Arrangements for reducing harmonics or ripples
- H—ELECTRICITY
- H02—GENERATION; CONVERSION OR DISTRIBUTION OF ELECTRIC POWER
- H02J—CIRCUIT ARRANGEMENTS OR SYSTEMS FOR SUPPLYING OR DISTRIBUTING ELECTRIC POWER; SYSTEMS FOR STORING ELECTRIC ENERGY
- H02J2203/00—Indexing scheme relating to details of circuit arrangements for AC mains or AC distribution networks
- H02J2203/20—Simulating, e g planning, reliability check, modelling or computer assisted design [CAD]
- Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
- Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
- Y02E—REDUCTION OF GREENHOUSE GAS [GHG] EMISSIONS, RELATED TO ENERGY GENERATION, TRANSMISSION OR DISTRIBUTION
- Y02E40/00—Technologies for an efficient electrical power generation, transmission or distribution
- Y02E40/40—Arrangements for reducing harmonics
Landscapes
- Engineering & Computer Science (AREA)
- Power Engineering (AREA)
- Physics & Mathematics (AREA)
- Theoretical Computer Science (AREA)
- Evolutionary Computation (AREA)
- General Health & Medical Sciences (AREA)
- Biomedical Technology (AREA)
- Biophysics (AREA)
- Computational Linguistics (AREA)
- Data Mining & Analysis (AREA)
- Life Sciences & Earth Sciences (AREA)
- Artificial Intelligence (AREA)
- Molecular Biology (AREA)
- Computing Systems (AREA)
- General Engineering & Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Mathematical Physics (AREA)
- Software Systems (AREA)
- Health & Medical Sciences (AREA)
- Control Of Electrical Variables (AREA)
Abstract
Translated fromChineseDescription
Translated fromChinese技术领域technical field
本发明涉及电力技术领域,具体涉及一种改进麻雀搜索算法优化三相SAPF直流侧控制方法。The invention relates to the field of electric power technology, in particular to an improved sparrow search algorithm to optimize a three-phase SAPF direct current side control method.
背景技术Background technique
随着电力电子技术的发展,微电网中有大量非线性负载投入使用,导致电网电流的谐波污染越来越严重。三相并联型有源电力滤波器(SAPF)可以有效补偿谐波。实际上,SAPF是由电流内环和电压外环构成的双闭环系统。当电网接入非线性负载时,许多谐波和无功电流注入其中,超过一定标准的谐波含量将会严重威胁电气设备的安全和稳定运行,因此,为了改善补偿后的电网电流波形,抑制谐波,就要让直流侧电压值稳定在给参考值附近。电容电压控制环节对完善补偿电流有重要作用,其控制参数对控制性能起着决定性作用,合理选择控制参数至关重要。With the development of power electronics technology, a large number of non-linear loads are put into use in the microgrid, resulting in more and more serious harmonic pollution of grid current. Three-phase parallel active power filter (SAPF) can effectively compensate for harmonics. In fact, the SAPF is a double closed-loop system consisting of an inner current loop and an outer voltage loop. When the power grid is connected to a nonlinear load, many harmonics and reactive currents are injected into it, and the harmonic content exceeding a certain standard will seriously threaten the safe and stable operation of electrical equipment. Therefore, in order to improve the grid current waveform after compensation, suppress the Harmonics, it is necessary to stabilize the DC side voltage value near the given reference value. The capacitor voltage control link plays an important role in improving the compensation current, and its control parameters play a decisive role in the control performance, and it is very important to select the control parameters reasonably.
直流侧电容电压的控制采用传统的PI控制器,在选取控制器参数方面,参数的整定方法主要有传统参数整定方法和智能参数优化方法。其中传统参数整定方法有:Z-N法、临界比例度法、衰减曲线法等,这类方法都是根据工程经验公式进行近似整定,还需要在实际运行中最后调整和完善,整定精度不高,并且需要精确的对象模型,而工业控制中,许多实际对象的模型不容易建立。智能算法优化方法主要有:神经网络、模糊控制、遗传算法、粒子群优化算法等。神经网络的整定参数效果受初始值的影响较大;模糊控制则需要整定人具有丰富的先验知识进行模糊规则的编写;遗传算法中的交叉变异操作可能将更优解变差;粒子群优化算法是群体智能算法中最为经典的一种方法,但是存在容易陷入局部最优区域和收敛较慢的缺陷。The control of the DC side capacitor voltage adopts the traditional PI controller. In terms of selecting the controller parameters, the parameter tuning methods mainly include the traditional parameter tuning method and the intelligent parameter optimization method. Among them, the traditional parameter setting methods include: Z-N method, critical proportionality method, decay curve method, etc. These methods are approximated by the formula of engineering experience, and they need to be adjusted and perfected in the actual operation. The setting accuracy is not high, and Accurate object models are required, and in industrial control, many actual object models are not easy to build. The intelligent algorithm optimization methods mainly include: neural network, fuzzy control, genetic algorithm, particle swarm optimization algorithm, etc. The effect of the tuning parameters of the neural network is greatly affected by the initial value; the fuzzy control requires the tuning person to have rich prior knowledge to write fuzzy rules; the crossover mutation operation in the genetic algorithm may make the better solution worse; particle swarm optimization Algorithm is the most classic method in swarm intelligence algorithm, but it has the defects of easy to fall into the local optimal area and slow convergence.
发明内容SUMMARY OF THE INVENTION
为解决上述问题,本发明提出采用改进麻雀搜索算法(ISSA)对SAPF直流侧的电容电压控制器进行参数整定,并且与传统粒子群算法优化结果进行对比,解决粒子群算法易陷入局部最优,收敛速度慢的缺点,提升电压侧PI控制器的控制性能。In order to solve the above problems, the present invention proposes to use an improved sparrow search algorithm (ISSA) to adjust the parameters of the capacitor-voltage controller on the DC side of the SAPF, and compares the optimization results with the traditional particle swarm optimization algorithm to solve the problem that the particle swarm optimization algorithm is easy to fall into local optimum, The disadvantage of slow convergence speed improves the control performance of the voltage-side PI controller.
本发明采用以下技术方案:The present invention adopts following technical scheme:
一种改进麻雀搜索算法优化三相SAPF直流侧控制方法,包括如下步骤:An improved sparrow search algorithm to optimize a three-phase SAPF DC side control method, comprising the following steps:
步骤1,非线性负载电流IL经过基于FBD法的参考电流检测模块,除去电流基波正序有功分量ipabc后,得到谐波电流ih。
步骤2,将SAPF直流侧电压参考值Ud*与实际电压值Ud的差值,进行绝对值乘以时间的积分作为算法优化的目标函数ITAE。Step 2: The difference between the SAPF DC side voltage reference value Ud* and the actual voltage value Ud is multiplied by the absolute value and integrated with time as the objective function ITAE for algorithm optimization.
步骤3,用改进麻雀搜索算法ISSA进行参数整定,找出Kp、Ki的最优值赋给仿真模型中的PI控制器,并且将电压偏差转换成稳定直流侧电压的补偿电流增量Δip。Step 3: Use the improved sparrow search algorithm ISSA to tune the parameters, find out the optimal values of Kp and Ki and assign them to the PI controller in the simulation model, and convert the voltage deviation into the compensation current increment Δi for the stable DC side voltage.p .
步骤4,把补偿电流增量Δip与电流基波正序分量ipabc相乘,与谐波电流ih做差,得到参考电流iref。Step 4: Multiply the compensation current incrementΔip by the current fundamental wave positive sequence component ipabc , and make a difference with the harmonic current ih to obtain the reference current iref .
步骤5,参考电流iref减去补偿电流Ic的差值,通过电流跟踪控制即PR控制,输出信号g。Step 5, the reference current iref subtracts the difference value of the compensation current Ic , and outputs the signal g through the current tracking control, that is, the PR control.
步骤6,输出信号g控制PWM变流器使得SAPF输出合理的补偿电流Ic,让补偿电流与负载电流中要补偿的谐波及无功等电流抵消,从而使电网电流IS接近正弦波。In
进一步的,所述步骤2中算法优化的目标函数由如下方法计算得到:Further, the objective function optimized by the algorithm in the
电压参考值Ud*与实际电压值Ud的差值定义为e(t),则The difference between the voltage reference value Ud* and the actual voltage value Ud is defined as e(t), then
进一步的,在所述步骤3中,改进麻雀搜索算法ISSA包括以下步骤:Further, in the step 3, the improved sparrow search algorithm ISSA includes the following steps:
(1)初始化麻雀种群RP,设置麻雀总数量为N,最大迭代次数为Max_iter,随机初始化麻雀群体位置,在初始种群中每个麻雀个体的反向个体构成反向种群OP,合并种群RP与OP,将其2N个麻雀个体按照适应度值进行升序排序,选取适应度值前N个麻雀作为初始种群。(1) Initialize the sparrow population RP, set the total number of sparrows as N, the maximum number of iterations as Max_iter, and initialize the sparrow population position randomly. , sort its 2N sparrow individuals in ascending order according to the fitness value, and select the first N sparrows with the fitness value as the initial population.
(2)计算初始种群中所有麻雀的适应度值fitness,并对这些位置进行排序。(2) Calculate the fitness value of all sparrows in the initial population, and sort these positions.
(3)在每次迭代的过程中,发现者的位置更新描述如下:(3) In the process of each iteration, the location update of the finder is described as follows:
其中,t代表当前迭代数,j=1,2,3,...d。itermax表示最大迭代次数,Xi,j表示第i个麻雀在第j维中的位置信息,R2和ST分别表示预警值与安全值。Among them, t represents the current iteration number, j=1, 2, 3, ... d. itermax represents the maximum number of iterations, Xi,j represents the position information of the i-th sparrow in the j-th dimension, and R2 and ST represent the warning value and the safety value, respectively.
当R2<ST时,这意味着此时的觅食环境周围没有捕食者,发现者可以执行广泛的搜索操作。如果R2≥ST,这表示种群中的一些麻雀已经发现了捕食者,并向种群中其它麻雀发出了警报,此时所有麻雀都需要迅速飞到其它安全的地方进行觅食。When R2 < ST, it means that there are no predators around the foraging environment at this time, and the finder can perform a wide range of search operations. If R2 ≥ ST, it means that some sparrows in the population have detected a predator and alerted other sparrows in the population, and all sparrows need to quickly fly to other safe places to forage.
(4)更新加入者的位置,其位置更新公式如下:(4) Update the position of the joiner, and its position update formula is as follows:
其中,Xp是目前发现者所占据的最优位置,Xworst则表示当前全局最差的位置。A表示一个1×d的矩阵,其中每个元素随机赋值为1或-1,并且A+=AT(AAT)-1。当i>n/2时,这表明适应度值较低的第i个加入者没有获得食物,处于十分饥饿的状态,此时需要飞往其它地方觅食,以获得更多的能量。Among them, Xp is the optimal position currently occupied by the discoverer, and Xworst represents the current global worst position. A represents a 1×d matrix in which each element is randomly assigned a value of 1 or -1, and A+ =AT (AAT )-1 . When i>n/2, it means that the i-th participant with a lower fitness value has not obtained food and is in a very hungry state, and needs to fly to other places for food to obtain more energy.
(5)实验中,假设这些意识到危险的麻雀占总数量的10%到20%。这些麻雀的初始位置是在种群中随机产生的。更新公式如下:(5) In the experiment, it is assumed that these sparrows who are aware of the danger make up 10% to 20% of the total population. The initial positions of these sparrows were randomly generated in the population. The update formula is as follows:
其中,Xbest是当前的全局最优位置。β作为步长控制参数,是服从均值为0,方差为1的正态分布的随机数。K∈[-1,1]是一个随机数,fi则是当前麻雀个体的适应度值。fg和fw分别是当前全局最佳和最差的适应度值。ε是最小的常数,以避免分母出现零。Among them, Xbest is the current global optimal position. β, as a step control parameter, is a random number that obeys a normal distribution with a mean of 0 and a variance of 1. K∈[-1,1] is a random number, and fi is the fitness value of the current sparrow individual. fg and fw are the current global best and worst fitness values, respectively. ε is the smallest constant to avoid zeros in the denominator.
为简单起见,当fi>fg表示此时的麻雀正处于种群的边缘,极其容易受到捕食者的攻击。Xbest表示这个位置的麻雀是种群中最好的位置也是十分安全的。fi=fg时,这表明处于种群中间的麻雀意识到了危险,需要靠近其它的麻雀以此尽量减少它们被捕食的风险。K表示麻雀移动的方向同时也是步长控制参数。For the sake of simplicity, when fi > fg , it means that the sparrow is at the edge of the population and is extremely vulnerable to predators. Xbest indicates that the sparrow in this position is the best position in the population and is very safe. When fi = fg , this indicates that sparrows in the middle of the population are aware of the danger and need to get close to other sparrows to minimize their risk of predation. K represents the direction in which the sparrow moves and is also a step size control parameter.
(6)计算出适应度值,并且更新麻雀的位置。(6) Calculate the fitness value and update the position of the sparrow.
(7)判断是否满足终止条件,若满足则输出最优解,结束程序;否则,重复以上改进麻雀搜索算法流程继续进行寻优迭代处理。(7) Judging whether the termination conditions are met, if so, output the optimal solution and end the program; otherwise, repeat the above process of the improved sparrow search algorithm to continue the optimization iterative process.
(8)将改进麻雀搜索算法寻优得到的参数Kp、Ki赋值给Simulink仿真模型中的PI控制器。(8) Assign the parameters Kp and Ki obtained by the improved sparrow search algorithm to the PI controller in the Simulink simulation model.
本发明的有益效果:Beneficial effects of the present invention:
相比直流侧电压PI控制,或用PSO算法参数整定,本发明提出的采用ISSA算法进行参数整定,SAPF直流侧电压稳定效果更好、补偿后电网电流的谐波畸变率THD值更小。大大提高了谐波补偿的有效性和实时性,降低了稳态误差。对有效治理谐波,提高电能质量具有重大意义。Compared with the PI control of the DC side voltage or the parameter setting with the PSO algorithm, the ISSA algorithm proposed by the present invention is used for parameter setting, the SAPF DC side voltage stabilization effect is better, and the harmonic distortion rate THD value of the grid current after compensation is smaller. The effectiveness and real-time performance of harmonic compensation are greatly improved, and the steady-state error is reduced. It is of great significance to effectively control harmonics and improve power quality.
附图说明Description of drawings
图1为本发明ISSA算法优化SAPF直流侧PI控制器的原理图;Fig. 1 is the schematic diagram of the ISSA algorithm of the present invention to optimize the SAPF DC side PI controller;
图2为PSO算法优化迭代曲线;Fig. 2 is the optimization iteration curve of PSO algorithm;
图3为PSO算法优化后SAPF直流侧电压结果图;Figure 3 shows the result of the SAPF DC side voltage after PSO algorithm optimization;
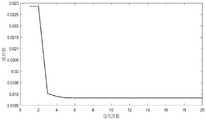
图4为本发明ISSA算法优化迭代曲线;Fig. 4 is the ISSA algorithm optimization iteration curve of the present invention;
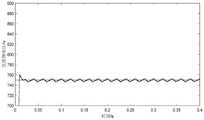
图5为本发明ISSA算法优化后SAPF直流侧电压结果图。FIG. 5 is a result diagram of the DC side voltage of the SAPF after the ISSA algorithm of the present invention is optimized.
具体实施方式Detailed ways
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述。The technical solutions in the embodiments of the present invention will be clearly and completely described below with reference to the accompanying drawings in the embodiments of the present invention.
如图1-5所示,本发明的一个实施算例,公开了一种改进麻雀搜索算法优化SAPF直流侧电压控制器参数方法,包括以下步骤:As shown in Figures 1-5, an embodiment of the present invention discloses a method for optimizing the parameters of the SAPF DC side voltage controller by improving the sparrow search algorithm, including the following steps:
步骤1,非线性负载电流IL经过基于FBD法的参考电流检测模块,除去电流基波正序有功分量ipabc后,得到谐波电流ih。
步骤2,将SAPF直流侧电压参考值Ud*与实际电压值Ud的差值,进行绝对值乘以时间的积分作为算法优化的目标函数ITAE。Step 2: The difference between the SAPF DC side voltage reference value Ud* and the actual voltage value Ud is multiplied by the absolute value and integrated with time as the objective function ITAE for algorithm optimization.
步骤3,用改进麻雀搜索算法ISSA进行参数整定,找出Kp、Ki的最优值赋给仿真模型中的PI控制器,并且将电压偏差转换成稳定直流侧电压的补偿电流增量Δip。Step 3: Use the improved sparrow search algorithm ISSA to tune the parameters, find out the optimal values of Kp and Ki and assign them to the PI controller in the simulation model, and convert the voltage deviation into the compensation current increment Δi for the stable DC side voltage.p .
步骤4,把补偿电流增量Δip与电流基波正序分量ipabc相乘,与谐波电流ih做差,得到参考电流iref。Step 4: Multiply the compensation current incrementΔip by the current fundamental wave positive sequence component ipabc , and make a difference with the harmonic current ih to obtain the reference current iref .
步骤5,参考电流iref减去补偿电流Ic的差值,通过电流跟踪控制即PR控制,输出信号g。Step 5, the reference current iref subtracts the difference value of the compensation current Ic , and outputs the signal g through the current tracking control, that is, the PR control.
步骤6,输出信号g控制PWM变流器使得SAPF输出合理的补偿电流Ic,让补偿电流与负载电流中要补偿的谐波及无功等电流抵消,从而使电网电流IS接近正弦波。In
进一步的,所述步骤2中算法优化的目标函数由如下方法计算得到:Further, the objective function optimized by the algorithm in the
电压参考值Ud*与实际电压值Ud的差值定义为e(t),则The difference between the voltage reference value Ud* and the actual voltage value Ud is defined as e(t), then
进一步的,在所述步骤3中,改进麻雀搜索算法ISSA包括以下步骤:Further, in the step 3, the improved sparrow search algorithm ISSA includes the following steps:
步骤3.1,初始化麻雀种群RP,设置麻雀总数量为N,最大迭代次数为Max_iter,随机初始化麻雀群体位置,在初始种群中每个麻雀个体的反向个体构成反向种群OP,合并种群RP与OP,将其2N个麻雀个体按照适应度值进行升序排序,选取适应度值前N个麻雀作为初始种群。Step 3.1, initialize the sparrow population RP, set the total number of sparrows to N, the maximum number of iterations to Max_iter, and initialize the sparrow population position randomly. , sort its 2N sparrow individuals in ascending order according to the fitness value, and select the first N sparrows with the fitness value as the initial population.
步骤3.2,计算初始种群中所有麻雀的适应度值fitness,并对这些位置进行排序。Step 3.2, calculate the fitness value of all sparrows in the initial population, and sort these positions.
步骤3.3,在每次迭代的过程中,发现者的位置更新描述如下:Step 3.3, in the process of each iteration, the location update of the finder is described as follows:
其中,t代表当前迭代数,j=1,2,3,...d。itermax表示最大迭代次数,Xi,j表示第i个麻雀在第j维中的位置信息,R2和ST分别表示预警值与安全值。Among them, t represents the current iteration number, j=1, 2, 3, ... d. itermax represents the maximum number of iterations, Xi,j represents the position information of the i-th sparrow in the j-th dimension, and R2 and ST represent the warning value and the safety value, respectively.
当R2<ST时,这意味着此时的觅食环境周围没有捕食者,发现者可以执行广泛的搜索操作。如果R2≥ST,这表示种群中的一些麻雀已经发现了捕食者,并向种群中其它麻雀发出了警报,此时所有麻雀都需要迅速飞到其它安全的地方进行觅食。When R2 < ST, it means that there are no predators around the foraging environment at this time, and the finder can perform a wide range of search operations. If R2 ≥ ST, it means that some sparrows in the population have detected a predator and alerted other sparrows in the population, and all sparrows need to quickly fly to other safe places to forage.
步骤3.4,更新加入者的位置,其位置更新公式如下:Step 3.4, update the position of the joiner, and its position update formula is as follows:
其中,Xp是目前发现者所占据的最优位置,Xworst则表示当前全局最差的位置。A表示一个1×d的矩阵,其中每个元素随机赋值为1或-1,并且A+=AT(AAT)-1。当i>n/2时,这表明,适应度值较低的第i个加入者没有获得食物,处于十分饥饿的状态,此时需要飞往其它地方觅食,以获得更多的能量。Among them, Xp is the optimal position currently occupied by the discoverer, and Xworst represents the current global worst position. A represents a 1×d matrix in which each element is randomly assigned a value of 1 or -1, and A+ =AT (AAT )-1 . When i>n/2, this indicates that the i-th participant with a lower fitness value has not obtained food and is in a very hungry state. At this time, it needs to fly to other places for food to obtain more energy.
步骤3.5,实验中,假设这些意识到危险的麻雀占总数量的10%到20%。这些麻雀的初始位置是在种群中随机产生的。更新公式如下:In step 3.5, the experiment assumes that these danger-aware sparrows make up 10% to 20% of the total population. The initial positions of these sparrows were randomly generated in the population. The update formula is as follows:
其中,Xbest是当前的全局最优位置。β作为步长控制参数,是服从均值为0,方差为1的正态分布的随机数。K∈[-1,1]是一个随机数,fi则是当前麻雀个体的适应度值。fg和fw分别是当前全局最佳和最差的适应度值。ε是最小的常数,以避免分母出现零。Among them, Xbest is the current global optimal position. β, as a step control parameter, is a random number that obeys a normal distribution with a mean of 0 and a variance of 1. K∈[-1,1] is a random number, and fi is the fitness value of the current sparrow individual. fg and fw are the current global best and worst fitness values, respectively. ε is the smallest constant to avoid zeros in the denominator.
为简单起见,当fi>fg表示此时的麻雀正处于种群的边缘,极其容易受到捕食者的攻击。Xbest表示这个位置的麻雀是种群中最好的位置也是十分安全的。fi=fg时,这表明处于种群中间的麻雀意识到了危险,需要靠近其它的麻雀以此尽量减少它们被捕食的风险。K表示麻雀移动的方向同时也是步长控制参数。For the sake of simplicity, when fi > fg , it means that the sparrow is at the edge of the population and is extremely vulnerable to predators. Xbest indicates that the sparrow in this position is the best position in the population and is very safe. When fi = fg , this indicates that sparrows in the middle of the population are aware of the danger and need to get close to other sparrows to minimize their risk of predation. K represents the direction in which the sparrow moves and is also a step size control parameter.
步骤3.6,计算出适应度值,并且更新麻雀的位置。Step 3.6, calculate the fitness value, and update the position of the sparrow.
步骤3.7,判断是否满足终止条件,若满足则输出最优解,结束程序;否则,重复以上改进麻雀搜索算法流程继续进行寻优迭代处理。Step 3.7, judge whether the termination condition is met, if so, output the optimal solution and end the program; otherwise, repeat the above process of improving the sparrow search algorithm to continue the optimization iterative process.
步骤3.8,将改进麻雀搜索算法寻优得到的参数Kp、Ki赋值给PI控制器。Step 3.8, assign the parameters Kp and Ki obtained by the improved sparrow search algorithm to the PI controller.
本实施算例中算法参数取值如下:The values of the algorithm parameters in this example are as follows:
PSO算法:粒子群群体大小为SwarmSize=20,维数Dim=2,最大迭代次数MaxIter=20。PSO algorithm: the particle swarm size is SwarmSize=20, the dimension Dim=2, and the maximum number of iterations MaxIter=20.
ISSA算法:麻雀群体大小为N=20,维数Dim=2,最大迭代次数Max_iter=20,捕食者的比例PD=20%,意识到有危险的麻雀比重SD=20%,预警值ST=0.8。ISSA algorithm: The sparrow population size is N=20, the dimension Dim=2, the maximum number of iterations Max_iter=20, the proportion of predators PD=20%, the proportion of sparrows aware of danger SD=20%, the warning value ST=0.8 .
采用本发明提出的改进麻雀搜索算法(ISSA)优化SAPF直流侧控制,并与粒子群算法(PSO)优化结果进行对比,通过图2至图5的结果可知,本发明相比传统PSO算法优化,收敛速度更快,寻优精度更高,SAPF直流侧电压稳定效果更好,谐波补偿效果更佳。The improved sparrow search algorithm (ISSA) proposed by the present invention is used to optimize the SAPF DC side control, and compared with the optimization results of the particle swarm algorithm (PSO), it can be seen from the results in Figs. The convergence speed is faster, the optimization accuracy is higher, the SAPF DC side voltage stabilization effect is better, and the harmonic compensation effect is better.
最后说明的是,以上仅对本发明具体实施例进行详细描述说明。但本发明并不限制于以上描述具体实施例。本领域的技术人员对本发明进行的等同修改和替代也都在本发明的范畴之中。因此,在不脱离本发明的精神和范围下所作的均等变换和修改,都涵盖在本发明范围内。Finally, it should be noted that the above only describes the specific embodiments of the present invention in detail. However, the present invention is not limited to the specific embodiments described above. Equivalent modifications and substitutions of the present invention made by those skilled in the art are also within the scope of the present invention. Therefore, equivalent changes and modifications made without departing from the spirit and scope of the present invention are all included within the scope of the present invention.
Claims (3)
Translated fromChinesePriority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110548777.1ACN113363963B (en) | 2021-05-20 | 2021-05-20 | Optimized three-phase SAPF direct current side control method by improving sparrow search algorithm |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110548777.1ACN113363963B (en) | 2021-05-20 | 2021-05-20 | Optimized three-phase SAPF direct current side control method by improving sparrow search algorithm |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN113363963A CN113363963A (en) | 2021-09-07 |
| CN113363963Btrue CN113363963B (en) | 2022-05-20 |
Family
ID=77527002
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202110548777.1AActiveCN113363963B (en) | 2021-05-20 | 2021-05-20 | Optimized three-phase SAPF direct current side control method by improving sparrow search algorithm |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN113363963B (en) |
Families Citing this family (6)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN113959448B (en)* | 2021-10-26 | 2023-08-29 | 江苏海洋大学 | An Underwater Terrain Aided Navigation Method Based on Improved Salp Swarm Algorithm |
| CN114792066B (en)* | 2022-03-15 | 2024-06-14 | 湖北工业大学 | Wireless charging system compensation network optimization method for improving sparrow search algorithm |
| CN115470601B (en)* | 2022-09-15 | 2025-09-23 | 辽宁大学 | A method for arranging joint microseismic monitoring stations in coal mines |
| CN116979931B (en)* | 2023-09-22 | 2024-01-12 | 中建八局第三建设有限公司 | Signal processing method for early warning feedback of bridge girder erection machine |
| CN117526326B (en)* | 2023-11-01 | 2024-10-01 | 哈尔滨电气科学技术有限公司 | Multi-target combined optimization method for three-level PWM rectifier, electronic equipment and storage medium |
| CN118596160B (en)* | 2024-08-08 | 2024-11-22 | 四川省机械研究设计院(集团)有限公司 | Industrial robot control method, system and platform based on mixed sparrow algorithm |
Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN112329934A (en)* | 2020-11-17 | 2021-02-05 | 江苏科技大学 | An RBF Neural Network Optimization Algorithm Based on Improved Sparrow Search Algorithm |
| CN112714397A (en)* | 2020-12-25 | 2021-04-27 | 杭州电子科技大学 | WSN node positioning method based on ranging optimization and improved sparrow search algorithm |
Family Cites Families (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| ATE420160T1 (en)* | 2003-06-18 | 2009-01-15 | Genelux Corp | MODIFIED RECOMBINANT VACCINIA VIRUSES, USES THEREOF |
| BRPI0702826B1 (en)* | 2007-06-26 | 2018-05-02 | Petrobras Distribuidora S.A. | CAUSIC EMULSION COMPOSITIONS OF CONTROLLED ASPHALTIC MICROCOATING |
| CN103151781B (en)* | 2013-03-19 | 2014-12-10 | 河海大学常州校区 | Self-adaptive fuzzy control method for active power filter based on feedback linearization |
| CN105846431A (en)* | 2016-06-06 | 2016-08-10 | 国网福建省电力有限公司 | Power harmonics current signal tracking control method |
| CN109066678A (en)* | 2018-08-28 | 2018-12-21 | 西安航空职业技术学院 | A kind of improved APF system harmonics electric current detecting method |
| CN111260015A (en)* | 2020-01-10 | 2020-06-09 | 南昌大学 | A method for parameter identification of lithium-ion battery model based on chaotic cat swarm algorithm |
| CN112260280A (en)* | 2020-09-29 | 2021-01-22 | 山东大学 | Harmonic control method for bidirectional AC/DC converter in hybrid micro-grid |
- 2021
- 2021-05-20CNCN202110548777.1Apatent/CN113363963B/enactiveActive
Patent Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN112329934A (en)* | 2020-11-17 | 2021-02-05 | 江苏科技大学 | An RBF Neural Network Optimization Algorithm Based on Improved Sparrow Search Algorithm |
| CN112714397A (en)* | 2020-12-25 | 2021-04-27 | 杭州电子科技大学 | WSN node positioning method based on ranging optimization and improved sparrow search algorithm |
Non-Patent Citations (1)
| Title |
|---|
| An Improved Salp Swarm Algorithm With Spiral Flight Search for Optimizing Hybrid Active Power Filters’ Parameters;Leyingyue Zhang等;《IEEE Access》;20200903(第8期);第154816-154832页* |
Also Published As
| Publication number | Publication date |
|---|---|
| CN113363963A (en) | 2021-09-07 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN113363963B (en) | Optimized three-phase SAPF direct current side control method by improving sparrow search algorithm | |
| CN108227494A (en) | The fuzzy fault tolerant control method of the non-linear optimal constraints of batch process 2D | |
| CN116961004B (en) | Intelligent power distribution network voltage adjusting method, system and readable storage medium | |
| CN108334679A (en) | Active Power Filter-APF total-sliding-mode control method based on double feedback fuzzy neural networks | |
| CN111371322A (en) | Boost type converter control method and system based on finite time convergence observer | |
| CN109103884A (en) | Active Power Filter-APF back stepping control method based on metacognition fuzzy neural network | |
| WO2024159591A1 (en) | Method for estimating leakage inductance parameter of high-frequency transformer of dab converter | |
| Fei et al. | Self-constructing Chebyshev fuzzy neural complementary sliding mode control and its application | |
| Kalim et al. | A graphical approach for controller design with desired stability margins for a DC–DC boost converter | |
| CN108828961A (en) | Active Power Filter-APF sliding-mode control based on metacognition fuzzy neural network | |
| CN116610029A (en) | Inverter control method based on fuzzy PID control of whale algorithm | |
| Ibrahim | Performance evaluation of PI controller for positive output Luo converter | |
| CN115987086A (en) | Single-switch DC-DC converter on-line control method based on neural network | |
| Round et al. | Comparison of frequency and time domain neural network controllers for an active power filter | |
| CN119171506A (en) | Photovoltaic inverter low voltage ride-through control method and system based on improved MPPT | |
| CN110350546A (en) | A kind of single-phase active electric-power filter control method | |
| CN114513060A (en) | Wireless charging control method based on particle swarm optimization fuzzy control | |
| Vijayal et al. | Integrated Renewable Smart Grid System Using Fuzzy Based Intelligent Controller. | |
| CN113690926A (en) | Method for optimizing control parameter setting of single-phase inverter by improving firework algorithm | |
| CN112072893A (en) | A Power Electronic Converter Control Method with Synthetic Variable Feedback | |
| Li et al. | An improved grid voltage feedforward compensation scheme of grid-connected inverter in weak grid | |
| CN116449682A (en) | A BP neural network PI parameter self-tuning method for three-phase PWM rectifier | |
| Qin et al. | Research and design of single phase inverter based on fuzzy PID control | |
| CN116125803A (en) | A Backstepping Fuzzy Neural Network Control Strategy of Inverter Based on Extreme Learning Machine | |
| Li et al. | WOA–PSO of fractional-order PID control for arc plasma power supply inverter modules |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |