CN111614571A - A distributed end-to-end delay optimization method and system for critical tasks - Google Patents
A distributed end-to-end delay optimization method and system for critical tasksDownload PDFInfo
- Publication number
- CN111614571A CN111614571ACN202010340849.9ACN202010340849ACN111614571ACN 111614571 ACN111614571 ACN 111614571ACN 202010340849 ACN202010340849 ACN 202010340849ACN 111614571 ACN111614571 ACN 111614571A
- Authority
- CN
- China
- Prior art keywords
- model
- link
- distributed
- delay
- delay optimization
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Granted
Links
Images
Classifications
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L47/00—Traffic control in data switching networks
- H04L47/10—Flow control; Congestion control
- H04L47/18—End to end
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L47/00—Traffic control in data switching networks
- H04L47/10—Flow control; Congestion control
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L47/00—Traffic control in data switching networks
- H04L47/10—Flow control; Congestion control
- H04L47/28—Flow control; Congestion control in relation to timing considerations
- H04L47/283—Flow control; Congestion control in relation to timing considerations in response to processing delays, e.g. caused by jitter or round trip time [RTT]
Landscapes
- Engineering & Computer Science (AREA)
- Computer Networks & Wireless Communication (AREA)
- Signal Processing (AREA)
- Data Exchanges In Wide-Area Networks (AREA)
Abstract
Translated fromChinese
Description
Translated fromChinese技术领域technical field
本发明涉及通信技术领域，尤其涉及一种分布式的关键型任务端到端时延优化方法及系统。The invention relates to the field of communication technologies, and in particular, to a distributed end-to-end delay optimization method and system for critical tasks.
背景技术Background technique
随着网络技术的高速发展，5G通信网络需要严格保证物联网设备的QoS端到端服务交付，则要求端到端服务交付更具有定制化以及延迟敏感的特性，并为物联网通信提供更细粒度的服务质量。典型的物联网应用场景包括智能电网、大规模移动社交网络、工业自动化与智能交通系统等。对于端到端服务交付，来自无线接入网络侧(RAN)的数据分组被聚合在一起，并根据服务类型分组到业务流中，然后通过有回程链路将其转发到核心网络的边缘路由器。With the rapid development of network technology, the 5G communication network needs to strictly guarantee the QoS end-to-end service delivery of IoT devices, which requires the end-to-end service delivery to be more customized and delay-sensitive, and provide more detailed information for IoT communication. Granular quality of service. Typical IoT application scenarios include smart grids, large-scale mobile social networks, industrial automation, and intelligent transportation systems. For end-to-end service delivery, data packets from the radio access network side (RAN) are aggregated and grouped into traffic flows according to service type, which are then forwarded to edge routers in the core network over a backhaul link.
智能电网作为典型的垂直行业，多样化的电力业务所需的QoS要求也不同。智能电网中一些时间关键的机器对机器通信业务，需要超高可靠性与低延迟的网络；实时控制类与动态过程自动化调度等业务则需要这种时延能力极致的通信网络，可以将这些业务称为电网中的关键任务通信。例如，面向低时延需求的配电自动化，通过检测配电网线路或设备状态信息，可快速实现配网线路区段或配网设备的故障判断及准确定位，这在电力通信中起着举足轻重的作用，其可靠性要求达到99.999％，同时需要高精度的时间同步需求以及低时延需求，通信端到端传输时延要求小于10ms甚至更低。As a typical vertical industry, smart grid has different QoS requirements for diversified power services. Some time-critical machine-to-machine communication services in the smart grid require ultra-high reliability and low-latency networks; services such as real-time control and dynamic process automation scheduling require such communication networks with extreme latency capabilities, which can integrate these services. Called mission critical communications in the grid. For example, in the distribution automation for low-latency requirements, by detecting the status information of the distribution network lines or equipment, the fault judgment and accurate positioning of the distribution network line sections or distribution network equipment can be quickly realized, which plays a pivotal role in power communication. Its reliability requirements reach 99.999%, high-precision time synchronization requirements and low-latency requirements are also required, and the end-to-end transmission delay of communication is required to be less than 10ms or even lower.
端到端电力网络可以包括无线接入(RAN)部分与核心网络(CN)部分。在CN侧，使用软件定义网络(SDN)和网络功能虚拟化(NFV)，可以使每个划分出的逻辑隔离的CN共享底层网络基础设施(如路由、交换机与有线链路等)。同时，在核心网络中，VNFs可以被灵活地放置在网络中，并且可以动态地请求和释放相应的资源。一组VNFs与连接它们的虚拟链路构成逻辑VNF链，称为服务功能链(SFC)，表示业务流需要遍历以进行E2E服务供应的特定网络功能序列。The end-to-end power network may include a radio access (RAN) part and a core network (CN) part. On the CN side, using software-defined networking (SDN) and network function virtualization (NFV), each logically isolated CN can share the underlying network infrastructure (such as routing, switches, and wired links, etc.). Meanwhile, in the core network, VNFs can be flexibly placed in the network, and corresponding resources can be dynamically requested and released. A set of VNFs and the virtual links connecting them form a logical VNF chain, called a service function chain (SFC), which represents a specific sequence of network functions that a traffic flow needs to traverse for E2E service provisioning.
面对不同种类的关键任务，服务于关键任务业务流的SFC将由不同设置在路由节点上的VNFs构成。对于关键任务来讲，历经SFC的延迟敏感业务流的E2E分组延迟是指示切片性能的主要度量。然而，关键任务通信仍然处于5G的早期标准化阶段，这带来了许多尚未解决的研究问题。Facing different kinds of key tasks, the SFC serving the mission-critical business flow will be composed of different VNFs set up on the routing nodes. For mission critical, the E2E packet delay of delay-sensitive traffic flows through the SFC is the primary metric indicative of slice performance. However, mission-critical communications are still in the early standardization stages of 5G, which brings up many unanswered research questions.
在大多数现有的研究中，每个业务流的E2E分组延迟计算为每个物理链路上的分组传输延迟的总和，而不考虑由于NFV节点上的CPU处理引起的分组处理延迟。因此，如何构建一种分析模型来评估业务流历经SFC时的平均分组延迟，这是一项具有挑战性的工作，并且对于实现SFC构成的时延感知的关键任务具有重要意义。In most existing studies, the E2E packet delay for each traffic flow is calculated as the sum of the packet transmission delays on each physical link, regardless of the packet processing delay due to CPU processing on the NFV node. Therefore, how to construct an analytical model to evaluate the average packet delay when a traffic flow goes through SFC is a challenging task, and it is of great significance for realizing the key task of delay-awareness constituted by SFC.
发明内容SUMMARY OF THE INVENTION
本发明实施例提供一种分布式的关键型任务端到端时延优化方法及系统，用以克服现有技术在端到端时延优化计算时，是获取每个物理链路上的分组传输延迟，再计算传输延迟的总和，导致计算效率低、精算精度差，受制约条件多等缺陷。The embodiments of the present invention provide a distributed key task end-to-end delay optimization method and system, which are used to overcome the need to obtain the packet transmission on each physical link during the end-to-end delay optimization calculation in the prior art. Delay, and then calculate the sum of the transmission delay, resulting in low computational efficiency, poor actuarial accuracy, and many constraints.
第一方面，本发明实施例提供一种分布式的关键型任务端到端时延优化方法，主要包括：In a first aspect, an embodiment of the present invention provides a distributed end-to-end delay optimization method for critical tasks, which mainly includes:
S1，根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；S2，根据权重有向图，以链路拥塞因子作为优化变量，考虑链路存在故障时的链路-路径流量恢复设计，构建最小化所述拥塞因子的时延优化模型；S3，采用基于交替方向乘法子的Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到端关键型任务的时延最小化。S1, according to the distributed mission-critical end-to-end network, construct the weighted directed graph of the underlying core network; S2, according to the weighted directed graph, take the link congestion factor as the optimization variable, and consider the link when the link is faulty -Path traffic recovery design, construct a delay optimization model that minimizes the congestion factor; S3, use Benders decomposition based on alternating direction multipliers to solve the delay optimization model to obtain a distributed link-path traffic planning scheme , which minimizes the latency of end-to-end critical tasks.
作为可选地，上述S1，根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图，可以包括：Optionally, in the above S1, according to the distributed end-to-end network of critical tasks, construct a weighted directed graph of the underlying core network, which may include:
确定关键型任务端到端网络的物理节点集合
作为可选地，上述根据权重有向图，以链路拥塞因子作为优化变量，考虑链路存在故障时的链路-路径流量恢复设计，构建最小化所述拥塞因子的时延优化模型，其目标函数为：Optionally, according to the weighted directed graph, the link congestion factor is used as the optimization variable, and the link-path traffic recovery design when the link is faulty is considered, and a delay optimization model that minimizes the congestion factor is constructed. The objective function is:
该时延优化模型的约束条件为：The constraints of the delay optimization model are:
C1-1：
C1-2：
C1-3:
C1-4:
C1-5:
C1-6:
其中，r为链路拥塞因子，e表示一条链路；p表示一条虚拟路径，h表示节点对之间的需求量，d表示需求的编号，hd表示第d个业务的需求量；s表示链路e的故障状态，其中s＝0表示链路e正常运行，s＝e表示链路e发生故障；
作为可选地，上述S3，采用基于交替方向乘子法的Benders分解，对时延优化模型进行求解，可以包括以下步骤：Optionally, in the above S3, the Benders decomposition based on the alternating direction multiplier method is used to solve the delay optimization model, which may include the following steps:
S3.1，基于Benders分解，将对时延优化模型的分解为一个首问题模型P2和一个主问题模型P6；S3.1, based on Benders decomposition, decompose the delay optimization model into a first problem model P2 and a main problem model P6;
S3.2，对首问题模型P2进行可行性检验；S3.2, to test the feasibility of the first problem model P2;
S3.3，若首问题模型P2可行，基于交替方向乘子法对首问题模型进行P2求解，获取到拉格朗日乘子最优割和上界信息，将拉格朗日乘子最优割反馈至主问题模型P6；S3.3, if the first problem model P2 is feasible, solve the first problem model P2 based on the alternating direction multiplier method, obtain the optimal cut and upper bound information of the Lagrangian multipliers, and optimize the Lagrange multipliers Cut feedback to the main problem model P6;
S3.4，基于分支定界法，根据拉格朗日乘子最优割，对主问题模型P6进行求解，以更新首问题模型P2的二元变量udp0、udps，并获取下界信息；S3.4, based on the branch and bound method, according to the optimal cut of Lagrangian multipliers, solve the main problem model P6 to update the binary variables udp0 and udps of the first problem model P2, and obtain the lower bound information;
S3.5，迭代执行S3.2-S3.4，直至判断首问题模型P2不可行，获取每条链路负载以及每条虚拟路径的流变量，以确定分布式的链路-路径流量规划方案。S3.5, iteratively execute S3.2-S3.4 until it is judged that the first problem model P2 is infeasible, obtain the load of each link and the flow variable of each virtual path to determine the distributed link-path flow planning scheme .
作为可选地，上述S3.1，基于Benders分解，将对时延优化模型的分解为一个首问题模型P2和一个主问题模型P6，可以包括以下步骤：Optionally, the above S3.1, based on Benders decomposition, decomposes the delay optimization model into a first problem model P2 and a main problem model P6, which may include the following steps:
在确定第v次迭代时候的二元变量udp0和udps之后，根据时延优化模型获取首问题模型P2；首问题模型P2的目标函数为：After determining the binary variables udp0 and udps at the vth iteration, the first problem model P2 is obtained according to the delay optimization model; the objective function of the first problem model P2 is:
首问题模型P2的约束条件为：The constraints of the first problem model P2 are:
C2-1:
C2-2:
C2-3:
C2-4:
主问题模型P6的目标函数为：The objective function of the main problem model P6 is:
主问题模型P6的约束条件为：The constraints of the main problem model P6 are:
C6-1:
C6-2:
C6-3:
C6-4:
其中，V1+V2＝v，v为总迭代次数，V1为当首问题可行时，解决首问题的迭代次数；V2为当首问题不可行时，解决l1-min问题时的迭代次数；
作为可选地，上述S3.3，若首问题模型P2可行，基于交替方向乘子法对所述首问题模型P2进行求解，具体包括以下步骤：Optionally, in the above S3.3, if the first problem model P2 is feasible, the first problem model P2 is solved based on the alternating direction multiplier method, which specifically includes the following steps:
S3.3.1，获取首问题模型P2的拉格朗日函数
其中，λ＝(λ1,λ2,λ3,λ4)为拉格朗日乘子，
S3.3.2，基于拉格朗日函数
对偶模型P2-Dual的约束条件为：The constraints of the dual model P2-Dual are:
λ≥0；λ≥0;
S3.3.3，将对偶模型P2-Dual分解为内层最小化模型P3和外层最大化模型P4，内层最小化模型的求解变量为二元变量xdps、ye，外层最大化模型的求解变量为拉格朗日乘子λ＝(λ1,λ2,λ3,λ4)；S3.3.3, decompose the dual model P2-Dual into an inner minimization model P3 and an outer maximization model P4, the solution variables of the inner minimization model are binary variables xdps , ye , and the outer maximization model is The solution variable is Lagrange multiplier λ=(λ1 ,λ2 ,λ3 ,λ4 );
内层最小化模型P3为无约束模型，其目标函数为：The inner minimization model P3 is an unconstrained model, and its objective function is:
外层最大化模型P4的目标函数为：The objective function of the outer maximization model P4 is:
外层最大化模型P4的约束条件为：The constraints of the outer maximization model P4 are:
λ≥0；λ≥0;
其中，
S3.3.4，基于交替方向乘子法对所述内层最小化模型P3求解；S3.3.4, solve the inner layer minimization model P3 based on the alternating direction multiplier method;
S3.3.5，对首问题模型P2中的拉格朗日乘子进行更新，完成对外层最大化模型P4进行求解。S3.3.5, update the Lagrange multiplier in the first problem model P2, and complete the solution of the outer layer maximization model P4.
作为可选地，上述S3.3.4，基于交替方向乘子法对内层最小化模型P3求解，包括单不限于以下步骤：Optionally, in the above S3.3.4, the inner layer minimization model P3 is solved based on the alternating direction multiplier method, including but not limited to the following steps:
引入辅助变量fe作为链路e上的负载变量ye的复制，获取首问题模型P2的增广拉格朗日函数
其中，μe是对应这个等式约束的拉格朗日乘子，ρ是惩罚参数；E为链路总数；Among them, μe is the Lagrange multiplier corresponding to this equality constraint, ρ is the penalty parameter; E is the total number of links;
获取转换后的内层最小化模型P3’：Get the transformed inner minimization model P3':
其中，变量ye，fe，xdps和乘子μe的更新方式分别如下：Among them, the update methods of variables ye , fe , xdps and multiplier μe are as follows:
μe[t+1]＝μe[t]+ρ(fe-ye)μe [t+1]=μe [t]+ρ(fe -ye )
其中，t为当前更新次数。Among them, t is the current number of updates.
作为可选地，在上述S3.3.5，对所述首问题模型P2中的拉格朗日乘子进行更新，完成对所述外层最大化模型P4进行求解中，所述拉格朗日乘子更新的步骤为：Optionally, in the above S3.3.5, the Lagrangian multiplier in the first problem model P2 is updated, and the Lagrangian multiplier in the solution of the outer layer maximization model P4 is completed. The steps for sub-update are:
其中，
作为可选地，在所述S3.5中，直至判断所述首问题模型P2不可行，获取每条链路负载以及每条虚拟路径的流变量，包括：Optionally, in S3.5, until it is judged that the first problem model P2 is infeasible, the load of each link and the flow variable of each virtual path are obtained, including:
若判断首问题模型P2不可行，则创建可行割确定模型l1-min；If it is judged that the first problem model P2 is infeasible, create a feasible cut determination model l1 -min;
可行割确定模型l1-min的目标函数为：The objective function of the feasible cut determination model l1 -min is:
可行割确定模型l1-min的约束条件为：The constraints of the feasible cut determination model l1 -min are:
C5-1:
C5-2:
C5-3:
C5-4:
其中，qj为新引入的约束破坏变量，所述约束破坏变量用于当无可行解满足首问题时，松弛对首问题的约束条件。Among them, qj is a newly introduced constraint breaking variable, which is used to relax the constraints on the first problem when no feasible solution satisfies the first problem.
根据可行割确定模型l1-min，获取拉格朗日乘子最优割
其中，
根据拉格朗日乘子最优割
第二方面，本发明实施例提供一种分布式的关键型任务端到端时延优化系统，主要包括：拓扑结构构建单元、时延优化模型单元和模型运算单元，其中：In a second aspect, an embodiment of the present invention provides a distributed end-to-end delay optimization system for critical tasks, which mainly includes: a topology structure construction unit, a delay optimization model unit, and a model operation unit, wherein:
拓扑结构构建单元主要用于根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；时延优化模型单元，用于根据所述权重有向图，以链路拥塞因子作为优化变量，构建最小化拥塞因子的时延优化模型；模型运算单元主要用于采用基于交替方向乘法子的Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到端关键型任务的时延最小化。The topology construction unit is mainly used to construct the weighted directed graph of the underlying core network according to the distributed key task end-to-end network; the delay optimization model unit is used to calculate the link congestion factor according to the weighted directed graph. As an optimization variable, a delay optimization model that minimizes the congestion factor is constructed; the model operation unit is mainly used to solve the delay optimization model by using Benders decomposition based on multipliers in alternating directions to obtain a distributed link-path traffic planning scheme , which minimizes the latency of end-to-end critical tasks.
第三方面，本发明实施例提供一种电子设备，包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序，其中，处理器执行所述程序时实现如第一方面任一所述的分布式的关键型任务端到端时延优化方法的步骤。In a third aspect, an embodiment of the present invention provides an electronic device, including a memory, a processor, and a computer program stored in the memory and executable on the processor, wherein, when the processor executes the program, any of the methods described in the first aspect are implemented. Steps of the described distributed end-to-end delay optimization method for critical tasks.
第四方面，本发明实施例提供一种非暂态计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现如第一方面任一所述的分布式的关键型任务端到端时延优化方法的步骤。In a fourth aspect, an embodiment of the present invention provides a non-transitory computer-readable storage medium on which a computer program is stored, and when the computer program is executed by a processor, implements the distributed critical type as described in any one of the first aspect. Steps of the task end-to-end latency optimization method.
本发明实施例提供的分布式的关键型任务端到端时延优化方法及系统，采用简洁的方法对底层核心网络进行设计，创建了一个针对最小化最大链路拥塞因子的问题模型，并采用基于交替方向乘法子的Benders分解对该模型进行求解，以得到分布式的链路-路径流量规划方案，使得端到端关键型任务时延最小化，兼顾了链路-路径的流量恢复设计，有效的提高了优化的效率和精度。The distributed key task end-to-end delay optimization method and system provided by the embodiments of the present invention use a concise method to design the underlying core network, create a problem model for minimizing the maximum link congestion factor, and adopt The model is solved based on the Benders decomposition of the alternating direction multipliers to obtain a distributed link-path traffic planning scheme, which minimizes the end-to-end critical task delay and takes into account the link-path traffic recovery design. Effectively improve the efficiency and precision of optimization.
附图说明Description of drawings
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作一简单地介绍，显而易见地，下面描述中的附图是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。In order to more clearly illustrate the embodiments of the present invention or the technical solutions in the prior art, the following briefly introduces the accompanying drawings that need to be used in the description of the embodiments or the prior art. Obviously, the accompanying drawings in the following description These are some embodiments of the present invention. For those of ordinary skill in the art, other drawings can also be obtained according to these drawings without creative efforts.
图1为本发明实施例提供的一种分布式的关键型任务端到端时延优化方法流程示意图；1 is a schematic flowchart of a distributed end-to-end delay optimization method for critical tasks provided by an embodiment of the present invention;
图2为本发明实施例提供的一种分布式的关键型任务端到端网络构架示意图；2 is a schematic diagram of a distributed end-to-end network architecture for critical tasks provided by an embodiment of the present invention;
图3为本发明实施例提供的一种底层网络模型示意图；3 is a schematic diagram of an underlying network model provided by an embodiment of the present invention;
图4为现有技术中的一种平均时延和链路利用率曲线示意图；4 is a schematic diagram of an average delay and link utilization curve in the prior art;
图5为本发明实施例提供的一种分布式的关键型任务端到端时延优化方法的框架图；5 is a framework diagram of a distributed end-to-end delay optimization method for critical tasks provided by an embodiment of the present invention;
图6为本发明实施例提供的一种ADMM实施方法的模型示意图；6 is a schematic diagram of a model of an ADMM implementation method provided by an embodiment of the present invention;
图7为本发明实施例提供的一种分布式的关键型任务端到端时延优化系统的结构示意图；7 is a schematic structural diagram of a distributed end-to-end delay optimization system for critical tasks provided by an embodiment of the present invention;
图8为本发明实施例提供的一种电子设备的实体结构图。FIG. 8 is a physical structure diagram of an electronic device according to an embodiment of the present invention.
具体实施方式Detailed ways
为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。In order to make the purposes, technical solutions and advantages of the embodiments of the present invention clearer, the technical solutions in the embodiments of the present invention will be clearly and completely described below with reference to the accompanying drawings in the embodiments of the present invention. Obviously, the described embodiments These are some embodiments of the present invention, but not all embodiments. Based on the embodiments of the present invention, all other embodiments obtained by those of ordinary skill in the art without creative efforts shall fall within the protection scope of the present invention.
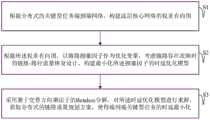
图1为本发明实施例提供的一种分布式的关键型任务端到端时延优化方法的流程示意图，如图1所示，该方法包括但不限于以下步骤：FIG. 1 is a schematic flowchart of a distributed end-to-end delay optimization method for critical tasks provided by an embodiment of the present invention. As shown in FIG. 1 , the method includes but is not limited to the following steps:
S1，根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；S1, according to the distributed mission-critical end-to-end network, construct the weighted directed graph of the underlying core network;
S2，根据权重有向图，以链路拥塞因子作为优化变量，考虑链路存在故障时的链路-路径流量恢复设计，构建最小化拥塞因子的时延优化模型；S2, according to the weighted directed graph, taking the link congestion factor as the optimization variable, and considering the link-path traffic recovery design when the link is faulty, construct a delay optimization model that minimizes the congestion factor;
S3，采用基于交替方向乘法子的Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到端关键型任务的时延最小化。S3, Benders decomposition based on alternating direction multipliers is used to solve the delay optimization model, and a distributed link-path traffic planning scheme is obtained to minimize the delay of end-to-end critical tasks.
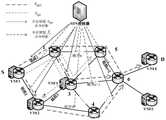
具体地，作为一种可选的实施例，对于分布式的关键型任务端到端网络，例如，电力底层核心网络的设计，考虑任一由软件定义网络(SDN)/网络功能虚拟化(NFV)技术支持的软件化网络为模型。在该底层网络上，虚拟网络功能(VNF)实例(例如VNF1、VNF2等)被创建在实际的数据转发节点上。作为可选地，相同类型的VNF实例可以部署在多个物理节点上，以便接近最终用户并实现负载平衡，且每个物理节点可以部署多个VNF实例。Specifically, as an optional embodiment, for the design of a distributed mission-critical end-to-end network, for example, the power underlying core network, consider either a software-defined network (SDN)/network function virtualization (NFV) ) technology-supported software-based network is modeled. On this underlying network, virtual network function (VNF) instances (eg VNF1, VNF2, etc.) are created on the actual data forwarding nodes. Alternatively, VNF instances of the same type can be deployed on multiple physical nodes for proximity to end users and for load balancing, and each physical node can deploy multiple VNF instances.
具体地，具有NFV能力的节点的处理能力是指计算资源的集合，可以包括CPU核心、内存和存储等。Specifically, the processing capability of an NFV-capable node refers to a collection of computing resources, which may include CPU cores, memory, and storage.
其中，节点集合
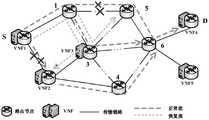
假定由底层网络基础设施支撑的VNF实例由集合Π＝{π|π＝1,2,...,N}表示，图2位本发明实施例提供的一种关键型任务端到端网络架构，图3为本发明实施例提供的与图2相对应的底层网络模型，如图2和图3所示，从源节点S到目的节点D的端到端需求可以由{VNF1,VNF2,VNF3,VNF4}构成的SFC进行服务。Assuming that the VNF instance supported by the underlying network infrastructure is represented by the set Π={π|π=1,2,...,N}, Figure 2 shows a mission-critical end-to-end network architecture provided by an embodiment of the
需要说明的是，VNF可能被创建在业务需求的源节点以及目的节点，也有可能作为中继节点上的VNF用于处理来自上个流段的业务流，即SFC序列{VNF1,VNF2,VNF3,VNF4}也有可能是一个长SFC序列{VNF1,…,VNF N}中的一个子集。It should be noted that the VNF may be created on the source node and destination node of the business requirements, or may be used as a VNF on the relay node to process the business flow from the previous flow segment, that is, the SFC sequence {VNF1, VNF2, VNF3, It is also possible that VNF4} is a subset of a long SFC sequence {VNF1,...,VNF N}.
同时，本发明实施例在分布式的关键型任务端到端网络的构建中，还可以进一步结合核心网络中故障的恢复设计问题，即不仅针对网络正常运行状态，并且还针对一组选定的故障情况相对应的状态集。其中，不同的故障情况由链路和节点的可用性状态指定，并且还由特定情况所需的需求量指定。故本发明实施例提供的分布式的关键型任务端到端时延优化方法，通过对利用上述方式构建的分布式的关键型任务端到端网络进行建模分析，可以对故障具有恢复能力，有效的提高时延优化模型的鲁棒性，致使即使部分网络资源暂时出现故障，网络也能够承载相应的需求。At the same time, in the construction of a distributed end-to-end network for critical tasks, the embodiments of the present invention can further combine the design problem of fault recovery in the core network, that is, not only for the normal operation state of the network, but also for a set of selected The set of states corresponding to the fault condition. Among them, the different failure conditions are specified by the availability status of links and nodes, and also by the amount of demand required for a particular situation. Therefore, in the distributed end-to-end delay optimization method for critical tasks provided by the embodiments of the present invention, by modeling and analyzing the distributed end-to-end network for critical tasks constructed in the above manner, it can recover from faults. The robustness of the delay optimization model is effectively improved, so that even if some network resources temporarily fail, the network can carry the corresponding demand.
作为一种可选实施例，在步骤S1中，所述的根据分布式的关键型任务端到端网络，考虑链路存在故障时的链路-路径流量恢复设计，构建底层核心网络的权重有向图，可以包括：As an optional embodiment, in step S1, according to the distributed mission-critical end-to-end network, considering the link-path traffic recovery design when the link is faulty, the weight of constructing the underlying core network is as follows: Directional graphs, which can include:
确定关键型任务端到端网络的物理节点集合
根据物理节点集合、链路集合、支持VNF功能的节点的处理容量集合以及链路容量集合，构建底层核心网络的权重有向图
具体地，在本发明实施例中，构建底层核心网络的权重有向图可以采用以下方法：Specifically, in this embodiment of the present invention, the following methods may be used to construct the weighted directed graph of the underlying core network:
用i表示一个节点，e表示一条链路，p表示一条虚拟路径，h表示节点对之间的需求量，并且用d来表示需求的编号，即hd表示第d个业务需求量大小，s表示链路e的故障状态，其中s＝0表示链路e正常运行，s＝e表示链路e发生故障。Use i to represent a node, e to represent a link, p to represent a virtual path, h to represent the demand between pairs of nodes, and d to represent the number of demands, that is, hd represents the size of the d-th business demand, s Indicates the failure state of link e, where s=0 indicates that link e is running normally, and s=e indicates that link e is faulty.
因此，可以定义节点集合为
进一步地，本发明实施例中，采用链路拥塞因子作为优化变量，构建最小化所述拥塞因子的时延优化模型，是基于以下考虑：Further, in this embodiment of the present invention, the link congestion factor is used as an optimization variable to construct a delay optimization model that minimizes the congestion factor, based on the following considerations:
电力网络中的关键型任务的传输需要时延能力极致的网络，例如电网中智能分布式配电自动化业务，其端到端最大时延不应超过10ms，而应用层端到端的时延需求需要对底层物理网络的合理设计来实现，故合理化的对底层网络中的拓扑流量进行设计，才能满足端到端关键任务通信的时延需求。更进一步来说，即如何最小化数据包通过网络的延迟是本发明实施例需要解决的一个技术问题。需要说明的是，关于网络的延迟的计算对象重点不是特定的包，而是源和目标(需求)之间整体包的流的平均延迟，甚至是整体包的平均行为。The transmission of critical tasks in the power network requires a network with extreme delay capability. For example, for intelligent distributed distribution automation services in the power grid, the maximum end-to-end delay should not exceed 10ms, and the end-to-end delay requirement of the application layer requires It is realized by the rational design of the underlying physical network, so the rational design of the topology traffic in the underlying network can meet the delay requirements of end-to-end mission-critical communication. Furthermore, how to minimize the delay of data packets passing through the network is a technical problem to be solved by the embodiments of the present invention. It should be noted that the calculation object of network delay does not focus on specific packets, but on the average delay of the entire packet flow between the source and the destination (demand), and even the average behavior of the entire packet.
为了进一步地说明本发明实施例中选择以链路拥塞因子作为优化变量的优点，下面将结合系统平均时延与链路拥塞因子之间的关系进行说明。In order to further illustrate the advantage of selecting the link congestion factor as the optimization variable in the embodiment of the present invention, the following description will be given in conjunction with the relationship between the system average delay and the link congestion factor.
为了说明典型的网络的延迟行为，可以从图4所示的现有技术中记载的平均时延和链路利用率曲线示意图，直观地获知：当一条链路的利用率越高，该链路上承载的流量就越多，即该链路就越拥塞。因此，在本发明实施例中选择采用链路拥塞因子(Linkcongestion factor)来替代图4中链路利用率(Link utilization)。在计算端到端延迟时，由于网络路由的瞬时存储和转发性质，延迟部分需要相加，从而保持每个链路/网络上的平均延迟尽可能低是很重要的。综上所述，出于网络设计考虑的目的，采用最大链路拥塞因子作为延迟标准的替代标准是符合客观规律的，通过构建最小化所述拥塞因子的时延优化模型，确定出最佳的分布式的链路-路径流量规划方案，提高端到端关键型任务的时延最小化的确定效率。In order to illustrate the delay behavior of a typical network, it can be intuitively known from the schematic diagram of the average delay and link utilization curve recorded in the prior art shown in FIG. 4: when the utilization rate of a link is higher, the link The more traffic is carried on the link, the more congested the link is. Therefore, in this embodiment of the present invention, a link congestion factor (Linkcongestion factor) is chosen to replace the link utilization (Link utilization) in FIG. 4 . When calculating end-to-end latency, it is important to keep the average latency on each link/network as low as possible due to the instantaneous store-and-forward nature of network routing. To sum up, for the purpose of network design consideration, it is in line with objective laws to use the maximum link congestion factor as a substitute for the delay standard. By constructing a delay optimization model that minimizes the congestion factor, the optimal The distributed link-path traffic planning scheme improves the efficiency of determining the delay minimization of end-to-end critical tasks.
进一步地，本发明实施例在对时延优化模型进行求解时，采用基于交替方向乘法子(ADMM)与Benders分解相结合，解决了对模型解耦涉及所有用户的约束，导致对于原始的最初问题通常会花费大量时间和资源的不足，通过将问题划分为小问题，可以节省端到端的通信时间和资源，求解速度快，收敛性能好。Further, when solving the delay optimization model in the embodiment of the present invention, the combination of alternating direction multiplier (ADMM) and Benders decomposition is adopted, which solves the constraint that all users are involved in the decoupling of the model, which leads to the original initial problem. Usually it takes a lot of time and lack of resources. By dividing the problem into small problems, end-to-end communication time and resources can be saved, the solution speed is fast, and the convergence performance is good.
本发明实施例提供的种分布式的关键型任务端到端时延优化方法，采用简洁的方法对底层核心网络进行设计，创建了一个针对最小化最大链路拥塞因子的问题模型，并采用基于交替方向乘法子的Benders分解对该模型进行求解，以得到分布式的链路-路径流量规划方案，使得端到端关键型任务时延最小化，兼顾了链路-路径的流量恢复设计，有效的提高了优化的效率和精度。The distributed end-to-end delay optimization method for critical tasks provided by the embodiment of the present invention adopts a concise method to design the underlying core network, creates a problem model aiming at minimizing the maximum link congestion factor, and adopts a method based on The Benders decomposition of the alternating direction multiplier is used to solve the model to obtain a distributed link-path traffic planning scheme, which minimizes the end-to-end critical task delay, and takes into account the link-path traffic recovery design. improves the efficiency and accuracy of the optimization.
基于上述实施例的内容，作为一种可选实施例，上述S22，根据权重有向图，以链路拥塞因子作为优化变量，构建最小化所述拥塞因子的时延优化模型，其目标函数可以为：Based on the content of the above embodiment, as an optional embodiment, in the above S22, according to the weighted directed graph, the link congestion factor is used as the optimization variable to construct a delay optimization model that minimizes the congestion factor, and its objective function can be for:
P1：
时延优化模型的约束条件设置为：The constraints of the delay optimization model are set as:
C1-1：
C1-2：
C1-3:
C1-4:
C1-5:
C1-6:
其中，r为链路拥塞因子，e表示一条链路；p表示一条虚拟路径，h表示节点对之间的需求量，d表示需求的编号，hd表示第d个业务的需求量；s表示链路e的故障状态，其中s＝0表示链路e正常运行，s＝e表示链路e发生故障；
具体地，在本发明实施例中，不仅考虑到链路正常时的第d个业务的需求量hd0，同时兼顾了在各种状态链路下的第d个业务的需求量hds，有效的提供了模型的精确性。Specifically, in the embodiment of the present invention, not only the demand hd0 of the d th service when the link is normal, but also the demand hds of the d th service under various state links are taken into account, and the effective provides the accuracy of the model.
进一步地，链路e的容量为ce，并且设链路e的实际负载为ye，xdp0表示正常状况下需求d在虚拟路径p上的流量，xdps表示在状态s下需求d在虚拟路径p上的流量。令二值常量δedp作为路径-链路指示记号，对于需求d，如果链路e在虚拟路径p上，δedp＝1，否则为0。引入二元变量udp0和udps分别指示在正常状况下和在状态s下需求d是否使用虚拟路径p，如果使用这条路径，udp0＝1、udps＝1，否则均为0。Further, the capacity of link e is ce , and the actual load of link e is set to be ye , xdp0 represents the flow of demand d on virtual path p under normal conditions, and xdps represents that in state s, demand d is at Traffic on virtual path p. Let the binary constant δedp be the path-link indicator, for the demand d, if the link e is on the virtual path p, δedp =1, otherwise it is 0. The binary variablesudp0 andudps are introduced to indicate whether the virtual path p is used by the demand d under normal conditions and in the state s, respectively. If this path is used,udp0 =1,udps =1, otherwise both are 0.
在本申请实施例中，基于每条链路的实际负载为ye，定义链路拥塞因子为
由于整个网络在正常状况下的业务流不会分支，即对于需求d所开通的虚拟路径p的总和应等于1，即可以构建所述约束条件C1-1。Since the service flow of the entire network does not branch under normal conditions, that is, the sum of the virtual paths p opened for the demand d should be equal to 1, the constraint condition C1-1 can be constructed.
由于
由于在故障状态s下，最多允许需求d的一个附加恢复流，当现有的正常流量不足以实现需求量时，需要此额外流量。所以二元变量udps应满足所述约束条件C1-3。Since in the fault state s, at most one additional recovery flow of demand d is allowed, this additional flow is required when the existing normal flow is insufficient to meet the demand. So the binary variableudps should satisfy the constraint C1-3.
由于xdps是一个事先未知的恢复流，则需要满足上述约束条件C1-4。Since xdps is a previously unknown recovery stream, the above constraint C1-4 needs to be satisfied.
进一步地，在本实施例中引入二元常量αes∈{0,1}αes＝1表示链路e是否处于故障状态s，如果是链路正常，则αes＝1，否则αes＝0。为了描述需求d的某一虚拟路径p在状态s下的可用性，引入二元常量
最后，对于链路e，也应该满足上述约束条件C1-6。需要说明的是，
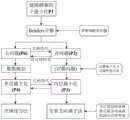
基于上述实施例的内容，作为一种可选实施例，在上述S3中，采用基于交替方向乘子法的Benders分解，对所述时延优化模型进行求解，包括单不限于以下步骤：Based on the content of the above embodiment, as an optional embodiment, in the above S3, the Benders decomposition based on the alternating direction multiplier method is used to solve the delay optimization model, including but not limited to the following steps:
S3.1，基于Benders分解，将对时延优化模型的分解为一个首问题模型P2和一个主问题模型P6；S3.1, based on Benders decomposition, decompose the delay optimization model into a first problem model P2 and a main problem model P6;
S3.2，对首问题模型P2进行可行性检验；S3.2, to test the feasibility of the first problem model P2;
S3.3，若首问题模型P2可行，基于交替方向乘子法对首问题模型进行P2求解，获取到拉格朗日乘子最优割和上界信息，将拉格朗日乘子最优割反馈至主问题模型P6；S3.3, if the first problem model P2 is feasible, solve the first problem model P2 based on the alternating direction multiplier method, obtain the optimal cut and upper bound information of the Lagrangian multipliers, and optimize the Lagrange multipliers Cut feedback to the main problem model P6;
S3.4，基于分支定界法，根据拉格朗日乘子最优割，对主问题模型P6进行求解，以更新首问题模型P2的二元变量udp0、udps，并获取下界信息；S3.4, based on the branch and bound method, according to the optimal cut of Lagrangian multipliers, solve the main problem model P6 to update the binary variables udp0 and udps of the first problem model P2, and obtain the lower bound information;
S3.5，迭代执行S3.2-S3.4，直至判断首问题模型P2不可行，获取每条链路负载以及每条虚拟路径的流变量，以确定分布式的链路-路径流量规划方案。S3.5, iteratively execute S3.2-S3.4 until it is judged that the first problem model P2 is infeasible, obtain the load of each link and the flow variable of each virtual path to determine the distributed link-path flow planning scheme .
具体地，在本实施例中所涉及的最小化端到端关键型任务的平均时延问题，以链路拥塞因子作为优化变量，在优化每条链路上的负载ye时，我们同时还引入了保护设计约束(C1-3至C1-6)。同时，优化变量还考虑到在正常状况与状态s下的路径指示变量udp0与udps，以及状态s下路径p的流变量xdps。通过对构建的时延优化模型分析，可以看出由于udp0与udps的二值性，使得上述问题是一个混合整数规划(MILP)问题。Specifically, in the problem of minimizing the average delay of end-to-end key tasks involved in this embodiment, the link congestion factor is used as the optimization variable. When optimizing the load ye on each link, we also Protection design constraints (C1-3 to C1-6) are introduced. At the same time, the optimization variables also take into account the path indicator variables udp0 andudps under normal conditions and state s, and the flow variable x dpsof path p under state s. By analyzing the constructed delay optimization model, it can be seen that the above problem is a mixed integer programming (MILP) problem due to the binary nature of udp0 and udps .
如图5所示，在本发明实施例中，由于时延优化模型的求解问题仍然是MILP问题，其中包括整数和连续变量。Benders(Benders Decomposition，简称BD)分解是一种有效解决此类问题的迭代算法。BD分解的基本原理是将原来的MILP问题分解成一个首问题和一个主问题，并且利用两个问题在每一步中的解，进行相互迭代求解。其中，与原问题相关的首问题需要固定二值变量，而对于首问题的解决，可以获取时延优化模型的上界信息(原问题为min问题)，并且可以得到和不等式约束相关的拉格朗日乘子的信息。As shown in FIG. 5 , in the embodiment of the present invention, the solution problem of the time delay optimization model is still a MILP problem, which includes integer and continuous variables. Benders (Benders Decomposition, BD for short) decomposition is an iterative algorithm that effectively solves such problems. The basic principle of BD decomposition is to decompose the original MILP problem into a head problem and a main problem, and use the solutions of the two problems in each step to iteratively solve each other. Among them, the first problem related to the original problem requires fixed binary variables, and for the solution of the first problem, the upper bound information of the delay optimization model can be obtained (the original problem is the min problem), and the Lager related to the inequality constraint can be obtained. Information on the Long Day Multiplier.
在本发明实施例中，主问题的求解则是利用对偶理论，并且利用从首问题获取的拉格朗日乘子进行推导求解。对于主问题的求解，可以获取时延优化模型的下界信息(原问题为min问题)，并且能获取到下一次迭代的首问题的二值变量的信息。In the embodiment of the present invention, the solution of the main problem is based on the dual theory, and the Lagrange multiplier obtained from the first problem is used for derivation and solution. For the solution of the main problem, the lower bound information of the delay optimization model (the original problem is the min problem) can be obtained, and the information of the binary variables of the first problem of the next iteration can be obtained.
基于上述实施例的内容，作为一种可选实施例，结合图6所示的ADMM实施方法示意图，上述S3.1，基于Benders分解，将时延优化模型的分解为一个首问题模型P2和一个主问题模型P6，具体可以包括：Based on the content of the above embodiment, as an optional embodiment, in conjunction with the schematic diagram of the ADMM implementation method shown in FIG. 6, the above S3.1, based on Benders decomposition, decomposes the delay optimization model into a first problem model P2 and a The main problem model P6, which can specifically include:
在确定第v次迭代时候的二元变量udp0和udps之后，根据时延优化模型获取所述首问题模型P2，其中：After determining the binary variables udp0 and udps at the vth iteration, the first problem model P2 is obtained according to the delay optimization model, where:
首问题模型P2的目标函数为：The objective function of the first problem model P2 is:
首问题模型P2的约束条件为：The constraints of the first problem model P2 are:
C2-1:
C2-2:
C2-3:
C2-4:
其中，主问题模型P6的目标函数为：Among them, the objective function of the main problem model P6 is:
主问题模型P6的约束条件为：The constraints of the main problem model P6 are:
C6-1:
C6-2:
C6-3:
C6-4:
其中，V1+V2＝v，v为总迭代次数，V1为当首问题可行时，解决首问题的迭代次数；V2为当首问题不可行时，解决l1-min问题时的迭代次数；
因为基于Benders分解的首问题仅包含连续变量，因此给定在第v次迭代时候的二元变量udp0和udps，则可以得到上述首问题P2。Because the first problem based on Benders decomposition contains only continuous variables, given the binary variables udp0 and udps at the vth iteration, the above first problem P2 can be obtained.
进一步地，在首问题P2中，由于优化变量只有在状态s下需求d在虚拟路径p上的流变量xdps和每条链路e的实际负载ye，同时约束C2-1～C2-4均为线性约束，因此问题P2是一个线性规划问题。Further, in the first problem P2, since the optimization variables are only the flow variable xdps on the virtual path p and the actual load ye of each link e in the state s, C2-1～C2-4 are constrained at the same time. Both are linear constraints, so problem P2 is a linear programming problem.
进一步地，在确定了首问题P2之后，对于Benders分解的主问题，可以相应的确定出主问题模型P6的目标函数及其约束条件。Further, after determining the first problem P2, for the main problem of Benders decomposition, the objective function of the main problem model P6 and its constraints can be determined accordingly.
进一步地，本发明实施例提供的分布式的关键型任务端到端时延优化方法，所述S3.3，若所述首问题模型P2可行，基于交替方向乘子法对所述首问题模型P2进行求解，包括但不限于以下步骤：Further, in the distributed end-to-end delay optimization method for critical tasks provided by the embodiment of the present invention, in S3.3, if the first problem model P2 is feasible, the first problem model is determined based on the alternating direction multiplier method. P2 is solved, including but not limited to the following steps:
S3.3.1，获取所述首问题模型P2的拉格朗日函数
其中，λ＝(λ1,λ2,λ3,λ4)为拉格朗日乘子，
S3.3.2，基于所述拉格朗日函数
所述对偶模型P2-Dual的约束条件为：The constraints of the dual model P2-Dual are:
λ≥0；λ≥0;
S3.3.3，将所述对偶模型P2-Dual分解为内层最小化模型P3和外层最大化模型P4，所述内层最小化模型的求解变量为二元变量xdps、ye，所述外层最大化模型的求解变量为拉格朗日乘子λ＝(λ1,λ2,λ3,λ4)；S3.3.3, decompose the dual model P2-Dual into an inner layer minimization model P3 and an outer layer maximization model P4, the solution variables of the inner layer minimization model are binary variables xdps , ye , the The solution variable of the outer maximization model is the Lagrange multiplier λ=(λ1 ,λ2 ,λ3 ,λ4 );
所述内层最小化模型P3为无约束模型，其目标函数为：The inner layer minimization model P3 is an unconstrained model, and its objective function is:
所述外层最大化模型P4的目标函数为：The objective function of the outer layer maximization model P4 is:
所述外层最大化模型P4的约束条件为：The constraints of the outer layer maximization model P4 are:
λ≥0；λ≥0;
其中，
S3.3.4，基于交替方向乘子法对所述内层最小化模型P3求解；S3.3.4, solve the inner layer minimization model P3 based on the alternating direction multiplier method;
S3.3.5，对所述首问题模型P2中的拉格朗日乘子进行更新，完成对所述外层最大化模型P4进行求解。S3.3.5, update the Lagrange multiplier in the first problem model P2, and complete the solution of the outer layer maximization model P4.
具体地，本发明实施例在对首问题模型P2进行求解的过程中，首先确定P2的拉格朗日函数
对于问题P2-Dual，在本实施例中，可以将其分离为内层最小化问题和外层最大化问题。其中，内层最小化问题的求解变量为状态s下需求d在虚拟路径p上的流变量xdps和每条链路e的实际负载ye；外层最大化问题的求解变量则是拉格朗日乘子λ＝(λ1,λ2,...)。For the problem P2-Dual, in this embodiment, it can be separated into an inner minimization problem and an outer maximization problem. Among them, the solution variables of the inner minimization problem are the flow variable xdps of the demand d on the virtual path p in the state s and the actual load ye of each link e; the solution variable of the outer maximization problem is Lager Rangian multiplier λ=(λ1 ,λ2 ,...).
具体地，关于内层最小化问题的求解步骤可以为：Specifically, the solution steps for the inner minimization problem can be as follows:
将问题P2-Dual分解获取到内层最小化问题P3，则内层最小化问题模型P3的目标函数为
该问题P3为无约束最小化问题，且优化变量为xdps和ye，可以采用ADMM(交替方向乘子法)进行求解。The problem P3 is an unconstrained minimization problem, and the optimization variables are xdps and ye , which can be solved by ADMM (Alternating Direction Multiplier Method).
ADMM被广泛用于解耦涉及所有用户的约束。对于原始的最初问题通常会花费大量时间和资源，但借助于ADMM，通过将问题划分为小问题，可以节省端到端的通信时间和资源。ADMM is widely used to decouple constraints involving all users. The original initial problem usually takes a lot of time and resources, but with ADMM, by dividing the problem into small problems, end-to-end communication time and resources can be saved.
对于一个一般的问题可以由下面的问题进行表示：A general problem can be represented by the following problem:
其中x是由等式约束耦合的变量。where x is the variable coupled by the equality constraints.
则对于原始问题的增广拉格朗日函数可以表述为：Then the augmented Lagrangian function for the original problem can be expressed as:
其中，γ是对应的拉格朗日乘子，μ是惩罚参数。where γ is the corresponding Lagrange multiplier and μ is the penalty parameter.
变量更新过程可以按如下顺序进行：The variable update process can be performed in the following order:
因此，在本实施例中，由于已经确定了拉格朗日函数，故需要按照ADMM变量更新的方式对问题P3中的变量进行更新。Therefore, in this embodiment, since the Lagrangian function has been determined, the variables in problem P3 need to be updated in the manner of ADMM variable update.
需要说明的是，在解决问题P3之前，需要首先将问题P3转化为可分离的形式，以便于分布式解法的进行：It should be noted that, before solving the problem P3, it is necessary to convert the problem P3 into a separable form to facilitate the distributed solution:
首先，引入辅助变量fe作为变量ye的复制，作为首问题P2的全局变量。该辅助变量fe的引入，相当于新增添了一个等式约束，且需要使得下式满足：First, the auxiliary variable fe is introduced as a copy of the variable ye as the global variable of the first problem P2. The introduction of the auxiliary variable fe is equivalent to adding a new equality constraint, and the following formula needs to be satisfied:
则需要进一步改写问题P3中的目标函数，将等式约束加入目标函数中，即问题P2的增广拉格朗日函数。Then it is necessary to further rewrite the objective function in problem P3, and add equality constraints to the objective function, that is, the augmented Lagrangian function of problem P2.
其中，μe是对应这个等式约束的拉格朗日乘子，系数ρ是惩罚参数。where μe is the Lagrange multiplier corresponding to this equality constraint, and the coefficient ρ is the penalty parameter.
其中，全局的复制变量fe由全局的SDN控制器进行处理，而原本的变量ye则由每条链路(借助路由节点或NFV进行处理)进行并行式地处理，因此问题P3可进一步转换为内层最小化模型P3’，并同时获取变量ye，fe，xdps和乘子μe的更新方式。Among them, the global replicated variable fe is processed by the global SDN controller, and the original variable ye is processed in parallel by each link (processed by means of routing nodes or NFV), so the problem P3 can be further transformed Minimize the model P3' for the inner layer, and obtain the update mode of the variables ye , fe , xdps and the multiplier μe at the same time.
基于上述实施例的内容，作为一种可选实施例，在上述S3.3.5，对首问题模型P2中的拉格朗日乘子进行更新，完成对外层最大化模型P4进行求解中，所述拉格朗日乘子更新的步骤为：Based on the content of the above embodiment, as an optional embodiment, in the above S3.3.5, the Lagrange multiplier in the first problem model P2 is updated, and the solution of the outer layer maximization model P4 is completed. The steps of Lagrange multiplier update are:
其中，
由于外层最大化问题主要是对P2中的拉格朗日乘子进行更新，则可以得到最大化模型P4的目标函数，其中，
基于上述实施的内容，在本发明实施例中，采用基于交替方向乘子法的Benders分解时，在每个迭代的过程中，对于在第v次迭代时候的二值
如果在第v次迭代时候，首问题是可行的，那么它的解可以为每条链路的实际负载以及在状态s下对于需求d的路径p上的流变量提供信息。在此基础上，则可以获取拉格朗日乘子最优割α，并且可以将其加到之后的主问题中：If the first problem is feasible at the vth iteration, its solution can provide information on the actual load on each link and the flow variables on path p for demand d in state s. On this basis, the optimal cut α of the Lagrangian multiplier can be obtained, and it can be added to the main problem after:
如果在第v次迭代时候，首问题是不可行的，则需要创建可行割确定模型l1-min。If the first problem is infeasible at the vth iteration, a feasible cut determination model l1 -min needs to be created.
其中，可行割确定模型l1-min的目标函数为：Among them, the objective function of the feasible cut determination model l1 -min is:
可行割确定模型l1-min的约束条件为：The constraints of the feasible cut determination model l1 -min are:
C5-1:
C5-2:
C5-3:
C5-4:
其中，qj为新引入的约束破坏变量，所述约束破坏变量用于当无可行解满足首问题时，松弛对首问题的约束条件。Among them, qj is a newly introduced constraint breaking variable, which is used to relax the constraints on the first problem when no feasible solution satisfies the first problem.
进一步地，可以根据可行割确定模型l1-min，获取拉格朗日乘子最优割
其中，
最后，根据拉格朗日乘子最优割
本发明实施例提供一种分布式的关键型任务端到端时延优化系统，如图7所示，包括但不限于拓扑结构构建单元1、时延优化模型单元2和模型运算单元3，其中：An embodiment of the present invention provides a distributed end-to-end delay optimization system for critical tasks, as shown in FIG. 7 , including but not limited to a topology
拓扑结构构建单元1主要用于根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；时延优化模型单元2主要用于根据权重有向图，以链路拥塞因子作为优化变量，考虑链路存在故障时的链路-路径流量恢复设计，构建最小化所述拥塞因子的时延优化模型；模型运算单元3主要用于采用基于交替方向乘法子的Benders分解，对所述时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到端关键型任务的时延最小化。The
需要说明的是，本发明实施例提供的分布式的关键型任务端到端时延优化系统在具体运行过程中，可以执行上述任一实施例所述的分布式的关键型任务端到端时延优化方法，对此本实施例不作赘述。It should be noted that, the distributed end-to-end delay optimization system for critical tasks provided by the embodiments of the present invention can perform the end-to-end time delay optimization of distributed critical tasks described in any of the foregoing embodiments during a specific operation process. The extension optimization method is not repeated in this embodiment.
本发明实施例提供的分布式的关键型任务端到端时延优化系统，采用简洁的方法对底层核心网络进行设计，创建了一个针对最小化最大链路拥塞因子的问题模型，并采用基于交替方向乘法子的Benders分解对该模型进行求解，以得到分布式的链路-路径流量规划方案，使得端到端关键型任务时延最小化，兼顾了链路-路径的流量恢复设计，有效的提高了优化的效率和精度。The distributed end-to-end delay optimization system for critical tasks provided by the embodiment of the present invention adopts a concise method to design the underlying core network, creates a problem model aiming at minimizing the maximum link congestion factor, and adopts an alternate The Benders decomposition of the direction multiplier is used to solve the model to obtain a distributed link-path traffic planning scheme, which minimizes the end-to-end critical task delay and takes into account the link-path traffic recovery design. Improved efficiency and accuracy of optimization.
图8示例了一种电子设备的实体结构示意图，如图8所示，该电子设备可以包括：处理器(processor)310、通信接口(Communications Interface)320、存储器(memory)330和通信总线340，其中，处理器310，通信接口320，存储器330通过通信总线340完成相互间的通信。处理器310可以调用存储器330中的逻辑指令，以执行如下方法：S1，根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；S2，根据权重有向图，以链路拥塞因子作为优化变量，构建最小化所述拥塞因子的时延优化模型；S3，采用基于交替方向乘法子的Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到端关键型任务的时延最小化。FIG. 8 illustrates a schematic diagram of the physical structure of an electronic device. As shown in FIG. 8 , the electronic device may include: a processor (processor) 310, a communication interface (Communications Interface) 320, a memory (memory) 330, and a
此外，上述的存储器330中的逻辑指令可以通过软件功能单元的形式实现并作为独立的数据集销售或使用时，可以存储在一个计算机可读取存储介质中。基于这样的理解，本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件数据集的形式体现出来，该计算机软件数据集存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：U盘、移动硬盘、只读存储器(ROM，Read-Only Memory)、随机存取存储器(RAM，Random Access Memory)、磁碟或者光盘等各种可以存储程序代码的介质。In addition, the above-mentioned logic instructions in the
另一方面，本发明实施例还提供一种非暂态计算机可读存储介质，其上存储有计算机程序，该计算机程序被处理器执行时实现以执行上述各实施例提供的优化方法，例如包括：S1，根据分布式的关键型任务端到端网络，构建底层核心网络的权重有向图；S2，根据权重有向图，以链路拥塞因子作为优化变量，构建最小化所述拥塞因子的时延优化模型；S3，采用基于交替方向乘法子的Benders分解，对时延优化模型进行求解，获取分布式的链路-路径流量规划方案，使得端到端关键型任务的时延最小化。On the other hand, an embodiment of the present invention further provides a non-transitory computer-readable storage medium, on which a computer program is stored, and the computer program is implemented by a processor to execute the optimization method provided by the foregoing embodiments, for example, including : S1, according to the distributed mission-critical end-to-end network, construct the weighted directed graph of the underlying core network; S2, according to the weighted directed graph, take the link congestion factor as the optimization variable, construct the method that minimizes the congestion factor Delay optimization model; S3, Benders decomposition based on alternating direction multipliers is used to solve the delay optimization model, and a distributed link-path traffic planning scheme is obtained to minimize the delay of end-to-end critical tasks.
以上所描述的装置实施例仅仅是示意性的，其中所述作为分离部件说明的单元可以是或者也可以不是物理上分开的，作为单元显示的部件可以是或者也可以不是物理单元，即可以位于一个地方，或者也可以分布到多个网络单元上。可以根据实际的需要选择其中的部分或者全部模块来实现本实施例方案的目的。本领域普通技术人员在不付出创造性的劳动的情况下，即可以理解并实施。The device embodiments described above are only illustrative, wherein the units described as separate components may or may not be physically separated, and the components shown as units may or may not be physical units, that is, they may be located in One place, or it can be distributed over multiple network elements. Some or all of the modules may be selected according to actual needs to achieve the purpose of the solution in this embodiment. Those of ordinary skill in the art can understand and implement it without creative effort.
通过以上的实施方式的描述，本领域的技术人员可以清楚地了解到各实施方式可借助软件加必需的通用硬件平台的方式来实现，当然也可以通过硬件。基于这样的理解，上述技术方案本质上或者说对现有技术做出贡献的部分可以以软件数据集的形式体现出来，该计算机软件数据集可以存储在计算机可读存储介质中，如ROM/RAM、磁碟、光盘等，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)执行各个实施例或者实施例的某些部分所述的方法。From the description of the above embodiments, those skilled in the art can clearly understand that each embodiment can be implemented by means of software plus a necessary general hardware platform, and certainly can also be implemented by hardware. Based on this understanding, the above-mentioned technical solutions can be embodied in the form of software data sets, which can be stored in a computer-readable storage medium, such as ROM/RAM. , disk, optical disk, etc., including several instructions for causing a computer device (which may be a personal computer, server, or network device, etc.) to perform the methods described in various embodiments or parts of embodiments.
最后应说明的是：以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。Finally, it should be noted that the above embodiments are only used to illustrate the technical solutions of the present invention, but not to limit them; although the present invention has been described in detail with reference to the foregoing embodiments, those of ordinary skill in the art should understand that it can still be The technical solutions described in the foregoing embodiments are modified, or some technical features thereof are equivalently replaced; and these modifications or replacements do not make the essence of the corresponding technical solutions deviate from the spirit and scope of the technical solutions of the embodiments of the present invention.
Claims (12)
Translated fromChinese
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010340849.9ACN111614571B (en) | 2020-04-26 | 2020-04-26 | Distributed key task end-to-end time delay optimization method and system |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010340849.9ACN111614571B (en) | 2020-04-26 | 2020-04-26 | Distributed key task end-to-end time delay optimization method and system |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN111614571Atrue CN111614571A (en) | 2020-09-01 |
| CN111614571B CN111614571B (en) | 2022-03-04 |
Family
ID=72201151
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202010340849.9AExpired - Fee RelatedCN111614571B (en) | 2020-04-26 | 2020-04-26 | Distributed key task end-to-end time delay optimization method and system |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN111614571B (en) |
Cited By (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN114900518A (en)* | 2022-04-02 | 2022-08-12 | 中国光大银行股份有限公司 | Task allocation method, device, medium and electronic equipment for directed distributed network |
| CN115499370A (en)* | 2021-06-17 | 2022-12-20 | 中国移动通信集团浙江有限公司 | Signaling network link fault processing method, device and computer-readable storage medium |
Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20120155262A1 (en)* | 2010-12-17 | 2012-06-21 | Microsoft Corporation | Kernel awareness of physical environment |
| US20160234077A1 (en)* | 2015-02-09 | 2016-08-11 | Mellanox Technologies Ltd. | Time-efficient network function virtualization architecture |
| CN108934029A (en)* | 2018-07-06 | 2018-12-04 | 南京邮电大学 | The acceleration distributed optimization algorithm rebuild towards perception big data |
| WO2019043446A1 (en)* | 2017-09-04 | 2019-03-07 | Nng Software Developing And Commercial Llc | A method and apparatus for collecting and using sensor data from a vehicle |
- 2020
- 2020-04-26CNCN202010340849.9Apatent/CN111614571B/ennot_activeExpired - Fee Related
Patent Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20120155262A1 (en)* | 2010-12-17 | 2012-06-21 | Microsoft Corporation | Kernel awareness of physical environment |
| US20160234077A1 (en)* | 2015-02-09 | 2016-08-11 | Mellanox Technologies Ltd. | Time-efficient network function virtualization architecture |
| WO2019043446A1 (en)* | 2017-09-04 | 2019-03-07 | Nng Software Developing And Commercial Llc | A method and apparatus for collecting and using sensor data from a vehicle |
| CN108934029A (en)* | 2018-07-06 | 2018-12-04 | 南京邮电大学 | The acceleration distributed optimization algorithm rebuild towards perception big data |
Non-Patent Citations (3)
| Title |
|---|
| DELONG YANG等: "E2E Delay Optimization for Smart Grids Mission-critical Slices in Core Networks", 《2019 11TH INTERNATIONAL CONFERENCE ON WIRELESS COMMUNICATIONS AND SIGNAL PROCESSING》* |
| LUHAN WANG等: "Joint Optimization of Service Function Chaining and Resource Allocation in Network Function Virtualization", 《IEEE ACCESS》* |
| 江卓等: "互联网端到端多路径传输跨层优化研究综述", 《软件学报》* |
Cited By (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN115499370A (en)* | 2021-06-17 | 2022-12-20 | 中国移动通信集团浙江有限公司 | Signaling network link fault processing method, device and computer-readable storage medium |
| CN115499370B (en)* | 2021-06-17 | 2023-08-15 | 中国移动通信集团浙江有限公司 | Method and device for processing link failure of signaling network and computer readable storage medium |
| CN114900518A (en)* | 2022-04-02 | 2022-08-12 | 中国光大银行股份有限公司 | Task allocation method, device, medium and electronic equipment for directed distributed network |
Also Published As
| Publication number | Publication date |
|---|---|
| CN111614571B (en) | 2022-03-04 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| EP3090517B1 (en) | Inter-domain sdn traffic engineering | |
| CN114286413A (en) | TSN network combined routing and stream distribution method and related equipment | |
| Renart et al. | Distributed operator placement for iot data analytics across edge and cloud resources | |
| CN107666412A (en) | The virtual network function dispositions method of service function chain | |
| CN108616394B (en) | A virtual network function backup and deployment method | |
| Hu et al. | Joint deployment and request routing for microservice call graphs in data centers | |
| CN113596868A (en) | 5G network slice resource management mechanism based on SDN and NFV | |
| CN111614571B (en) | Distributed key task end-to-end time delay optimization method and system | |
| CN111865681A (en) | End-to-end delay optimization method, system and storage medium for core network slicing | |
| De Souza et al. | An optimal model for optimizing the placement and parallelism of data stream processing applications on cloud-edge computing | |
| Xu et al. | On the joint design of microservice deployment and routing in cloud data centers | |
| Shang et al. | Network congestion-aware online service function chain placement and load balancing | |
| Zhou et al. | Network function parallelization for high reliability and low latency services | |
| CN117519927A (en) | A hybrid workflow scheduling method, system and medium in a cloud computing environment | |
| CN107579852A (en) | System and method for virtual network performance isolation based on history model in cloud server | |
| Saha et al. | SAFAR: Simulated annealing-based flow allocation rules for industrial networks | |
| Peng et al. | Large-Scale Service Mesh Orchestration with Probabilistic Routing in Cloud Data Centers | |
| CN118573630A (en) | Flow scheduling method and system for time delay sensitive task | |
| de Souza et al. | A throughput model for data stream processing on fog computing | |
| Xiao et al. | Joint Service Deployment and Task Offloading for Datacenters with Edge Heterogeneous Servers | |
| CN115002038B (en) | An intelligent peak shaving method and system based on cloud distributed coordination service | |
| WO2024146193A1 (en) | Sdn-based routing path selection method and apparatus, and storage medium | |
| CN118802696A (en) | A differentiated routing method for cloud scenarios based on SRv6 technology | |
| JP2006287919A (en) | Communication network, content distribution node, tree construction method, and content distribution control program | |
| Yang et al. | E2E delay optimization for smart grids mission-critical slices in core networks |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant | ||
| CF01 | Termination of patent right due to non-payment of annual fee | Granted publication date:20220304 | |
| CF01 | Termination of patent right due to non-payment of annual fee |