CN111402303A - A Target Tracking Architecture Based on KFSTRCF - Google Patents

Abstract

Translated fromChinese

本发明涉及一种基于KFSTRCF的目标跟踪架构，包括离散时间卡尔曼估计器DKE以及STRCF，DKE包括离散时间系统测量以及离散时间系统副本子系统；STRCF的目标跟踪结果输出作为离散时间系统测量中观测模型的测量值输入，通过离散时间系统副本子系统对DKE的模型进行更新，获得状态估计观测更新方程。本发明将卡尔曼滤波器与STRCF相结合实现视觉跟踪，以克服由于大规模应用变化带来的不稳定性问题；并且，还引入步长控制方法来限制所提出的框架的输出状态的最大振幅，以克服由突然加速和转向引起的丢失目标问题，在大多数情况下都优于STRCF，特别是在体育赛事中，表现出比竞争对手更好的性能和更强的鲁棒性。

The invention relates to a target tracking framework based on KFSTRCF, including discrete time Kalman estimator DKE and STRCF, DKE includes discrete time system measurement and discrete time system replica subsystem; the target tracking result of STRCF is output as the observation in the discrete time system measurement The measured value of the model is input, and the DKE model is updated through the discrete-time system replica subsystem to obtain the state estimation observation update equation. The present invention combines Kalman filter and STRCF to realize visual tracking to overcome the instability problem caused by large-scale application changes; and also introduces a step size control method to limit the maximum amplitude of the output state of the proposed framework , to overcome the problem of missing targets caused by sudden acceleration and steering, outperforms STRCF in most cases, especially in sporting events, showing better performance and stronger robustness than competitors.

Description

Translated fromChinese

一种基于KFSTRCF的目标跟踪架构A Target Tracking Architecture Based on KFSTRCF

技术领域：Technical field:

本发明涉及计算机视觉的目标跟踪技术领域，具体涉及一种基于 KFSTRCF的目标跟踪架构。The invention relates to the technical field of target tracking of computer vision, in particular to a target tracking architecture based on KFSTRCF.

背景技术：Background technique:

近年来，视觉跟踪技术在计算机视觉领域得到了广泛的应用，借助于共享代码和数据集，如OTB-2015和Temple-Color，我们可以使用各种评估标准来了解该视觉跟踪方法如何执行，并确定这些领域未来的研究方向。在许多现实场景中，只要获得图像序列帧中目标对象的初始状态(如位置和大小)，视觉跟踪算法就可以对后续帧中的目标进行跟踪。虽然几十年来许多研究者都在努力提高跟踪性能，但仍然存在许多具有挑战性的问题，如背景杂波、遮挡以及视场外等，至今还没有一种算法能在所有场景下都表现出优异的性能。因此，为了克服现有跟踪器的缺点，设计出更为健壮的跟踪方法法是至关重要的。In recent years, visual tracking technology has been widely used in the field of computer vision, with the help of shared codes and datasets, such as OTB-2015 and Temple-Color, we can use various evaluation criteria to understand how this visual tracking method performs, and Identify future research directions in these areas. In many real-world scenarios, as long as the initial state (such as position and size) of the target object in the frame of the image sequence is obtained, the visual tracking algorithm can track the target in the subsequent frames. Although many researchers have worked hard to improve tracking performance for decades, there are still many challenging problems such as background clutter, occlusion, and out-of-view, and so far no algorithm can perform well in all scenarios. Excellent performance. Therefore, in order to overcome the shortcomings of existing trackers, it is crucial to design more robust tracking methods.

如今，许多国家的最先进的跟踪器的源代码已经公开可用，并在实时救灾场景中实现态势感知，但一些跟踪器采用的策略是通过增加复杂性的代价来提高跟踪精度；相反，排名第一的跟踪器，时空正则相关滤波器 (spatial-temporal regularized correlationfilters,STRCF)能够以5倍的速度实现实时视觉跟踪，并提供比其竞争对手空间正则判别相关滤波器(spatially regularized discriminative correlation filters,SRDCF)更为健壮的外观模型。利用多种训练样本，STRCF可以实现对SRDCF的合理逼近，并对大尺度外观变化具有鲁棒性。利用乘法器交替方向法(alternating direction method ofmultipliers,ADMM)，可以有效地求出STRCF的解。然而，这种方法在背景杂波、光照变化、遮挡、平面外旋转和视场外等方面仍有改进的潜力。特别是对于应用的大规模变化中，仍然存在不稳定性问题。Today, the source code of many state-of-the-art trackers is publicly available and enables situational awareness in real-time disaster relief scenarios, but some trackers employ strategies to improve tracking accuracy at the cost of added complexity; The first tracker, spatial-temporal regularized correlation filters (STRCF), can achieve real-time visual tracking at 5 times the speed, and provides spatially regularized discriminative correlation filters (SRDCF) than its competitors. ) for a more robust appearance model. With multiple training samples, STRCF can achieve a reasonable approximation to SRDCF and is robust to large-scale appearance changes. Using the alternating direction method of multipliers (ADMM), the solution of STRCF can be efficiently obtained. However, this approach still has potential for improvement in terms of background clutter, illumination changes, occlusion, out-of-plane rotation, and out-of-view. Especially for large-scale changes in applications, instability issues still exist.

由于自然灾害的破坏性和人类无法到达特点，自主移动机器人是探索未知灾后地区实现救灾的替代选择。由于卡尔曼滤波(Kalman filter,KF)能够平滑和优化定位算法的目标状态，为了提高移动机器人的定位精度，KF成为解决定位误差校正的有力手段。尤其是对于无线传感器网络(wireless sensor networks,WSN)中的网络盲区，仿真和实验结果表明，基于卡尔曼滤波的改进最大似然估计(Kalman filtered grid-based improvedmaximum likelihood estimation,KGIMLE)可以有效地降低环境噪声，提高节点部署不佳的网络盲点中的定位精度。WSN环境噪声和网络盲区中的副作用类似于视觉跟踪中的背景杂波、光照变化、遮挡、平面外旋转和视场外现象。因此，将KF技术与最先进的跟踪器相结合，对计算机视觉领域中各种场景下的视觉跟踪误差进行校正，提高跟踪性能是一种合理的解决方案。Due to the destructive nature of natural disasters and the inaccessibility of humans, autonomous mobile robots are an alternative to explore unknown post-disaster areas for disaster relief. Since the Kalman filter (KF) can smooth and optimize the target state of the positioning algorithm, in order to improve the positioning accuracy of the mobile robot, KF has become a powerful means to solve the positioning error correction. Especially for the network dead zone in wireless sensor networks (WSN), simulation and experimental results show that Kalman filtered grid-based improved maximum likelihood estimation (KGIMLE) can effectively reduce Environmental noise, improving localization accuracy in network blind spots where nodes are poorly deployed. Side effects in WSN ambient noise and network dead zones are similar to background clutter, illumination changes, occlusion, out-of-plane rotation, and out-of-field phenomena in visual tracking. Therefore, it is a reasonable solution to combine KF technology with state-of-the-art trackers to correct visual tracking errors in various scenarios in the field of computer vision and improve tracking performance.

申请号为201910988383.0的中国发明专利公开一种基于STRCF的抗遮挡目标跟踪方法，该方法中通过遮挡判断函数与阈值的关系、以及分块匹配数与阈值的关系来决定是否运行卡尔曼滤波器，一旦判断函数不符合条件，则只能执行STRCF跟踪，并没有将卡尔曼滤波器与STRCF真正有效结合应用，在需要图片帧环节，卡尔曼滤波器并没有参加到目标跟踪中，甚至放弃了对于卡尔曼增益等模型的更新，无法对目标进行连续跟踪，并传播随机动态干扰和传感器噪声的均方不确定性等知识到后续帧的目标跟踪。并且，该方法中使用卡尔曼滤波器对待检测目标进行位置估计时增加了二次检测，这是在卡尔曼模型更新之前完成的，不仅增加了更新模型的噪声干扰，也降低了卡尔曼滤波器对于目标状态的随机动态干扰和传感器噪声的均方不确定性等知识的学习和理解能力。The Chinese invention patent with the application number of 201910988383.0 discloses an anti-occlusion target tracking method based on STRCF. In this method, whether to run the Kalman filter is determined by the relationship between the occlusion judgment function and the threshold, and the relationship between the block matching number and the threshold. Once the judgment function does not meet the conditions, only STRCF tracking can be performed, and the Kalman filter and STRCF are not truly combined and applied. In the link where picture frames are required, the Kalman filter does not participate in the target tracking, and even gives up for Updates of models such as Kalman gain, cannot continuously track the target, and propagate knowledge such as random dynamic disturbance and the mean square uncertainty of sensor noise to the target tracking of subsequent frames. In addition, in this method, the Kalman filter is used to estimate the position of the target to be detected, which is completed before the Kalman model is updated, which not only increases the noise interference of the updated model, but also reduces the Kalman filter. The ability to learn and understand knowledge such as random dynamic disturbance of target state and mean square uncertainty of sensor noise.

由于我们关注的是灾后救援行动中的智能监控，因此，跟踪对象的连续运动状态是人工智能(artificial intelligent,AI)了解其在感兴趣区域(region of interest,ROI)中的行为和目的的关键信息。一方面，跟踪对象的运动状态应该是连续的，以使当前轨迹平滑到前一轨迹。另一方面，跟踪对象的运动状态应该对新实例的修改敏感。为了解决在各种情况下跟踪目标状态的视觉跟踪优化问题(visual tracking optimizationproblem,VTOP)，我们提出了一种新颖的基于卡尔曼滤波的时空正则相关滤波器(KFSTRCF)框架来平滑和优化在大规模应用变化中排名靠前的STRCF跟踪器的估计结果，该框架既保持了 STRCF良好实时跟踪性能，又提高了背景杂波、光照变化、遮挡、平面外旋转和视场外等因素的跟踪精度。并且，我们还引入步长控制方法来限制所提出的框架的输出状态的最大振幅，以克服由突然加速和转向引起的丢失目标问题，本案由此而生。Since we focus on intelligent monitoring in post-disaster relief operations, tracking the continuous motion state of an object is the key for artificial intelligence (AI) to understand its behavior and purpose in a region of interest (ROI) information. On the one hand, the motion state of the tracked object should be continuous to smooth the current trajectory to the previous trajectory. On the other hand, the motion state of the tracked object should be sensitive to the modification of new instances. To address the visual tracking optimization problem (VTOP) of tracking object states in various situations, we propose a novel Kalman filter-based spatiotemporal regular correlation filter (KFSTRCF) framework to smooth and optimize in large Estimation results of the top-ranked STRCF tracker in scale application variation, the framework not only maintains the good real-time tracking performance of STRCF, but also improves the tracking accuracy for factors such as background clutter, illumination changes, occlusion, out-of-plane rotation, and out-of-field of view. . And, we also introduce a step size control method to limit the maximum amplitude of the output state of the proposed framework to overcome the problem of missing targets caused by sudden acceleration and steering, from which this case arises.

发明内容：Invention content:

本发明旨在有效地解决目标跟踪中背景杂波、光照变化、遮挡、平面外旋转和视场外等因素对大规模应用中定位算法目标状态的平滑和优化问题，提出一种基于KFSTRCF的目标跟踪架构，不仅保持了STRCF优秀实时跟踪性能，还克服了大规模应用变化带来的不稳定性问题。The invention aims to effectively solve the problem of smoothing and optimizing the target state of the positioning algorithm in large-scale applications due to factors such as background clutter, illumination change, occlusion, out-of-plane rotation and out-of-view field in target tracking, and proposes a target based on KFSTRCF. The tracking architecture not only maintains the excellent real-time tracking performance of STRCF, but also overcomes the instability problem caused by large-scale application changes.

为了实现上述发明目的，本发明所采用的技术方案为：In order to realize the above-mentioned purpose of the invention, the technical scheme adopted in the present invention is:

一种基于KFSTRCF的目标跟踪架构，包括离散时间卡尔曼估计器DKE 以及STRCF，所述DKE包括离散时间系统测量以及离散时间系统副本子系统；所述STRCF的目标跟踪结果输出作为离散时间系统测量中观测模型的测量值输入，通过离散时间系统副本子系统对DKE的模型进行更新，获得状态估计观测更新方程。A target tracking architecture based on KFSTRCF, including discrete-time Kalman estimator DKE and STRCF, the DKE includes discrete-time system measurement and discrete-time system replica subsystem; the target tracking result of the STRCF is output as the discrete-time system measurement. The measured value input of the observation model is used to update the DKE model through the discrete-time system replica subsystem to obtain the state estimation observation update equation.

所述离散时间系统副本子系统更新后的输出环节，通过步长控制环节来限制整个目标跟踪架构输出状态最大振幅，所述步长控制具体如下：The updated output link of the replica subsystem of the discrete time system limits the maximum amplitude of the output state of the entire target tracking architecture through a step size control link, and the step size control is as follows:

定义最大步长为：len_max＝v×dt.，v表示跟踪目标的速度，t为采样时刻；The maximum step size is defined as: len_max =v×dt., v represents the speed of the tracking target, and t is the sampling time;

建立以下条件约束：Establish the following conditional constraints:

上式中，

表示

的第1行和第1列元素，x_t(1,1)表示x_t的第1行和第1列元素；x_t表示DKE目标运动输入状态向量，

表示输出状态向量后验值。In the above formula,

express

The 1st row and 1st column elements of x_t (1,1) represent the 1st row and 1st column elements of x_t ; x_t represents the DKE target motion input state vector,

Represents the posterior value of the output state vector.

所述离散时间系统测量中的系统动态模型如下：The system dynamic model in the discrete-time system measurement is as follows:

x_t＝Μx_t-1+Γu_t-1.x_t = Μx_t-1 +Γu_t-1 .

其中，x_t表示DKE目标的n×1维运动输入状态向量，u_t-1表示控制状态的 r×1维确定性输入向量，t为采样时刻；Μ表示n×n维状态转移矩阵，它是一个时不变矩阵；Γ表示n×r维离散时间输入耦合矩阵，它是一个时不变矩阵；Among them, x_t represents the n×1-dimensional motion input state vector of the DKE target, u_t-1 represents the r×1-dimensional deterministic input vector of the control state, t is the sampling time; M represents the n×n-dimensional state transition matrix, which is a time-invariant matrix; Γ represents an n×r-dimensional discrete-time input coupling matrix, which is a time-invariant matrix;

用目标的速度v将状态转移矩阵定义为：The state transition matrix is defined by the velocity v of the target as:

使用单位矩阵I来描述离散时间输入耦合矩阵Γ；Use the identity matrix I to describe the discrete-time input coupling matrix Γ;

确定性输入向量可由下式确定，e表示环境噪声：The deterministic input vector can be determined by the following equation, where e represents the ambient noise:

利用测量值更新目标的跟踪结果，将测量值Z_t和跟踪结果x_t之间的线性相关方程定义为：Using the measurement value to update the tracking result of the target, the linear correlation equation between the measurement value Z_t and the tracking result x_t is defined as:

z_t＝Νx_t+υ.z_t = Nx_t +υ.

其中，Ν表示测量灵敏度矩阵，它是时不变矩阵，采用系统中的n×n维单位矩阵I；υ表示测量噪声，它是一个常数参数[1 0]^T。Among them, N represents the measurement sensitivity matrix, which is a time-invariant matrix and adopts the n×n-dimensional unit matrix I in the system; υ represents the measurement noise, which is a constant parameter [1 0]^T .

所述STRCF与DKE的融合方式具体如下：The fusion method of the STRCF and DKE is as follows:

针对STRCF，将离散采样时刻t的每个样本表示为

由S 个特征映射组成，其大小为M×N；并且yt是预定义的高斯形状标签，通过最小化以下目标函数来实现STRCF模型：For STRCF, each sample at discrete sampling time t is denoted as

consists of S feature maps of size M × N; and yt is a predefined Gaussian shape label, the STRCF model is implemented by minimizing the following objective function:

其中Hadamard积表示为·，卷积算子表示为*，w_t和f_t分别表示空间正则化矩阵和相关滤波器；将第(t-1)帧的STRCF结果表示为f_t-1，惩罚参数表示为σ，

和||f_t-f_t-1||²代表空间正则化和时间正则化；where the Hadamard product is denoted as ·, the convolution operator is denoted as *, wt and ft represent the spatial regularization matrix and the correlation filter, respectively; the_STRCF result of the (_t -1)th frame is denoted as ft_-1 , and the penalty The parameter is denoted as σ,

and ||f_t -f_t-1 ||² represent space regularization and temporal regularization;

由于上述模型是凸函数，STRCF可以通过ADMM算法最小化公式(1)得到全局最优解，因此，将辅助变量表示为g_t，并要求f_t＝g_t和将步长参数表示为ρ，然后将公式(1)的增广拉格朗日形式表示为：Since the above model is a convex function, STRCF can obtain the global optimal solution by minimizing formula (1) through ADMM algorithm. Therefore, the auxiliary variable is denoted as g_t , and f_t = g_t is required and the step size parameter is denoted as ρ, Then the augmented Lagrangian form of formula (1) is expressed as:

其中

s_t是拉格朗日乘数，σ是惩罚因子；in

s_t is the Lagrange multiplier and σ is the penalty factor;

基于式(1)，相关滤波器

表示在采样时刻t第s特征层的M×N卷积滤波器，滤波器f_t对样本x_t的卷积响应为：Based on equation (1), the correlation filter

Denotes the M×N convolution filter of the s-th feature layer at sampling time_{t, and the convolution response of filter ft to sample x tis} :

通过求解数目为M×N的S×S线性方程组，可以得到离散傅里叶变换滤波器为：By solving a system of S×S linear equations with a number of M×N, the discrete Fourier transform filter can be obtained as:

由于STRCF以滑动窗口的方式计算帧的所有循环移位上的分类分数，因此使用DFT的卷积特性来获得第t帧中所有像素的分类分数

为：Since STRCF computes the classification scores over all cyclic shifts of a frame in a sliding window fashion, the convolutional properties of DFT are used to obtain the classification scores for all pixels in the t-th frame

for:

其中，运算符·表示逐点乘法，bar运算符表示DFT运算，而运算符Δ-1表示 DFT的逆运算。Among them, operator · represents pointwise multiplication, operator bar represents DFT operation, and operator Δ-1 represents the inverse operation of DFT.

在检测阶段，通过使用在第(t-1)帧中更新后的滤波器

来定位在t时刻新实例中的目标，由于在式(2)中使用了步长ρ大于一个像素的网格策略，因此通过计算DFT系数，从而应用三角多项式来有效地插值分类分数，即：首先，将分类分数

的DFT定义为：In the detection stage, by using the filter updated in the (t-1)th frame

To locate the target in the new instance at time t, since a grid strategy with a step size ρ larger than one pixel is used in Eq. (2), the triangular polynomial is applied to effectively interpolate the classification score by calculating the DFT coefficients, namely: First, the classification score

The DFT is defined as:

其次，定义了样本x_t针对第u个虚单元中图像坐标

处的插值检测分数

为：Second, the sample_xt is defined for the image coordinates in the uth imaginary unit

Interpolated detection score at

for:

通过评估在所有像素位置的检测得分d(m,n)来定义最大检测得分

The maximum detection score is defined by evaluating the detection score d(m,n) at all pixel locations

其中，图像坐标

穿过样本x_t中的所有像素位置，

然后，利用Newton方法从像素(0,0)开始寻找最大得分，通过计算式(15)中梯度和Hessian的差分，通过有限次数的迭代得到收敛；Among them, the image coordinates

through all pixel positions in sample_xt ,

Then, use the Newton method to find the maximum score from the pixel (0,0), and obtain convergence through a finite number of iterations by calculating the difference between the gradient and the Hessian in equation (15).

最后，在测量模型中应用STRCF的跟踪结果

实现STRCF算法与DKE的融合，有：Finally, the tracking results of STRCF are applied in the measurement model

To realize the fusion of STRCF algorithm and DKE, there are:

所述DKE中的误差协方差获得方法如下：The method for obtaining the error covariance in the DKE is as follows:

将跟踪结果的传播估计误差的期望值定义为：The expected value of the propagation estimation error of the tracking results is defined as:

并将状态估计的先验值定义为：And define the prior value of the state estimate as:

其中，

表示为x_t的预先估计，

表示为先验估计

的传播估计误差，

表示为x_t-1的后验估计；in,

is denoted as a pre-estimation of x_t ,

represented as a priori estimate

The propagation estimation error of ,

Denoted as the posterior estimate of x_t-1 ;

因此，可以得到误差协方差矩阵为：Therefore, the error covariance matrix can be obtained as:

其中，w设为一个常数[1 0]^T，将Q定义为环境噪声矩阵，并表示为eI，e表示环境噪声，I表示n×n维单位矩阵，这表明误差协方差矩阵在t时刻的先验值是其t-1时刻的后验值函数；where w is set to a constant [1 0]^T , Q is defined as the environmental noise matrix, and denoted as eI, e is the environmental noise, and I is the n×n-dimensional identity matrix, which indicates that the error covariance matrix at time t The prior value is its posterior value function at time t-1;

由于先验协方差矩阵是式(18)，它满足以下方程：Since the prior covariance matrix is Eq. (18), it satisfies the following equation:

因此，可以得到卡尔曼增益为：Therefore, the Kalman gain can be obtained as:

其中，R表示n×n维测量噪声矩阵，它是时不变矩阵eI；Among them, R represents the n×n-dimensional measurement noise matrix, which is the time-invariant matrix eI;

此外，基于式(18)可得到后验协方差矩阵的相似方程为：In addition, based on equation (18), the similar equation of the posterior covariance matrix can be obtained as:

因此，又可以得到状态估计观测的更新方程为：Therefore, the update equation of the state estimation observation can be obtained as:

又可以写为：

It can also be written as:

最后，基于期望

和式(23)，可以得到误差协方差的更新方程为：Finally, based on expectations

With Equation (23), the update equation of the error covariance can be obtained as:

本发明为了在不同的评估标准下寻求最优的跟踪精度和鲁棒性，并有助于灾后救援行动中的智能监控，提出了一种新的目标跟踪架构，即：融合KF 和STRCF进行视觉跟踪，STRCF的目标跟踪结果作为DKE的观测模型的测量值参加到DKE的计算中，视频流中的每一帧都完整无缺的成为DKE的输入数据，实现了目标跟踪的连续性和完整性，符合“连续思考，离散处理”原则，克服了大规模应用变化带来的不稳定性问题。然后，为了解决由突然加速和转向引起的丢失目标问题，采用步长控制方法来限制框架的输出状态的最大幅值；以步长控制方法作为误差修正机制，在DKE的模型更新后执行，不会影响到DKE对于目标当前状态和随机动态干扰和传感器噪声的均方不确定性等知识的学习和理解，只是在输出阶段，对于存在明显偏差的估计结果进行误差修正，是对现有方法的改进和补充。In order to seek the optimal tracking accuracy and robustness under different evaluation standards, and to help intelligent monitoring in post-disaster rescue operations, the present invention proposes a new target tracking architecture, namely: fusion of KF and STRCF for vision Tracking, the target tracking result of STRCF is used as the measurement value of the DKE observation model to participate in the DKE calculation. Each frame in the video stream becomes the input data of the DKE intact, realizing the continuity and integrity of the target tracking. In line with the principle of "continuous thinking, discrete processing", it overcomes the instability problem caused by large-scale application changes. Then, in order to solve the problem of missing targets caused by sudden acceleration and steering, a step size control method is used to limit the maximum amplitude of the output state of the framework; the step size control method is used as an error correction mechanism, which is executed after the model update of DKE, without It will affect the learning and understanding of DKE's knowledge of the current state of the target, random dynamic interference and the mean square uncertainty of sensor noise. It is only in the output stage that the error correction is performed on the estimation results with obvious deviations, which is an improvement on the existing methods. Improvements and additions.

本发明所给出的DKE协方差方程没有有限的稳态值，这表明本发明的架构性能在很大程度上取决于环境噪声和目标运动特性。经过大规模实验验证，本发明给出的KFSTRCF架构在大多数情况下都优于STRCF，特别是在体育赛事中，表现出比竞争对手更好的性能和更强的鲁棒性。The DKE covariance equation given by the present invention has no finite steady-state value, which indicates that the architecture performance of the present invention depends to a large extent on the environmental noise and target motion characteristics. After large-scale experimental verification, the KFSTRCF architecture given by the present invention is superior to STRCF in most cases, especially in sports events, showing better performance and stronger robustness than competitors.

附图说明：Description of drawings:

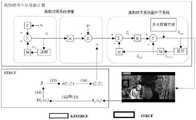
图1为本发明基于KFSTRCF目标跟踪架构示意图。FIG. 1 is a schematic diagram of the target tracking architecture based on KFSTRCF in the present invention.

具体实施方式：Detailed ways:

本实施例公开一种基于KFSTRCF的目标跟踪架构，如图1所示，主要包括离散时间卡尔曼估计器DKE以及STRCF，DKE包括离散时间系统测量以及离散时间系统副本子系统；STRCF的目标跟踪结果输出作为离散时间系统测量中观测模型的测量值输入，通过离散时间系统副本子系统对DKE的模型进行更新，获得状态估计观测更新方程。下面，将结合附图对本发明所涉及的内容展开详细介绍。This embodiment discloses a KFSTRCF-based target tracking architecture, as shown in FIG. 1 , which mainly includes a discrete-time Kalman estimator DKE and STRCF. DKE includes a discrete-time system measurement and a discrete-time system replica subsystem; the target tracking result of the STRCF The output is used as the measurement value input of the observation model in the discrete-time system measurement, and the DKE model is updated through the discrete-time system replica subsystem to obtain the state estimation observation update equation. Hereinafter, the content involved in the present invention will be introduced in detail with reference to the accompanying drawings.

本发明所公开的基于KFSTRCF的目标跟踪架构，主要用于在大规模应用变化中平滑和优化定位算法的目标状态。为了有效地描述目标的运动模型，并保持STRCF良好的实时跟踪性能，我们提出了一种基于KF的视觉跟踪方法，采用基于离散时间卡尔曼估计器(discrete-time Kalman estimator,DKE) 优化STRCF算法输出结果，克服了后续帧的不稳定性问题。与此同时，为了解决由突然加速和转向引起的丢失目标问题，我们提出了一种步长控制方法来限制所提出的框架的输出状态的最大幅值，它是对现实场景中物体运动规律的合理约束。为了分析图1中架构的跟踪性能，我们还验证了本发明的DKE 的协方差方程没有有限的稳态值，该架构的性能主要取决于环境噪声和目标运动特性。以下展开详细说明。The KFSTRCF-based target tracking architecture disclosed in the present invention is mainly used for smoothing and optimizing the target state of the positioning algorithm in large-scale application changes. In order to effectively describe the motion model of the target and maintain the good real-time tracking performance of STRCF, we propose a KF-based visual tracking method, which uses the discrete-time Kalman estimator (DKE) to optimize the STRCF algorithm. The output results, overcoming the instability problem of subsequent frames. At the same time, in order to solve the problem of missing targets caused by sudden acceleration and steering, we propose a step size control method to limit the maximum magnitude of the output state of the proposed framework, which is sensitive to the motion laws of objects in real scenes Reasonable constraints. In order to analyze the tracking performance of the architecture in Fig. 1, we also verified that the covariance equation of the DKE of the present invention has no finite steady-state value, and the performance of this architecture mainly depends on the environmental noise and target motion characteristics. The detailed description is expanded below.

STRCF提出了一种比SRDCF更为稳健的外观模型，并将空间和时间正则化结合到DCF框架中。STRCF利用ADMM算法有效地寻找闭式解，并在很少的迭代次数内实现收敛。采用手工提取的特征，STRCF可以实时运行，比SRDCF具有更好的跟踪精度。STRCF proposes a more robust appearance model than SRDCF and incorporates both spatial and temporal regularization into the DCF framework. STRCF utilizes the ADMM algorithm to efficiently find closed-form solutions and achieve convergence in a small number of iterations. With hand-extracted features, STRCF can run in real-time and has better tracking accuracy than SRDCF.

针对STRCF，我们将离散采样时刻t的每个样本表示为

由 S个特征映射组成，其大小为M×N。并且y_t是预定义的高斯形状标签。我们通过最小化以下目标函数来实现STRCF模型：For STRCF, we denote each sample at discrete sampling time t as

Consists of S feature maps whose size is M×N. And y_t is a predefined Gaussian shape label. We implement the STRCF model by minimizing the following objective function:

其中Hadamard积表示为·，卷积算子表示为*，w_t和f_t分别表示空间正则化矩阵和相关滤波器。我们还将第(t-1)帧的STRCF结果表示为f_t-1，惩罚参数表示为σ。

和||f_t-f_t-1||²代表空间正则化和时间正则化。where the Hadamard product is denoted as ·, the convolution operator is denoted as *, and_wt and ft denote the spatial regularization matrix and correlation filter_, respectively. We also denote the STRCF result at frame (t-1) as f_t-1 and the penalty parameter as σ.

and ||f_t -f_t-1 ||² represent spatial regularization and temporal regularization.

由于上述模型是凸函数，STRCF可以通过ADMM算法最小化式(1)得到全局最优解。因此，我们将辅助变量表示为g_t，并要求f_t＝g_t和将步长参数表示为ρ。然后我们可以将(1)的增广拉格朗日形式表示为：Since the above model is a convex function, STRCF can obtain the global optimal solution by minimizing equation (1) through ADMM algorithm. Therefore, we denote the auxiliary variable as g_t and require f_t = g_t and the step size parameter as ρ. Then we can express the augmented Lagrangian form of (1) as:

其中

s_t是拉格朗日乘数，σ是惩罚因子。in

s_t is the Lagrange multiplier and σ is the penalty factor.

我们可以通过ADMM算法将上述模型分解为以下可选子问题：We can decompose the above model into the following optional subproblems via the ADMM algorithm:

上述f_t，g_t和ρ的解可以在文献中找到(F.Li,C.Tian,W.Zuo,et al,Learningspatial-temporal regularized correlation filters for visual tracking,Proceedings ofthe IEEE Conference on Computer Vision and Pattern Recognition(2018)4904-4913.)。STRCF算法的总成本是O(SMNlog(MN)N_M)，其中N_M是最大迭代次数。The solutions for the above f_t , g_t and ρ can be found in the literature (F.Li, C.Tian, W.Zuo, et al, Learningspatial-temporal regularized correlation filters for visual tracking, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2018) 4904-4913.). The total cost of the STRCF algorithm is O(SMNlog(MN)N_M ), where N_M is the maximum number of iterations.

虽然STRCF能以5倍的速度实现实时的视觉跟踪，并提供比竞争对手 SRDCF更为健壮的外观模型，但对于应用的大规模变化，仍然存在不稳定性问题。正因为如此，我们提出的架构将KF算法集成到STRCF模型中，有效地解决了这个问题，因为它可以在数学上传播跟踪对象的当前运动状态的知识，包括来自随机动态干扰和传感器噪声的均方不确定性。这些特性对估计模型的统计分析和设计具有重要意义。Although STRCF can achieve real-time visual tracking 5 times faster and provide a more robust appearance model than the competitor SRDCF, it still suffers from instability issues for large-scale changes in applications. Because of this, our proposed architecture integrates the KF algorithm into the STRCF model, which effectively addresses this problem as it can mathematically propagate the knowledge of the current motion state of the tracked object, including the average from random dynamic disturbances and sensor noise. square uncertainty. These properties have important implications for the statistical analysis and design of estimation models.

我们首先引入KF算法，要求STRCF的当前输出状态作为KF算法的初始状态。在我们的KFSTRCF架构中，当每轮出现一个新的实例时，STRCF 首先预测其标签并定位目标的质心，然后提取目标的当前运动状态，并将它们反馈给KF算法。此外，我们还可以通过KF模型实现误差修正。最后，通过对KF模型的更新，可以实现更为稳健的目标定位，并传播随机动态干扰和传感器噪声的均方不确定性等知识。We first introduce the KF algorithm, requiring the current output state of the STRCF as the initial state of the KF algorithm. In our KFSTRCF architecture, when a new instance appears in each round, STRCF first predicts its label and locates the object's centroid, then extracts the object's current motion state and feeds them back to the KF algorithm. In addition, we can also achieve error correction through the KF model. Finally, through updates to the KF model, more robust target localization can be achieved and knowledge such as random dynamic disturbances and the mean square uncertainty of sensor noise are propagated.

为了澄清我们的目标，我们提出了我们的优化问题是将我们的KFSTRCF 与STRCF相比较，如何实现最大的改进。我们用符号Inc表示成功率的曲线下面积(area under thecurve,AUC)的增加：To clarify our goal, we pose our optimization problem as comparing our KFSTRCF with STRCF, how to achieve the maximum improvement. We use the symbol Inc to denote the increase in the area under the curve (AUC) of the success rate:

Inc＝auc_KFSTRCF-auc_STRCF. (4)Inc=auc_KFSTRCF- auc_STRCF . (4)

因此，auc_KFSTRCF和auc_STRCF是KFSTRCF和STRCF的成功率AUC得分。Therefore, auc_KFSTRCF and auc_STRCF are the success rate AUC scores of KFSTRCF and STRCF.

因此，我们的视觉跟踪优化问题(visual tracking optimization problem,VTOP)可以表述为：Therefore, our visual tracking optimization problem (VTOP) can be formulated as:

subject tosubject to

andand

其中，

表示在离散采样时刻t的每个样本，包括S个特征映射，其大小为M×N。

表示在t采样时刻第s个特征层的M×N卷积滤波器。x_t表示本文提出的DKE的目标运动状态向量。

and

表示第t帧的水平和垂直图像坐标，

此外，我们定义st_t为离散线性系统针对t时刻的感兴趣采样时间。因此我们可以得到时间间隔dt为dt＝st_t-st_t-1。in,

represents each sample at discrete sampling time t, including S feature maps, and its size is M×N.

represents the M × N convolutional filters of the s-th feature layer at t sampling time. x_t represents the target motion state vector of the DKE proposed in this paper.

and

represent the horizontal and vertical image coordinates of the t-th frame,

Furthermore, we define st_t as the sampling time of interest for the discrete linear system at time t. So we can get the time interval dt as dt=st_t -st_t-1 .

为了降低随机动态干扰和传感器噪声的风险，我们遵循连续思考和离散处理的原则。因此，我们利用DKE来描述目标的连续运动状态以及对新实例的修正。系统动态模型可以描述为：To reduce the risk of random dynamic disturbances and sensor noise, we follow the principles of continuous thinking and discrete processing. Therefore, we utilize DKE to describe the continuous motion state of the target and the correction to new instances. The system dynamic model can be described as:

x_t＝Μx_t-1+Γu_t-1. (8)x_t = Μx_t-1 +Γu_t-1 . (8)

其中，x_t表示目标的n×1维运动状态向量，u_t-1表示控制状态的r×1维确定性输入向量。Μ表示n×n维状态转移矩阵，它是一个时不变矩阵。Γ表示n×r维离散时间输入耦合矩阵，它是一个时不变矩阵。Among them, x_t represents the n×1-dimensional motion state vector of the target, and u_t-1 represents the r×1-dimensional deterministic input vector of the control state. M represents an n×n-dimensional state transition matrix, which is a time-invariant matrix. Γ denotes an n×r-dimensional discrete-time input coupling matrix, which is a time-invariant matrix.

在初始阶段，我们设计了DKE的系统动态模型参数。我们利用第一帧的预定目标位置

作为离散时间模型的输入。然后，我们设计了系统动力学模型的等效常数参数，以在感兴趣的采样时刻之间传播状态向量。首先，我们使用目标的速度v将状态转移矩阵定义为：In the initial stage, we design the system dynamic model parameters of DKE. We utilize the predetermined target position of the first frame

as input to discrete-time models. We then design the equivalent constant parameters of the system dynamics model to propagate the state vector between the sampling instants of interest. First, we define the state transition matrix using the velocity v of the target as:

其次，我们使用单位矩阵I来描述离散时间输入耦合矩阵Γ。最后，我们定义了基于步长控制方法的确定性输入向量u_t。Second, we use the identity matrix I to describe the discrete-time input coupling matrix Γ. Finally, we define the deterministic input vector_ut based on the step size control method.

为了定义测量模型，我们可以得到每个采样时刻t的测量值。此外，利用测量值可以更新目标的跟踪结果x_t。我们将测量值z_t和跟踪结果x_t之间的线性相关方程定义为：To define the measurement model, we can get the measurements at each sampling time t. Furthermore, the tracking result x_t of the target can be updated with the measured value. We define the linear correlation equation between the measured value z_t and the tracking result x_t as:

z_t＝Νx_t+υ. (10)z_t = Nx_t +υ. (10)

其中，Ν表示测量灵敏度矩阵，它是时不变矩阵，采用系统中的n×n维单位矩阵I。υ表示测量噪声，它是一个常数参数[1 0]^T。Among them, N represents the measurement sensitivity matrix, which is a time-invariant matrix and adopts the n×n-dimensional identity matrix I in the system. υ represents measurement noise, which is a constant parameter [1 0]^T .

为了准确地描述目标的运动状态，我们基于STRCF的估计结果定义DKE 的测量模型，因为STRCF在较大的外观变化情况下比其他算法具有更强的鲁棒性。In order to accurately describe the motion state of the target, we define the measurement model of DKE based on the estimation results of STRCF, because STRCF is more robust than other algorithms in the case of large appearance changes.

基于式(1)，相关滤波器

表示在采样时刻t第s特征层的M×N卷积滤波器。我们给出了滤波器f_t对样本x_t的卷积响应为：Based on equation (1), the correlation filter

represents the M×N convolutional filters of the s-th feature layer at sampling time t. We give the convolutional response of the filter f_t to the sample x_t as:

通过求解数目为M×N的S×S线性方程组，我们可以得到离散傅里叶变换(discrete Fourier transformed,DFT)滤波器为：By solving a system of S×S linear equations of number M×N, we can obtain the discrete Fourier transformed (DFT) filter as:

由于STRCF以滑动窗口的方式计算帧的所有循环移位上的分类分数，因此我们使用DFT的卷积特性来获得第t帧中所有像素的分类分数

为：Since STRCF computes the classification scores over all cyclic shifts of a frame in a sliding window fashion, we use the convolutional properties of DFT to obtain the classification scores for all pixels in the t-th frame

for:

其中，运算符·表示逐点乘法。bar运算符表示DFT运算，而运算符Δ^-1表示DFT的逆运算。该方法的时间复杂度为O(SMNlogMN)。where operator · represents pointwise multiplication. The bar operator represents the DFT operation, while the operator Δ^-1 represents the inverse of the DFT. The time complexity of this method is O(SMNlogMN).

此外，在检测阶段，我们通过使用在第(t-1)帧中更新后的滤波器

来定位在t时刻新实例中的目标。由于我们在式(2)中使用了步长ρ大于一个像素的网格策略，因此我们通过计算DFT系数，从而应用三角多项式来有效地插值分类分数。首先，我们将分类分数

的DFT定义为：In addition, in the detection stage, we use the filter updated in the (t-1)th frame by using

to locate the target in the new instance at time t. Since we used a grid strategy with a step size ρ larger than one pixel in Eq. (2), we effectively interpolate the classification scores by computing the DFT coefficients and thus applying triangular polynomials. First, we will classify the score

The DFT is defined as:

其次，我们定义了样本x_t针对第u个虚单元中图像坐标

处的插值检测分数

为：Second, we define the sample_xt for the image coordinates in the uth imaginary unit

Interpolated detection score at

for:

第三，我们通过评估在所有像素位置的检测得分d(m,n)来定义最大检测得分

Third, we define the maximum detection score by evaluating the detection score d(m,n) at all pixel locations

其中，图像坐标

穿过样本x_t中的所有像素位置，

然后，我们利用Newton方法从像素(0,0)开始寻找最大得分。通过计算式(15) 中梯度和Hessian的差分，我们可以通过有限次数的迭代得到收敛。Among them, the image coordinates

through all pixel positions in sample_xt ,

Then, we use Newton's method to find the maximum score starting from pixel (0,0). By computing the difference between the gradient and the Hessian in Eq. (15), we can achieve convergence with a finite number of iterations.

最后，我们可以在测量模型中应用STRCF的跟踪结果

实现STRCF 算法与DKE的融合：Finally, we can apply the tracking results of STRCF in the measurement model

Implement the fusion of STRCF algorithm and DKE:

为了获得DKE的误差协方差，我们将跟踪结果的传播估计误差的期望值定义为：To obtain the error covariance of DKE, we define the expected value of the propagation estimation error of the tracking result as:

并将状态估计的先验值定义为：And define the prior value of the state estimate as:

因此，

表示为x_t的预先估计。

表示为先验估计

的传播估计误差。

表示为x_t-1的后验估计。therefore,

is denoted as a pre-estimation of_xt .

represented as a priori estimate

Propagation estimation error.

Denoted as the posterior estimate of x_t-1 .

因此，我们可以得到误差协方差矩阵为：Therefore, we can get the error covariance matrix as:

因此，w设为一个常数[1 0]^T，那么我们可以将Q定义为环境噪声矩阵，并表示为eI。其中，e表示环境噪声，I表示n×n维单位矩阵。这表明误差协方差矩阵在t时刻的先验值是其t-1时刻的后验值函数。Therefore, w is set to a constant [1 0]^T , then we can define Q as the environmental noise matrix and denote it as eI. Among them, e represents the environmental noise, and I represents the n×n-dimensional identity matrix. This shows that the prior value of the error covariance matrix at time t is a function of its posterior value at time t-1.

由于先验协方差矩阵是式(18)，它满足以下方程：Since the prior covariance matrix is Eq. (18), it satisfies the following equation:

因此，我们可以得到卡尔曼增益为：Therefore, we can get the Kalman gain as:

其中，R表示n×n维测量噪声矩阵，它是时不变矩阵eI。where R represents the n×n-dimensional measurement noise matrix, which is the time-invariant matrix eI.

此外，基于式(18)我们可得到后验协方差矩阵的相似方程为：In addition, based on Equation (18), we can obtain the similar equation of the posterior covariance matrix as:

因此，我们可以得到状态估计观测的更新方程为：Therefore, we can obtain the update equation of the state estimate observation as:

最后，基于期望

和(23)，我们可以得到误差协方差的更新方程为：Finally, based on expectations

and (23), we can get the update equation of the error covariance as:

另外，DKE的一个显著特点为即使无采样的协方差方程是不稳定的，测量估计不确定性的协方差方程仍然具有有限的稳态值。考虑到没有测量的情况，我们需要确定协方差方程的稳定性。这表明当t趋向于正无穷大时，解是否趋向于有限常数值。In addition, a distinctive feature of DKE is that even if the unsampled covariance equation is unstable, the covariance equation measuring the estimation uncertainty still has a finite steady-state value. Considering the absence of measurements, we need to determine the stability of the covariance equation. This shows whether the solution tends to a finite constant value as t tends to positive infinity.

命题1:假设采样时间t→+∞，我们将协方差方程定义为：Proposition 1: Assuming the sampling time t→+∞, we define the covariance equation as:

P_∞＝ΜP_∞Μ^T+Q. (27)P_∞ = MPa_∞ Μ^T +Q. (27)

如果我们将Μ定义为式(9)，则协方差方程没有有限的稳态值。它与协方差P的初始值无关。If we define M as equation (9), the covariance equation has no finite steady-state value. It has nothing to do with the initial value of the covariance P.

证明:因为我们将Μ定义为式(9)，我们可以计算特征值为：Proof: Since we define M as Eq. (9), we can calculate the eigenvalues as:

因此，Μ的特征值是唯一值1。那么，它的复数形式是1+0i。从而得到它在复平面上的点是(1,0)。由于该点不在单位圆内，协方差方程没有解。Therefore, the eigenvalue of M is theunique value 1. Well, its plural form is 1+0i. So that its point on the complex plane is (1,0). Since the point is not inside the unit circle, the covariance equation has no solution.

在现实世界中，跟踪目标可以自由地改变速度和方向。特别是当存在突然加速和转向时，跟踪算法不能进行正确的调整，导致跟踪目标在边界框中丢失。为了解决这个问题，我们提出了一种步长控制方法来限制我们架构的输出状态最大振幅。它是对现实场景中物体运动规律的合理约束。In the real world, the tracking target can freely change speed and direction. Especially when there are sudden accelerations and turns, the tracking algorithm cannot make correct adjustments, resulting in the loss of the tracked target in the bounding box. To address this issue, we propose a step size control method to limit the output state maximum amplitude of our architecture. It is a reasonable constraint on the laws of motion of objects in real scenes.

为了更清楚地讨论KFSTRCF，图1描述了我们的系统架构。在大规模应用中(比如，OTB-2015数据集中的dragonbaby)，我们可以建立基于式(8) 和式(10)的离散时间系统测量，并采用状态转移矩阵Μ和输入耦合矩阵Γ。然后，利用式(12)和式(13)得到第t帧(比如，dragonbaby的第65帧)中所有像素的分类分数

将STRCF融合到我们的框架中，利用其更加健壮的外观模型。此外，我们可以通过式(14)和式(15)获得图像坐标处的插值检测分数

而且，我们可以通过评估式(16)在所有像素位置的检测分数d(m,n)来确定最大检测得分

这也是我们DKE的测量值z_t。因此，在我们的体系结构的离散时间系统副本子系统中，我们可以通过式(25)得到状态估计观测的更新方程。最后，我们可以应用步长控制方法来纠正由于突然加速和转向导致跟踪算法失败而产生的显著偏差。通过在dragonbaby第65帧中的具有竞争力的实验结果表明，当STRCF在图1左侧边界框中失败时，我们的 KFSTRCF能够成功地将目标定位在右侧人脸处边界框中，特别是在运动项目中，KFSTRCF表现出卓越的性能。To discuss KFSTRCF more clearly, Figure 1 depicts our system architecture. In large-scale applications (eg, dragonbaby in the OTB-2015 dataset), we can establish discrete-time system measurements based on equations (8) and (10), and employ the state transition matrix M and the input coupling matrix Γ. Then, use equations (12) and (13) to get the classification scores of all pixels in the t-th frame (for example, the 65th frame of dragonbaby)

STRCF is incorporated into our framework, leveraging its more robust appearance model. Furthermore, we can obtain the interpolated detection scores at the image coordinates by Eqs. (14) and (15)

Moreover, we can determine the maximum detection score by evaluating the detection score d(m,n) at all pixel positions of Eq. (16)

This is also our DKE measurement z_t . Therefore, in the discrete-time system replica subsystem of our architecture, we can obtain the update equation for the state estimation observations by Eq. (25). Finally, we can apply a step-size control method to correct significant deviations due to the failure of the tracking algorithm due to sudden acceleration and steering. Competitive experimental results in the 65th frame of dragonbaby show that when STRCF fails in the left bounding box of Fig. 1, our KFSTRCF can successfully locate the object in the right bounding box of the face, especially In sports, KFSTRCF shows excellent performance.

接下来，我们详细介绍本发明提出的步长控制方法。首先，为了有效地控制跟踪结果的步长，我们需要清楚地分析框架的输入和输出状态。因此，我们应用奇异值分解(singular value decomposition,SVD)方法来深入了解状态矩阵的特性。我们将SVD函数定义为：Next, we introduce the step size control method proposed by the present invention in detail. First, in order to effectively control the stride of the tracking results, we need to clearly analyze the input and output states of the framework. Therefore, we apply the singular value decomposition (SVD) method to gain insight into the properties of the state matrix. We define the SVD function as:

[L^*,D^*,R^*]＝svd(x). (29)[L^* ,D^* ,R^* ]=svd(x).(29)

其中，x表示为目标的n×1维空间运动状态向量。如果x＝x_t，它表示我们框架的输入状态。如果

它表示我们框架的输出状态。svd(·)函数将x分解为x＝L^*D^*R^*。L^*表示n×n维矩阵，其列表示x的左特征向量。D^*表示n×1维矩阵，其主对角线为按降序排列的非负元素，它表示x的奇异值，其它位置的元素为0。R^*表示单一值，它表示x的右特征向量。Among them, x is represented as the n×1-dimensional spatial motion state vector of the target. If x=_xt , it represents the input state of our framework. if

It represents the output state of our framework. The svd(·) function decomposes x into x=L^* D^* R^* . L^* denotes an n×n-dimensional matrix whose columns represent the left eigenvectors of x. D^* represents an n×1-dimensional matrix whose main diagonal is the non-negative elements in descending order, which represents the singular value of x, and the elements in other positions are 0. R^* represents a single value, which represents the right eigenvector of x.

其次，通过求SVD矩阵中的最大值，我们可以得到最大奇异值，x的欧几里德范数定义为：Second, by finding the maximum value in the SVD matrix, we can get the largest singular value, the Euclidean norm of x is defined as:

n^*(x)＝max(L^*,D^*,R^*). (30)n^* (x)=max(L^* ,D^* ,R^* ).(30)

第三，我们可以根据我们的框架的输入状态x_t和输出状态

之间的最大奇异值的差异来更新t≥0时刻确定性输入向量为：Third, we can take the input state_xt and output state of our framework according to

The difference between the largest singular values to update the deterministic input vector at time t ≥ 0 is:

因此，我们可以根据框架的输入输出状态之间的关系，自动地稍微增加或减少确定性输入向量

此外，我们可以得到

这表明当t＜0时我们关闭输入控制。该策略可以逐渐平滑由于突然加速和转向引起的跟踪结果的剧烈波动。Therefore, we can automatically slightly increase or decrease the deterministic input vector based on the relationship between the input and output states of the framework

Furthermore, we can get

This indicates that we turn off input control when t<0. This strategy can gradually smooth out sharp fluctuations in tracking results caused by sudden acceleration and steering.

最后，为了修正由于跟踪算法失败引起的显著偏差，我们提出最大步长约束来将框架的输出状态限制在合理的范围。这表明如果跟踪算法不能在边界框中对目标进行定位，则所提出的约束条件应能提供符合真实场景中目标运动规律的合理结果。因此，我们定义最大步长为：Finally, to correct the significant bias caused by the failure of the tracking algorithm, we propose a maximum step size constraint to limit the output state of the framework to a reasonable range. This suggests that if the tracking algorithm cannot locate the target within the bounding box, the proposed constraints should provide reasonable results that conform to the laws of target motion in real scenes. Therefore, we define the maximum step size as:

len_max＝v×dt. (32)len_max = v × dt. (32)

我们可以通过应用以下约束将跟踪目标限制在合理的范围内：We can limit the tracking target to a reasonable range by applying the following constraints:

因此，

和x_t(1,1)分别表示

和x_t的第1行、第1列元素。因此，无论跟踪目标如何改变速度和方向，目标的最大步长都应该在约束len_max之内。即使在跟踪算法失效的情况下，也能为跟踪目标建立一个合理的出现区域。therefore,

and x_t (1,1) respectively represent

and the 1st row, 1st column element of x_t . Therefore, no matter how the tracking target changes speed and direction, the maximum step size of the target should be within the constraint len_max . Even in the event of failure of the tracking algorithm, a reasonable appearance area for the tracking target can be established.

最后，将对我们提出的目标跟踪架构进行全面评估，实验在OTB-2013、 OTB-2015和Temple-Color三个基准数据集上进行。Finally, our proposed object tracking architecture will be comprehensively evaluated, and the experiments are conducted on three benchmark datasets, OTB-2013, OTB-2015 and Temple-Color.

实验参数如下：The experimental parameters are as follows:

使用MATLAB R2018b进行了实验，计算机操作系统为Windows 8.1 64 位。CPU为i7-4500U，2核4线程。处理器的基频为1.8GHz，最大turbo频率为3GHz。RAM为8GB 1600GHz。GPU是AMD Radeon HD 8870M，具有775MHz的核心时钟和2048MB的图形内存。Experiments were carried out using MATLAB R2018b, and the computer operating system was Windows 8.1 64-bit. The CPU is i7-4500U, 2 cores and 4 threads. The processor has a base frequency of 1.8GHz and a maximum turbo frequency of 3GHz. RAM is 8GB 1600GHz. The GPU is an AMD Radeon HD 8870M with a core clock of 775MHz and 2048MB of graphics memory.

实验参数列在表I中。为了实现集成STRCF的高性能，我们将惩罚因子σ和初始步长参数ρ设置为16和10。然后我们提取灰度、方向梯度直方图 (histogram of orientedgradient,HOG)和颜色名称(color names,CN)特征来描述跟踪目标。此外，为了提高计算效率，我们将迭代的最大次数N_M设置为 2。由于我们需要提出的架构适应大规模的应用变化，因此融合的DKE参数应该在所有情况下都是一致和适当的。因此，我们将时间间隔dt、速度v和环境噪声e分别设置为恒定值0.5、50和1.0×10^-3。最后，我们将不变矩阵维数n、 r、初始确定性输入向量u₀和初始误差协方差矩阵P₀₍₊₎分别设为2、2、[1 1]^T和

The experimental parameters are listed in Table I. To achieve the high performance of the integrated STRCF, we set the penalty factor σ and the initial step size parameter ρ to 16 and 10. Then we extract grayscale, histogram of oriented gradient (HOG) and color names (CN) features to describe the tracking target. Furthermore, to improve computational efficiency, we set the maximum number of iterations_NM to 2. Since we need the proposed architecture to adapt to large-scale application changes, the fused DKE parameters should be consistent and appropriate in all cases. Therefore, we set the time interval dt, velocity v and ambient noise e to constant values of 0.5, 50 and 1.0×10⁻³ , respectively. Finally, we set the invariant matrix dimensions n, r, the initial deterministic input vector u₀ and the initial error covariance matrix P₀₍₊₎ to 2, 2, [1 1]^T and

通过实验对比验证，本发明公开的KFSTRCF架构与STRCF相比，在 OTB-2015数据集的重叠区域评价标准中，本方法对背景杂波、光照变化、遮挡、平面外旋转和视场外等因素的AUC得分分别提高了2.8％、2％、1.8％、 1.3％和2.4％。本发明公开的方法在OTB-2013、OTB-2015和Temple-Color数据集的某些特定类别中均优于STRCF方法，实现了计算机视觉中的最优视觉跟踪。Through experimental comparison and verification, the KFSTRCF architecture disclosed in the present invention is compared with STRCF. In the evaluation standard of the overlapping area of the OTB-2015 data set, this method has no effect on factors such as background clutter, illumination change, occlusion, out-of-plane rotation and out-of-view. The AUC scores were improved by 2.8%, 2%, 1.8%, 1.3% and 2.4%, respectively. The method disclosed in the present invention is superior to the STRCF method in some specific categories of OTB-2013, OTB-2015 and Temple-Color datasets, and achieves optimal visual tracking in computer vision.

Claims (6)

Translated fromChinese

1.一种基于KFSTRCF的目标跟踪架构，其特征在于：包括离散时间卡尔曼估计器DKE以及STRCF，所述DKE包括离散时间系统测量以及离散时间系统副本子系统；所述STRCF的目标跟踪结果输出作为离散时间系统测量中观测模型的测量值输入，通过离散时间系统副本子系统对DKE的模型进行更新，获得状态估计观测更新方程。1. a target tracking architecture based on KFSTRCF, it is characterized in that: comprise discrete-time Kalman estimator DKE and STRCF, and described DKE comprises discrete-time system measurement and discrete-time system replica subsystem; The target tracking result output of described STRCF As the measurement value input of the observation model in the discrete-time system measurement, the DKE model is updated through the discrete-time system replica subsystem, and the state estimation observation update equation is obtained.2.根据权利要求1所述的一种基于KFSTRCF的目标跟踪架构，其特征在于：所述离散时间系统副本子系统更新后的输出环节，通过步长控制环节来限制整个目标跟踪架构输出状态最大振幅，所述步长控制具体如下：2. a kind of target tracking architecture based on KFSTRCF according to claim 1, it is characterized in that: the output link after the update of described discrete time system replica subsystem limits the output state of the entire target tracking architecture to the maximum by step size control link Amplitude, the step size control is as follows:定义最大步长为：len_max＝v×dt.，v表示跟踪目标的速度，t为采样时刻；The maximum step size is defined as: len_max =v×dt., v represents the speed of the tracking target, and t is the sampling time;建立以下条件约束：Establish the following conditional constraints:

上式中，

表示

的第1行和第1列元素，x_t(1,1)表示x_t的第1行和第1列元素；x_t表示DKE目标运动输入状态向量，

表示输出状态向量后验值。In the above formula,

express

The 1st row and 1st column elements of x_t (1,1) represent the 1st row and 1st column elements of x_t ; x_t represents the DKE target motion input state vector,

Represents the posterior value of the output state vector.3.根据权利要求1或2所述的一种基于KFSTRCF的目标跟踪架构，其特征在于：所述离散时间系统测量中的系统动态模型如下：3. a kind of target tracking architecture based on KFSTRCF according to claim 1 and 2, is characterized in that: the system dynamic model in described discrete-time system measurement is as follows:x_t＝Μx_t-1+Γu_t-1.x_t = Μx_t-1 +Γu_t-1 .其中，x_t表示DKE目标的n×1维运动输入状态向量，u_t-1表示控制状态的r×1维确定性输入向量，t为采样时刻；Μ表示n×n维状态转移矩阵，它是一个时不变矩阵；Γ表示n×r维离散时间输入耦合矩阵，它是一个时不变矩阵；Among them, x_t represents the n×1-dimensional motion input state vector of the DKE target, u_t-1 represents the r×1-dimensional deterministic input vector of the control state, t is the sampling time; M represents the n×n-dimensional state transition matrix, which is a time-invariant matrix; Γ represents an n×r-dimensional discrete-time input coupling matrix, which is a time-invariant matrix;用目标的速度v将状态转移矩阵定义为：The state transition matrix is defined by the velocity v of the target as:

使用单位矩阵I来描述离散时间输入耦合矩阵Γ；Use the identity matrix I to describe the discrete-time input coupling matrix Γ;确定性输入向量可由下式确定，e表示环境噪声：The deterministic input vector can be determined by the following equation, where e represents the ambient noise:

利用测量值更新目标的跟踪结果，将测量值Z_t和跟踪结果x_t之间的线性相关方程定义为：Using the measurement value to update the tracking result of the target, the linear correlation equation between the measurement value Z_t and the tracking result x_t is defined as:z_t＝Νx_t+υ.z_t = Nx_t +υ.其中，Ν表示测量灵敏度矩阵，它是时不变矩阵，采用系统中的n×n维单位矩阵I；υ表示测量噪声，它是一个常数参数[1 0]^T。Among them, N represents the measurement sensitivity matrix, which is a time-invariant matrix and adopts the n×n-dimensional unit matrix I in the system; υ represents the measurement noise, which is a constant parameter [1 0]^T .4.根据权利要求3所述的一种基于KFSTRCF的目标跟踪架构，其特征在于：所述STRCF与DKE的融合方式具体如下：4. a kind of target tracking architecture based on KFSTRCF according to claim 3, is characterized in that: the fusion mode of described STRCF and DKE is specifically as follows:针对STRCF，将离散采样时刻t的每个样本表示为

由S个特征映射组成，其大小为M×N；并且y_t是预定义的高斯形状标签，通过最小化以下目标函数来实现STRCF模型：For STRCF, each sample at discrete sampling time t is denoted as

consists of S feature maps of size M × N; and y_t is a predefined Gaussian shape label, the STRCF model is implemented by minimizing the following objective function:

其中Hadamard积表示为·，卷积算子表示为*，w_t和f_t分别表示空间正则化矩阵和相关滤波器；将第(t-1)帧的STRCF结果表示为f_t-1，惩罚参数表示为σ，

和||f_t-f_t-1||²代表空间正则化和时间正则化；where the Hadamard product is denoted as ·, the convolution operator is denoted as *, wt and ft represent the spatial regularization matrix and the correlation filter, respectively; the_STRCF result of the (_t -1)th frame is denoted as ft_-1 , and the penalty The parameter is denoted as σ,

and ||f_t -f_t-1 ||² represent space regularization and temporal regularization;由于上述模型是凸函数，STRCF可以通过ADMM算法最小化公式(1)得到全局最优解，因此，将辅助变量表示为g_t，并要求f_t＝g_t和将步长参数表示为ρ，然后将公式(1)的增广拉格朗日形式表示为：Since the above model is a convex function, STRCF can obtain the global optimal solution by minimizing formula (1) through ADMM algorithm. Therefore, the auxiliary variable is denoted as g_t , and f_t = g_t is required and the step size parameter is denoted as ρ, Then the augmented Lagrangian form of formula (1) is expressed as:

其中

s_t是拉格朗日乘数，σ是惩罚因子；in

s_t is the Lagrange multiplier and σ is the penalty factor;基于式(1)，相关滤波器

表示在采样时刻t第s特征层的M×N卷积滤波器，滤波器f_t对样本x_t的卷积响应为：Based on equation (1), the correlation filter

Denotes the M×N convolution filter of the s-th feature layer at sampling time_{t, and the convolution response of filter ft to sample x tis} :

通过求解数目为M×N的S×S线性方程组，可以得到离散傅里叶变换滤波器为：By solving a system of S×S linear equations with a number of M×N, the discrete Fourier transform filter can be obtained as:

由于STRCF以滑动窗口的方式计算帧的所有循环移位上的分类分数，因此使用DFT的卷积特性来获得第t帧中所有像素的分类分数

为：Since STRCF computes the classification scores over all cyclic shifts of the frame in a sliding window fashion, the convolutional properties of DFT are used to obtain the classification scores of all pixels in the t-th frame

for:

其中，运算符·表示逐点乘法，bar运算符表示DFT运算，而运算符Δ^-1表示DFT的逆运算。Among them, the operator · represents pointwise multiplication, the bar operator represents the DFT operation, and the operator Δ^-1 represents the inverse operation of the DFT.5.根据权利要求4所述的一种基于KFSTRCF的目标跟踪架构，其特征在于：在检测阶段，通过使用在第(t-1)帧中更新后的滤波器

来定位在t时刻新实例中的目标，由于在式(2)中使用了步长ρ大于一个像素的网格策略，因此通过计算DFT系数，从而应用三角多项式来有效地插值分类分数，即：首先，将分类分数

的DFT定义为：5. A KFSTRCF-based target tracking architecture according to claim 4, characterized in that: in the detection stage, by using the updated filter in the (t-1)th frame

To locate the target in the new instance at time t, since a grid strategy with a step size ρ larger than one pixel is used in Eq. (2), the triangular polynomial is applied to effectively interpolate the classification score by calculating the DFT coefficients, namely: First, the classification score

The DFT is defined as:

其次，定义了样本x_t针对第u个虚单元中图像坐标

处的插值检测分数

为：Second, the sample_xt is defined for the image coordinates in the uth imaginary unit

Interpolated detection score at

for:

通过评估在所有像素位置的检测得分d(m,n)来定义最大检测得分

The maximum detection score is defined by evaluating the detection score d(m,n) at all pixel locations

其中，图像坐标

穿过样本x_t中的所有像素位置，

然后，利用Newton方法从像素(0,0)开始寻找最大得分，通过计算式(15)中梯度和Hessian的差分，通过有限次数的迭代得到收敛；Among them, the image coordinates

through all pixel positions in sample_xt ,

Then, use the Newton method to find the maximum score from the pixel (0,0), and obtain convergence through a finite number of iterations by calculating the difference between the gradient and the Hessian in equation (15).最后，在测量模型中应用STRCF的跟踪结果

实现STRCF算法与DKE的融合，有：Finally, the tracking results of STRCF are applied in the measurement model

To realize the fusion of STRCF algorithm and DKE, there are:

6.根据权利要求5所述的一种基于KFSTRCF的目标跟踪架构，其特征在于：所述DKE中的误差协方差获得方法如下：6. a kind of target tracking architecture based on KFSTRCF according to claim 5, is characterized in that: the error covariance obtaining method in described DKE is as follows:将跟踪结果的传播估计误差的期望值定义为：The expected value of the propagation estimation error of the tracking results is defined as:

并将状态估计的先验值定义为：And define the prior value of the state estimate as:

其中，

表示为x_t的预先估计，

表示为先验估计

的传播估计误差，

表示为x_t-1的后验估计；in,

is denoted as a pre-estimation of x_t ,

represented as a priori estimate

The propagation estimation error of ,

Denoted as the posterior estimate of x_t-1 ;因此，可以得到误差协方差矩阵为：Therefore, the error covariance matrix can be obtained as:

其中，w设为一个常数[1 0]^T，将Q定义为环境噪声矩阵，并表示为eI，e表示环境噪声，I表示n×n维单位矩阵，这表明误差协方差矩阵在t时刻的先验值是其t-1时刻的后验值函数；where w is set to a constant [1 0]^T , Q is defined as the environmental noise matrix, and denoted as eI, e is the environmental noise, and I is the n×n-dimensional identity matrix, which indicates that the error covariance matrix at time t The prior value is its posterior value function at time t-1;由于先验协方差矩阵是式(18)，它满足以下方程：Since the prior covariance matrix is Eq. (18), it satisfies the following equation:

因此，可以得到卡尔曼增益为：Therefore, the Kalman gain can be obtained as:

其中，R表示n×n维测量噪声矩阵，它是时不变矩阵eI；Among them, R represents the n×n-dimensional measurement noise matrix, which is the time-invariant matrix eI;此外，基于式(18)可得到后验协方差矩阵的相似方程为：In addition, based on equation (18), the similar equation of the posterior covariance matrix can be obtained as:

因此，又可以得到状态估计观测的更新方程为：Therefore, the update equation of the state estimation observation can be obtained as:

又可以写为：

It can also be written as:

最后，基于期望

和式(23)，可以得到误差协方差的更新方程为：Finally, based on expectations

With Equation (23), the update equation of the error covariance can be obtained as:

Images