Movatterモバイル変換

[0]ホーム
URL:

CN110942258A - A performance-driven approach to monitoring anomalies in industrial processes - Google Patents

A performance-driven approach to monitoring anomalies in industrial processesDownload PDF

Info

Publication number
CN110942258A
CN110942258ACN201911254450.2ACN201911254450ACN110942258ACN 110942258 ACN110942258 ACN 110942258ACN 201911254450 ACN201911254450 ACN 201911254450ACN 110942258 ACN110942258 ACN 110942258A
Authority
CN
China
Prior art keywords
equation
formula
matrix
detection
calculate
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Granted
Application number
CN201911254450.2A
Other languages
Chinese (zh)
Other versions
CN110942258B (en
Inventor
周东华
陈茂银
吴德浩
纪洪泉
高明
朱继峰
闫飞
郑水明
郭恩陶
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Shandong University of Science and Technology
Original Assignee
Shandong University of Science and Technology
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Shandong University of Science and TechnologyfiledCriticalShandong University of Science and Technology
Priority to CN201911254450.2ApriorityCriticalpatent/CN110942258B/en
Publication of CN110942258ApublicationCriticalpatent/CN110942258A/en
Application grantedgrantedCritical
Publication of CN110942258BpublicationCriticalpatent/CN110942258B/en
Activelegal-statusCriticalCurrent
Anticipated expirationlegal-statusCritical

Links

Images

Classifications

Landscapes

Abstract

The invention discloses a performance-driven industrial process abnormity monitoring method, and particularly relates to the technical field of industrial process monitoring. The method defines a detection performance index on the basis of fault detectability analysis, and selects components according to the index; the component selection problem is then described as a random optimization problem, and the optimal solution to the problem is given in a statistical sense. The method comprises two parts of off-line training and on-line monitoring. In the off-line training stage, historical data under normal working conditions are utilized to calculate the detection statistics of each sample, and the monitoring control limit is determined under the given significance level; in the on-line monitoring stage, the detection statistic is calculated according to the new sample, and if the detection statistic exceeds the control limit, the process is considered to be abnormal. Compared with a principal component analysis method based on the CPV criterion, the method selects principal components according to the detection performance, weakens sufficient conditions of detectability, and can generally obtain better monitoring performance.

Description

Translated fromChinese
一种性能驱动的工业过程异常监测方法A performance-driven approach to monitoring anomalies in industrial processes

技术领域technical field

本发明工业过程监控技术领域，具体涉及一种性能驱动的工业过程异常监测方法。The present invention is in the technical field of industrial process monitoring, in particular to a performance-driven abnormality monitoring method for an industrial process.

背景技术Background technique

主元分析(Principal component analysis，简称PCA)作为一种经典的数据降维技术，在图像处理、信号处理等诸多领域取得了广泛的应用。近年来，PCA及其各种改进方法成为了工业过程监控领域的有效技术手段。Principal component analysis (PCA), as a classic data dimensionality reduction technique, has been widely used in many fields such as image processing and signal processing. In recent years, PCA and its various improvement methods have become effective technical means in the field of industrial process monitoring.

利用PCA建立工业过程数据模型的关键问题之一是选择合适个数的主元，这关乎所建模型的监控性能。过多的主元可能会包含测量噪声，过少的主元可能会丢失关键信息而不能反映过程的某些变化。针对主元选择问题，研究人员相继提出了许多准则或方法，例如特征值限制、交叉验证、CPV准则、VRE准则等。但是这些方法都没有考虑监控性能，比如特征值限制和CPV准则都认为小特征值对应的主元是测量噪声，二者都是以保留最大的信息量为出发点来选择主元的；VRE准则考虑的是重构性能，希望选出的主元具有最小的重构误差。因此，根据上述方式选出的主元可能对异常不敏感。One of the key issues in using PCA to build an industrial process data model is to select an appropriate number of pivots, which is related to the monitoring performance of the model. Too many pivots may contain measurement noise, and too few pivots may lose key information and fail to reflect some changes in the process. For the pivot selection problem, researchers have successively proposed many criteria or methods, such as eigenvalue restriction, cross-validation, CPV criterion, VRE criterion, etc. However, these methods do not consider the monitoring performance. For example, the eigenvalue limit and the CPV criterion both consider that the pivot corresponding to the small eigenvalue is the measurement noise. is the reconstruction performance, and it is hoped that the selected pivot has the smallest reconstruction error. Therefore, pivots selected in the above manner may be insensitive to anomalies.

目前，仅有少数方法在选择主元时考虑了监控性能。但是这些方法都有几个共同的缺陷。第一，严重依赖于故障方向，因而仅限于检测传感器故障，对复杂的过程故障则需要利用异常数据估计故障方向，但实际中故障数据通常难以获得且故障方向难以估计准确；第二，对于没有先验信息的未知故障，有学者提出了同时监控多个模型的并行监控方案，但是这会造成巨大的计算复杂度，不利于对过程进行实时监控；第三，这些方法都是离线确定主元的个数，且在在线监控阶段保持不变，因此对未知故障的监控性能并不理想。Currently, only a few methods consider monitoring performance when selecting pivots. But these methods share several common flaws. First, it depends heavily on the fault direction, so it is limited to detecting sensor faults. For complex process faults, abnormal data needs to be used to estimate the fault direction, but in practice, the fault data is usually difficult to obtain and the fault direction is difficult to estimate accurately; Unknown faults of prior information, some scholars have proposed a parallel monitoring scheme to monitor multiple models at the same time, but this will cause huge computational complexity, which is not conducive to real-time monitoring of the process; third, these methods are offline to determine the pivot And it remains unchanged in the online monitoring stage, so the monitoring performance for unknown faults is not ideal.

发明内容SUMMARY OF THE INVENTION

本发明的目的是针对上述不足，提出了一种依据检测性能指标动态地选择主元，不需要异常数据，也无需估计故障的方向和幅值的性能驱动的工业过程异常监测方法。The purpose of the present invention is to address the above deficiencies, and propose a performance-driven industrial process anomaly monitoring method that dynamically selects the main element according to the detection performance index, does not require abnormal data, and does not need to estimate the direction and amplitude of the fault.

本发明具体采用如下技术方案：The present invention specifically adopts following technical scheme:

一种性能驱动的工业过程异常监测方法，包括离线训练阶段和在线监测阶段；A performance-driven method for monitoring anomalies in industrial processes, including an offline training phase and an online monitoring phase;

离线训练阶段包括以下步骤：The offline training phase includes the following steps:

1.1、采集正常工况下的历史数据，得到训练数据集

Figure BDA0002309844270000011
其中N为样本的数目，m为测量变量的数目；1.1. Collect historical data under normal working conditions to obtain a training data set
Figure BDA0002309844270000011
where N is the number of samples and m is the number of measurement variables;

1.2、用式(1)计算样本均值μx，并利用式(2)计算样本协方差矩阵Σx：1.2. Use formula (1) to calculate the sample mean μx , and use formula (2) to calculate the sample covariance matrix Σx :

Figure BDA0002309844270000021
Figure BDA0002309844270000021

Figure BDA0002309844270000022
Figure BDA0002309844270000022

其中，

Figure BDA0002309844270000023
in,
Figure BDA0002309844270000023

1.3、对样本协方差矩阵Σx进行特征值分解，得到式(3)：1.3. Decompose the eigenvalues of the sample covariance matrix Σx to obtain formula (3):

Σx＝QΛQT (3)Σx = QΛQT (3)

其中，Q为一个正交矩阵，Λ＝diag(λ[1],λ[2],…,λ[m])为一个对角矩阵，且有λ[1]≥λ[2]≥…≥λ[m]；Among them, Q is an orthogonal matrix, Λ=diag(λ[1] ,λ[2] ,…,λ[m] ) is a diagonal matrix, and λ[1] ≥λ[2] ≥…≥ λ[m] ;

1.4、对训练数据集X中的第k个样本，1≤k≤N，

Figure BDA0002309844270000024
根据式(4)计算其成分向量yk：1.4. For the kth sample in the training data set X, 1≤k≤N,
Figure BDA0002309844270000024
Calculate its component vector yk according to formula (4):

yk＝QT(xk-μx) (4)；yk =QT (xk -μx ) (4);

1.5、根据检测性能指标P的定义，计算成分向量yk对应的检测性能指标

Figure BDA0002309844270000025
1.5. According to the definition of the detection performance index P, calculate the detection performance index corresponding to the component vectoryk
Figure BDA0002309844270000025

1.6、基于选择矩阵W∈{0,1}m×d，得到选择之后的成分向量

Figure BDA0002309844270000026
并计算相应的检测性能指标
Figure BDA0002309844270000027
1.6. Based on the selection matrix W∈{0,1}m ×d , the component vector after selection is obtained
Figure BDA0002309844270000026
And calculate the corresponding detection performance indicators
Figure BDA0002309844270000027

1.7、将维度d从1到m依次遍历，得到使检测性能指标

Figure BDA0002309844270000028
最大的最优选择矩阵
Figure BDA0002309844270000029
1.7. Traverse the dimension d from 1 to m in order to obtain the detection performance index
Figure BDA0002309844270000028
The largest optimal choice matrix
Figure BDA0002309844270000029

1.8、根据选出的最优成分子集，计算第k个样本的检测统计量Dk，如式(5)所示：1.8. Calculate the detection statistic Dk of the kth sample according to the selected optimal component subset, as shown in formula (5):

Figure BDA00023098442700000210
Figure BDA00023098442700000210

其中，

Figure BDA00023098442700000211
表示自由度为
Figure BDA00023098442700000212
的卡方分布的α分位点；in,
Figure BDA00023098442700000211
represents the degrees of freedom as
Figure BDA00023098442700000212
The alpha quantile of the chi-square distribution;

1.9、给定显著性水平α，利用经验方法确定检测控制限ηα；1.9. Given the significance level α, use the empirical method to determine the detection control limitηα ;

在线监测阶段包括以下步骤：The online monitoring phase includes the following steps:

2.1、对于实时样本x，根据式(6)计算其成分向量y：2.1. For real-time sample x, calculate its component vector y according to formula (6):

y＝QT(x-μx) (6)；y=QT (x-μx ) (6);

2.2、根据检测性能指标P的定义，计算成分向量y对应的检测性能指标Py；2.2, according to the definition of the detection performance index P, calculate the detection performance index P y corresponding to the component vectory ;

2.3、基于选择矩阵W∈{0,1}m×d，得到选择之后的成分向量

Figure BDA0002309844270000031
并计算相应的检测性能指标
Figure BDA0002309844270000032
2.3. Based on the selection matrix W∈{0,1}m ×d , the component vector after selection is obtained
Figure BDA0002309844270000031
And calculate the corresponding detection performance indicators
Figure BDA0002309844270000032

2.4、将维度d从1到m依次遍历，得到使检测性能指标

Figure BDA0002309844270000033
最大的最优选择矩阵
Figure BDA0002309844270000034
2.4. Traverse the dimension d from 1 to m in turn to obtain the detection performance index
Figure BDA0002309844270000033
The largest optimal choice matrix
Figure BDA0002309844270000034

2.5、根据选出的最优成分子集，计算实时样本x的检测统计量D，如式(7)所示：2.5. Calculate the detection statistic D of the real-time sample x according to the selected optimal component subset, as shown in formula (7):

Figure BDA0002309844270000035
Figure BDA0002309844270000035

其中，

Figure BDA0002309844270000036
表示自由度为d*的卡方分布的α分位点；in,
Figure BDA0002309844270000036
represents the alpha quantile of a chi-square distribution with degrees of freedom d*;

2.6、将检测统计量D与控制限ηα比较，如果D大于ηα，则认为过程发生了异常，反之则处于正常状态。2.6. Compare the detection statistic D with the control limit ηα , if D is greater than ηα , it is considered that the process is abnormal, otherwise, it is in a normal state.

优选的，步骤1.5和2.2具体为：Preferably, steps 1.5 and 2.2 are specifically:

成分向量的均值μy和协方差矩阵Σy分别如式(8)和式(9)所示：The mean μy of the component vector and the covariance matrix Σy are shown in equations (8) and (9), respectively:

Figure BDA0002309844270000037
Figure BDA0002309844270000037

Figure BDA0002309844270000038
Figure BDA0002309844270000038

基于式(10)所示的加性故障模型：Based on the additive fault model shown in equation (10):

x＝x*+Ξif (10)x = x* +Ξi f (10)

其中，x是故障样本，x*是对应的正常样本，Ξi是故障

Figure BDA0002309844270000039
的方向矩阵，||f||表示故障的幅值；where x is the fault sample, x* is the corresponding normal sample, Ξi is the fault
Figure BDA0002309844270000039
The direction matrix of , ||f|| represents the magnitude of the fault;

成分向量y对应的马氏距离如式(11)所示：The Mahalanobis distance corresponding to the component vector y is shown in formula (11):

Figure BDA00023098442700000310
Figure BDA00023098442700000310

其中，y*＝QT(x*-μx)；Wherein, y* =QT (x* -μx );

根据向量的三角不等式，得到式(12)：According to the triangular inequality of vectors, Equation (12) is obtained:

Figure BDA00023098442700000311
Figure BDA00023098442700000311

考虑到

Figure BDA00023098442700000312
为确保故障
Figure BDA00023098442700000313
充分地被检测到，应有
Figure BDA00023098442700000314
于是，故障可检测的充分条件如式(13)所示：considering
Figure BDA00023098442700000312
To ensure failure
Figure BDA00023098442700000313
adequately detected, there should be
Figure BDA00023098442700000314
Therefore, the sufficient condition for fault detection is shown in equation (13):

||Λ-1/2QTΞif||＞2χα(m) (13)；||Λ-1/2 QT Ξif ||>2χα (m) (13);

成分向量y对应的检测性能指标定义为式(14)：The detection performance index corresponding to the component vector y is defined as formula (14):

Figure BDA0002309844270000041
Figure BDA0002309844270000041

优选的，步骤1.6和2.3具体为：Preferably, steps 1.6 and 2.3 are specifically:

定义选择矩阵W如式(15)所示：The definition selection matrix W is shown in formula (15):

Figure BDA0002309844270000042
Figure BDA0002309844270000042

其中，d≤m，而且

Figure BDA0002309844270000043
是一个除了第
Figure BDA00023098442700000413
个元素为1，其余元素都为0的列向量；where d≤m, and
Figure BDA0002309844270000043
is an addition to the
Figure BDA00023098442700000413
A column vector whose elements are 1 and the rest are 0;

对于成分向量y，选择之后的成分子集ys由式(16)给出：For the component vector y, the selected component subset ys is given by equation (16):

Figure BDA0002309844270000044
Figure BDA0002309844270000044

其均值为

Figure BDA0002309844270000045
协方差如式(17)所示：Its mean is
Figure BDA0002309844270000045
The covariance is shown in equation (17):

Figure BDA0002309844270000046
Figure BDA0002309844270000046

成分子集ys对应的马氏距离如式(18)所示：The Mahalanobis distance corresponding to the component subset ys is shown in formula (18):

Figure BDA0002309844270000047
Figure BDA0002309844270000047

类似地，得到故障可检测的充分条件，即式(19)：Similarly, a sufficient condition for fault detectability is obtained, that is, equation (19):

||(WTΛW)-1/2WTQTΞif||＞2χα(d) (19)；||(WT ΛW)-1/2 WT QT Ξi f||>2χα (d) (19);

于是，成分子集ys对应的性能指标

Figure BDA0002309844270000048
如式(20)所示：Therefore, the performance index corresponding to the component subset ys
Figure BDA0002309844270000048
As shown in formula (20):

Figure BDA0002309844270000049
Figure BDA0002309844270000049

优选的，步骤1.7和2.4具体为：Preferably, steps 1.7 and 2.4 are specifically:

将式(15)中定义的选择矩阵记为

Figure BDA00023098442700000410
那么使检测性能指标
Figure BDA00023098442700000411
最大的最优选择矩阵W*由式(21)给出：Denote the selection matrix defined in Eq. (15) as
Figure BDA00023098442700000410
Then make the detection performance indicator
Figure BDA00023098442700000411
The largest optimal selection matrix W* is given by equation (21):

Figure BDA00023098442700000412
Figure BDA00023098442700000412

给定d(1≤d≤m)的情况下，式(21)转化为式(22)：Given d (1≤d≤m), equation (21) is transformed into equation (22):

Figure BDA0002309844270000051
Figure BDA0002309844270000051

由于Ξif的值是未知的，式(22)其实是一个随机优化问题；Since the value ofΞif is unknown, equation (22) is actually a stochastic optimization problem;

根据式(10)所示的故障模型，可得Ξif＝x-x*，因此Ξif可被视为一个服从高斯分布的随机变量，即有

Figure BDA0002309844270000052
则其表示为式(23)所示的形式：According to the fault model shown in equation (10), Ξi f=xx* can be obtained, so Ξi f can be regarded as a random variable obeying a Gaussian distribution, that is, we have
Figure BDA0002309844270000052
Then it can be expressed in the form shown in formula (23):

Ξif＝x-μx+e (23)Ξi f=x-μx +e (23)

其中，

Figure BDA0002309844270000053
表示测量噪声；in,
Figure BDA0002309844270000053
represents measurement noise;

将式(23)代入F(W)中，得到式(24)：Substituting equation (23) into F(W), we get equation (24):

F(W)＝(y+g)TW(WTΛW)-1WT(y+g) (24)F(W)=(y+g)T W(WT ΛW)-1 WT (y+g) (24)

其中，

Figure BDA0002309844270000054
是一个高斯随机变量；in,
Figure BDA0002309844270000054
is a Gaussian random variable;

考虑到(WTΛW)-1＝WTΛ-1W，在统计意义下得到式(25)：Considering (WT ΛW)-1 =WT Λ-1 W, equation (25) is obtained in statistical significance:

Figure BDA0002309844270000055
Figure BDA0002309844270000055

由于WWT是一个对角线元素全为0或1的对角矩阵，因此式(25)等号右边的两项分别化成式(26)和式(27)所示的形式：Since WWT is a diagonal matrix whose diagonal elements are all 0 or 1, the two terms on the right side of the equation (25) are transformed into the forms shown in equations (26) and (27), respectively:

Figure BDA0002309844270000056
Figure BDA0002309844270000056

Figure BDA0002309844270000057
Figure BDA0002309844270000057

其中，

Figure BDA0002309844270000058
因此可以进一步得到式(28)：in,
Figure BDA0002309844270000058
Therefore, formula (28) can be further obtained:

Figure BDA0002309844270000059
Figure BDA0002309844270000059

在给定d的情况下，为了最大化

Figure BDA00023098442700000510
应将σi中最大的d个值相加，假设σ[1]≥σ[2]≥…≥σ[m]，最优选择矩阵
Figure BDA00023098442700000511
由式(29)给出：Given d, in order to maximize
Figure BDA00023098442700000510
The largest d values in σi should be added, assuming σ[1] ≥σ[2] ≥…≥σ[m] , the optimal selection matrix
Figure BDA00023098442700000511
It is given by equation (29):

Figure BDA00023098442700000512
Figure BDA00023098442700000512

将维度d从1到m依次遍历，得到全局最优的选择矩阵W*如式(30)所示：Traverse the dimension d from 1 to m in turn to obtain the globally optimal selection matrix W* , as shown in formula (30):

Figure BDA0002309844270000061
Figure BDA0002309844270000061

本发明具有如下有益效果：The present invention has the following beneficial effects:

该方法依据检测性能指标动态地选择主元，所选的主元对异常敏感，可以获得较好的监控性能；该方法不需要异常数据，也无需估计故障的方向和幅值，对于没有先验信息的未知异常也可获得较好的监控性能；而且在线计算复杂度较低，有利于对工业过程进行实时监测。The method dynamically selects the pivot element according to the detection performance index. The selected pivot element is sensitive to anomalies and can obtain better monitoring performance; this method does not require abnormal data, nor does it need to estimate the direction and amplitude of the fault. The unknown anomaly of information can also obtain better monitoring performance; and the online computing complexity is low, which is conducive to real-time monitoring of industrial processes.

附图说明Description of drawings

图1是本发明离线训练和在线监测的流程图；Fig. 1 is the flow chart of off-line training and on-line monitoring of the present invention;

图2是基于马氏距离的监测结果示意图；Fig. 2 is a schematic diagram of monitoring results based on Mahalanobis distance;

图3是基于PCA的Q统计量的监测结果示意图；Fig. 3 is the monitoring result schematic diagram of the Q statistic based on PCA;

图4是基于PCA的T2统计量的监测结果示意图；Figure 4 is a schematic diagram of the monitoring results of PCA-based T2 statistics;

图5是基于本发明所提方法的监测结果示意图；Fig. 5 is the monitoring result schematic diagram based on the proposed method of the present invention;

图6是基于本发明所提方法选择的主元个数示意图6 is a schematic diagram of the number of pivots selected based on the method proposed in the present invention

具体实施方式Detailed ways

结合图1，一种性能驱动的工业过程异常监测方法，包括离线训练阶段和在线监测阶段；Combined with Figure 1, a performance-driven industrial process anomaly monitoring method includes an offline training phase and an online monitoring phase;

离线训练阶段包括以下步骤：The offline training phase includes the following steps:

1.1、采集正常工况下的历史数据，得到训练数据集

Figure BDA0002309844270000062
其中N为样本的数目，m为测量变量的数目；1.1. Collect historical data under normal working conditions to obtain a training data set
Figure BDA0002309844270000062
where N is the number of samples and m is the number of measurement variables;

1.2、用式(1)计算样本均值μx，并利用式(2)计算样本协方差矩阵Σx：1.2. Use formula (1) to calculate the sample mean μx , and use formula (2) to calculate the sample covariance matrix Σx :

Figure BDA0002309844270000063
Figure BDA0002309844270000063

Figure BDA0002309844270000064
Figure BDA0002309844270000064

其中，

Figure BDA0002309844270000065
in,
Figure BDA0002309844270000065

1.3、对样本协方差矩阵Σx进行特征值分解，得到式(3)：1.3. Decompose the eigenvalues of the sample covariance matrix Σx to obtain formula (3):

Σx＝QΛQT (3)Σx = QΛQT (3)

其中，Q为一个正交矩阵，Λ＝diag(λ[1],λ[2],…,λ[m])为一个对角矩阵，且有λ[1]≥λ[2]≥…≥λ[m]；Among them, Q is an orthogonal matrix, Λ=diag(λ[1] ,λ[2] ,…,λ[m] ) is a diagonal matrix, and λ[1] ≥λ[2] ≥…≥ λ[m] ;

1.4、对训练数据集X中的第k个样本，1≤k≤N，

Figure BDA0002309844270000066
根据式(4)计算其成分向量yk：1.4. For the kth sample in the training data set X, 1≤k≤N,
Figure BDA0002309844270000066
Calculate its component vector yk according to formula (4):

yk＝QT(xk-μx) (4)；yk =QT (xk -μx ) (4);

1.5、根据检测性能指标P的定义，计算成分向量yk对应的检测性能指标

Figure BDA0002309844270000071
1.5. According to the definition of the detection performance index P, calculate the detection performance index corresponding to the component vectoryk
Figure BDA0002309844270000071

1.6、基于选择矩阵W∈{0,1}m×d，得到选择之后的成分向量

Figure BDA0002309844270000072
并计算相应的检测性能指标
Figure BDA0002309844270000073
1.6. Based on the selection matrix W∈{0,1}m×d , the component vector after selection is obtained
Figure BDA0002309844270000072
And calculate the corresponding detection performance indicators
Figure BDA0002309844270000073

1.7、将维度d从1到m依次遍历，得到使检测性能指标

Figure BDA0002309844270000074
最大的最优选择矩阵
Figure BDA0002309844270000075
1.7. Traverse the dimension d from 1 to m in order to obtain the detection performance index
Figure BDA0002309844270000074
The largest optimal choice matrix
Figure BDA0002309844270000075

1.8、根据选出的最优成分子集，计算第k个样本的检测统计量Dk，如式(5)所示：1.8. Calculate the detection statistic Dk of the kth sample according to the selected optimal component subset, as shown in formula (5):

Figure BDA0002309844270000076
Figure BDA0002309844270000076

其中，

Figure BDA0002309844270000077
表示自由度为
Figure BDA0002309844270000078
的卡方分布的α分位点；in,
Figure BDA0002309844270000077
represents the degrees of freedom as
Figure BDA0002309844270000078
The alpha quantile of the chi-square distribution;

1.9、给定显著性水平α，利用经验方法确定检测控制限ηα。1.9. Given the significance level α, use empirical methods to determine the detection control limit ηα .

在线监测阶段包括以下步骤：The online monitoring phase includes the following steps:

2.1、对于实时样本x，根据式(6)计算其成分向量y：2.1. For real-time sample x, calculate its component vector y according to formula (6):

y＝QT(x-μx) (6)；y=QT (x-μx ) (6);

2.2、根据检测性能指标P的定义，计算成分向量y对应的检测性能指标Py；2.2, according to the definition of the detection performance index P, calculate the detection performance index P y corresponding to the component vectory ;

2.3、基于选择矩阵W∈{0,1}m×d，得到选择之后的成分向量

Figure BDA0002309844270000079
并计算相应的检测性能指标
Figure BDA00023098442700000710
2.3. Based on the selection matrix W∈{0,1}m×d , the component vector after selection is obtained
Figure BDA0002309844270000079
And calculate the corresponding detection performance indicators
Figure BDA00023098442700000710

2.4、将维度d从1到m依次遍历，得到使检测性能指标

Figure BDA00023098442700000711
最大的最优选择矩阵
Figure BDA00023098442700000712
2.4. Traverse the dimension d from 1 to m in turn to obtain the detection performance index
Figure BDA00023098442700000711
The largest optimal choice matrix
Figure BDA00023098442700000712

2.5、根据选出的最优成分子集，计算实时样本x的检测统计量D，如式(7)所示：2.5. Calculate the detection statistic D of the real-time sample x according to the selected optimal component subset, as shown in formula (7):

Figure BDA00023098442700000713
Figure BDA00023098442700000713

其中，

Figure BDA00023098442700000714
表示自由度为d*的卡方分布的α分位点；in,
Figure BDA00023098442700000714
represents the alpha quantile of a chi-square distribution with degrees of freedom d* ;

2.6、将检测统计量D与控制限ηα比较，如果D大于ηα，则认为过程发生了异常，反之则处于正常状态。2.6. Compare the detection statistic D with the control limit ηα , if D is greater than ηα , it is considered that the process is abnormal, otherwise, it is in a normal state.

步骤1.5和2.2具体包括以下过程：Steps 1.5 and 2.2 specifically include the following processes:

成分向量的均值μy和协方差矩阵Σy分别如式(8)和式(9)所示：The mean μy of the component vector and the covariance matrix Σy are shown in equations (8) and (9), respectively:

Figure BDA0002309844270000081
Figure BDA0002309844270000081

Figure BDA0002309844270000082
Figure BDA0002309844270000082

基于式(10)所示的加性故障模型：Based on the additive fault model shown in equation (10):

x＝x*+Ξif (10)x = x* +Ξi f (10)

其中，x是故障样本，x*是对应的正常样本，Ξi是故障

Figure BDA0002309844270000083
的方向矩阵，||f||表示故障的幅值；where x is the fault sample, x* is the corresponding normal sample, Ξi is the fault
Figure BDA0002309844270000083
The direction matrix of , ||f|| represents the magnitude of the fault;

成分向量y对应的马氏距离如式(11)所示：The Mahalanobis distance corresponding to the component vector y is shown in formula (11):

Figure BDA0002309844270000084
Figure BDA0002309844270000084

其中，y*＝QT(x*-μx)；Wherein, y* =QT (x* -μx );

根据向量的三角不等式，得到式(12)：According to the triangular inequality of vectors, Equation (12) is obtained:

Figure BDA0002309844270000085
Figure BDA0002309844270000085

考虑到

Figure BDA0002309844270000086
为确保故障
Figure BDA0002309844270000087
充分地被检测到，应有
Figure BDA0002309844270000088
于是，故障可检测的充分条件如式(13)所示：considering
Figure BDA0002309844270000086
To ensure failure
Figure BDA0002309844270000087
adequately detected, there should be
Figure BDA0002309844270000088
Therefore, the sufficient condition for fault detection is shown in equation (13):

||Λ-1/2QTΞif||＞2χα(m) (13)；||Λ-1/2 QT Ξi f||>2χα (m) (13);

成分向量y对应的检测性能指标定义为式(14)：The detection performance index corresponding to the component vector y is defined as formula (14):

Figure BDA0002309844270000089
Figure BDA0002309844270000089

步骤1.6和2.3具体包括以下过程：Steps 1.6 and 2.3 specifically include the following processes:

定义选择矩阵W如式(15)所示：The definition selection matrix W is shown in formula (15):

Figure BDA00023098442700000810
Figure BDA00023098442700000810

其中，d≤m，而且

Figure BDA00023098442700000811
是一个除了第
Figure BDA00023098442700000812
个元素为1，其余元素都为0的列向量；where d≤m, and
Figure BDA00023098442700000811
is an addition to the
Figure BDA00023098442700000812
A column vector whose elements are 1 and the rest are 0;

对于成分向量y，选择之后的成分子集ys由式(16)给出：For the component vector y, the selected component subset ys is given by equation (16):

Figure BDA0002309844270000091
Figure BDA0002309844270000091

其均值为

Figure BDA0002309844270000092
协方差如式(17)所示：Its mean is
Figure BDA0002309844270000092
The covariance is shown in equation (17):

Figure BDA0002309844270000093
Figure BDA0002309844270000093

成分子集ys对应的马氏距离如式(18)所示：The Mahalanobis distance corresponding to the component subset ys is shown in formula (18):

Figure BDA0002309844270000094
Figure BDA0002309844270000094

类似地，得到故障可检测的充分条件，即式(19)：Similarly, a sufficient condition for fault detectability is obtained, that is, equation (19):

||(WTΛW)-1/2WTQTΞif||＞2χα(d) (19)；||(WT ΛW)-1/2 WT QT Ξi f||>2χα (d) (19);

于是，成分子集ys对应的性能指标

Figure BDA0002309844270000095
如式(20)所示：Therefore, the performance index corresponding to the component subset ys
Figure BDA0002309844270000095
As shown in formula (20):

Figure BDA0002309844270000096
Figure BDA0002309844270000096

步骤1.7和2.4具体过程为：The specific process of steps 1.7 and 2.4 is:

将式(15)中定义的选择矩阵记为

Figure BDA0002309844270000097
那么使检测性能指标
Figure BDA0002309844270000098
最大的最优选择矩阵W*由式(21)给出：Denote the selection matrix defined in Eq. (15) as
Figure BDA0002309844270000097
Then make the detection performance indicator
Figure BDA0002309844270000098
The largest optimal selection matrix W* is given by equation (21):

Figure BDA0002309844270000099
Figure BDA0002309844270000099

给定d(1≤d≤m)的情况下，式(21)转化为式(22)：Given d (1≤d≤m), equation (21) is transformed into equation (22):

Figure BDA00023098442700000910
Figure BDA00023098442700000910

由于Ξif的值是未知的，式(22)其实是一个随机优化问题；Since the value ofΞif is unknown, equation (22) is actually a stochastic optimization problem;

根据式(10)所示的故障模型，可得Ξif＝x-x*，因此Ξif可被视为一个服从高斯分布的随机变量，即有

Figure BDA00023098442700000911
则其表示为式(23)所示的形式：According to the fault model shown in equation (10), Ξi f=xx* can be obtained, so Ξi f can be regarded as a random variable obeying a Gaussian distribution, that is, we have
Figure BDA00023098442700000911
Then it can be expressed in the form shown in formula (23):

Ξif＝x-μx+e (23)Ξi f=x-μx +e (23)

其中，

Figure BDA00023098442700000912
表示测量噪声；in,
Figure BDA00023098442700000912
represents measurement noise;

将式(23)代入F(W)中，得到式(24)：Substituting equation (23) into F(W), we get equation (24):

F(W)＝(y+g)TW(WTΛW)-1WT(y+g) (24)F(W)=(y+g)T W(WT ΛW)-1 WT (y+g) (24)

其中，

Figure BDA0002309844270000101
是一个高斯随机变量；in,
Figure BDA0002309844270000101
is a Gaussian random variable;

考虑到(WTΛW)-1＝WTΛ-1W，在统计意义下得到式(25)：Considering (WT ΛW)-1 =WT Λ-1 W, equation (25) is obtained in statistical significance:

Figure BDA0002309844270000102
Figure BDA0002309844270000102

由于WWT是一个对角线元素全为0或1的对角矩阵，因此式(25)等号右边的两项分别化成式(26)和式(27)所示的形式：Since WWT is a diagonal matrix whose diagonal elements are all 0 or 1, the two terms on the right side of the equation (25) are transformed into the forms shown in equations (26) and (27), respectively:

Figure BDA0002309844270000103
Figure BDA0002309844270000103

Figure BDA0002309844270000104
Figure BDA0002309844270000104

其中，

Figure BDA0002309844270000105
因此可以进一步得到式(28)：in,
Figure BDA0002309844270000105
Therefore, formula (28) can be further obtained:

Figure BDA0002309844270000106
Figure BDA0002309844270000106

在给定d的情况下，为了最大化

Figure BDA0002309844270000107
应将σi中最大的d个值相加，假设σ[1]≥σ[2]≥…≥σ[m]，最优选择矩阵
Figure BDA0002309844270000108
由式(29)给出：Given d, in order to maximize
Figure BDA0002309844270000107
The largest d values in σi should be added, assuming σ[1] ≥σ[2] ≥…≥σ[m] , the optimal selection matrix
Figure BDA0002309844270000108
It is given by equation (29):

Figure BDA0002309844270000109
Figure BDA0002309844270000109

将维度d从1到m依次遍历，得到全局最优的选择矩阵W*如式(30)所示：Traverse the dimension d from 1 to m in turn, and obtain the globally optimal selection matrix W* as shown in formula (30):

Figure BDA00023098442700001010
Figure BDA00023098442700001010

下面基于连续搅拌釜式加热器(Continuous stirred tank heater,简称CSTH)，验证该监测方法，该过程提供了一个在工业过程监控领域被广泛研究的标准模型库。The monitoring method is validated below based on a continuous stirred tank heater (CSTH), which provides a standard model library that has been extensively studied in the field of industrial process monitoring.

在该过程中，热水和冷水混合且被蒸汽加热，其中温度和液位是具有标称值的被控变量。该过程模型中有三个PI控制器，分别控制温度、液位和冷水流量。不失一般性，在本实验室中该过程运行在第一种工况。测量样本由液位、冷水流量和温度三个传感器的测量值以及三个控制器的输出值组成，即x＝[L,F,T,CL,CF,CT]T。In this process, hot and cold water are mixed and heated by steam, where temperature and liquid level are controlled variables with nominal values. There are three PI controllers in this process model, which control temperature, liquid level, and cold water flow. Without loss of generality, in this laboratory the process was run under the first condition. The measurement sample consists of the measured values of the three sensors of liquid level, cold water flow and temperature, and the output values of the three controllers, namely x=[L, F, T, CL , CF , CT ]T .

在离线训练阶段，采集正常工况下的2000个样本用于离线建模，显著性水平选为α＝0.01，利用经验方法确定控制限。在在线监测阶段，产生1500个样本，其中前500个样本是正常的，从第501个样本开始引入异常状况，并一直持续到最后。该异常是一个幅值为+0.02，施加在液位传感器上的恒偏差故障。In the offline training stage, 2000 samples under normal working conditions were collected for offline modeling, the significance level was selected as α=0.01, and the control limit was determined by empirical method. In the online monitoring stage, 1500 samples are generated, of which the first 500 samples are normal, and abnormal conditions are introduced from the 501st sample and continue to the end. The anomaly is a constant deviation fault with an amplitude of +0.02 applied to the level sensor.

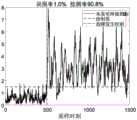
为了更清楚地展示本发明所提方法的优点，采用马氏距离和PCA方法作为对比。图2给出了基于马氏距离的监测结果示意图，图3和图4分别给出了基于PCA的Q统计量和T2统计量的监测结果示意图，图5给出了基于本发明所提方法的监测结果示意图。比较这四个图，可以得出：PCA在该方案中的监测结果较差，无论是Q统计量还是T2统计量，几乎都无法监测出异常，原因在于该故障的幅值较小，容易被噪声所掩盖；马氏距离可以部分监测出异常，但仍有20％以上的漏报率；本发明所提方法有着最优的监测结果，能以90％以上的检测率监测出异常。此外，图6给出了基于本发明所提方法选择的主元个数示意图。从图6可以看出，在异常发生之前所选主元个数有较大的变化，原因在于过程正常运行且存在测量噪声；但在异常发生之后，该方法能够迅速定位到对该异常最敏感的主元子集上，因而可以得到较好的监控性能。In order to demonstrate the advantages of the method proposed in the present invention more clearly, the Mahalanobis distance and the PCA method are used as a comparison. Figure 2 shows a schematic diagram of the monitoring results based on Mahalanobis distance, Figure 3 and Figure 4 respectively provide a schematic diagram of the monitoring results based on PCA's Q statistic and T2 statistic, and Figure 5 shows the method based on the present invention. Schematic diagram of the monitoring results. Comparing these four graphs, it can be concluded that the monitoring results of PCA in this scheme are poor. No matter it is the Q statistic or the T2 statistic, it is almost impossible to monitor the abnormality. The reason is that the amplitude of the fault is small and it is easy to Masked by noise; Mahalanobis distance can partially detect abnormality, but still has a false negative rate of more than 20%; the method proposed in the invention has the best monitoring result, and can detect abnormality with a detection rate of more than 90%. In addition, FIG. 6 shows a schematic diagram of the number of pivots selected based on the method proposed in the present invention. It can be seen from Figure 6 that the number of selected pivot elements changes greatly before the anomaly occurs, because the process is running normally and there is measurement noise; but after the anomaly occurs, the method can quickly locate the most sensitive to the anomaly. Therefore, better monitoring performance can be obtained.

当然，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的技术人员在本发明的实质范围内所做出的变化、改型、添加或替换，也应属于本发明的保护范围。Of course, the above description is not intended to limit the present invention, and the present invention is not limited to the above examples. Changes, modifications, additions or substitutions made by those skilled in the art within the essential scope of the present invention should also belong to the present invention. The scope of protection of the invention.

Claims (4)

Translated fromChinese
1.一种性能驱动的工业过程异常监测方法，其特征在于，包括离线训练阶段和在线监测阶段；1. A performance-driven method for monitoring anomalies in an industrial process, comprising an offline training phase and an online monitoring phase;离线训练阶段包括以下步骤：The offline training phase includes the following steps:1.1、采集正常工况下的历史数据，得到训练数据集
Figure FDA0002309844260000011
其中N为样本的数目，m为测量变量的数目；1.1. Collect historical data under normal working conditions to obtain a training data set
Figure FDA0002309844260000011
where N is the number of samples and m is the number of measurement variables;1.2、用式(1)计算样本均值μx，并利用式(2)计算样本协方差矩阵Σx：1.2. Use formula (1) to calculate the sample mean μx , and use formula (2) to calculate the sample covariance matrix Σx :
Figure FDA0002309844260000012
Figure FDA0002309844260000012
Figure FDA0002309844260000013
Figure FDA0002309844260000013
其中，
Figure FDA0002309844260000014
in,
Figure FDA0002309844260000014
1.3、对样本协方差矩阵Σx进行特征值分解，得到式(3)：1.3. Decompose the eigenvalues of the sample covariance matrix Σx to obtain formula (3):Σx＝QΛQT (3)Σx = QΛQT (3)其中，Q为一个正交矩阵，Λ＝diag(λ[1],λ[2],…,λ[m])为一个对角矩阵，且有λ[1]≥λ[2]≥…≥λ[m]；Among them, Q is an orthogonal matrix, Λ=diag(λ[1] ,λ[2] ,…,λ[m] ) is a diagonal matrix, and λ[1] ≥λ[2] ≥…≥ λ[m] ;1.4、对训练数据集X中的第k个样本，1≤k≤N，
Figure FDA0002309844260000015
根据式(4)计算其成分向量yk：1.4. For the kth sample in the training data set X, 1≤k≤N,
Figure FDA0002309844260000015
Calculate its component vector yk according to formula (4):yk＝QT(xk-μx) (4)；yk =QT (xk -μx ) (4);1.5、根据检测性能指标P的定义，计算成分向量yk对应的检测性能指标
Figure FDA0002309844260000016
1.5. According to the definition of the detection performance index P, calculate the detection performance index corresponding to the component vectoryk
Figure FDA0002309844260000016
1.6、基于选择矩阵W∈{0,1}m×d，得到选择之后的成分向量
Figure FDA0002309844260000017
并计算相应的检测性能指标
Figure FDA0002309844260000018
1.6. Based on the selection matrix W∈{0,1}m×d , the component vector after selection is obtained
Figure FDA0002309844260000017
And calculate the corresponding detection performance indicators
Figure FDA0002309844260000018
1.7、将维度d从1到m依次遍历，得到使检测性能指标
Figure FDA0002309844260000019
最大的最优选择矩阵
Figure FDA00023098442600000110
1.7. Traverse the dimension d from 1 to m in order to obtain the detection performance index
Figure FDA0002309844260000019
The largest optimal choice matrix
Figure FDA00023098442600000110
1.8、根据选出的最优成分子集，计算第k个样本的检测统计量Dk，如式(5)所示：1.8. Calculate the detection statistic Dk of the kth sample according to the selected optimal component subset, as shown in formula (5):
Figure FDA00023098442600000111
Figure FDA00023098442600000111
其中，
Figure FDA00023098442600000112
表示自由度为
Figure FDA00023098442600000113
的卡方分布的α分位点；in,
Figure FDA00023098442600000112
represents the degrees of freedom as
Figure FDA00023098442600000113
The alpha quantile of the chi-square distribution;1.9、给定显著性水平α，利用经验方法确定检测控制限ηα；1.9. Given the significance level α, use the empirical method to determine the detection control limitηα ;在线监测阶段包括以下步骤：The online monitoring phase includes the following steps:2.1、对于实时样本x，根据式(6)计算其成分向量y：2.1. For real-time sample x, calculate its component vector y according to formula (6):y＝QT(x-μx) (6)；y=QT (x-μx ) (6);2.2、根据检测性能指标P的定义，计算成分向量y对应的检测性能指标Py；2.2, according to the definition of the detection performance index P, calculate the detection performance index P y corresponding to the component vectory ;2.3、基于选择矩阵W∈{0,1}m×d，得到选择之后的成分向量
Figure FDA0002309844260000021
并计算相应的检测性能指标
Figure FDA0002309844260000022
2.3. Based on the selection matrix W∈{0,1}m×d , the component vector after selection is obtained
Figure FDA0002309844260000021
And calculate the corresponding detection performance indicators
Figure FDA0002309844260000022
2.4、将维度d从1到m依次遍历，得到使检测性能指标
Figure FDA0002309844260000023
最大的最优选择矩阵
Figure FDA0002309844260000024
2.4. Traverse the dimension d from 1 to m in turn to obtain the detection performance index
Figure FDA0002309844260000023
The largest optimal choice matrix
Figure FDA0002309844260000024
2.5、根据选出的最优成分子集，计算实时样本x的检测统计量D，如式(7)所示：2.5. Calculate the detection statistic D of the real-time sample x according to the selected optimal component subset, as shown in formula (7):
Figure FDA0002309844260000025
Figure FDA0002309844260000025
其中，
Figure FDA0002309844260000026
表示自由度为d*的卡方分布的α分位点；in,
Figure FDA0002309844260000026
represents the alpha quantile of a chi-square distribution with degrees of freedom d* ;2.6、将检测统计量D与控制限ηα比较，如果D大于ηα，则认为过程发生了异常，反之则处于正常状态。2.6. Compare the detection statistic D with the control limit ηα , if D is greater than ηα , it is considered that the process is abnormal, otherwise, it is in a normal state.2.如权利要求1所述的一种性能驱动的工业过程异常监测方法，其特征在于，1.5和2.2具体为：2. A performance-driven abnormality monitoring method for an industrial process as claimed in claim 1, wherein 1.5 and 2.2 are specifically:成分向量的均值μy和协方差矩阵Σy分别如式(8)和式(9)所示：The mean μy of the component vector and the covariance matrix Σy are shown in equations (8) and (9), respectively:
Figure FDA0002309844260000027
Figure FDA0002309844260000027
Figure FDA0002309844260000028
Figure FDA0002309844260000028
基于式(10)所示的加性故障模型：Based on the additive fault model shown in equation (10):x＝x*+Ξif (10)x = x* +Ξi f (10)其中，x是故障样本，x*是对应的正常样本，Ξi是故障
Figure FDA0002309844260000029
的方向矩阵，||f||表示故障的幅值；where x is the fault sample, x* is the corresponding normal sample, Ξi is the fault
Figure FDA0002309844260000029
The direction matrix of , ||f|| represents the magnitude of the fault;成分向量y对应的马氏距离如式(11)所示：The Mahalanobis distance corresponding to the component vector y is shown in formula (11):
Figure FDA0002309844260000031
Figure FDA0002309844260000031
其中，y*＝QT(x*-μx)；Wherein, y* =QT (x* -μx );根据向量的三角不等式，得到式(12)：According to the triangular inequality of vectors, Equation (12) is obtained:
Figure FDA0002309844260000032
Figure FDA0002309844260000032
考虑到
Figure FDA0002309844260000033
为确保故障
Figure FDA0002309844260000034
充分地被检测到，应有
Figure FDA0002309844260000035
于是，故障可检测的充分条件如式(13)所示：considering
Figure FDA0002309844260000033
To ensure failure
Figure FDA0002309844260000034
adequately detected, there should be
Figure FDA0002309844260000035
Therefore, the sufficient condition for fault detection is shown in equation (13):||Λ-1/2QTΞif||＞2χα(m) (13)；||Λ-1/2 QT Ξi f||>2χα (m) (13);成分向量y对应的检测性能指标定义为式(14)：The detection performance index corresponding to the component vector y is defined as formula (14):
Figure FDA0002309844260000036
Figure FDA0002309844260000036
3.如权利要求1所述的一种性能驱动的工业过程异常监测方法，其特征在于，1.6和2.3具体为：3. A performance-driven abnormality monitoring method for an industrial process as claimed in claim 1, wherein 1.6 and 2.3 are specifically:定义选择矩阵W如式(15)所示：The definition selection matrix W is shown in formula (15):
Figure FDA0002309844260000037
Figure FDA0002309844260000037
其中，d≤m，而且
Figure FDA0002309844260000038
是一个除了第
Figure FDA0002309844260000039
个元素为1，其余元素都为0的列向量；where d≤m, and
Figure FDA0002309844260000038
is an addition to the
Figure FDA0002309844260000039
A column vector whose elements are 1 and the rest are 0;对于成分向量y，选择之后的成分子集ys由式(16)给出：For the component vector y, the selected component subset ys is given by equation (16):
Figure FDA00023098442600000310
Figure FDA00023098442600000310
其均值为
Figure FDA00023098442600000311
协方差如式(17)所示：Its mean is
Figure FDA00023098442600000311
The covariance is shown in equation (17):
Figure FDA00023098442600000312
Figure FDA00023098442600000312
成分子集ys对应的马氏距离如式(18)所示：The Mahalanobis distance corresponding to the component subset ys is shown in formula (18):
Figure FDA00023098442600000313
Figure FDA00023098442600000313
类似地，得到故障可检测的充分条件，即式(19)：Similarly, a sufficient condition for fault detectability is obtained, that is, equation (19):||(WTΛW)-1/2WTQTΞif||＞2χα(d) (19)；||(WT ΛW)-1/2 WT QT Ξi f||>2χα (d) (19);于是，成分子集ys对应的性能指标
Figure FDA0002309844260000041
如式(20)所示：Therefore, the performance index corresponding to the component subset ys
Figure FDA0002309844260000041
As shown in formula (20):
Figure FDA0002309844260000042
Figure FDA0002309844260000042
4.如权利要求3所述的一种性能驱动的工业过程异常监测方法，其特征在于，1.7和2.4具体为：4. A performance-driven industrial process abnormality monitoring method as claimed in claim 3, characterized in that 1.7 and 2.4 are specifically:将式(15)中定义的选择矩阵记为
Figure FDA0002309844260000043
那么使检测性能指标
Figure FDA0002309844260000044
最大的最优选择矩阵W*由式(21)给出：Denote the selection matrix defined in Eq. (15) as
Figure FDA0002309844260000043
Then make the detection performance indicator
Figure FDA0002309844260000044
The largest optimal choice matrix W* is given by equation (21):
Figure FDA0002309844260000045
Figure FDA0002309844260000045
给定d(1≤d≤m)的情况下，式(21)转化为式(22)：Given d (1≤d≤m), equation (21) is transformed into equation (22):
Figure FDA0002309844260000046
Figure FDA0002309844260000046
由于Ξif的值是未知的，式(22)其实是一个随机优化问题；Since the value ofΞif is unknown, equation (22) is actually a stochastic optimization problem;根据式(10)所示的故障模型，可得Ξif＝x-x*，因此Ξif可被视为一个服从高斯分布的随机变量，即有
Figure FDA0002309844260000047
则其表示为式(23)所示的形式：According to the fault model shown in equation (10), Ξi f=xx* can be obtained, so Ξi f can be regarded as a random variable obeying a Gaussian distribution, that is, we have
Figure FDA0002309844260000047
Then it can be expressed in the form shown in formula (23):Ξif＝x-μx+e (23)Ξi f=x-μx +e (23)其中，
Figure FDA0002309844260000048
表示测量噪声；in,
Figure FDA0002309844260000048
represents measurement noise;将式(23)代入F(W)中，得到式(24)：Substituting equation (23) into F(W), we get equation (24):F(W)＝(y+g)TW(WTΛW)-1WT(y+g) (24)F(W)=(y+g)T W(WT ΛW)-1 WT (y+g) (24)其中，
Figure FDA0002309844260000049
是一个高斯随机变量；in,
Figure FDA0002309844260000049
is a Gaussian random variable;考虑到(WTΛW)-1＝WTΛ-1W，在统计意义下得到式(25)：Considering (WT ΛW)-1 =WT Λ-1 W, equation (25) is obtained in statistical significance:
Figure FDA00023098442600000410
Figure FDA00023098442600000410
由于WWT是一个对角线元素全为0或1的对角矩阵，因此式(25)等号右边的两项分别化成式(26)和式(27)所示的形式：Since WWT is a diagonal matrix whose diagonal elements are all 0 or 1, the two terms on the right side of the equation (25) are transformed into the forms shown in equations (26) and (27), respectively:
Figure FDA00023098442600000411
Figure FDA00023098442600000411
Figure FDA0002309844260000051
Figure FDA0002309844260000051
其中，
Figure FDA0002309844260000052
因此可以进一步得到式(28)：in,
Figure FDA0002309844260000052
Therefore, formula (28) can be further obtained:
Figure FDA0002309844260000053
Figure FDA0002309844260000053
在给定d的情况下，为了最大化
Figure FDA0002309844260000054
应将σi中最大的d个值相加，假设σ[1]≥σ[2]≥…≥σ[m]，最优选择矩阵
Figure FDA0002309844260000055
由式(29)给出：Given d, in order to maximize
Figure FDA0002309844260000054
The largest d values in σi should be added, assuming σ[1] ≥σ[2] ≥…≥σ[m] , the optimal selection matrix
Figure FDA0002309844260000055
It is given by equation (29):
Figure FDA0002309844260000056
Figure FDA0002309844260000056
将维度d从1到m依次遍历，得到全局最优的选择矩阵W*如式(30)所示：Traverse the dimension d from 1 to m in turn to obtain the globally optimal selection matrix W* , as shown in formula (30):
Figure FDA0002309844260000057
Figure FDA0002309844260000057
CN201911254450.2A2019-12-102019-12-10Performance-driven industrial process anomaly monitoring methodActiveCN110942258B (en)

Priority Applications (1)

Application NumberPriority DateFiling DateTitle
CN201911254450.2ACN110942258B (en)2019-12-102019-12-10Performance-driven industrial process anomaly monitoring method

Applications Claiming Priority (1)

Application NumberPriority DateFiling DateTitle
CN201911254450.2ACN110942258B (en)2019-12-102019-12-10Performance-driven industrial process anomaly monitoring method

Publications (2)

Publication NumberPublication Date
CN110942258Atrue CN110942258A (en)2020-03-31
CN110942258B CN110942258B (en)2022-02-25

Family

ID=69909928

Family Applications (1)

Application NumberTitlePriority DateFiling Date
CN201911254450.2AActiveCN110942258B (en)2019-12-102019-12-10Performance-driven industrial process anomaly monitoring method

Country Status (1)

CountryLink
CN (1)CN110942258B (en)

Cited By (3)

* Cited by examiner, † Cited by third party
Publication numberPriority datePublication dateAssigneeTitle
CN111931349A (en)*2020-07-152020-11-13中南大学 Multiplicative Fault Diagnosis Method of CSTH Based on Dynamic Principal Component Analysis
CN113254874A (en)*2021-04-142021-08-13山东科技大学Uncertainty non-stationary industrial process oriented anomaly monitoring method
CN116861224A (en)*2023-09-042023-10-10鲁东大学Intermittent process soft measurement modeling system based on intermittent process soft measurement modeling method

Citations (4)

* Cited by examiner, † Cited by third party
Publication numberPriority datePublication dateAssigneeTitle
CN105676833A (en)*2015-12-212016-06-15海南电力技术研究院Power generation process control system fault detection method
CN108958226A (en)*2018-08-082018-12-07太原理工大学Based on existence information potential-Principal Component Analysis Algorithm TE procedure failure testing method
CN109407652A (en)*2018-12-102019-03-01中国石油大学(华东)Multivariable industrial process fault detection method based on major-minor pca model
CN109459993A (en)*2018-12-062019-03-12湖南师范大学A kind of process flow industry process online adaptive Fault monitoring and diagnosis method

Patent Citations (4)

* Cited by examiner, † Cited by third party
Publication numberPriority datePublication dateAssigneeTitle
CN105676833A (en)*2015-12-212016-06-15海南电力技术研究院Power generation process control system fault detection method
CN108958226A (en)*2018-08-082018-12-07太原理工大学Based on existence information potential-Principal Component Analysis Algorithm TE procedure failure testing method
CN109459993A (en)*2018-12-062019-03-12湖南师范大学A kind of process flow industry process online adaptive Fault monitoring and diagnosis method
CN109407652A (en)*2018-12-102019-03-01中国石油大学(华东)Multivariable industrial process fault detection method based on major-minor pca model

Non-Patent Citations (7)

* Cited by examiner, † Cited by third party
Title
GANG LI 等: "Reconstruction based fault prognosis for continuous processes", 《CONTROL ENGINEERING PRACTICE》*
HONGQUAN JI 等: "On the use of recognition-based contribution for fault diagnosis", 《JOURNAL OF PROCESS CONTROL》*
JUN SHANG 等: "Fault detection based on augmented kernel Mahalanobis distance for nonlinear dynamic processes", 《COMPUTERS AND CHEMICAL ENGINEERING》*
JUN SHANG: "Recursive transformed component statistical analysis for incipient fault detection", 《AUTOMATICA》*
常玉清 等: "基于多 PCA 模型的过程监测方法", 《仪器仪表学报》*
荣智海 等: "基于核主成分分析的油色谱在线监测装置 异常状态快速辨识", 《高电压技术》*
郭金玉 等: "基于 DMOLPP 的间歇过程在线故障检测", 《仪器仪表学报》*

Cited By (5)

* Cited by examiner, † Cited by third party
Publication numberPriority datePublication dateAssigneeTitle
CN111931349A (en)*2020-07-152020-11-13中南大学 Multiplicative Fault Diagnosis Method of CSTH Based on Dynamic Principal Component Analysis
CN113254874A (en)*2021-04-142021-08-13山东科技大学Uncertainty non-stationary industrial process oriented anomaly monitoring method
CN113254874B (en)*2021-04-142022-04-15山东科技大学 An Anomaly Monitoring Method for Uncertain Non-stationary Industrial Processes
CN116861224A (en)*2023-09-042023-10-10鲁东大学Intermittent process soft measurement modeling system based on intermittent process soft measurement modeling method
CN116861224B (en)*2023-09-042023-12-01鲁东大学 Intermittent process soft sensor modeling system based on intermittent process soft sensor modeling method

Also Published As

Publication numberPublication date
CN110942258B (en)2022-02-25

Similar Documents

PublicationPublication DateTitle
Harrou et al.Statistical process monitoring using advanced data-driven and deep learning approaches: theory and practical applications
Joe QinStatistical process monitoring: basics and beyond
Mansouri et al.Kernel PCA-based GLRT for nonlinear fault detection of chemical processes
Yoon et al.Fault diagnosis with multivariate statistical models part I: using steady state fault signatures
Ma et al.Fault detection for dynamic processes based on recursive innovational component statistical analysis
Xiao et al.An isolation enhanced PCA method with expert-based multivariate decoupling for sensor FDD in air-conditioning systems
CN107092242B (en)A kind of Industrial Process Monitoring method based on missing variable pca model
CN110942258B (en)Performance-driven industrial process anomaly monitoring method
Wang et al.KPCA-CCA-based quality-related fault detection and diagnosis method for nonlinear process monitoring
Baklouti et al.Iterated robust kernel fuzzy principal component analysis and application to fault detection
Harrou et al.Amalgamation of anomaly-detection indices for enhanced process monitoring
CN102183699A (en)Method for model mismatching detection and positioning of multivariate predictive control system in chemical process
Wang et al.Efficient nonlinear fault diagnosis based on kernel sample equivalent replacement
CN108153267B (en)Industrial process monitoring method based on error principal component analysis model
Ma et al.A novel three-stage quality oriented data-driven nonlinear industrial process monitoring strategy
CN111368428A (en)Sensor precision reduction fault detection method based on monitoring second-order statistics
CN108181893B (en)PCA-KDR-based fault detection method
SzegaMethodology of advanced data validation and reconciliation application in industrial thermal processes
JiData-driven sensor fault diagnosis under closed-loop control with slow feature analysis
Wang et al.Orthogonal stationary component analysis for nonstationary process monitoring
CN114879612A (en)Blast furnace iron-making process monitoring method based on Local-DBKSSA
Wang et al.Concurrent fault detection and anomaly location in closed-loop dynamic systems with measured disturbances
CN103207567A (en)Low-false-alarm-rate improved principal component analysis process monitoring method and system
Li et al.Twofold weighted-based statistical feature KECA for nonlinear industrial process fault diagnosis
Ma et al.Dynamic process monitoring based on dot product feature analysis for thermal power plants

Legal Events

DateCodeTitleDescription
PB01Publication
PB01Publication
SE01Entry into force of request for substantive examination
SE01Entry into force of request for substantive examination
GR01Patent grant
GR01Patent grant
[8]ページ先頭
©2009-2025 Movatter.jp