CN110852416A - CNN accelerated computing method and system based on low-precision floating-point data expression form - Google Patents
CNN accelerated computing method and system based on low-precision floating-point data expression formDownload PDFInfo
- Publication number
- CN110852416A CN110852416ACN201910940659.8ACN201910940659ACN110852416ACN 110852416 ACN110852416 ACN 110852416ACN 201910940659 ACN201910940659 ACN 201910940659ACN 110852416 ACN110852416 ACN 110852416A
- Authority
- CN
- China
- Prior art keywords
- point number
- low
- precision floating
- floating point
- floating
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Granted
Links
Images
Classifications
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06N—COMPUTING ARRANGEMENTS BASED ON SPECIFIC COMPUTATIONAL MODELS
- G06N3/00—Computing arrangements based on biological models
- G06N3/02—Neural networks
- G06N3/04—Architecture, e.g. interconnection topology
- G06N3/045—Combinations of networks
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F7/00—Methods or arrangements for processing data by operating upon the order or content of the data handled
- G06F7/38—Methods or arrangements for performing computations using exclusively denominational number representation, e.g. using binary, ternary, decimal representation
- G06F7/48—Methods or arrangements for performing computations using exclusively denominational number representation, e.g. using binary, ternary, decimal representation using non-contact-making devices, e.g. tube, solid state device; using unspecified devices
- G06F7/483—Computations with numbers represented by a non-linear combination of denominational numbers, e.g. rational numbers, logarithmic number system or floating-point numbers
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F7/00—Methods or arrangements for processing data by operating upon the order or content of the data handled
- G06F7/38—Methods or arrangements for performing computations using exclusively denominational number representation, e.g. using binary, ternary, decimal representation
- G06F7/48—Methods or arrangements for performing computations using exclusively denominational number representation, e.g. using binary, ternary, decimal representation using non-contact-making devices, e.g. tube, solid state device; using unspecified devices
- G06F7/57—Arithmetic logic units [ALU], i.e. arrangements or devices for performing two or more of the operations covered by groups G06F7/483 – G06F7/556 or for performing logical operations
- G—PHYSICS
- G06—COMPUTING OR CALCULATING; COUNTING
- G06N—COMPUTING ARRANGEMENTS BASED ON SPECIFIC COMPUTATIONAL MODELS
- G06N3/00—Computing arrangements based on biological models
- G06N3/02—Neural networks
- G06N3/06—Physical realisation, i.e. hardware implementation of neural networks, neurons or parts of neurons
- G06N3/063—Physical realisation, i.e. hardware implementation of neural networks, neurons or parts of neurons using electronic means
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Theoretical Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Computing Systems (AREA)
- General Engineering & Computer Science (AREA)
- Life Sciences & Earth Sciences (AREA)
- Biophysics (AREA)
- Pure & Applied Mathematics (AREA)
- Mathematical Optimization (AREA)
- Mathematical Analysis (AREA)
- Health & Medical Sciences (AREA)
- Computational Mathematics (AREA)
- Biomedical Technology (AREA)
- Evolutionary Computation (AREA)
- Artificial Intelligence (AREA)
- Computational Linguistics (AREA)
- Data Mining & Analysis (AREA)
- General Health & Medical Sciences (AREA)
- Molecular Biology (AREA)
- Mathematical Physics (AREA)
- Software Systems (AREA)
- Neurology (AREA)
- Nonlinear Science (AREA)
- Complex Calculations (AREA)
Abstract
Description
Translated fromChinese技术领域technical field
本发明涉及深度卷积神经网络量化领域，尤其是基于低精度浮点数数据表现形式的CNN加速计算方法及系统。The invention relates to the field of deep convolutional neural network quantization, in particular to a CNN acceleration calculation method and system based on the representation of low-precision floating point number data.
背景技术Background technique
近年来，AI(Artificial Intelligence，人工智能)的应用已经渗透到很多方面，如人脸识别、游戏对战、图像处理、仿真模拟等等，虽然提高了处理准确性，但由于神经网络包含很多层和大量参数，需要非常大的计算代价和存储空间。对此，技术人员提出了神经网络压缩处理方案，即通过改变网络结构或利用量化、近似的方法来减少网络的参数或存储空间，在不大影响神经网络性能的情况下，降低网络代价和存储空间。In recent years, the application of AI (Artificial Intelligence) has penetrated into many aspects, such as face recognition, game battle, image processing, simulation, etc. Although the processing accuracy has been improved, the neural network contains many layers and A large number of parameters require very large computational cost and storage space. In this regard, technicians have proposed a neural network compression processing scheme, that is, by changing the network structure or using quantization and approximation methods to reduce network parameters or storage space, and reduce the network cost and storage space without affecting the performance of the neural network. space.
现有技术中的专利号：CN109740737A、专利名称：卷积神经网络量化处理方法、装置及计算机设备，方法包括步骤：获取卷积神经网络中各卷积层的最大权值及最大偏差量；计算所述最大权值的第一动态比特位精度值，及最大偏差量的第二动态比特位精度值，所述第一动态比特位精度值与所述第二动态比特位精度值不同；利用各卷积层对应的所述第一动态比特位精度值和所述第二动态比特位精度值，对相应卷积层的权值和偏差量进行量化；基于各卷积层中量化后的权值及量化后的偏差量，得到所述卷积神经网络的卷积结果。上述方案采用双精度量化处理方法提高量化后的准确率，具体的，获取卷积神经网络中卷积层的最大权值及最大偏差量，分别计算最大权值的动态比特位精度值及最大偏差量的动态比特位精度值，之后，利用这两个动态比特位精度值实现卷积计算，由于本申请从卷积层的权值和偏差值两方面进行量化，避免了单精度量化，容易导致权值或偏差值精度损失，影响量化准确性的情况发生。Patent number in the prior art: CN109740737A, patent name: convolutional neural network quantization processing method, device and computer equipment, the method includes the steps: obtaining the maximum weight and maximum deviation of each convolutional layer in the convolutional neural network; calculating The first dynamic bit precision value of the maximum weight, and the second dynamic bit precision value of the maximum deviation, the first dynamic bit precision value is different from the second dynamic bit precision value; using each The first dynamic bit precision value and the second dynamic bit precision value corresponding to the convolutional layer are used to quantize the weights and deviations of the corresponding convolutional layers; based on the quantized weights in each convolutional layer and the quantized deviation to obtain the convolution result of the convolutional neural network. The above scheme adopts the double-precision quantization processing method to improve the accuracy rate after quantization. Specifically, the maximum weight and maximum deviation of the convolutional layer in the convolutional neural network are obtained, and the dynamic bit precision value and the maximum deviation of the maximum weight are calculated respectively. After that, the two dynamic bit precision values are used to realize the convolution calculation. Since the application is quantized from the weight value and the deviation value of the convolution layer, single-precision quantization is avoided, which is easy to cause Loss of accuracy of weights or bias values, which affects the accuracy of quantization.
虽然目前技术对量化进行改进，提高量化准确性，但仍然存在几个方面的限制：1)对于量化深度卷积神经网络(卷积层/全连接层的数量超过100层)，需要重新训练来保证准确率；2)量化需要使用16比特浮点数或者8比特定点数来保证准确率；3)在不使用重新训练和保证准确率的前提下，目前技术在一个DSP中，最多只能实现两个乘法运算，从而导致FPGA上加速性能较低。Although the current technology improves quantization and improves quantization accuracy, there are still limitations in several aspects: 1) For quantized deep convolutional neural networks (the number of convolutional layers/fully connected layers exceeds 100 layers), retraining is required to Guaranteed accuracy; 2) Quantization needs to use 16-bit floating point numbers or 8-bit specific points to ensure accuracy; 3) Without using retraining and ensuring accuracy, the current technology in one DSP can only achieve at most two a multiplication operation, resulting in lower acceleration performance on the FPGA.
因此，需要一种基于低精度浮点数数据表现形式的CNN加速计算方法及系统，克服以上问题，实现在不需要重新训练的情况下，找到最优的数据表示形式MaEb，通过DSP实现Nm个MaEb浮点数乘法器，保证量化后卷积神经网络的准确率和提升定制电路或者非定制电路的加速性能。Therefore, a CNN acceleration calculation method and system based on the representation of low-precision floating-point data is needed to overcome the above problems, and to find the optimal data representation MaEb without retraining, and realize Nm data through DSP. The MaEb floating-point multiplier ensures the accuracy of the quantized convolutional neural network and improves the acceleration performance of custom circuits or non-custom circuits.
发明内容SUMMARY OF THE INVENTION
本发明的目的在于：本发明提供了一种基于低精度浮点数数据表现形式的CNN加速计算方法及系统，使用低精度浮点数的表示形式MaEb，在不需要重新训练的情况下，保证量化后卷积神经网络的准确率，并通过MaEb的浮点数进行低精度浮点数乘法运算，通过DSP实现Nm个MaEb浮点数乘法器，提升定制电路或者非定制电路的加速性能。The purpose of the present invention is: the present invention provides a CNN acceleration calculation method and system based on the representation of low-precision floating-point number data, using the representation of low-precision floating-point number MaEb, without retraining, to ensure that after quantization The accuracy of the convolutional neural network, and the low-precision floating-point multiplication operation is performed through MaEb floating-point numbers, and Nm MaEb floating-point number multipliers are implemented through DSP to improve the acceleration performance of custom circuits or non-custom circuits.
本发明采用的技术方案如下：The technical scheme adopted in the present invention is as follows:
基于低精度浮点数数据表现形式的CNN加速计算方法，包括如下步骤：The CNN acceleration calculation method based on the representation of low-precision floating-point data includes the following steps:
中心控制模块生成控制信号仲裁浮点数功能模块和存储系统；The central control module generates the control signal to arbitrate the floating point number function module and the storage system;
浮点数功能模块根据控制信号从存储系统中接收输入激活值和权重，将所述输入激活值和权重分发至不同的处理单元PE进行每一卷积层的卷积计算，完成CNN加速计算；The floating-point number function module receives the input activation value and weight from the storage system according to the control signal, and distributes the input activation value and weight to different processing units PE to perform the convolution calculation of each convolution layer to complete the CNN acceleration calculation;
所述卷积计算包括对通过低精度浮点数表现形式量化的MaEb浮点数进行点积计算完成的卷积层的前向计算，其中，a、b均为正整数。The convolution calculation includes the forward calculation of the convolution layer completed by performing dot product calculation on MaEb floating-point numbers quantized by the low-precision floating-point number representation, wherein a and b are both positive integers.
优选地，所述通过低精度浮点数表现形式量化的MaEb浮点数进行点积计算完成的卷积层的前向计算包括如下步骤：Preferably, the forward calculation of the convolutional layer completed by performing dot product calculation on MaEb floating-point numbers quantized by low-precision floating-point numbers includes the following steps:
步骤a：将单精度浮点数的输入数据量化为低精度浮点数表现形式的MaEb的浮点数，所述输入数据包括输入激活值、权重和偏置，其中，0＜a+b≤31；Step a: quantize the input data of single-precision floating-point numbers into floating-point numbers of MaEb in the form of low-precision floating-point numbers, the input data includes input activation values, weights and biases, where 0<a+b≤31;
步骤b：将MaEb的浮点数分发至浮点数功能模块中并行的Nm个低精度浮点数乘法器进行前向计算得到全精度浮点数乘积，其中，Nm表示浮点数功能模块中一个处理单元PE低精度浮点数乘法器的数量；Step b: Distribute the floating-point number of MaEb to Nm low-precision floating-point number multipliers in parallel in the floating-point number function module to perform forward calculation to obtain a full-precision floating-point number product, where Nm represents a processing unit in the floating-point number function module Number of PE low-precision floating-point multipliers;
步骤c：将所述全精度浮点数乘积传输至数据转换模块获取无精度损失的定点数结果；Step c: transmitting the full-precision floating-point number product to the data conversion module to obtain a fixed-point number result without precision loss;
步骤b：将所述定点数结果分配至并行的4T个定点数加法树后，将定点数加法树结果和输入数据中的偏置经过后处理单元依次进行累加、池化和激活完成卷积层计算，其中，T为正整数。Step b: After allocating the fixed-point number result to the parallel 4T fixed-point number addition trees, the result of the fixed-point number addition tree and the offset in the input data are accumulated, pooled and activated in turn through the post-processing unit to complete the convolution layer. Calculate, where T is a positive integer.
优选地，所述步骤a、b、c包括如下步骤：Preferably, the steps a, b and c include the following steps:
原始图片、权重通过低精度浮点数表现形式量化为MaEb的浮点数，偏置量化为16比特的定点数，将上述量化后的原始图片、权重和偏置输入所述网络并存储至外部存储器；The original picture and weight are quantized into MaEb floating-point numbers through low-precision floating-point number representation, and the offset is quantized into a 16-bit fixed-point number, and the above-mentioned quantized original picture, weight and offset are input into the network and stored in the external memory;
将量化后的图片和权重进行低精度浮点数乘法运算得到(2a+b+4)比特浮点数后，将上述(2a+b+4)比特浮点数转换为(2a+2(b+1)-1)比特定点数后进行累加计算，将上述累加计算结果与所述偏置量化的16比特的定点数相加得到32比特定点数；After multiplying the quantized image and weight with low-precision floating-point numbers to obtain (2a+b+4)-bit floating-point numbers, convert the above (2a+b+4)-bit floating-point numbers to (2a+2(b+1) -1) Accumulation calculation is performed after the ratio of specific points, and the above-mentioned cumulative calculation result is added to the 16-bit fixed-point number of the offset quantization to obtain 32 ratios of specific points;
将上述32比特定点数转换为MaEb的浮点数作为所述网络下一层的输入，并保存至外部存储器。Convert the above-mentioned 32-ratio specific point number to a floating point number of MaEb as the input of the next layer of the network, and save it to the external memory.
优选地，所述原始图片、权重量化为MaEb的浮点数如下包括步骤：Preferably, the original picture and the weight are quantized to a floating point number of MaEb as follows:
定义所述网络的低精度浮点数表现形式MaEb，所述低精度浮点数表现形式包括符号位、尾数和指数；defining a low-precision floating-point number representation MaEb of the network, the low-precision floating-point number representation including a sign bit, a mantissa, and an exponent;
在优化低精度浮点数表示形式过程中，同时更改比例因子、更改a和b的组合和计算所述网络每一层量化前后的权重和激活值均方差，根据量化前后的权重和激活值均方差最小值获取最优的低精度浮点数表示形式和所述表示形式下的最优比例因子；In the process of optimizing the representation of low-precision floating-point numbers, simultaneously changing the scale factor, changing the combination of a and b, and calculating the mean square error of weights and activation values before and after quantization of each layer of the network, according to the mean square error of weights and activation values before and after quantization The minimum value obtains the optimal low-precision floating-point representation and the optimal scale factor under said representation;
基于上述低精度浮点数表示形式和最优比例因子，完成将原始图片、权重的单精度浮点数量化为以低精度浮点数表现形式MaEb表示的浮点数；Based on the above-mentioned low-precision floating-point number representation and optimal scale factor, the single-precision floating-point number of the original image and weight is quantized into a floating-point number represented by the low-precision floating-point number representation MaEb;
当a＝4或者5时，用此低精度浮点数表示形式量化的网络即为最优结果。When a=4 or 5, the network quantized with this low-precision floating-point representation is the optimal result.
优选地，所述MaEb的浮点数进行低精度浮点数乘法运算包括如下步骤：Preferably, performing the low-precision floating-point multiplication operation on the floating-point number of MaEb includes the following steps:
将MaEb的浮点数拆分为一个a比特的乘加器和一个b比特的加法器，计算公式如下：The floating-point number of MaEb is split into an a-bit multiplier-adder and a b-bit adder, and the calculation formula is as follows:
其中，Mx，My，Ex，Ey分别表示X和Y的尾数与指数，式子0.Mx×0.My+(1.Mx+0.My)由一个a比特的无符号定点数乘加器实现，式子Ex+Ey可以由一个b比特的无符号定点数加法器实现；Among them, Mx , My , Ex , Ey represent the mantissa and exponent of X andY respectively, and the formula 0.Mx ×0.My +(1.Mx +0.My ) consists of an a-bit The unsigned fixed-point multiplier-adder of , the formula Ex +Ey can be realized by a b-bit unsigned fixed-point adder;
基于DSP实现的乘加器P＝A×B+C，在输入端口添加的空白比特实现若干个a比特的乘加器，其中，A、B、C表示DSP的三个输入端。Based on the multiplier-accumulator P=A×B+C realized by DSP, the blank bits added at the input port realize several a-bit multiplier-adders, wherein A, B, and C represent the three input ends of the DSP.
优选地，所述A、B、C比特位宽最大取值分别为25、18、48。Preferably, the maximum value of the bit width of the A, B, and C bits is 25, 18, and 48, respectively.
一种系统，包括定制电路或者非定制电路，所述定制电路或者非定制电路包括浮点数功能模块，所述浮点数功能模块用于根据控制信号从存储系统中接收输入激活值和权重，将输入激活值和权重分发至不同的处理单元PE并行计算通过低精度浮点数表现形式量化为MaEb浮点数的卷积，其中，a、b均为正整数；A system includes a custom circuit or a non-custom circuit, the custom circuit or non-custom circuit includes a floating-point number function module, the floating-point number function module is used to receive input activation values and weights from a storage system according to a control signal, and input an input activation value and a weight. Activation values and weights are distributed to different processing units PE for parallel computing, and the convolution quantized as MaEb floating point numbers through low-precision floating point number representation, where a and b are both positive integers;
存储系统，用于缓存输入特征图、权重和输出特征图；A storage system for caching input feature maps, weights, and output feature maps;
中心控制模块，用于将指令解码为控制信号后仲裁浮点数功能模块和存储系统；The central control module is used to arbitrate the floating-point number function module and the storage system after decoding the instruction into a control signal;
所述浮点数功能模块包括n个并行处理单元PE，所述处理单元PE通过DSP实现Nm个MaEb浮点数乘法器，其中，n为正整数，Nm表示浮点数功能模块中一个处理单元PE低精度浮点数乘法器的数量。The floating-point number function module includes n parallel processing units PE, and the processing unit PE implements Nm MaEb floating-point number multipliers through DSP, where n is a positive integer, and Nm represents a processing unit PE in the floating-point number function module. The number of low-precision floating-point multipliers.
优选地，所述每个处理单元PE包括4T个并行支路，所述每个并行支路包含Nm/(4T)个乘法器、Nm/(4T)个数据转换模块、1个定点数加法树和1个后处理单元PPM，所述乘法器、数据转换模块、定点数加法树、后处理单元依次连接，其中，T为正整数。Preferably, each processing unit PE includes 4T parallel branches, and each parallel branch includes Nm /(4T) multipliers, Nm /(4T) data conversion modules, and 1 fixed-point number The addition tree and a post-processing unit PPM, the multiplier, the data conversion module, the fixed-point number addition tree, and the post-processing unit are connected in sequence, wherein T is a positive integer.
优选地，所述存储系统包括具有乒乓结构的输入特征图缓存模块IFMB、权重缓存模块WB和输出特征图缓存OFMB。Preferably, the storage system includes an input feature map cache module IFMB, a weight cache module WB and an output feature map cache OFMB with a ping-pong structure.
优选地，所述后处理单元包括依次连接的累加器、池化层和激活函数。Preferably, the post-processing unit includes an accumulator, a pooling layer and an activation function connected in sequence.
优选地，所述a、b满足0＜a+b≤31，当a＝4或者5时，用此低精度浮点数表示形式量化的网络即为最优结果。Preferably, the a and b satisfy 0<a+b≤31, and when a=4 or 5, the network quantized using this low-precision floating-point number representation is the optimal result.
优选地，所述定制电路包括ASIC或者SOC，所述非定制电路包括FPGA。Preferably, the customized circuit includes an ASIC or an SOC, and the non-customized circuit includes an FPGA.
综上所述，由于采用了上述技术方案，本发明的有益效果是：To sum up, due to the adoption of the above-mentioned technical solutions, the beneficial effects of the present invention are:
1.本发明使用低精度浮点数表现形式MaEb，在不需要重新训练的情况下，可以找到最优的数据表示形式，只需要4比特或者5比特的尾数，保证top-1/top-5的准确率丢失可以忽略不计，top-1/top-5准确率的降低值分别在0.5％/0.3％以内；1. The present invention uses the low-precision floating-point number representation MaEb, and can find the optimal data representation without retraining, and only needs a 4-bit or 5-bit mantissa to ensure top-1/top-5. The loss of accuracy is negligible, and the reduction in top-1/top-5 accuracy is within 0.5%/0.3%, respectively;
2.本发明在使用一个4比特的乘加器和一个3比特的加法器的方式实现一个8比特的低精度浮点数的乘法运算，并且在一个DSP内实现4个这种方式的低精度浮点数乘法运算，相当于在一个DSP内部实现四个卷积运算中的乘法运算，比起现有最多只能用一个DSP实现两个乘法运算，实现在保证准确率的情况下，大大提升定制电路或者非定制电路上加速的性能，定制电路包括ASIC或者SOC，非定制电路包括FPGA；2. The present invention uses a 4-bit multiplier-adder and a 3-bit adder to realize the multiplication of an 8-bit low-precision floating-point number, and implements 4 low-precision floating-point numbers in this way in a DSP. The point multiplication operation is equivalent to realizing the multiplication operation of four convolution operations in one DSP. Compared with the existing one, which can only realize two multiplication operations with one DSP, it can greatly improve the customized circuit while ensuring the accuracy. Or accelerated performance on non-custom circuits, custom circuits include ASIC or SOC, and non-custom circuits include FPGA;
3.本发明的吞吐量相比于Intel i9 CPU提升了64.5倍，相比于现有的FPGA加速器提升了1.5倍；针对VGG16和YOLO卷积神经网络而言，本申请与现有的六个FPGA加速器相比，在吞吐量方面，分别提升了3.5倍和27.5倍，在单个DSP吞吐量方面，分别提升了4.1倍和5倍；3. The throughput of the present invention is increased by 64.5 times compared with the Intel i9 CPU, and by 1.5 times compared with the existing FPGA accelerator; for VGG16 and YOLO convolutional neural networks, the present application and the existing six Compared with the FPGA accelerator, the throughput is increased by 3.5 times and 27.5 times respectively, and the throughput of a single DSP is increased by 4.1 times and 5 times respectively;
4.本发明的数据表示形式也可以运用在ASIC方面，在ASIC设计中，实现低精度浮点数乘法器比8比特定点数乘法器，需要的标准单元数量更少；4. The data representation form of the present invention can also be used in ASIC. In ASIC design, the number of standard cells required to realize a low-precision floating-point multiplier is less than that of a specific point multiplier of 8;
5.本发明基于量化方法进行卷积层的前向计算时，将累加结果定点数转换为浮点数，利于节省存储资源；将浮点数累加转换为定点数累加，可以节省大量定制电路或者非定制电路资源，从而提升定制电路或者非定制电路实现的吞吐量。5. When the present invention performs the forward calculation of the convolution layer based on the quantization method, the accumulated result fixed-point number is converted into a floating-point number, which is conducive to saving storage resources; the floating-point number accumulation is converted into a fixed-point number accumulation, which can save a lot of customized circuits or non-customized circuits. circuit resources, thereby improving the throughput achieved by custom circuits or non-custom circuits.
附图说明Description of drawings
为了更清楚地说明本发明实施例的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，应当理解，以下附图仅示出了本发明的某些实施例，因此不应被看作是对范围的限定，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他相关的附图。In order to illustrate the technical solutions of the embodiments of the present invention more clearly, the following briefly introduces the accompanying drawings used in the embodiments. It should be understood that the following drawings only show some embodiments of the present invention, and therefore do not It should be regarded as a limitation of the scope, and for those of ordinary skill in the art, other related drawings can also be obtained according to these drawings without any creative effort.
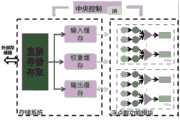
图1为本发明的系统框图；1 is a system block diagram of the present invention;
图2为本发明的量化方法流程图；Fig. 2 is the quantization method flow chart of the present invention;
图3为本发明的量化后卷积神经网络的前向计算数据流示意图；3 is a schematic diagram of the forward calculation data flow of the quantized convolutional neural network of the present invention;
图4为本发明的浮点数功能模块的全流水结构示意图；4 is a schematic diagram of a full pipeline structure of a floating-point number functional module of the present invention;
图5为本发明的卷积计算示意图；Fig. 5 is the convolution calculation schematic diagram of the present invention;
图6为本发明的DSP端口的输入形式示意图。FIG. 6 is a schematic diagram of the input form of the DSP port of the present invention.
具体实施方式Detailed ways
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明，即所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。通常在此处附图中描述和示出的本发明实施例的组件可以以各种不同的配置来布置和设计。In order to make the objectives, technical solutions and advantages of the present invention clearer, the present invention will be further described in detail below with reference to the accompanying drawings and embodiments. It should be understood that the specific embodiments described herein are only used to explain the present invention, but not to limit the present invention, that is, the described embodiments are only a part of the embodiments of the present invention, rather than all the embodiments. The components of the embodiments of the invention generally described and illustrated in the drawings herein may be arranged and designed in a variety of different configurations.
因此，以下对在附图中提供的本发明的实施例的详细描述并非旨在限制要求保护的本发明的范围，而是仅仅表示本发明的选定实施例。基于本发明的实施例，本领域技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。Thus, the following detailed description of the embodiments of the invention provided in the accompanying drawings is not intended to limit the scope of the invention as claimed, but is merely representative of selected embodiments of the invention. Based on the embodiments of the present invention, all other embodiments obtained by those skilled in the art without creative work fall within the protection scope of the present invention.
需要说明的是，术语“第一”和“第二”等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者设备中还存在另外的相同要素。It should be noted that relational terms such as the terms "first" and "second" are only used to distinguish one entity or operation from another entity or operation, and do not necessarily require or imply any relationship between these entities or operations. any such actual relationship or sequence exists. Moreover, the terms "comprising", "comprising" or any other variation thereof are intended to encompass a non-exclusive inclusion such that a process, method, article or device that includes a list of elements includes not only those elements, but also includes not explicitly listed or other elements inherent to such a process, method, article or apparatus. Without further limitation, an element qualified by the phrase "comprising a..." does not preclude the presence of additional identical elements in a process, method, article or apparatus that includes the element.
以下结合实施例对本发明的特征和性能作进一步的详细描述。The features and performances of the present invention will be further described in detail below in conjunction with the embodiments.
实施例1Example 1
本实施例提供一种基于低精度浮点数数据表现形式的CNN加速计算方法及系统，使用低精度浮点数的表示形式MaEb，在不需要重新训练的情况下，保证量化后卷积神经网络的准确率，并通过MaEb的浮点数进行低精度浮点数乘法运算，通过DSP实现Nm个MaEb浮点数乘法器，提升定制电路或者非定制电路的加速性能，具体如下：This embodiment provides a CNN acceleration calculation method and system based on the representation form of low-precision floating-point number data. Using the representation form of low-precision floating-point number MaEb, the accuracy of the quantized convolutional neural network is guaranteed without retraining. rate, and perform low-precision floating-point multiplication operations through MaEb floating-point numbers, and implement Nm MaEb floating-point number multipliers through DSP to improve the acceleration performance of custom circuits or non-custom circuits, as follows:
基于低精度浮点数数据表现形式的CNN加速计算方法，包括如下步骤：The CNN acceleration calculation method based on the representation of low-precision floating-point data includes the following steps:
中心控制模块生成控制信号仲裁浮点数功能模块和存储系统；The central control module generates the control signal to arbitrate the floating point number function module and the storage system;
浮点数功能模块根据控制信号从存储系统中接收输入激活值和权重，将所述输入激活值和权重分发至不同的处理单元PE进行每一卷积层的卷积计算，完成CNN加速计算；The floating-point number function module receives the input activation value and weight from the storage system according to the control signal, and distributes the input activation value and weight to different processing units PE to perform the convolution calculation of each convolution layer to complete the CNN acceleration calculation;
所述卷积计算包括对通过低精度浮点数表现形式量化的MaEb浮点数进行点积计算完成的卷积层的前向计算，其中，a、b均为正整数。The convolution calculation includes the forward calculation of the convolution layer completed by performing dot product calculation on MaEb floating-point numbers quantized by the low-precision floating-point number representation, wherein a and b are both positive integers.
如图4所示，通过低精度浮点数表现形式量化的MaEb浮点数进行点积计算完成的卷积层的前向计算包括如下步骤：As shown in Figure 4, the forward calculation of the convolutional layer completed by the dot product calculation of MaEb floating-point numbers quantized by low-precision floating-point numbers includes the following steps:
步骤a：将单精度浮点数的输入数据量化为低精度浮点数表现形式的MaEb的浮点数，所述输入数据包括输入激活值、权重和偏置，0＜a+b≤31；Step a: quantize the input data of the single-precision floating-point number into the floating-point number of MaEb in the form of low-precision floating-point number, the input data includes the input activation value, weight and bias, 0<a+b≤31;
步骤b：将MaEb的浮点数分发至浮点数功能模块中并行的Nm个低精度浮点数乘法器进行前向计算得到全精度浮点数乘积，其中，Nm表示浮点数功能模块中一个处理单元PE低精度浮点数乘法器的数量；Step b: Distribute the floating-point number of MaEb to Nm low-precision floating-point number multipliers in parallel in the floating-point number function module to perform forward calculation to obtain a full-precision floating-point number product, where Nm represents a processing unit in the floating-point number function module Number of PE low-precision floating-point multipliers;
步骤c：将所述全精度浮点数乘积传输至数据转换模块获取无精度损失的定点数结果；Step c: transmitting the full-precision floating-point number product to the data conversion module to obtain a fixed-point number result without precision loss;
步骤b：将所述定点数结果分配至并行的4T个定点数加法树后，将定点数加法树结果和输入数据中的偏置经过后处理单元依次进行累加、池化和激活完成卷积层计算，T为正整数。Step b: After allocating the fixed-point number result to the parallel 4T fixed-point number addition trees, the result of the fixed-point number addition tree and the offset in the input data are accumulated, pooled and activated in turn through the post-processing unit to complete the convolution layer. Calculate, T is a positive integer.
所述步骤a、b、c包括如下步骤：Described steps a, b, c comprise the following steps:
如图3所示，原始图片、权重通过低精度浮点数表现形式量化为MaEb的浮点数，偏置量化为16比特的定点数，将上述量化后的原始图片、权重和偏置输入所述网络并存储至外部存储器，其中，0＜a+b≤31，a、b均为正整数；As shown in Figure 3, the original picture and weight are quantized into MaEb floating-point numbers through the representation of low-precision floating-point numbers, and the offset is quantized into a 16-bit fixed-point number, and the above-mentioned quantized original picture, weight and offset are input into the network and store it in the external memory, where 0<a+b≤31, a and b are both positive integers;
将量化后的图片和权重进行低精度浮点数乘法运算得到(2a+b+4)比特浮点数后，将上述(2a+b+4)比特浮点数转换为(2a+2(b+1)-1)比特定点数后进行累加计算，将上述累加计算结果与所述偏置量化的16比特的定点数相加得到32比特定点数；After multiplying the quantized image and weight with low-precision floating-point numbers to obtain (2a+b+4)-bit floating-point numbers, convert the above (2a+b+4)-bit floating-point numbers to (2a+2(b+1) -1) Accumulation calculation is performed after the ratio of specific points, and the above-mentioned cumulative calculation result is added to the 16-bit fixed-point number of the offset quantization to obtain 32 ratios of specific points;
将上述32比特定点数转换为MaEb的浮点数作为所述网络下一层的输入，并保存至外部存储器。Convert the above-mentioned 32-ratio specific point number to a floating point number of MaEb as the input of the next layer of the network, and save it to the external memory.
如图2所示，所述原始图片、权重量化为MaEb的浮点数如下包括步骤：As shown in Figure 2, the original picture and the weight are quantized into floating point numbers of MaEb as follows:
定义所述网络的低精度浮点数表现形式MaEb，所述低精度浮点数表现形式包括符号位、尾数和指数，其中，0＜a+b≤31，a、b均为正整数；Define a low-precision floating-point number representation MaEb of the network, the low-precision floating-point number representation includes a sign bit, a mantissa and an exponent, where 0<a+b≤31, a and b are both positive integers;
在优化低精度浮点数表示形式过程中，同时更改比例因子、更改a和b的组合和计算所述网络每一层量化前后的权重和激活值均方差，根据量化前后的权重和激活值均方差最小值获取最优的低精度浮点数表示形式和所述表示形式下的最优比例因子；In the process of optimizing the representation of low-precision floating-point numbers, simultaneously changing the scale factor, changing the combination of a and b, and calculating the mean square error of weights and activation values before and after quantization of each layer of the network, according to the mean square error of weights and activation values before and after quantization The minimum value obtains the optimal low-precision floating-point representation and the optimal scale factor under said representation;
基于上述低精度浮点数表示形式和最优比例因子，完成将原始图片、权重的单精度浮点数量化为以低精度浮点数表现形式MaEb表示的浮点数；Based on the above-mentioned low-precision floating-point number representation and optimal scale factor, the single-precision floating-point number of the original image and weight is quantized into a floating-point number represented by the low-precision floating-point number representation MaEb;
当a＝4或者5时，用此低精度浮点数表示形式量化的网络即为最优结果。When a=4 or 5, the network quantized with this low-precision floating-point representation is the optimal result.
所述MaEb的浮点数进行低精度浮点数乘法运算包括如下步骤：The floating-point number of MaEb to perform low-precision floating-point number multiplication includes the following steps:
将MaEb的浮点数拆分为一个a比特的乘加器和一个b比特的加法器，计算公式如下：The floating-point number of MaEb is split into an a-bit multiplier-adder and a b-bit adder, and the calculation formula is as follows:
其中，Mx，My，Ex，Ey分别表示X和Y的尾数与指数，式子0.Mx+0.My+(1.Mx+0.My)由一个a比特的无符号定点数乘加器实现，式子Ex+Ey可以由一个b比特的无符号定点数加法器实现；Among them, Mx , My , Ex , and Ey represent the mantissa and exponent ofX andY respectively, and the formula 0.Mx +0.My +(1.Mx +0.My ) consists of an a-bit The unsigned fixed-point multiplier-adder of , the formula Ex +Ey can be realized by a b-bit unsigned fixed-point adder;
基于DSP实现的乘加器P＝A×B+C，在输入端口添加的空白比特实现若干个a比特的乘加器，其中，A、B、C表示DSP的三个输入端。Based on the multiplier-accumulator P=A×B+C realized by DSP, the blank bits added at the input port realize several a-bit multiplier-adders, wherein A, B, and C represent the three input ends of the DSP.
所述A、B、C比特位宽最大取值分别为25、18、48。The maximum values of the bit widths of the A, B, and C bits are 25, 18, and 48, respectively.
量化细节：Quantization details:
定义所述网络的低精度浮点数表现形式MaEb，所述低精度浮点数表现形式包括符号位、尾数和指数，其中，a、b均为正整数；Define a low-precision floating-point number representation form MaEb of the network, the low-precision floating-point number representation form includes a sign bit, a mantissa and an exponent, wherein a and b are both positive integers;
在优化低精度浮点数表示形式过程中，同时更改比例因子、更改a和b的组合和计算所述网络每一层量化前后的权重和激活值均方差，根据量化前后的权重和激活值均方差最小值获取最优的低精度浮点数表示形式和所述表示形式下的最优比例因子；In the process of optimizing the representation of low-precision floating-point numbers, simultaneously changing the scale factor, changing the combination of a and b, and calculating the mean square error of weights and activation values before and after quantization of each layer of the network, according to the mean square error of weights and activation values before and after quantization The minimum value obtains the optimal low-precision floating-point representation and the optimal scale factor under said representation;
基于上述低精度浮点数表示形式和最优比例因子，完成单精度浮点数量化为低精度浮点数。Based on the above-mentioned low-precision floating-point number representation and optimal scale factor, the quantization of single-precision floating-point numbers to low-precision floating-point numbers is completed.
步骤1中低精度浮点数表现形式的十进制值计算如下：The decimal value of the low-precision floating-point representation in
其中，Vdec表示低精度浮点数表现形式的十进制值，S，M和E分别表示符号位，尾数和指数，均为无符号的值，Eb表示指数的偏置，用于为指数引入正数和负数，表示为：where Vdec represents the decimal value of the low-precision floating-point representation, S, M, and E represent the sign bit, mantissa, and exponent, respectively, all unsigned values, and Eb represents the bias of the exponent, which is used to introduce positive values for the exponent. numbers and negative numbers, expressed as:
其中，DWE表示指数的位宽，尾数和指数的位宽均为非固定的。Among them,DWE represents the bit width of the exponent, and the bit width of the mantissa and the exponent are both non-fixed.
量化中的优化包括如下步骤：Optimization in quantization includes the following steps:
步骤aa：将单精度浮点数乘以比例因子映射至低精度浮点数能够表示的动态范围内，将映射后的数四舍五入成最接近的低精度浮点数，并将超过动态范围的数据保留成最大值或者最小值，计算公式如下：Step aa: Multiply the single-precision floating-point number by the scale factor and map it to the dynamic range that the low-precision floating-point number can represent, round the mapped number to the nearest low-precision floating-point number, and keep the data that exceeds the dynamic range to the maximum value or minimum value, the calculation formula is as follows:
Vlfp＝quan(Vfp32×2sf，MINlfb，MAXlfp)Vlfp =quan(Vfp32 ×2sf , MINlfb , MAXlfp )
其中，Vlfp和Vfp32表示由低精度浮点数和单精度浮点数形式表示的十进制的值，MINlfp和MAXlfp表示低精度浮点数能够表示的最小值和最大值，sf表示比例因子，quan(x，IN，MAX)表示对任意浮点数x在范围MIN到MAX之间进行量化，round(x)表示表示对任意浮点数x进行四舍五入；Among them, Vlfp and Vfp32 represent decimal values represented by low-precision floating-point numbers and single-precision floating-point numbers, MINlfp and MAXlfp represent the minimum and maximum values that low-precision floating-point numbers can represent, sf represents the scale factor, and quan (x, IN, MAX) means to quantize any floating-point number x in the range MIN to MAX, and round(x) means to round up any floating-point number x;
步骤bb：计算量化前后权重和激活值均方差MSE，所述量化前后的权重和激活值均方差表示量化误差，计算如下：Step bb: Calculate the weight and activation value mean square error MSE before and after quantization, and the weight and activation value mean square error before and after quantization represent the quantization error, and the calculation is as follows:
其中，N表示权重和激活值的数量；where N represents the number of weights and activation values;
步骤cc：更改比例因子，重复步骤aa和bb；Step cc: change the scale factor, repeat steps aa and bb;
步骤dd：更改低精度浮点数表示形式即MaEb中a和b的组合，重复步骤aa、bb和cc；Step dd: Change the representation of low-precision floating-point numbers, that is, the combination of a and b in MaEb, and repeat steps aa, bb, and cc;
步骤ee：将权重和激活值均方差最小值对应的低精度表示形式和比例因子作为最优的结果。Step ee: Take the low-precision representation and scale factor corresponding to the minimum mean square error of the weights and activation values as the optimal result.
如图2所示，针对每个卷积神经网络，为其寻找最优的低精度浮点数数据表示形式(不同的尾数和指数的位宽组合)，从而保证量化误差最小；CNN的量化过程中，针对每一层可以选择量化或者不量化，同时在量化时，每一层的低精度浮点数表示形式可以不同，即a和b只需满足0＜a+b≤31即可。具体来说，针对每一个需要量化的卷积神经网络，优化低精度浮点数表示形式的过程中(优化可采用遍历或者其他搜索方式)，为卷积神经网络每一层的权重和激活值，寻找该低精度浮点数表示形式下的最优的比例因子，保证量化前后权重和激活值的均方差最小；通过本申请的量化方法实现不需要重新训练的情况下保证准确率的原因在于：对于量化前的卷积神经网络，它本身有一个准确率的结果，通常把这个结果定义为标准值。本申请目的是在保证这个标准的准确率的前提下，量化卷积神经网络；量化前网络的权重和激活值，这些数据更接近于一个高斯分布，伽马分布等非均匀分布，即这些值集中出现在某一个范围内，而在这个范围外出现的概率较小；量化权重和激活值，就是用更低精度的数去近似表示原来的数据，本申请提出的用低精度浮点数去做量化，低精度浮点数的特点是在零附近能够表示的数更多，而往两边则能够表示的数更少即低精度浮点数的特点更接近于量化前权重和激活值的分布。将量化前后的数据进行对比，当量化后的数据越接近于量化前的数据，则该量化后的网络会带来的准确率的丢失会更小。而均方差就能够表示量化后的数据与量化前的数据之间的差别，均方差越小，代表量化后的数据更接近于量化前的数据。所以能够说明，均方差最小的情况，能够保证准确率丢失最小从而实现在不需要重新训练的情况下。通过本申请的量化方法可以找到最优的数据表示形式，只需要4比特或者5比特的尾数，保证top-1/top-5的准确率丢失可以忽略不计，top-1/top-5准确率降低值分别在0.5％/0.3％以内。As shown in Figure 2, for each convolutional neural network, find the optimal low-precision floating-point data representation (different combinations of mantissa and exponent bit width), so as to ensure the smallest quantization error; in the quantization process of CNN , quantization or non-quantization can be selected for each layer, and during quantization, the low-precision floating-point number representation of each layer can be different, that is, a and b only need to satisfy 0<a+b≤31. Specifically, for each convolutional neural network that needs to be quantized, in the process of optimizing the representation of low-precision floating-point numbers (the optimization can use traversal or other search methods), the weights and activation values of each layer of the convolutional neural network, Find the optimal scale factor under the low-precision floating-point number representation to ensure that the mean square error of the weights and activation values before and after quantization is the smallest; the quantization method of the present application realizes the reason for ensuring the accuracy without retraining: for Before quantization, the convolutional neural network itself has an accuracy result, which is usually defined as the standard value. The purpose of this application is to quantify the convolutional neural network under the premise of ensuring the accuracy of this standard; the weights and activation values of the network before quantization, these data are closer to a Gaussian distribution, gamma distribution and other non-uniform distributions, that is, these values Concentrated in a certain range, and the probability of appearing outside this range is small; quantization weights and activation values are to use lower precision numbers to approximate the original data, and this application proposes to use low precision floating point numbers to do Quantization, the characteristics of low-precision floating-point numbers are that more numbers can be represented near zero, and less numbers can be represented on both sides, that is, the characteristics of low-precision floating-point numbers are closer to the distribution of weights and activation values before quantization. Comparing the data before and after quantization, when the quantized data is closer to the data before quantization, the loss of accuracy caused by the quantized network will be smaller. The mean square error can represent the difference between the data after quantization and the data before quantization. The smaller the mean square error, the closer the data after quantization is to the data before quantization. Therefore, it can be shown that in the case of the smallest mean square error, the accuracy loss can be minimized so that retraining is not required. The optimal data representation can be found through the quantization method of the present application. Only a 4-bit or 5-bit mantissa is required to ensure that the top-1/top-5 accuracy loss is negligible, and the top-1/top-5 accuracy is negligible. The reduction values are within 0.5%/0.3%, respectively.
量化后神经网络的前向计算数据流如图3所示。为清晰的解释该数据流，在图3中使用M4E3的低精度浮点数表示形式作为例子即a为4，b为3，列出数据流中每一个步骤的数据位宽；所有的输入图片，权重以及偏置都是用单精度浮点数表示的。首先，原始图片和权重都用M4E3的数据表示形式进行量化，而偏置则是量化成16比特定点数，为了减小量化误差，将量化后的输入图片，权重以及偏置存储在外部存储器中。其次，针对量化后的图片和权重，进行低精度浮点数乘法运算，其乘积保存为15比特的浮点数M10E4。随后，15比特浮点数乘积被转化为23比特的定点数，结合偏置量化的16比特定点数进行累加计算，累加的最后结果保存为32比特定点数。上述操作有两个优点：1、在整个过程中不会有任何精度损失，从而保证最后推理结果的准确率；2、将浮点数累加转化为定点数累加，可以节省大量的定制电路(例如ASIC/SOC)或非定制电路(例如FPGA)的资源，从而提升定制电路(例如ASIC/SOC)或非定制电路(例如FPGA)实现的吞吐量。最后，在被另一个CNN层使用前，最终的输出结果会被重新转化为M4E3的浮点数，并且保存到外部存储器，节约存储空间。在整个数据流中，只有最后的数据转化步骤会带来比特位宽的减少和精度损失。而这部分的精度损失并不会给最后的精度带来影响，根据实验可验证。The forward computing data flow of the quantized neural network is shown in Figure 3. In order to explain the data flow clearly, the low-precision floating-point representation of M4E3 is used as an example in Figure 3, that is, a is 4, b is 3, and the data bit width of each step in the data flow is listed; all input pictures, Weights and biases are expressed in single-precision floating-point numbers. First, the original image and weight are quantized using M4E3 data representation, and the offset is quantized into 16-bit specific points. In order to reduce the quantization error, the quantized input image, weight and offset are stored in the external memory. . Secondly, for the quantized picture and weight, a low-precision floating-point number multiplication operation is performed, and the product is stored as a 15-bit floating-point number M10E4. Then, the product of 15-bit floating-point numbers is converted into 23-bit fixed-point numbers, and combined with the 16-bit specific point number of offset quantization for accumulation calculation, and the final result of accumulation is stored as a 32-bit specific point number. The above operation has two advantages: 1. There will be no loss of precision in the whole process, thus ensuring the accuracy of the final inference result; 2. Converting the accumulation of floating-point numbers into accumulation of fixed-point numbers can save a lot of custom circuits (such as ASICs). /SOC) or non-custom circuits (such as FPGA), thereby increasing the throughput realized by custom circuits (such as ASIC/SOC) or non-custom circuits (such as FPGA). Finally, before being used by another CNN layer, the final output will be re-converted to M4E3 floating-point numbers and saved to external memory to save storage space. In the entire data stream, only the final data transformation step brings about a reduction in bit width and a loss of precision. This part of the accuracy loss will not affect the final accuracy, which can be verified by experiments.
每个PE中的乘法器，都是针对低精度浮点数设计的。根据低精度浮点数的表示形式，两个低精度浮点数的乘法可以分成三个部分：1)符号位异或；2)尾数相乘；3)指数相加。以MaEb的形式为例。我们需要一个a比特的无符号数乘加器和一个b比特的无符号数加法器来实现这两个数的乘法。尽管在考虑到第一个隐藏比特后(规约数是1，非规约数是0)，尾数的相乘应该使用(a+1)比特的乘法器，本申请将其设计为a比特的乘加器，这是为了提升DSP的使用效率。与此同时，指数偏置并没有包含在加法中，这是因为本申请的实施例中，所有数据的表示形式都是一样的，那么指数偏置也是一样的，这样可以在最后一步处理，从而简化加法器的设计。The multipliers in each PE are designed for low-precision floating-point numbers. According to the representation of low-precision floating-point numbers, the multiplication of two low-precision floating-point numbers can be divided into three parts: 1) XOR of the sign bit; 2) Mantissa multiplication; 3) Exponent addition. Take the form of MaEb as an example. We need an a-bit unsigned multiplier-adder and a b-bit unsigned adder to multiply these two numbers. Although after taking into account the first hidden bit (the reduction number is 1, the non-reduction number is 0), the multiplication of the mantissa should use a multiplier of (a+1) bits, which is designed as a bit multiplication and addition in this application This is to improve the use efficiency of DSP. At the same time, the exponential bias is not included in the addition, because in the embodiment of this application, the representation of all data is the same, so the exponential bias is also the same, so that it can be processed in the last step, thus Simplify the design of the adder.
如图5所示，在卷积计算过程中，输出通道每一个像素点由下式计算得到：As shown in Figure 5, during the convolution calculation process, each pixel of the output channel is calculated by the following formula:
其中，IC表示输入通道的数量，KW和KH表示卷积核的宽和高，x，y，w和b分别表示输入激活值，输出激活值，权重和偏置。由于用一个DSP实现4个低精度浮点数乘法，并按以下方式计算：(a+b)×(c+d)＝ac+bc+ad+bd，因此，每个PE都是设计成可以同时计算两个输出通道，并且在每个输出通道上，可以同时计算两个卷积结果，如图5所示。具体来说，在第一个周期，在IC个输入通道上的第一个像素点和对应的第一个卷积核的值被送入PE进行计算，在图5中分别标记为a和c。为了遵从四个乘法器中的并行计算模式，在IC个输入通道上的第二个像素点(图5中标记为b)和用于计算另一个输出通道的对应的卷积核的值(图5中标记为d)同样被送入到PE中进行计算。这样，a和b是重复使用的，可以计算出相同输出通道上不同位置的值，而c和d是共用的，可以计算出不同输出通道上的值。在第二个周期，按照同样的方式，输入第二个位置的数据。这样，在KW×KH个周期后，一个PE就可以计算出四个卷积结果。Among them, IC represents the number of input channels, KW and KH represent the width and height of the convolution kernel, and x, y, w and b represent the input activation value, output activation value, weight and bias, respectively. Since four low-precision floating-point multiplications are implemented with one DSP and calculated as follows: (a+b)×(c+d)=ac+bc+ad+bd, therefore, each PE is designed to simultaneously Two output channels are computed, and on each output channel, two convolution results can be computed simultaneously, as shown in Figure 5. Specifically, in the first cycle, the values of the first pixel on the IC input channels and the corresponding first convolution kernel are sent to PE for calculation, which are marked as a and c respectively in Figure 5 . In order to comply with the parallel computing mode among the four multipliers, the second pixel on the IC input channels (labeled b in Figure 5) and the corresponding convolution kernel value used to compute the other output channel (Figure 5) Marked as d) in 5 is also sent to PE for calculation. In this way, a and b are reused and can calculate values at different positions on the same output channel, while c and d are shared and can calculate values on different output channels. In the second cycle, in the same way, enter the data for the second position. In this way, one PE can calculate four convolution results after KW×KH cycles.
在本申请中，每个PE中使用Nm个乘法器，所以IC的值设计为Nm/4，因此，在每个PE内并行计算Nm/4个输入通道。在使用对应的权重和偏置过后，并行计算两个输出通道，每个输出通道上的两个像素点。当输入通道的数量大于Nm/4时，或者每个输出通道上的数量大于2时或者输出通道的数量大于2时，需要多轮计算来完成一次卷积运算。由于PE和CNN卷积层的规模，很多时候CNN卷积层并不能在PE上通过一次计算得到最后结果，计算会将卷积层分成多个部分，先将其中一部分放在PE上计算，这个计算结果就是中间结果。这个中间结果就会存储在OFMB中，等到计算下一个部分的时候，从OFMB中取出中间结果进行计算。为了能够提升并行度，本设计中使用Np个PE在不同的PE之间，可以送入不同输入特征图上面的像素点和不同的权重来进行不同维度的并行计算。举例来说，所有的PE可以共享相同的输入特征图和使用不同的权重，从而并行计算不同的输出通道。或者所有的PE共享相同的参数和使用不同的输入特征图来并行计算输入通道。参数Nm和Np是考虑CNN网络结构，吞吐量，带宽需求来决定。In this application, Nm multipliers are used in each PE, so the value of IC is designed to be Nm /4, therefore, Nm /4 input channels are calculated in parallel in each PE. After applying the corresponding weights and biases, two output channels are computed in parallel, with two pixels on each output channel. When the number of input channels is greater than Nm /4, or when the number on each output channel is greater than 2, or when the number of output channels is greater than 2, multiple rounds of computation are required to complete a convolution operation. Due to the scale of the PE and CNN convolutional layers, in many cases the CNN convolutional layer cannot obtain the final result through one calculation on the PE. The calculation will divide the convolutional layer into multiple parts, and part of them will be calculated on the PE first. The result of the calculation is the intermediate result. This intermediate result will be stored in OFMB, and when the next part is calculated, the intermediate result will be taken out of OFMB for calculation. In order to improve the degree of parallelism, in this design, Np PEs are used between different PEs, and pixels on different input feature maps and different weights can be sent to perform parallel computations of different dimensions. For example, all PEs can share the same input feature map and use different weights, thereby computing different output channels in parallel. Or all PEs share the same parameters and use different input feature maps to compute input channels in parallel. The parameters Nm and Np are determined by considering the CNN network structure, throughput, and bandwidth requirements.
根据PE中的计算模式，IFMB和WB都设置为每个周期分别向每个PE提供Nm/2个输入激活值和权重，同时OFMB每个周期需要保存四个输出激活值。尽管在输出特征图上的每个像素点最后都会保存成低精度浮点数形式，但是在中间结果时，保存成16bit以减少精度损失。这样，对于每个PE来说，OFMB的比特位宽需要设置为64比特。由于输入激活值或权重在不同的并行计算模式下，可以被不同的PE共享，定义Pifm和Pofm(Pifm×Pofm＝Np)这两个参数来分别表示用于并行计算输入特征图和输出特征图的PE的数量。因此，Pifm个PE会共享相同的权重，Pofm个PE会共享相同的输入激活值。对于IFMB，WB，和OFMB的位宽，则需要分别设置为：
一个DSP中实现4个乘法器的具体实现方式。在FPGA实现中，使用M4E3这种数据表示形式。为了能够更清楚的解释在一个DSP中实现四个低精度浮点数乘法器，使用两个规约数的乘法作为例子。两个数的乘积的尾数可以表示为：The specific implementation of 4 multipliers in a DSP. In the FPGA implementation, the M4E3 data representation is used. To be able to explain more clearly the realization of four low-precision floating-point multipliers in one DSP, the multiplication of two reduced numbers is used as an example. The mantissa of the product of two numbers can be expressed as:
其中Mx，My，Ex，Ey分别表示X和Y的尾数与指数，式子0.Mx×0.My+(1.Mx+0.My)可以由一个4-bit的无符号定点数乘加器实现，式子Ex+Ey可以由一个3-bit的无符号定点数加法器实现。由于Xilinx 7系列FPGA中的DSP可以实现一个乘加器P＝A×B+C(其中A，B，C的最大比特位宽分别为25，18和48)，在每个输入端口中添加空白比特，从而充分使用DSP来实现四个4比特的乘加器，DSP每一个端口的具体输入形式如图6所示。在计算过程中，小数点位置设定在最右边，也就是说0.Mx和0.My转化成4比特的正数，1.Mx+0.My转化为10比特的正数以确保在计算过程中不会出现重叠的情况。以这样一种方式，在使用少量的查找表(LUT)和少量的触发器(FF)来实现指数以及式子1.Mx+0.My的加法的情况下，可以使用一个DSP来实现4个M4E3数据表示形式的数的乘法，从而大大增加单个DSP的吞吐量。where Mx , My , Ex , and Ey represent the mantissa and exponent ofX andY , respectively. The formula 0.Mx ×0.My +(1.Mx +0.My ) can be represented by a Bit unsigned fixed-point multiplier-adder implementation, the formula Ex +Ey can be implemented by a 3-bit unsigned fixed-point adder. Since the DSP in the Xilinx 7 series FPGA can implement a multiplier-adder P=A×B+C (where the maximum bit widths of A, B, and C are 25, 18, and 48, respectively), add blanks to each input port Therefore, the DSP is fully used to realize four 4-bit multiplier-accumulators. The specific input form of each port of the DSP is shown in Figure 6. During the calculation process, the decimal point position is set to the far right, that is to say, 0.Mx and 0.My are converted into 4-bit positive numbers, and 1.Mx +0.My is converted into 10-bit positive numbers with Make sure that there is no overlap during the calculation. In such a way, with a small number of look-up tables (LUTs) and a small number of flip-flops (FF) to implement the exponent and the addition of the formula 1.Mx +0.My , one DSP can be used to implement Multiplication of 4 numbers in the M4E3 data representation, thereby greatly increasing the throughput of a single DSP.
综上，本实施例基于低精度浮点数表示形式和最优比例因子，将原始图片、权重的单精度浮点数量化为以低精度浮点数表现形式MaEb表示的浮点数，所述MaEb的浮点数进行低精度浮点数乘法运算包括将MaEb的浮点数拆分为一个a比特的乘加器和一个b比特的加法器；基于DSP实现的乘加器P＝A×B+C，在输入端口添加的空白比特实现a比特的乘加器。比如使用一个4比特的乘加器和一个3比特的加法器的方式实现一个8比特的低精度浮点数的乘法运算，并且在一个DSP内实现4个这种方式的低精度浮点数乘法运算，相当于在一个DSP内部实现四个卷积运算中的乘法运算，比起现有最多只能用一个DSP实现两个乘法运算，实现在保证准确率的情况下，大大提升定制电路或者非定制电路上加速的性能；吞吐量相比于Intel i9 CPU提升了64.5倍，相比于现有的FPGA加速器提升了1.5倍；针对VGG16和YOLO卷积神经网络而言，本申请与现有的六个FPGA加速器相比，在吞吐量方面，分别提升了3.5倍和27.5倍，在单个DSP吞吐量方面，分别提升了4.1倍和5倍；同时，基于量化方法进行卷积层的前向计算时，将累加结果定点数转换为浮点数，利于节省存储资源；将浮点数累加转换为定点数累加，可以节省大量定制电路或者非定制电路资源，从而更加利于提升定制电路或者非定制电路实现的吞吐量。To sum up, this embodiment quantifies the single-precision floating-point number of the original image and the weight into a floating-point number represented by the low-precision floating-point number representation MaEb based on the low-precision floating-point number representation and the optimal scale factor. The floating-point number of MaEb Multiplication of low-precision floating-point numbers includes splitting the floating-point numbers of MaEb into an a-bit multiplier-adder and a b-bit adder; the multiplier-adder P=A×B+C implemented based on DSP is added at the input port The blank bits implement an a-bit multiplier-adder. For example, a 4-bit multiplier-adder and a 3-bit adder are used to implement an 8-bit low-precision floating-point multiplication operation, and four low-precision floating-point multiplication operations are implemented in one DSP. It is equivalent to implementing the multiplication operations in four convolution operations in one DSP. Compared with the existing one, only one DSP can be used to implement two multiplication operations, which greatly improves the custom circuit or non-custom circuit while ensuring the accuracy. Compared with the Intel i9 CPU, the throughput is increased by 64.5 times, and compared with the existing FPGA accelerator by 1.5 times; for VGG16 and YOLO convolutional neural networks, this application is comparable to the existing six Compared with the FPGA accelerator, the throughput is increased by 3.5 times and 27.5 times respectively, and the throughput of a single DSP is increased by 4.1 times and 5 times respectively; at the same time, when the forward calculation of the convolution layer is performed based on the quantization method, Converting the accumulation result from fixed-point numbers to floating-point numbers saves storage resources; converting floating-point accumulation to fixed-point accumulation can save a lot of custom circuit or non-custom circuit resources, which is more conducive to improving the throughput of custom circuits or non-custom circuits. .
实施例2Example 2
基于实施例1，一种系统包括定制电路或者非定制电路，定制电路包括ASIC或者SOC，所述非定制电路包括FPGA，如图1所示，所述定制电路或者非定制电路包括浮点数功能模块，浮点数功能模块用于根据控制信号从存储系统中接收输入激活值和权重，将输入激活值和权重分发至不同的处理单元PE并行计算通过低精度浮点数表现形式量化为MaEb浮点数的卷积，其中，0＜a+b≤31，a、b均为正整数；Based on
存储系统，用于缓存输入特征图、权重和输出特征图；A storage system for caching input feature maps, weights, and output feature maps;
中心控制模块，用于将指令解码为控制信号后仲裁浮点数功能模块和存储系统；The central control module is used to arbitrate the floating-point number function module and the storage system after decoding the instruction into a control signal;
所述浮点数功能模块包括n个并行处理单元PE，所述处理单元PE通过DSP实现Nm个MaEb浮点数乘法器，其中，n为正整数，Nm表示浮点数功能模块中一个处理单元PE低精度浮点数乘法器的数量。The floating-point number function module includes n parallel processing units PE, and the processing unit PE implements Nm MaEb floating-point number multipliers through DSP, where n is a positive integer, and Nm represents a processing unit PE in the floating-point number function module. The number of low-precision floating-point multipliers.
每个处理单元PE包括4T个并行支路，所述每个并行支路包含Nm/(4T)个乘法器、Nm/(4T)个数据转换模块、1个定点数加法树和1个后处理单元PPM，所述乘法器、数据转换模块、定点数加法树、后处理单元依次连接，其中，T为正整数。Each processing unit PE includes 4T parallel branches, each parallel branch includes Nm /(4T) multipliers, Nm /(4T) data conversion modules, 1 fixed-point number addition tree, and 1 The post-processing unit PPM, the multiplier, the data conversion module, the fixed-point number addition tree, and the post-processing unit are connected in sequence, wherein T is a positive integer.
存储系统包括具有乒乓结构的输入特征图缓存模块IFMB、权重缓存模块WB和输出特征图缓存OFMB。The storage system includes an input feature map cache module IFMB, a weight cache module WB and an output feature map cache OFMB with a ping-pong structure.
所述后处理单元包括依次连接的累加器、池化层和激活函数。The post-processing unit includes an accumulator, a pooling layer, and an activation function connected in sequence.
MaEb中a、b取值为4、3即M4E3，T为1，Nm为8，每个处理单元PE包括4个并行支路，所述每个并行支路包含2个乘法器、2个数据转换模块、1个定点数加法树和1个后处理单元PPM。In MaEb, the values of a and b are 4 and 3, that is, M4E3, T is 1, and Nm is 8. Each processing unit PE includes 4 parallel branches, and each parallel branch includes 2 multipliers, 2 Data conversion module, a fixed-point addition tree and a post-processing unit PPM.
将MaEb的浮点数分发至浮点数功能模块中并行的Nm个低精度浮点数乘法器进行前向计算得到全精度浮点数乘积，其中，Nm表示浮点数功能模块中一个处理单元PE低精度浮点数乘法器的数量；将所述全精度浮点数乘积传输至数据转换模块获取无精度损失的定点数结果；将所述定点数结果分配至并行的四个(T为1时)定点数加法树后，将定点数加法树结果和输入数据中的偏置经过后处理单元依次进行累加、池化和激活完成卷积层计算。Distribute the floating-point number of MaEb to the parallel Nm low-precision floating-point number multipliers in the floating-point number function module for forward calculation to obtain the full-precision floating-point number product, where Nm represents a processing unit PE low-precision in the floating-point number function module. The number of floating-point multipliers; transfer the full-precision floating-point product to the data conversion module to obtain fixed-point results without loss of precision; assign the fixed-point results to four parallel (when T is 1) fixed-point additions After the tree, the result of the fixed-point addition tree and the bias in the input data are sequentially accumulated, pooled and activated by the post-processing unit to complete the calculation of the convolution layer.
综上，上述模块计算一个卷积层，针对一个卷积神经网络CNN的加速，每一层都需要经过上述模块计算，结合中心控制模块和存储系统，浮点数功能模块用于根据控制信号从存储系统中接收输入激活值和权重，将输入激活值和权重分发至不同的处理单元PE并行计算通过低精度浮点数表现形式量化为MaEb浮点数的卷积；本申请基于MaEb浮点数实现不进行重新训练即可保证量化后卷积神经网络的准确率，所述处理单元PE通过DSP实现Nm个MaEb浮点数乘法器；实现在保证准确率的情况下，大大提升定制电路或者非定制电路上加速的性能。To sum up, the above modules calculate a convolution layer. For the acceleration of a convolutional neural network CNN, each layer needs to be calculated by the above modules. Combined with the central control module and the storage system, the floating-point number function module is used to store data from the storage system according to the control signal. The input activation value and weight are received in the system, and the input activation value and weight are distributed to different processing units PE for parallel calculation through the low-precision floating-point number representation quantized into the convolution of MaEb floating-point numbers; this application is based on MaEb floating-point numbers. Training can ensure the accuracy of the quantized convolutional neural network. The processing unit PE implements Nm MaEb floating-point multipliers through DSP; it can greatly improve the acceleration on custom circuits or non-custom circuits while ensuring the accuracy. performance.
以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。The above descriptions are only preferred embodiments of the present invention and are not intended to limit the present invention. Any modifications, equivalent replacements and improvements made within the spirit and principles of the present invention shall be included in the protection of the present invention. within the range.
Claims (12)
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201910940659.8ACN110852416B (en) | 2019-09-30 | 2019-09-30 | CNN hardware-accelerated computing method and system based on low-precision floating-point data representation |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201910940659.8ACN110852416B (en) | 2019-09-30 | 2019-09-30 | CNN hardware-accelerated computing method and system based on low-precision floating-point data representation |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN110852416Atrue CN110852416A (en) | 2020-02-28 |
| CN110852416B CN110852416B (en) | 2022-10-04 |
Family
ID=69596180
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN201910940659.8AActiveCN110852416B (en) | 2019-09-30 | 2019-09-30 | CNN hardware-accelerated computing method and system based on low-precision floating-point data representation |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN110852416B (en) |
Cited By (14)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN111414994A (en)* | 2020-03-03 | 2020-07-14 | 哈尔滨工业大学 | An FPGA-based Yolov3 network computing acceleration system and its acceleration method |
| CN111507465A (en)* | 2020-06-16 | 2020-08-07 | 电子科技大学 | Configurable convolutional neural network processor circuit |
| CN111696149A (en)* | 2020-06-18 | 2020-09-22 | 中国科学技术大学 | Quantization method for stereo matching algorithm based on CNN |
| CN112148249A (en)* | 2020-09-18 | 2020-12-29 | 北京百度网讯科技有限公司 | Dot product operation implementation method and device, electronic equipment and storage medium |
| CN112541583A (en)* | 2020-12-16 | 2021-03-23 | 华中光电技术研究所（中国船舶重工集团公司第七一七研究所） | Neural network accelerator |
| CN112598078A (en)* | 2020-12-28 | 2021-04-02 | 北京达佳互联信息技术有限公司 | Hybrid precision training method and device, electronic equipment and storage medium |
| CN112632878A (en)* | 2020-12-10 | 2021-04-09 | 中山大学 | High-speed low-resource binary convolution unit based on FPGA |
| CN112734020A (en)* | 2020-12-28 | 2021-04-30 | 中国电子科技集团公司第十五研究所 | Convolution multiplication accumulation hardware acceleration device, system and method of convolution neural network |
| CN113222130A (en)* | 2021-04-09 | 2021-08-06 | 广东工业大学 | Reconfigurable convolution neural network accelerator based on FPGA |
| CN113762498A (en)* | 2020-06-04 | 2021-12-07 | 合肥君正科技有限公司 | Method for quantizing RoiAlign operator |
| CN114580628A (en)* | 2022-03-14 | 2022-06-03 | 北京宏景智驾科技有限公司 | Efficient quantization acceleration method and hardware circuit for neural network convolution layer |
| CN116127255A (en)* | 2022-12-14 | 2023-05-16 | 北京登临科技有限公司 | Convolution operation circuit and related circuit or device with same |
| CN117806590A (en)* | 2023-12-18 | 2024-04-02 | 上海无问芯穹智能科技有限公司 | A matrix multiplication hardware architecture |
| KR20240084631A (en)* | 2022-12-06 | 2024-06-14 | 삼성전자주식회사 | Computing apparatus and operating method thereof |
Citations (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN106570559A (en)* | 2015-10-09 | 2017-04-19 | 阿里巴巴集团控股有限公司 | Data processing method and device based on neural network |
| CN107239829A (en)* | 2016-08-12 | 2017-10-10 | 北京深鉴科技有限公司 | A kind of method of optimized artificial neural network |
| CN108133262A (en)* | 2016-12-01 | 2018-06-08 | 上海兆芯集成电路有限公司 | With for perform it is efficient 3 dimension convolution memory layouts neural network unit |
| CN108647184A (en)* | 2018-05-10 | 2018-10-12 | 杭州雄迈集成电路技术有限公司 | A kind of Dynamic High-accuracy bit convolution multiplication Fast implementation |
| US20180307980A1 (en)* | 2017-04-24 | 2018-10-25 | Intel Corporation | Specialized fixed function hardware for efficient convolution |
| CN109800877A (en)* | 2019-02-20 | 2019-05-24 | 腾讯科技（深圳）有限公司 | Parameter regulation means, device and the equipment of neural network |
| CN109902745A (en)* | 2019-03-01 | 2019-06-18 | 成都康乔电子有限责任公司 | A CNN-based low-precision training and 8-bit integer quantization inference method |
| CN110058883A (en)* | 2019-03-14 | 2019-07-26 | 成都恒创新星科技有限公司 | A kind of CNN accelerated method and system based on OPU |
- 2019
- 2019-09-30CNCN201910940659.8Apatent/CN110852416B/enactiveActive
Patent Citations (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN106570559A (en)* | 2015-10-09 | 2017-04-19 | 阿里巴巴集团控股有限公司 | Data processing method and device based on neural network |
| CN107239829A (en)* | 2016-08-12 | 2017-10-10 | 北京深鉴科技有限公司 | A kind of method of optimized artificial neural network |
| CN108133262A (en)* | 2016-12-01 | 2018-06-08 | 上海兆芯集成电路有限公司 | With for perform it is efficient 3 dimension convolution memory layouts neural network unit |
| US20180307980A1 (en)* | 2017-04-24 | 2018-10-25 | Intel Corporation | Specialized fixed function hardware for efficient convolution |
| CN108647184A (en)* | 2018-05-10 | 2018-10-12 | 杭州雄迈集成电路技术有限公司 | A kind of Dynamic High-accuracy bit convolution multiplication Fast implementation |
| CN109800877A (en)* | 2019-02-20 | 2019-05-24 | 腾讯科技（深圳）有限公司 | Parameter regulation means, device and the equipment of neural network |
| CN109902745A (en)* | 2019-03-01 | 2019-06-18 | 成都康乔电子有限责任公司 | A CNN-based low-precision training and 8-bit integer quantization inference method |
| CN110058883A (en)* | 2019-03-14 | 2019-07-26 | 成都恒创新星科技有限公司 | A kind of CNN accelerated method and system based on OPU |
Non-Patent Citations (2)
| Title |
|---|
| 吴焕等: "《基于Caffe加速卷积神经网络前向推理》", 《计算机工程与设计》* |
| 王慧丽等: "《基于通用向量DSP的深度学习硬件加速技术》", 《中国科学》* |
Cited By (24)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN111414994A (en)* | 2020-03-03 | 2020-07-14 | 哈尔滨工业大学 | An FPGA-based Yolov3 network computing acceleration system and its acceleration method |
| CN113762498A (en)* | 2020-06-04 | 2021-12-07 | 合肥君正科技有限公司 | Method for quantizing RoiAlign operator |
| CN113762498B (en)* | 2020-06-04 | 2024-01-23 | 合肥君正科技有限公司 | Method for quantizing RoiAlign operator |
| CN111507465B (en)* | 2020-06-16 | 2020-10-23 | 电子科技大学 | A Configurable Convolutional Neural Network Processor Circuit |
| CN111507465A (en)* | 2020-06-16 | 2020-08-07 | 电子科技大学 | Configurable convolutional neural network processor circuit |
| CN111696149A (en)* | 2020-06-18 | 2020-09-22 | 中国科学技术大学 | Quantization method for stereo matching algorithm based on CNN |
| CN112148249A (en)* | 2020-09-18 | 2020-12-29 | 北京百度网讯科技有限公司 | Dot product operation implementation method and device, electronic equipment and storage medium |
| JP2022552046A (en)* | 2020-09-18 | 2022-12-15 | ベイジン バイドゥ ネットコム サイエンス テクノロジー カンパニー リミテッド | Dot product operation implementation method, device, electronic device, and storage medium |
| WO2022057502A1 (en)* | 2020-09-18 | 2022-03-24 | 北京百度网讯科技有限公司 | Method and device for implementing dot product operation, electronic device, and storage medium |
| CN112148249B (en)* | 2020-09-18 | 2023-08-18 | 北京百度网讯科技有限公司 | Dot product operation realization method, device, electronic equipment and storage medium |
| CN112632878A (en)* | 2020-12-10 | 2021-04-09 | 中山大学 | High-speed low-resource binary convolution unit based on FPGA |
| CN112632878B (en)* | 2020-12-10 | 2023-11-24 | 中山大学 | A high-speed and low-resource binary convolution unit based on FPGA |
| CN112541583A (en)* | 2020-12-16 | 2021-03-23 | 华中光电技术研究所（中国船舶重工集团公司第七一七研究所） | Neural network accelerator |
| CN112598078A (en)* | 2020-12-28 | 2021-04-02 | 北京达佳互联信息技术有限公司 | Hybrid precision training method and device, electronic equipment and storage medium |
| CN112734020A (en)* | 2020-12-28 | 2021-04-30 | 中国电子科技集团公司第十五研究所 | Convolution multiplication accumulation hardware acceleration device, system and method of convolution neural network |
| CN112598078B (en)* | 2020-12-28 | 2024-04-19 | 北京达佳互联信息技术有限公司 | Hybrid precision training method and device, electronic equipment and storage medium |
| CN113222130A (en)* | 2021-04-09 | 2021-08-06 | 广东工业大学 | Reconfigurable convolution neural network accelerator based on FPGA |
| CN114580628A (en)* | 2022-03-14 | 2022-06-03 | 北京宏景智驾科技有限公司 | Efficient quantization acceleration method and hardware circuit for neural network convolution layer |
| KR20240084631A (en)* | 2022-12-06 | 2024-06-14 | 삼성전자주식회사 | Computing apparatus and operating method thereof |
| KR102737112B1 (en) | 2022-12-06 | 2024-12-02 | 삼성전자주식회사 | Computing apparatus and operating method thereof |
| CN116127255A (en)* | 2022-12-14 | 2023-05-16 | 北京登临科技有限公司 | Convolution operation circuit and related circuit or device with same |
| CN116127255B (en)* | 2022-12-14 | 2023-10-03 | 北京登临科技有限公司 | Convolution operation circuit and related circuit or device with same |
| CN117806590A (en)* | 2023-12-18 | 2024-04-02 | 上海无问芯穹智能科技有限公司 | A matrix multiplication hardware architecture |
| US12287844B1 (en) | 2023-12-18 | 2025-04-29 | Shanghai Infinigence Ai Intelligent Technology Co., Ltd. | Matrix multiplication hardware architecture |
Also Published As
| Publication number | Publication date |
|---|---|
| CN110852416B (en) | 2022-10-04 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN110852416B (en) | CNN hardware-accelerated computing method and system based on low-precision floating-point data representation | |
| CN110852434B (en) | CNN quantization method, forward calculation method and hardware device based on low-precision floating point numbers | |
| CN105844330B (en) | The data processing method and neural network processor of neural network processor | |
| CN111832719A (en) | A Fixed-Point Quantized Convolutional Neural Network Accelerator Computing Circuit | |
| CN110598839A (en) | Convolutional neural network system and method for quantizing convolutional neural network | |
| CN110880038A (en) | System for accelerating convolution calculation based on FPGA and convolution neural network | |
| CN108021537A (en) | A kind of softmax implementations based on hardware platform | |
| CN107330515A (en) | A device and method for performing forward operation of artificial neural network | |
| Wang et al. | Sole: Hardware-software co-design of softmax and layernorm for efficient transformer inference | |
| CN109002881A (en) | The fixed point calculation method and device of deep neural network based on FPGA | |
| CN110555516B (en) | Implementation method of low-latency hardware accelerator for YOLOv2-tiny neural network based on FPGA | |
| CN112434801B (en) | A Convolution Operation Acceleration Method for Weight Splitting According to Bit Accuracy | |
| CN113283587A (en) | Winograd convolution operation acceleration method and acceleration module | |
| CN115982528A (en) | Approximate precoding convolution operation method and system based on Booth algorithm | |
| CN114418057A (en) | Operation method and related equipment of convolutional neural network | |
| CN110110852B (en) | Method for transplanting deep learning network to FPAG platform | |
| CN109165006B (en) | Design optimization and hardware implementation method and system of Softmax function | |
| CN113419779B (en) | Scalable multi-precision data pipeline system and method | |
| CN110210611B (en) | A Dynamic Adaptive Data Truncation Method for Convolutional Neural Network Computing | |
| WO2022170811A1 (en) | Fixed-point multiply-add operation unit and method suitable for mixed-precision neural network | |
| JP2020098469A (en) | Arithmetic processing device and method for controlling arithmetic processing device | |
| CN114154631A (en) | Convolutional neural network quantization implementation method and device based on FPGA | |
| US20240345806A1 (en) | Computing apparatus and method, electronic device and storage medium | |
| US20210044303A1 (en) | Neural network acceleration device and method | |
| CN113516235A (en) | A Deformable Convolution Accelerator and Deformable Convolution Acceleration Method |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| TA01 | Transfer of patent application right | ||
| TA01 | Transfer of patent application right | Effective date of registration:20200609 Address after:Room 305, building 9, meizhuang new village, 25 Yangzi Jiangbei Road, Weiyang District, Yangzhou City, Jiangsu Province 225000 Applicant after:Liang Lei Address before:610094 China (Sichuan) Free Trade Pilot Area, Chengdu City, Sichuan Province, 1402, Block 199, Tianfu Fourth Street, Chengdu High-tech Zone Applicant before:Chengdu Star Innovation Technology Co.,Ltd. | |
| GR01 | Patent grant | ||
| GR01 | Patent grant | ||
| TR01 | Transfer of patent right | ||
| TR01 | Transfer of patent right | Effective date of registration:20221220 Address after:518017 1110, Building 3, Northwest Shenjiu Science and Technology Pioneer Park, the intersection of Taohua Road and Binglang Road, Fubao Community, Fubao Street, Shenzhen, Guangdong Patentee after:Shenzhen biong core technology Co.,Ltd. Address before:Room 305, Building 9, Meizhuang New Village, No. 25, Yangzijiang North Road, Weiyang District, Yangzhou City, Jiangsu Province, 225000 Patentee before:Liang Lei | |
| EE01 | Entry into force of recordation of patent licensing contract | ||
| EE01 | Entry into force of recordation of patent licensing contract | Application publication date:20200228 Assignee:Suzhou Heyu Finance Leasing Co.,Ltd. Assignor:Shenzhen biong core technology Co.,Ltd. Contract record no.:X2025980012788 Denomination of invention:A CNN hardware acceleration computing method and system based on the data representation of low-precision floating-point numbers Granted publication date:20221004 License type:Exclusive License Record date:20250711 | |
| PE01 | Entry into force of the registration of the contract for pledge of patent right | ||
| PE01 | Entry into force of the registration of the contract for pledge of patent right | Denomination of invention:A CNN hardware acceleration computing method and system based on the data representation of low-precision floating-point numbers Granted publication date:20221004 Pledgee:Suzhou Heyu Finance Leasing Co.,Ltd. Pledgor:Shenzhen biong core technology Co.,Ltd. Registration number:Y2025980028513 |