CN110826145B - Automobile multi-parameter operation condition design method based on heuristic Markov chain evolution - Google Patents

Abstract

The invention discloses a method for designing multi-parameter operation working conditions of an automobile based on a hyper-heuristic Markov chain evolution. Firstly, defining a strategy boundary variable and designing a plurality of strategy factors based on an operation operator meeting Markov property and by combining strategy functions and diversity; then, based on expected operation conditions, a strategy factor and working condition sequence distribution mechanism and a working condition population and optimal working condition sequence updating mechanism are formulated, and an evaluation function is designed; and finally, selecting a genetic algorithm as a high-level heuristic algorithm, taking the process of applying the multi-strategy factors to the working condition sequence population as a low-level heuristic algorithm, and establishing the high-efficiency multi-parameter working condition design method. The self-adaptability of the policy factor proportion in the design framework enables the operation efficiency to be further obviously improved compared with a Markov chain evolution method, and the method is strong in transportability and convenient for actual operation and use of automobile engineers.

Description

Translated fromChinese

基于超启发式马氏链进化的汽车多参数运行工况设计方法Design method of automobile multi-parameter operating conditions based on hyperheuristic Markov chain evolution

技术领域technical field

本发明涉及一种汽车运行工况设计方法，尤其涉及一种基于超启发式马氏链进化的汽车多参数运行工况设计方法。The invention relates to a method for designing an automobile operating condition, in particular to a method for designing a multi-parameter operating condition of an automobile based on a hyper-heuristic Markov chain evolution.

背景技术Background technique

汽车代表性运行工况的生成是当前汽车测试、评估、控制以及预测等研究的基本需求。为提高适应性，需要多方面考虑实际影响因素，例如，混合动力汽车的动力元件尺寸的选择对道路坡度具有敏感性，因此需要考虑含道路坡度的工况设计。又如，对运行工况进行仿真验证时，仅考虑速度和加速度两参数的代表性工况设计，由于车辆传动系仿真软件中换挡策略固定，与实际驾驶员换挡风格存在差距，导致设计工况很难满足发动机负荷一致性要求。因此，需要考虑包含挡位、转速和转矩参数的工况设计。总之，设计多参数车辆运行工况的需求变得强烈。The generation of vehicle representative operating conditions is the basic requirement of current research on vehicle testing, evaluation, control and prediction. In order to improve the adaptability, it is necessary to consider the actual influencing factors in many aspects. For example, the selection of the size of the power components of the hybrid vehicle is sensitive to the road gradient, so the design of the working conditions including the road gradient needs to be considered. For another example, when simulating and verifying the operating conditions, only the representative operating conditions of the two parameters of speed and acceleration are considered. Due to the fixed shifting strategy in the vehicle powertrain simulation software, there is a gap with the actual driver's shifting style, which leads to the design of It is difficult to meet the requirements of engine load consistency under working conditions. Therefore, it is necessary to consider the design of operating conditions including gear, speed and torque parameters. In conclusion, the need to design multi-parameter vehicle operating conditions becomes strong.

当前多参数工况设计方法包含基于马尔可夫链方法及其衍生的智能方法两类主流方法。虽然现有文献广泛通过建立速度、加速度和坡度三参数的马尔可夫链模型，应用于评估混合动力汽车能量源的额定功率以及优化传动系等。然而，由于马尔可夫链随机生成的本质，该方法设计高维运行工况的优势并不那么明显。针对多维马尔可夫链模型仿真时间过长的问题，虽然可以通过增大参量步长减小状态数，例如三维度马尔可夫链模型中速度、加速度和坡度的步长相对于二维度速度和坡度的步长适当增大，进而缩短仿真时长，但会导致生成明显波动的工况序列。此外，随着设计精度要求更高和更多参数工况设计需求，马尔可夫链设计方法远不能应对。比较有潜力设计高维运行工况的方法是马尔可夫链进化方法，该方法将马尔可夫链与进化方法结合，设计满足马尔可夫性的操作策略，使工况设计过程具有方向性从而逼近目标工况；相对于马尔可夫链方法，该方法可显著提高设计工况的运行效率。然而，马尔可夫链进化方法存在两个问题，一是无法调整算子占比，即缺少自适应性能；二是算法的灵活性差，即工程应用时，设计的新策略因子需移植到传统遗传算法或者其他功能中。因此有必要继续对现有的马尔可夫链进化方法进行改进。The current multi-parameter working condition design method includes two mainstream methods based on Markov chain method and its derived intelligent method. Although the existing literature is widely used to establish the Markov chain model with three parameters of speed, acceleration and slope, it is applied to evaluate the rated power of the energy source of hybrid electric vehicles and optimize the power train. However, due to the randomly generated nature of Markov chains, the advantage of this method for designing high-dimensional operating cases is not so obvious. For the problem that the simulation time of the multi-dimensional Markov chain model is too long, although the number of states can be reduced by increasing the parameter step size, for example, the step size of velocity, acceleration and gradient in the three-dimensional Markov chain model is relative to the two-dimensional velocity and gradient. The step size is appropriately increased to shorten the simulation time, but it will result in a significantly fluctuating sequence of operating conditions. In addition, with the design requirements of higher design accuracy and more parameter conditions, the Markov chain design method is far from being able to cope. A more promising method for designing high-dimensional operating conditions is the Markov chain evolution method, which combines the Markov chain with the evolutionary method to design an operating strategy that satisfies the Markov property, so that the operating condition design process is directional. Approach the target condition; compared to the Markov chain method, this method can significantly improve the operating efficiency of the design condition. However, there are two problems in the Markov chain evolution method. One is that the proportion of operators cannot be adjusted, that is, it lacks self-adaptive performance; the other is that the algorithm has poor flexibility, that is, when engineering applications, the designed new strategy factors need to be transplanted to traditional genetics. algorithms or other functions. Therefore, it is necessary to continue to improve the existing Markov chain evolution methods.

发明内容SUMMARY OF THE INVENTION

本发明所要解决的技术问题是提供一种基于超启发式马氏链进化的汽车多参数运行工况设计方法，能够有效解决策略因子占比的自适应调整和工程应用灵活性的问题，拓宽当前方法设计工况的参数维度，且能提高设计效率的巨大潜力。The technical problem to be solved by the present invention is to provide an automobile multi-parameter operating condition design method based on hyperheuristic Markov chain evolution, which can effectively solve the problems of self-adaptive adjustment of the proportion of strategy factors and flexibility of engineering application, broaden the current The parameter dimension of the method design case, and it has great potential to improve the design efficiency.

本发明为解决上述技术问题而采用的技术方案是提供一种基于超启发式马氏链进化的汽车多参数运行工况设计方法，包括如下步骤：S1)基于马尔可夫链进化方法的操作策略，通过定义策略边界变量，选定满足马尔可夫性的多个策略因子；S2)设计策略因子与工况序列的分配机制和更新机制，进而生成基于期望运行工况的评价函数；S3)采用传统遗传算法作为超启发式架构的高层控制算法，进化迭代由策略因子序列组成的策略因子种群，最终获得期望评价值的运行工况。The technical solution adopted by the present invention to solve the above-mentioned technical problems is to provide a method for designing a multi-parameter operating condition of an automobile based on the evolution of the hyper-heuristic Markov chain, which includes the following steps: S1) an operation strategy based on the evolution method of the Markov chain , by defining the strategy boundary variables, select multiple strategy factors that satisfy the Markov property; S2) design the allocation mechanism and update mechanism of strategy factors and the sequence of operating conditions, and then generate an evaluation function based on the expected operating conditions; S3) adopt As a high-level control algorithm with a hyper-heuristic architecture, the traditional genetic algorithm evolves and iterates the strategy factor population composed of strategy factor sequences, and finally obtains the operating conditions of the expected evaluation value.

进一步地，所述步骤S1包括：Further, the step S1 includes:

步骤S11：基于车辆实际的采集数据，设定每个参数的步长，划分各个参数状态，统计多参数的状态转移概率矩阵P，并利用马尔可夫链随机模拟方法生成目标工况长度L且起止状态为怠速的候选工况；Step S11: Based on the actual collected data of the vehicle, set the step size of each parameter, divide each parameter state, count the multi-parameter state transition probability matrix P, and use the Markov chain stochastic simulation method to generate the target operating condition length L and The start-stop state is the candidate working condition of idle speed;

步骤S12：基于步骤S11统计的多参数状态转移概率矩阵，设计任意两条工况序列发生等长交叉段交换时，生成个体序列一定满足马尔可夫链状态转移关系的交叉算子策略，以及将基于步骤S11中候选工况随机选择一条工况序列代替要变异的工况序列的过程，作为变异算子策略；Step S12: Based on the multi-parameter state transition probability matrix calculated in step S11, design a crossover operator strategy that generates an individual sequence that must satisfy the Markov chain state transition relationship when any two operating condition sequences are exchanged with an equal-length crossover segment, and the The process of randomly selecting a sequence of working conditions to replace the sequence of working conditions to be mutated based on the candidate working conditions in step S11 is used as the mutation operator strategy;

步骤S13：将任意两条工况序列发生交换的状态位置定义为策略边界变量R，设定策略边界变量向量R＝[R₁,R₂,...,R_i,...,R_j,...,R_n]，i,j∈[1,n]，且R_i≠R_j，n为不同的R个数；Step S13: Define the state position where any two working condition sequences are exchanged as the strategy boundary variable R, and set the strategy boundary variable vector R=[R₁ , R₂ ,...,R_i ,...,R_j ,...,R_n ], i,j∈[1,n], and R_i ≠R_j , n is the number of different Rs;

步骤S14：依据步骤S13的向量R，首先将基于步骤S12中满足马尔可夫性的两种算子策略的所有等长可交换段划分成多个不同的n+1组，n+1个组的等长可交换段产生n+1个等长交叉算子策略，即进化过程中能发挥局部搜索、全局搜索能力的n+1个等长策略因子，其次，根据设计工况长度偏差保持在一定阈值T_r范围内和向量R，n+1组的非等长可交换段产生n+1个非等长策略因子；最后，包含发挥工况状态更新能力的变异算子策略共2n+3个策略因子；Step S14: According to the vector R in step S13, firstly divide all the commutative segments of equal length based on the two operator strategies satisfying the Markov property in step S12 into multiple different n+1 groups, n+1 groups. The equal-length exchangeable segment generates n+1 equal-length crossover operator strategies, that is, n+1 equal-length strategy factors that can exert local search and global search capabilities in the evolution process. Secondly, according to the design conditions, the length deviation is kept at Within the range of a certain threshold T_r and the non-equal-length exchangeable segments of the vector R and n+1 groups, n+1 non-equal-length strategy factors are generated; finally, there are 2n+3 mutation operator strategies including the ability to update the state of the working condition. a strategic factor;

步骤S15：基于步骤S14获得的2n+3个策略因子，设定各个策略因子占比p_r，并随机组成长度为t的策略因子序列Y(θ)＝[θ¹,θ²,...,θⁱ,...,θ^t]，其中t＞(2n+3)，θ∈[θ_e1,θ_e2,…,θ_e(n+1),θ_ne1,θ_ne2,…,θ_ne(n+1),θ_m]，θ_e1,θ_e2,…,θ_e(n+1)对应等长交叉策略因子，θ_ne1,θ_ne2,…,θ_ne(n+1)对应非等长交叉策略因子，θ_m为完全变异算子；同时构建由工况状态序列随机组成的种群大小为t的工况序列种群Pop(²){X}＝[X₁；X₂；...；X_t]，其中X为工况状态序列，在工况序列初始种群Pop(²){X}的条件下，设定运行工况的评价指标和相对偏差阈值T_r，借助满意准则，计算工况序列种群的初始函数值F{X}＝[F(X₁),F(X₂),...,F(X_t)]，并由公式(1)获取该工况序列种群最佳函数值F(X_*)和最佳工况序列X_*；Step S15: Based on the 2n+3 strategy factors obtained in step S14, set the proportion pr of each strategy factor, and randomly form a strategy factor sequence of length_t Y(θ)=[θ¹ ,θ² ,... ,θⁱ ,...,θ^t ], where t>(2n+3), θ∈[θ_e1 ,θ_e2 ,…,θ_e(n+1) ,θ_ne1 ,θ_ne2 ,…,θ_{ne (n+1)} ,θ_m ], θ_e1 ,θ_e2 ,…,θ_e(n+1) correspond to equal-length crossover strategy factors, θ_ne1 ,θ_ne2 ,…,θ_ne(n+1) correspond to non-equal length Long crossover strategy factor, θ_m is a complete mutation operator; at the same time, a population Pop(² ){X}=[X₁ ; X₂ ;... ; X_t ], where X is the state sequence of working conditions, under the condition of the initial population Pop(² ){X} of the working condition sequence, set the evaluation index of the working condition and the relative deviation threshold T_r , with the help of the satisfaction criterion, calculate The initial function value F{X}=[F(X₁ ), F(X₂ ),..., F(X_t )] of the working condition sequence population, and the maximum value of the working condition sequence population is obtained by formula (1). The optimal function value F(X_* ) and the optimal operating condition sequence X_* ;

F(X_*)＝min(F{X})(1)。F(X_* )=min(F{X})(1).

进一步地，所述步骤S11中的参数包含速度、加速度和道路坡度，L的取值为1800s；所述步骤S13中n的取值为6，R的取值为[10,20,50,100,150,200]；所述步骤S13中T_r的取值为10％；所述步骤S13中p_r的取值为(1:1:1:2:3:3:3:1:1:1:2:3:3:3:2)，t的取值为30。Further, the parameters in the step S11 include speed, acceleration and road gradient, and the value of L is 1800s; the value of n in the step S13 is 6, and the value of R is [10, 20, 50, 100, 150, 200]; In the step_S13 , the value of Tr is 10%; in the step_S13 , the value of pr is (1:1:1:2:3:3:3:1:1:1:2:3: 3:3:2), the value of t is 30.

进一步地，所述步骤S2包括：Further, the step S2 includes:

步骤S21：在当前第k条策略因子序列Y(θ)下，对步骤S15的工况序列个体的函数值F{X}进行轮盘赌操作，产生新工况序列个体排序的种群

并将种群中工况序列一一对应分配给策略因子序列Y(θ)中策略因子，进行策略操作，生成工况序列子代种群

计算工况序列种群

的函数值

Step S21: Under the current k-th strategy factor sequence Y(θ), perform a roulette operation on the function value F{X} of the individual working condition sequence in step S15, and generate a population sorted by the individual working condition sequence

Assign the working condition sequences in the population to the strategy factors in the strategy factor sequence Y(θ) one-to-one, and perform the strategy operation to generate the working condition sequence subpopulation.

Calculate the population of the sequence of operating conditions

the function value of

步骤S22：更新种群Pop⁽²⁾{X}和函数值F{X}，将子代种群

和函数值

分别替换父代种群Pop⁽²⁾{X}和种群函数值F{X}；按照公式(2)获取工况序列子代种群

的最佳函数值

和最佳序列

Step S22: Update the population Pop⁽²⁾ {X} and the function value F{X}, and update the offspring population

and function value

Replace the parent population Pop⁽²⁾ {X} and the population function value F{X} respectively; obtain the daughter population of the working condition sequence according to formula (2)

The best function value of

and the best sequence

当

通过将

赋给X_*更新最佳工况序列X_*，通过将

赋给F(X_*)更新最佳函数值F(X_*)；when

by putting

Assign X_* to update the optimal case sequence X_* by putting

Assign F(X_* ) to update the best function value F(X_* );

当

时，将X_*赋到种群Pop⁽²⁾{X}中

在

位置，将对应函数值

赋到函数值F(X_*)的相同位置，实现最佳工况序列X_*和最佳函数值F(X_*)的更新；when

, assign X_* to the population Pop⁽²⁾ {X}

exist

position, which will correspond to the function value

Assign it to the same position of the function value F(X_* ) to realize the update of the optimal operating condition sequence X_* and the optimal function value F(X_* );

步骤S23：输出当前第k条策略序列Y(θ)下的最佳函数值F(X_*)。Step S23: Output the optimal function value F(X_* ) under the current k-th strategy sequence Y(θ).

进一步地，所述步骤S3包括：Further, the step S3 includes:

步骤S31：基于步骤S15的策略因子序列，随机组成大小为K_max的初始策略因子序列种群

计算策略因子序列个体函数值

Step S31: Based on the strategy factor sequence of step S15, randomly form an initial strategy factor sequence population of size_Kmax

Calculate the individual function value of the policy factor sequence

步骤S32：根据策略因子序列函数值F{Y}，按照默认的精英概率p_d，选择保留当前种群中最佳的K_max×p_d个精英个体，然后对序列个体进行传统选择算子操作；Step S32: According to the strategy factor sequence function value F{Y}, according to the default elite probability p_d , select and retain the best K_max ×p_d elite individuals in the current population, and then perform the traditional selection operator operation on the sequence individuals;

步骤S33：按照默认交叉概率p_c，在(K_max-K_max×p_d)个剩余个体中选择(K_max-K_max×p_d)×p_c个序列个体进行随机两点交叉操作，生成(K_max-K_max×p_d)×p_c个交叉个体；Step S33: According to the default crossover probability p_c , select (K_max -K_max ×p_d )×p_c sequence individuals from the (K_max -K_max ×p_d ) remaining individuals to perform random two-point crossover operation to generate (K_max -K_max ×p_d ) × p_c crossover individuals;

步骤S34：对剩余K_max-K_max×p_d-(K_max-K_max×p_d)×p_c个个体进行单点变异操作，生成K_max-K_max×p_d-(K_max-K_max×p_d)×p_c个变异个体；Step S34: Perform single-point mutation operation on the remaining K_max -K_max ×p_d -(K_max -K_max ×p_d )×pc individuals to generate K_max -K_max ×p_d -₍ K_max -K_max ×p_d )×p_c variant individuals;

步骤S35：由步骤S32的精英个体、步骤S33的交叉个体和步骤S34的变异个体组成新的策略因子序列种群；Step S35: A new strategy factor sequence population is formed by the elite individuals in step S32, the crossover individuals in step S33 and the mutant individuals in step S34;

步骤S36：判断输出最佳评价值F(Y_*)是否达到期望阈值T_r范围，若F(Y_*)≤T_r，此时F(Y_*)＝F(X_*)，其中Y_*为最佳策略序列组合，执行步骤S37，否则，返回步骤S32；Step S36: Determine whether the output best evaluation value F(Y_* ) reaches the expected threshold Tr range, if F(Y_*)≤Tr , then F(Y_* )=F(X_* ), where Y_* is For the best strategy sequence combination, go to step S37, otherwise, go back to step S32;

步骤S37：将最佳工况状态序列X_*解码，并输出多参数期望运行工况时间序列。Step S37: Decode the optimal operating condition state sequence X_* , and output the multi-parameter expected operating operating condition time series.

进一步地，所述步骤S31中K_max的取值为24。Further, the value of K_max in the step S31 is 24.

本发明对比现有技术有如下的有益效果：本发明将超启发式架构与马尔可夫链进化方法进行结合，有效解决面向汽车运行工况设计的策略因子占比的自适应调整和程序封装的问题，本发明能够拓宽当前方法设计工况的参数维度，且能提高设计效率的巨大潜力。此外，本发明提出的框架可移植性强，为汽车工程师的操作使用提供支持。Compared with the prior art, the present invention has the following beneficial effects: the present invention combines the hyperheuristic architecture with the Markov chain evolution method, and effectively solves the problem of self-adaptive adjustment and program encapsulation of the ratio of strategy factors for the design of automobile operating conditions. The problem is that the present invention can widen the parameter dimension of the design conditions of the current method, and has a great potential to improve the design efficiency. In addition, the framework proposed by the present invention is highly portable, and provides support for the operation and use of automobile engineers.

附图说明Description of drawings

图1为本发明超启发式马尔可夫链进化方法框图；Fig. 1 is the block diagram of the super-heuristic Markov chain evolution method of the present invention;

图2为本发明设计结果的速度随着时间的变化曲线；Fig. 2 is the change curve of the speed of the design result of the present invention with time;

图3为本发明设计结果的加速度随着时间的变化曲线；Fig. 3 is the change curve of the acceleration with time of the design result of the present invention;

图4为本发明设计结果的坡度随着时间的变化曲线；Fig. 4 is the change curve of the gradient with time of the design result of the present invention;

图5为本发明随机10个策略因子种群的输出期望运行工况时的策略因子平均个数分布柱状图；Fig. 5 is a histogram of the distribution of the average number of strategy factors when the output expected operating conditions of 10 random strategy factor populations of the present invention;

图6为本发明超启发式马尔可夫链进化方法和马尔可夫链进化方法各10次设计试验的运行时间柱状图。FIG. 6 is a histogram of the running time of 10 design experiments each of the hyperheuristic Markov chain evolution method and the Markov chain evolution method of the present invention.

具体实施方式Detailed ways

下面结合附图和实施例对本发明作进一步的描述。The present invention will be further described below with reference to the accompanying drawings and embodiments.

图1为本发明超启发式马尔可夫链进化方法框图。FIG. 1 is a block diagram of the hyperheuristic Markov chain evolution method of the present invention.

请参见图1，本发明提供的基于超启发式马氏链进化的汽车多参数运行工况设计方法，包括以下步骤：Referring to Fig. 1, the method for designing a multi-parameter operating condition of an automobile based on the evolution of the hyper-heuristic Markov chain provided by the present invention includes the following steps:

步骤S1：基于马尔可夫链进化方法的操作策略，通过定义策略边界变量，设计满足马尔可夫性的多个策略因子，具体过程包含步骤S11到步骤S14。Step S1: Based on the operation strategy of the Markov chain evolution method, by defining strategy boundary variables, a plurality of strategy factors satisfying the Markov property are designed, and the specific process includes steps S11 to S14.

步骤S11：基于车辆实际的采集数据，包含速度、加速度和道路坡度等参数，设定速度、加速度和道路坡度步长以及最值，其中Δv＝0.5m/s，Δa＝0.1m/s²，Δg＝1％，v_min＝0m/s，v_max＝35m/s，a_min＝-2m/s²，a_max＝2m/s²，g_min＝-10％和g_max＝10％，划分各个参数状态，按照公式(3)统计三参数的状态转移概率矩阵P，并利用马尔可夫链随机模拟方法生成目标工况长度L且起止状态为怠速的候选工况；其中L为1800s；Step S11: Based on the actual collected data of the vehicle, including parameters such as speed, acceleration and road gradient, set the step size and maximum value of the speed, acceleration and road gradient, where Δv=0.5m/s, Δa=0.1m/s² , Δg=¹ %, vmin=0m/s,_vmax =35m/s,_amin =_-2m /s2,_amax =^2m /s2,_gmin =-10% and_gmax =10%, divided For each parameter state, the state transition probability matrix P of the three parameters is counted according to formula (3), and the Markov chain stochastic simulation method is used to generate the candidate working condition with the target working condition length L and the starting and ending state is idle speed; where L is 1800s;

式中：

为一维空间状态个数,N_i′j′为一维空间状态s_i′到一维空间状态s_j′的转移次数，N_i′为一维空间状态s_i′到其他状态的转移次数和，p_i′j′为一维空间状态s_i′到一维空间状态s_j′的转移概率，S为空间状态集合；where:

is the number of one-dimensional space states, N_i'j' is the transition times from one-dimensional space state_si' to one-dimensional space state s_j ', and N_i' is the transition times from one-dimensional space state_si' to other states and, p_i'j' is the transition probability from one-dimensional space state_si' to one-dimensional space state s_j' , S is the set of space states;

在w时刻的状态s_w按照公式(4)计算The state s_w at time w is calculated according to formula (4)

s_w＝m_w+(u_w-1)×M+(h_w-1)×M×N (4)s_w =m_w +(u_w -1)×M+(h_w -1)×M×N (4)

式中：m_w-w时刻的速度状态，u_w-w时刻的加速度状态，h_w-w时刻的坡度状态，M-速度状态个数，N-加速度状态个数，计算方式分别参见公式(5)到公式(9)。In the formula: the speed state at the time of m_w -w, the acceleration state at the time of u_w -w, the slope state at the time of h_w -w, M - the number of speed states, N - the number of acceleration states, and the calculation methods are shown in the formula ( 5) to formula (9).

步骤S12：基于步骤S11统计的三参数状态转移概率矩阵P，设计任意两条工况序列发生等长交叉段交换时，生成个体序列一定满足马尔可夫链状态转移关系的交叉算子策略，以及将基于步骤S11中候选工况随机选择一条工况序列代替要变异的工况序列的过程，作为变异算子策略；Step S12: Based on the three-parameter state transition probability matrix P calculated in Step S11, design a crossover operator strategy that generates an individual sequence that must satisfy the Markov chain state transition relationship when any two operating condition sequences are exchanged with equal-length crossover segments, and The process of randomly selecting a working condition sequence to replace the working condition sequence to be mutated based on the candidate working conditions in step S11 is used as the mutation operator strategy;

步骤S13：将任意两条工况序列发生交换的状态位置定义为策略边界变量R，设定策略边界变量向量R＝[R₁,R₂,...,R_i,...,R_j,...,R_n]，i,j∈[1,n]，且R_i≠R_j，n为不同的R个数；其中R为[10,20,50,100,150,200]，n为6；Step S13: Define the state position where any two working condition sequences are exchanged as the strategy boundary variable R, and set the strategy boundary variable vector R=[R₁ , R₂ ,...,R_i ,...,R_j ,...,R_n ], i,j∈[1,n], and R_i ≠R_j , n is the number of different R; where R is [10, 20, 50, 100, 150, 200], n is 6;

步骤S14：依据步骤S13的向量R，将基于步骤S12中满足马尔可夫性的两种算子策略的所有等长可交换段划分成多个不同的n+1组，n+1组的等长可交换段产生n+1个等长交叉算子策略，即进化过程中能发挥局部搜索、全局搜索能力的n+1个等长策略因子，其次，根据设计工况长度偏差保持在一定阈值T_r范围内和向量R，n+1个组的非等长可交换段产生n+1个非等长策略因子；最后，包含发挥工况状态更新能力的变异算子策略共2n+3个策略因子；即对应着15个策略因子，分别是交叉段在[1:10]s，[10:20]s，[20:50]s，[50:100]s，[100:150]s，[150:200]s，[>200]s区间的等长交叉策略因子，和交叉段在[1:10]s，[10:20]s，[20:50]s，[50:100]s，[100:150]s，[150:200]s，[>200]s区间的非等长交叉策略因子以及完全变异策略因子，T_r为10％；Step S14: According to the vector R in step S13, divide all the commutative segments of equal length based on the two operator strategies satisfying the Markov property in step S12 into multiple different n+1 groups, n+1 groups, etc. The long exchangeable segment generates n+1 equal-length crossover operator strategies, that is, n+1 equal-length strategy factors that can exert local search and global search capabilities in the evolution process. Secondly, the length deviation is kept at a certain threshold according to the design conditions. Within the range of T_r and the vector R, the non-equal-length exchangeable segments of n+1 groups generate n+1 non-equal-length strategy factors; finally, there are 2n+3 mutation operator strategies including the ability to update the state of the working condition. Strategy factors; that is, corresponding to 15 strategy factors, which are the intersections at [1:10]s, [10:20]s, [20:50]s, [50:100]s, [100:150]s , [150:200]s, [>200]s interval isometric crossover strategy factor, and crossover segments at [1:10]s, [10:20]s, [20:50]s, [50:100 ]s, [100:150]s, [150:200]s, [>200]s interval non-isometric crossover strategy factor and full mutation strategy factor, T_r is 10%;

步骤S15：基于步骤S14获得的2n+3个策略因子，设定各个策略因子占比p_r，并随机组成长度为t的策略因子序列Y(θ)＝[θ¹,θ²,…,θⁱ,...,θ^t]，其中t＞(2n+3)，θ∈[θ_e1,θ_e2,...,θ_e(n+1),θ_ne1,θ_ne2,...,θ_ne(n+1),θ_m]，θ_e1,θ_e2,...,θ_e(n+1)对应等长交叉策略因子，θ_ne1,θ_ne2,...,θ_ne(n+1)对应非等长交叉策略因子，θ_m为完全变异算子；同时构建由工况状态序列随机组成的种群大小为t的工况序列种群Pop⁽²⁾{X}＝[X₁；X₂；...；X_t]，其中X为工况状态序列，在工况序列初始种群Pop⁽²⁾{X}的条件下，设定运行工况的评价指标和相对偏差阈值T_r，借助满意函数准则，计算工况序列种群的初始函数值F{X}＝[F(X₁),F(X₂),...,F(X_t)]，并由公式(10)获取该工况序列种群最佳函数值F(X_*)和最佳工况序列X_*；其中p_r为(1:1:1:2:3:3:3:1:1:1:2:3:3:3:2)，t为30；Step S15: Based on the 2n+3 strategy factors obtained in Step S14, set the proportion pr of each strategy factor, and randomly form a strategy factor sequence of length_t Y(θ)=[θ¹ ,θ² ,...,θⁱ ,...,θ^t ], where t>(2n+3), θ∈[θ_e1 ,θ_e2 ,...,θ_e(n+1) ,θ_ne1 ,θ_ne2 ,..., θ_ne(n+1) ,θ_m ], θ_e1 ,θ_e2 ,...,θ_e(n+1) correspond to equal-length crossover strategy factors, θ_ne1 ,θ_ne2 ,...,θ_{ne(n +1)} Corresponding to the non-equal-length crossover strategy factor, θ_m is a complete mutation operator; at the same time, construct a working condition sequence population Pop⁽²⁾ {X}=[X₁ , which is randomly composed of working condition state sequences and whose population size is t; X₂ ;...;X_t ], where X is the state sequence of working conditions, under the condition of the initial population Pop⁽²⁾ {X} of the working condition sequence, set the evaluation index of the working condition and the relative deviation threshold_Tr , with the help of the satisfaction function criterion, calculate the initial function value F{X}=[F(X₁ ), F(X₂ ),..., F(X_t )] of the population of the working condition sequence, and by formula (10) Obtain the optimal function value F(X_* ) of the population of the working condition sequence and the optimal working condition sequence X_* ; where p_r is (1:1:1:2:3:3:3:1:1:1:2 :3:3:3:2), t is 30;

F(X_*)＝min(F{X}) (10)F(X_* )=min(F{X}) (10)

其中，设定的评价指标包含：怠速时间比例，加速时间比例，匀速时间比例，减速时间比例，平均速度，平均行驶速度，行驶速度标准差，单位距离上的正加速动能、平均爬坡度、平均下坡度、速度和加速度的概率分布相关系数，共11个。Among them, the set evaluation indicators include: idle speed ratio, acceleration time ratio, uniform speed time ratio, deceleration time ratio, average speed, average driving speed, driving speed standard deviation, positive acceleration kinetic energy per unit distance, average grade, average There are 11 correlation coefficients for probability distribution of downhill gradient, speed and acceleration.

步骤S2：设计策略因子与工况序列的分配机制和更新机制，进而设计基于期望运行工况的评价函数，具体过程包含步骤S21到步骤S23。Step S2: Design the allocation mechanism and update mechanism of the strategy factor and the sequence of operating conditions, and then design the evaluation function based on the expected operating conditions. The specific process includes steps S21 to S23.

步骤S21：在当前第k条策略因子序列Y(θ)下，对步骤S15的工况序列个体的函数值F{X}进行轮盘赌操作，产生新工况序列个体排序的种群

并将种群中工况序列一一对应分配给策略因子序列Y(θ)中策略因子，进行策略操作，生成工况序列子代种群

计算工况序列种群

的函数值

Step S21: Under the current k-th strategy factor sequence Y(θ), perform a roulette operation on the function value F{X} of the individual working condition sequence in step S15, and generate a population sorted by the individual working condition sequence

Assign the working condition sequences in the population to the strategy factors in the strategy factor sequence Y(θ) one-to-one, and perform the strategy operation to generate the working condition sequence subpopulation.

Calculate the population of the sequence of operating conditions

the function value of

步骤S22：更新种群Pop⁽²⁾{X}和函数值F{X}，即将子代种群

和函数值

分别替换父代种群Pop⁽²⁾{X}和种群函数值F{X}；按照公式(11)获取工况序列子代种群

的最佳函数值

和最佳序列

Step S22: Update the population Pop⁽²⁾ {X} and the function value F{X}, that is, the descendant population

and function value

Replace the parent population Pop⁽²⁾ {X} and the population function value F{X} respectively; obtain the child population of the working condition sequence according to formula (11)

The best function value of

and the best sequence

当

通过将

赋给X_*更新最佳工况序列X_*，通过将

赋给F(X_*)更新最佳函数值F(X_*)，当

时，将X_*赋到种群Pop⁽²⁾{X}中

在

的位置，将对应函数值

赋到函数值F(X_*)的相同位置的，实现最佳工况序列X_*和最佳函数值F(X_*)的更新；when

by putting

Assign X_* to update the optimal case sequence X_* by putting

Assign F(X_* ) to update the optimal function value F(X_* ), when

, assign X_* to the population Pop⁽²⁾ {X}

exist

The position of , will correspond to the function value

If it is assigned to the same position of the function value F(X_* ), the update of the optimal operating condition sequence X_* and the optimal function value F(X_* ) is realized;

步骤S23：输出当前第k策略序列Y(θ)下的最佳函数值F(X_*)。Step S23: Output the optimal function value F(X_* ) under the current kth strategy sequence Y(θ).

步骤S3：采用传统遗传算法作为超启发式架构的高层控制算法，进化迭代由策略因子序列组成的策略因子种群，最终获得期望评价值的运行工况；具体过程包含步骤S31到步骤S37。Step S3: using traditional genetic algorithm as the high-level control algorithm of the super-heuristic architecture, iterates the strategy factor population composed of strategy factor sequences, and finally obtains the operation condition of the expected evaluation value; the specific process includes steps S31 to S37.

步骤S31：基于步骤S15的策略因子序列，随机组成大小为K_max的初始策略因子序列种群

基于步骤S2计算策略因子序列个体函数值

其中K_max为24；Step S31: Based on the strategy factor sequence of step S15, randomly form an initial strategy factor sequence population of size_Kmax

Calculate the individual function value of the strategy factor sequence based on step S2

where K_max is 24;

步骤S32：根据策略因子序列函数值F{Y}，按照默认的精英概率p_d，选择保留当前种群中最佳的K_max×p_d个精英个体，然后对序列个体进行传统选择算子操作；Step S32: According to the strategy factor sequence function value F{Y}, according to the default elite probability p_d , select and retain the best K_max ×p_d elite individuals in the current population, and then perform the traditional selection operator operation on the sequence individuals;

步骤S33：按照默认交叉概率p_c，在(K_max-K_max×p_d)个剩余个体中选择(K_max-K_max×p_d)×p_c个序列个体进行随机两点交叉操作，生成(K_max-K_max×p_d)×p_c个交叉个体；Step S33: According to the default crossover probability p_c , select (K_max -K_max ×p_d )×p_c sequence individuals from the (K_max -K_max ×p_d ) remaining individuals to perform random two-point crossover operation to generate (K_max -K_max ×p_d ) × p_c crossover individuals;

步骤S34：对剩余K_max-K_max×p_d-(K_max-K_max×p_d)×p_c个个体进行单点变异操作，生成K_max-K_max×p_d-(K_max-K_max×p_d)×p_c个变异个体；Step S34: Perform single-point mutation operation on the remaining K_max -K_max ×p_d -(K_max -K_max ×p_d )×pc individuals to generate K_max -K_max ×p_d -₍ K_max -K_max ×p_d )×p_c variant individuals;

步骤S35：由步骤S32的精英个体、步骤S33的交叉个体和步骤S34的变异个体组成新的策略因子序列种群；Step S35: A new strategy factor sequence population is formed by the elite individuals in step S32, the crossover individuals in step S33 and the mutant individuals in step S34;

步骤S36：判断输出最佳评价值F(Y_*)是否达到期望阈值T_r范围，若F(Y_*)≤T_r，此时F(Y_*)＝F(X_*)，其中Y_*为最佳策略序列组合，执行步骤S37，否则，返回步骤S32；Step S36: Determine whether the output best evaluation value F(Y_* ) reaches the expected threshold Tr range, if F(Y_*)≤Tr , then F(Y_* )=F(X_* ), where Y_* is For the best strategy sequence combination, go to step S37, otherwise, go back to step S32;

步骤S37：将最佳工况状态序列X_*解码，并输出多参数期望运行工况时间序列。Step S37: Decode the optimal operating condition state sequence X_* , and output the multi-parameter expected operating operating condition time series.

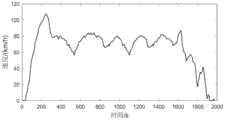
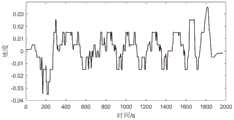
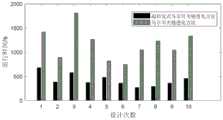
图2至图4为本发明某次试验输出期望运行工况的速度、加速度和道路坡度时间序列；图5为本发明进化由策略因子随机组成10个策略因子种群直至输出期望运行工况时种群中策略因子平均个数分布柱状图，表现了本发明可以实现策略因子自适应组合的特性；图6为本发明超启发式马尔可夫链进化方法和马尔可夫链进化方法各10次设计试验的运行时间柱状图。经统计，本发明较基于马尔可夫链进化的工况设计方法，运行效率提高了63.52％。此外，本发明超启发式架构中每个部分的功能易于区分与封装，可移植性强，为汽车工程师的操作使用提供支持。Fig. 2 to Fig. 4 are the time series of speed, acceleration and road gradient of outputting expected operating conditions in a certain test of the present invention; Fig. 5 is the evolution of the present invention, which is randomly composed of 10 strategy factor populations by strategy factors until the population when expected operating conditions are output The histogram of the distribution of the average number of strategy factors in the present invention shows the characteristic that the present invention can realize the adaptive combination of strategy factors; Fig. 6 is a design experiment of 10 times each of the hyper-heuristic Markov chain evolution method and the Markov chain evolution method of the present invention The running time histogram of . According to statistics, compared with the working condition design method based on Markov chain evolution, the operation efficiency of the present invention is improved by 63.52%. In addition, the function of each part in the hyper-heuristic architecture of the present invention is easy to distinguish and encapsulate, and has strong portability, which provides support for the operation and use of automobile engineers.

虽然本发明已以较佳实施例揭示如上，然其并非用以限定本发明，任何本领域技术人员，在不脱离本发明的精神和范围内，当可作些许的修改和完善，因此本发明的保护范围当以权利要求书所界定的为准。Although the present invention has been disclosed above with preferred embodiments, it is not intended to limit the present invention. Any person skilled in the art can make some modifications and improvements without departing from the spirit and scope of the present invention. Therefore, the present invention The scope of protection shall be defined by the claims.

Claims (3)

1. A method for designing the multi-parameter operation condition of an automobile based on the meta-heuristic Mahalanobis chain evolution is characterized by comprising the following steps:

s1) selecting a plurality of strategy factors meeting Markov property by defining strategy boundary variables based on the operation strategy of the Markov chain evolution method;

s2) designing a strategy factor and a distribution mechanism and an updating mechanism of the working condition sequence, and further generating an evaluation function based on the expected operation working condition;

s3) adopting a traditional genetic algorithm as a high-level control algorithm of a hyper-heuristic architecture, evolving and iterating a strategy factor population consisting of strategy factor sequences, and finally obtaining the operation condition of the expected evaluation value;

the step S1 includes:

step S11: setting the step length of each parameter based on the actual data collected by the vehicle, dividing the states of each parameter, counting a multi-parameter state transition probability matrix P, and generating a target working condition length L by using a Markov chain random simulation method, wherein the starting and stopping states are candidate working conditions of idle speed;

step S12: based on the multi-parameter state transition probability matrix counted in the step S11, when any two working condition sequences are designed to have equal-length cross section exchange, a cross operator strategy that an individual sequence must meet the Markov chain state transition relation is generated, and a process of randomly selecting a working condition sequence to replace the working condition sequence to be mutated based on the candidate working condition in the step S11 is used as a mutation operator strategy;

step S13: defining the state position of any two working condition sequences as a strategy boundary variable R, and setting a strategy boundary variable vector R as [ R ═ R₁,R₂,...,R_i,...,R_j,...,R_n]，i,j∈[1,n]And R is_i≠R_jN is different R numbers;

step S14: according to the vector R of the step S13, firstly dividing all equal-length exchangeable segments of the two operator strategies based on Markov property in the step S12 into a plurality of different n +1 groups, generating n +1 equal-length cross operator strategies by the equal-length exchangeable segments of the n +1 groups, namely n +1 equal-length strategy factors capable of playing local search and global search capacities in the evolution process, and then keeping the length deviation at a certain threshold T according to the design working condition_rThe non-isometric exchangeable segments of the in-range sum vector R, n +1 group generate n +1 non-isometric strategy factors; finally, the mutation operator strategy including the working condition state updating capability has 2n +3 strategy factors;

step S15: based on the 2n +3 policy factors obtained in step S14, each policy factor ratio p is set_rAnd randomly composing a strategy factor sequence Y (theta) with the length t [ theta ]¹,θ²,...,θⁱ,...,θ^t]Where t > (2n +3), θ ∈ [ θ [ ]_e1,θ_e2,...,θ_e(n+1),θ_ne1,θ_ne2,...,θ_ne(n+1),θ_m]，θ_e1,θ_e2,...,θ_e(n+1)Corresponding to an equal length cross policy factor, θ_ne1,θ_ne2,...,θ_ne(n+1)Corresponding to a non-equal length cross policy factor, θ_mIs a complete mutation operator; simultaneously constructing a working condition sequence population Pop with the population size of t and randomly composed of working condition state sequences⁽²⁾{X}＝[X₁；X₂；...；X_t]Wherein X is a working condition state sequence, and the initial population Pop is in the working condition sequence⁽²⁾Setting an evaluation index and a relative deviation threshold T of an operation condition under the condition of { X }_rAnd calculating an initial function value F { X } - [ F (X) of the working condition sequence population by means of a satisfaction criterion₁),F(X₂),...,F(X_t)]And obtaining the optimal function value F (X) of the population of the working condition sequence by the formula (1)_*) And optimum operating mode sequence X_*；

F(X_*)＝min(F{X}) (1)；

The step S2 includes:

step S21: under the current k-th strategy factor sequence Y (theta), the function value F { X } of the condition sequence individuals in the step S15 is subjected to roulette operation, and a new condition sequence individual-ordered population is generated

And correspondingly distributing the working condition sequences in the population to strategy factors in a strategy factor sequence Y (theta) one by one, performing strategy operation, and generating working condition sequence child population

Calculating working condition sequence population

Function value of

Step S22: updating population Pop⁽²⁾X and function values F X, to group the offspring

Sum function value

Respectively replacing parent population Pop⁽²⁾{ X } and a population function value F { X }; acquiring a working condition sequence filial generation population according to a formula (2)

Best function value of

And optimal sequence

When in use

By mixing

Is given to X_*Updating the optimal operating regime sequence X_*By passing through

Is given to F (X)_*) Updating the optimum function value F (X)_*)；

When in use

When it is, X is_*Assigned to population Pop⁽²⁾{ X } in

In that

Position will correspond to function value

Is given to function value F (X)_*) To achieve the optimal working condition sequence X_*And the optimum function value F (X)_*) Updating of (1);

step S23: outputting the optimal function value F (X) under the current k-th strategy sequence Y (theta)_*)；

The step S3 includes:

step S31: randomly forming a size K based on the strategy factor sequence of step S15_maxInitial policy factor sequence population of

Calculating individual function values of strategy factor sequence

Step S32: according to the strategy factor sequence function value F { Y }, according to the default elite probability p_dSelecting the best K in the current population_max×p_dCarrying out traditional operator selection operation on the sequence individuals;

step S33: according to a default cross probability p_cIn (K)_max-K_max×p_d) Selection from one of the remaining individuals (K)_max-K_max×p_d)×p_cThe individual sequences are subjected to random two-point crossing operation to generate (K)_max-K_max×p_d)×p_cA plurality of crossing individuals;

step S34: for the rest K_max-K_max×p_d-(K_max-K_max×p_d)×p_cPerforming single point mutation operation on the individual to generate K_max-K_max×p_d-(K_max-K_max×p_d)×p_c(ii) individual variants;

step S35: forming a new strategy factor sequence population by the elite individuals in the step S32, the crossover individuals in the step S33 and the variant individuals in the step S34;

step S36: the best evaluation value F (Y) is judged and output_*) Whether the desired threshold T has been reached_rRange, if F (Y)_*)≤T_rAt this time, F (Y)_*)＝F(X_*) Wherein Y is_*Executing step S37 for the optimal strategy sequence combination, otherwise, returning to step S32;

step S37: the optimal working condition state sequence X_*And decoding and outputting the multi-parameter expected operation condition time sequence.

2. The method for designing the multi-parameter operating condition of the automobile based on the heuristic mahalanobis link evolution of claim 1, wherein the parameters in the step S11 include speed, acceleration and road gradient, and the value of L is 1800S; the value of n in the step S13Is 6, R takes the value of [10,20,50,100,150,200](ii) a T in the step S13_rThe value of (a) is 10%; p in said step S13_rThe value of (1:1:1:2:3:3:3:1:1: 2:3:3: 2) and the value of t is 30.

3. The method for designing the multi-parameter operation condition of the automobile based on the meta-heuristic mahalanobis chain evolution as claimed in claim 1, wherein K in the step S31_maxIs 24.

Images