CN110807531A - Maintenance Strategy of Photovoltaic Power Plant Based on Component-System Hierarchical Optimization - Google Patents

Abstract

Translated fromChinese

本发明公开了一种基于元件‑系统分级优化的光伏电站维护策略，包括以下步骤：先根据马尔科夫链对各个元件进行状态预测，根据状态预测结果计算元件故障风险损失，在元件级优化阶段依据平均维护费用分析，确定每个元件最经济的预防性维修时间和接近最优维修时间，得到每个元件的维修策略集合。在系统级优化阶段，依据元件之间的维修费用相关性与结构依赖性计算元件共同维修的时间阈值，确定系统最优维修策略。本发明使各个元件之间的维护相互协调，从而最大限度地节省维修费用和减少系统停机损失。

The invention discloses a photovoltaic power station maintenance strategy based on component-system hierarchical optimization, which includes the following steps: firstly performing state prediction on each component according to the Markov chain; calculating the component failure risk loss according to the state prediction result; According to the analysis of the average maintenance cost, the most economical preventive maintenance time and near-optimal maintenance time of each component are determined, and the maintenance strategy set of each component is obtained. In the system-level optimization stage, the time threshold for common maintenance of components is calculated according to the maintenance cost correlation and structural dependence between components, and the optimal maintenance strategy of the system is determined. The invention makes the maintenance among the various components coordinated with each other, thereby saving the maintenance cost to the greatest extent and reducing the loss of system downtime.

Description

Translated fromChinese

基于元件-系统分级优化的光伏电站维护策略Maintenance strategy of photovoltaic power station based on component-system hierarchical optimization

技术领域technical field

本发明涉及光伏电站的维护策略分析，具体是根据光伏电站各个元件故障率进行状态预测，再对维护费用进行优化，从而经济合理的安排光伏电站的维修计划。The invention relates to the maintenance strategy analysis of the photovoltaic power station. Specifically, the state prediction is carried out according to the failure rate of each element of the photovoltaic power station, and then the maintenance cost is optimized, so as to arrange the maintenance plan of the photovoltaic power station economically and reasonably.

背景技术Background technique

太阳能作为一种可再生能源，越来越受到重视，光伏发电的装机容量在逐年递增。但是光伏发电也存在明显的缺陷和不足，比如随机性和不稳定性，加之光伏电站运行条件恶劣，使得光伏电站各元件故障频发。所以，为光伏电站安排经济合理的维护策略有很大的研究价值。As a renewable energy, solar energy has been paid more and more attention, and the installed capacity of photovoltaic power generation is increasing year by year. However, photovoltaic power generation also has obvious defects and deficiencies, such as randomness and instability, coupled with the poor operating conditions of photovoltaic power plants, which cause frequent failures of various components of photovoltaic power plants. Therefore, it is of great research value to arrange economical and reasonable maintenance strategies for photovoltaic power plants.

光伏电站的维修策略主要包含事后维修和预防性维修两种方式：事后维修是指当系统或元件发生故障后再进行维修的方式，其目的是恢复系统或部件原有的功能属性，但是事后维修会造成元件或系统故障停机，降低系统的可靠性；预防性维修是指当系统或部件已经工作较长时间，在预定的时间进行维修，防止元件发生故障，避免停机损失，但是预防性维修存在过修或欠修的情况，导致维修费用昂贵。国内外研究学者对多元件系统的维修原理进行了大量研究。其中，赵洪山等人在中国电机工程学报，2016，36(3)：701-708.“考虑不完全维修的风电机组状态-机会维修策略”提出了状态-机会维修策略，根据元件的可靠度函数，确定机会维修和状态维修的阈值，从而合理安排元件是否共同维修，节省维修成本；刘璐洁等人在中国电机工程学报，2016，36(21)：5732-5740.“基于可靠性和维修优先级的海上风电机组预防性维护策略优化”中，将维护的等待时间进行分类，考虑维护等待时间对元件和风电机组可靠性更新的影响，以维护期单位成本最低为准则优化运维策略；苏永新等在电工技术学报，2015，30(22)：190-198.“海上风电场疲劳分布与有功功率统一控制”中提出了研究了考虑随机故障的机会维修，通过优化系统各部件预防性维修役龄和机会维修役龄，使系统的维修费用最少。以上分析方法维修时间的确定一般都是基于元件运行状态，分析元件可靠性以确定是否进行状态维修或机会维修，在此基础上才考虑优化维修策略的总费用。这种方法确定的维修时间可以保证元件的可靠性，但不一定是每个元件最经济的维护方案。The maintenance strategy of photovoltaic power plants mainly includes two ways: post-event maintenance and preventive maintenance: post-event maintenance refers to the maintenance method after the system or component fails. The purpose is to restore the original functional properties of the system or component, but the post-event maintenance It will cause the failure of components or systems and reduce the reliability of the system; preventive maintenance means that when the system or components have been working for a long time, maintenance is carried out at a predetermined time to prevent component failure and avoid downtime losses, but preventive maintenance exists. Over-repair or under-repair, resulting in expensive repair costs. Domestic and foreign researchers have done a lot of research on the maintenance principles of multi-component systems. Among them, Zhao Hongshan et al. in Chinese Journal of Electrical Engineering, 2016, 36(3): 701-708. "Condition-opportunity maintenance strategy for wind turbines considering incomplete maintenance" proposed a state-opportunity maintenance strategy, according to the reliability of components function to determine the thresholds of opportunistic maintenance and condition maintenance, so as to reasonably arrange whether components are repaired together and save maintenance costs; Liu Lujie et al. in Chinese Journal of Electrical Engineering, 2016, 36(21): 5732-5740. "Based on reliability and maintenance priority In “Optimization of Preventive Maintenance Strategy for Offshore Wind Turbines at the Advanced Level”, the maintenance waiting time is classified, the influence of maintenance waiting time on the reliability update of components and wind turbines is considered, and the operation and maintenance strategy is optimized based on the minimum unit cost during the maintenance period; Su Yongxin et al. in the Journal of Electrotechnical Technology, 2015, 30(22): 190-198. "Fatigue distribution and active power unified control of offshore wind farms" proposed and studied opportunistic maintenance considering random faults, and by optimizing the preventive maintenance service of each component of the system. age and opportunity maintenance service age to minimize system maintenance costs. The maintenance time of the above analysis methods is generally determined based on the operating status of the components, and the reliability of the components is analyzed to determine whether to perform condition maintenance or opportunity maintenance. On this basis, the total cost of the optimized maintenance strategy is considered. The repair time determined by this method can guarantee the reliability of the component, but it is not necessarily the most economical maintenance plan for each component.

发明内容SUMMARY OF THE INVENTION

本发明的目的针对现有技术的不足，提出了一种基于元件-系统分级优化的光伏电站维护策略分析方法，以解决上述背景技术中提出的问题。The purpose of the present invention is to propose a maintenance strategy analysis method for photovoltaic power plants based on component-system hierarchical optimization in view of the deficiencies of the prior art, so as to solve the problems raised in the above background technology.

本发明采用下述技术方案：The present invention adopts following technical scheme:

一种基于元件-系统分级优化的光伏电站维护策略分析方法，包括以下步骤：A photovoltaic power station maintenance strategy analysis method based on component-system hierarchical optimization, comprising the following steps:

步骤1：利用平均无故障工作时间MTBF(Mean time between failure)可以计算出光伏电站各个元件的故障率λ，计算式如式(1)所示。Step 1: Using the mean time between failure (MTBF), the failure rate λ of each component of the photovoltaic power station can be calculated, and the calculation formula is shown in formula (1).

步骤2：光伏电站中直流汇流箱、逆变器、箱式三绕组变压器均视为两状态元件，状态集合由故障停运和正常运行两种状态组成。在状态1下，元件正常运行，完成预设功能，状态0情况下，元件发生故障导致停运，状态集合S＝{1，0}，对应的状态信息η_i分别为100％和0％。Step 2: The DC combiner box, inverter, and box-type three-winding transformer in the photovoltaic power station are all regarded as two-state elements, and the state set consists of two states: fault shutdown and normal operation. Instate 1, the component runs normally and completes the preset function. In state 0, the component fails and causes shutdown. The state set S={1,0}, and the corresponding state information η_i is 100% and 0%, respectively.

根据式(1)计算得到的元件故障率λ，获得两状态元件状态转移矩阵P如式(2)所示：According to the element failure rate λ calculated by Equation (1), the state transition matrix P of the two-state element is obtained as shown in Equation (2):

步骤3：光伏组件也属于两状态元件，但是光伏阵列由多个光伏组件串并联组成，某一个光伏组件的故障不会导致整个光伏阵列停运，因此需要对光伏阵列进行多状态划分。m×n的子阵列由n个组串并联而成，每个组串由m个组件串联组成。根据式(1)计算光伏组件故障率为λ，则每个组串的故障率λ_s如式(3)所示。子阵列的状态集有n+1个元素，S＝{s_i(i＝n，n-1，…，1，0)}，对应的状态信息η_i表达式如式(4)所示，i为正常工作组串个数。Step 3: Photovoltaic modules are also two-state elements, but the photovoltaic array is composed of multiple photovoltaic modules in series and parallel. The failure of one photovoltaic module will not cause the entire photovoltaic array to be shut down. Therefore, it is necessary to divide the photovoltaic array into multiple states. The m×n sub-array is formed by n groups of strings in parallel, and each group string is formed by m components in series. Calculate the failure rate λ of photovoltaic modules according to formula (1), then the failure rate_λs of each string is shown in formula (3). The state set of the sub-array has n+1 elements, S={s_i (_i =n, n-1, . i is the number of normal working group strings.

λ_s＝m·λ (3)λ_s = m·λ (3)

η_i＝i·P_s/P_a×100％ (4)η_i =i·P_s /P_a ×100% (4)

根据光伏阵列状态转移图确定阵列的状态转移矩阵P，则光伏阵列状态转移矩阵各元素如式(5)所示：The state transition matrix P of the array is determined according to the state transition diagram of the photovoltaic array, and the elements of the state transition matrix of the photovoltaic array are shown in formula (5):

步骤4：基于马尔科夫过程，结合状态转移概率矩阵，建立光伏电站各元件状态预测模型：Step 4: Based on the Markov process, combined with the state transition probability matrix, establish a state prediction model for each component of the photovoltaic power station:

π(k)＝π(k-1)P＝π(0)P^k＝π(i)P^k-i (6)π(k)=π(k-1)P=π(0)P^k =π(i)P^ki (6)

式中，π(0)为初始状态概率分布，π(i)为iΔt时刻状态概率分布，P为状态转移矩阵。In the formula, π(0) is the initial state probability distribution, π(i) is the state probability distribution at time iΔt, and P is the state transition matrix.

步骤5：元件的平均维修成本分为三部分，平均直接维修费用C_m(t)、平均停机损失C_i(t)和故障风险损失C_r(t)，计算式分别为式(7)-(9)。Step 5: The average maintenance cost of components is divided into three parts, the average direct maintenance cost C_m (t), the average downtime loss C_i (t) and the failure risk loss C_r (t), the calculation formulas are equation (7)- (9).

式中，c_m表示维修的直接成本，包含物流、人工等费用；t_mnt表示上一次维修时间。In the formula, cm represents the direct cost of maintenance, including logistics, labor and other costs;_tmnt represents the last maintenance time.

式中，c_i表示维修时元件的停机损失。In the formula, c_i represents the downtime loss of components during maintenance.

式中，π_j(t)表示元件在t时刻处于状态的j概率；Γ为子阵列的平均一天发电量，kWh；v为电价；l表示元件状态个数；m_j(t|Θ_j)表示t时刻元件处于状态j的功率损失率；In the formula, π_j (t) represents the j probability that the element is in the state at time t; Γ is the average daily power generation of the sub-array, kWh; v is the electricity price; l represents the number of element states; m_j (t|Θ_j ) Represents the power loss rate of the element in state j at time t;

步骤6：c_m和c_i均为固定值，所以C_m(t)和C_i(t)是随维修时间间隔的增加而减小的，但是随着时间的推移，元件故障停运的风险会逐渐增大，所以C_r(t)是随时间增加的，根据式(10)确定最优维护动作时间t^*和最低平均费用C^*；Step 6: Both c_m and c_i are fixed values, so C_m (t) and C_i (t) decrease as the maintenance interval increases, but over time, the risk of component failure outages will gradually increase, so C_r (t) increases with time, according to formula (10) to determine the optimal maintenance action time t^* and the minimum average cost C^* ;

步骤7：除最优维护时间外，其他可选择的接近最优的维护时间也需要确定，为系统级维护策略的优化提供选择。接近最优维修时间可以通过排除搜索空间中的最优时间来求取，如式(11)所示，确定每个元件的维修策略集合A^*，A^*＝{a₁^*，a₂^*，…}＝{(t₁^*，C₁^*)，(t₂^*，C₂^*)，…}，其中(t_j^*，C_j^*)表示维护策略集合中第j个策略的维护时间和平均维护费用；Step 7: In addition to the optimal maintenance time, other optional near-optimal maintenance times also need to be determined to provide options for the optimization of system-level maintenance strategies. The near-optimal maintenance time can be obtained by excluding the optimal time in the search space, as shown in equation (11), to determine the maintenance strategy set A^* for each component, A^* ={a₁^* , a₂^* , …}={(t₁^* , C₁^* ), (t₂^* , C₂^* ), …}, where (t_j^* , C_j^* ) represents the maintenance time of the jth policy in the maintenance policy set and average maintenance cost;

步骤8：对于N个元件构成的系统，通过元件级维护策略优化分别确定每个元件所对应的策略集合A_k^*＝{a_1，k^*，a_2，k^*，…}＝{(t_1，k^*，C_1，k^*)，(t_2，k^*，C^2，k*)，...}，k表示第k个元件，k＝1，2，...，N。元件单独维修时，系统总的维修费用c₀如式(12)所示：Step 8: For a system composed of N elements, determine the strategy set A_k^* = {a_{1, k}^* , a_{2, k}^* , ...} = {(t_1,k^* ,C1_,k^* ),(t2_,k^* ,C2^,k* ),...}, k denotes the kth element, k=1,2,...,N. When the components are repaired individually, the total maintenance cost c₀ of the system is shown in formula (12):

式中c_k表示第k个元件选择维修策略x_k时的维修费用；c_mk表示第k个元件的直接维修费用；c_ik表示第k个元件的维修停机损失。In the formula,_ck represents the maintenance cost when the kth component chooses the maintenance strategy_xk ;_cmk represents the direct maintenance cost of the kth component;_cik represents the maintenance downtime loss of the kth component.

步骤9：为了方便计算元件共同维修节省成本，将元件的直接维修费用c_m分成两部分，如式(13)所示：Step 9: In order to conveniently calculate the cost savings of common maintenance of components, the direct maintenance cost cm of components is_divided into two parts, as shown in formula (13):

c_m＝c_m1+c_m2 (13)c_m =c_m1 +c_m2 (13)

式中，c_m1表示固定成本；c_m2表示非技术维修人员的人工费用，元件共同维修时可以节省的支出费用。因此，共同维修节省的直接维修费用c_EOS如式(14)所示：In the formula, c_m1 represents the fixed cost; c_m2 represents the labor cost of non-technical maintenance personnel, and the expenses that can be saved when the components are repaired together. Therefore, the direct maintenance cost c_EOS saved by joint maintenance is shown in formula (14):

式中，X表示系统维修策略；n(X_t)表示策略X中在t时刻共同维修的元件个数。In the formula, X represents the system maintenance strategy; n(X_t ) represents the number of components to be jointly maintained at time t in the strategy X.

用c_i2表示在某一时刻元件共同维修时重复的停机损失，根据式(15)确定，则共同维修节省的总停机损失c_DT如式(16)所示。C_i2 is used to represent the repeated downtime loss when the components are repaired together at a certain time. According to the formula (15), the total downtime loss c_DT saved by the joint repair is shown in the formula (16).

式中，X_t为t时刻共同维修元件的组合，元件数为n(X_t)；c_ik(X_t)表示X_t中第k个元件的停机损失。In the formula, X_t is the combination of common maintenance components at time t, and the number of components is n(X_t ); c_ik (X_t ) represents the shutdown loss of the kth component in X_t .

系统中元件共同维修除了会节省维修费用和停机损失外，还可能会产生额外的功率损失，因此，需要在成本中引入额外损失变量。为了便于计算多个元件共同维修引发的额外损失费用，根据元件之间的结构特征将系统中的元件分为v个组别，分别为g₁，g₂，...，g_v，额外损失c_LF表达式为式(17)：In addition to saving maintenance costs and downtime losses, the common maintenance of components in the system may also generate additional power losses. Therefore, additional loss variables need to be introduced into the cost. In order to facilitate the calculation of the additional loss cost caused by the common maintenance of multiple components, the components in the system are divided into v groups according to the structural characteristics between the components, which are respectively g₁ , g₂ , ..., g_v , the additional loss c_LF expression is formula (17):

式中，χ_t(X)表示维修策略X中在t时刻共同维修会产生额外损失的集合；f_LF表示共同维修产生的损失函数。In the formula, χ_t (X) represents the set of additional losses caused by joint maintenance at time t in the maintenance strategy X; f_LF represents the loss function caused by joint maintenance.

步骤10：综合以上分析，得到系统级维修策略X总成本c_SL表达式如式(18)所示：Step 10: Based on the above analysis, the system-level maintenance strategy X total cost c_SL expression is obtained as shown in formula (18):

c_SL(X)＝c₀(X)-c_EOS(X)-c_DT(X)+c_LF(X) (18)c_SL (X)=c₀ (X)-c_EOS (X)-c_DT (X)+c_LF (X) (18)

步骤11：根据式(10)确定了元件最优维修时间t^*和最低平均费用C^*，则在系统级优化阶段选择A^*中其他非最优的维修时间对应的平均费用的增量C_t如式(19)所示：Step 11: According to the formula (10), the optimal maintenance time t^* and the minimum average cost C^* of the component are determined, then in the system-level optimization stage, the increment C_t of the average cost corresponding to other non-optimal maintenance time in A^* is selected As shown in formula (19):

根据步骤9成本分析，元件共同维修节省的成本及产生的额外损失分别为，c_EOS、c_DT和c_LF，因此系统中元件同时维修导致的平均减额费用C_sim如式(20)所示：According to the cost analysis in step 9, the cost saved and the additional losses generated by the joint maintenance of components are c_EOS , c_DT and c_LF respectively. Therefore, the average derating cost C_sim caused by the simultaneous maintenance of components in the system is shown in equation (20) :

步骤12：通过比较共同维修带来的成本优势与选择非最优维护时间引起的费用增额，确定光伏电站中元件共同维修时间阈值，确定电站最优维护策略。Step 12: Determine the common maintenance time threshold of components in the photovoltaic power station and determine the optimal maintenance strategy of the power station by comparing the cost advantage brought by the common maintenance and the cost increase caused by selecting a non-optimal maintenance time.

本发明与现有技术相比的优点在于：The advantages of the present invention compared with the prior art are:

1.本发明能够在保证可靠性的前提下得到元件的最经济维护时间，不同于状态维修仅仅根据元件可靠性确定维修时间，从而有效的避免过修或欠修。1. The present invention can obtain the most economical maintenance time of the components under the premise of ensuring reliability, which is different from the condition maintenance which only determines the maintenance time according to the reliability of the components, thereby effectively avoiding over-repair or under-repair.

2.本发明在对各个元件维护时间进行优化的基础上再对光伏电站总的维护费用进行优化，在元件级和系统级均进行经济性分析，从而获得最优的维护策略。2. The present invention optimizes the total maintenance cost of the photovoltaic power station on the basis of optimizing the maintenance time of each component, and performs economic analysis at the component level and the system level, thereby obtaining the optimal maintenance strategy.

附图说明Description of drawings

图1是本发明的流程图；Fig. 1 is the flow chart of the present invention;

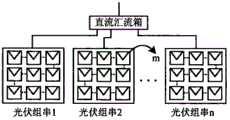
图2是光伏电站电气结构图；Figure 2 is the electrical structure diagram of the photovoltaic power station;

图3是光伏阵列电气结构图；Figure 3 is an electrical structure diagram of a photovoltaic array;

图4是光伏阵列状态转移图；Figure 4 is a state transition diagram of a photovoltaic array;

图5是平均直接维修费用C_m(t)、平均停机损失C_i(t)和故障风险损失C_r(t)变化趋势图。Figure 5 is a trend diagram of the average direct maintenance cost C_m (t), the average downtime loss C_i (t) and the failure risk loss C_r (t).

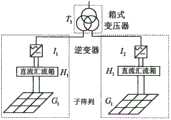
图6是发电单元电气结构图Figure 6 is a diagram of the electrical structure of the power generation unit

具体实施方式Detailed ways

一种基于元件-系统分级优化的光伏电站维护策略分析方法，流程图如图1所示，包括以下步骤：A method for analyzing the maintenance strategy of photovoltaic power plants based on component-system hierarchical optimization, the flow chart is shown in Figure 1, including the following steps:

步骤1：光伏电站电气结构如图2所示，在对光伏电站各个元件进行状态预测时，只考虑了光伏组件，直流汇流箱、逆变器、箱式三绕组变压器4种主要元件。根据美国桑迪亚实验室提供的数据，利用平均无故障工作时间MTBF(Mean time between failure)可以计算出光伏电站各个元件的故障率λ，计算式如式(1)所示，数据及结果如表1所示。Step 1: The electrical structure of the photovoltaic power station is shown in Figure 2. When predicting the state of each component of the photovoltaic power station, only four main components, the photovoltaic module, the DC combiner box, the inverter, and the box-type three-winding transformer, are considered. According to the data provided by Sandia Laboratories in the United States, the failure rate λ of each component of the photovoltaic power station can be calculated by using the mean time between failure (MTBF), the calculation formula is shown in formula (1), and the data and results are as follows shown in Table 1.

表1 元件平均故障时间和故障修复时间Table 1 Component mean time to failure and failure repair time

Table1 MTBF and MTTR of componentsTable1 MTBF and MTTR of components

步骤2：光伏电站中直流汇流箱、逆变器、箱式三绕组变压器均视为两状态元件，状态集合由故障停运和正常运行两种状态组成。在状态1下，元件正常运行，完成预设功能，状态0情况下，元件发生故障导致停运，状态集合S＝{1，0}，对应的状态信息η_i分别为100％和0％。Step 2: The DC combiner box, inverter, and box-type three-winding transformer in the photovoltaic power station are all regarded as two-state elements, and the state set consists of two states: fault shutdown and normal operation. Instate 1, the component runs normally and completes the preset function. In state 0, the component fails and causes shutdown. The state set S={1,0}, and the corresponding state information η_i is 100% and 0%, respectively.

根据式(1)计算得到的元件故障率λ，获得两状态元件状态转移矩阵P如式(2)所示：According to the element failure rate λ calculated by Equation (1), the state transition matrix P of the two-state element is obtained as shown in Equation (2):

步骤3：光伏组件也属于两状态元件，但是光伏阵列由多个光伏组件串并联组成，某一个光伏组件的故障不会导致整个光伏阵列停运，因此需要对光伏阵列进行多状态划分。子阵列结构图如图3所示，m×n的子阵列由n个组串并联而成，每个组串由m个组件串联组成。根据式(1)计算光伏组件故障率为λ，则每个组串的故障率λ_s如式(3)所示。子阵列的状态集有n+1个元素，S＝{s_i(i＝n，n-1，…，1，0)}，对应的状态信息η_i表达式如式(4)所示，i为正常工作组串个数。Step 3: Photovoltaic modules are also two-state elements, but the photovoltaic array is composed of multiple photovoltaic modules in series and parallel. The failure of one photovoltaic module will not cause the entire photovoltaic array to be shut down. Therefore, it is necessary to divide the photovoltaic array into multiple states. The sub-array structure diagram is shown in Figure 3. The m×n sub-array is formed by n groups of strings in parallel, and each group string is composed of m components in series. Calculate the failure rate λ of photovoltaic modules according to formula (1), then the failure rate_λs of each string is shown in formula (3). The state set of the sub-array has n+1 elements, S={s_i (_i =n, n-1, . i is the number of normal working group strings.

λ_s＝m·λ (3)λ_s = m·λ (3)

η_i＝i·P_s/P_a×100％ (4)η_i =i·P_s /P_a ×100% (4)

子阵列的状态转移图如图4所示，根据光伏阵列状态转移图确定阵列的状态转移矩阵P，则光伏阵列状态转移矩阵各元素如式(5)所示：The state transition diagram of the sub-array is shown in Figure 4. According to the state transition diagram of the photovoltaic array, the state transition matrix P of the array is determined, and then the elements of the photovoltaic array state transition matrix are shown in formula (5):

步骤4：基于马尔科夫过程，结合状态转移概率矩阵，建立光伏电站各元件状态预测模型：Step 4: Based on the Markov process, combined with the state transition probability matrix, establish a state prediction model for each component of the photovoltaic power station:

π(k)＝π(k-1)P＝π(0)P^k＝π(i)P^k-i (6)π(k)=π(k-1)P=π(0)P^k =π(i)P^ki (6)

式中，π(0)为初始状态概率分布，π(i)为iΔt时刻状态概率分布，P为状态转移矩阵。In the formula, π(0) is the initial state probability distribution, π(i) is the state probability distribution at time iΔt, and P is the state transition matrix.

步骤5：元件的平均维修成本分为三部分，平均直接维修费用C_m(t)、平均停机损失C_i(t)和故障风险损失C_r(t)，计算式分别为式(7)-(9)。Step 5: The average maintenance cost of components is divided into three parts, the average direct maintenance cost C_m (t), the average downtime loss C_i (t) and the failure risk loss C_r (t), the calculation formulas are equation (7)- (9).

式中，c_m表示维修的直接成本，包含物流、人工等费用；t_mnt表示上一次维修时间。In the formula, cm represents the direct cost of maintenance, including logistics, labor and other costs;_tmnt represents the last maintenance time.

式中，c_i表示维修时元件的停机损失。In the formula, c_i represents the downtime loss of components during maintenance.

式中，π_j(t)表示元件在t时刻处于状态的j概率；Γ为子阵列的平均一天发电量，kWh；v为电价；l表示元件状态个数；m_j(t|Θ_j)表示t时刻元件处于状态j的功率损失率；In the formula, π_j (t) represents the j probability that the element is in the state at time t; Γ is the average daily power generation of the sub-array, kWh; v is the electricity price; l represents the number of element states; m_j (t|Θ_j ) Represents the power loss rate of the element in state j at time t;

步骤6：c_m和c_i均为固定值，所以C_m(t)和C_i(t)是随维修时间间隔的增加而减小的，但是随着时间的推移，元件故障停运的风险会逐渐增大，所以C_r(t)是随时间增加的，C_m(t)、C_i(t)和C_r(t)变化趋势如图5所示，根据式(10)确定最优维护动作时间t^*和最低平均费用C^*；Step 6: Both c_m and c_i are fixed values, so C_m (t) and C_i (t) decrease as the maintenance interval increases, but over time, the risk of component failure outages will gradually increase, so C_r (t) increases with time, and the trends of C_m (t), C_i (t) and C_r (t) are shown in Figure 5. According to formula (10) to determine the optimal Maintenance action time t^* and minimum average cost C^* ;

步骤7：除最优维护时间外，其他可选择的接近最优的维护时间也需要确定，为系统级维护策略的优化提供选择。接近最优维修时间可以通过排除搜索空间中的最优时间来求取，如式(11)所示，确定每个元件的维修策略集合A^*，A^*＝{a₁^*，a₂^*，…}＝{(t₁^*，C₁^*)，(t₂^*，C₂^*)，…}，其中(t_j^*，C_j^*)表示维护策略集合中第j个策略的维护时间和平均维护费用；Step 7: In addition to the optimal maintenance time, other optional near-optimal maintenance times also need to be determined to provide options for the optimization of system-level maintenance strategies. The near-optimal maintenance time can be obtained by excluding the optimal time in the search space, as shown in equation (11), to determine the maintenance strategy set A^* for each component, A^* ={a₁^* , a₂^* , …}={(t₁^* , C₁^* ), (t₂^* , C₂^* ), …}, where (t_j^* , C_j^* ) represents the maintenance time of the jth policy in the maintenance policy set and average maintenance cost;

步骤8：对于N个元件构成的系统，通过元件级维护策略优化分别确定每个元件所对应的策略集合A_k^*＝{a_1，k^*，a_2，k^*，…}＝{(t_i，k^*，C_1，k^*)，(t_2，k^*，C_2，k^*)，...}，k表示第k个元件，k＝1，2，...，N。元件单独维修时，系统总的维修费用c₀如式(12)所示：Step 8: For a system composed of N elements, determine the strategy set A_k^* = {a_{1, k}^* , a_{2, k}^* , ...} = {(t_{i, k}^* , C1_{, k}^* ), (t2_{, k}^* , C2_{, k}^* ),...}, k denotes the kth element, k=1, 2,...,N. When the components are repaired individually, the total maintenance cost c₀ of the system is shown in formula (12):

式中c_k表示第k个元件选择维修策略x_k时的维修费用；c_mk表示第k个元件的直接维修费用；c_ik表示第k个元件的维修停机损失。In the formula,_ck represents the maintenance cost when the kth component chooses the maintenance strategy_xk ;_cmk represents the direct maintenance cost of the kth component;_cik represents the maintenance downtime loss of the kth component.

步骤9：为了方便计算元件共同维修节省成本，将元件的直接维修费用c_m分成两部分，如式(13)所示：Step 9: In order to conveniently calculate the cost savings of common maintenance of components, the direct maintenance cost cm of components is_divided into two parts, as shown in formula (13):

c_m＝c_m1+c_m2 (13)c_m =c_m1 +c_m2 (13)

式中，c_m1表示固定成本；c_m2表示非技术维修人员的人工费用，元件共同维修时可以节省的支出费用。因此，共同维修节省的直接维修费用c_EOS如式(14)所示：In the formula, c_m1 represents the fixed cost; c_m2 represents the labor cost of non-technical maintenance personnel, and the expenses that can be saved when the components are repaired together. Therefore, the direct maintenance cost c_EOS saved by joint maintenance is shown in formula (14):

式中，X表示系统维修策略；n(X_t)表示策略X中在t时刻共同维修的元件个数。In the formula, X represents the system maintenance strategy; n(X_t ) represents the number of components to be jointly maintained at time t in the strategy X.

用c_i2表示在某一时刻元件共同维修时重复的停机损失，根据式(15)确定，则共同维修节省的总停机损失c_DT如式(16)所示。C_i2 is used to represent the repeated downtime loss when the components are repaired together at a certain time. According to the formula (15), the total downtime loss c_DT saved by the joint repair is shown in the formula (16).

式中，X_t为t时刻共同维修元件的组合，元件数为n(X_t)；c_ik(X_t)表示X_t中第k个元件的停机损失。In the formula, X_t is the combination of common maintenance components at time t, and the number of components is n(X_t ); c_ik (X_t ) represents the shutdown loss of the kth component in X_t .

系统中元件共同维修除了会节省维修费用和停机损失外，还可能会产生额外的功率损失，因此，需要在成本中引入额外损失变量。为了便于计算多个元件共同维修引发的额外损失费用，根据元件之间的结构特征将系统中的元件分为v个组别，分别为g₁，g₂，...，g_v，发电单元分组如图6所示，额外损失c_LF表达式为式(17)：In addition to saving maintenance costs and downtime losses, the common maintenance of components in the system may also generate additional power losses. Therefore, additional loss variables need to be introduced into the cost. In order to facilitate the calculation of the additional loss cost caused by the common maintenance of multiple components, the components in the system are divided into v groups according to the structural characteristics between the components, namely g₁ , g₂ , ..., g_v , the power generation units The grouping is shown in Figure 6, and the additional loss c_LF is expressed as formula (17):

式中，χ_t(X)表示维修策略X中在t时刻共同维修会产生额外损失的集合；f_LF表示共同维修产生的损失函数。In the formula, χ_t (X) represents the set of additional losses caused by joint maintenance at time t in the maintenance strategy X; f_LF represents the loss function caused by joint maintenance.

步骤10：综合以上分析，得到系统级维修策略X总成本c_SL表达式如式(18)所示：Step 10: Based on the above analysis, the system-level maintenance strategy X total cost c_SL expression is obtained as shown in formula (18):

c_SL(X)＝c₀(X)-c_EOS(X)-c_DT(X)+c_LF(X) (18)c_SL (X)=c₀ (X)-c_EOS (X)-c_DT (X)+c_LF (X) (18)

步骤11：根据式(10)确定了元件最优维修时间t^*和最低平均费用C^*，则在系统级优化阶段选择A^*中其他非最优的维修时间对应的平均费用的增量C_t如式(19)所示：Step 11: According to the formula (10), the optimal maintenance time t^* and the minimum average cost C^* of the component are determined, then in the system-level optimization stage, the increment C_t of the average cost corresponding to other non-optimal maintenance time in A^* is selected As shown in formula (19):

根据步骤9成本分析，元件共同维修节省的成本及产生的额外损失分别为，c_EOS、c_DT和c_LF，因此系统中元件同时维修导致的平均减额费用C_sim如式(20)所示：According to the cost analysis in step 9, the cost saved and the additional losses generated by the joint maintenance of components are c_EOS , c_DT and c_LF respectively. Therefore, the average derating cost C_sim caused by the simultaneous maintenance of components in the system is shown in equation (20) :

步骤12：通过比较共同维修带来的成本优势C_sim与选择非最优维护时间引起的费用增额C_t，确定光伏电站中元件共同维修时间阈值，确定电站最优维护策略，计算最优维修策略节省的维修费用与停机时间。Step 12: Determine the common maintenance time threshold of components in the photovoltaic power station by comparing the cost advantage C_sim brought by common maintenance and the cost increase C_t caused by selecting non-optimal maintenance time, determine the optimal maintenance strategy of the power station, and calculate the optimal maintenance Maintenance costs and downtime saved by the strategy.

Claims (1)

1. A photovoltaic power station maintenance strategy based on element-system hierarchical optimization comprises the following steps:

step 1: calculating the fault rate lambda of each element of the photovoltaic power station by using the Mean Time Between Failures (MTBF), wherein the calculation formula is shown as formula (1).

And step 2, regarding the direct current combiner box, the inverter and the box type three-winding transformer as two-state elements, wherein a state set consists of two states of fault shutdown and normal operation, in a state 1, the elements normally operate to complete a preset function, in a state 0, the elements are in fault to cause shutdown, the state set S is {1, 0}, and corresponding state information η_i100% and 0%, respectively.

Obtaining a two-state element state transition matrix P according to the element failure rate lambda calculated by the formula (1) as shown in the formula (2):

and step 3: the photovoltaic module also belongs to two-state elements, but the photovoltaic array is composed of a plurality of photovoltaic modules in series-parallel connection, and the failure of one photovoltaic module cannot cause the shutdown of the whole photovoltaic array, so that the photovoltaic array needs to be divided in a multi-state mode. The m x n sub-array is formed by connecting n group strings in parallel, and each group string is formed by connecting m components in series. Calculating the failure rate of the photovoltaic module to be lambda according to the formula (1), and then calculating the failure rate lambda of each group string_sAs shown in formula (3). The state set of the subarray has n +1 elements, S ═ S_i(i ═ n, n-1, …, 1, 0) }, corresponding status information η_iThe expression is shown in formula (4), i is normalNumber of workgroup strings.

λ_s＝m·λ (3)

η_i＝i·P_s/P_a×100％ (4)

Determining a state transition matrix P of the array according to a photovoltaic array state transition diagram, wherein the state transition matrix is an upper triangular matrix when maintenance is not considered, the array is in an absorption state when i, j is n +1, and P is in the absorption state_ij1. Then, each element of the state transition matrix of the photovoltaic array is as shown in formula (5):

and 4, step 4: based on a Markov process and in combination with a state transition probability matrix, establishing a state prediction model of each element of the photovoltaic power station:

π(k)＝π(k-1)P＝π(0)P^k＝π(i)P^k-i(6)

in the formula, pi (0) is the initial state probability distribution, pi (i) is the state probability distribution at the moment i Δ t, and P is the state transition matrix.

And 5: average maintenance cost of elements is divided into three parts, average direct maintenance cost C_m(t) average shutdown loss C_i(t) and failure risk loss C_r(t) the calculation expressions are respectively expressed as expressions (7) to (9).

In the formula, c_mRepresents the direct cost of maintenance, including logistics, labor, etc; t is t_mntIndicating the last repair time.

In the formula, c_iIndicating a loss of component downtime during maintenance.

In the formula, pi_j(t) represents the j probability that the element is in the state at time t; Γ is the average one-day power generation of the subarrays, kWh; v is the electricity price; l represents the number of element states; m is_j(t|Θ_j) Representing the power loss rate of the element in state j at time t;

step 6: c. C_mAnd c_iAre all fixed values, so C_m(t) and C_i(t) decreases with increasing maintenance intervals, but over time the risk of a component failure shutdown increases, so C_r(t) is increased with time, and the optimal maintenance action time t is determined according to equation (10)^*And minimum average cost C^*；

And 7: in addition to the optimal maintenance time, other selectable near optimal maintenance times may also need to be determined to provide options for optimization of the system level maintenance strategy. The near-optimal repair time can be found by excluding the optimal time in the search space, as shown in equation (11), determining the repair strategy set A for each component^*，A^*＝{a₁^*，a₂^*，…}＝{(t₁^*，C₁^*)，(t₂^*，C₂^*) … }, where (t)_j^*，C_j^*) Representing the maintenance time and the average maintenance cost of the jth strategy in the maintenance strategy set;

and 8: for a system composed of N elements, a strategy set Ak corresponding to each element is respectively determined through element-level maintenance strategy optimization^*＝{a_1，k^*，a_2，k^*，…}＝{(t_1，k^*，C_1，k^*)，(t_2，k^*，C_2，k^*) ,., k denotes the kth element, k 1, 2. Total maintenance cost c of the system when the components are maintained individually₀As shown in equation (12):

in the formula c_kIndicates that the kth element selects a repair strategy x_kMaintenance costs per hour; c. C_mkRepresents the direct maintenance cost of the kth element; c. C_ikIndicating a maintenance outage loss for the kth element.

And step 9: to facilitate the calculation of the cost saving of the common maintenance of the components, the direct maintenance cost c of the components is calculated_mIs divided into two parts as shown in formula (13):

c_m＝c_m1+c_m2(13)

in the formula, c_m1Represents a fixed cost; c. C_m2The labor cost of non-technical maintenance personnel is shown, and the expenditure cost can be saved when the elements are maintained together. Thus, the common maintenance saves direct maintenance costs c_EOSAs shown in equation (14):

wherein X represents a system maintenance strategy; n (X)_t) Indicating the number of components that are commonly serviced at time t in strategy X.

By c_i2Representing repeated outage losses at a time of component co-maintenance, as determined by equation (15), the total outage loss saved by the co-maintenance is shown as equation (16).

In the formula, X_tFor combinations of commonly maintained components at time t, the number of components being n (X)_t)；c_ik(X_t) Represents X_tMiddle k elementA loss of downtime of the part.

In addition to saving maintenance costs and downtime losses, the common maintenance of components in the system may also result in additional power losses, thus introducing additional loss variables in cost. In order to calculate the extra loss cost caused by the common maintenance of a plurality of elements, the elements in the system are divided into v groups, g respectively, according to the structural characteristics among the elements₁，g₂，...，g_vExtra loss c_LFThe expression is formula (17):

in the formula, x_t(X) represents the set of extra losses that would result from the common repair at time t in repair strategy X; f. of_LFRepresenting the loss function resulting from the common repair.

Step 10: the system level maintenance strategy X total cost c is obtained by combining the analysis_SLThe expression is shown in formula (18):

c_SL(X)＝c₀(X)-c_EOS(X)-c_DT(X)+c_LF(X) (18)

step 11: the optimum maintenance time t of the component is determined according to equation (10)^*And minimum average cost C^*Then A is selected during the system level optimization phase^*Increment C of average cost corresponding to other non-optimal maintenance time_tAs shown in equation (19):

according to the cost analysis of step 9, the cost saved by the component common maintenance and the additional loss generated are respectively, c_EOS、c_DTAnd c_LFThus the average reduction cost C caused by the simultaneous maintenance of elements in the system_simAs shown in equation (20):

step 12: cost advantage by comparison of common maintenance C_simCost increase C caused by selecting non-optimal maintenance time_tAnd determining a common maintenance time threshold value of elements in the photovoltaic power station and determining an optimal maintenance strategy of the power station.

Images