CN109901146B - Hemispherical array and differential angle decoupling method based on spiral distribution - Google Patents

Abstract

Translated fromChinese

本发明公开了一种基于螺旋分布的半球形阵列和差测角解耦合方法，包括如下步骤：首先按照螺旋分布的排列方式将N个阵元分布在一个半径为R的半球面上；然后重新定义某方向到来的信号方位角

和俯仰角θ，得到重新定义的慢速矢量r；再分别求得方位向偏差为

和俯仰向偏差为±△θ的四个波束，对四个波束分别求得和波束、方位向差波束和俯仰向差波束，再求得方位向差和比与俯仰向差和比；然后设置方位向观察窗

和俯仰向观察窗θ_win，从而得到观察窗内的不耦合的方位向和俯仰向的鉴角曲线。该方法在减少预存储的数据量的同时，方法本身的测角误差也比较小，测角速度快，保证了雷达阵列测角的速度和精度的要求。

The invention discloses a hemispherical array based on helical distribution and a decoupling method for differential angle measurement. Define the azimuth of the signal coming from a certain direction

and the pitch angle θ to obtain the redefined slow vector r; and then obtain the azimuth deviation as

For the four beams whose sum and pitch deviations are ±△θ, the sum beam, the azimuth difference beam and the pitch difference beam are respectively obtained for the four beams, and then the azimuth difference sum ratio and the pitch difference sum ratio are obtained; then set Azimuth observation window

and the observation window θ_win in the elevation direction, so as to obtain the uncoupled azimuth and elevation angle discrimination curves in the observation window. While the method reduces the amount of pre-stored data, the error of the method itself is relatively small, and the angle measurement speed is fast, which ensures the requirements of the speed and accuracy of the radar array angle measurement.

Description

Translated fromChinese

一种基于螺旋分布的半球形阵列和差测角解耦合方法A Hemispherical Array and Differential Angle Decoupling Method Based on Helical Distribution

技术领域technical field

本发明属于雷达信号处理技术领域，特别涉及一种基于半球形阵列和差测角解耦合方法，适用于螺旋分布的半球形雷达阵列，在和差测角时存在的方位向和俯仰向耦合，导致需要预存储的数据量非常巨大的问题。The invention belongs to the technical field of radar signal processing, and in particular relates to a hemispherical array and differential angle decoupling method, which is suitable for spirally distributed hemispherical radar arrays, and the coupling of azimuth and pitch that exists when summing and differential angle measurement, This leads to the problem that the amount of data that needs to be pre-stored is very huge.

背景技术Background technique

早期的雷达阵列，主要有线阵和面阵等，因为阵列分布比较规则，天线单元的指向一致，因此进行理论分析比较容易，缺点是阵列的接收视角有限，半球形分布的雷达视角，具有指向性好、干扰杂波抑制能力强、探测距离远和广波束视角等优点，但是半球形阵列的天线单元指向不一致，导致半球形的阵列理论分析比较困难。The early radar arrays mainly include linear arrays and area arrays. Because the array distribution is relatively regular and the antenna units point in the same direction, it is relatively easy to conduct theoretical analysis. The disadvantage is that the receiving angle of the array is limited, and the radar angle of hemispherical distribution is directional. Good, strong interference clutter suppression ability, long detection distance and wide beam viewing angle, etc., but the antenna elements of the hemispherical array are inconsistent, which makes the theoretical analysis of the hemispherical array more difficult.

和差测角技术起源较早，优点很明显，可以在一个脉冲内测出目标的角度信息，随着雷达算法的研究，和差测角的精度大大提高，在工程实践中获得了巨大的应用，尤其是线阵的和差测角技术，目前为止发展的非常成熟，有双波束指向法、直接加权法、对称取反法等。面阵的和差测角主要问题存在于方位向和俯仰向信息耦合，主要的解决方法有坐标系变换和导向矢量变换等两种方法，将该方法应用于半球形阵列时，由于基于有向阵元的半球形阵列中，每个天线单元指向不一致，导致理论分析较难；同时，方位向信息和俯仰向信息耦合，而且面阵的解耦合方法不再完全适用，因此基于半球形阵列的和差测角技术存在困难。The sum-difference angle measurement technology originated earlier, and its advantages are obvious. The angle information of the target can be measured within one pulse. With the research of radar algorithms, the accuracy of the sum-difference angle measurement has been greatly improved, and it has been widely used in engineering practice. , especially the sum-and-difference angle measurement technology of linear arrays, has been developed very maturely so far, including dual-beam pointing methods, direct weighting methods, and symmetrical inversion methods. The main problem of sum and difference angle measurement of area array lies in the coupling of azimuth and elevation information. The main solutions include coordinate system transformation and steering vector transformation. When this method is applied to a hemispherical array, due to the In the hemispherical array of array elements, each antenna unit points inconsistently, which makes theoretical analysis difficult; at the same time, the azimuth information and the elevation information are coupled, and the decoupling method of the area array is no longer fully applicable, so the hemispherical array-based Difficulties exist in sum-and-difference angle measurement techniques.

发明内容Contents of the invention

为解决上述问题，本发明公开了一种基于半球形阵列的和差测角解耦合方法，本发明的方法在螺旋分布的半球形阵列的基础上，重新定义坐标系的方位角和俯仰角，分别合成四个波束，分别求得期望方向的俯仰向和俯仰向差和比，在期望方向一定的小角度范围内，近似认为方位向差和比与俯仰角无关，俯仰向的差和比与方位角无关，从而达到方位向与俯仰向解耦合的目的。In order to solve the above problems, the present invention discloses a decoupling method based on a hemispherical array and a difference measurement angle. The method of the present invention redefines the azimuth and elevation angles of the coordinate system on the basis of a hemispherical array with helical distribution, Synthesize four beams respectively, and obtain the pitch direction and pitch difference sum ratio in the desired direction respectively. Within a certain small angle range in the desired direction, it is approximately considered that the azimuth difference sum ratio has nothing to do with the pitch angle, and the pitch difference sum ratio is related to The azimuth angle is irrelevant, so as to achieve the purpose of decoupling the azimuth and pitch directions.

为达到上述目的，本发明采用如下技术方案予以实现：In order to achieve the above object, the present invention adopts the following technical solutions to achieve:

一种基于半球形阵列的和差测角解耦合方法，包括如下步骤：A hemispherical array-based sum-and-difference angle decoupling method, comprising the steps of:

步骤1：按照螺旋分布的排列方式将N个阵元分布在一个半径为R的半球面上；Step 1: Distribute N array elements on a hemispherical surface with radius R according to the arrangement of spiral distribution;

步骤2：重新定义某方向到来的信号方位角

和俯仰角θ，得到重新定义的慢速矢量r；Step 2: Redefine the azimuth of the incoming signal in a certain direction

And the pitch angle θ, get the redefined slow vector r;

步骤3：假定目标波束期望方向为

在步骤1和步骤2的基础上，分别合成波束指向分别为

和

四个波束，分别记为P₁、P₂、P₃和P₄；其中，△θ和

分别为方位向和俯仰向的角度偏差；Step 3: Assume that the desired direction of the target beam is

On the basis ofstep 1 and step 2, the synthetic beam points are respectively

and

The four beams are denoted as P₁ , P₂ , P₃ and P₄ respectively; among them, △θ and

are the angular deviations in azimuth and pitch, respectively;

步骤4：分别计算和波束P_sum、俯仰向差波束P_ele、方位向差波束P_azi、俯仰向差和比r_ele和方位向差和比r_azi；Step 4: Calculate sum beam P_sum , pitch difference beam P_ele , azimuth difference beam P_azi , pitch difference sum ratio r_ele , and azimuth difference sum ratio_razi ;

步骤5：设置方位向观察窗

和俯仰向观察窗θ_win，分别取方位向观察窗

和俯仰向观察窗θ_win内的俯仰向差和比r_ele和方位向差和比r_azi，得到方位向和俯仰向的鉴角曲线，从而达到解耦合的目的。Step 5: Set the azimuth viewing window

and pitch observation window θ_win , respectively take the azimuth observation window

and the pitch difference sum ratio r_ele and the azimuth difference sum ratio r_azi in the pitch observation window θ_win to obtain the angle discrimination curves in the azimuth and pitch directions, so as to achieve the purpose of decoupling.

本发明与现有技术相比，具有以下优点：Compared with the prior art, the present invention has the following advantages:

(1)本方法有效解决了方位向与俯仰向耦合的问题，因此有效降低了和差测角算法需要存储的鉴角曲线的数据量，使得测角算法的工程实现复杂度降低，数据量变小；(1) This method effectively solves the problem of azimuth and pitch coupling, thus effectively reducing the amount of data of the angle detection curves that need to be stored by the sum-difference angle measurement algorithm, reducing the complexity of the engineering implementation of the angle measurement algorithm and reducing the amount of data ;

(2)本方法在取近似的基础上得到的鉴角曲线，减小数据量的同时，误差没有显著增大，提升了该算法的综合性能。(2) The angle discrimination curve obtained by this method on the basis of approximation reduces the amount of data and at the same time, the error does not increase significantly, which improves the comprehensive performance of the algorithm.

附图说明Description of drawings

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。In order to more clearly illustrate the technical solutions in the embodiments of the present invention or the prior art, the following will briefly introduce the drawings that need to be used in the description of the embodiments or the prior art. Obviously, the accompanying drawings in the following description are only These are some embodiments of the present invention. Those skilled in the art can also obtain other drawings based on these drawings without creative work.

图1为基于螺旋分布的半球形阵列和差测角解耦合方法流程示意图；Fig. 1 is a schematic flow chart of a hemispherical array based on a helical distribution and a decoupling method of differential angle measurement;

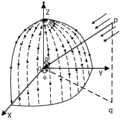
图2为第m个阵元在半球形阵列的阵元坐标图；Fig. 2 is the array element coordinate diagram of the mth array element in the hemispherical array;

图3为直角坐标系中慢速矢量定义图；Fig. 3 is the slow vector definition diagram in the Cartesian coordinate system;

图4为仿真实验的半球形阵列螺旋分布图；Fig. 4 is the hemispherical array spiral distribution figure of simulation experiment;

图5为仿真实验的指向(0°,0°)方向的波束图；Fig. 5 is the beam pattern pointing to (0°, 0°) direction of the simulation experiment;

图6为仿真实验的波束P₁、P₂、P₃、P₄图；Fig. 6 is a diagram of beams P₁ , P₂ , P₃ , and P₄ in the simulation experiment;

图7为图6的X-Y维视图；Fig. 7 is the X-Y dimensional view of Fig. 6;

图8为图7的局部放大图；Figure 8 is a partially enlarged view of Figure 7;

图9为仿真实验的和波束图；Fig. 9 is the sum beam diagram of the simulation experiment;

图10为仿真实验的方位向差波束图；Fig. 10 is the azimuth difference beam diagram of the simulation experiment;

图11为仿真实验的俯仰向差波束图；Figure 11 is the pitch difference beam pattern of the simulation experiment;

图12为仿真实验的观察窗内方位向差和比图；Fig. 12 is the azimuth difference and ratio diagram in the observation window of the simulation experiment;

图13为仿真实验的观察窗内方位向差和比X-Z视图；Fig. 13 is the azimuth direction difference and ratio X-Z view in the observation window of the simulation experiment;

图14为仿真实验的方位向观察窗内鉴角曲线拟合结果图；Fig. 14 is the fitting result figure of the angle-discriminating curve in the azimuth direction observation window of the simulation experiment;

图15为仿真实验的观察窗内俯仰向差和比图；Fig. 15 is the pitch difference and ratio diagram in the observation window of the simulation experiment;

图16为仿真实验的观察窗内俯仰向差和比Y-Z维视图；Fig. 16 is the pitch difference and ratio Y-Z dimension view in the observation window of the simulation experiment;

图17为仿真实验的方位向观察窗内鉴角曲线拟合结果图；Fig. 17 is the fitting result figure of the angle detection curve in the azimuth direction observation window of the simulation experiment;

图18为仿真实验的SNR-方位向估计误差曲线图；Fig. 18 is the SNR-azimuth estimation error curve diagram of the simulation experiment;

图19为仿真实验的SNR-俯仰向估计误差曲线图；Fig. 19 is the SNR-pitch estimation error curve diagram of the simulation experiment;

图20为对比实验的常规的阵列坐标系中慢速矢量定义图；Fig. 20 is a slow vector definition diagram in the conventional array coordinate system of the comparative experiment;

图21为对比实验的常规坐标系下的四个波束图的原始视图；Figure 21 is the original view of the four beam patterns under the conventional coordinate system of the comparative experiment;

图22为图21的X-Y视图；Fig. 22 is the X-Y view of Fig. 21;

图23为对比实验的观察窗内方位向差和比的原始视图；Figure 23 is the original view of the azimuth difference and ratio in the observation window of the comparative experiment;

图24为图23的X-Z视图；Fig. 24 is the X-Z view of Fig. 23;

图25为对比实验的观察窗内俯仰向差和比的原始视图；Figure 25 is the original view of the pitch difference and ratio in the observation window of the comparative experiment;

图26为图25的Y-Z视图。Fig. 26 is a Y-Z view of Fig. 25 .

具体实施方式Detailed ways

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。The following will clearly and completely describe the technical solutions in the embodiments of the present invention with reference to the accompanying drawings in the embodiments of the present invention. Obviously, the described embodiments are only some, not all, embodiments of the present invention. Based on the embodiments of the present invention, all other embodiments obtained by persons of ordinary skill in the art without making creative efforts belong to the protection scope of the present invention.

图1所示为本发明实施例提供的一种基于螺旋分布的半球形阵列和差测角解耦合方法的流程示意图。FIG. 1 is a schematic flowchart of a hemispherical array based on a helical distribution and a decoupling method for differential angle measurement provided by an embodiment of the present invention.

如图1所示，本发明实施例提供的基于螺旋分布的半球形阵列和差测角解耦合方法，包括如下步骤：As shown in Figure 1, the hemispherical array based on the helical distribution provided by the embodiment of the present invention and the differential angle decoupling method include the following steps:

步骤1：按照螺旋分布的排列方式将N个阵元分布在一个半径为R的半球面上；Step 1: Distribute N array elements on a hemispherical surface with radius R according to the arrangement of spiral distribution;

N个阵元分布在半球形球面上，整个半球体统称为雷达阵列，即雷达阵列包含N个阵元。N array elements are distributed on a hemispherical surface, and the entire hemisphere is collectively called a radar array, that is, the radar array includes N array elements.

子步骤1a，N个阵元中，其中将第m个阵元在如图2所示坐标系中的位置记为点p_m，记q_m为点p_m在平面XOY的投影点，其中

∠ZOp_m＝θ_m，则根据螺旋分布的定义可得：Sub-step 1a, among the N array elements, the position of the mth array element in the coordinate system shown in Figure 2 is recorded as point p_m , and q_m is the projection point of point p_m on the plane XOY, where

∠ZOp_m ＝θ_m , then according to the definition of spiral distribution:

θ_m＝arccos(h_m)，

其中，1≤m≤N；θ_m = arccos(h_m ),

Among them, 1≤m≤N;

其中，2≤m≤N-1，

Among them, 2≤m≤N-1,

子步骤1b，根据子步骤1a可以得到，第m个阵元在如图所示直角坐标系中的XYZ坐标为：Sub-step 1b, according to sub-step 1a, it can be obtained that the XYZ coordinates of the mth array element in the Cartesian coordinate system shown in the figure are:

z_m＝R sinθ_mz_m =R sinθ_m

子步骤1c，根据子步骤1b得到的第m个阵元的阵元坐标，由此可以将N个阵元按照螺旋分布在一个半径为R的半球体上。In sub-step 1c, according to the array element coordinates of the mth array element obtained in sub-step 1b, N array elements can be spirally distributed on a hemisphere with a radius of R.

步骤2：重新定义某方向到来的信号方位角

和俯仰角θ，由此得到重新定义的慢速矢量r；具体包含如下子步骤：Step 2: Redefine the azimuth of the incoming signal in a certain direction

and the pitch angle θ, thus obtaining the redefined slow vector r; specifically includes the following sub-steps:

子步骤2a，假设一来波信号如图3中

所示，q为p点在平面XOZ的投影点，图中的黑色实心圆点为阵元，定义∠qOZ＝θ，

Sub-step 2a, assuming an incoming wave signal as shown in Figure 3

As shown, q is the projection point of point p on the plane XOZ, the black solid circle in the figure is the array element, define ∠qOZ=θ,

子步骤2b，根据慢速矢量的定义，得到慢速矢量为：Sub-step 2b, according to the definition of the slow vector, the slow vector is obtained as:

步骤3：假定目标波束期望方向为

在步骤1和步骤2的基础上，合成波束指向分别为

和

四个波束，分别记为P₁、P₂、P₃和P₄；其中，△θ和

分别为方位向和俯仰向的角度偏差；Step 3: Assume that the desired direction of the target beam is

On the basis ofstep 1 and step 2, the synthetic beam points are respectively

and

The four beams are denoted as P₁ , P₂ , P₃ and P₄ respectively; among them, △θ and

are the angular deviations in azimuth and pitch, respectively;

具体包含以下子步骤：It specifically includes the following sub-steps:

子步骤3a，根据半球形阵列波束形成的定义，得到指向

的波束为：Sub-step 3a, according to the definition of hemispherical array beamforming, get the pointing

The beam is:

其中，

和θ如图3中的定义所示，

为目标方位角的角度，θ₀为目标俯仰角的角度，N为雷达阵列中阵元的总个数，H表示共轭转置，

表示汉德蒙德积，L_i为雷达阵列中第i个阵元的空间位置，且L_i＝[x_i y_i z_i]^T,1≤i≤N，r为慢速矢量，

为第i个阵元的空间位置指向

的加权值，且

j为虚数因子，λ为来波信号波长，

为第i个阵元方向图函数，且

in,

and θ are defined in Fig. 3,

is the angle of target azimuth angle,_θ0 is the angle of target pitch angle, N is the total number of array elements in the radar array, H represents the conjugate transpose,

Represents the Handmond product, L_i is the spatial position of the i-th array element in the radar array, and L_i =[xi_yi z_i ]^T , 1≤i≤N, r is the slow vector,

is the spatial position of the i-th array element pointing to

weighted value of , and

j is the imaginary factor, λ is the wavelength of the incoming signal,

is the pattern function of the i-th array element, and

根据上述定义可以得到P₁、P₂、P₃和P₄分别为：According to the above definitions, P₁ , P₂ , P₃ and P₄ can be obtained as:

步骤4：计算和波束P_sum、俯仰向差波束P_ele、方位向差波束P_azi、俯仰向差和比r_ele和方位向差和比r_azi；Step 4: Calculate sum beam P_sum , pitch difference beam P_ele , azimuth difference beam P_azi , pitch difference sum ratio r_ele and azimuth difference sum ratio_razi ;

具体包含如下子步骤：It specifically includes the following sub-steps:

子步骤4a，根据和波束的定义，得到和波束P_sum的计算公式为：In sub-step 4a, according to the definition of the sum beam, the calculation formula of the sum beam P_sum is obtained as:

P_sum＝P₁+P₂+P₃+P₄；P_sum =P₁ +P₂ +P₃ +P₄ ;

子步骤4b，根据俯仰向差波束的定义，得到俯仰向差波束P_ele的计算公式为：In sub-step 4b, according to the definition of the pitch difference beam, the calculation formula of the pitch difference beam P_ele is obtained as:

P_ele＝P₁+P₂-P₃-P₄；P_ele =P₁ +P₂ -P₃ -P₄ ;

子步骤4c，根据方位向差波束的定义，得到方位向差波束P_azi的计算公式为：In sub-step 4c, according to the definition of the azimuth difference beam, the calculation formula of the azimuth difference beam P_azi is obtained as:

P_azi＝P₁-P₂+P₃-P₄；P_azi =P₁ -P₂ +P₃ -P₄ ;

子步骤4d，根据俯仰向差和比的定义，得到俯仰向差和比r_ele的计算公式为：In sub-step 4d, according to the definition of the pitch difference and ratio, the calculation formula of the pitch difference and ratio r_ele is:

子步骤4e，根据方位向差和比的定义，得到方位向差和比r_azi的计算公式为：In sub-step 4e, according to the definition of the azimuth difference and ratio, the formula for calculating the azimuth difference and ratio r_azi is:

由此得到和波束P_sum、俯仰向差波束P_ele、方位向差波束P_azi、俯仰向差和比r_ele和方位向差和比r_azi。Thus, the sum beam P_sum , the elevation difference beam P_ele , the azimuth difference beam P_azi , the elevation difference sum ratio r_ele , and the azimuth difference sum ratio_razi are obtained.

步骤5：设置方位向观察窗

和俯仰向观察窗θ_win，分别取方位向观察窗

和俯仰向观察窗θ_win内的俯仰向差和比r_ele和方位向差和比r_azi，得到方位向和俯仰向的鉴角曲线，从而达到解耦合的目的。Step 5: Set the azimuth viewing window

and pitch observation window θ_win , respectively take the azimuth observation window

and the pitch difference sum ratio r_ele and the azimuth difference sum ratio r_azi in the pitch observation window θ_win to obtain the angle discrimination curves in the azimuth and pitch directions, so as to achieve the purpose of decoupling.

具体的，设置1-2°的方位向观察窗

和俯仰向观察窗θ_win。上述步骤4得到的俯仰向差和比r_ele和方位向差和比r_azi实际上是一个关于θ和

的函数，通过设置一个小范围的方位向观察窗

和俯仰向观察窗θ_win，近似认为俯仰向差和比r_ele与方位角

无关，方位向差和比r_azi与俯仰角θ无关，从而达到解耦合的目的。那么方位向的鉴角曲线就是方位向差和比曲面在θ_o处的切片，俯仰向的鉴角曲线就是俯仰向差和比曲面在

处的切片。Specifically, set a 1-2° azimuth observation window

and pitch to the observation window θ_win . The pitch difference sum ratio r_ele and the azimuth difference ratio r_azi obtained in the above step 4 are actually a relationship between θ and

function, by setting a small range of azimuth observation window

and pitch observation window θ_win , it is approximately considered that pitch difference sum ratio r_ele and azimuth angle

The_azimuth difference and ratio razi have nothing to do with the pitch angle θ, so as to achieve the purpose of decoupling. Then the angle detection curve in azimuth is the slice of the difference in azimuth and the ratio surface at θ_o , and the angle detection curve in the pitch direction is the difference in pitch and the ratio surface at

slices at.

以下通过仿真实验对本发明实施例提供的上述方法的效果进行验证：The effect of the above-mentioned method provided by the embodiment of the present invention is verified by simulation experiments as follows:

1.仿真实验环境和数据：1. Simulation experiment environment and data:

实验环境：Inter(R)Core(TM)i5-6500 CPU@3.20HGz，64位Windows操作系统和MATLAB 2016b仿真软件。Experimental environment: Inter(R) Core(TM) i5-6500 CPU@3.20HGz, 64-bit Windows operating system and MATLAB 2016b simulation software.

实验参数：雷达阵列的阵元总个数N为200个，方位角

的取值范围为-90°～90°，俯仰角θ的取值范围为-90°～90°，目标指向

为(0°,0°)，俯仰向偏角△θ＝1°，方位向偏角

俯仰向观察窗θ_win＝1°，方位向观察窗

Experimental parameters: The total number N of radar array elements is 200, and the azimuth angle

The value range of θ is -90°～90°, the value range of pitch angle θ is -90°～90°, and the target pointing

is (0°,0°), the pitch angle is △θ=1°, the azimuth angle is

Pitch to the observation window θ_win = 1°, azimuth to the observation window

2.仿真实验结果：2. Simulation results:

由步骤1得到的半球形阵列螺旋分布如图4所示；The spiral distribution of the hemispherical array obtained instep 1 is shown in Figure 4;

根据步骤3可以得到指向目标方位(0°,0°)的波束如图5所示；According to step 3, the beam pointing to the target azimuth (0°, 0°) can be obtained as shown in Figure 5;

波束P₁、P₂、P₃和P₄如图6所示，图7为图6的X-Y维视图，图8为图7的局部放大图。从图8中可以看出，四个波束分别指向(-1°,-1°)、(-1°,1°)、(1°,-1°)和(1°,1°)。Beams P₁ , P₂ , P₃ and P₄ are shown in FIG. 6 , FIG. 7 is an XY-dimensional view of FIG. 6 , and FIG. 8 is a partially enlarged view of FIG. 7 . It can be seen from Figure 8 that the four beams point to (-1°, -1°), (-1°, 1°), (1°, -1°) and (1°, 1°) respectively.

从图9中可以看出，和波束指向(0°,0°)。由图10和图11可以得到，方位向差波束和俯仰向差波束在(0°,0°)点旁边分别存在一个波峰和一个波谷，所不同的是，方位向差波束(0°,0°)旁的波峰和波谷是在

这个维度，俯仰向差波束(0°,0°)旁的波峰和波谷是在θ这个维度。As can be seen from Figure 9, and the beam points to (0°,0°). From Figure 10 and Figure 11, it can be obtained that the azimuth difference beam and the elevation difference beam have a peak and a trough respectively next to the point (0°, 0°). The difference is that the azimuth difference beam (0°, 0°) °) next to the peaks and troughs are in

In this dimension, the crest and trough beside the pitch difference beam (0°,0°) are in the dimension θ.

从图12和图13可以得到，观察窗内方位向差和比只与方位角

有关，与俯仰角θ无关，在观察窗内，本发明认为，方位向差和比近似于方位角

是线性关系，对其进行拟合得到的曲线如图14所示，从图14可以看出，拟合效果良好，拟合直线的表达式为

It can be obtained from Figure 12 and Figure 13 that the azimuth difference sum ratio in the observation window is only related to the azimuth angle

It is related and has nothing to do with the pitch angle θ. In the observation window, the present invention considers that the azimuth difference sum ratio is approximately the azimuth angle

is a linear relationship, and the curve obtained by fitting it is shown in Figure 14. It can be seen from Figure 14 that the fitting effect is good, and the expression of the fitted line is

从图15和图16可以得到，观察窗内俯仰向差和比只与俯仰角θ有关，与方位角

无关，在观察窗内，本发明认为，俯仰向差和比近似与俯仰角θ是线性关系，对其进行拟合得到的曲线如图17所示，从图17可以看出，拟合效果良好，拟合直线的表达式为r_ele＝-0.1175θ。From Fig. 15 and Fig. 16, it can be obtained that the pitch difference sum ratio in the observation window is only related to the pitch angle θ, and is not related to the azimuth angle

Nothing to do, in the observation window, the present invention believes that the pitch difference sum ratio is approximately linear with the pitch angle θ, and the curve obtained by fitting it is shown in Figure 17, and it can be seen from Figure 17 that the fitting effect is good , the expression of the fitting line is r_ele =-0.1175θ.

在图14和图17所示的鉴角曲线的基础上，对其进行和差测角和误差分析，可以得到误差-SNR曲线如图18和图19所示。On the basis of the angle detection curves shown in Figure 14 and Figure 17, the sum and difference angle measurement and error analysis can be performed on it, and the error-SNR curve can be obtained as shown in Figure 18 and Figure 19.

由图18和图19可知，在图14和图17所获得鉴角曲线的基础上，用半球形螺旋分布的阵列对其进行和差测角，得到的误差大概在0.07左右，误差处于一个比较小的范围，并且信噪比SNR对误差的影响不是很大，这主要是因为和波束和差波束在做比值前，信号对其进行积累导致的。It can be seen from Figure 18 and Figure 19 that, on the basis of the angle discrimination curves obtained in Figure 14 and Figure 17, the array of hemispherical spiral distribution is used to measure the sum and difference of the angle, and the error obtained is about 0.07, which is in a comparison The range is small, and the signal-to-noise ratio SNR does not have a great influence on the error, which is mainly caused by the signal accumulation before the sum beam and the difference beam are compared.

由图18和图19所示，设置的方位向和俯仰向的观察窗大小分别为2°，因为方位向和俯仰向已经解耦合，因此需要预存储的直线数据为180条直线；但是如果没有解耦合，那么需要预存储的数据量大约为上千个平面，而且每个平面假设都由几百条直线组成，那么需要存储的直线大约为10⁵条。As shown in Figure 18 and Figure 19, the size of the observation window in the azimuth direction and the pitch direction is set to 2° respectively, because the azimuth direction and the pitch direction have been decoupled, so the straight line data that needs to be pre-stored is 180 straight lines; but if there is no Decoupling, the amount of data that needs to be pre-stored is about thousands of planes, and each plane is assumed to be composed of hundreds of straight lines, then the number of straight lines that need to be stored is about 10⁵ .

3.对比实验结果：3. Compare the experimental results:

常规的阵列坐标系定义，如图20所示，图中p为空间一电磁波向量，q为p在XOY平面的投影，其中

∠ZOp＝θ。那么慢速矢量为：Conventional array coordinate system definition, as shown in Figure 20, p in the figure is a space-electromagnetic wave vector, q is the projection of p on the XOY plane, where

∠ZOp=θ. Then the slow vector is:

假定球面半径R＝10λ，中心波束的指向的角度为(10°,10°)，那么分别合成指向(11°,9°)、(9°,11°)、(9°,9°)和(11°,11°)四个方向的波束，四个波束如图21和图22所示：Assuming that the radius of the sphere is R=10λ, and the pointing angle of the center beam is (10°, 10°), then the synthetic points are (11°, 9°), (9°, 11°), (9°, 9°) and (11°, 11°) beams in four directions, the four beams are shown in Figure 21 and Figure 22:

图21为常规坐标系下的四个波束图的原始视图，图22为图21的X-Y视图；可以看出：图中只有俯仰向的两个波束。这是因为波束在方位向上比较宽，但是其指向的角度却相差很小，所以方位向的两个波束重合到在一起，因此，在图中只能看到俯仰向的两个波束。综上所述，可以得出结论：在常规坐标系下，螺旋分布的四个波束图在俯仰向上完全不对称。Figure 21 is the original view of the four beam patterns in the conventional coordinate system, and Figure 22 is the X-Y view of Figure 21; it can be seen that there are only two beams in the elevation direction in the figure. This is because the beam is relatively wide in azimuth, but the difference in pointing angle is very small, so the two beams in azimuth overlap together, so only the two beams in elevation can be seen in the figure. In summary, it can be concluded that in the conventional coordinate system, the four beam patterns of the helical distribution are completely asymmetrical in the pitch direction.

假设方位向观察窗

俯仰向观察窗θ_win＝1°，求得的观察窗内方位向差和比和俯仰向差和比如图23-图26所示。图23为观察窗内方位向差和比的原始视图，图24为图23的X-Z视图，图25为观察窗内俯仰向差和比的原始视图，图26为图25的Y-Z视图。从图中可以看出，方位向差和比与俯仰向差和比不仅与方位角有关，还与俯仰角有关，因此，在常规坐标系下，螺旋分布的半球形阵列方位向和俯仰向相耦合，和差测角时，预存储的数据将会很多。Assumed azimuth towards observation window

The pitch observation window θ_win =1°, and the ratio of azimuth difference sum and pitch difference sum ratio in the observation window obtained is shown in Fig. 23-Fig. 26 . Figure 23 is the original view of the azimuth difference and ratio in the observation window, Figure 24 is the XZ view of Figure 23, Figure 25 is the original view of the pitch difference and ratio in the observation window, and Figure 26 is the YZ view of Figure 25. It can be seen from the figure that the azimuth difference sum ratio and the pitch difference sum ratio are not only related to the azimuth angle, but also related to the pitch angle. When coupling and measuring angles, there will be a lot of pre-stored data.

由上述仿真实验和对比实验结果可知，本发明的方法在坐标重新定义和取近似的基础上，有效的在部分范围内解决了半球形阵列螺旋分布和差测角时存在的方位向和俯仰向耦合的问题，大大减少了和差测角需要预存储的数据量，并且使得和差测角的误差处于一个比较小的范围。It can be seen from the results of the above-mentioned simulation experiments and comparative experiments that the method of the present invention effectively solves the azimuth and pitch directions that exist in the hemispherical array helical distribution and differential angle measurement on the basis of coordinate redefinition and approximation. The problem of coupling greatly reduces the amount of data that needs to be pre-stored in the sum and difference angle measurement, and makes the error of the sum and difference angle measurement in a relatively small range.

本领域普通技术人员可以理解：实现上述方法实施例的全部或部分步骤可以通过程序指令相关的硬件来完成，前述的程序可以存储于计算机可读取存储介质中，该程序在执行时，执行包括上述方法实施例的步骤；而前述的存储介质包括：ROM、RAM、磁碟或者光盘等各种可以存储程序代码的介质。Those of ordinary skill in the art can understand that all or part of the steps to realize the above method embodiments can be completed by hardware related to program instructions, and the aforementioned programs can be stored in computer-readable storage media. When the program is executed, the execution includes The steps of the above-mentioned method embodiments; and the aforementioned storage medium includes: ROM, RAM, magnetic disk or optical disk and other various media that can store program codes.

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以所述权利要求的保护范围为准。The above is only a specific embodiment of the present invention, but the scope of protection of the present invention is not limited thereto. Anyone skilled in the art can easily think of changes or substitutions within the technical scope disclosed in the present invention. Should be covered within the protection scope of the present invention. Therefore, the protection scope of the present invention should be determined by the protection scope of the claims.

Claims (6)

Translated fromChinese

1.一种基于螺旋分布的半球形阵列和差测角解耦合方法，其特征在于，包括如下步骤：1. A hemispherical array based on helical distribution and a method for decoupling the angle of difference measurement, is characterized in that, comprises the steps:步骤1：按照螺旋分布的排列方式将N个阵元分布在一个半径为R的半球面上；Step 1: Distribute N array elements on a hemispherical surface with radius R according to the arrangement of spiral distribution;步骤2：重新定义某方向到来的信号方位角

和俯仰角θ，得到重新定义的慢速矢量r；Step 2: Redefine the azimuth of the incoming signal in a certain direction

And the pitch angle θ, get the redefined slow vector r;步骤3：假定目标波束期望方向为

在步骤1和步骤2的基础上，合成波束指向分别为

和

四个波束，分别记为P₁、P₂、P₃和P₄；其中，△θ和

分别为方位向和俯仰向的角度偏差；Step 3: Assume that the desired direction of the target beam is

On the basis of step 1 and step 2, the synthetic beam points are respectively

and

The four beams are denoted as P₁ , P₂ , P₃ and P₄ respectively; among them, △θ and

are the angular deviations in azimuth and pitch, respectively;步骤4：计算和波束P_sum、俯仰向差波束P_ele、方位向差波束P_azi、俯仰向差和比r_ele和方位向差和比r_azi；Step 4: Calculate sum beam P_sum , pitch difference beam P_ele , azimuth difference beam P_azi , pitch difference sum ratio r_ele and azimuth difference sum ratio_razi ;步骤5：设置方位向观察窗

和俯仰向观察窗θ_win，分别取方位向观察窗

和俯仰向观察窗θ_win内的俯仰向差和比r_ele和方位向差和比r_azi，得到方位向和俯仰向的鉴角曲线，从而达到解耦合的目的。Step 5: Set the azimuth viewing window

and pitch observation window θ_win , respectively take the azimuth observation window

and the pitch difference sum ratio r_ele and the azimuth difference sum ratio r_azi in the pitch observation window θ_win to obtain the angle discrimination curves in the azimuth and pitch directions, so as to achieve the purpose of decoupling.2.根据权利要求1所述的基于螺旋分布的半球形阵列和差测角解耦合方法，其特征在于，步骤1中，所述按照螺旋分布的排列方式将N个阵元分布在一个半径为R的半球面上，具体包含如下子步骤：2. The hemispherical array based on the helical distribution according to claim 1 and the method for decoupling the difference measurement angle, characterized in that, in step 1, the N array elements are distributed in a radius of On the hemispherical surface of R, it specifically includes the following sub-steps:子步骤1a，N个阵元中，其中将第m个阵元在坐标系中的位置记为点p_m，记q_m为点p_m在平面XOY的投影点，其中

则根据螺旋分布的定义，得到：Sub-step 1a, among the N array elements, the position of the mth array element in the coordinate system is recorded as point p_m , and q_m is the projection point of point p_m on the plane XOY, where

According to the definition of spiral distribution, we get:

其中，1≤m≤N；

Among them, 1≤m≤N;

其中，2≤m≤N-1，

Among them, 2≤m≤N-1,

子步骤1b，根据子步骤1a可得，第m个阵元在直角坐标系中的XYZ坐标为：Sub-step 1b, according to sub-step 1a, the XYZ coordinates of the mth array element in the Cartesian coordinate system are:

z_m＝Rsinθ_mz_m = Rsinθ_m子步骤1c，根据子步骤1b得到的第m个阵元的阵元坐标，由此将N个阵元按照螺旋分布在一个半径为R的半球体上。In sub-step 1c, according to the array element coordinates of the mth array element obtained in sub-step 1b, N array elements are spirally distributed on a hemisphere with a radius of R.3.根据权利要求1所述的基于螺旋分布的半球形阵列和差测角解耦合方法，其特征在于，步骤2中，所述得到重新定义的慢速矢量r具体包含如下子步骤：3. The hemispherical array based on helical distribution according to claim 1 and the method for decoupling angles by difference measurement, wherein in step 2, the redefined slow vector r obtained specifically includes the following sub-steps:子步骤2a，假设一来波信号

q为p点在平面XOZ的投影点，定义∠qOZ＝θ，

Sub-step 2a, assuming an incoming wave signal

q is the projection point of point p on the plane XOZ, define ∠qOZ=θ,

子步骤2b，根据慢速矢量的定义，得到慢速矢量为：Sub-step 2b, according to the definition of the slow vector, the slow vector is obtained as:

4.根据权利要求1所述的基于螺旋分布的半球形阵列和差测角解耦合方法，其特征在于，步骤3中，四个波束P₁、P₂、P₃和P₄的计算算法包含如下子步骤：4. The hemispherical array based on the helical distribution according to claim 1 and the method for decoupling the angle of difference measurement, it is characterized in that, in step 3, the calculation algorithm of the four beams P₁ , P₂ , P₃ and P₄ includes The following sub-steps:子步骤3a，根据半球形阵列波束形成的定义，得到指向

的波束为：Sub-step 3a, according to the definition of hemispherical array beamforming, get the pointing

The beam is:

其中，

为目标方位角的角度，θ₀为目标俯仰角的角度，N为雷达阵列中阵元的总个数，H表示共轭转置，

表示汉德蒙德积，L_i为雷达阵列中第i个阵元的空间位置，且L_i＝[x_i y_iz_i]^T,1≤i≤N，r为慢速矢量，

为第i个阵元的空间位置指向

的加权值，且

j为虚数因子，λ为来波信号波长，

为第i个阵元方向图函数，且

in,

is the angle of target azimuth angle,_θ0 is the angle of target pitch angle, N is the total number of array elements in the radar array, H represents the conjugate transpose,

Represents the Handmond product, L_i is the spatial position of the i-th array element in the radar array, and L_i =[xi_yi z_i ]^T , 1≤i≤N, r is the slow vector,

is the spatial position of the i-th array element pointing to

weighted value of , and

j is the imaginary factor, λ is the wavelength of the incoming signal,

is the pattern function of the i-th array element, and

子步骤3b，根据子步骤3a，得到指向

方向的波束P₁为：Sub-step 3b, according to sub-step 3a, get pointing to

The direction of beam_P1 is:

子步骤3c，根据子步骤3a，得到指向

方向的波束P₂为：Sub-step 3c, according to sub-step 3a, get pointing to

The direction of beam_P2 is:

子步骤3d，根据子步骤3a，得到指向

方向的波束P₃为：Sub-step 3d, according to sub-step 3a, get pointing to

The direction of beam_P3 is:

子步骤3e，根据子步骤3a，得到指向

方向的波束P₄为：Sub-step 3e, according to sub-step 3a, get pointing to

The direction of beam P₄ is:

5.根据权利要求1所述的基于螺旋分布的半球形阵列和差测角解耦合方法，其特征在于，步骤4中，所述计算包含如下子步骤：5. the hemispherical array based on helical distribution according to claim 1 and the method for decoupling angles by difference measurement, is characterized in that, in step 4, the calculation includes the following sub-steps:子步骤4a，根据和波束的定义，得到和波束P_sum的计算公式为：In sub-step 4a, according to the definition of the sum beam, the calculation formula of the sum beam P_sum is obtained as:P_sum＝P₁+P₂+P₃+P₄；P_sum =P₁ +P₂ +P₃ +P₄ ;其中，P₁为指向

方向的波束；P₂为指向

方向的波束；P₃为指向

方向的波束；P₄为指向

方向的波束；where P₁ is pointing to

Beam in direction; P₂ is pointing

Beam in direction; P₃ is pointing

Beam in direction; P₄ is pointing

the direction of the beam;子步骤4b，根据俯仰向差波束的定义，得到俯仰向差波束P_ele的计算公式为：In sub-step 4b, according to the definition of the pitch difference beam, the calculation formula of the pitch difference beam P_ele is obtained as:P_ele＝P₁+P₂-P₃-P₄；P_ele =P₁ +P₂ -P₃ -P₄ ;子步骤4c，根据方位向差波束的定义，得到方位向差波束P_azi的计算公式为：In sub-step 4c, according to the definition of the azimuth difference beam, the calculation formula of the azimuth difference beam P_azi is obtained as:P_azi＝P₁-P₂+P₃-P₄；P_azi =P₁ -P₂ +P₃ -P₄ ;子步骤4d，根据俯仰向差和比的定义，得到俯仰向差和比r_ele的计算公式为：In sub-step 4d, according to the definition of the pitch difference and ratio, the calculation formula of the pitch difference and ratio r_ele is:

子步骤4e，根据方位向差和比的定义，得到方位向差和比r_azi的计算公式为：In sub-step 4e, according to the definition of the azimuth difference and ratio, the formula for calculating the azimuth difference and ratio r_azi is:

6.根据权利要求1所述的基于螺旋分布的半球形阵列和差测角解耦合方法，其特征在于，步骤5中，所述得到方位向和俯仰向的鉴角曲线，具体包含如下子步骤：6. The hemispherical array based on the helical distribution according to claim 1 and the differential angle decoupling method, characterized in that, in step 5, the obtaining of the angle discrimination curves in the azimuth direction and the pitch direction specifically includes the following sub-steps :子步骤5a，设置1-2°的方位向观察窗

和俯仰向观察窗θ_win，观察在方位向观察窗

和俯仰向观察窗θ_win范围内的方位向差和比r_azi与俯仰向差和比r_ele；Sub-step 5a, set the azimuth observation window of 1-2°

and the observation window θ_win in the pitch direction, observe the observation window in the azimuth direction

and the azimuth difference and ratio r_azi and the pitch difference and ratio r_ele within the scope of the observation window θ_win ;子步骤5b，认为俯仰向差和比r_ele与方位角

无关，方位向差和比r_azi与俯仰角θ无关，分别得到方位向和俯仰向的鉴角曲线，即所述方位向的鉴角曲线为方位向差和比曲面在θ_o处的切片，俯仰向的鉴角曲线为俯仰向差和比曲面在

处的切片。Sub-step 5b, it is considered that the pitch difference sum ratio r_ele and the azimuth angle

Irrelevant, the azimuth difference and ratio r_azi have nothing to do with the pitch angle θ, and the angle discrimination curves of the azimuth direction and the pitch direction are respectively obtained, that is, the angle discrimination curve of the azimuth direction is a slice of the azimuth difference and ratio surface at θ_o , The angle discrimination curve in the pitch direction is the pitch difference sum ratio surface in

slices at.

Images