Bit-Interleaved Coded Modulation (BICM)
In this notebook you will learn about the principles of bit interleaved coded modulation (BICM) and focus on the interface between LDPC decoding and demapping for higher order modulation. Further, we will discuss the idea ofall-zero codeword simulations that enable bit-error rate simulations without having an explicit LDPC encoder available. In the last part, we analyze what happens for mismatched demapping, e.g., if the SNR is unknown and show how min-sum decoding can have practicaladvantages in such cases.
“From the coding viewpoint, the modulator, waveform channel, and demodulator together constitute a discrete channel with\(q\)input letters and\(q'\)output letters. […] the real goal of the modulation system is to create the “best” discrete memoryless channel (DMC) as seen by the coding system.” James L. Massey, 1974 [4, cf. preface in 5].
The fact that we usually separate modulation and coding into two individual tasks is strongly connected to the concept of bit-interleaved coded modulation (BICM) [1,2,5]. However, the joint optimization of coding and modulation has a long history, for example by Gottfried Ungerböck’sTrellis coded modulation (TCM) [3] and we refer the interested reader to [1,2,5,6] for theseprinciples of coded modulation [5]. Nonetheless, BICM has become thede facto standard in virtually any moderncommunication system due to its engineering simplicity.
In this notebook, you will use the following components:
Mapper / demapper and the constellation class
LDPC5GEncoder / LDPC5GDecoder
AWGN channel
BinarySource and GaussianPriorSource
Interleaver / deinterleaver
Scrambler / descrambler
Table of Contents
System Block Diagram
We introduce the following terminology:
udenotes thekuncoded information bitscdenotes thencodewords bitsxdenotes the complex-valued symbols after mappingmbits to one symbolydenotes the (noisy) channel observationsl_chdenotes the demappers llr estimate on each bitcu_hatdenotes the estimated information bits at the decoder output
GPU Configuration and Imports
[1]:
importosifos.getenv("CUDA_VISIBLE_DEVICES")isNone:gpu_num=0# Use "" to use the CPUos.environ["CUDA_VISIBLE_DEVICES"]=f"{gpu_num}"os.environ['TF_CPP_MIN_LOG_LEVEL']='3'# Import Sionnatry:importsionna.phyexceptImportErrorase:importsysif'google.colab'insys.modules:# Install Sionna in Google Colabprint("Installing Sionna and restarting the runtime. Please run the cell again.")os.system("pip install sionna")os.kill(os.getpid(),5)else:raisee# Configure the notebook to use only a single GPU and allocate only as much memory as needed# For more details, see https://www.tensorflow.org/guide/gpuimporttensorflowastfgpus=tf.config.list_physical_devices('GPU')ifgpus:try:tf.config.experimental.set_memory_growth(gpus[0],True)exceptRuntimeErrorase:print(e)# Avoid warnings from TensorFlowtf.get_logger().setLevel('ERROR')%matplotlib inlineimportmatplotlib.pyplotaspltimportnumpyasnp# Load the required Sionna componentsfromsionna.phyimportBlockfromsionna.phy.mappingimportConstellation,Mapper,Demapper,BinarySourcefromsionna.phy.fec.ldpcimportLDPC5GEncoder,LDPC5GDecoder,LDPCBPDecoder,EXITCallbackfromsionna.phy.fec.interleavingimportRandomInterleaver,Deinterleaverfromsionna.phy.fec.scramblingimportScrambler,Descramblerfromsionna.phy.fec.utilsimportGaussianPriorSource,load_parity_check_examples, \get_exit_analytic,plot_exit_chart,plot_trajectoryfromsionna.phy.utilsimportebnodb2no,hard_decisions,PlotBERfromsionna.phy.channelimportAWGNsionna.phy.config.seed=42# Set seed for reproducible random number generation
A Simple BICM System
The principle idea of higher order modulation is to mapm bits to one (complex-valued) symbolx. As each received symbol now contains information aboutm transmitted bits, the demapper producesm bit-wise LLR estimates (one per transmitted bit) where each LLR contains information about an individual bit. This scheme allows a simple binary interface between demapper and decoder.
From a decoder’s perspective, the transmission of allm bits - mapped onto one symbol - could be modeled as if they have been transmitted overm differentsurrogate channels with certain properties as shown in the figure below.
In the following, we are now interested in the LLR distribution at the decoder input (= demapper output) for each of thesesurrogate channels (denoted asbit-channels in the following). Please note that in some scenario these surrogate channels can share the same statistical properties, e.g., for QPSK, both bit-channels behave equally due to symmetry.
Advanced note: them binary LLR values are treated as independent estimates which is not exactly true for higher order modulation. As a result, the sum of thebitwise mutual information of allm transmitted bits does not exactly coincide with thesymbol-wise mutual information describing the relation between channel input / output from a symbol perspective. However, in practice the (small) losses are usually neglected if a QAM with a rectangular grid and Gray labeling is used.
Constellations and Bit-Channels
Let us first look at some higher order constellations.
[2]:
# show QPSK constellationconstellation=Constellation("qam",num_bits_per_symbol=2)constellation.show();

Assuming an AWGN channel and QPSK modulation all symbols behave equally due to the symmetry (all constellation points are located on a circle). However, for higher order modulation such as 16-QAM the situation changes and the LLRs after demapping are not equally distributed anymore.
[3]:
# generate 16QAM with Gray labelingconstellation=Constellation("qam",num_bits_per_symbol=4)constellation.show();

We can visualize this by applyinga posteriori propability (APP) demapping and plotting of the corresponding LLR distributions for each of them transmitted bits per symbol individually. As each bit could be either0 or1, we flip the signs of the LLRsafter demapping accordingly. Otherwise, we would observe two symmetric distributions per bitb_i forb_i=0 andb_i=1, respectively. See [10] for a closed-form approximation and further details.
[4]:
# simulation parametersbatch_size=int(1e6)# number of symbols to be analyzednum_bits_per_symbol=4# bits per modulated symbol, i.e., 2^4 = 16-QAMebno_db=4# simulation SNR# init system componentssource=BinarySource()# generates random info bits# we use a simple AWGN channelchannel=AWGN()# calculate noise var for given Eb/No (no code used at the moment)no=ebnodb2no(ebno_db,num_bits_per_symbol,coderate=1)# and generate bins for the histogramllr_bins=np.arange(-20,20,0.1)# initialize mapper and demapper for constellation objectconstellation=Constellation("qam",num_bits_per_symbol=num_bits_per_symbol)mapper=Mapper(constellation=constellation)# APP demapperdemapper=Demapper("app",constellation=constellation)# Binary source that generates random 0s/1sb=source([batch_size,num_bits_per_symbol])# init mapper, channel and demapperx=mapper(b)y=channel(x,no)llr=demapper(y,no)# we flip the sign of all LLRs where b_i=0# this ensures that all positive LLRs mark correct decisions# all negative LLR values would lead to erroneous decisionsllr_b=tf.multiply(llr,(2.*b-1.))# calculate LLR distribution for all bit-channels individuallyllr_dist=[]foriinrange(num_bits_per_symbol):llr_np=tf.reshape(llr_b[:,i],[-1]).numpy()t,_=np.histogram(llr_np,bins=llr_bins,density=True);llr_dist.append(t)# and plot the resultsplt.figure(figsize=(20,8))plt.xticks(fontsize=18)plt.yticks(fontsize=18)plt.grid(which="both")plt.xlabel("LLR value",fontsize=25)plt.ylabel("Probability density",fontsize=25)foridx,llr_histinenumerate(llr_dist):leg_str=f"Demapper output for bit_channel{idx} (sign corrected)".format()plt.plot(llr_bins[:-1],llr_hist,label=leg_str)plt.title("LLR distribution after demapping (16-QAM / AWGN)",fontsize=25)plt.legend(fontsize=20);

This also shows up in the bit-wise BER without any forward-error correction (FEC).
[5]:
# calculate bitwise BERsb_hat=hard_decisions(llr)# hard decide the LLRs# each bit where b != b_hat is defines a decision error# cast to tf.float32 to allow tf.reduce_mean operationerrors=tf.cast(tf.not_equal(b,b_hat),tf.float32)# calculate ber PER bit_channel# axis = 0 is the batch-dimension, i.e. contains individual estimates# axis = 1 contains the m individual bit channelsber_per_bit=tf.reduce_mean(errors,axis=0)print("BER per bit-channel: ",ber_per_bit.numpy())
BER per bit-channel: [0.039031 0.038787 0.077408 0.078288]
So far, we have not applied any outer channel coding. However, from the previous histograms it is obvious that the quality of the received LLRs depends bit index within a symbol. Further, LLRs may become correlated and each symbol error may lead to multiple erroneous received bits (mapped to the same symbol). The principle idea of BICM is tobreak the local dependencies by adding an interleaver between channel coding and mapper (or demapper and decoder, respectively).
For sufficiently long codes (and well-suited interleavers), the channel decoder effectivelysees one channel. This separation enables the - from engineering’s perspective - simplified and elegant design of channel coding schemes based on binary bit-metric decoding while following Massey’s original spirit thatthe real goal of the modulation system is to create the “best” discrete memoryless channel (DMC) as seen by the coding system” [1].
Simple BER Simulations
We are now interested to simulate the BER of the BICM system including LDPC codes. For this, we use the classPlotBER which essentially provides convenience functions for BER simulations. It internally callssim_ber() to simulate each SNR point until reaching a pre-defined target number of errors.
Note: a custom BER simulation is always possible. However, without early stopping the simulations can take significantly more simulation time andPlotBER directly stores the results internally for later comparison.
[6]:
# generate new figureber_plot_allzero=PlotBER("BER Performance of All-zero Codeword Simulations")# and define baselinenum_bits_per_symbol=2# QPSKnum_bp_iter=20# number of decoder iterations# LDPC code parametersk=600# number of information bits per codewordn=1200# number of codeword bits# and the initialize the LDPC encoder / decoderencoder=LDPC5GEncoder(k,n)decoder=LDPC5GDecoder(encoder,# connect encoder (for shared code parameters)cn_update="boxplus-phi",# use the exact boxplus functionnum_iter=num_bp_iter)# initialize a random interleaver and corresponding deinterleaverinterleaver=RandomInterleaver()deinterleaver=Deinterleaver(interleaver)# mapper and demapperconstellation=Constellation("qam",num_bits_per_symbol=num_bits_per_symbol)mapper=Mapper(constellation=constellation)demapper=Demapper("app",constellation=constellation)# APP demapper# define system@tf.function()# we enable graph mode for faster simulationsdefrun_ber(batch_size,ebno_db):# calculate noise varianceno=ebnodb2no(ebno_db,num_bits_per_symbol=num_bits_per_symbol,coderate=k/n)u=source([batch_size,k])# generate random bit sequence to transmitc=encoder(u)# LDPC encode (incl. rate-matching and CRC concatenation)c_int=interleaver(c)x=mapper(c_int)# map to symbol (QPSK)y=channel(x,no)# transmit over AWGN channelllr_ch=demapper(y,no)# demappllr_deint=deinterleaver(llr_ch)u_hat=decoder(llr_deint)# run LDPC decoder (incl. de-rate-matching)returnu,u_hat
We simulate the BER at each SNR point inebno_db for a givenbatch_size of samples. In total, per SNR pointmax_mc_iter batches are simulated.
To improve the simulation throughput, several optimizations are available:
) Continue with next SNR point if
num_target_bit_errorsis reached (ornum_target_block_errors).) Stop simulation if current SNR point returned no error (usually the BER is monotonic w.r.t. the SNR, i.e., a higher SNR point will also return BER=0)
Note: by settingforward_keyboard_interrupt=False, the simulation can be interrupted at any time and returns the intermediate results.
[7]:
# the first argument must be a callable (function) that yields u and u_hat for batch_size and ebnober_plot_allzero.simulate(run_ber,# the function have defined previouslyebno_dbs=np.arange(0,5,0.25),# sim SNR rangelegend="Baseline (with encoder)",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,early_stop=True,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 1.6391e-01 | 1.0000e+00 | 98344 | 600000 | 1000 | 1000 | 4.5 |reached target bit errors 0.25 | 1.3859e-01 | 9.9000e-01 | 83152 | 600000 | 990 | 1000 | 0.1 |reached target bit errors 0.5 | 1.0644e-01 | 9.3700e-01 | 63863 | 600000 | 937 | 1000 | 0.1 |reached target bit errors 0.75 | 6.6673e-02 | 7.5900e-01 | 40004 | 600000 | 759 | 1000 | 0.1 |reached target bit errors 1.0 | 3.0815e-02 | 4.7800e-01 | 18489 | 600000 | 478 | 1000 | 0.1 |reached target bit errors 1.25 | 1.0355e-02 | 1.9600e-01 | 6213 | 600000 | 196 | 1000 | 0.1 |reached target bit errors 1.5 | 1.9367e-03 | 5.8000e-02 | 1162 | 600000 | 58 | 1000 | 0.1 |reached target bit errors 1.75 | 6.0944e-04 | 1.6667e-02 | 1097 | 1800000 | 50 | 3000 | 0.3 |reached target bit errors 2.0 | 5.0556e-05 | 1.6970e-03 | 1001 | 19800000 | 56 | 33000 | 2.9 |reached target bit errors 2.25 | 5.8000e-06 | 2.4000e-04 | 174 | 30000000 | 12 | 50000 | 4.3 |reached max iterations 2.5 | 1.0000e-06 | 8.0000e-05 | 30 | 30000000 | 4 | 50000 | 4.3 |reached max iterations 2.75 | 0.0000e+00 | 0.0000e+00 | 0 | 30000000 | 0 | 50000 | 4.3 |reached max iterationsSimulation stopped as no error occurred @ EbNo = 2.8 dB.

All-zero Codeword Simulations
In this section you will learn about how to simulate accurate BER curves without the need for having an actual encoder in-place. We compare each step with the ground truth from the Sionna encoder:
) Simulate baseline with encoder as done above.
) Remove encoder: Simulate QPSK with all-zero codeword transmission.
) Gaussian approximation (for BPSK/QPSK): Remove (de-)mapping and mimic the LLR distribution for the all-zero codeword.
) Learn that a scrambler is required for higher order modulation schemes.
An important property of linear codes is that each codewords has - in average - the same behavior. Thus, for BER simulations the all-zero codeword is sufficient.
Note: strictly speaking, this requiressymmetric decoders in a sense that the decoder is not biased towards positive or negative LLRs (e.g., by interpreting\(\ell_\text{ch}=0\) as positive value). However, in practice this can be either avoided or is often neglected.
Recall that we have simulated the following setup as baseline. Note: for simplicity and readability, the interleaver is omitted in the following.
Let us implement a Sionna Block that can be re-used and configured for the later experiments.
[8]:
classLDPC_QAM_AWGN(Block):"""System model for channel coding BER simulations This model allows to simulate BERs over an AWGN channel with QAM modulation. It can enable/disable multiple options to analyse all-zero codeword simulations. If active, the system uses the 5G LDPC encoder/decoder module. Parameters ---------- k: int number of information bits per codeword. n: int codeword length. num_bits_per_symbol: int number of bits per QAM symbol. demapping_method: str A string defining the demapping method. Can be either "app" or "maxlog". cn_update: str A string defining the check node update function type of the LDPC decoder. use_allzero: bool A boolean defaults to False. If True, no encoder is used and all-zero codewords are sent. use_scrambler: bool A boolean defaults to False. If True, a scrambler after the encoder and a descrambler before the decoder is used, respectively. use_ldpc_output_interleaver: bool A boolean defaults to False. If True, the output interleaver as defined in 3GPP 38.212 is applied after rate-matching. no_est_mismatch: float A float defaults to 1.0. Defines the SNR estimation mismatch of the demapper such that the effective demapping noise variance estimate is the scaled by ``no_est_mismatch`` version of the true noise_variance Input ----- batch_size: int or tf.int The batch_size used for the simulation. ebno_db: float or tf.float A float defining the simulation SNR. Output ------ (u, u_hat): Tuple: u: tf.float32 A tensor of shape `[batch_size, k] of 0s and 1s containing the transmitted information bits. u_hat: tf.float32 A tensor of shape `[batch_size, k] of 0s and 1s containing the estimated information bits. """def__init__(self,k,n,num_bits_per_symbol,demapping_method="app",cn_update="boxplus",use_allzero=False,use_scrambler=False,use_ldpc_output_interleaver=False,no_est_mismatch=1.):super().__init__()self.k=kself.n=nself.num_bits_per_symbol=num_bits_per_symbolself.use_allzero=use_allzeroself.use_scrambler=use_scrambler# adds noise to SNR estimation at demapper# see last section "mismatched demapping"self.no_est_mismatch=no_est_mismatch# init componentsself.source=BinarySource()# initialize mapper and demapper with constellation objectself.constellation=Constellation("qam",num_bits_per_symbol=self.num_bits_per_symbol)self.mapper=Mapper(constellation=self.constellation)self.demapper=Demapper(demapping_method,constellation=self.constellation)self.channel=AWGN()# LDPC encoder / decoderifuse_ldpc_output_interleaver:# the output interleaver needs knowledge of the modulation orderself.encoder=LDPC5GEncoder(self.k,self.n,num_bits_per_symbol)else:self.encoder=LDPC5GEncoder(self.k,self.n)self.decoder=LDPC5GDecoder(self.encoder,cn_update=cn_update)self.scrambler=Scrambler()# connect descrambler to scramblerself.descrambler=Descrambler(self.scrambler,binary=False)@tf.function()# enable graph mode for higher throughputsdefcall(self,batch_size,ebno_db):# calculate noise varianceno=ebnodb2no(ebno_db,num_bits_per_symbol=self.num_bits_per_symbol,coderate=self.k/self.n)ifself.use_allzero:u=tf.zeros([batch_size,self.k])# only needed forc=tf.zeros([batch_size,self.n])# replace enc. with all-zero codewordelse:u=self.source([batch_size,self.k])c=self.encoder(u)# explicitly encode# scramble codeword if actively requiredifself.use_scrambler:c=self.scrambler(c)x=self.mapper(c)# map c to symbolsy=self.channel(x,no)# transmit over AWGN channel# add noise estimation mismatch for demapper (see last section)# set to 1 per default -> no mismatchno_est=no*self.no_est_mismatchllr_ch=self.demapper(y,no_est)# demappifself.use_scrambler:llr_ch=self.descrambler(llr_ch)u_hat=self.decoder(llr_ch)# run LDPC decoder (incl. de-rate-matching)returnu,u_hat
Remove Encoder: Simulate QPSK with All-zero Codeword Transmission
We now simulate the same systemwithout encoder and transmit constant0s.
Due to the symmetry of the QPSK, no scrambler is required. You will learn about the effect of the scrambler in the last section.
[9]:
model_allzero=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=2,use_allzero=True,# disable encoderuse_scrambler=False)# we do not use a scrambler for the moment (QPSK!)# and simulate the new curve# Hint: as the model is callable, we can directly pass it to the# Monte Carlo simulationber_plot_allzero.simulate(model_allzero,ebno_dbs=np.arange(0,5,0.25),legend="All-zero / QPSK (no encoder)",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 1.6394e-01 | 1.0000e+00 | 98366 | 600000 | 1000 | 1000 | 0.5 |reached target bit errors 0.25 | 1.4105e-01 | 9.8900e-01 | 84628 | 600000 | 989 | 1000 | 0.1 |reached target bit errors 0.5 | 1.0657e-01 | 9.2900e-01 | 63942 | 600000 | 929 | 1000 | 0.1 |reached target bit errors 0.75 | 6.8887e-02 | 7.6200e-01 | 41332 | 600000 | 762 | 1000 | 0.1 |reached target bit errors 1.0 | 3.3478e-02 | 4.8800e-01 | 20087 | 600000 | 488 | 1000 | 0.1 |reached target bit errors 1.25 | 1.0825e-02 | 2.0900e-01 | 6495 | 600000 | 209 | 1000 | 0.1 |reached target bit errors 1.5 | 2.5000e-03 | 5.9000e-02 | 1500 | 600000 | 59 | 1000 | 0.1 |reached target bit errors 1.75 | 4.2767e-04 | 1.3200e-02 | 1283 | 3000000 | 66 | 5000 | 0.3 |reached target bit errors 2.0 | 5.2323e-05 | 1.8485e-03 | 1036 | 19800000 | 61 | 33000 | 2.3 |reached target bit errors 2.25 | 2.9000e-06 | 2.6000e-04 | 87 | 30000000 | 13 | 50000 | 3.4 |reached max iterations 2.5 | 7.0000e-07 | 2.0000e-05 | 21 | 30000000 | 1 | 50000 | 3.4 |reached max iterations 2.75 | 0.0000e+00 | 0.0000e+00 | 0 | 30000000 | 0 | 50000 | 3.4 |reached max iterationsSimulation stopped as no error occurred @ EbNo = 2.8 dB.

As expected, the BER curves are identical (within the accuracy of the Monte Carlo simulation).
Remove (De-)Mapping: Approximate the LLR Distribution of the All-zero Codeword (and BPSK/QPSK)
For the all-zero codeword, the BPSK mapper generates theall-one signal (as each0 is mapped to a1).
Assuming an AWGN channel with noise variance\(\sigma_\text{ch}^2\), it holds that the output of the channel\(y\) is Gaussian distributed with mean\(\mu=1\) and noise variance\(\sigma_\text{ch}^2\). Demapping of the BPSK symbols is given as\(\ell_\text{ch} = -\frac{2}{\sigma_\text{ch}^2}y\).
This leads to the effective LLR distribution of\(\ell_\text{ch} \sim \mathcal{N}(-\frac{2}{\sigma_\text{ch}^2},\frac{4}{\sigma_\text{ch}^2})\) and, thereby, allows to mimic the mapper, AWGN channel and demapper by a Gaussian distribution. TheGaussianPriorSource block provides such a source for arbitrary shapes.
The same derivation holds for QPSK. Let us quickly verify the correctness of these results by a Monte Carlo simulation.
Note: the negative sign for the BPSK demapping rule comes from the (in communications) unusual definition of logits\(\ell = \operatorname{log} \frac{p(x=1)}{p(x=0)}\).
[10]:
num_bits_per_symbol=2# we use QPSKebno_db=4# choose any SNRbatch_size=100000# we only simulate 1 symbol per batch# calculate noise varianceno=ebnodb2no(ebno_db,num_bits_per_symbol=num_bits_per_symbol,coderate=k/n)# generate bins for the histogramllr_bins=np.arange(-20,20,0.2)c=tf.zeros([batch_size,num_bits_per_symbol])# all-zero codewordx=mapper(c)# mapped to constant symboly=channel(x,no)llr=demapper(y,no)# and generate LLRsllr_dist,_=np.histogram(llr.numpy(),bins=llr_bins,density=True);# negative mean value due to different logit/llr definition# llr = log[(x=1)/p(x=0)]mu_llr=-2/nono_llr=4/no# generate Gaussian pdfllr_pred=1/np.sqrt(2*np.pi*no_llr)*np.exp(-(llr_bins-mu_llr)**2/(2*no_llr))# and compare the resultsplt.figure(figsize=(20,8))plt.xticks(fontsize=18)plt.yticks(fontsize=18)plt.grid(which="both")plt.xlabel("LLR value",fontsize=25)plt.ylabel("Probability density",fontsize=25)plt.plot(llr_bins[:-1],llr_dist,label="Measured LLR distribution")plt.plot(llr_bins,llr_pred,label="Analytical LLR distribution (GA)")plt.title("LLR distribution after demapping",fontsize=25)plt.legend(fontsize=20);

[11]:
num_bits_per_symbol=2# QPSK# initialize LLR sourcega_source=GaussianPriorSource()@tf.function()# enable graph modedefrun_ber_ga(batch_size,ebno_db):# calculate noise varianceno=ebnodb2no(ebno_db,num_bits_per_symbol=num_bits_per_symbol,coderate=k/n)u=tf.zeros([batch_size,k])# only needed for ber calculationsllr_ch=ga_source([batch_size,n],no)# generate LLRs directlyu_hat=decoder(llr_ch)# run LDPC decoder (incl. de-rate-matching)returnu,u_hat# and simulate the new curveber_plot_allzero.simulate(run_ber_ga,ebno_dbs=np.arange(0,5,0.25),# simulation SNR,max_mc_iter=50,num_target_bit_errors=1000,legend="Gaussian Approximation of LLRs",batch_size=10000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 1.6492e-01 | 9.9980e-01 | 989546 | 6000000 | 9998 | 10000 | 0.9 |reached target bit errors 0.25 | 1.3964e-01 | 9.8840e-01 | 837867 | 6000000 | 9884 | 10000 | 0.5 |reached target bit errors 0.5 | 1.0591e-01 | 9.2990e-01 | 635482 | 6000000 | 9299 | 10000 | 0.5 |reached target bit errors 0.75 | 6.5787e-02 | 7.5730e-01 | 394723 | 6000000 | 7573 | 10000 | 0.5 |reached target bit errors 1.0 | 3.0858e-02 | 4.7990e-01 | 185149 | 6000000 | 4799 | 10000 | 0.5 |reached target bit errors 1.25 | 1.0535e-02 | 2.0960e-01 | 63213 | 6000000 | 2096 | 10000 | 0.5 |reached target bit errors 1.5 | 2.5652e-03 | 6.0300e-02 | 15391 | 6000000 | 603 | 10000 | 0.5 |reached target bit errors 1.75 | 4.7950e-04 | 1.3400e-02 | 2877 | 6000000 | 134 | 10000 | 0.5 |reached target bit errors 2.0 | 6.2278e-05 | 1.7000e-03 | 1121 | 18000000 | 51 | 30000 | 1.5 |reached target bit errors 2.25 | 6.4691e-06 | 2.4074e-04 | 1048 | 162000000 | 65 | 270000 | 13.7 |reached target bit errors 2.5 | 7.5333e-07 | 5.0000e-05 | 226 | 300000000 | 25 | 500000 | 25.3 |reached max iterations 2.75 | 2.1333e-07 | 1.0000e-05 | 64 | 300000000 | 5 | 500000 | 25.3 |reached max iterations 3.0 | 2.3333e-08 | 2.0000e-06 | 7 | 300000000 | 1 | 500000 | 25.3 |reached max iterations 3.25 | 0.0000e+00 | 0.0000e+00 | 0 | 300000000 | 0 | 500000 | 25.3 |reached max iterationsSimulation stopped as no error occurred @ EbNo = 3.2 dB.

The Role of the Scrambler
So far, we have seen that the all-zero codeword yields the same error-rates as any other sequence. Intuitively, theall-zero codeword trick generates a constant stream of0s at the input of the mapper. However, if the channel is not symmetric we need to ensure that we capture theaverage behavior of all possible symbols equally. Mathematically this symmetry condition can be expressed as\(p(Y=y|c=0)=p(Y=-y|c=1)\)
As shown in the previous experiments, for QPSK bothbit-channels have the same behavior but for 16-QAM systems this does not hold anymore and our simulated BER does not represent the average decoding performance of the original system.
One possible solution is to scramble the all-zero codeword before transmission and descramble the received LLRs before decoding (i.e., flip the sign accordingly). This ensures that the mapper/demapper (+channel) operate on (pseudo-)random data, but from decoder’s perspective the the all-zero codeword assumption is still valid. This avoids the need for an actual encoder. For further details, we refer toi.i.d. channel adapters in [9].
Note: another example is that the recorded LLRs can be even used to evaluate different codes as the all-zero codeword is a valid codeword for all linear codes. Going one step further, one can even simulate codes of different rates with the same pre-recorded LLRs.
[12]:
# we generate a new plotber_plot_allzero16qam=PlotBER("BER Performance for 64-QAM")
[13]:
# simulate a new baseline for 16-QAMmodel_baseline_16=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_allzero=False,# baseline without all-zerouse_scrambler=False)# and simulate the new curve# Hint: as the model is callable, we can directly pass it to the# Monte Carlo simulationber_plot_allzero16qam.simulate(model_baseline_16,ebno_dbs=np.arange(0,5,0.25),legend="Baseline 16-QAM",max_mc_iter=50,num_target_bit_errors=2000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 2.4785e-01 | 1.0000e+00 | 148713 | 600000 | 1000 | 1000 | 0.6 |reached target bit errors 0.25 | 2.4023e-01 | 1.0000e+00 | 144136 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.5 | 2.3140e-01 | 1.0000e+00 | 138842 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.75 | 2.2230e-01 | 1.0000e+00 | 133381 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 2.1468e-01 | 1.0000e+00 | 128809 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.25 | 2.0553e-01 | 1.0000e+00 | 123321 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 1.9343e-01 | 1.0000e+00 | 116060 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.75 | 1.8374e-01 | 1.0000e+00 | 110243 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 1.6868e-01 | 1.0000e+00 | 101207 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.25 | 1.5363e-01 | 9.9900e-01 | 92180 | 600000 | 999 | 1000 | 0.1 |reached target bit errors 2.5 | 1.2842e-01 | 9.8100e-01 | 77051 | 600000 | 981 | 1000 | 0.1 |reached target bit errors 2.75 | 9.6925e-02 | 9.1500e-01 | 58155 | 600000 | 915 | 1000 | 0.1 |reached target bit errors 3.0 | 6.0137e-02 | 7.4600e-01 | 36082 | 600000 | 746 | 1000 | 0.1 |reached target bit errors 3.25 | 3.2578e-02 | 5.1700e-01 | 19547 | 600000 | 517 | 1000 | 0.1 |reached target bit errors 3.5 | 1.5235e-02 | 2.7400e-01 | 9141 | 600000 | 274 | 1000 | 0.1 |reached target bit errors 3.75 | 3.7325e-03 | 9.1000e-02 | 4479 | 1200000 | 182 | 2000 | 0.2 |reached target bit errors 4.0 | 1.1721e-03 | 3.4250e-02 | 2813 | 2400000 | 137 | 4000 | 0.3 |reached target bit errors 4.25 | 2.3433e-04 | 7.2667e-03 | 2109 | 9000000 | 109 | 15000 | 1.1 |reached target bit errors 4.5 | 2.1900e-05 | 1.1600e-03 | 657 | 30000000 | 58 | 50000 | 3.7 |reached max iterations 4.75 | 2.1333e-06 | 1.0000e-04 | 64 | 30000000 | 5 | 50000 | 3.7 |reached max iterations

We now apply theall-zero trick as above and simulate ther BER performance without scrambling.
[14]:
# and repeat the experiment for a 16QAM WITHOUT scramblermodel_allzero_16_no_sc=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_allzero=True,# all-zero codeworduse_scrambler=False)# no scrambler used# and simulate the new curve# Hint: as the model is callable, we can directly pass it to the# Monte Carlo simulationber_plot_allzero16qam.simulate(model_allzero_16_no_sc,ebno_dbs=np.arange(0,5,0.25),legend="All-zero / 16-QAM (no scrambler!)",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 3.0101e-01 | 1.0000e+00 | 180604 | 600000 | 1000 | 1000 | 0.4 |reached target bit errors 0.25 | 2.9716e-01 | 1.0000e+00 | 178294 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.5 | 2.9111e-01 | 1.0000e+00 | 174664 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.75 | 2.8768e-01 | 1.0000e+00 | 172605 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 2.7976e-01 | 1.0000e+00 | 167854 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.25 | 2.7443e-01 | 1.0000e+00 | 164659 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 2.6708e-01 | 1.0000e+00 | 160245 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.75 | 2.6155e-01 | 1.0000e+00 | 156932 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 2.5305e-01 | 1.0000e+00 | 151832 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.25 | 2.4513e-01 | 1.0000e+00 | 147075 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.5 | 2.3768e-01 | 1.0000e+00 | 142609 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.75 | 2.2895e-01 | 1.0000e+00 | 137367 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.0 | 2.1695e-01 | 1.0000e+00 | 130169 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.25 | 2.0914e-01 | 1.0000e+00 | 125482 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.5 | 1.9582e-01 | 1.0000e+00 | 117493 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.75 | 1.8141e-01 | 1.0000e+00 | 108844 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 4.0 | 1.6221e-01 | 1.0000e+00 | 97326 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 4.25 | 1.3627e-01 | 9.9400e-01 | 81761 | 600000 | 994 | 1000 | 0.1 |reached target bit errors 4.5 | 1.0323e-01 | 9.5200e-01 | 61938 | 600000 | 952 | 1000 | 0.1 |reached target bit errors 4.75 | 6.1143e-02 | 7.4600e-01 | 36686 | 600000 | 746 | 1000 | 0.1 |reached target bit errors
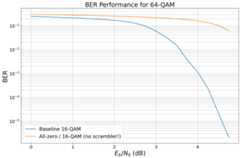
As expected the results are wrong as we have transmitted all bits over theless reliable channel (cfBER per bit-channel).
Let us repeat this experiment with scrambler and descrambler at the correct position.
[15]:
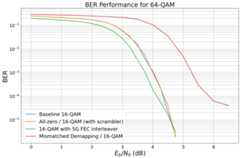
# and repeat the experiment for a 16QAM WITHOUT scramblermodel_allzero_16_sc=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_allzero=True,# all-zero codeworduse_scrambler=True)# activate scrambler# and simulate the new curve# Hint: as the model is callable, we can directly pass it to the# Monte Carlo simulationber_plot_allzero16qam.simulate(model_allzero_16_sc,ebno_dbs=np.arange(0,5,0.25),legend="All-zero / 16-QAM (with scrambler)",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 2.4785e-01 | 1.0000e+00 | 148710 | 600000 | 1000 | 1000 | 0.7 |reached target bit errors 0.25 | 2.4052e-01 | 1.0000e+00 | 144314 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.5 | 2.3189e-01 | 1.0000e+00 | 139133 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.75 | 2.2409e-01 | 1.0000e+00 | 134457 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 2.1497e-01 | 1.0000e+00 | 128980 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.25 | 2.0492e-01 | 1.0000e+00 | 122955 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 1.9380e-01 | 1.0000e+00 | 116280 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.75 | 1.8171e-01 | 1.0000e+00 | 109027 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 1.6793e-01 | 1.0000e+00 | 100760 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.25 | 1.5074e-01 | 9.9600e-01 | 90441 | 600000 | 996 | 1000 | 0.1 |reached target bit errors 2.5 | 1.2801e-01 | 9.8500e-01 | 76808 | 600000 | 985 | 1000 | 0.1 |reached target bit errors 2.75 | 9.7045e-02 | 9.2000e-01 | 58227 | 600000 | 920 | 1000 | 0.1 |reached target bit errors 3.0 | 6.0937e-02 | 7.4500e-01 | 36562 | 600000 | 745 | 1000 | 0.1 |reached target bit errors 3.25 | 3.4122e-02 | 5.0500e-01 | 20473 | 600000 | 505 | 1000 | 0.1 |reached target bit errors 3.5 | 1.3368e-02 | 2.6200e-01 | 8021 | 600000 | 262 | 1000 | 0.1 |reached target bit errors 3.75 | 5.3417e-03 | 1.0800e-01 | 3205 | 600000 | 108 | 1000 | 0.1 |reached target bit errors 4.0 | 1.0100e-03 | 3.3000e-02 | 1212 | 1200000 | 66 | 2000 | 0.1 |reached target bit errors 4.25 | 2.2250e-04 | 7.5000e-03 | 1068 | 4800000 | 60 | 8000 | 0.6 |reached target bit errors 4.5 | 4.1138e-05 | 1.2927e-03 | 1012 | 24600000 | 53 | 41000 | 2.9 |reached target bit errors 4.75 | 1.8333e-06 | 1.2000e-04 | 55 | 30000000 | 6 | 50000 | 3.5 |reached max iterations

The 5G standard defines an additional output interleaver after the rate-matching (see Sec. 5.4.2.2 in [11]).
We now activate this additional interleaver to enable additional BER gains.
[16]:
# activate output interleavermodel_output_interleaver=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_ldpc_output_interleaver=True,use_allzero=False,use_scrambler=False)# and simulate the new curve# Hint: as the model is callable, we can directly pass it to the# Monte Carlo simulationber_plot_allzero16qam.simulate(model_output_interleaver,ebno_dbs=np.arange(0,5,0.25),legend="16-QAM with 5G FEC interleaver",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 1.9832e-01 | 1.0000e+00 | 118994 | 600000 | 1000 | 1000 | 0.6 |reached target bit errors 0.25 | 1.8933e-01 | 1.0000e+00 | 113597 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.5 | 1.8310e-01 | 1.0000e+00 | 109862 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 0.75 | 1.7523e-01 | 1.0000e+00 | 105138 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 1.6596e-01 | 1.0000e+00 | 99575 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.25 | 1.5853e-01 | 1.0000e+00 | 95116 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 1.4718e-01 | 1.0000e+00 | 88305 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.75 | 1.3444e-01 | 1.0000e+00 | 80666 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 1.1917e-01 | 9.9400e-01 | 71500 | 600000 | 994 | 1000 | 0.1 |reached target bit errors 2.25 | 9.9625e-02 | 9.8600e-01 | 59775 | 600000 | 986 | 1000 | 0.1 |reached target bit errors 2.5 | 7.6272e-02 | 9.3600e-01 | 45763 | 600000 | 936 | 1000 | 0.1 |reached target bit errors 2.75 | 5.0847e-02 | 8.1400e-01 | 30508 | 600000 | 814 | 1000 | 0.1 |reached target bit errors 3.0 | 2.7878e-02 | 5.5900e-01 | 16727 | 600000 | 559 | 1000 | 0.1 |reached target bit errors 3.25 | 1.1997e-02 | 3.2900e-01 | 7198 | 600000 | 329 | 1000 | 0.1 |reached target bit errors 3.5 | 3.4583e-03 | 1.1200e-01 | 2075 | 600000 | 112 | 1000 | 0.1 |reached target bit errors 3.75 | 9.9667e-04 | 4.7000e-02 | 1196 | 1200000 | 94 | 2000 | 0.2 |reached target bit errors 4.0 | 1.9067e-04 | 1.2700e-02 | 1144 | 6000000 | 127 | 10000 | 0.7 |reached target bit errors 4.25 | 5.7333e-05 | 2.9333e-03 | 1032 | 18000000 | 88 | 30000 | 2.2 |reached target bit errors 4.5 | 1.5867e-05 | 9.4000e-04 | 476 | 30000000 | 47 | 50000 | 3.7 |reached max iterations 4.75 | 3.0667e-06 | 2.0000e-04 | 92 | 30000000 | 10 | 50000 | 3.7 |reached max iterations

EXIT Charts
You now learn about how the convergence behavior of iterative receivers can be visualized.
Extrinsic Information Transfer (EXIT) charts [7] are a widely adopted tool to analyze the convergence behavior of iterative receiver algorithms. The principle idea is to treat each component decoder (or demapper etc.) as individual entity with its own EXIT characteristic. EXIT charts not only allow to predict the decoding behavior (open decoding tunnel) but also enable LDPC code design (cf. [8]). However, this is beyond the scope of this notebook.
We can analytically derive the EXIT characteristic for check node (CN) and variable node (VN) decoder for a given code withget_exit_analytic. Further, if theLDPCBPDecoder is initialized with optiontrack_exit=True, it internally stores the average extrinsic mutual information after each iteration at the output of the VN/CN decoder.
Please note that this is only an approximation for the AWGN channel and assumes infinite code length. However, it turns out that the results are often accurate enough and
[17]:
# parametersebno_db=2.3batch_size=10000num_bits_per_symbol=2pcm_id=4# decide which parity check matrix should be used (0-2: BCH; 3: (3,6)-LDPC 4: LDPC 802.11npcm,k_exit,n_exit,coderate=load_parity_check_examples(pcm_id,verbose=True)# init callbacks for tracking of EXIT chartsnum_iter=20cb_exit_vn=EXITCallback(num_iter)cb_exit_cn=EXITCallback(num_iter)# init componentsdecoder_exit=LDPCBPDecoder(pcm,hard_out=False,cn_update="boxplus",track_exit=True,num_iter=num_iter,v2c_callbacks=[cb_exit_vn,],c2v_callbacks=[cb_exit_cn,])# generates fake llrs as if the all-zero codeword was transmitted over an AWNG channel with BPSK modulation (see early sections)llr_source=GaussianPriorSource()noise_var=ebnodb2no(ebno_db=ebno_db,num_bits_per_symbol=num_bits_per_symbol,coderate=coderate)# use fake llrs from GAllr=llr_source([batch_size,n_exit],noise_var)# simulate free runing trajectorydecoder_exit(llr)# calculate analytical EXIT characteristics# Hint: these curves assume asymptotic code length, i.e., may become inaccurate in the short length regimeIa,Iev,Iec=get_exit_analytic(pcm,ebno_db)# and plot the EXIT curvesplt=plot_exit_chart(Ia,Iev,Iec)# however, as track_exit=True, the decoder logs the actual exit trajectory during decoding. This can be accessed by decoder.ie_v/decoder.ie_c after the simulation# and add simulated trajectory to plotplot_trajectory(plt,cb_exit_vn.mi.numpy(),cb_exit_cn.mi.numpy(),ebno_db)
n: 648, k: 324, coderate: 0.500
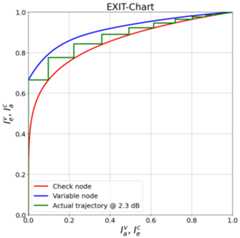
As can be seen, the simulated trajectory of the decoder matches (relatively) well with the predicted EXIT functions of the VN and CN decoder, respectively.
A few things to try:
Change the SNR; which curves change? Why is one curve constant? Hint: does every component directlysee the channel?
What happens for other codes?
Can you predict thethreshold of this curve (i.e., the minimum SNR required for successful decoding)
Verify the correctness of this threshold via BER simulations (hint: the codes are relatively short, thus the prediction is less accurate)
Mismatched Demapping and the Advantages of Min-sum Decoding
So far, we have demapped with exact knowledge of the underlying noise distribution (including the exact SNR). However, in practice estimating the SNR can be a complicated task and, as such, the estimated SNR used for demapping can be inaccurate.
In this part, you will learn about the advantages of min-sum decoding and we will see that it is more robust against mismatched demapping.
[18]:
# let us first remove the non-scrambled result from the previous experimentber_plot_allzero16qam.remove(idx=1)# remove curve with index 1
[19]:
# simulate with mismatched noise estimationmodel_allzero_16_no=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_allzero=False,# full simulationno_est_mismatch=0.15)# noise variance estimation mismatch (no scaled by 0.15 )ber_plot_allzero16qam.simulate(model_allzero_16_no,ebno_dbs=np.arange(0,7,0.5),legend="Mismatched Demapping / 16-QAM",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 2.9166e-01 | 1.0000e+00 | 174996 | 600000 | 1000 | 1000 | 0.6 |reached target bit errors 0.5 | 2.8154e-01 | 1.0000e+00 | 168924 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 2.6981e-01 | 1.0000e+00 | 161887 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 2.5988e-01 | 1.0000e+00 | 155928 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 2.4820e-01 | 1.0000e+00 | 148921 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.5 | 2.3444e-01 | 1.0000e+00 | 140661 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.0 | 2.1729e-01 | 9.9800e-01 | 130371 | 600000 | 998 | 1000 | 0.1 |reached target bit errors 3.5 | 1.8174e-01 | 9.7800e-01 | 109047 | 600000 | 978 | 1000 | 0.1 |reached target bit errors 4.0 | 1.0665e-01 | 7.9000e-01 | 63988 | 600000 | 790 | 1000 | 0.1 |reached target bit errors 4.5 | 3.5353e-02 | 3.9900e-01 | 21212 | 600000 | 399 | 1000 | 0.1 |reached target bit errors 5.0 | 4.8633e-03 | 1.2000e-01 | 2918 | 600000 | 120 | 1000 | 0.1 |reached target bit errors 5.5 | 2.9417e-04 | 3.7833e-02 | 1059 | 3600000 | 227 | 6000 | 0.4 |reached target bit errors 6.0 | 6.1790e-05 | 2.3333e-02 | 1001 | 16200000 | 630 | 27000 | 2.0 |reached target bit errors 6.5 | 3.9881e-05 | 1.5786e-02 | 1005 | 25200000 | 663 | 42000 | 3.1 |reached target bit errors
[20]:
# simulate with mismatched noise estimationmodel_allzero_16_ms=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_allzero=False,# full simulationcn_update="minsum",# activate min-sum decodingno_est_mismatch=1.)# no mismatchber_plot_allzero16qam.simulate(model_allzero_16_ms,ebno_dbs=np.arange(0,7,0.5),legend="Min-sum decoding / 16-QAM (no mismatch)",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 2.9541e-01 | 1.0000e+00 | 177247 | 600000 | 1000 | 1000 | 0.7 |reached target bit errors 0.5 | 2.8625e-01 | 1.0000e+00 | 171747 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 2.7540e-01 | 1.0000e+00 | 165242 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 2.6427e-01 | 1.0000e+00 | 158559 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 2.5289e-01 | 1.0000e+00 | 151733 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.5 | 2.3922e-01 | 1.0000e+00 | 143533 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.0 | 2.2233e-01 | 1.0000e+00 | 133396 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.5 | 1.8174e-01 | 9.5000e-01 | 109046 | 600000 | 950 | 1000 | 0.1 |reached target bit errors 4.0 | 9.7517e-02 | 6.5700e-01 | 58510 | 600000 | 657 | 1000 | 0.1 |reached target bit errors 4.5 | 1.8880e-02 | 1.5600e-01 | 11328 | 600000 | 156 | 1000 | 0.1 |reached target bit errors 5.0 | 1.3183e-03 | 1.3500e-02 | 1582 | 1200000 | 27 | 2000 | 0.2 |reached target bit errors 5.5 | 1.8300e-05 | 1.8000e-04 | 549 | 30000000 | 9 | 50000 | 4.1 |reached max iterations 6.0 | 0.0000e+00 | 0.0000e+00 | 0 | 30000000 | 0 | 50000 | 4.1 |reached max iterationsSimulation stopped as no error occurred @ EbNo = 6.0 dB.

[21]:
# simulate with mismatched noise estimationmodel_allzero_16_ms=LDPC_QAM_AWGN(k,n,num_bits_per_symbol=4,use_allzero=False,# full simulationcn_update="minsum",# activate min-sum decodingno_est_mismatch=0.15)# noise_var mismatch at demapperber_plot_allzero16qam.simulate(model_allzero_16_ms,ebno_dbs=np.arange(0,7,0.5),legend="Min-sum decoding / 16-QAM (with mismatch)",max_mc_iter=50,num_target_bit_errors=1000,batch_size=1000,soft_estimates=False,show_fig=True,forward_keyboard_interrupt=False);
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status--------------------------------------------------------------------------------------------------------------------------------------- 0.0 | 2.9553e-01 | 1.0000e+00 | 177321 | 600000 | 1000 | 1000 | 0.7 |reached target bit errors 0.5 | 2.8743e-01 | 1.0000e+00 | 172459 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.0 | 2.7644e-01 | 1.0000e+00 | 165863 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 1.5 | 2.6585e-01 | 1.0000e+00 | 159512 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.0 | 2.5385e-01 | 1.0000e+00 | 152312 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 2.5 | 2.4186e-01 | 1.0000e+00 | 145116 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.0 | 2.2458e-01 | 1.0000e+00 | 134748 | 600000 | 1000 | 1000 | 0.1 |reached target bit errors 3.5 | 1.9949e-01 | 9.9000e-01 | 119694 | 600000 | 990 | 1000 | 0.1 |reached target bit errors 4.0 | 1.3280e-01 | 8.3600e-01 | 79682 | 600000 | 836 | 1000 | 0.1 |reached target bit errors 4.5 | 4.9195e-02 | 4.4300e-01 | 29517 | 600000 | 443 | 1000 | 0.1 |reached target bit errors 5.0 | 7.4567e-03 | 1.0000e-01 | 4474 | 600000 | 100 | 1000 | 0.1 |reached target bit errors 5.5 | 4.6000e-04 | 1.9750e-02 | 1104 | 2400000 | 79 | 4000 | 0.3 |reached target bit errors 6.0 | 2.0933e-05 | 7.2800e-03 | 628 | 30000000 | 364 | 50000 | 4.1 |reached max iterations 6.5 | 1.1133e-05 | 4.5800e-03 | 334 | 30000000 | 229 | 50000 | 4.1 |reached max iterations

Interestingly,min-sum decoding is more robust w.r.t. inaccurate LLR estimations. It is worth mentioning thatmin-sum decoding itself causes a performance loss. However, more advanced min-sum-based decoding approaches (offset-corrected min-sum) can operate close tofull BP decoding.
You can also try:
What happens with max-log demapping?
Implement offset corrected min-sum decoding
Have a closer look at the error-floor behavior
Apply the concept ofWeighted BP to mismatched demapping
References
[1] E. Zehavi, “8-PSK Trellis Codes for a Rayleigh Channel,” IEEE Transactions on Communications, vol. 40, no. 5, 1992.
[2] G. Caire, G. Taricco and E. Biglieri, “Bit-interleaved Coded Modulation,” IEEE Transactions on Information Theory, vol. 44, no. 3, 1998.
[3] G. Ungerböck, “Channel Coding with Multilevel/Phase Signals.”IEEE Transactions on Information Theory, vol. 28, no. 1, 1982.
[4] J. L. Massey, “Coding and modulation in digital communications,” in Proc. Int. Zurich Seminar Commun., 1974.
[5] G. Böcherer, “Principles of Coded Modulation,” Habilitation thesis, Tech. Univ. Munich, Munich, Germany, 2018.
[6] F. Schreckenbach, “Iterative Decoding of Bit-Interleaved Coded Modulation”, PhD thesis, Tech. Univ. Munich, Munich, Germany, 2007.
[7] S. ten Brink, “Convergence Behavior of Iteratively Decoded Parallel Concatenated Codes,” IEEE Transactions on Communications, vol. 49, no. 10, pp. 1727-1737, 2001.
[8] S. ten Brink, G. Kramer, and A. Ashikhmin, “Design of low-density parity-check codes for modulation and detection,” IEEE Trans. Commun., vol. 52, no. 4, pp. 670–678, Apr. 2004.
[9] J. Hou, P. H. Siegel, L. B. Milstein, and H. D. Pfister, “Capacity-approaching bandwidth-efficient coded modulation schemes based on low-density parity-check codes,” IEEE Trans. Inform. Theory, vol. 49, no. 9, pp. 2141–2155, 2003.
[10] A. Alvarado, L. Szczecinski, R. Feick, and L. Ahumada, “Distribution of L-values in Gray-mapped M 2-QAM: Closed-form approximations and applications,” IEEE Transactions on Communications, vol. 57, no. 7, pp. 2071-2079, 2009.
[11] ETSI 3GPP TS 38.212 “5G NR Multiplexing and channel coding”, v.16.5.0, 2021-03.