Note
Go to the endto download the full example code.
Histogram bins, density, and weight#
TheAxes.hist method can flexibly create histograms in a few different ways,which is flexible and helpful, but can also lead to confusion. In particular,you can:
bin the data as you want, either with an automatically chosen number ofbins, or with fixed bin edges,
normalize the histogram so that its integral is one,
and assign weights to the data points, so that each data point affects thecount in its bin differently.
The Matplotlibhist method callsnumpy.histogram and plots the results,therefore users should consult the numpy documentation for a definitive guide.
Histograms are created by defining bin edges, and taking a dataset of valuesand sorting them into the bins, and counting or summing how much data is ineach bin. In this simple example, 9 numbers between 1 and 4 are sorted into 3bins:
importmatplotlib.pyplotaspltimportnumpyasnprng=np.random.default_rng(19680801)xdata=np.array([1.2,2.3,3.3,3.1,1.7,3.4,2.1,1.25,1.3])xbins=np.array([1,2,3,4])# changing the style of the histogram bars just to make it# very clear where the boundaries of the bins are:style={'facecolor':'none','edgecolor':'C0','linewidth':3}fig,ax=plt.subplots()ax.hist(xdata,bins=xbins,**style)# plot the xdata locations on the x axis:ax.plot(xdata,0*xdata,'d')ax.set_ylabel('Number per bin')ax.set_xlabel('x bins (dx=1.0)')

Modifying bins#
Changing the bin size changes the shape of this sparse histogram, so its agood idea to choose bins with some care with respect to your data. Here wemake the bins half as wide.
xbins=np.arange(1,4.5,0.5)fig,ax=plt.subplots()ax.hist(xdata,bins=xbins,**style)ax.plot(xdata,0*xdata,'d')ax.set_ylabel('Number per bin')ax.set_xlabel('x bins (dx=0.5)')

We can also let numpy (via Matplotlib) choose the bins automatically, orspecify a number of bins to choose automatically:
fig,ax=plt.subplot_mosaic([['auto','n4']],sharex=True,sharey=True,layout='constrained')ax['auto'].hist(xdata,**style)ax['auto'].plot(xdata,0*xdata,'d')ax['auto'].set_ylabel('Number per bin')ax['auto'].set_xlabel('x bins (auto)')ax['n4'].hist(xdata,bins=4,**style)ax['n4'].plot(xdata,0*xdata,'d')ax['n4'].set_xlabel('x bins ("bins=4")')

Normalizing histograms: density and weight#
Counts-per-bin is the default length of each bar in the histogram. However,we can also normalize the bar lengths as a probability density function usingthedensity parameter:
fig,ax=plt.subplots()ax.hist(xdata,bins=xbins,density=True,**style)ax.set_ylabel('Probability density [$V^{-1}$])')ax.set_xlabel('x bins (dx=0.5 $V$)')

This normalization can be a little hard to interpret when just exploring thedata. The value attached to each bar is divided by the total number of datapointsand the width of the bin, and thus the values _integrate_ to onewhen integrating across the full range of data.e.g.
density=counts/(sum(counts)*np.diff(bins))np.sum(density*np.diff(bins))==1
This normalization is howprobability density functions are defined instatistics. If\(X\) is a random variable on\(x\), then\(f_X\)is is the probability density function if\(P[a<X<b] = \int_a^b f_X dx\).If the units of x are Volts, then the units of\(f_X\) are\(V^{-1}\)or probability per change in voltage.
The usefulness of this normalization is a little more clear when we draw froma known distribution and try to compare with theory. So, choose 1000 pointsfrom anormal distribution, and also calculate theknown probability density function:
If we don't usedensity=True, we need to scale the expected probabilitydistribution function by both the length of the data and the width of thebins:
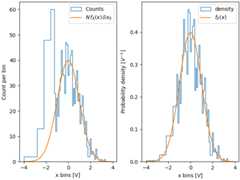
fig,ax=plt.subplot_mosaic([['False','True']],layout='constrained')dx=0.1xbins=np.arange(-4,4,dx)ax['False'].hist(xdata,bins=xbins,density=False,histtype='step',label='Counts')# scale and plot the expected pdf:ax['False'].plot(xpdf,pdf*len(xdata)*dx,label=r'$N\,f_X(x)\,\delta x$')ax['False'].set_ylabel('Count per bin')ax['False'].set_xlabel('x bins [V]')ax['False'].legend()ax['True'].hist(xdata,bins=xbins,density=True,histtype='step',label='density')ax['True'].plot(xpdf,pdf,label='$f_X(x)$')ax['True'].set_ylabel('Probability density [$V^{-1}$]')ax['True'].set_xlabel('x bins [$V$]')ax['True'].legend()

One advantage of using the density is therefore that the shape and amplitudeof the histogram does not depend on the size of the bins. Consider anextreme case where the bins do not have the same width. In this example, thebins belowx=-1.25 are six times wider than the rest of the bins. Bynormalizing by density, we preserve the shape of the distribution, whereas ifwe do not, then the wider bins have much higher counts than the thinner bins:
fig,ax=plt.subplot_mosaic([['False','True']],layout='constrained')dx=0.1xbins=np.hstack([np.arange(-4,-1.25,6*dx),np.arange(-1.25,4,dx)])ax['False'].hist(xdata,bins=xbins,density=False,histtype='step',label='Counts')ax['False'].plot(xpdf,pdf*len(xdata)*dx,label=r'$N\,f_X(x)\,\delta x_0$')ax['False'].set_ylabel('Count per bin')ax['False'].set_xlabel('x bins [V]')ax['False'].legend()ax['True'].hist(xdata,bins=xbins,density=True,histtype='step',label='density')ax['True'].plot(xpdf,pdf,label='$f_X(x)$')ax['True'].set_ylabel('Probability density [$V^{-1}$]')ax['True'].set_xlabel('x bins [$V$]')ax['True'].legend()
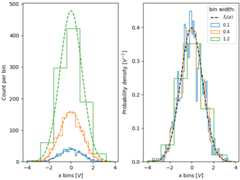
Similarly, if we want to compare histograms with different bin widths, we maywant to usedensity=True:
fig,ax=plt.subplot_mosaic([['False','True']],layout='constrained')# expected PDFax['True'].plot(xpdf,pdf,'--',label='$f_X(x)$',color='k')fornn,dxinenumerate([0.1,0.4,1.2]):xbins=np.arange(-4,4,dx)# expected histogram:ax['False'].plot(xpdf,pdf*1000*dx,'--',color=f'C{nn}')ax['False'].hist(xdata,bins=xbins,density=False,histtype='step')ax['True'].hist(xdata,bins=xbins,density=True,histtype='step',label=dx)# Labels:ax['False'].set_xlabel('x bins [$V$]')ax['False'].set_ylabel('Count per bin')ax['True'].set_ylabel('Probability density [$V^{-1}$]')ax['True'].set_xlabel('x bins [$V$]')ax['True'].legend(fontsize='small',title='bin width:')
Sometimes people want to normalize so that the sum of counts is one. This isanalogous to aprobability mass function for a discretevariable where the sum of probabilities for all the values equals one. Usinghist, we can get this normalization if we set theweights to 1/N.Note that the amplitude of this normalized histogram still depends onwidth and/or number of the bins:
fig,ax=plt.subplots(layout='constrained',figsize=(3.5,3))fornn,dxinenumerate([0.1,0.4,1.2]):xbins=np.arange(-4,4,dx)ax.hist(xdata,bins=xbins,weights=1/len(xdata)*np.ones(len(xdata)),histtype='step',label=f'{dx}')ax.set_xlabel('x bins [$V$]')ax.set_ylabel('Bin count / N')ax.legend(fontsize='small',title='bin width:')

The value of normalizing histograms is comparing two distributions that havedifferent sized populations. Here we compare the distribution ofxdatawith a population of 1000, andxdata2 with 100 members.
xdata2=rng.normal(size=100)fig,ax=plt.subplot_mosaic([['no_norm','density','weight']],layout='constrained',figsize=(8,4))xbins=np.arange(-4,4,0.25)ax['no_norm'].hist(xdata,bins=xbins,histtype='step')ax['no_norm'].hist(xdata2,bins=xbins,histtype='step')ax['no_norm'].set_ylabel('Counts')ax['no_norm'].set_xlabel('x bins [$V$]')ax['no_norm'].set_title('No normalization')ax['density'].hist(xdata,bins=xbins,histtype='step',density=True)ax['density'].hist(xdata2,bins=xbins,histtype='step',density=True)ax['density'].set_ylabel('Probability density [$V^{-1}$]')ax['density'].set_title('Density=True')ax['density'].set_xlabel('x bins [$V$]')ax['weight'].hist(xdata,bins=xbins,histtype='step',weights=1/len(xdata)*np.ones(len(xdata)),label='N=1000')ax['weight'].hist(xdata2,bins=xbins,histtype='step',weights=1/len(xdata2)*np.ones(len(xdata2)),label='N=100')ax['weight'].set_xlabel('x bins [$V$]')ax['weight'].set_ylabel('Counts / N')ax['weight'].legend(fontsize='small')ax['weight'].set_title('Weight = 1/N')plt.show()

Tags:plot-type: histogramdomain: statistics
References
The use of the following functions, methods, classes and modules is shownin this example:
Total running time of the script: (0 minutes 5.490 seconds)