3.1.1 What is this about?

This chapter covers the following topics:

• The best variables ranking from conventional machine learning algorithms, either predictive or clustering.
• The nature of selecting variables with and without predictive models.
• The effect of variables working in groups (intuition and information theory).
• Exploring the best variable subset in practice using R.

Selecting the best variables is also known as feature selection, selecting the most important predictors, selecting the best predictors, among others.

Figure 3.1: As above, so below

Image: Is it a neural network? Nope. Dark matter, from the “The Millennium Simulation Project”.

3.3.1 Going deeper into variable ranking

It’s quite common to find in literature and algorithms, that covers this topic an univariate analysis, which is a ranking of variables given a particular metric.

We’re going to create two models: random forest and gradient boosting machine (GBM) usingcaret R package to cross-validate the data. Next, we’ll compare the best variable ranking that every model returns.

library(caret)library(funModeling)library(dplyr)# Excluding all NA rows from the data, in this case, NAs are not the main issue to solve, so we'll skip the 6 cases which have NA (or missing values).heart_disease=na.omit(heart_disease)# Setting a 4-fold cross-validationfitControl =trainControl(method ="cv",number =4,classProbs =TRUE,summaryFunction = twoClassSummary)# Creating the random forest model, finding the best tuning parameter setset.seed(999)fit_rf =train(x=select(heart_disease,-has_heart_disease,-heart_disease_severity),y = heart_disease$has_heart_disease,method ="rf",trControl = fitControl,verbose =FALSE,metric ="ROC")# Creating the gradient boosting machine model, finding the best tuning parameter setfit_gbm =train(x=select(heart_disease,-has_heart_disease,-heart_disease_severity),y = heart_disease$has_heart_disease,method ="gbm",trControl = fitControl,verbose =FALSE,metric ="ROC")

Now we can proceed with the comparison.

The columnsimportance_rf andimportance_gbm represent the importance measured by each algorithm. Based on each metric, there arerank_rf andrank_gbm which represent the importance order, finallyrank_diff (rank_rf -rank_gbm) represents how different each algorithm rank the variables.

# Here we manipulate to show a nice the table described beforevar_imp_rf=data.frame(varImp(fit_rf,scale=T)["importance"])%>%dplyr::mutate(variable=rownames(.))%>%dplyr::rename(importance_rf=Overall)%>%dplyr::arrange(-importance_rf)%>%dplyr::mutate(rank_rf=seq(1:nrow(.)))var_imp_gbm=as.data.frame(varImp(fit_gbm,scale=T)["importance"])%>%dplyr::mutate(variable=rownames(.))%>%dplyr::rename(importance_gbm=Overall)%>%dplyr::arrange(-importance_gbm)%>%dplyr::mutate(rank_gbm=seq(1:nrow(.)))                                                                                                                            final_res=merge(var_imp_rf, var_imp_gbm,by="variable")final_res$rank_diff=final_res$rank_rf-final_res$rank_gbm# Printing the results!final_res

Figure 3.2: Comparing different variable ranking

We can see that there are variables which are not important at all to both models (fasting_blood_sugar). There are others that maintain a position at the top of importance likechest_pain andthal.

Different predictive model implementations have their criteria to report what are the best features, according to that particular model. This ends up in different ranking across different algorithms.More info about the inner importance metrics can be found at thecaret documentation.

Even more, in tree based models like GBM and Random Forest there is a random component to picking up variables, and the importance is based on prior -and automatic- variable selection when building the trees. The importance of each variable depends on the others, not only on its isolated contribution:Variables work in groups. We’ll back on this later on this chapter.

Although the ranking will vary from algorithm to algorithm, in general terms there is a correlation between all of these results as we mentioned before.

Conclusion: Every ranking list is not the“final truth”, it gives us orientation about where the information is.

Figure 3.3: Variables work in groups

3.7.1 Example in R: Variables working in groups

Figure 3.4: Aristotle (384 BC322 BC)

The following code illustrates what Aristotle saidsome years ago.

It creates 3 models based on different variable subsets:

• model 1 is based onmax_heart_rate input variable
• model 2 is based onchest_pain input variable
• model 3 is based onmax_heart_rateandchest_pain input variables

Each model returns the metric ROC, and the result contains the improvement of considering the two variables at the same time vs. taking each variable isolated.

library(caret)library(funModeling)library(dplyr)# setting cross-validation 4-foldfitControl =trainControl(method ="cv",number =4,classProbs =TRUE,summaryFunction = twoClassSummary               )create_model<-function(input_variables) {# create gradient boosting machine model# based on input variables  fit_model =train(x=select(heart_disease,one_of(input_variables)                             ),y = heart_disease$has_heart_disease,method ="gbm",trControl = fitControl,verbose =FALSE,metric ="ROC")# returning the ROC as the performance metric  max_roc_value=max(fit_model$results$ROC)return(max_roc_value)}roc_1=create_model("max_heart_rate")roc_2=create_model("chest_pain")roc_3=create_model(c("max_heart_rate","chest_pain"))avg_improvement=round(100*(((roc_3-roc_1)/roc_1)+((roc_3-roc_2)/roc_2))/2,2)avg_improvement_text=sprintf("Average improvement: %s%%",                              avg_improvement)results =sprintf("ROC model based on 'max_heart_rate': %s.;  based on 'chest_pain': %s; and based on both: %s",round(roc_1,2),round(roc_2,2),round(roc_3,2)  )# printing the results!cat(c(results, avg_improvement_text),sep="\n\n")

## ROC model based on 'max_heart_rate': 0.71.;##   based on 'chest_pain': 0.75; and based on both: 0.81## ## Average improvement: 11.67%

3.7.2 Tiny example (based on Information Theory)

Consider the followingbig data table 😜 4 rows, 2 input variables (var_1,var_2) and one outcome (target):

Figure 3.5: Unity gives strength: Combining variables

If we build a predictive model based onvar_1 only, what it willsee?, the valuea is correlated with outputblue andred in the same proportion (50%):

• Ifvar_1='a' then likelihood of target=‘red’ is 50% (row 1)
• Ifvar_1='b' then likelihood of target=‘blue’ is 50% (row 2)

Same analysis goes forvar_2

When the same input is related to different outcomes it’s defined asnoise. The intuition is the same as one person telling us:“Hey it’s going to rain tomorrow!”, and another one saying:“For sure tomorrow it’s not going to rain”. We’d think…“OMG! do I need the umbrella or not 😱?”

Going back to the example, taking the two variables at the same time, the correspondence between the input and the output in unique: “Ifvar_1='a' andvar_2='x' then the likelihood of beingtarget='red' is 100%”. You can try other combinations.

Summing-up:

That was an example ofvariables working in groups, consideringvar_1 andvar_2 at the same time increases the predictive power.

Nonetheless, it’s a deeper topic to cover, considering the last analysis; how about taking anId column (every value is unique) to predict something? The correspondence between input-output will also be unique… but is it a useful model? There’ll be more to come about information theory in this book.

3.7.3 Conclusions

• The proposed R example based onheart_disease data shows an averageimprovement of 9% when considering two variables at a time, not too bad. This percentage of improvement is the result of thevariables working in groups.
• This effect appears if the variables contain information, such is the case ofmax_heart_rate andchest_pain (orvar_1 andvar_2).
• Puttingnoisy variables next to good variableswill usually affect overall performance.
• Also thework in groups effect is higher if the input variablesare not correlated between them. This is difficult to optimize in practice. More on this on the next section…

3.7.4 Rank best features using information theory

As introduced at the beginning of the chapter, we can get variable importance without using a predictive model using information theory.

From version 1.6.6 the packagefunModeling introduces the functionvar_rank_info, which takes two arguments, the data and the target variable, because it follows:

variable_importance =var_rank_info(heart_disease,"has_heart_disease")# Printing resultsvariable_importance

##                       var    en    mi           ig           gr## 1  heart_disease_severity 1.846 0.995 0.9950837595 0.5390655068## 2                    thal 2.032 0.209 0.2094550580 0.1680456709## 3             exer_angina 1.767 0.139 0.1391389302 0.1526393841## 4            exter_angina 1.767 0.139 0.1391389302 0.1526393841## 5              chest_pain 2.527 0.205 0.2050188327 0.1180286190## 6       num_vessels_flour 2.381 0.182 0.1815217813 0.1157736478## 7                   slope 2.177 0.112 0.1124219069 0.0868799615## 8       serum_cholestoral 7.481 0.561 0.5605556771 0.0795557228## 9                  gender 1.842 0.057 0.0572537665 0.0632970555## 10                oldpeak 4.874 0.249 0.2491668741 0.0603576874## 11         max_heart_rate 6.832 0.334 0.3336174096 0.0540697329## 12 resting_blood_pressure 5.567 0.143 0.1425548155 0.0302394591## 13                    age 5.928 0.137 0.1371752885 0.0270548944## 14        resting_electro 2.059 0.024 0.0241482908 0.0221938072## 15    fasting_blood_sugar 1.601 0.000 0.0004593775 0.0007579095

# Plottingggplot(variable_importance,aes(x =reorder(var, gr),y = gr,fill = var)       )+geom_bar(stat ="identity")+coord_flip()+theme_bw()+xlab("")+ylab("Variable Importance       (based on Information Gain)"       )+guides(fill =FALSE)

Figure 3.6: Variable Importance (based on Gain Ratio)

Isheart_disease_severity the feature that explains the target the most?

No, this variable was used to generate the target, thus we must exclude it. It is a typical mistake when developing a predictive model to have either an input variable that was built in the same way as the target (as in this case) or adding variables from the future as explained inConsiderations involving time.

Going back to the result ofvar_rank_info, the resulting metrics come from information theory:

• en: entropy measured in bits
• mi: mutual information
• ig: information gain
• gr: gain ratio

We are not going to cover what is behind these metrics at this point as this will be covered exclusively in a future chapter, However, thegain ratio is the most important metric here, ranged from 0 to 1, with higher being better.

Fuzzy boundaries

We’ve just seen how to calculate importance based on information theory metrics. This topic is not exclusive to this chapter; this concept is also present in theExploratory Data Analysis - Correlation and Relationship section.

Toselect best features is related tọexploratory data analysis and vice-versa.

Figure 3.7: Fractals in Nature

Figure 3.8: ROC values for different variables subset

Figure 3.9: Example of cluster segmentation

3.11.1 The short answer

Pick up the topN variables from the algorithm you’re using and then re-build the model with this subset. Not every predictive model retrieves variable rankings, but if it does, use the same model (for example gradient boosting machine) to get the ranking and to build the final model.

For those models like k-nearest neighbors which don’t have a built-in select best features procedure, it’s valid to use the selection of another algorithm. It will lead to better results than using all the variables.

3.11.2 The long answer

• When possible,validate the list with someone who knows about the context, the business or the data source. Either for the topN or the bottomM variables. As regards thosebad variables, we may be missing something in the data munging that could be destroying their predictive power.
• Understand each variable, its meaning in context (business, medical, other).
• Doexploratory data analysis to see the distributions of the most important variables regarding a target variable,does the selection make sense? If the target is binary then the functionProfiling target using cross_plot can be used.
• Does the average of any variablesignificantly change over time? Check for abrupt changes in distributions.
• Suspect about high cardinality top-ranked variables (like postal code, let’s say above +100 categories). More information atHigh Cardinality Variable in Predictive Modeling.
• When making the selection -as well as a predictive modeling-, try and use methods which contain some mechanism of re-sampling (like bootstrapping), and cross-validation. More information in theknowing the error chapter.
• Try other methods to findgroups of variables, like the one mentioned before: mRMR.
• If the selection doesn’t meet the needs, try creating new variables, you can check thedata preparation chapter. Coming soon: Feature engineering chapter.

3.11.3 Generate your own knowledge

It’s difficult to generalize when the nature of the data is so different, fromgenetics in which there are thousands of variables and a few rows, to web-navigation when new data is coming all the time.

The same applies to the objective of the analysis. Is it to be used in a competition where precision is highly necessary? Perhaps the solution may include more correlated variables in comparison to an ad-hoc study in which the primary goal is a simple explanation.

There is no one-size-fits-all answer to face all possible challenges; you’ll find powerful insights using your experience. It’s just a matter of practice.

3.12.1 Usingcross_plot (dataViz)

3.12.1.2 Example 1: Is gender correlated with heart disease?

cross_plot(heart_disease,input="gender",target="has_heart_disease")

Figure 3.10: Using cross-plot to analyze and report variable importance

Last two plots have the same data source, showing the distribution ofhas_heart_disease regardinggender. The one on the left shows in percentage value, while the one on the right shows in absolute value.

3.12.1.2.1 How to extract conclusions from the plots? (Short version)

Gender variable seems to be agood predictor, since the likelihood of having heart disease is different given the female/male groups.it gives an order to the data.

3.12.1.4 Example 2: Crossing with numerical variables

Numerical variables should bebinned to plot them with a histogram, otherwise, the plot is not showing information, as it can be seen here:

3.12.1.4.1 Equal frequency binning

There is a function included in the package (inherited from Hmisc package):equal_freq, which returns the bins/buckets based on theequal frequency criteria. Which is-or tries to- have the same quantity of rows per bin.

For numerical variables,cross_plot has by default theauto_binning=T, which automatically calls theequal_freq function withn_bins=10 (or the closest number).

cross_plot(heart_disease,input="max_heart_rate",target="has_heart_disease")

Figure 3.11: Numeric variable as input (automatic binning)

3.12.1.5 Example 3: Manual binning

If you don’t want the automatic binning, then set theauto_binning=F incross_plot function.

For example, creatingoldpeak_2 based on equal frequency, with three buckets.

heart_disease$oldpeak_2 =equal_freq(var=heart_disease$oldpeak,n_bins =3)summary(heart_disease$oldpeak_2)

## [0.0,0.2) [0.2,1.5) [1.5,6.2] ##       106       107        90

Plotting the binned variable (auto_binning = F):

cross_oldpeak_2=cross_plot(heart_disease,input="oldpeak_2",target="has_heart_disease",auto_binning = F)

Figure 3.12: Disabling automatic binning shows the original variable

3.12.1.5.1Conclusion

This new plot based onoldpeak_2 shows clearly how: the likelihood ofhaving heart disease increases asoldpeak_2 increases as well.Again, it gives an order to the data.

3.12.1.6 Example 4: Noise reducing

Converting variablemax_heart_rate into a one of 10 bins:

heart_disease$max_heart_rate_2 =equal_freq(var=heart_disease$max_heart_rate,n_bins =10)cross_plot(heart_disease,input="max_heart_rate_2",target="has_heart_disease"           )

Figure 3.13: Plotting using custom binning

At first glance,max_heart_rate_2 shows a negative and linear relationship. However, there are some buckets which add noise to the relationship. For example, the bucket(141, 146] has a higher heart disease rate than the previous bucket, and it was expected to have a lower.This could be noise in data.

Key note: One way to reduce thenoise (at the cost oflosing some information), is to split with less bins:

heart_disease$max_heart_rate_3 =equal_freq(var=heart_disease$max_heart_rate,n_bins =5)cross_plot(heart_disease,input="max_heart_rate_3",target="has_heart_disease"           )

Figure 3.14: Reducing the bins may help to better expose the relationship

Conclusion: As it can be seen, now the relationship is much clean and clear. Bucket‘N’ has a higher rate than‘N+1’, which implies a negative correlation.

How about saving the cross_plot result into a folder?

Just set the parameterpath_out with the folder you want -It creates a new one if it doesn’t exists-.

cross_plot(heart_disease,input="max_heart_rate_3",target="has_heart_disease",path_out="my_plots")

It creates the foldermy_plots into the working directory.

vars_to_analyze=c("age","oldpeak","max_heart_rate")

cross_plot(data=heart_disease,target="has_heart_disease",input=vars_to_analyze)

plotar(data=heart_disease,input=c('max_heart_rate','resting_blood_pressure'),target="has_heart_disease",plot_type ="boxplot",path_out ="my_awsome_folder")

3.12.2 Using BoxPlots

3.12.2.1 What is this about?

The use of Boxplots in importance variable analysis gives a quick view of how different the quartiles are among the various values in a binary target variable.

# Loading funModeling !library(funModeling)data(heart_disease)

plotar(data=heart_disease,input="age",target="has_heart_disease",plot_type ="boxplot")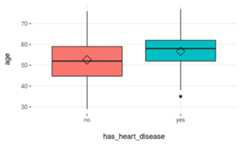

Figure 3.15: Profiling target using boxplot

Rhomboid near the mean line represents themedian.

Figure 3.16: How to interpret a boxplot

When to use boxplots?

When we need to analyze different percentiles across the classes to predict. Note this is a powerful technique since the bias produced due to outliers doesn’t affect as much as it does to the mean.

3.12.2.2 Boxplot: Good vs. Bad variable

Using more than one variable as inputs is useful in order to compare boxplots quickly, and thus getting the best variables…

plotar(data=heart_disease,input=c('max_heart_rate','resting_blood_pressure'),target="has_heart_disease",plot_type ="boxplot")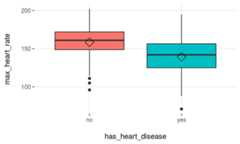

Figure 3.17: plotar function for multiple variables

Figure 3.17: plotar function for multiple variables

We can conclude thatmax_heart_rate is a better predictor thanresting_blood_pressure.

As a general rule, a variable will rank asmore important if boxplots arenot aligned horizontally.

Statistical tests: percentiles are another used feature used by them in order to determine -for example- if means across groups are or not the same.

plotar(data=heart_disease,input=c('max_heart_rate','resting_blood_pressure'),target="has_heart_disease",plot_type ="boxplot",path_out ="my_awsome_folder")

3.12.3 Using Density Histograms

3.12.3.1 What is this about?

Density histograms are quite standard in any book/resource when plotting distributions. To use them in selecting variables gives a quick view on how well certain variable separates the class.

plotar(data=heart_disease,input="age",target="has_heart_disease",plot_type ="histdens")

Figure 3.18: Profiling target using density histograms

Note: The dashed-line represents variable mean.

Density histograms are helpful to visualize the general shape of a numeric distribution.

Thisgeneral shape is calculated based on a technique calledKernel Smoother, its general idea is to reduce high/low peaks (noise) present in near points/bars by estimating the function that describes the points. Here some pictures to illustrate the concept:https://en.wikipedia.org/wiki/Kernel_smoother

3.12.3.3 Good vs. bad variable

plotar(data=heart_disease,input=c('resting_blood_pressure','max_heart_rate'),target="has_heart_disease",plot_type ="histdens")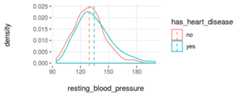

Figure 3.19: plotar function for multiple variables

Figure 3.19: plotar function for multiple variables

And the model will see the same… if the curves are quite overlapped, like it is inresting_blood_pressure, then it’snot a good predictor as if they weremore spaced -likemax_heart_rate.

• Key in mind this when using Histograms & BoxPlots They are nice to see when the variable:
  • Has a good spread -not concentrated on a bunch of3, 4..6.. different values,and
  • It has not extreme outliers…(this point can be treated withprep_outliers function present in this package)

---

---