# Loading funModeling!library(funModeling)library(dplyr)data(heart_disease)

1.1.1.1 Checking missing values, zeros, data type, and unique values

Probably one of the first steps, when we get a new dataset to analyze, is to know if there are missing values (NA inR) and the data type.

Thedf_status function coming infunModeling can help us by showing these numbers in relative and percentage values. It also retrieves the infinite and zeros statistics.

# Profiling the data inputdf_status(heart_disease)

Figure 1.1: Dataset health status

• q_zeros: quantity of zeros (p_zeros: in percent)
• q_inf: quantity of infinite values (p_inf: in percent)
• q_na: quantity of NA (p_na: in percent)
• type: factor or numeric
• unique: quantity of unique values

1.1.1.2 Why are these metrics important?

• Zeros: Variables withlots of zeros may not be useful for modeling and, in some cases, they may dramatically bias the model.
• NA: Several models automatically exclude rows with NA (random forest for example). As a result, the final model can be biased due to several missing rows because of only one variable. For example, if the data contains only one out of 100 variables with 90% of NAs, the model will be training with only 10% of the original rows.
• Inf: Infinite values may lead to an unexpected behavior in some functions in R.
• Type: Some variables are encoded as numbers, but they are codes or categories and the modelsdon’t handle them in the same way.
• Unique: Factor/categorical variables with a high number of different values (~30) tend to do overfitting if the categories have low cardinality (decision trees, for example).

1.1.1.3 Filtering unwanted cases

The functiondf_status takes a data frame and returns astatus table that can help us quickly remove features (or variables) based on all the metrics described in the last section. For example:

Removing variables with ahigh number of zeros

# Profiling the Data Inputmy_data_status=df_status(heart_disease,print_results = F)# Removing variables with 60% of zero valuesvars_to_remove=filter(my_data_status, p_zeros>60)%>%.$variablevars_to_remove

## [1] "fasting_blood_sugar" "exer_angina"         "exter_angina"

# Keeping all columns except the ones present in 'vars_to_remove' vectorheart_disease_2=select(heart_disease,-one_of(vars_to_remove))

Ordering data by percentage of zeros

arrange(my_data_status,-p_zeros)%>%select(variable, q_zeros, p_zeros)

##                  variable q_zeros p_zeros## 1     fasting_blood_sugar     258   85.15## 2             exer_angina     204   67.33## 3            exter_angina     204   67.33## 4       num_vessels_flour     176   58.09## 5  heart_disease_severity     164   54.13## 6         resting_electro     151   49.83## 7                 oldpeak      99   32.67## 8                     age       0    0.00## 9                  gender       0    0.00## 10             chest_pain       0    0.00## 11 resting_blood_pressure       0    0.00## 12      serum_cholestoral       0    0.00## 13         max_heart_rate       0    0.00## 14                  slope       0    0.00## 15                   thal       0    0.00## 16      has_heart_disease       0    0.00

The same reasoning applies when we want to remove (or keep) those variables above or below a certain threshold. Please check the missing values chapter to get more information about the implications when dealing with variables containing missing values.

1.1.1.4 Going deep into these topics

Values returned bydf_status are deeply covered in other chapters:

• Missing values (NA) treatment, analysis, and imputation are deeply covered in theMissing Data chapter.
• Data type, its conversions and implications when handling different data types and more are covered in theData Types chapter.
• A high number ofunique values is synonymous for high-cardinality variables. This situation is studied in both chapters:
  • High Cardinality Variable in Descriptive Stats
  • High Cardinality Variable in Predictive Modeling

1.1.1.5 Getting other common statistics:total rows,total columns andcolumn names:

# Total rowsnrow(heart_disease)

## [1] 303

# Total columnsncol(heart_disease)

## [1] 16

# Column namescolnames(heart_disease)

##  [1] "age"                    "gender"                ##  [3] "chest_pain"             "resting_blood_pressure"##  [5] "serum_cholestoral"      "fasting_blood_sugar"   ##  [7] "resting_electro"        "max_heart_rate"        ##  [9] "exer_angina"            "oldpeak"               ## [11] "slope"                  "num_vessels_flour"     ## [13] "thal"                   "heart_disease_severity"## [15] "exter_angina"           "has_heart_disease"

freq(data=heart_disease,input =c('thal','chest_pain'))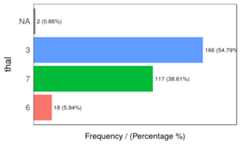

Figure 1.2: Frequency analysis 1

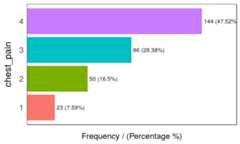
Figure 1.2: Frequency analysis 2

freq(data=heart_disease)

freq(data=heart_disease$thal,plot =FALSE,na.rm =TRUE)

freq(data=heart_disease,path_out='my_folder')

1.1.2.0.1 Analysis

The output is ordered by thefrequency variable, which quickly analyzes the most frequent categories and how many shares they represent (cummulative_perc variable). In general terms, we as human beings like order. If the variables are not ordered, then our eyes start moving over all the bars to do the comparison and our brains place each bar in relation to the other bars.

Check the difference for the same data input, first without order and then with order:

Figure 1.3: Order and beauty

Generally, there are just a few categories that appear most of the time.

A more complete analysis is inHigh Cardinality Variable in Descriptive Stats

1.1.2.1 Introducing thedescribe function

This function comes in theHmisc package and allows us to quickly profile a complete dataset for both numerical and categorical variables. In this case, we’ll select only two variables and we will analyze the result.

# Just keeping two variables to use in this exampleheart_disease_3=select(heart_disease, thal, chest_pain)# Profiling the data!describe(heart_disease_3)

## heart_disease_3 ## ##  2  Variables      303  Observations## ---------------------------------------------------------------------------## thal ##        n  missing distinct ##      301        2        3 ##                             ## Value          3     6     7## Frequency    166    18   117## Proportion 0.551 0.060 0.389## ---------------------------------------------------------------------------## chest_pain ##        n  missing distinct ##      303        0        4 ##                                   ## Value          1     2     3     4## Frequency     23    50    86   144## Proportion 0.076 0.165 0.284 0.475## ---------------------------------------------------------------------------

Where:

• n: quantity of non-NA rows. In this case, it indicates there are301 patients containing a number.
• missing: number of missing values. Summing this indicator ton gives us the total number of rows.
• unique: number of unique (or distinct) values.

The other information is pretty similar to thefreq function and returns between parentheses the total number in relative and absolute values for each different category.

1.1.3.1 Part 1: Introducing the World Data case study

This contains many indicators regarding world development. Regardless the profiling example, the idea is to provide a ready-to-use table for sociologists, researchers, etc. interested in analyzing this kind of data.

The original data source is:http://databank.worldbank.org. There you will find a data dictionary that explains all the variables.

First, we have to do some data wrangling. We are going to keep with the newest value per indicator.

library(Hmisc)# Loading data from the book repository without altering the formatdata_world=read.csv(file ="https://goo.gl/2TrDgN",header = T,stringsAsFactors = F,na.strings ="..")# Excluding missing values in Series.Code. The data downloaded from the web page contains four lines with "free-text" at the bottom of the file.data_world=filter(data_world, Series.Code!="")# The magical function that keeps the newest values for each metric. If you're not familiar with R, then skip it.max_ix<-function(d) {  ix=which(!is.na(d))  res=ifelse(length(ix)==0,NA, d[max(ix)])return(res)}data_world$newest_value=apply(data_world[,5:ncol(data_world)],1,FUN=max_ix)# Printing the first three rowshead(data_world,3)

##                                          Series.Name       Series.Code## 1 Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS## 2 Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS## 3 Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS##   Country.Name Country.Code X1990..YR1990. X2000..YR2000. X2007..YR2007.## 1  Afghanistan          AFG             NA             NA             NA## 2      Albania          ALB             NA             NA             NA## 3      Algeria          DZA           11.8             NA             NA##   X2008..YR2008. X2009..YR2009. X2010..YR2010. X2011..YR2011.## 1             NA             NA             NA             NA## 2             NA             NA             NA             NA## 3             NA             NA             NA             NA##   X2012..YR2012. X2013..YR2013. X2014..YR2014. X2015..YR2015.## 1             NA             NA           62.7             NA## 2             NA             NA             NA             NA## 3             NA             NA             NA             NA##   X2016..YR2016. newest_value## 1             NA         62.7## 2             NA           NA## 3             NA         11.8

The columnsSeries.Name andSeries.Code are the indicators to be analyzed.Country.Name andCountry.Code are the countries. Each row represents a unique combination of country and indicator. Remaining columns,X1990..YR1990. (year 1990),X2000..YR2000. (year 2000),X2007..YR2007. (year 2007), and so on indicate the metric value for that year, thus each column is a year.

1.1.3.2 Making a data scientist decision

There are manyNAs because some countries don’t have the measure of the indicator in those years. At this point, we need tomake a decision as a data scientist. Probably no the optimal if we don’t ask to an expert, e.g., a sociologist.

What to do with theNA values? In this case, we are going to to keep with thenewest value for all the indicators. Perhaps this is not the best way to extract conclusions for a paper as we are going to compare some countries with information up to 2016 while other countries will be updated only to 2009. To compare all the indicators with the newest data is a valid approach for the first analysis.

Another solution could have been to keep with the newest value, but only if this number belongs to the last five years. This would reduce the number of countries to analyze.

These questions are impossible to answer for anartificial intelligence system, yet the decision can change the results dramatically.

The last transformation

The next step will convert the last table fromlong towide format. In other words, each row will represent a country and each column an indicator (thanks to the last transformation that has thenewest value for each combination of indicator-country).

The indicator names are unclear, so we will “translate” a few of them.

# Get the list of indicator descriptions.names=unique(select(data_world, Series.Name, Series.Code))head(names,5)

##                                            Series.Name       Series.Code## 1   Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS## 218                    Income share held by second 20%    SI.DST.02ND.20## 435                     Income share held by third 20%    SI.DST.03RD.20## 652                    Income share held by fourth 20%    SI.DST.04TH.20## 869                   Income share held by highest 20%    SI.DST.05TH.20

# Convert a fewdf_conv_world=data.frame(new_name=c("urban_poverty_headcount","rural_poverty_headcount","gini_index","pop_living_slums","poverty_headcount_1.9"),Series.Code=c("SI.POV.URHC","SI.POV.RUHC","SI.POV.GINI","EN.POP.SLUM.UR.ZS","SI.POV.DDAY"),stringsAsFactors = F)# adding the new indicator valuedata_world_2 =left_join(data_world,                          df_conv_world,by="Series.Code",all.x=T)data_world_2 =mutate(data_world_2,Series.Code_2=ifelse(!is.na(new_name),as.character(data_world_2$new_name),                   data_world_2$Series.Code)         )

Any indicator meaning can be checked in data.worldbank.org. For example, if we want to know whatEN.POP.SLUM.UR.ZS means, then we type:http://data.worldbank.org/indicator/EN.POP.SLUM.UR.ZS

# The package 'reshape2' contains both 'dcast' and 'melt' functionslibrary(reshape2)data_world_wide=dcast(data_world_2, Country.Name~Series.Code_2,value.var ="newest_value")

Note: To understand more aboutlong andwide format usingreshape2 package, and how to convert from one to another, please go tohttp://seananderson.ca/2013/10/19/reshape.html.

Now we have the final table to analyze:

# Printing the first three rowshead(data_world_wide,3)

##   Country.Name gini_index pop_living_slums poverty_headcount_1.9## 1  Afghanistan         NA             62.7                    NA## 2      Albania      28.96               NA                  1.06## 3      Algeria         NA             11.8                    NA##   rural_poverty_headcount SI.DST.02ND.20 SI.DST.03RD.20 SI.DST.04TH.20## 1                    38.3             NA             NA             NA## 2                    15.3          13.17          17.34          22.81## 3                     4.8             NA             NA             NA##   SI.DST.05TH.20 SI.DST.10TH.10 SI.DST.FRST.10 SI.DST.FRST.20 SI.POV.2DAY## 1             NA             NA             NA             NA          NA## 2          37.82          22.93           3.66           8.85        6.79## 3             NA             NA             NA             NA          NA##   SI.POV.GAP2 SI.POV.GAPS SI.POV.NAGP SI.POV.NAHC SI.POV.RUGP SI.POV.URGP## 1          NA          NA         8.4        35.8         9.3         5.6## 2        1.43        0.22         2.9        14.3         3.0         2.9## 3          NA          NA          NA         5.5         0.8         1.1##   SI.SPR.PC40 SI.SPR.PC40.ZG SI.SPR.PCAP SI.SPR.PCAP.ZG## 1          NA             NA          NA             NA## 2        4.08        -1.2205        7.41        -1.3143## 3          NA             NA          NA             NA##   urban_poverty_headcount## 1                    27.6## 2                    13.6## 3                     5.8

1.1.3.3 Part 2: Doing the numerical profiling in R

We will see the following functions:

• describe fromHmisc
• profiling_num (full univariate analysis), andplot_num (hisotgrams) fromfunModeling

We’ll pick up only two variables as an example:

library(Hmisc)# contains the `describe` functionvars_to_profile=c("gini_index","poverty_headcount_1.9")data_subset=select(data_world_wide,one_of(vars_to_profile))# Using the `describe` on a complete dataset. # It can be run with one variable; for example, describe(data_subset$poverty_headcount_1.9)describe(data_subset)

## data_subset ## ##  2  Variables      217  Observations## ---------------------------------------------------------------------------## gini_index ##        n  missing distinct     Info     Mean      Gmd      .05      .10 ##      140       77      136        1     38.8    9.594    26.81    27.58 ##      .25      .50      .75      .90      .95 ##    32.35    37.69    43.92    50.47    53.53 ## ## lowest : 24.09 25.59 25.90 26.12 26.13, highest: 56.24 60.46 60.79 60.97 63.38## ---------------------------------------------------------------------------## poverty_headcount_1.9 ##        n  missing distinct     Info     Mean      Gmd      .05      .10 ##      116      101      107        1    18.33    23.56    0.025    0.075 ##      .25      .50      .75      .90      .95 ##    1.052    6.000   33.815   54.045   67.328 ## ## lowest :  0.00  0.01  0.03  0.04  0.06, highest: 68.64 68.74 70.91 77.08 77.84## ---------------------------------------------------------------------------

Takingpoverty_headcount_1.9 (Poverty headcount ratio at $1.90 a day is the percentage of the population living on less than $1.90 a day at 2011 international prices.), we can describe it as:

• n: quantity of non-NA rows. In this case, it indicates116 countries that contain a number.
• missing: number of missing values. Summing this indicator ton gives us the total number of rows. Almost half of the countries have no data.
• unique: number of unique (or distinct) values.
• Info: an estimator of the amount of information present in the variable and not important at this point.
• Mean: the classical mean or average.
• Numbers:.05,.10,.25,.50,.75,.90 and.95 stand for the percentiles. These values are really useful since it helps us to describe the distribution. It will be deeply covered later on, i.e.,.05 is the 5th percentile.
• lowest andhighest: the five lowest/highest values. Here, we can spot outliers and data errors. For example, if the variable represents a percentage, then it cannot contain negative values.

The next function isprofiling_num which takes a data frame and retrieves abig table, easy to get overwhelmed in asea of metrics. This is similar to what we can see in the movieThe Matrix.

Figure 1.4: The matrix of data

Picture from the movie: “The Matrix” (1999). The Wachowski Brothers (Directors).

The idea of the following table is to give to the user afull set of metrics,, for then, she or he can decide which ones to pick for the study.

Note: Every metric has a lot of statistical theory behind it. Here we’ll be covering just a tiny andoversimplified approach to introduce the concepts.

library(funModeling)# Full numerical profiling in one function automatically excludes non-numerical variablesprofiling_num(data_world_wide)

##                   variable mean std_dev variation_coef   p_01   p_05## 1               gini_index 38.8    8.49           0.22 25.711 26.815## 2         pop_living_slums 45.7   23.66           0.52  6.830 10.750## 3    poverty_headcount_1.9 18.3   22.74           1.24  0.000  0.025## 4  rural_poverty_headcount 41.2   21.91           0.53  2.902  6.465## 5           SI.DST.02ND.20 10.9    2.17           0.20  5.568  7.361## 6           SI.DST.03RD.20 15.2    2.03           0.13  9.137 11.828## 7           SI.DST.04TH.20 21.5    1.49           0.07 16.286 18.288## 8           SI.DST.05TH.20 45.9    7.14           0.16 35.004 36.360## 9           SI.DST.10TH.10 30.5    6.75           0.22 20.729 21.988## 10          SI.DST.FRST.10  2.5    0.87           0.34  0.916  1.147## 11          SI.DST.FRST.20  6.5    1.87           0.29  2.614  3.369## 12             SI.POV.2DAY 32.4   30.64           0.95  0.061  0.393## 13             SI.POV.GAP2 14.2   16.40           1.16  0.012  0.085## 14             SI.POV.GAPS  6.9   10.10           1.46  0.000  0.000## 15             SI.POV.NAGP 12.2   10.12           0.83  0.421  1.225## 16             SI.POV.NAHC 30.7   17.88           0.58  1.842  6.430## 17             SI.POV.RUGP 15.9   11.83           0.75  0.740  1.650## 18             SI.POV.URGP  8.3    8.24           0.99  0.300  0.900## 19             SI.SPR.PC40 10.3    9.75           0.95  0.857  1.228## 20          SI.SPR.PC40.ZG  2.0    3.62           1.85 -6.232 -3.021## 21             SI.SPR.PCAP 21.1   17.44           0.83  2.426  3.138## 22          SI.SPR.PCAP.ZG  1.5    3.21           2.20 -5.897 -3.805## 23 urban_poverty_headcount 23.3   15.06           0.65  0.579  3.140##      p_25 p_50 p_75 p_95 p_99 skewness kurtosis  iqr       range_98## 1  32.348 37.7 43.9 53.5 60.9    0.552      2.9 11.6  [25.71, 60.9]## 2  25.175 46.2 65.6 83.4 93.4    0.087      2.0 40.5  [6.83, 93.41]## 3   1.052  6.0 33.8 67.3 76.2    1.125      2.9 32.8     [0, 76.15]## 4  25.250 38.1 57.6 75.8 81.7    0.051      2.0 32.3    [2.9, 81.7]## 5   9.527 11.1 12.6 14.2 14.6   -0.411      2.7  3.1  [5.57, 14.57]## 6  13.877 15.5 16.7 17.9 18.1   -0.876      3.8  2.8  [9.14, 18.14]## 7  20.758 21.9 22.5 23.0 23.4   -1.537      5.6  1.8 [16.29, 23.39]## 8  40.495 44.8 49.8 58.1 65.9    0.738      3.3  9.3    [35, 65.89]## 9  25.710 29.5 34.1 42.2 50.6    0.905      3.6  8.4 [20.73, 50.62]## 10  1.885  2.5  3.2  3.9  4.3    0.043      2.2  1.4   [0.92, 4.35]## 11  5.092  6.5  8.0  9.4 10.0   -0.119      2.2  2.9     [2.61, 10]## 12  3.828 20.3 63.2 84.6 90.3    0.536      1.8 59.4  [0.06, 90.34]## 13  1.305  5.5 26.3 48.5 56.2    1.063      2.9 25.0  [0.01, 56.18]## 14  0.287  1.4 10.3 31.5 38.3    1.654      4.7 10.0     [0, 38.29]## 15  4.500  8.7 16.9 32.4 36.7    1.129      4.0 12.4  [0.42, 36.72]## 16 16.350 26.6 44.2 63.0 71.6    0.529      2.4 27.9  [1.84, 71.64]## 17  5.950 13.6 22.5 37.7 45.3    0.801      3.0 16.5  [0.74, 45.29]## 18  2.900  6.3  9.9 25.1 35.2    2.316      9.8  7.0   [0.3, 35.17]## 19  3.475  6.9 12.7 28.9 35.4    1.251      3.4  9.2  [0.86, 35.35]## 20 -0.084  1.7  4.6  7.9  9.0   -0.294      3.3  4.7     [-6.23, 9]## 21  8.003 15.3 25.4 52.8 67.2    1.132      3.3 17.4  [2.43, 67.17]## 22 -0.486  1.3  3.6  7.0  8.5   -0.018      3.6  4.0   [-5.9, 8.48]## 23 12.708 20.1 31.2 51.0 61.8    0.730      3.0 18.5  [0.58, 61.75]##          range_80## 1  [27.58, 50.47]## 2    [12.5, 75.2]## 3   [0.08, 54.05]## 4  [13.99, 71.99]## 5    [8.28, 13.8]## 6   [12.67, 17.5]## 7  [19.73, 22.81]## 8  [36.99, 55.24]## 9  [22.57, 39.89]## 10   [1.48, 3.67]## 11   [3.99, 8.89]## 12  [0.79, 78.29]## 13  [0.16, 40.85]## 14  [0.02, 23.45]## 15     [1.85, 27]## 16  [9.86, 58.22]## 17    [3.3, 32.2]## 18    [1.3, 19.1]## 19  [1.81, 27.63]## 20  [-2.64, 6.48]## 21  [4.25, 49.22]## 22  [-2.07, 5.17]## 23  [5.98, 46.11]

Each indicator hasits raison d’être:

• variable: variable name

• mean: the well-known mean or average

• std_dev: standard deviation, a measure ofdispersion orspread around the mean value. A value around0 means almost no variation (thus, it seems more like a constant); on the other side, it is harder to set whathigh is, but we can tell that the higher the variation the greater the spread.Chaos may look like infinite standard variation. The unit is the same as the mean so that it can be compared.

• variation_coef: variation coefficient=std_dev/mean. Because thestd_dev is an absolute number, it’s good to have an indicator that puts it in a relative number, comparing thestd_dev against themean A value of0.22 indicates thestd_dev is 22% of themean If it were close to0 then the variable tends to be more centered around the mean. If we compare two classifiers, then we may prefer the one with lessstd_dev andvariation_coef on its accuracy.

• p_01,p_05,p_25,p_50,p_75,p_95,p_99:Percentiles at 1%, 5%, 25%, and so on. Later on in this chapter is a complete review about percentiles.

For a full explanation about percentiles, please go to:Annex 1: The magic of percentiles.

• skewness: is a measure ofasymmetry. Close to0 indicates that the distribution isequally distributed (or symmetrical) around its mean. Apositive number implies a long tail on the right, whereas anegative number means the opposite. After this section, check the skewness in the plots. The variablepop_living_slums is close to 0 (“equally” distributed),poverty_headcount_1.9 is positive (tail on the right), andSI.DST.04TH.20 is negative (tail on the left). The further the skewness is from 0 the more likely the distribution is to haveoutliers

• kurtosis: describes the distributiontails; keeping it simple, a higher number may indicate the presence of outliers (just as we’ll see later for the variableSI.POV.URGP holding an outlier around the value50 For a complete skewness and kurtosis review, check Refs.(McNeese2016) and(Handbook2013).

• iqr: the inter-quartile range is the result of looking at percentiles0.25 and0.75 and indicates, in the same variable unit, the dispersion length of 50% of the values. The higher the value the more sparse the variable.

• range_98 andrange_80: indicates the range where98% of the values are. It removes the bottom and top 1% (thus, the98% number). It is good to know the variable range without potential outliers. For example,pop_living_slums goes from0 to76.15 It’smore robust than comparing themin andmax values. Therange_80 is the same as therange_98 but without the bottom and top10%

iqr,range_98 andrange_80 are based on percentiles, which we’ll be covering later in this chapter.

Important: All the metrics are calculated having removed theNA values. Otherwise, the table would be filled with NA`s.

my_profiling_table=profiling_num(data_world_wide,print_results =FALSE)%>%select(variable, mean, p_01, p_99, range_80)# Printing only the first three rowshead(my_profiling_table,3)

##                variable mean p_01 p_99       range_80## 1            gini_index   39 25.7   61 [27.58, 50.47]## 2      pop_living_slums   46  6.8   93   [12.5, 75.2]## 3 poverty_headcount_1.9   18  0.0   76  [0.08, 54.05]

1.1.3.3.2 Profiling numerical variables by plotting

Another function infunModeling isplot_num which takes a dataset and plots the distribution of every numerical variable while automatically excluding the non-numerical ones:

plot_num(data_world_wide)

Figure 1.5: Profiling numerical data

We can adjust the number of bars used in the plot by changing thebins parameter (default value is set to 10). For example:plot_num(data_world_wide, bins = 20).

---

# Loading needed librarieslibrary(funModeling)# contains heart_disease datalibrary(minerva)# contains MIC statisticlibrary(ggplot2)library(dplyr)library(reshape2)library(gridExtra)# allow us to plot two plots in a rowoptions(scipen=999)# disable scientific notation

correlation_table(data=heart_disease,target="has_heart_disease")

1.2.2.1 Correlation on Anscombe’s Quartet

Take a look at theAnscombe’s quartet, quotingWikipedia:

They were constructed in 1973 by the statistician Francis Anscombe to demonstrate both the importance of graphing data before analyzing it and the effect of outliers on statistical properties.

1973 and still valid, fantastic.

These four relationships are different, but all of them have the same R2:0.816.

Following example calculates the R2 and plot every pair.

# Reading anscombe quartet dataanscombe_data =read.delim(file="https://goo.gl/mVLz5L",header = T)# calculating the correlation (R squared, or R2) for#every pair, every value is the same: 0.86.cor_1 =cor(anscombe_data$x1, anscombe_data$y1)cor_2 =cor(anscombe_data$x2, anscombe_data$y2)cor_3 =cor(anscombe_data$x3, anscombe_data$y3)cor_4 =cor(anscombe_data$x4, anscombe_data$y4)# defining the functionplot_anscombe <-function(x, y, value, type){# 'anscombe_data' is a global variable, this is# a bad programming practice ;)  p=ggplot(anscombe_data,aes_string(x,y))+geom_smooth(method='lm',fill=NA)+geom_point(aes(colour=factor(1),fill =factor(1)),shape=21,size =2               )+ylim(2,13)+xlim(4,19)+theme_minimal()+theme(legend.position="none")+annotate("text",x =12,y =4.5,label =sprintf("%s: %s",                        type,round(value,2)                       )             )return(p)}# plotting in a 2x2 gridgrid.arrange(plot_anscombe("x1","y1", cor_1,"R2"),plot_anscombe("x2","y2", cor_2,"R2"),plot_anscombe("x3","y3", cor_3,"R2"),plot_anscombe("x4","y4", cor_4,"R2"),ncol=2,nrow=2)

Figure 1.6: Anscombe set

4-different plots, having the samemean for everyx andy variable (9 and 7.501 respectively), and the same degree of correlation. You can check all the measures by typingsummary(anscombe_data).

This is why is so important to plot relationships when analyzing correlations.

We’ll back on this data later. It can be improved! First, we’ll introduce some concepts of information theory.

1.2.3.1 An example in R: A perfect relationship

Let’s plot a non-linear relationship, directly based on a function (negative exponential), and print the MIC value.

x=seq(0,20,length.out=500)df_exp=data.frame(x=x,y=dexp(x,rate=0.65))ggplot(df_exp,aes(x=x,y=y))+geom_line(color='steelblue')+theme_minimal()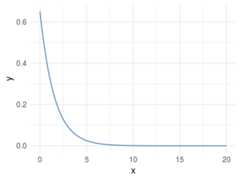

Figure 1.7: A perfect relationship

# position [1,2] contains the correlation of both variables, excluding the correlation measure of each variable against itself.# Calculating linear correlationres_cor_R2=cor(df_exp)[1,2]^2sprintf("R2: %s",round(res_cor_R2,2))

## [1] "R2: 0.39"

# now computing the MIC metricres_mine=mine(df_exp)sprintf("MIC: %s", res_mine$MIC[1,2])

## [1] "MIC: 1"

MIC value goes from 0 to 1. Being 0 implies no correlation and 1 highest correlation. The interpretation is the same as the R-squared.

1.2.3.2 Results analysis

TheMIC=1 indicates there is a perfect correlation between the two variables. If we were doingfeature engineering this variable should be included.

Further than a simple correlation, what the MIC says is: “Hey these two variables show a functional relationship”.

In machine learning terms (and oversimplifying): “variabley is dependant of variablex and a function -that we don’t know which one- can be found model the relationship.”

This is tricky because that relationship was effectively created based on a function, an exponential one.

But let’s continue with other examples…

df_exp$y_noise_1=jitter(df_exp$y,factor =1000,amount =NULL)ggplot(df_exp,aes(x=x,y=y_noise_1))+geom_line(color='steelblue')+theme_minimal()

Figure 1.8: Adding some noise

# calculating R squaredres_R2=cor(df_exp)^2res_R2

# Calculating mineres_mine_2=mine(df_exp)# Printing MICres_mine_2$MIC

# MIC r2: non-linearity metricround(res_mine_2$MICR2,3)# calculating MIC r2 manuallyround(res_mine_2$MIC-res_R2,3)

# creating data exampledf_example=data.frame(x=df_exp$x,y_exp=df_exp$y,y_linear=3*df_exp$x+2)# getting mine metricsres_mine_3=mine(df_example)# generating labels to print the resultsresults_linear =sprintf("MIC: %s\n MIC-R2 (non-linearity): %s",          res_mine_3$MIC[1,3],round(res_mine_3$MICR2[1,3],2)          )results_exp =sprintf("MIC: %s\n MIC-R2 (non-linearity): %s",           res_mine_3$MIC[1,2],round(res_mine_3$MICR2[1,2],4)          )# Plotting results# Creating plot exponential variablep_exp=ggplot(df_example,aes(x=x,y=y_exp))+geom_line(color='steelblue')+annotate("text",x =11,y =0.4,label = results_exp)+theme_minimal()# Creating plot linear variablep_linear=ggplot(df_example,aes(x=x,y=y_linear))+geom_line(color='steelblue')+annotate("text",x =8,y =55,label = results_linear)+theme_minimal()grid.arrange(p_exp,p_linear,ncol=2)

Figure 1.9: Comparing relationships

# calculating the MIC for every pairmic_1=mine(anscombe_data$x1, anscombe_data$y1,alpha=0.8)$MICmic_2=mine(anscombe_data$x2, anscombe_data$y2,alpha=0.8)$MICmic_3=mine(anscombe_data$x3, anscombe_data$y3,alpha=0.8)$MICmic_4=mine(anscombe_data$x4, anscombe_data$y4,alpha=0.8)$MIC# plotting MIC in a 2x2 gridgrid.arrange(plot_anscombe("x1","y1", mic_1,"MIC"),plot_anscombe("x2","y2", mic_2,"MIC"),plot_anscombe("x3","y3", mic_3,"MIC"),plot_anscombe("x4","y4", mic_4,"MIC"),ncol=2,nrow=2)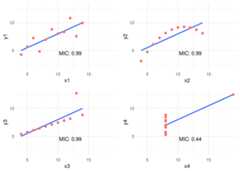

Figure 1.10: MIC statistic

# Calculating the MIC for every pair, note the "MIC-R2" object has the hyphen when the input are two vectors, unlike when it takes a data frame which is "MICR2".mic_r2_1=mine(anscombe_data$x1, anscombe_data$y1,alpha =0.8)$`MIC-R2`mic_r2_2=mine(anscombe_data$x2, anscombe_data$y2,alpha =0.8)$`MIC-R2`mic_r2_3=mine(anscombe_data$x3, anscombe_data$y3,alpha =0.8)$`MIC-R2`mic_r2_4=mine(anscombe_data$x4, anscombe_data$y4,alpha =0.8)$`MIC-R2`# Ordering according mic_r2df_mic_r2=data.frame(pair=c(1,2,3,4),mic_r2=c(mic_r2_1,mic_r2_2,mic_r2_3,mic_r2_4))%>%arrange(-mic_r2)df_mic_r2

# creating sample data (simulating time series)time_x=sort(runif(n=1000,min=0,max=1))y_1=4*(time_x-0.5)^2y_2=4*(time_x-0.5)^3# Calculating MAS for both seriesmas_y1=round(mine(time_x,y_1)$MAS,2)mas_y2=mine(time_x,y_2)$MAS# Putting all togetherdf_mono=data.frame(time_x=time_x,y_1=y_1,y_2=y_2)# Plottinglabel_p_y_1 =sprintf("MAS=%s (goes down\n and up => not-monotonic)",           mas_y1)p_y_1=ggplot(df_mono,aes(x=time_x,y=y_1))+geom_line(color='steelblue')+theme_minimal()+annotate("text",x =0.45,y =0.75,label = label_p_y_1)label_p_y_2=sprintf("MAS=%s (goes up => monotonic)", mas_y2)p_y_2=ggplot(df_mono,aes(x=time_x,y=y_2))+geom_line(color='steelblue')+theme_minimal()+annotate("text",x =0.43,y =0.35,label = label_p_y_2)grid.arrange(p_y_1,p_y_2,ncol=2)

Figure 1.11: Monotonicity in functions

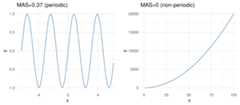
Figure 1.12: Periodicity in functions

1.2.7.1 A more real example: Time Series

Consider the following case which contains three-time series:y1,y2 andy3. They can be profiled concerning its non-monotonicity or overall growth trend.

# reading datadf_time_series =read.delim(file="https://goo.gl/QDUjfd")# converting to long format so they can be plotteddf_time_series_long=melt(df_time_series,id="time")# Plottingplot_time_series =ggplot(data=df_time_series_long,aes(x=time,y=value,colour=variable))+geom_line()+theme_minimal()+scale_color_brewer(palette="Set2")plot_time_series

Figure 1.13: Time series example

# Calculating and printing MAS values for time series datamine_ts=mine(df_time_series)mine_ts$MAS

##      time    y1    y2    y3## time 0.00 0.120 0.105 0.191## y1   0.12 0.000 0.068 0.081## y2   0.11 0.068 0.000 0.057## y3   0.19 0.081 0.057 0.000

We need to look attime column, so we’ve got the MAS value of each series regarding the time.y2 is the most monotonic (and less periodic) series, and it can be confirmed by looking at it. It seems to be always up.

MAS summary:

• MAS ~ 0 indicates monotonic or non-periodic function (“always” up or down)
• MAS ~ 1 indicates non-monotonic or periodic function

# printing again the 3-time seriesplot_time_series

Figure 1.14: Time series example

# Printing MIC valuesmine_ts$MIC

1.2.8.1 Going further: Dynamic Time Warping

MIC will not be helpful for more complex esenarios having time series which vary in speed, you would usedynamic time warping technique (DTW).

Let’s use an image to catch up the concept visually:

Figure 1.15: Dynamic time warping

Image source:Dynamic time wrapping Converting images into time series for data mining(Izbicki2011).

The last image shows two different approaches to compare time series, and theeuclidean is more similar to MIC measure. While DTW can track similarities occurring at different times.

A nice implementation inR:dtw package.

Finding correlations between time series is another way of performingtime series clustering.

library(caret)# selecting just a few variablesheart_disease_2 =select(heart_disease, max_heart_rate, oldpeak,          thal, chest_pain,exer_angina, has_heart_disease)# this conversion from categorical to a numeric is merely# to have a cleaner plotheart_disease_2$has_heart_disease=ifelse(heart_disease_2$has_heart_disease=="yes",1,0)# it converts all categorical variables (factor and# character for R) into numerical variables.# skipping the original so the data is ready to usedmy =dummyVars(" ~ .",data = heart_disease_2)heart_disease_3 =data.frame(predict(dmy,newdata = heart_disease_2))# Important: If you recieve this message# `Error: Missing values present in input variable 'x'.# Consider using use = 'pairwise.complete.obs'.`# is because data has missing values.# Please don't omit NA without an impact analysis first,# in this case it is not important.heart_disease_4=na.omit(heart_disease_3)# compute the mic!mine_res_hd=mine(heart_disease_4)

mine_res_hd$MIC[1:5,1:5]

1.2.9.1 Printing some fancy plots!

We’ll usecorrplot package in R which can plot acor object (classical correlation matrix), or any other matrix. We will plotMIC matrix in this case, but any other can be used as well, for example,MAS or another metric that returns an squared matrix of correlations.

The two plots are based on the same data but display the correlation in different ways.

# library wto plot that matrixlibrary(corrplot)

## corrplot 0.84 loaded

# to use the color pallete brewer.pallibrary(RColorBrewer)# hack to visualize the maximum value of the# scale excluding the diagonal (variable against itself)diag(mine_res_hd$MIC)=0# Correlation plot with circles.corrplot(mine_res_hd$MIC,method="circle",col=brewer.pal(n=10,name="PuOr"),# only display upper diagonaltype="lower",#label color, size and rotationtl.col="red",tl.cex =0.9,tl.srt=90,# dont print diagonal (var against itself)diag=FALSE,# accept a any matrix, mic in this case#(not a correlation element)is.corr = F         )

Figure 1.16: Correlation plot

# Correlation plot with color and correlation MICcorrplot(mine_res_hd$MIC,method="color",type="lower",number.cex=0.7,# Add coefficient of correlationaddCoef.col ="black",tl.col="red",tl.srt=90,tl.cex =0.9,diag=FALSE,is.corr = F )

Figure 1.16: Correlation plot

Just change the first parameter -mine_res_hd$MIC- to the matrix you want and reuse with your data.

1.2.9.2 A comment about this kind of plots

They are useful only when the number of variables are not big. Or if you perform a variable selection first, keeping in mind that every variable should be numerical.

If there is some categorical variable in the selection you can convert it into numerical first and inspect the relationship between the variables, thus sneak peak how certain values in categorical variables are more related to certain outcomes, like in this case.

1.2.9.3 How about some insights from the plots?

Since the variable to predict ishas_heart_disease, it appears something interesting, to have a heart disease is more correlated tothal=3 than to valuethal=6.

Same analysis for variablechest_pain, a value of 4 is more dangerous than a value of 1.

And we can check it with other plot:

cross_plot(heart_disease,input ="chest_pain",target ="has_heart_disease",plot_type ="percentual")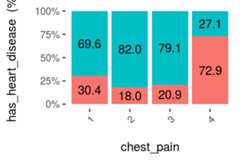

Figure 1.17: Visual analysis using cross-plot

The likelihood of having a heart disease is 72.9% if the patient haschest_pain=4. More than 2x more likely if she/(he) haschest_pain=1 (72.9 vs 30.4%).

Some thoughts…

The data is the same, but the approach to browse it is different. The same goes when we are creating a predictive model, the input data in theN-dimensional space can be approached through different models like support vector machine, a random forest, etc.

Like a photographer shooting from different angles, or different cameras. The object is always the same, but the perspective gives different information.

Combining raw tables plus different plots gives us a more real and complementary object perspective.

# Getting the index of the variable to# predict: has_heart_diseasetarget="has_heart_disease"index_target=grep(target,colnames(heart_disease_4))# master takes the index column number to calculate all# the correlationsmic_predictive=mine(heart_disease_4,master = index_target)$MIC# creating the data frame containing the results,# ordering descently by its correlation and excluding# the correlation of target vs itselfdf_predictive =data.frame(variable=rownames(mic_predictive),mic=mic_predictive[,1],stringsAsFactors = F)%>%arrange(-mic)%>%filter(variable!=target)# creating a colorful plot showing importance variable# based on MIC measureggplot(df_predictive,aes(x=reorder(variable, mic),y=mic,fill=variable)       )+geom_bar(stat='identity')+coord_flip()+theme_bw()+xlab("")+ylab("Variable Importance (based on MIC)")+guides(fill=FALSE)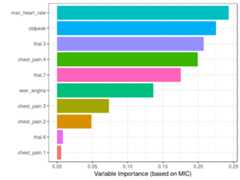

Figure 1.18: Correlation using information theory

1.2.10.1 Practice advice for usingmine

If it lasts too much time to finish, consider taking a sample. If the amount of data is too little, consider setting a higher number inalpha parameter, 0.6 is its default. Also, it can be run in parallel, just settingn.cores=3 in case you have 4 cores. A general good practice when running parallel processes, the extra core will be used by the operating system.

1.2.11.1 Another correlation example (mutual information)

This time we’ll useinfotheo package, we need first to do adata preparation step, applying adiscretize function (or binning) function present in the package. It converts every numerical variable into categorical based on equal frequency criteria.

Next code will create the correlation matrix as we seen before, but based on the mutual information index.

library(infotheo)# discretizing every variableheart_disease_4_disc=discretize(heart_disease_4)# calculating "correlation" based on mutual informationheart_info=mutinformation(heart_disease_4_disc,method="emp")# hack to visualize the maximum value of the scale excluding the diagonal (var against itself)diag(heart_info)=0# Correlation plot with color and correlation Mutual Information from Infotheo package. This line only retrieves the plot of the right.corrplot(heart_info,method="color",type="lower",number.cex=0.6,addCoef.col ="black",tl.col="red",tl.srt=90,tl.cex =0.9,diag=FALSE,is.corr = F)

Figure 1.19: Comparing variable importance

Correlation score based on mutual information ranks relationships pretty similar to MIC, doesn’t it?