引言

不同与我们之前介绍的线性结构，今天我们介绍一种非线性结构：树，树的内容比较多，包括BST树、AVL树、Trie树等，这部分内容将放在下几个章节陆续放出，本章将介绍树与二叉树的基础必会内容，在开始这一章节前，请思考以下内容：

• 什么是树？
• 树的高度怎么计算？
• 什么是二叉树？
• 什么是平衡二叉树？
• 在代码中如何表示一棵二叉树？
• 二叉树的前序、中序、后序遍历又是什么？如何实现？
• 能否用递归及迭代两种方式实现喃？

下面进入本节内容👇

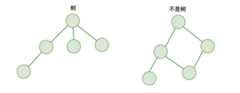
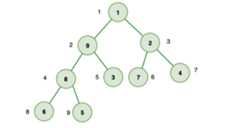
一、树

不同于我们上面介绍的线性结构，树是一种非线性结构。

图：

它遵循：

• 仅有唯一一个根节点，没有节点则为空树
• 除根节点外，每个节点都有并仅有唯一一个父节点
• 节点间不能形成闭环

这就是树！

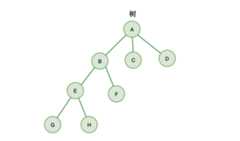
树有几个概念：

• 拥有相同父节点的节点，互称为兄弟节点
• 节点的深度 ：从根节点到该节点所经历的边的个数
• 节点的高度 ：节点到叶节点的最长路径
• 树的高度：根节点的高度

B、C、D就互称为兄弟节点，其中，节点B的高度为2，节点B的深度为 1，树的高度为3

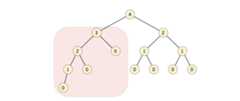
高度

树的高度计算公式：

下图每个节点值都代表来当前节点的高度：

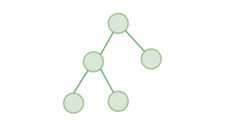
二、二叉树

二叉树，故名思义，最多仅有两个子节点的树（最多能分两个叉的树🤦‍♀️）：

图：

三、平衡二叉树

二叉树中，每一个节点的左右子树的高度相差不能大于 1，称为平衡二叉树。

另外还有满二叉树、完全二叉树等：

• 满二叉树：除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树
• 完全二叉树：深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h 层所有的结点都连续集中在最左边

四、在代码中如何去表示一棵二叉树

1. 链式存储法

二叉树的存储很简单，在二叉树中，我们看到每个节点都包含三部分：

• 当前节点的 val
• 左子节点 left
• 右子节点 right

所以我们可以将每个节点定义为：

functionNode(val){// 保存当前节点 key 值this.val=val// 指向左子节点this.left=null// 指向右子节点this.right=null}

一棵二叉树可以由根节点通过左右指针连接起来形成一个树。

functionBinaryTree(){letNode=function(val){this.val=valthis.left=nullthis.right=null}letroot=null}

2. 数组存储法（适用于完全二叉树）

下图就是一棵完全二叉树，

如果我们把根节点存放在位置i=1 的位置，则它的左子节点位置为2i = 2 ，右子节点位置为2i+1 = 3 。

如果我们选取 B 节点i=2 ，则它父节点为i/2 = 1 ，左子节点2i=4 ，右子节点2i+1=5 。

以此类推，我们发现所有的节点都满足这三种关系：

• 位置为 i 的节点，它的父节点位置为i/2
• 它的左子节点2i
• 它的右子节点2i+1

因此，如果我们把完全二叉树存储在数组里（从下标为 1 开始存储），我们完全可以通过下标找到任意节点的父子节点。从而完整的构建出这个完全二叉树。这就是数组存储法。

数组存储法相对于链式存储法不需要为每个节点创建它的左右指针，更为节省内存。

五、二叉树的遍历

二叉树的遍历可分为：

• 前序遍历
• 中序遍历
• 后序遍历

所谓前、中、后，不过是根的顺序，即也可以称为先根遍历、中根遍历、后根遍历

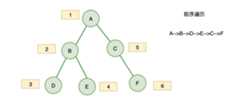
1. 前序遍历

对于二叉树中的任意一个节点，先打印该节点，然后是它的左子树，最后右子树

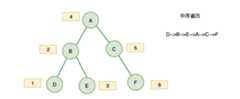
2. 中序遍历

对于二叉树中的任意一个节点，先打印它的左子树，然后是该节点，最后右子树

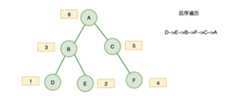
3. 后序遍历

对于二叉树中的任意一个节点，先打印它的左子树，然后是右子树，最后该节点

4. 代码实现（前序遍历为例）

所以，遍历二叉树的过程也就是一个递归的过程，例如前序遍历，先遍历根节点，然后是根的左子树，最后右子树；遍历根节点的左子树的时候，又是先遍历左子树的根节点，然后左子树的左子树，左子树的右子树…….

所以，它的核心代码就是：

// 前序遍历核心代码varpreOrderTraverseNode=(node)=>{if(node){// 先根节点result.push(node.val)// 然后遍历左子树preOrderTraverseNode(node.left)// 再遍历右子树preOrderTraverseNode(node.right)}}

完整代码如下：

递归实现

// 前序遍历varpreorderTraversal=(root)=>{letresult=[]varpreOrderTraverseNode=(node)=>{if(node){// 先根节点result.push(node.val)// 然后遍历左子树preOrderTraverseNode(node.left)// 再遍历右子树preOrderTraverseNode(node.right)}}preOrderTraverseNode(root)returnresult};

我们既然可以使用递归实现，那么是否也可以使用迭代实现喃？

迭代实现

利用栈来记录遍历的过程，实际上，递归就使用了调用栈，所以这里我们可以使用栈来模拟递归的过程

• 首先根入栈
• 将根节点出栈，将根节点值放入结果数组中
• 然后遍历左子树、右子树，因为栈是先入后出，所以，我们先右子树入栈，然后左子树入栈
• 继续出栈（左子树被出栈）…….

依次循环出栈遍历入栈，直到栈为空，遍历完成

// 前序遍历constpreorderTraversal=(root)=>{constlist=[];conststack=[];// 当根节点不为空的时候，将根节点入栈if(root)stack.push(root)while(stack.length>0){constcurNode=stack.pop()// 第一步的时候，先访问的是根节点list.push(curNode.val)// 我们先打印左子树，然后右子树// 所以先加入栈的是右子树，然后左子树if(curNode.right!==null){stack.push(curNode.right)}if(curNode.left!==null){stack.push(curNode.left)}}returnlist}

复杂度分析：

空间复杂度：O(n)

时间复杂度：O(n)

至此，我们已经实现了二叉树的前序遍历，尝试思考一下二叉树的中序遍历如何实现喃？

六、leetcode94：二叉树的中序遍历

给定一个二叉树，返回它的中序 遍历。

示例:

输入:[1,null,2,3]1    \2/3输出:[1,3,2]

进阶:  递归算法很简单，你可以通过迭代算法完成吗？

欢迎将解答提交到JavaScript-Algorithms ，这里我们提交了前端所用到的算法系列文章以及题目（已解答），欢迎star，如果感觉不错，点个赞支持一下呗😊

七、前端算法集训营第一期免费加入啦

欢迎关注「前端瓶子君」，回复「算法」自动加入，从0到1构建完整的数据结构与算法体系！

在这里，瓶子君不仅介绍算法，还将算法与前端各个领域进行结合，包括浏览器、HTTP、V8、React、Vue源码等。

在这里，你可以每天学习一道大厂算法题（阿里、腾讯、百度、字节等等）或 leetcode，瓶子君都会在第二天解答哟！

⬆️扫码关注公众号「前端瓶子君」，回复「算法」即可自动加入 👍👍👍