Repository files navigation

#> Warning: package 'ggplot2' was built under R version 4.1.2

TheR packagesplithalf provides tools to estimate the internalconsistency reliability of cognitive measures. In particular, the toolswere developed for application to tasks that use difference scores asthe main outcome measure, for instance the Stroop score or dot-probeattention bias index (average RT in incongruent trials minus average RTin congruent trials).

The methods insplithalf are built around split half reliabilityestimation. To increase the robustness of these estimates, the packageimplements a permutation approach that takes a large number of random(without replacement) split halves of the data. For each permutation thecorrelation between halves is calculated, with the Spearman-Browncorrection applied (Spearman 1904). This process generates adistribution of reliability estimates from which we can extract summarystatistics (e.g. average and 95% HDI).

While many cognitive tasks yield robust effects (e.g. everybody shows aStroop effect) they may not yield reliable individual differences(Hedge, Powell, and Sumner 2018). As these measures are used inquestions of individual differences researchers need to have somepsychometric information for the outcome measures. Recently, it wasproposed that psychological science should set a standard expectationfor the reporting of reliability information for cognitive andbehavioural measures (Parsons, Kruijt, and Fox 2019).splithalf wasdeveloped to support this proposition by providing a tool to easilyextract internal consistency reliability estimates from behaviouralmeasures.

The latest release version (0.7.2 unofficial version name: KittenMittens) can be installed from CRAN:

install.packages("splithalf")

The current developmental version (0.8.1 unofficial version name: RumHam) can be installed from Github with:

devtools::install_github("sdparsons/splithalf")

splithalf requires thetidyr (Wickham and Henry 2019) anddplyr (Wickham et al. 2018) packages for data handling within thefunctions. Therobustbase package is used to extract median scoreswhen applicable. The computationally heavy tasks (extracting many randomhalf samples of the data) are written inc++ via theR packageRcpp (Eddelbuettel et al. 2018). Figures use theggplot package(Wickham 2016), raincloud plots use code adapted from Allen et al.(Allen et al. 2019), and thepatchwork package (Pedersen 2019) isused for plotting the multiverse analyses.

Citing packages is one way for developers to gain some recognition forthe time spent maintaining the work. I would like to keep track of howthe package is used so that I can solicit feedback and improve thepackage more generally. This would also help me track the uptake ofreporting measurement reliability over time.

Please use the following reference for the code: Parsons, S., (2021).splithalf: robust estimates of split half reliability.Journal of OpenSource Software, 6(60), 3041,https://doi.org/10.21105/joss.03041

Developing the splithalf package is a labour of love (and occasionallyburning hatred). If you have any suggestions for improvement, additionalfunctionality, or anything else, please contact me(sam.parsons@psy.ox.ac.uk) or raise an issue on github(https://github.com/sdparsons/splithalf). Likewise, if you are havingtrouble using the package (e.g. scream fits at your computer screen –we’ve all been there) do contact me and I will do my best to help asquickly as possible. These kind of help requests are super welcome. Infact, the package has seen several increases in performance andusability due to people asking for help.

Version 0.8.1 now out! [unofficial version name: “Rum Ham”] Lotsof fixed issues in the multiverse functions, and lots moredocumentation/examples!

Now on github and submitted to CRAN: VERSION 0.7.2 [unofficialversion name: “Kitten Mittens”] Featuring reliability multiverseanalyses!!!

This update includes the addition of reliability multiverse functions. Asplithalf object can be inputted intosplithalf.multiverse toestimate reliability across a user-defined list of data-processingspecifications (e.g. min/max RTs). Then, because sometimes science ismore art than science, the multiverse output can be plotted withmultiverse.plot. A brief tutorial can be found below, and a morecomprehensive one can be found in a recent preprint (Parsons 2020).

Additionally, the output of splithalf has been reworked. Now a list isreturned including the specific function calls, the processed data.

Since version 0.6.2 a user can also setplot = TRUE insplithalf togenerate a raincloud plot of the distribution of reliability estimates.

It is important that we have a similar understanding of the terminologyI use in the package and documentation. Each is also discussed inreference to the functions later in the documentation.

• Trial – whatever happens in this task, e.g. a stimuli is presented.Importantly, participants give one response per trial
• Trial type – often trials can be split into different trial types(e.g. to compare congruent and incongruent trials)
• Condition - this might be different blocks of trials, or somethingto be assessed separately within the functions. e.g. a task mighthave a block of ‘positive’ trials and a block of ‘negative’ trials.
• Datatype - I use this to refer to the outcome of interest.specifically whether one is interested in average response times oraccuracy rates
• Score - I use score to indicate how the final outcome is measured;e.g. the average RT, or the difference between two average RTs, oreven the difference between two differences between two RTs (yes,the final one is confusing)

The core functionsplithalf requires that the input dataset hasalready undergone preprocessing (e.g. removal of error trials, RTtrimming, and participants with high error rates). Splithalf shouldtherefore be used with the same data that will be used to calculatesummary scores and outcome indices. The exception is in multiverseanalyses, as described below.

For those unfamiliar with R, the following snippets may help with commondata-processing steps. I also highly recommend the Software Carpentrycourse “R for Reproducible Scientific Analysis”(https://swcarpentry.github.io/r-novice-gapminder/).

Note == indicates ‘is equal to,’ :: indicates that the function uses thepackage indicated, in the first case thedplyr package (Wickham etal. 2018).

dataset %>%dplyr::filter(accuracy==1) %>%## keeps only trials in which participants made an accurate responsedplyr::filter(RT>=100,RT<=2000)  %>%## removes RTs less than 100ms and greater than 2000msdplyr::filter(participant!= c(“p23”, “p45”)## removes participants “p23” and “p45”

If following rt trims you also trimmed by SD, use the following as well.Note that this is for two standard deviations from the mean, within eachparticipant, and within each condition and trialtype.

dataset %>%dplyr::group_by(participant,condition,compare) %>%dplyr::mutate(low=  mean(RT)- (2* sd(RT)),high= mean(RT)+ (2* sd(RT))) %>%dplyr::filter(RT>=low&RT<=high)

If you want to save yourself effort in running splithalf, you could alsorename your variable (column) names to the function defaults using thefollowing

dplyr::rename(dataset,RT="latency",condition=FALSE,participant="subject",correct="correct",trialnum="trialnum",compare="congruency")

The following examples assume that you have already processed your datato remove outliers, apply any RT cutoffs, etc. A reminder: the data youinput intosplithalf should be the same as that used to create yourfinal scores - otherwise the resultant estimates will not accuratelyreflect the reliability of your data.

These questions should feed into what settings are appropriate for yourneed, and are aimed to make thesplithalf function easy to use.

1. What type of data do you have?

Are you interested in response times, or accuracy rates?

Knowing this, you can setoutcome = "RT", oroutcome = "accuracy"

2. How is your outcome score calculated?

Say that your response time based task has two trial types;“incongruent” and “congruent.” When you analyse your data will you usethe average RT in each trial type, or will you create a difference score(or bias) by e.g. subtracting the average RT in congruent trials fromthe average RT in incongruent trials. The first can be called withscore = "average" and the second withscore = "difference".

3. Which method would you like to use to estimate (split-half)reliability?

A super common way is to split the data into odd and even trials.Another is to split by the first half and second half of the trials.Both approaches are implemented in thesplithalf funciton. However, Ibelieve that the permutation splithalf approach is the most applicablein general and so the default ishalftype = "random"

For this brief example, we will simulate some data for 60 participants,who each completed a task with two blocks (A and B) of 80 trials. Trialsare also evenly distributed between “congruent” and “incongruent”trials. For each trial we have RT data, and are assuming thatparticipants were accurate in all trials.

n_participants=60## sample sizen_trials=80n_blocks=2sim_data<-data.frame(participant_number= rep(1:n_participants,each=n_blocks*n_trials),trial_number= rep(1:n_trials,times=n_blocks*n_participants),block_name= rep(c("A","B"),each=n_trials,length.out=n_participants*n_trials*n_blocks),trial_type= rep(c("congruent","incongruent"),length.out=n_participants*n_trials*n_blocks),RT= rnorm(n_participants*n_trials*n_blocks,500,200),ACC=1)

This is by far the most common outcome measure I have come across, solets start with that.

Our data will be analysed so that we have two ‘bias’ or ‘differencescore’ outcomes. So, within each block, we will take the average RT incongruent trials and subtract the average RT in incongruent trials.Calculating the final scores for each participant and for each blockseparately could be done as follows:

library("dplyr")library("tidyr")sim_data %>%dplyr::group_by(participant_number,block_name,trial_type) %>%dplyr::summarise(average= mean(RT)) %>%tidyr::spread(trial_type,average) %>%dplyr::mutate(bias=congruent-incongruent)# A tibble: 120 x 5# Groups:   participant_number, block_name [120]participant_numberblock_namecongruentincongruentbias<int><chr><dbl><dbl><dbl>11A550.430.120.21B512.433.78.932A525.496.28.642B488.523.-35.253A457.500.-43.663B478.518.-39.374A492.479.13.184B593.458.135.95A568.565.2.72105B485.555.-70.3# ... with 110 more rows

To estimate reliability withsplithalf we run the following.

library("splithalf")difference<- splithalf(data=sim_data,outcome="RT",score="difference",conditionlist= c("A","B"),halftype="random",permutations=5000,var.RT="RT",var.condition="block_name",var.participant="participant_number",var.compare="trial_type",compare1="congruent",compare2="incongruent",average="mean",plot=TRUE)

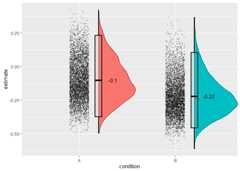
  condition  n splithalf 95_low 95_high spearmanbrown SB_low SB_high1         A 60     -0.06  -0.23    0.13         -0.10  -0.37    0.232         B 60     -0.13  -0.30    0.06         -0.22  -0.46    0.10

Specifyingplot = TRUE will also allow you to plot the distributionsof reliability estimates. you can extract the plot from a saved objectwith e.g. difference$plot.

Thesplithalf output gives estimates separately for each conditiondefined (if no condition is defined, the function assumes that you haveonly a single condition, which it will call “all” to represent that alltrials were included).

The second column (n) gives the number of participants analysed. If, forsome reason one participant has too few trials to analyse, or did notcomplete one condition, this will be reflected here. I suggest youcompare this n to your expected n to check that everything is runningcorrectly. If the ns dont match, we have a problem. More likely, R willgive an error message, but useful to know.

Next are the estimates; the splithalf column and the associated 95%percentile intervals, and the Spearman-Brown corrected estimate with itsown percentile intervals. Unsurprisingly, our simlated random data doesnot yield internally consistant measurements.

What should I report? My preference is to report everything. 95%percentiles of the estimates are provided to give a picture of thespread of internal consistency estimates. Also included is thespearman-brown corrected estimates, which take into account that theestimates are drawn from half the trials that they could have been.Negative reliabilities are near uninterpretable and the spearman-brownformula is not useful in this case.

We estimated the internal consitency of bias A and B using apermutation-based splithalf approach (Parsons 2019) with 5000 randomsplits. The (Spearman-Brown corrected) splithalf internal consistencyof bias A was werer_SB = -0.1, 95%CI [-0.37,0.23].

— Parsons, 2020

For some tasks the outcome measure may simply be the average RT. In thiscase, we will ignore the trial type option. We will extract separateoutcome scores for each block of trials, but this time it is simply theaverage RT in each block. Note that the main difference in this code isthat we have omitted the inputs about what trial types to ‘compare,’ asthis is irrelevant for the current task.

average<- splithalf(data=sim_data,outcome="RT",score="average",conditionlist= c("A","B"),halftype="random",permutations=5000,var.RT="RT",var.condition="block_name",var.participant="participant_number",average="mean")

  condition  n splithalf 95_low 95_high spearmanbrown SB_low SB_high1         A 60      0.16  -0.02    0.34          0.26  -0.03    0.512         B 60      0.05  -0.13    0.24          0.09  -0.23    0.39

The difference of differences score is a bit more complex, and perhapsalso less common. I programmed this aspect of the package initiallybecause I had seen a few papers that used a change in bias score intheir analysis, and I wondered “I wonder how reliable that is as anindividual difference measure.” Be warned, difference scores are nearlyalways less reliable than raw averages, and differences-of-differenceswill be less reliable again.

Our difference-of-difference variable in our task is the differencebetween bias observed in block A and B. So our outcome is calculatedsomething like this.

BiasA = incongruent_A - congruent_A

BiasB = incongruent_B - congruent_B

Outcome = BiasB - BiasA

In our function, we specify this very similarly as in the differencescore example. The only change will be changing the score to“difference_of_difference.” Note that we will keep the condition listconsisting of A and B. But, specifying that we are interested in thedifference of differences will lead the function to calculate theoutcome scores apropriately.

diff_of_diff<- splithalf(data=sim_data,outcome="RT",score="difference_of_difference",conditionlist= c("A","B"),halftype="random",permutations=5000,var.RT="RT",var.condition="block_name",var.participant="participant_number",var.compare="trial_type",compare1="congruent",compare2="incongruent",average="mean")

                       condition  n splithalf 95_low 95_high spearmanbrown1 difference_of_difference score 60     -0.12  -0.29    0.07         -0.21  SB_low SB_high1  -0.45    0.13

This example is simplified from Parsons (2020). The process takes foursteps. First, specify a list of data processing decisions. Here, we’llspecify only removing trials greater or lower than a specified amount.More options are available, such as total accuracy cutoff thresholds forparticipant removals.

specifications<-list(RT_min= c(0,100,200),RT_max= c(1000,2000),averaging_method= c("mean","median"))

Second, performsplithalf(...). The key difference here, compared tothe earlier examples is that we are no longer assuming that all dataprocessing has already occurred. Instead, the data processing will beperformed as part ofsplithalf.multiverse, next.

difference<- splithalf(data=sim_data,outcome="RT",score="difference",conditionlist= c("A"),halftype="random",permutations=5000,var.RT="RT",var.condition="block_name",var.participant="participant_number",var.compare="trial_type",var.ACC="ACC",compare1="congruent",compare2="incongruent",average="mean")

Third, performsplithalf.multiverse with the specification list andsplithalf objects as inputs

multiverse<- splithalf.multiverse(input=difference,specifications=specifications)

Finally, plot the multiverse with plot.multiverse.

multiverse.plot(multiverse=multiverse,title="README multiverse")

For more information, see Parsons (2020).

To examine how many random splits are required to provide a preciseestimate, a short simulation was performed including 20 estimates of thespearman-brown reliability estimate, for each of 1, 10, 50, 100, 1000,2000, 5000, 10000, and 20000 random splits. This simulation wasperformed on data from one block of 80 trials. Based on this simulation,I recommend 5000 (or more) random splits be used to calculate split-halfreliability. 5000 permutations yielded a standard deviation of .002 anda total range of .008, indicating that the reliability estimates arestable to two decimal places with this number of random splits.Increasing the number of splits improved precision, however 20000 splitswere required to reduce the standard deviation to .001.

The speed ofsplithalf rests entirely on the number of conditions,participants, and permutations. The biggest factor will be your machinespeed. For relative times, I ran a simulation with a range of samplesizes, numbers of conditions, numbers of trials, and permutations. Thedata is contained within the package asdata/speedtest.rda

Thesplithalf package is still under development. If you havesuggestions for improvements to the package, or bugs to report, pleaseraise an issue on github (https://github.com/sdparsons/splithalf).Currently, I have the following on my immediate to do list:

• error tracking
  • I plan to develop a function that catches potential issues thatcould arise with the functions.
  • I also plan to document common R warnings and errors that ariseand why (as sometimes without knowing exactly how the functionswork these issues can be harder to trace back).
• include other scoring methods:
  • signal detection, e.g. d prime
  • potentially customisable methods, e.g. where the outcome isscored in formats similar to A - B / A + B

splithalf is the only package to implement all of these tools, inparticular reliability multiverse analyses. Some otherR packagesoffer a bootstrapped approach to split-half reliabilitymulticon(Sherman 2015),psych (Revelle 2019), andsplithalfr (Pronk2020)