- Notifications
You must be signed in to change notification settings - Fork0
Bayesian modal regression models based on the GUD
License
rh8liuqy/Bayesian_modal_regression
Folders and files
| Name | Name | Last commit message | Last commit date | |
|---|---|---|---|---|
Repository files navigation
TheGUDpackage provides probability density functions and sampling algorithmsfor three key distributions from the General Unimodal Distribution (GUD)family: the Flexible Gumbel (FG) distribution, the Double Two-Piece(DTP) Student-t distribution, and the Two-Piece Scale (TPSC) Student-tdistribution. Additionally, this package includes a function forBayesian linear modal regression, leveraging these three distributionsfor model fitting.
You can install theGUD package:
if (! require(GUD)) { install.packages(pkgs="GUD",repos="https://cran.rstudio.com/" )}else { require(GUD)}#> Loading required package: GUD
The general unimodal distribution (GUD) family is essentially a familyof two-component mixture distributions. The probability density function(pdf) of a member of GUD family is $$f\left(y \mid w, \theta, \boldsymbol{\xi}_1, \boldsymbol{\xi}_2\right)=w f_1\left(y \mid \theta, \boldsymbol{\xi}_1\right)+(1-w) f_2\left(y \mid \theta, \boldsymbol{\xi}_2\right),$$ where
- The pdfs
$f_1\left(\cdot \mid \theta, \boldsymbol{\xi}_1\right)$ and$f_2\left(\cdot \mid \theta, \boldsymbol{\xi}_2\right)$ are unimodalat$\theta$ . - The pdfs
$f_1\left(\cdot \mid \theta, \boldsymbol{\xi}_1\right)$ and$f_2\left(\cdot \mid \theta, \boldsymbol{\xi}_2\right)$ areleft-skewed and right-skewed respectively. - The mixture pdf
$f\left(\cdot \mid w, \theta, \boldsymbol{\xi}_1, \boldsymbol{\xi}_2\right)$ in (1) is continuous in its domain.
More details of the GUD family can be found inLiu, Q., Huang, X., &Bai, R. (2024).
In this section, we demonstrate how to use theGUD package to analyze2003 United States Crime Data as in Section 2 ofLiu, Q., Huang, X., &Bai, R. (2024).
In “The Art and Science of Learning from Data, 5th edition” by AlanAgresti, Christine A. Franklin, and Bernhard Klingenberg, an interestingexample about the 2003 United States crime data is presented todemonstrate the influence of outliers in the classic linear regressionmodel. This example is very compelling and partially motivates theconstruction of the Bayesian modal regression based on the GUD family.This data contains the murder rate, percentage of college education,poverty percentage, and metropolitan rate for the 50 states in theUnited States and the District of Columbia (D.C.) from 2003. The murderrate is defined as the annual number of murders per
# load data crime from the GUD packagedf1<-crime# the conditional scatter plot matrices of U.S. crime dataif (require(lattice)) {lattice::splom(~df1[c(6,4,9,3)],main=NULL,panel=function(x,y,...) { panel.splom(x,y,...) })}#> Loading required package: lattice
In the conditional scatter plot matrices, we notice an outlier,Washington, D.C., which stands out and does not follow the commonpattern of other states.
Next, we demonstrate how to fit the Bayesian modal regression modelbased on the TPSC distribution to the 2003 United States crime data.
TPSC_model<- modal_regression(`murder rate`~college+poverty+metropolitan,data=df1,model="TPSC",chains=2,iter=2000)#>#> SAMPLING FOR MODEL 'TPSC' NOW (CHAIN 1).#> Chain 1:#> Chain 1: Gradient evaluation took 3.2e-05 seconds#> Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.32 seconds.#> Chain 1: Adjust your expectations accordingly!#> Chain 1:#> Chain 1:#> Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)#> Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)#> Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)#> Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)#> Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)#> Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)#> Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)#> Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)#> Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)#> Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)#> Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)#> Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)#> Chain 1:#> Chain 1: Elapsed Time: 1.095 seconds (Warm-up)#> Chain 1: 0.674 seconds (Sampling)#> Chain 1: 1.769 seconds (Total)#> Chain 1:#>#> SAMPLING FOR MODEL 'TPSC' NOW (CHAIN 2).#> Chain 2:#> Chain 2: Gradient evaluation took 1.1e-05 seconds#> Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.11 seconds.#> Chain 2: Adjust your expectations accordingly!#> Chain 2:#> Chain 2:#> Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)#> Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)#> Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)#> Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)#> Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)#> Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)#> Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)#> Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)#> Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)#> Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)#> Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)#> Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)#> Chain 2:#> Chain 2: Elapsed Time: 1.028 seconds (Warm-up)#> Chain 2: 0.591 seconds (Sampling)#> Chain 2: 1.619 seconds (Total)#> Chain 2:
One can summarize the Bayesian analysis using the summary function.
print(summary(TPSC_model),n=7)#> # A tibble: 113 × 10#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>#> 1 w 0.276 0.282 0.117 0.126 0.0756 0.464 1.01 368. 235.#> 2 delta 1.90 1.78 0.677 0.566 1.09 3.15 1.01 447. 582.#> 3 sigma 1.17 1.16 0.265 0.257 0.760 1.62 1.00 540. 343.#> 4 (Interc… 1.13 1.31 2.73 2.69 -3.71 5.26 1.00 698. 971.#> 5 college -0.197 -0.201 0.0825 0.0812 -0.325 -0.0554 1.00 648. 995.#> 6 poverty 0.244 0.248 0.138 0.147 0.0150 0.462 1.00 568. 784.#> 7 metropo… 0.0627 0.0616 0.0143 0.0138 0.0413 0.0889 1.00 521. 640.#> # ℹ 106 more rows
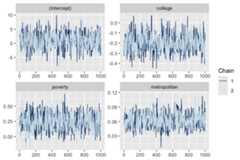
One can present the traceplot of the MCMC chain using thebayesplot::mcmc_trace function.
if (require(bayesplot)) {bayesplot::mcmc_trace(TPSC_model,pars= c("(Intercept)","college","poverty","metropolitan"))}#> Loading required package: bayesplot#> Warning: package 'bayesplot' was built under R version 4.3.1#> This is bayesplot version 1.11.1#> - Online documentation and vignettes at mc-stan.org/bayesplot#> - bayesplot theme set to bayesplot::theme_default()#> * Does _not_ affect other ggplot2 plots#> * See ?bayesplot_theme_set for details on theme setting
The summary of posterior predictive distribution can be assessed usingthe following command. Hereystar[1] represents the posteriorprediction of the first observation in the dataset, and so on.
summary(posterior::subset_draws(TPSC_model,variable="ystar"))#> # A tibble: 51 × 10#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>#> 1 ystar[1] 7.25 6.20 15.3 2.03 3.28 13.4 1.00 1791. 1717.#> 2 ystar[2] 2.67 1.35 12.6 2.02 -1.55 9.87 1.00 2016. 1885.#> 3 ystar[3] 7.12 6.06 7.78 1.90 3.36 12.7 1.00 1691. 2043.#> 4 ystar[4] 6.62 5.54 11.3 2.36 2.24 12.5 1.00 1688. 1793.#> 5 ystar[5] 7.37 6.20 8.39 1.96 3.36 13.6 1.00 1811. 1809.#> 6 ystar[6] 3.85 2.71 6.18 2.09 -0.315 11.1 1.00 1937. 1937.#> 7 ystar[7] 5.22 3.86 14.0 2.04 0.856 12.4 1.00 1475. 1937.#> 8 ystar[8] 5.79 4.91 5.04 1.80 2.16 11.7 1.00 1891. 1478.#> 9 ystar[9] 6.72 5.28 17.6 2.61 1.18 14.4 1.00 1422. 1693.#> 10 ystar[10] 7.75 6.41 10.4 1.94 3.58 14.7 1.00 2065. 1687.#> # ℹ 41 more rows
Further comparisons between mean, median, and modal regression can befound in Section 2 ofLiu, Q., Huang, X., & Bai, R.(2024) and Section 6 ofLiu, Q.,Huang, X., & Zhou, H. (2024).
About
Bayesian modal regression models based on the GUD
Resources
License
Uh oh!
There was an error while loading.Please reload this page.