Uh oh!
There was an error while loading.Please reload this page.
- Notifications
You must be signed in to change notification settings - Fork24
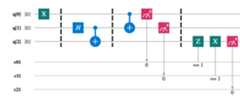
Quantum computing examples with QISKit.
License
NotificationsYou must be signed in to change notification settings
mrtkp9993/QuantumComputingExamples
About
Quantum computing examples with QISKit.
Topics
Resources
License
Uh oh!
There was an error while loading.Please reload this page.
Stars
Watchers
Forks
Sponsor this project
Uh oh!
There was an error while loading.Please reload this page.
Packages0
No packages published
Uh oh!
There was an error while loading.Please reload this page.
Contributors2
Uh oh!
There was an error while loading.Please reload this page.