Repository files navigation

Implementation of algorithms that extend Iterative Proportional Fitting(IPF) to nested structures.

The IPF algorithm operates on count data. This package offersimplementations for several algorithms that extend this to nestedstructures: “parent” and “child” items for both of which constraints canbe provided.

Install from CRAN with:

install.packages("mlfit")

Or the development version from GitHub:

# install.packages("devtools")devtools::install_github("mlfit/mlfit")

Here is a multi-level fitting example with a reference sample(reference_sample) and two control tables (individual_control andgroup_control). Each row ofreference_sample represents anindividual in a sample of a population, whereHHNR is their group IDandPNR is their individual ID,APER andWKSTAT areindividial-level charateristics, andCAR is the only householdcharacteristic of the sample population. The ‘N’ columns in both controltables denote how many units of individuals or groups belong to eachcategory.

library(mlfit)library(tibble)reference_sample<-tibble::tribble(~HHNR,~PNR,~APER,~CAR,~WKSTAT,1L,1L,3L,"0","1",1L,2L,3L,"0","2",1L,3L,3L,"0","3",2L,4L,2L,"0","1",2L,5L,2L,"0","3",3L,6L,3L,"0","1",3L,7L,3L,"0","1",3L,8L,3L,"0","2",4L,9L,3L,"1","1",4L,10L,3L,"1","3",4L,11L,3L,"1","3",5L,12L,3L,"1","2",5L,13L,3L,"1","2",5L,14L,3L,"1","3",6L,15L,2L,"1","1",6L,16L,2L,"1","2",7L,17L,5L,"1","1",7L,18L,5L,"1","1",7L,19L,5L,"1","2",7L,20L,5L,"1","3",7L,21L,5L,"1","3",8L,22L,2L,"1","1",8L,23L,2L,"1","2"  )individual_control<-tibble::tribble(~WKSTAT,~N,"1",91L,"2",65L,"3",104L  )group_control<-tibble::tribble(~CAR,~N,"0",35L,"1",65L  )

First we need to create aml_problem object which defines ourmulti-level fitting problem.special_field_names() is useful for thefield_names argument toml_problem(), this is where we need tospecific the names of the ID columns in our reference sample and thecount column in the control tables.

fitting_problem<- ml_problem(ref_sample=reference_sample,controls=list(individual=list(individual_control),group=list(group_control)  ),field_names= special_field_names(groupId="HHNR",individualId="PNR",count="N"  ))

You can use one of theml_fit_*() functions to calibrate your fittingproblem, or you can useml_fit(ml_problem, algorithm = "<your-selected-algorithm>").

fit<- ml_fit(ml_problem=fitting_problem,algorithm="ipu")fit#> An object of class ml_fit#>   Algorithm: ipu#>   Success: TRUE#>   Residuals (absolute): min = -6.41906e-05, max = 0#>   Flat problem:#>   An object of class flat_ml_fit_problem#>     Dimensions: 5 groups, 8 target values#>     Model matrix type: separate#>     Original fitting problem:#>     An object of class ml_problem#>       Reference sample: 23 observations#>       Control totals: 1 at individual, and 1 at group level

mlfit also provides a function that helps to replicate the referencesample based on the fitted/calibrated weights. See?ml_replicate tofind out which integerisation algorithms are available.

syn_pop<- ml_replicate(fit,algorithm="trs")syn_pop#> # A tibble: 259 x 5#>     HHNR   PNR  APER CAR   WKSTAT#>    <int> <int> <int> <chr> <chr>#>  1     1     1     3 0     1#>  2     1     2     3 0     2#>  3     1     3     3 0     3#>  4     2     4     3 0     1#>  5     2     5     3 0     2#>  6     2     6     3 0     3#>  7     3     7     2 0     1#>  8     3     8     2 0     3#>  9     4     9     2 0     1#> 10     4    10     2 0     3#> # ... with 249 more rows

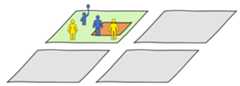
This example is almost identical to the previous example, except we arecreating sub-fitting problems based on zones.ml_problem() has thegeo_hierarchy argument, where it lets you specify a geographicalhierarchy, adata.frame with two columns:region andzone. To putit simply, a zone can only belong to one region. The image below showsan example of that, where the orange patch is a zone that is within thegreen region.

Whengeo_hierarchy is validly specified,ml_problem() would return alist of fitting problems, one fitting problem per zone. Each fittingproblem will contain only relevant subsets of the reference sample andcontrol totals for its zone. Basically, the reference sample is apopulation survey sample taken at a regional level and the controltotals should be at a zonal level.

ref_sample<-tibble::tribble(~HHNR,~PNR,~APER,~HH_VAR,~P_VAR,~REGION,1,1,3,1,1,1,1,2,3,1,2,1,1,3,3,1,3,1,2,4,2,1,1,1,2,5,2,1,3,1,3,6,3,1,1,1,3,7,3,1,1,1,3,8,3,1,2,1,4,9,3,2,1,1,4,10,3,2,3,1,4,11,3,2,3,1,5,12,3,2,2,1,5,13,3,2,2,1,5,14,3,2,3,1,6,15,2,2,1,1,6,16,2,2,2,1,7,17,5,2,1,1,7,18,5,2,1,1,7,19,5,2,2,1,7,20,5,2,3,1,7,21,5,2,3,1,8,22,2,2,1,1,8,23,2,2,2,1,9,24,3,1,1,2,9,25,3,1,2,2,9,26,3,1,3,2,10,27,2,1,1,2,10,28,2,1,3,2,11,29,3,1,1,2,11,30,3,1,1,2,11,31,3,1,2,2,12,32,3,2,1,2,12,33,3,2,3,2,12,34,3,2,3,2,13,35,3,2,2,2,13,36,3,2,2,2,13,37,3,2,3,2,14,38,2,2,1,2,14,39,2,2,2,2,15,40,5,2,1,2,15,41,5,2,1,2,15,42,5,2,2,2,15,43,5,2,3,2,15,44,5,2,3,2,16,45,2,2,1,2,16,46,2,2,2,2  )hh_ctrl<-tibble::tribble(~ZONE,~HH_VAR,~N,1,1,35,1,2,65,2,1,35,2,2,65,3,1,35,3,2,65,4,1,35,4,2,65)ind_ctrl<-tibble::tribble(~ZONE,~P_VAR,~N,1,1,91,1,2,65,1,3,104,2,1,91,2,2,65,2,3,104,3,1,91,3,2,65,3,3,104,4,1,91,4,2,65,4,3,104)geo_hierarchy<-tibble::tribble(~REGION,~ZONE,1,1,1,2,2,3,2,4)fitting_problems<- ml_problem(ref_sample=ref_sample,field_names= special_field_names(groupId="HHNR",individualId="PNR",count="N",zone="ZONE",region="REGION"    ),group_controls=list(hh_ctrl),individual_controls=list(ind_ctrl),geo_hierarchy=geo_hierarchy  )#> Creating a list of fitting problems by zonefits<-fitting_problems %>%  lapply(ml_fit,algorithm="ipu") %>%  lapply(ml_replicate,algorithm="trs")

• grake: A reimplementation ofgeneralized raking (Deville and Särndal,1992;Deville, Särndal and Sautory,1993)

• wrswoR: An implementation offast weighted random sampling without replacement (Efraimidis andSpirakis,2006)
• mangow: Embed the Gowerdistance metric in L1
• RANN.L1:k-nearest neighbors using the L1 metric

From version0.4.0 onwards the package is now to be known asmlfit.If you would like to install any version that is older than0.4.0please use:

# See https://github.com/mlfit/mlfit/releases for the releases that are available# To install a certain branch or commit or tag, append it to the repo name, after an @:devtools::install_github("mlfit/mlfit@v0.3-7")

Note that, all versions prior to0.4.0 should be used asMultiLeveLIPF notmlfit.

To cite package ‘mlfit’ in publications use:

Kirill Müller and Amarin Siripanich (2021). mlfit: IterativeProportional Fitting Algorithms for Nested Structures.https://mlfit.github.io/mlfit/,https://github.com/mlfit/mlfit.

A BibTeX entry for LaTeX users is

@Manual{,  title = {mlfit: Iterative Proportional Fitting Algorithms for Nested Structures},  author = {Kirill Müller and Amarin Siripanich},  year = {2021},  note = {https://mlfit.github.io/mlfit/, https://github.com/mlfit/mlfit},}

• Casati, D., Müller, K., Fourie, P. J., Erath, A., & Axhausen, K. W.(2015). Synthetic population generation by combining a hierarchical,simulation-based approach with reweighting by generalized raking.Transportation Research Record, 2493(1), 107-116.
• Bösch, P. M., Müller, K., & Ciari, F. (2016). The IVT 2015 baselinescenario. In 16th Swiss Transport Research Conference (STRC 2016).16th Swiss Transport Research Conference (STRC 2016).
• Müller, K. (2017). A generalized approach to population synthesis(Doctoral dissertation, ETH Zurich).
• Ilahi, A., & Axhausen, K. W. (2018). Implementing Bayesian networkand generalized raking multilevel IPF for constructing populationsynthesis in megacities. In 18th Swiss Transport Research Conference(STRC 2018). STRC.
• Ilahi, A., & Axhausen, K. W. (2019). Integrating Bayesian networkand generalized raking for population synthesis in Greater Jakarta.Regional Studies, Regional Science, 6(1), 623-636.
• Yameogo, B. F., Vandanjon, P. O., Gastineau, P., & Hankach, P.(2021). Generating a two-layered synthetic population for Frenchmunicipalities: Results and evaluation of four syntheticreconstruction methods. JASSS-Journal of Artificial Societies andSocial Simulation, 24, 27p.
• Zhou, M., Li, J., Basu, R., & Ferreira, J. (2022). Creatingspatially-detailed heterogeneous synthetic populations foragent-based microsimulation. Computers, Environment and UrbanSystems, 91, 101717.