Repository files navigation

ggvfields extendsggplot2 by providing suiteof tools to visualize vector and stream fields. In addition to standardvector and stream plotting,ggvfields automatically computes andvisualizes smoothed vector fields, smooth gradient fields, gradientfields derived from scalar functions, and potential fields fromgradients. This integrated framework simplifies the analysis andinterpretation of complex vector and scalar field data.

A manuscript describing the theoretical foundations and detailedmethodologies behind ggvfields is forthcoming.

ggvfields is available on CRAN and can be installed with:

install.packages("ggvfields")

Alternatively, you can install the latest development version fromGitHub with:

remotes::install_github("dusty-turner/ggvfields")

Load the package in R:

library("ggvfields")#> Loading required package: ggplot2options(ggplot2.continuous.colour="viridis")

• geom_vector_field(): Computes vector fields from a user-definedfunction over the domain${(x,y) \in \mathbb{R}^2 : -1 < x < 1,\ -1 < y < 1}$ on an$n \times n$ grid (default:$11 \times 11$) and maps the norm tocolor. Vectors are centered and normalized by default.

The norm$\mathbf{w} = (u, v)$ is calculated$$|\mathbf{w}| = \sqrt{u^2 + v^2}$$ .

f<-function(v) c(-v[2],v[1])# Define a function for the fieldggplot()+  geom_vector_field(fun=f)

• geom_vector_field2(): Similar togeom_vector_field(), but mapsthe norm of vectors to their lengths instead of color.

ggplot()+  geom_vector_field2(fun=f)

Why Length Mapping Matters

Mapping vector lengths to their norms allows viewers to immediatelyunderstand magnitude differences without relying solely on color. Thisfeature ofgeom_vector2() enhances interpretability by using actualvector lengths to represent magnitude. The legend reflects the scalingand ensures correct interpretation.

• geom_vector_field() options

Length

We can set theL parameter to visualize vectors at a specified length.

ggplot()+  geom_vector_field(fun=f,n=4,L=2)

Center

By default, all vectors are centered on their origin. We can turn offcentering.

ggplot()+  geom_vector_field(fun=f,n=4,center=FALSE)

normalize

If we turn off normalization and centering, we get a raw look at thevector field data.

ggplot()+  geom_vector_field(fun=f,n=4,normalize=FALSE,center=FALSE)

• geom_stream_field(): Computes stream fields from a user-definedfunction and maps the average speed to color. Average speed is theoverall rate at which a particle traverses the shown stream. If thedisplacement vector has length$|\mathbf{d}|$ and it takes time$t$,the integration time of streams, to traverse that distance, then theaverage speed is given by$\text{Average Speed} = \frac{|\mathbf{d}|}{t}$

ggplot()+  geom_stream_field(fun=f)

• geom_stream_field2(): Similar togeom_stream_field(), butremoves mapping, arrow heads, and designates stream origins with adot.

ggplot()+  geom_stream_field2(fun=f)

• geom_stream_field() options

geom_stream_field() maintains similar options togeom_vector_field(). Some arguments yield slightly different behavior.

Length

By adjusting theL parameter, we can control the length of eachstream.

ggplot()+  geom_stream_field(fun=f,n=4,L=.8)

Normalization

By default, the lengths of each stream is normalized to be the samelength. By turning normalization off, each stream becomes timenormalized. In other words, each stream grows for the same amount oftime.

ggplot()+  geom_stream_field(fun=f,n=4,normalize=FALSE)

We can control the length of the longest stream whennormalize = FALSEby altering theL argument.

ggplot()+  geom_stream_field(fun=f,n=4,normalize=FALSE,L=.8)

Time

Whennormalize = FALSE, we can grow each stream for the same amount oftime by using theT parameter.

ggplot()+  geom_stream_field(fun=f,n=4,normalize=FALSE,T=.5)

Thegeom_gradient_field() function computes and visualizes gradientfields derived from scalar functions and displays the gradient vectorfield of a scalar function,$f(x, y)$. The gradient is given by:

$$\nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$$

This vector field points in the direction of the greatest rate ofincrease of the scalar function. The function numerically evaluatesthese partial derivatives and visualizes the resulting vectors.

• Gradient Fields as Vectors The resulting vector field has all thesame defaults and same options asgeom_vector_field()

field<-function(v) {x<-v[1]y<-v[2]x^3+y^3}ggplot()+  geom_gradient_field(fun=field)

• Gradient Fields as Streams The resulting stream field has all thesame defaults and same options asgeom_stream_field()

ggplot()+  geom_gradient_field(fun=field,type="stream")

A potential function represents a scalar field whose gradient produces avector field. It is used to describe conservative vector fields whichexist when the curl of the vector field is 0.

Thegeom_potential() function computes and visualizes the scalarpotential function for a given conservative vector field. The inputfunction must represent a 2D vector field and the output is thecorresponding potential function. If the input field is notconservative, the function checks this condition numerically based on atolerance parameter. The tolerance determines how strictly the fieldmust satisfy the conservation condition.

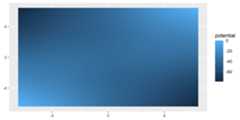
conservative_fun<-function(v) {x<-v[1]y<-v[2] c(sin(x)+y,x- sin(y))}ggplot()+  geom_potential(fun=conservative_fun,xlim= c(-2*pi,2*pi),ylim= c(-2*pi,2*pi))

Thetol parameter can be adjusted to control the sensitivity of theconservativeness check. Decreasing the tolerance makes the checkstricter, while increasing it allows for more numerical error. You canturn this functionality on withverify_conservative = TRUE.

non_conservative_fun<-function(v) {x<-v[1]y<-v[2] c(-y,x)}ggplot()+  geom_potential(fun=non_conservative_fun,xlim= c(-2*pi,2*pi),ylim= c(-2*pi,2*pi),verify_conservative=TRUE,tol=1e-6                 )#> Warning: ! The provided vector field does not have a potential function everywhere#>   within the specified domain.#> → Ensure that the vector field satisfies the necessary conditions for a#>   potential function.

So far, these layers have supported visualizing functions.ggvfieldscan also visualize raw data.

Generate sample wind data:

set.seed(1234)n<-10wind_data<-data.frame(lon= rnorm(n),lat= rnorm(n),dir= runif(n,-pi/2,pi/2),spd= rchisq(n,df=2))|>   within({fx<-spd* cos(dir)# Compute the x-component of the vectorfy<-spd* sin(dir)# Compute the y-component of the vectorxend<-lon+fx# Compute the end x-coordinateyend<-lat+fy# Compute the end y-coordinate  })round(wind_data,digits=2)|> head(6)#>     lon   lat   dir   spd  yend xend    fy    fx#> 1 -1.21 -0.48  0.17  3.55  0.11 2.29  0.59  3.50#> 2  0.28 -1.00  0.46  2.19 -0.03 2.24  0.97  1.96#> 3  1.08 -0.78 -0.59  2.99 -2.44 3.56 -1.66  2.48#> 4 -2.35  0.06  0.38 10.81  4.10 7.68  4.04 10.03#> 5  0.43  0.96 -0.53  3.45 -0.80 3.40 -1.76  2.97#> 6  0.51 -0.11  0.01  3.91 -0.09 4.41  0.02  3.91

• geom_vector(): By default, this maps the norm (magnitude) of avector to its color.

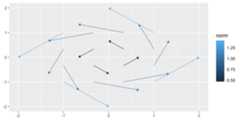
ggplot(wind_data)+  geom_vector(aes(x=lon,y=lat,xend=xend,yend=yend))

geom_vector() also supports bothxend/yend format as well asfx/fy format.

ggplot(wind_data)+  geom_vector(aes(x=lon,y=lat,fx=fx,fy=fy))

• geom_vector2(): Maps the norm of a vector directly to itslength. This provides a more intuitive representation of magnitude.This is done by mappinglength = after_stat(norm) by default.

ggplot(wind_data)+  geom_vector2(aes(x=lon,y=lat,fx=fx,fy=fy))

Polar Coordinates Support

Bothgeom_vector() andgeom_vector2() also support polarcoordinates, where vectors are specified using magnitude (distance)and direction (angle). Instead of providing Cartesian components(fx,fy orxend,yend), users can directly supply polar data.This feature simplifies workflows for directional data and works for allsubsequent relevant functions that handle polar coordinates.

Polar coordinates can be visualized like this:

ggplot(wind_data)+  geom_vector(aes(x=lon,y=lat,distance=spd,angle=dir))

Normalize and Center

• normalize: When set toTRUE, this option scales each vector tohave a unit length, which can help avoid overplotting in dense vectorfields. This is especially useful when the direction of vectors ismore important than their magnitude. However, it’s important to notethat normalize is different from mapping the norm of the vector to thelength aesthetic. While normalization ensures that all vectors arevisually uniform in length, mapping the norm to length preserves therelative differences in magnitude by varying the vector lengths basedon their actual norms.

• center: By default,center is also set toTRUE, meaning themidpoint of each vector is placed at the corresponding (x,y)coordinate, effectively “centering” the vector on the point. Whencenter isFALSE, the base of the vector is anchored at the (x,y) point, and the vector extends outward from there.

The example below turns off this default behavior:

ggplot(wind_data)+  geom_vector(aes(x=lon,y=lat,fx=fx,fy=fy),center=FALSE,normalize=FALSE)

ggvfields offers techniques for smoothing noisy vector field datageom_stream_smooth() andgeom_vector_smooth()

geom_stream_smooth() uses a dynamical systems approach andgeom_vector_smooth() offers a multivariate regression approach thataccounts for uncertainty.

ggplot(wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector(alpha=.5,color="black")+  geom_stream_smooth(aes(x=lon,y=lat,fx=fx,fy=fy))

Provides smoothed estimates of vector fields by applying statisticaltechniques to observed vectors.

Smoothing is performed using a multivariate linear model defined by:

$$\begin{pmatrix}\hat{dx} \\\hat{dy}\end{pmatrix} = \beta_0 + \beta_1 x + \beta_2 y + \beta_3 xy$$

where$\beta$ are coefficients estimated by ordinary least squares(OLS). This approach captures linear and interaction effects toapproximate the underlying vector field. This function also creates aprediction interval around the vector specified by theconf_levelargument and defaults to.95.

• Evaluating Specific Points:

When evaluation points are provided, smoothing is performed at thoselocations and prediction intervals can be visualized using either wedgesor ellipses to indicate uncertainty.

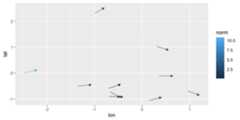
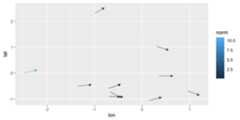
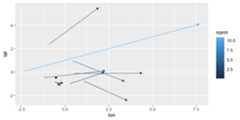
eval_point<-data.frame(x=.5,y=.5) ggplot(wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector(normalize=FALSE)+  geom_vector_smooth(eval_points=eval_point)+  lims(x= c(-7,10),y= c(-3,3))#> Warning: Removed 2 rows containing missing values or values outside the scale range#> (`geom_stream()`).

• Using Wedges to Visualize Uncertainty:

ggplot(wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector(normalize=FALSE)+  geom_vector_smooth(eval_points=eval_point,pi_type="wedge")

• Grid-Based Smoothing:

ggplot(wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector_smooth(pi_type="wedge")+   geom_vector()

• Custom Grid Resolution:

ggplot(wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector_smooth(n=6,pi_type="wedge")

• Altering Confidence Level

For all options, you can change the confidence level from the default toanother value by using theconf_level argument.

ggplot(wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector(normalize=FALSE)+  geom_vector_smooth(eval_points=eval_point,pi_type="wedge")+  geom_vector_smooth(eval_points=eval_point,pi_type="wedge",conf_level=.7)

geom_gradient_smooth() creates asmoothed gradient field from rawscalar data using a fitted linear model. This function estimatesgradients when only scalar values (z) are observed at spatiallocations (x,y). It is designed for cases where you have scalardata and wish to estimate the gradient.

The gradients are computed numerically from a fitted scalar field modeland the resulting gradient vectors are visualized using eitherstreamlines or vector arrows.

f1<-function(u) {x<-u[1]y<-u[2]x^2-y^2}grid_data<- expand.grid(x= seq(-5,5,length.out=30),y= seq(-5,5,length.out=30))set.seed(123)grid_data$z<- apply(grid_data,1,f1)+ rnorm(nrow(grid_data),mean=0,sd=5)ggplot(grid_data, aes(x=x,y=y,z=z))+  geom_gradient_smooth()

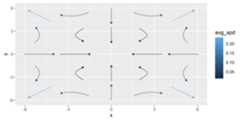
To illustrate howgeom_gradient_smooth() can adapt to nonlinearsurfaces, we can change the formula used to fit the scalar field andswitch to a streamline visualization usingtype = "stream". Theexample below uses a smooth but noisy scalar function that generatescurved gradients and fits a flexible smoothing model to capture thesevariations.

h1<-function(u) {x<-u[1]y<-u[2]  sin(x/2)* cos(y/2)}grid_data$z<- apply(grid_data,1,h1)+ rnorm(nrow(grid_data),mean=0,sd=1)ggplot(grid_data, aes(x=x,y=y,z=z))+  geom_gradient_smooth(formula=z~ I(x^2)* I(y^2),n=5,type="stream")

These functions can automatically determine plot limits based on thefunction provided. This happens when data exists in previous layers orin the base ggplot object. This allows the limits to be inferred fromcontext. Customize limits with thexlim andylim parameters ifneeded for more control.

ggplot(data=wind_data, aes(x=lon,y=lat,fx=fx,fy=fy))+  geom_vector()+  geom_stream_field(fun=f)# Automatically determines limits based on existing data

Thegeom_*_field functions allow the user to plot with customevaluation locations. The user can specify specific points to beevaluated over the field or can also use a “hex” pattern.

ggplot()+  geom_stream_field(fun=f,grid="hex")

This shows a custom grid.

custom<-data.frame(x= c(1,3,5),y= c(3,4,5))ggplot()+  geom_stream_field(fun=f,grid=custom,normalize=FALSE,center=FALSE,L=4)

This package is licensed under the MIT License.

For questions or feedback, pleaseopen anissue.

• metR:Meteorological visualizations with tools for vector fields.
• ggfields: Vector fieldlayers similar togeom_spoke.
• ggquiver: Quiver plotsfor vector fields.
• ggarchery: Arrow segmentvisualizations.