|
5 | 5 |
|
6 | 6 | ##题目大意 |
7 | 7 |
|
8 | | -给定一个二维数组`grid`,每个单元格为`0`(代表海)或`1`(代表陆地)。我们可以从一个陆地走到另一个陆地上(朝四个方向之一),然后从边界上的陆地离开网络的边界。 |
| 8 | +**描述**:给定一个二维数组`grid`,每个单元格为`0`(代表海)或`1`(代表陆地)。我们可以从一个陆地走到另一个陆地上(朝四个方向之一),然后从边界上的陆地离开网络的边界。 |
9 | 9 |
|
10 | | -要求:返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。 |
| 10 | +**要求**:返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。 |
| 11 | + |
| 12 | +**说明**: |
| 13 | + |
| 14 | +- $m == grid.length$。 |
| 15 | +- $n == grid[i].length$。 |
| 16 | +- $1 \le m, n \le 500$。 |
| 17 | +- $grid[i][j]$ 的值为 $0$ 或 $1$。 |
| 18 | + |
| 19 | +**示例**: |
| 20 | + |
| 21 | +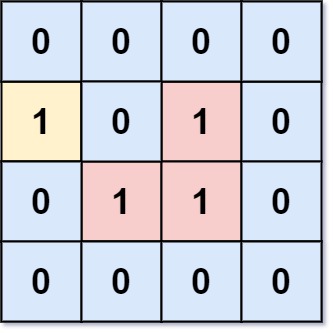 |
| 22 | + |
| 23 | +```Python |
| 24 | +输入:grid= [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] |
| 25 | +输出:3 |
| 26 | +解释:有三个1 被0 包围。一个1 没有被包围,因为它在边界上。 |
| 27 | +``` |
| 28 | + |
| 29 | +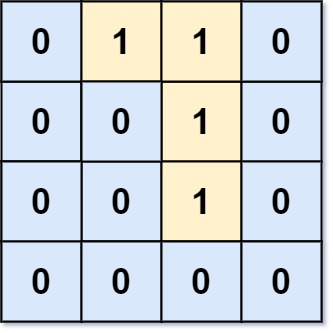 |
| 30 | + |
| 31 | +```Python |
| 32 | +输入:grid= [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]] |
| 33 | +输出:0 |
| 34 | +解释:所有1 都在边界上或可以到达边界。 |
| 35 | +``` |
11 | 36 |
|
12 | 37 | ##解题思路 |
13 | 38 |
|
14 | | -与四条边界相连的陆地单元是肯定能离开网络边界的。先通过深度优先搜索将与四条边界相关的陆地全部变为海(赋值为`0`)。然后统计网格中`1` 的数量即为答案。 |
| 39 | +###思路 1:深度优先搜索 |
| 40 | + |
| 41 | +与四条边界相连的陆地单元是肯定能离开网络边界的。 |
15 | 42 |
|
16 | | -##代码 |
| 43 | +我们可以先通过深度优先搜索将与四条边界相关的陆地全部变为海(赋值为`0`)。 |
| 44 | + |
| 45 | +然后统计网格中`1` 的数量,即为答案。 |
| 46 | + |
| 47 | +###思路 1:代码 |
17 | 48 |
|
18 | 49 | ```Python |
19 | 50 | classSolution: |
@@ -54,3 +85,7 @@ class Solution: |
54 | 85 | return ans |
55 | 86 | ``` |
56 | 87 |
|
| 88 | +###思路 1:复杂度分析 |
| 89 | + |
| 90 | +-**时间复杂度**:$O(m \times n)$。其中 $m$ 和 $n$ 分别为行数和列数。 |
| 91 | +-**空间复杂度**:$O(m \times n)$。 |