- Notifications
You must be signed in to change notification settings - Fork2
INCEPTdk/adaptr
Folders and files
| Name | Name | Last commit message | Last commit date | |
|---|---|---|---|---|
Repository files navigation
Theadaptr package simulates adaptive (multi-arm, multi-stage)clinical trials using adaptive stopping, adaptive arm dropping and/orresponse-adaptive randomisation.
The package has been developed as part of theINCEPT (Intensive CarePlatform Trial) project, primarily supported by agrant fromSygeforsikringen “danmark”.
- Website - stand-alone websitewith full package documentation
- adaptr: an R package for simulating and comparing adaptive clinicaltrials - article in theJournal of Open Source Software describing the package
- An overview of methodological considerations regarding adaptivestopping, arm dropping and randomisation in clinicaltrials - article inJournal of Clinical Epidemiology describing key methodologicalconsiderations in adaptive trials with description of the workflowand a simulation-based example using the package
Examples:
- Effects of duration of follow-up and lag in data collection on theperformance of adaptive clinicaltrials - article inPharmaceutical Statistics describing a simulation study (with code)using
adaptrto assess the performance of adaptive clinical trialsaccording to different follow-up/data collection lags. - Effects of sceptical priors on the performance of adaptive clinicaltrials with binary outcomes -article in Pharmaceutical Statistics describing a simulation study(with code) using
adaptrto assess the performance of adaptiveclinical trials according to different sceptical priors.
The easiest way is to install from CRAN directly:
install.packages("adaptr")Alternatively, you can install thedevelopment version from GitHub -this requires theremotes-package installed. The development versionmay contain additional features not yet available in the CRAN version,but may not be stable or fully documented:
# install.packages("remotes")remotes::install_github("INCEPTdk/adaptr@dev")
The central functionality ofadaptr and the typical workflow isillustrated here.
First, the package is loaded and a cluster of parallel workers isinitiated by thesetup_cluster() function to facilitate parallelcomputing:
library(adaptr)#> Loading 'adaptr' package v1.4.0.#> For instructions, type 'help("adaptr")'#> or see https://inceptdk.github.io/adaptr/.setup_cluster(2)
Setup a trial specification (defining the trial design and scenario)using the generalsetup_trial() function, or one of the special casevariants using default priorssetup_trial_binom() (for binary,binomially distributed outcomes; used in this example) orsetup_trial_norm() (for continuous, normally distributed outcomes).
# Setup a trial using a binary, binomially distributed, undesirable outcomebinom_trial<- setup_trial_binom(arms= c("Arm A","Arm B","Arm C"),# Scenario with identical outcomes in all armstrue_ys= c(0.25,0.25,0.25),# Response-adaptive randomisation with minimum 20% allocation in all armsmin_probs= rep(0.20,3),# Number of patients with data available at each analysisdata_looks= seq(from=300,to=2000,by=100),# Number of patients randomised at each analysis (higher than the numbers# with data, except at last look, due to follow-up/data collection lag)randomised_at_looks= c(seq(from=400,to=2000,by=100),2000),# Stopping rules for inferiority/superiority not explicitly defined# Stop for equivalence at > 90% probability of differences < 5 %-pointsequivalence_prob=0.9,equivalence_diff=0.05)# Print trial specificationprint(binom_trial,prob_digits=3)#> Trial specification: generic binomially distributed outcome trial#> * Undesirable outcome#> * No common control arm#> * Best arms: Arm A and Arm B and Arm C#>#> Arms, true outcomes, starting allocation probabilities#> and allocation probability limits:#> arms true_ys start_probs fixed_probs min_probs max_probs#> Arm A 0.25 0.333 NA 0.2 NA#> Arm B 0.25 0.333 NA 0.2 NA#> Arm C 0.25 0.333 NA 0.2 NA#>#> Maximum sample size: 2000#> Maximum number of data looks: 18#> Planned data looks after: 300, 400, 500, 600, 700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000 patients have reached follow-up#> Number of patients randomised at each look: 400, 500, 600, 700, 800, 900, 1000, 1100, 1200, 1300, 1400, 1500, 1600, 1700, 1800, 1900, 2000, 2000#>#> Superiority threshold: 0.99 (all analyses)#> Inferiority threshold: 0.01 (all analyses)#> Equivalence threshold: 0.9 (all analyses) (no common control)#> Absolute equivalence difference: 0.05#> No futility threshold (not relevant - no common control)#> Soften power for all analyses: 1 (no softening)
In the example trial specification, there are no true between-armdifferences, and stopping rules for inferiority and superiority are notexplicitly defined. This is intentional, as these stopping rules will becalibrated to obtain a desired probability of stopping for superiorityin the scenario with no between-arm differences (corresponding to theBayesian type 1 error rate). Trial specifications do not necessarilyhave to be calibrated, and simulations can be run directly using therun_trials() function covered below (orrun_trial() for a singlesimulation).
Calibration of a trial specification is done using thecalibrate_trial() function, which defaults to calibrate constant,symmetrical stopping rules for inferiority and superiority (expecting atrial specification with identical outcomes in each arm), but can beused to calibrate any parameter in a trial specification towards anyperformance metric.
# Calibrate the trial specificationcalibrated_binom_trial<- calibrate_trial(trial_spec=binom_trial,n_rep=1000,# 1000 simulations for each step (more generally recommended)base_seed=4131,# Base random seed (for reproducible results)target=0.05,# Target value for calibrated metric (default value)search_range= c(0.9,1),# Search range for superiority stopping thresholdtol=0.01,# Tolerance rangedir=-1# Tolerance range only applies below target)# Print result (to check if calibration is successful)calibrated_binom_trial#> Trial calibration:#> * Result: calibration successful#> * Best x: 0.9814318#> * Best y: 0.048#>#> Central settings:#> * Target: 0.05#> * Tolerance: 0.01 (at or below target, range: 0.04 to 0.05)#> * Search range: 0.9 to 1#> * Gaussian process controls:#> * - resolution: 5000#> * - kappa: 0.5#> * - pow: 1.95#> * - lengthscale: 1 (constant)#> * - x scaled: yes#> * Noisy: no#> * Narrowing: yes#>#> Calibration/simulation details:#> * Total evaluations: 7 (previous + grid + iterations)#> * Repetitions: 1000#> * Calibration time: 3.66 mins#> * Base random seed: 4131#>#> See 'help("calibrate_trial")' for details.
The calibration is successful - the calibrated, constant stoppingthreshold for superiority is printed with the results (0.9814318) andcan be extracted usingcalibrated_binom_trial$best_x. Using thedefault calibration functionality, the calibrated, constant stoppingthreshold for inferiority is symmetrical, i.e.,1 - stopping threshold for superiority (0.0185682). The calibratedtrial specification may be extracted usingcalibrated_binom_trial$best_trial_spec and, if printed, will alsoinclude the calibrated stopping thresholds.
Calibration results may be saved (and reloaded) by using thepathargument, to avoid unnecessary repeated simulations.
The results of the simulations using the calibrated trial specificationconducted during the calibration procedure may be extracted usingcalibrated_binom_trial$best_sims. These results can be summarised withseveral functions. Most of these functions support different ‘selectionstrategies’ for simulations not ending with superiority, i.e.,performance metrics can be calculated assuming different arms would beused in clinical practice if no arm is ultimately superior.
Thecheck_performance() function summarises performance metrics in atidydata.frame, with uncertainty measures (bootstrapped confidenceintervals) if requested. Here, performance metrics are calculatedconsidering the ‘best’ arm (i.e., the one with the highest probabilityof being overall best) selected in simulations not ending withsuperiority:
# Calculate performance metrics with uncertainty measuresbinom_trial_performance<- check_performance(calibrated_binom_trial$best_sims,select_strategy="best",uncertainty=TRUE,# Calculate uncertainty measuresn_boot=1000,# 1000 bootstrap samples (more typically recommended)ci_width=0.95,# 95% confidence intervals (default)boot_seed="base"# Use same random seed for bootstrapping as for simulations)# Print resultsprint(binom_trial_performance,digits=2)#> metric est err_sd err_mad lo_ci hi_ci#> 1 n_summarised 1000.00 0.00 0.00 1000.00 1000.00#> 2 size_mean 1749.60 11.36 10.97 1727.20 1772.10#> 3 size_sd 373.74 9.64 9.74 355.15 392.58#> 4 size_median 2000.00 0.00 0.00 2000.00 2000.00#> 5 size_p25 1400.00 52.43 0.00 1400.00 1500.00#> 6 size_p75 2000.00 0.00 0.00 2000.00 2000.00#> 7 size_p0 400.00 NA NA NA NA#> 8 size_p100 2000.00 NA NA NA NA#> 9 sum_ys_mean 438.69 2.95 2.85 432.74 444.66#> 10 sum_ys_sd 96.20 2.42 2.37 91.28 100.79#> 11 sum_ys_median 486.00 1.98 2.97 483.00 490.00#> 12 sum_ys_p25 364.75 10.95 9.64 352.00 395.00#> 13 sum_ys_p75 506.00 1.15 1.48 504.00 508.00#> 14 sum_ys_p0 88.00 NA NA NA NA#> 15 sum_ys_p100 565.00 NA NA NA NA#> 16 ratio_ys_mean 0.25 0.00 0.00 0.25 0.25#> 17 ratio_ys_sd 0.01 0.00 0.00 0.01 0.01#> 18 ratio_ys_median 0.25 0.00 0.00 0.25 0.25#> 19 ratio_ys_p25 0.24 0.00 0.00 0.24 0.24#> 20 ratio_ys_p75 0.26 0.00 0.00 0.26 0.26#> 21 ratio_ys_p0 0.20 NA NA NA NA#> 22 ratio_ys_p100 0.30 NA NA NA NA#> 23 prob_conclusive 0.43 0.02 0.01 0.40 0.46#> 24 prob_superior 0.05 0.01 0.01 0.04 0.06#> 25 prob_equivalence 0.38 0.02 0.01 0.35 0.41#> 26 prob_futility 0.00 0.00 0.00 0.00 0.00#> 27 prob_max 0.57 0.02 0.01 0.54 0.60#> 28 prob_select_arm_Arm A 0.32 0.02 0.01 0.29 0.35#> 29 prob_select_arm_Arm B 0.31 0.01 0.01 0.28 0.34#> 30 prob_select_arm_Arm C 0.37 0.02 0.02 0.34 0.40#> 31 prob_select_none 0.00 0.00 0.00 0.00 0.00#> 32 rmse 0.02 0.00 0.00 0.02 0.02#> 33 rmse_te NA NA NA NA NA#> 34 mae 0.01 0.00 0.00 0.01 0.01#> 35 mae_te NA NA NA NA NA#> 36 idp NA NA NA NA NA
Similar results inlist format (without uncertainty measures) can beobtained using thesummary() method, which comes with aprint()method providing formatted results:
binom_trial_summary<- summary(calibrated_binom_trial$best_sims,select_strategy="best")print(binom_trial_summary)#> Multiple simulation results: generic binomially distributed outcome trial#> * Undesirable outcome#> * Number of simulations: 1000#> * Number of simulations summarised: 1000 (all trials)#> * No common control arm#> * Selection strategy: best remaining available#> * Treatment effect compared to: no comparison#>#> Performance metrics (using posterior estimates from final analysis [all patients]):#> * Sample sizes: mean 1749.6 (SD: 373.7) | median 2000.0 (IQR: 1400.0 to 2000.0) [range: 400.0 to 2000.0]#> * Total summarised outcomes: mean 438.7 (SD: 96.2) | median 486.0 (IQR: 364.8 to 506.0) [range: 88.0 to 565.0]#> * Total summarised outcome rates: mean 0.251 (SD: 0.011) | median 0.250 (IQR: 0.244 to 0.258) [range: 0.198 to 0.295]#> * Conclusive: 42.9%#> * Superiority: 4.8%#> * Equivalence: 38.1%#> * Futility: 0.0% [not assessed]#> * Inconclusive at max sample size: 57.1%#> * Selection probabilities: Arm A: 31.8% | Arm B: 31.0% | Arm C: 37.2% | None: 0.0%#> * RMSE / MAE: 0.01730 / 0.01102#> * RMSE / MAE treatment effect: not estimated / not estimated#> * Ideal design percentage: not estimable#>#> Simulation details:#> * Simulation time: 33.1 secs#> * Base random seed: 4131#> * Credible interval width: 95%#> * Number of posterior draws: 5000#> * Estimation method: posterior medians with MAD-SDs
Individual simulation results may be extracted in a tidydata.frameusingextract_results().
Finally, the probabilities of different remaining arms and theirstatuses (with uncertainty) at the last adaptive analysis can besummarised using thecheck_remaining_arms() function.
Several visualisation functions are included (all are optional, and allrequire theggplot2 package installed).
Convergence and stability of one or more performance metrics may bevisually assessed usingplot_convergence() function:
plot_convergence(calibrated_binom_trial$best_sims,metrics= c("size mean","prob_superior","prob_equivalence"),# select_strategy can be specified, but does not affect the chosen metrics)
The empirical cumulative distribution functions for continuousperformance metrics may also be visualised:
plot_metrics_ecdf(calibrated_binom_trial$best_sims,metrics="size")
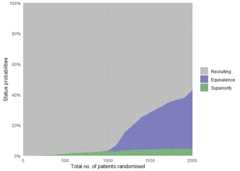
The status probabilities for the overall trial (or for specific arms)according to trial progress can be visualised using theplot_status()function:
# Overall trial status probabilitiesplot_status(calibrated_binom_trial$best_sims,x_value="total n"# Total number of randomised patients at X-axis)
Finally, various metrics may be summarised over the progress of one ormultiple trial simulations using theplot_history() function, whichrequires non-sparse results (thesparse argument must beFALSE incalibrate_trials(),run_trials(), orrun_trial(), leading toadditional results being saved).
The calibrated stopping thresholds (calibrated in a scenario with nobetween-arm differences) may be used to run simulations with the sameoverall trial specification, but according to a different scenario(i.e., with between-arm differences present) to assess performancemetrics (including the Bayesian analogue of power).
First, a new trial specification is setup using the same settings asbefore, except for between-arm differences and the calibrated stoppingthresholds:
binom_trial_calib_diff<- setup_trial_binom(arms= c("Arm A","Arm B","Arm C"),true_ys= c(0.25,0.20,0.30),# Different outcomes in the armsmin_probs= rep(0.20,3),data_looks= seq(from=300,to=2000,by=100),randomised_at_looks= c(seq(from=400,to=2000,by=100),2000),# Stopping rules for inferiority/superiority explicitly defined# using the calibration resultsinferiority=1-calibrated_binom_trial$best_x,superiority=calibrated_binom_trial$best_x,equivalence_prob=0.9,equivalence_diff=0.05)
Simulations using the trial specification with calibrated stoppingthresholds and differences present can then be conducted using therun_trials() function and performance metrics calculated as above:
binom_trial_diff_sims<- run_trials(binom_trial_calib_diff,n_rep=1000,# 1000 simulations (more generally recommended)base_seed=1234# Reproducible results)check_performance(binom_trial_diff_sims,select_strategy="best",uncertainty=TRUE,n_boot=1000,# 1000 bootstrap samples (more typically recommended)ci_width=0.95,boot_seed="base")#> metric est err_sd err_mad lo_ci hi_ci#> 1 n_summarised 1000.000 0.000 0.000 1000.000 1000.000#> 2 size_mean 1242.300 16.620 16.976 1209.895 1273.025#> 3 size_sd 531.190 7.251 7.604 516.617 544.091#> 4 size_median 1200.000 22.220 0.000 1200.000 1300.000#> 5 size_p25 800.000 36.095 0.000 700.000 800.000#> 6 size_p75 1700.000 42.453 0.000 1700.000 1800.000#> 7 size_p0 400.000 NA NA NA NA#> 8 size_p100 2000.000 NA NA NA NA#> 9 sum_ys_mean 284.999 3.695 3.726 277.724 291.991#> 10 sum_ys_sd 117.265 1.701 1.732 113.765 120.311#> 11 sum_ys_median 279.000 5.268 4.448 269.500 289.512#> 12 sum_ys_p25 186.000 6.682 7.413 174.000 197.019#> 13 sum_ys_p75 390.000 7.633 7.413 374.000 402.250#> 14 sum_ys_p0 81.000 NA NA NA NA#> 15 sum_ys_p100 519.000 NA NA NA NA#> 16 ratio_ys_mean 0.232 0.000 0.001 0.231 0.233#> 17 ratio_ys_sd 0.016 0.000 0.000 0.015 0.017#> 18 ratio_ys_median 0.230 0.001 0.000 0.230 0.232#> 19 ratio_ys_p25 0.221 0.000 0.000 0.220 0.222#> 20 ratio_ys_p75 0.242 0.001 0.001 0.240 0.243#> 21 ratio_ys_p0 0.195 NA NA NA NA#> 22 ratio_ys_p100 0.298 NA NA NA NA#> 23 prob_conclusive 0.877 0.011 0.010 0.857 0.898#> 24 prob_superior 0.731 0.014 0.015 0.706 0.759#> 25 prob_equivalence 0.146 0.011 0.011 0.125 0.167#> 26 prob_futility 0.000 0.000 0.000 0.000 0.000#> 27 prob_max 0.123 0.011 0.010 0.102 0.143#> 28 prob_select_arm_Arm A 0.038 0.006 0.006 0.026 0.049#> 29 prob_select_arm_Arm B 0.962 0.006 0.006 0.951 0.974#> 30 prob_select_arm_Arm C 0.000 0.000 0.000 0.000 0.000#> 31 prob_select_none 0.000 0.000 0.000 0.000 0.000#> 32 rmse 0.020 0.001 0.001 0.019 0.022#> 33 rmse_te NA NA NA NA NA#> 34 mae 0.011 0.000 0.000 0.010 0.012#> 35 mae_te NA NA NA NA NA#> 36 idp 98.100 0.306 0.297 97.549 98.700
Again, simulations may be saved and reloaded using thepath argument.
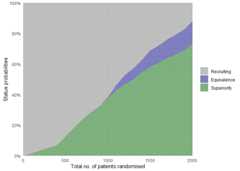
Similarly, overall trial statuses for the scenario with differences canbe visualised:
plot_status(binom_trial_diff_sims,x_value="total n")
We use theGitHub issuetracker for all bug/issuereports and proposals for enhancements.
We welcome contributions directly to the code to improve performance aswell as new functionality. For the latter, please first explain andmotivate it in anissue.
Changes to the code base should follow these steps:
- Forkthe repository
- Make abranchwith an appropriate name in your fork
- Implement changes in your fork, make sure it passes R CMD check(with neither errors, warnings, nor notes) and add a bullet at thetop of NEWS.md with a short description of the change, your GitHubhandle and the id of the pull request implementing the change (checkthe
NEWS.mdfile to see the formatting) - Create apullrequestinto the
devbranch ofadaptr
If you use the package, please consider citing it:
citation(package="adaptr")#>#> To cite package 'adaptr' in publications use:#>#> Granholm A, Jensen AKG, Lange T, Kaas-Hansen BS (2022). adaptr: an R#> package for simulating and comparing adaptive clinical trials.#> Journal of Open Source Software, 7(72), 4284. URL#> https://doi.org/10.21105/joss.04284.#>#> A BibTeX entry for LaTeX users is#>#> @Article{,#> title = {{adaptr}: an R package for simulating and comparing adaptive clinical trials},#> author = {Anders Granholm and Aksel Karl Georg Jensen and Theis Lange and Benjamin Skov Kaas-Hansen},#> journal = {Journal of Open Source Software},#> year = {2022},#> volume = {7},#> number = {72},#> pages = {4284},#> url = {https://doi.org/10.21105/joss.04284},#> doi = {10.21105/joss.04284},#> }
About
Adaptive Trial Simulator
Resources
License
Uh oh!
There was an error while loading.Please reload this page.
Stars
Watchers
Forks
Packages0
Uh oh!
There was an error while loading.Please reload this page.
Contributors2
Uh oh!
There was an error while loading.Please reload this page.