原题链接

子问题

dp[i]: 表示以 s[i] 结尾的最长有效括号长度。

状态转移方程

分情况讨论出所有可能：

s[i] 可能为 '(' 或者 ')'：

1. s[i] === '(' 时，不可能组成有效的括号，所以 dp[i] = 0。
2. s[i] === ')' 时，需要查看 s[i - 1]。
   • s[i - 1] === '(' 时，s[i - 1] 和 s[i] 可以组成一对有效括号，需要查看 s[i - 2]。
     • s[i - 2] 不存在，则有效长度为 2。dp[i] = 2
     • s[i - 2] 存在，则需要在 2 的基础上加上以 s[i - 2] 为结尾的最长有效长度。dp[i] = dp[i - 2] + 2
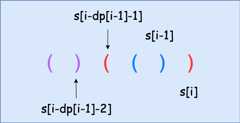
   • s[i - 1] === ')' 时，此时 s[i - 1] 和 s[i] 合起来是 '))'，需要查看 s[i - dp[i - 1] - 1]。
     • s[i - dp[i - 1] - 1] 不存在或为 ')'，则 s[i] 找不到匹配，所以 dp[i] = 0。
     • s[i - dp[i - 1] - 1] 是 '('，与 s[i] 匹配。此时需要查看 s[i - dp[i - 1] - 2]是否存在。
       • s[i - dp[i - 1] - 2] 不存在，dp[i] = dp[i - 1] + 2
       • s[i - dp[i - 1] - 2] 存在，dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2

用代码表示出来即可：

constlongestValidParentheses=function(s){letres=0constlen=s.lengthconstdp=newArray(len).fill(0)for(leti=1;i<len;i++){if(s[i]==')'){if(s[i-1]=='('){if(i-2>=0){dp[i]=dp[i-2]+2}else{dp[i]=2}}elseif(s[i-dp[i-1]-1]=='('){if(i-dp[i-1]-2>=0){dp[i]=dp[i-1]+2+dp[i-dp[i-1]-2]}else{dp[i]=dp[i-1]+2}}}res=Math.max(res,dp[i])}returnres}

• 时间复杂度：O(n)
• 空间复杂度：O(n)