the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Timing and climatic-driven mechanisms of glacier advances in Bhutanese Himalaya during the Little Ice Age
Mountain glaciers provide us a window into past climate changesand landscape evolution, but the pattern of glacier evolution at centennialor suborbital timescale remains elusive, especially in monsoonal Himalayas.We simulated the glacier evolution in Bhutanese Himalaya (BH), a typicalmonsoon-influenced region, during the Little Ice Age (LIA) using the OpenGlobal Glacier Model driven by six paleoclimate datasets and their average.Compared with geomorphologically mapped glacial landforms, the model canwell capture the patterns of glacier length change. Simulation resultsrevealed four glacial substages (the 1270s, 1470s, 1710s, and 1850s) during LIAin the study area. Statistically, a positive correlation between the numberof glacial substages and glacier slope was found, indicating that the occurrenceof glacial substages might be a result from heterogeneous responses ofglaciers to climate change. Monthly climate change analysis and sensitivityexperiments indicated that the summer temperature largely dominates the regionalglacier evolution during the LIA in BH.
- Article
(4501 KB) - Full-text XML
- Supplement
(783 KB) - BibTeX
- EndNote
Mountain glaciers over the high Himalayas provide us with a critical window toexplore the linkage between climatic, tectonic, and glacial systems(Oerlemans et al., 1998; Owen, 2009; Dortch et al., 2013; Owen andDortch, 2014; Saha et al., 2018). Many scientists have investigated theglacial history of the Himalaya at orbital scale, indicating that a generaltrend of glacier advances is related to overall summer temperature, forcedby orbitally controlled insolation (Murari et al., 2014; Yan et al., 2018,2020, 2021). However, the latest observations with finer temporal resolutionhave revealed that the evolution of some glaciers in monsoonal Himalayas hassuborbital scale fluctuations, which has generated increasing interest inexploring its mechanisms (Solomina et al., 2015; Peng et al., 2020).
The Little Ice Age (LIA; from 1300 to 1850 CE; Grove, 2013; Qureshi et al.,2021) is the latest cooling event during the Holocene, during which mostmountain glaciers advanced, forming abundant well-preserved and distinctivegeomorphic landforms (Murari et al., 2014; Qiao and Yi, 2017; Peng et al.,2019, 2020). Previous studies reconstructed the timing and extent ofglacier evolution during the LIA based on field investigation,geomorphological mapping, and cosmogenic nuclide dating (Owen and Dortch,2014, and references therein; Zhang et al., 2018a, b; Carrivick et al.,2019; Qureshi et al., 2021). However, it is still unclear how many substages(glacial advances) existed during the LIA (Yi et al., 2008; Murari et al.,2014; Xu and Yi, 2014), due to the post-glacial degradation and the largeuncertainties in the dating methods (Heyman et al., 2011; Fu et al., 2013).In addition, Carrivick et al. (2019) indicated that the reconstructionsusing individual glaciers or a small number of glaciers may not berepresentative for the regional average.
Numerical glacial modeling is a powerful way to study glacier evolution onthe centennial timescale (Parkes and Goosse, 2020) and quantify the response ofglaciers to climate change (Eis et al., 2019). It can also be a complementfor a field-based approach in capturing the glacier evolution on regionalscale. Meanwhile, the model simulations can be evaluated via multipleobservations to ensure the reliability. However, evaluating the simulationresults is still challenging due to the scarcity of the direct observationalrecord for glacier changes during the LIA (Goosse et al., 2018).
Based on the above issues, this study provides a possible approach to how tobring observation and simulation together, what the contribution ofindividual glacier to regional glacier evolution is, and how climate changedrives glacier evolution (Goosse et al., 2018; Carrivick et al., 2019; Penget al., 2019, 2020). We chose a typical monsoon-influenced area, BhutaneseHimalaya (BH) as an example, using the Open Global Glacier Model (OGGM) toimprove our understanding of the pattern of LIA glacier changes (Fig. 1).The BH (27.5–28.3∘ N, 89.1–91.0∘ E) is an east–west trending mountain range with an averageelevation above 5000 m above sea level (a.s.l.), nourishing abundant highmountain glaciers (Peng et al., 2019, 2020; Fig. 1b). According to theRandolph Glacier Inventory V6.2 (RGI; RGI Consortium, 2017), there are 803modern glaciers in BH, covering an area of∼1233.685 km2(Fig. 1b). There are 57 glaciers in the RGI13 region (Central Asia) and746 glaciers in the RGI15 region (Southeast Asia). The distribution ofglacier lengths is shown in Fig. 1c, with an average length of 1596 m (950 mfor the median value) ranging from 135 to 20 011 m. Small glaciers (of lengthshorter than 3000 m) are prevalent in BH (accounting for 88.9 %).
We systematically simulated the BH glacier changes during the LIA based onthe climate data from six different general circulation models (GCMs) andtheir average. The simulated glacier length changes are validated bygeomorphological maps and previous studies. The pattern of regional glacialevolution is compared with10Be and14C glacial chronologiesacross the monsoon-influenced Himalayas. The dominant climatic factors of BHglacial evolution are explored through analyzing the glacier surface massbalance (SMB) changes and a series of sensitivity experiments.
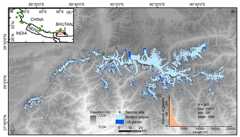
Figure 1An overview of study area and moraine sites. The red box in(a) shows the location of the study area, and the green circles in(a) displaythe spatial distribution of the10Be exposure dating moraines. Thebasic information of these moraine sites can refer to Table S1 in the Supplement.(b) Theextent of the modern glaciers (in light blue; RGI Consortium, 2017) and LIAglaciers (in navy blue). The background DEM was obtained from the ShuttleRadar Topography Mission (SRTM) 90 m Digital Elevation Model v4.1 (Jarvis etal., 2008;http://srtm.csi.cgiar.org/, last access: 17 September 2022).(c) The length distribution ofmodern glaciers.
2.1 Model description
The OGGM (v1.50) is a 1.5D ice-flow model, able to simulate past and futuremass balance, volume, and the geometry of glaciers (Maussion et al., 2019).Previous studies confirmed a good performance of this model insimulating alpine glaciers (Farinotti et al., 2017; Pelto et al., 2020) andreproducing the millennial trend of glacial evolution in mountainous regions(Goosse et al., 2018; Parkes and Goosse, 2020). For example, OGGM has beensuccessfully applied to simulate High Mountain Asia glaciers, includingtheir thickness, velocity, and future evolutions (Dixit et al., 2021; Pronket al., 2021; Shafeeque and Luo, 2021; Furian et al., 2022; Chen et al.,2022).
The OGGM couples a surface mass balance (SMB) scheme with a dynamic core(Marzeion et al., 2012; Maussion et al., 2019). The dynamic core adopts theshallow-ice approximation (SIA), computing the depth-integrated ice flux ofeach cross-section along multiple connected flowlines diagnosed by apre-process algorithm (via geometrical centerlines). Two key parameters, thecreep parameterA and the sliding parameterfs, in the dynamic core areset to their default values ( s−1 Pa−3,fs=0 s−1 Pa−3,without lateral drag). The spatial resolution (dx; m) of the target grid isscale dependent, determined by the size of the glacier (, withS representing the glacier area in km2) but truncated by minimum(10 m) and maximum (200 m) values, respectively (Maussion et al., 2019).According to the observations, the largest simulation domain is set to 160grid points outside the modern glacier boundaries to ensure that the domainis large enough for the LIA glaciers (Fig. S3; Qiao and Yi, 2017). If aglacier advance exceeds the domain during the simulation, we will excludethis glacier in the further analysis due to its large simulation bias.
The ice accumulation is estimated by a solid precipitation scheme toseparate the total precipitation into rain and snow based on monthly airtemperature. In this scheme, the amount of solid precipitation is computedas a fraction of the total precipitation. Specifically, precipitation isentirely solid ifTi≤TSolid (the default setting is 0 ∘C),entirely liquid ifTi≥TLiquid (defaults to 2 ∘C) ordivided into solid and liquid parts based on a linear relationship withthose two temperature values. The ablation is estimated using a positivedegree-day (PDD) scheme (Eq. 1). Melting occurs if the monthly temperature(Ti(z)) is aboveTmelt, which is equal to−1 ∘C.
wheremi(z) is the monthly SMB at elevationz of monthi;is the monthly solid precipitation, andPf is a general precipitationcorrection factor (the default setting is 2.5);μ∗ is thetemperature sensitivity parameter, andβ is the temperature bias. Aresidual bias term (ε) is added as a tuning parameter torepresent the collective effects of non-climate factors (Marzeion et al.,2012; Maussion et al., 2019). Different from the conventional PDD schemesembedded in other ice sheet models, such as the Parallel Ice Sheet Model (Buelerand Brown, 2009; Winkelmann et al., 2011), SICOPOLIS (Greve, 1997a, b)or CISM (Lipscomb et al., 2019), that assumeε andμ∗ as constant values, these parameters vary with glacier in OGGM.However, there are 16 glaciers (1.0 % of the total area) that cannot besimulated because theμ∗ is infinite or out of specifiedbounds (Maussion et al., 2019).
The monthly temperature and precipitation from six different GCMs (BCC,CCSM4, CESM, GISS, IPSL, and MPI), covering a period from 850 to 2000 CE,are used to drive OGGM. These data are available in the Past ModelIntercomparison Project (PMIP3) and the Coupled Model IntercomparisonProject (CMIP5) protocols (Schmidt et al., 2012; Taylor et al., 2012; PAGES2k-PMIP3 group, 2015) – with details listed in Goosse et al. (2018) andTable S2. The climate data cannot be directly used in glacial models due tothe large systematical bias of GCMs. A calibration algorithm is adopted byOGGM to correct the GCMs climate data by taking the anomalies between GCMsand the Climate Research Unit (CRU) TS 4.01 (Harris et al., 2020) meanclimate from 1961 to 1990 (Parkes and Goosse, 2020). In addition, the meanclimate (MC) from six different GCMs is also calculated and calibrated todrive OGGM (hereafter MC experiment) to further alleviate the climate biasof each GCM. Therefore, we would focus on analyzing the results from the MCexperiment but also involve some discussions on the difference between the MCexperiment and six GCM experiments.
2.2 Identification of glacial substages and related concepts
Similarly to Goosse et al. (2018) and Parkes and Goosse (2020), we usea simulated glacier length change (, whereL1950 represents the simulated glacier length at 1950) to representglacier evolution. In order to alleviate the influence of glacier size(length) to the mean value, we further convertΔL into glacier length change ratio (GLR = ). Firstly, we exclude the glaciers of which thesimulated lengths equal to zero at 1950 because these glaciers have largesimulation biases according to the observations (RGI). Then, the decadal meanGLR is calculated for each glacier in order to remove the interannualvariabilities. Next, the Gaussian filter (with the standard deviation setting tobe 3) is applied to the decadal mean GLR for each glacier to extract themain oscillations. After that, we obtain the regional average GLR byaveraging all glaciers' GLR (decadal averaged and Gaussian filtered) withinthe domain. Finally, we try to find all peaks and their corresponding timesin the regional average GLR time series based on the “findpeaks” functionembedded in the Matlab software. A local peak is a data sample that is largerthan its two neighboring samples. We set the minimum peak prominence to 0.2to eliminate the peaks that drop smaller than 0.2 on either side. Each peakfound is defined as a glacial substage during the LIA. We name the substages from new to old(LIA-1, LIA-2, LIA-3, LIA-4, and maybe more).
A concept related to GLR ismaximum peak GLR, defined as the GLR when a glacier reaches itsmaximum peak during a period. Notice that maximum peak GLR is different from the maximumGLR. For example, in Fig. 2d, the maximum peak GLR occurs around 1270 CE rather than 1100 CE. Based on this concept, the simulatedsecond/third/fourth peak GLR is defined as the GLR when aglacier reaches it second/third/fourth maximum peak during a period.
2.3 Spinup, tuning strategy, and experiment design
We spin up the model to avoid the influence of the pre-run condition andtuned the parameter, temperature bias (β) in Eq. (1), to obtain abetter post-spinup condition. Note that the post-spinup condition would be usedas the initial condition for the historical run. Theβ directlyregulates the post-spinup condition and largely impacts the GLR during earlyLIA (e.g., LIA4). We alterβ from−1 to 1 ∘C with anincrement of 0.1 ∘C during the spinup period to select the bestinitial condition for the historical run. For all experiments, a 5000-yearspinup forced by the climate data selected randomly from a 51-year windowof 875–925 CE is conducted prior to the historical run. After spinup, wemodel the LIA glacier changes withβ=0, forced by the past climatetime series from 900 to 2000 CE. In addition, we start our analysis at theyear 1100 for a better display of the glacial fluctuations during the LIA(1300–1850 CE; Grove, 2013; Qureshi et al., 2021).
The tuning procedure is based on the MC experiment, while six GCM experimentsshare the sameβ with the MC experiment during the spinup period. Our tuningstrategy is threefold. First, we should ensure that the regional average GLR islarger during LIA4 than LIA1 as in the observations because previous studiesindicated that the majority of glaciers advanced to their LIA maximumextents at the early LIA rather than the late LIA (Murari et al., 2014; Xuand Yi, 2014). Second, we need to ensure the simulated maximum peak GLR closer to theobservations. Notice that we choose to use maximum peak GLR because the observations derivedfrom the geomorphological mapping methods can only obtain this variableduring LIA (Sect. 2.4). Third, let more glaciers be available in theanalysis, as a smallerβ will decrease the number of availableglaciers (Fig. 2c).
A series of sensitivity experiments are also conducted to further validatethe effect of climate changes on BH glacier advances on both seasonal andannual scales. We apply a “constant climate scenario”, using the CRUdatasets as climate forcing, and run the simulation until reachingequilibrium (here, 5000 years). The window size of CRU data is set to 51 yearsand centered ont∗;t∗ is the year when the model bestreproduces the observed SMB for glaciers in the World Glacier MonitoringService (WGMS; WGMS, 2021) datasets (Marzeion et al., 2012; Maussion et al.,2019). We setε to 0 in Eq. (1) in order to maintain thecontemporary glacier geometry under the contemporary climate condition. Thecontrol experiment is forced by the default monthly temperature andprecipitation. Keeping the same precipitation, we alterβ from−1 to1 ∘C with an increment of 0.1 ∘C to the originalseasonal/annual temperature to test the sensitivity of temperature onglacier evolution. A similar approach is also applied to theprecipitation. Keeping the temperature, we adjust the precipitation from−20 %to 20 % with an increment of 2 % in the original seasonal/annualprecipitation data.
2.4 Establishing regional chronology and mapping LIA glaciers
The simulated timing and extent of glacial advances are validated with the10Be surface exposure ages and14C ages of the LIA moraines acrossthe monsoonal Himalaya and the mapped LIA glaciers over BH. Here, we assumethat the dated moraines outside of the study area can also represent thedates of glacial advances within the study area because the terrain andclimatic conditions are similar (Owen and Dortch, 2014; Murari et al.,2014). With this assumption, more observations can be included in thisstudy, making them more representative of regional features. Five10Beages from moraine M1 of Cogarbu valley and seven10Be ages from moraineM1 of the Shi Mo valley were selected to determine the regional glaciationchronology establishment in BH (Figs. 1b and S1), and 12610Besurface exposure ages and 714C across the monsoonal Himalayas are usedas a supplement (Fig. 1a; Table S1; Xu and Yi, 2014).
All10Be ages are recalculated using the CRONUS Earth V3 online calculatorwith the time and nuclide-dependent scaling scheme “LSDn” (Balco et al.,2008; Lifton, et al., 2014;http://hess.ess.washington.edu/math/, last access: 17 September 2022). We thenadopt the method advocated by Chevalier et al. (2011) and Dong et al. (2018)to exclude potential outliers. The potential outliers are defined as the10Be ages that did not overlap within1σ external uncertaintywith others for a moraine. After removing outliers, we use the oldest age ofa moraine sample set to represent the moraine depositional age (Chevalier etal., 2011; Dong et al., 2018; Peng et al., 2020).
Based on regional glacial chronology and the evidence of sediment-landformassemblages (Chandler et al., 2019), we map the outermost lateral andterminal moraines in BH to represent the maximum extent of glaciers duringthe LIA (the maximum peak GLR). These moraines are usually well preserved with sharp crests,locating from several hundred meters to a few kilometers away from thetermini of modern glaciers and damming a lake in front of modern glaciers(Qiao and Yi, 2017; Zhang et al., 2018b; Qureshi et al., 2021). We use theworld imagery ESRI (http://goto.arcgisonline.com/maps/World_Imagery, last access: 17 September 2022) and Google Earth high-resolution imagery to delineate the LIAmoraines and outlines. However, not all LIA glaciers could be identified dueto the destruction of moraines. Only 408 glaciers out of the 803 BH glacierscould be mapped (Fig. 1b). The length of contemporary glaciers is providedin Randolph Glacier Inventory V6.2 datasets (RGI; RGI Consortium, 2017), andthat of the LIA glaciers is calculated in ArcGIS based on the main modelflowline in OGGM.
3.1 The choice of post-spinup condition
In order to obtain a better estimation of the post-spinup condition, wetuned theβ during the spinup period. As shown in Fig. 2,βstrongly influences the post-spinup condition and, thus, the LIA simulationresults, especially for the first 600 years (Fig. 2b). With a decreasedβ, the regional average glacier volume increases (Fig. 2a), but thenumber of available glaciers (i.e., glaciers that do not exceed theprescribed domain boundaries) decreases during the spinup period (Fig. 2c).The number of available glaciers for the LIA simulation is approximatelyequal to that during the spinup period, except for a reduction whenβ is positive (Fig. 2c). This is probably because smallerβ can kickout the glaciers that would potentially suffer from large simulation biasduring LIA simulation. In addition, more glaciers disappear in 1950(L1950=0) with largerβ because the model isunable to capture some small glaciers, which rely on local topography,preferential deposition and redistribution of snow, or avalanching for theirexistence. Although about 100 glaciers are excluded, they are rathersmall glaciers that account for only 2.1 % of the total glacier areas(Fig. S3). Therefore, the results are still sufficiently representative forthe regional average.
The post-spinup condition slightly impacts the time and number of glacialsubstages but largely influences the strength of glacial substages (GLR)during LIA simulation (Figs. 2d and S1). Four substages occurred at∼1250s–1280s (LIA-4),∼1470s–1480s(LIA-3),∼1700s–1720s (LIA-2), and∼1850s(LIA-1) are detected under a wide range ofβ (from−0.7 to1.0 ∘C) in the MC experiment. However, the number of substagesbecome less whenβ is smaller than−0.7. Only two substages have beendetected with (LIA2 and LIA1) and(LIA3 and LIA1), while only the latest substage could be probed with. This is because smallerβ causes excessively largeinitial glaciers, so that a smaller climate perturbation is not powerfulenough for the glaciers to stop retreating during the early LIA period. Inaddition, the occurrence time of LIA-4, LIA-3, and LIA-2 becomes earlierwith a smallerβ, but the occurrence time of LIA-1 is stable withvariousβ.
The GLR during the early LIA periods (LIA-4 and LIA-3) are stronglyregulated by the post-spinup condition (Fig. 2d). Smallerβ will leadto a larger GLR during LIA-4 and LIA-3. According to the tuning strategiesin Sect. 2.3, simulations with should be excluded,as larger GLR must be ensured during LIA-4 than LIA-1. The root mean squarederror (RMSE) of maximum peak GLR between the simulation and observation is the smallest when (RMSE = 133.3 %), although a decreasing trend isfound when (Fig. 3). However, the number of availableglaciers when is less than that when. Therefore, we finally choose the simulation results with based on the tuning strategies.
The modern ice volume is estimated by the ice inversion module in OGGM(Maussion et al., 2019). This module is designed to diagnose the glacierthickness distribution under the constraints of modern glacier extents (suchas RGI outlines) and climate scenario (such as CRU dataset), which canprovide the best estimation of glacier volume (Maussion et al., 2019;Farinotti et al., 2019). The simulated BH ice volume at 2000 increases withdecreasedβ, resulting from the reduction of available glacier numbers.Compared with best estimation, the simulated regional average ice volume hasa small bias ranging from−0.006 to 0.010 km3, especially for a zerobias when. This confirms the ability of OGGM to simulatethe glaciers at regional scale, and is the best choicefor our study.
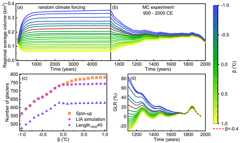
Figure 2(a) The regional average glacier volume during the 5000-yearspinup with variousβ.(b) The simulated regional average glaciervolume from 900 to 2000 CE with different post-spinup conditions.(c) Thenumber of available glaciers with variousβ.(d) The simulatedregional average GLR from 1100 to 1950 CE.
3.2 The pattern of glacier changes during the LIA
We focus on the pattern of glacier changes during the LIA in MCexperiment, but six GCM simulations are also shown in Fig. 4a forcomparison. The simulation results in most experiments indicate four LIAglacial substages in BH, except for the CESM experiment losing the LIA-3substage. The timings of the four LIA glacial substages are 1270s (LIA-4),1470s (LIA-3), 1710s (LIA-2), and 1850s (LIA-1) in the MC experiment. Thesetimes vary slightly among the six GCM experiments, around the 1230s–1320s,1470s–1520s, 1620s–1730s, and 1800s–1850s, respectively.
The most extensive glaciers occurred during LIA-4 in MC and six GCMexperiments because our tuning strategy is to ensure the larger regionalaverage GLR at the early LIA. The second peak GLR occurred during LIA-1 in the MC experiment. Thisfinding is the same as the results in the CCSM4, GISS, and MPI experimentsbut different from the results in BCC (LIA-2), CESM (LIA-2), and IPSL(LIA-3) experiments. The third and fourth peak GLR occurred during LIA-3 and LIA-2, respectively,in the MC experiment, which is also consistent with the simulations forced by CCSM4, GISS,and MPI climate datasets.

Figure 4(a) Time series of regional average GLR from 1100 to 1950 CE.(b) Theobservational timing when glaciers in the monsoonal Himalaya reached theirmaximum peak GLR. We grouped the moraine ages based on their temporal distances to eachglacial substage simulated in the MC experiment. Detailed information on themoraine ages measured by10Be and14C can be found in Table S1 andXu and Yi (2014), respectively.
4.1 Comparison between simulations and observations
We validated the simulation results using the moraine ages across themonsoonal Himalaya and mapped LIA glaciers (Sect. 2.4). The simulatedregional average maximum peak GLR (57.4 %; Fig. 3b) in the MC experiment agrees well withthat of the mapped glaciers (60.2 %). Similarly, the simulation results inBCC (55.7 %), GISS (54.2 %), and MPI (66.6 %) experiments are alsoconsistent with the observations. Observations from adjacent regions alsosupport the simulation results (Qiao and Yi, 2017; Zhang et al., 2018b).For example, Qiao and Yi (2017) found that the maximum peak GLR increased about 53.8 %during LIA in the central and western Himalayas relative to 2015. Zhang etal. (2018b) reported a 71.5 % increase of maximum peak GLR during LIA in the GangdiseMountains relative to 2010, based on the glacial geomorphological maps.However, the CCSM4 (89.6 %) and CESM (78.0 %) experimentsoverestimated the maximum peak GLR, while the IPSL (28.0 %) experiment underestimated it(Fig. S1). In addition, the negative bias for the median value in thesimulations compared with observations was identified in the MC and six GCMexperiments (Figs. 3b and S1). The difference between the mean value and themedian value indicates that some extrema might impact the average.
Based on our tuning strategy (Murari et al., 2014; Xu and Yi, 2014),the maximum peak GLR occurred during LIA-4 in the MC experiment, which was also confirmed by thedated moraine ages in monsoon-influenced Himalaya in that the majority ofglaciers advanced to their LIA maximum extents at the early LIA rather thanthe late LIA (Fig. 4b). Specifically, about 12 of the 30 moraine ages acrossthe monsoonal Himalaya show that the related glaciers reached theirmaximum peak GLR during LIA-4 compared with only two during LIA-1. However, there isstill a large number of glaciers reaching their maximum peak GLR during LIA-3 (about tenglaciers) and LIA-2 (about six glaciers). Ignoring the large uncertainties inthe dating methods, the collective and individual differences in glacierchanges are worth exploring. We will discuss this issue further in Sect. 4.2.
The simulated number of LIA substages is also comparable with observations,including some moraine dating results and climatic proxy records. Forexample, Murari et al. (2014) and Zhang et al. (2018a) identified fourLIA moraines in the Bhillangana and Dudhganga valleys, Garwal Himalaya, and the LopuKangri area, central Gangdise Mountains, respectively. Liu et al. (2017)found at least three LIA moraines in the Lhagoi Kangri Range, Karola Pass.Yang et al. (2003) found four cold phases during AD 1100–1150, 1500–1550,1650–1700, and 1800–1850 over TP and eastern China according to the proxydata of paleoclimate. A regional moraine chronologies framework composed of14C, lichenometry and cosmogenic radionuclide ages found threesubstages during late fourteenth, sixteenth to early eighteenth, andlate eighteenth to early nineteenth, corresponding to LIA-3, LIA-2, and LIA-1,respectively (Xu and Yi, 2014). However, the divergent number of LIAsubstages was also confirmed by some dating results and records. Forexample, only one moraine was dated in the Cogarbu valley (1484±44 CE;Table S1; Peng et al., 2019) and the Shi Mo valley (1514±69 CE; Table S1; Peng et al., 2020), but two substages were constrained in the Lato valley,Lahul Himalaya (Saha et al., 2018), Langtang Khola valley, Nepal Himalaya(Barnard et al., 2006), and the Gongotri Ganga valley, Garhwal Himalaya (Barnardet al., 2004). By applying dendroglaciology approach, Hochreuther et al. (2015) and Bräuning (2006) only detected one LIA substage in the Gongpuglacier, the Zepu glacier, the Baitong glacier, and the Gyalaperi glacier, while moresubstages were found in the Lhamcoka glacier (Bräuning, 2006), the Xinpu glacier(Hochreuther et al., 2015), the Gangapurna glacier, and the Annapurna III glacier(Sigdel et al., 2020). Yi et al. (2008) identified three substages during AD 950–1820 based on 5314C dating ages.
4.2 Why do four LIA substages exist in BH?
Clearly, the MC and GCM experiments (excluding the CESM experiment)indicate four glacial substages over BH during LIA. However, due to theindividualities of the glaciers (different slopes and lengths), this does not meanthat in each glacier in our study area there exist four LIA substages (Fig. 5a),consistent with the moraine dating results. Instead, it just reflects thatthe majority of glaciers in BH have four glacial substages. For example, inthe MC experiment, only about 33.8 % glaciers have four substages during theLIA, while the remaining glaciers have with zero (4.0 %), one (15.5 %), two(17.9 %), three (26.6 %), and five (2.2 %) substages. We argue thatthe difference in LIA substages is caused by the sensitivity of differentglaciers, even though many studies have ascribed it to the different climateconditions (Owen and Dortch, 2014; Murari et al., 2014; Saha et al., 2019).An analysis found that the number of glacial substages are significantly correlatedto the properties of the glacier (length and slope). The number glacial substageshas a significantly positive correlation with the glacier slopes andan obviously negative correlation with the glacier length (Fig. 5b and c).The correlation coefficient (CC) between the number of glacial substages andglacier length at 1950 is−0.31, and the CC between the number of glacialsubstages and glacier slope at 1950 is 0.41. Both of the CCs can pass a 95 %significance test. However, when zooming into the main glacial substagesnumbers (2, 3, 4), the relationship between the number of glacial substagesand the glacier length does not become that clear (Fig. 5b). Therefore, we arguethat the glacial slope may dominate the glacial substage numbers during LIA(Lüthi, 2009; Zekollari and Huybrechts, 2015; Bach et al., 2018; Eis etal., 2019). The negative correlation between the glacier length and glacialsubstage numbers might be a result of the fact that the longer (larger)glacier has a smaller slope (CC = −0.50). Moreover, the analysis also suggests aweak relationship between glacial substage numbers and glacialthe equilibrium-line altitude (ELA; Fig. 5d).
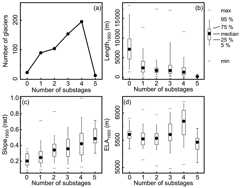
Figure 5(a) The identified glacial substage number distribution in the MCexperiment. The relationship between the identified glacial substages with(b) glacier length,(c) glacier slope, and(d) glacial ELA at 1950 in the MCexperiment.
The occurrence time of each glacial substage also varies between the glaciers,supported by the dispersal of moraine ages across the monsoonal Himalaya(Fig. 4b). Note that not all glaciers in BH reached their maximum peak GLRs during LIA-4,and taking a step back, even among the glaciers with the maximum peak GLR during LIA-4, theoccurrence times were also different (Fig. 6a). Statistically, about 48.1 % of glaciers experienced their maximum peak GLR during LIA-4 followed by 36.1 % of glaciersreaching their maximum peak GLR during LIA-1. Therefore, the occurrence time of maximum peak GLR at regionalscale is associated with the occurrence time of the majority of glaciersreaching their maximum peak GLRs. In addition, this can, in turn, explain the lack of somemoraines. Considering two glaciers both having four glacial substages butdifferent occurrence times of maximum GLR peak (one at LIA-4 and another at LIA-1) duringLIA, we might find four moraines for the glacier that reaches its maximum GLR peak at LIA-4but only one moraine for the other because the first three moraines aredestroyed by the last glacier advance. Similarly, this phenomenon alsoremains in the occurrence times of the second/third/fourth peak GLR (Fig. 6b–d).
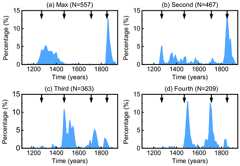
Figure 6Percentage of glaciers with(a) maximum peak GLR,(b) the second largest peak GLR,(c) thethird largest peak GLR, and(d) the fourth largest peak GLR over time in the MC experiment. The arrows representthe time of the four glacial substages, the 1270s (LIA-4), 1470s (LIA-3), 1710s(LIA-2), and 1850s (LIA-1).
In summary, four LIA glacial substages during the 1270s, 1470s, 1710s, and 1850swere found in BH based on the MC experiment. The maximum glacier extentappeared during LIA-4, which was confirmed by the moraine ages in the monsoonalinfluenced Himalaya. The regional glacial evolution is a collective effectof individual glacier changes. Four substages during LIA at the regionalscale does not guarantee that each individual glacier has four substages.Likewise, not all glaciers in BH reached their maximum peak GLRs during LIA-4. Instead, itonly represents the characteristics of most typical glaciers that accountedfor the vast majority of the total glaciers. This can explain why thereexist four substages in regional scale in the simulation, but it was difficultto capture in previous studies, which only focussed on one individual glacier. Thishelps us to thoroughly understand the relationship between regionalglacial evolution and the individual glacier response to climate change.
4.3 Climate-forcing mechanisms
The above discussions have explained why there are four glacial substages in BH,but the climatic mechanisms behind these substages described here are stillunclear. A better understanding of the possible forcing mechanism ofregional paleoglacier fluctuations at centennial timescales benefitsprojecting glacier outlooks in the future (Solomina et al., 2015). However,due to the limitations of field investigations, previous studies simplyascribed the glacier change to the temperature variation in themonsoon-influenced Himalaya by comparing the regional glacial sequences withtheδ18O record from Greenland and the Tibetan or North Atlantic (Penget al., 2019, 2020). As the model can explicitly link the glacier changeswith climate forcings (PDD scheme), which provides us with an opportunity toexplore this issue further.
Our study revealed that the regional glacial fluctuations are related to thetemperature changes rather than precipitation change (Figs. 4a and7a, b, d). Four cold intervals around the 1320s, 1510s, 1760s, and 1870s in theMC experiment corresponds to LIA-4 (1270s), LIA-3 (1470s), LIA-2 (1710s),and LIA-1 (1850s), respectively. However, this signal cannot be detected inprecipitation changes. Results from six GCM experiments also support thisargument, although with different times and strengths. The four cold intervalsduring the LIA in BH are forced by four large stratospheric sulfur-richexplosive eruptions events (sulfate aerosol loadings>60 Tg;Fig. 7c; Gao et al., 2008), as the volcanic aerosols will inject abundantaerosol into the upper atmosphere, cooling the climate (Schmidt et al.,2012). The beginning of oldest cold period (LIA-4) might have been forced by aseries of volcanic activities, including a massive tropical volcaniceruption in 1257, followed by three smaller eruptions in 1268, 1275, and 1284(Miller et al., 2012). The Billy Mitchell (1580), Huaynaputina(1600), Mount Parker (1641), Long Island (1660), and Laki (1783) volcanoes mayhave contributed to the cooling events during LIA-3 and LIA-2 (Jonathan, 2007).The 1815 eruption of Tambora and the 1883 eruption of Krakatau are believedto have promoted the youngest cold period of LIA (LIA-1; Rampino and Self, 1982).
Although temperature determines whether BH can run into a glacial substage,precipitation still has the ability to regulate the time of the glacieradvancing to its maximum in a glacial substage due to the fact that SMB isdetermined by the combination of temperature and precipitation, according tothe PDD scheme (Eq. 1; Marzeion et al., 2012; Maussion et al., 2019).Positive or negative SMB determines whether a glacier advances or retreats,and the amplitude of glacier change is directly influenced by the amplitudeof SMB change and the duration of the positive or negative SMB (Marzeion etal., 2012; Maussion et al., 2019; Figs. 4a and 7e). Four peaks of SMBwere found in the MC experiment, around the 1260s, 1460s, 1670s, and 1820s,corresponding to each substage. Stronger precipitation, associated withlarger SMB, at the beginning of the cold interval will drive the glacieradvance rapidly, shortening the time for it to reach its maximum extent. Inaddition, we also found that ELA has a good correlation of the SMB, which can beused as a proxy for SMB. ELA is the elevation where accumulation equalsablation for a certain glacier (Fig. 7f; Benn and Lehmkuhl, 2000; Heyman,2014). Four periods of ELA dropping around the 1270s (−132.2 m), 1470s (−115 m),1690s (−113.4 m), and 1820s (−112 m) were detected in the MC experiment,agreeing well with SMB change. This finding, to some extent, would benefitfield investigations, as paleo ELA is easily available, while paleo SMB is hardto measure.
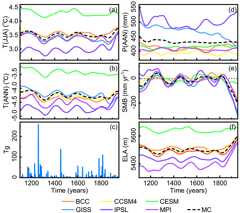
Figure 7The regional average(a) summer temperature (T(JJA)),(b) annualtemperature (T(ANN)),(d) annual precipitation (P(ANN)),(e) SMB,(f) ELAfrom 1100 to 1950 CE at a decadal timescale.(c) Global stratosphericsulfate aerosol loadings (Gao et al., 2008).
The seasonal climate is believed to have a more important impact on glacierevolutions than the annual climate (Yan et al., 2020, 2021). We calculated theregional average monthly temperature, precipitation, cumulative SMBanomalies (relative to the 1950s) from the 1100s to the 1950s (Fig. 8a–c) in theMC experiment to investigate the effect of monthly climate changes onglacial fluctuation. Consistent with Fig. 7e, four significant periods of increaseof the monthly SMB changes around the 1270s, 1470s, 1710s, and 1850s areidentified (Fig. 8c) as a result of monthly temperature decreases (Fig. 8a). The monthly precipitation does not show any obvious change, expect for anabrupt increase in August (Fig. 8b). The abnormal increase of Augustprecipitation is polluted by the GISS climate dataset, which suffers fromlarge precipitation bias.

Figure 8The monthly(a) temperature,(b) precipitation, and(c) SMBchanges relative to the 1950s at a decadal timescale in the MC experiment. Thearrows in(a)–(c) represent the times of the four glacial substages, the 1270s(LIA-4), the 1470s (LIA-3), the 1710s (LIA-2), and the 1850s (LIA-1).(d) The monthlytemperature, precipitation, and SMB distribution in the 1950s. Sensitivity ofGLR to annual or seasonal(e) temperature and(d) precipitation.
Strong cumulative SMB change only occurs in JJA, despite the fact that the temperaturechange is distributed almost uniformly and precipitation varies slightly(excluding August) throughout the year. The pattern of seasonal SMB changeindicates that the summer temperature might dominate the annual cumulativeSMB. This is because JJA is the main ablation season of glaciers in themonsoon-influenced Himalaya due to a higher temperature (Fig. 8d). Areduction of summer temperature will not only decrease the number ofpositive degree days but also decrease the average temperature during thepositive degree days, resulting in the reduction in summer ablation (Eq. 1).Meanwhile, JJA is also the wettest season in the study area. Decreasingtemperature will lead to an increasing probability of solid precipitation,enhancing the accumulation. As the SMB is determined by the sum of ablationand the accumulation, the JJA SMB is largely increased. However, although thetemperature also decreases in DJF, more precipitation will not increasethe accumulation. Therefore, the SMB change is weak.
We also conducted a series of the sensitivity tests to examine the influenceof seasonal temperature or precipitation on BH glacier change (Fig. 8e and f).Glaciers retreat gradually as a response to the temperature increases orprecipitation decreases. The sensitivity of glaciers totemperature or precipitation changes – in the form of the rate of change forGLR per∘C or % respectively – is the highest for unmodifiedtemperature or precipitation and decreases as they are varied further from thevalues given in the historical climate runs. The average GLR changing ratesare−160.1 % ∘C−1 and 4.0 % %−1 for annual temperature andprecipitation changes, respectively. The maximal sensitivity at unmodifiedtemperature/precipitation is the expected case due to the negative feedbackmechanism of changing ELA as glacier length changes. Glaciers are mostsensitive to summer temperature changes, with an average change rate of 110.4 % ∘C−1, followed by autumn (51.6 % ∘C−1) and spring (25.2 % ∘C−1). Glaciers are not sensitive to winter temperature changes(0.0 % ∘C−1), which supports the results in Fig. 8c. This indicatesthat the temperature changes in warm seasons, especially in summer, explainthe most variance of GLR changes. Fixing temperature, the sensitivity ofglaciers to precipitation changes is higher in spring (2.4 % %−1),followed by autumn (1.1 % %−1), summer (0.4 % %−1), and winter (0.4 % %−1). Therefore, the precipitation changes in spring and autumn hasa larger influence on glacier evolution. In order to compare the relativesensitivity of temperature and precipitation to glacier change, weintroduced an index, which is a measure of howmuch precipitation changes in response to temperature changes at present(Jeevanjee and Romps, 2018). This is an index only related to the localclimate and is about 1.7 % ∘C−1 in the MC experiment. From oursensitivity tests, we need ak=53.0 % ∘C−1 tomaintain the LIA glacier pattern (GLR = 60.6 %), which is much largerthan local climatek, indicating that the temperature dominates the LIA glacialfluctuation in BH.
In summary, seasonal analysis and sensitivity tests indicate that the changein temperature, especially summer temperature, is the dominant forcingfactor for glacier changes during the LIA (suborbital scale) in monsoonalinfluenced Himalaya. In contrast, the impact of precipitation change islimited. This conclusion has been drawn by Yan et al. (2020, 2021) atorbital scales but can now be extended to the suborbital scale. Inaddition, we also found that the temperature changes during LIA are closelyrelated to volcanic activities (Gao et al., 2008; Miller et al., 2012;Schmidt et al., 2012).
We simulated the glacial evolution across BH during LIA using the coupledmass balance and ice flow model, OGGM. Compared with the geomorphologicalmaps and moraine ages, OGGM broadly captures the pattern of glacier lengthchange. The regional pattern of glacier changes is the collective effect ofeach glacier. The dispersal of the observations could be reproduced by themodel due to the individualities of each glacier. On the regional scale,four LIA substages were identified at about the 1270s, 1470s, 1710s, and 1850s(from LIA-4 to LIA-1) in the MC experiment. The most extensive glacialadvances occurred during LIA-4, which is consistent with regional glacialchronological and geomorphic evidence. The number of glacial substages forindividual glaciers has a positive correlation with glacier slope. Theregional glacier advances are dominated by the reduction of summer ablation.
Although limitations still exist in the simulations, such as the applicationof OGGM on individual glacier changes, this study presented the firstsimulation of submillennium glacial evolutions during LIA in BH usingOGGM. We found a testable relationship between seasonal climate change andglacier expansion, explained the dispersal of moraine ages, and revealed thereasons for the four glacial substages during LIA in BH. Our findings linkthe limited observations with the model simulations and provides importantinsights into the climate forcing mechanism on glacier change at the centennialtimescale.
Code to run OGGM v1.5.0 is available athttps://doi.org/10.5281/zenodo.4765924 (Maussion et al., 2021). The extent of LIA glaciers is available athttps://doi.org/10.5281/zenodo.7033379 (Yang et al., 2022). The10Be surface exposure ages and the related references are listed in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-16-3739-2022-supplement.
Study concept devised by WC. WY performed the modelruns and analysis and wrote the original draft. YL and GL reviewed andrevised the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the Second Tibetan PlateauScientific Expedition and Research (STEP; grant no. 2019QZKK0205) and theNational Natural Science Foundation (NSFC; grant nos. 41771005, 41371082). Weare grateful to Atle Nesje, Julia Eis, David Parkes, and one anonymousreferee for their constructive comments/suggestions that help us a lot toimprove the quality of the paper.
This research has been supported by the Second Tibetan Plateau Scientific Expedition and Research (STEP; grant no. 2019QZKK0205) and the National Natural Science Foundation of China, Innovative Research Group Project of the National Natural Science Foundation of China (grant nos. 41771005 and 41371082).
This paper was edited by Ben Marzeion and reviewed by Julia Eis, Atle Nesje, David Parkes, and one anonymous referee.
Bach, E., Radić, V., and Schoof, C.: How sensitive are mountain glaciersto climate change? Insights from a block model, J. Glaciol., 64, 247–258,https://doi.org/10.1017/jog.2018.15, 2018.
Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J.: A complete and easilyaccessible means of calculating surface exposure ages or erosion rates from10Be and26Al measurements, Quat. Geochronol., 3, 174–195,https://doi.org/10.1016/j.quageo.2007.12.001, 2008.
Barnard, P. L., Owen, L. A., Sharma, M. C., and Finkel, R. C.: Late Quaternary(Holocene) landscape evolution of a monsoon-influenced high Himalayanvalley, Gori Ganga, Nanda Devi, NE Garhwal, Geomorphology, 61, 91–110,https://doi.org/10.1016/j.geomorph.2003.12.002, 2004.
Barnard, P. L., Owen, L. A., Finkel, R. C., and Asahi, K.: Landscape responseto deglaciation in a high relief, monsoon-influenced alpine environment,Langtang Himal, Nepal, Quaternary. Sci. Rev., 25, 2162–2176,https://doi.org/10.1016/j.quascirev.2006.02.002, 2006.
Benn, D. I. and Lehmkuhl, F.: Mass balance and equilibrium-line altitudes ofglaciers in high-mountain environments, Quatern. Int., 65/66, 15–29,https://doi.org/10.1016/S1040-6182(99)00034-8, 2000.
Bräuning, A.: Tree-ring evidence of “Little Ice Age” glacier advances insouthern Tibet, Holocene, 16, 369–380,https://doi.org/10.1191/0959683606hl922rp,2006.
Bueler, E. and Brown, J.: Shallow shelf approximation as a “sliding law”in a thermo mechanically coupled ice sheet model, J. Geophys. Res-Earth., 114, F03008,https://doi.org/10.1029/2008JF001179, 2009.
Carrivick, J. L., Boston, C. M., King, W., James, W. H., Quincey, D. J., Smith,M. W., Grimes, M., and Evans, J.: Accelerated volume loss in glacier ablationzones of NE Greenland, Little Ice Age to present, Geophys. Res. Lett., 46, 1476–1484,https://doi.org/10.1029/2018GL081383, 2019.
Chandler, B. M. P., Boston, C. M., and Lukas, S.: A spatially-restrictedYounger Dryas plateau icefield in the Gaick, Scotland: Reconstruction andpalaeoclimatic implications, Quaternary. Sci. Rev., 211, 107–135,https://doi.org/10.1016/j.quascirev.2019.03.019, 2019.
Chen, W., Yao, T., Zhang, G., Li, F., Zheng, G., Zhou, Y., and Xu, F.: Towards ice-thickness inversion: an evaluation of global digital elevation models (DEMs) in the glacierized Tibetan Plateau, The Cryosphere, 16, 197–218,https://doi.org/10.5194/tc-16-197-2022, 2022.
Chevalier, M.-L., Hilley, G., Tapponnier, P., Woerd, J. V. D., Liu-Zeng, J.,Finkel, R. C., Ryerson, F. J., Li, H., and Liu, X.: Constraints on the lateQuaternary glaciations in Tibet from cosmogenic exposure ages of moraineages, Quaternary. Sci. Rev., 30, 528–554,https://doi.org/10.1016/j.quascirev.2010.11.005, 2011.
Dixit, A., Sahany, S., and Kulkarni, A. V.: Glacial changes over theHimalayan Beas basin under global warming, J. Environ. Manage., 295, 113101,https://doi.org/10.1016/j.jenvman.2021.113101, 2021.
Dong, G., Zhou, W., Yi, C., Fu, Y., Zhang, L., and Li, M.: The timing andcause of glacial activity during the last glacial in central Tibet based on10Be surface exposure dating east of Mount Jagang, the Xianza range,Quaternary. Sci. Rev., 186, 284–297,https://doi.org/10.1016/j.quascirev.2018.03.007, 2018.
Dortch, J. M., Owen, L. A., and Caffee, M. W.: Timing and climatic drivers forglaciation across semi-arid western Himalayan-Tibetan orogen, Quaternary. Sci. Rev., 78, 188–208,https://doi.org/10.1016/j.quascirev.2013.07.025, 2013.
Eis, J., Maussion, F., and Marzeion, B.: Initialization of a global glacier model based on present-day glacier geometry and past climate information: an ensemble approach, The Cryosphere, 13, 3317–3335,https://doi.org/10.5194/tc-13-3317-2019, 2019.
Farinotti, D., Brinkerhoff, D. J., Clarke, G. K. C., Fürst, J. J., Frey, H., Gantayat, P., Gillet-Chaulet, F., Girard, C., Huss, M., Leclercq, P. W., Linsbauer, A., Machguth, H., Martin, C., Maussion, F., Morlighem, M., Mosbeux, C., Pandit, A., Portmann, A., Rabatel, A., Ramsankaran, R., Reerink, T. J., Sanchez, O., Stentoft, P. A., Singh Kumari, S., van Pelt, W. J. J., Anderson, B., Benham, T., Binder, D., Dowdeswell, J. A., Fischer, A., Helfricht, K., Kutuzov, S., Lavrentiev, I., McNabb, R., Gudmundsson, G. H., Li, H., and Andreassen, L. M.: How accurate are estimates of glacier ice thickness? Results from ITMIX, the Ice Thickness Models Intercomparison eXperiment, The Cryosphere, 11, 949–970,https://doi.org/10.5194/tc-11-949-2017, 2017.
Farinotti, D., Huss, M., Fürst, J. J., Landmann, J., Machguth, H.,Maussion, F., and Pandit, A.: A consensus estimate for the ice thicknessdistribution of all glaciers on Earth, Nat. Geosci., 12, 168–173,https://doi.org/10.1038/s41561-019-0300-3, 2019.
Fu, P., Stroeven, A. P., Harbor, J. M., Hättestrand, C., Heyman, J.,Caffee, M. W., and Zhou, P.: Paleoglaciation of Shaluli Shan, southeasternTibetan Plateau, Quaternary. Sci. Rev., 64, 121–135,https://doi.org/10.1016/j.quascirev.2012.12.009, 2013.
Furian, W., Maussion, F., and Schneider, C.: Projected 21st-Century GlacialLake Evolution in High Moutain Asia, Front. Earth. Sci., 10, 821798,https://doi.org/10.3389/feart.2022.821798, 2022.
Gao, C., Robock, A., and Ammann, C.: Volcanic forcing of climate over the past1500 years: An improved ice core-based index for climate models, J. Geophys. Res., 113,D23111,https://doi.org/10.1029/2008JD010239, 2008.
Goosse, H., Barriat, P.-Y., Dalaiden, Q., Klein, F., Marzeion, B., Maussion, F., Pelucchi, P., and Vlug, A.: Testing the consistency between changes in simulated climate and Alpine glacier length over the past millennium, Clim. Past, 14, 1119–1133,https://doi.org/10.5194/cp-14-1119-2018, 2018.
Greve, R.: A continuum-mechanical formulation for shallow polythermal icesheets, Philos. T.R. Soc. A., 355, 921–974,https://doi.org/10.1175/1520-0442(1997)010<0901:AOAPTD>2.0.CO;2, 1997a.
Greve, R.: Application of a polythermal three-dimensional ice sheet model tothe Greenland ice sheet: Response to steady-state and transient climatescenarios, J. Climate, 10, 901–918,https://doi.org/10.1098/rsta.1997.0050, 1997b.
Grove, J. M.: Little Ice Age, 2 edn., Routledge,https://doi.org/10.4324/9780203402863, 2013.
Harris, I., Osborn, T. J., Jones, P., and Lister, D.: Version 4 of the CRU TSmonthly high-resolution gridded multivariate climate dataset, Sci. Data, 7, 109, 109,https://doi.org/10.1038/s41597-020-0453-3, 2020.
Heyman, J.: Paleoglaciation of the Tibetan Plateau and surrounding mountainsbased on exposure ages and ELA depression estimates, Quaternary. Sci. Rev., 91, 30–41,https://doi.org/10.1016/j.quascirev.2014.03.018, 2014.
Heyman, J., Stroeven, A. P., Harbor, J. M., and Caffee, M. W.: Too young or tooold: Evaluating cosmogenic exposure dating based on an analysis of compiledboulder exposure ages, Earth. Planet. Sc. Lett., 302, 71–80,https://doi.org/10.1016/j.epsl.2010.11.040, 2011.
Hochreuther, P., Loibl, D., Wernicke, J., Zhu, H., Grießinger, J., andBräuning, A.: Ages of major Little Ice Age glacier fluctuations on thesoutheast Tibetan Plateau derived from tree-ring-based moraine dating,Palaeogeogr. Palaeocl., 422, 1–10,https://doi.org/10.1016/j.palaeo.2015.01.002, 2015.
Jarvis, A., Reuter, H., Nelson, A., and Guevara, E.: Hole-filledSRTM for theglobe Version 4, CGIAR Consortium for Spatial Inf ormation, University ofTwente, 2008.
Jeevanjee, N. and Romps, D. M.: Mean precipitation change from a deepeningtroposphere, P. Natl. Acad. Sci. USA, 115, 11465–11470,https://doi.org/10.1073/pnas.1720683115,2018.
Jonathan, C.: Climate change: biological and human aspects, CambridgeUniversity Press, 164, ISBN 978-0-521-69619-7, 2007.
Lifton, N., Sato, T., and Dunai, T. J.: Scaling in situ cosmogenic nuclideproduction rates using analytical approximations to atmospheric cosmic-rayfluxes, Earth. Planet. Sc. Lett., 386, 149–160,https://doi.org/10.1016/j.epsl.2013.10.052, 2014.
Lipscomb, W. H., Price, S. F., Hoffman, M. J., Leguy, G. R., Bennett, A. R., Bradley, S. L., Evans, K. J., Fyke, J. G., Kennedy, J. H., Perego, M., Ranken, D. M., Sacks, W. J., Salinger, A. G., Vargo, L. J., and Worley, P. H.: Description and evaluation of the Community Ice Sheet Model (CISM) v2.1, Geosci. Model Dev., 12, 387–424,https://doi.org/10.5194/gmd-12-387-2019, 2019.
Liu, J., Yi, C., Li, Y., Bi, W., Zhang, Q., and Hu, G.: Glacial fluctuationsaround the Karola Pass, eastern Lhagoi Kangri Range, since the Last GlacialMaximum, J. Quaternary. Sci., 32, 516–527,https://doi.org/10.1002/jqs.2946, 2017.
Lüthi, M. P.: Transient response of idealized glaciers to climatevariations, J. Glaciol., 55, 918–903,https://doi.org/10.3189/002214309790152519,2009.
Marzeion, B., Jarosch, A. H., and Hofer, M.: Past and future sea-level change from the surface mass balance of glaciers, The Cryosphere, 6, 1295–1322,https://doi.org/10.5194/tc-6-1295-2012, 2012.
Maussion, F., Butenko, A., Champollion, N., Dusch, M., Eis, J., Fourteau, K., Gregor, P., Jarosch, A. H., Landmann, J., Oesterle, F., Recinos, B., Rothenpieler, T., Vlug, A., Wild, C. T., and Marzeion, B.: The Open Global Glacier Model (OGGM) v1.1, Geosci. Model Dev., 12, 909–931,https://doi.org/10.5194/gmd-12-909-2019, 2019.
Maussion, F., Roth, T., Dusch, M., Recinos, B., Vlug, A., Champollion, N., Marzeion, B., Schuster, L., Oberrauch, M., Landmann, J., Eis, J.,Jarosch, A., sarah-hanus, Li, F., Rounce, D., Castellani, M., Bartholomew, S. L., Merrill, C., Loibl, D., Ultee, L., Smith, S., anton-ub, and Gregor, P.: OGGM/oggm: v1.5.0 (v1.5.0), Zenodo [code],https://doi.org/10.5281/zenodo.4765924, 2021.
Miller, G. H., Geirsdttir, Á., Zhong, Y., Larsen, D. J., Otto-Bliesner,B. L., Holland, M. M., Bailey, D. A., Refsnider, K. A., Lehman, S. J., Southon,J. R., Anderson, C., Björnsson, H., and Thordarson, T.: Abrupt onse of theLittle Ice Age triggered by volcanism and sustained by sea-ice/oceanfeedbacks, Geophys. Res. Lett., 39, L02708,https://doi.org/10.1029/2011GL050168, 2012.
Murari, M. K., Owen, L. A., Dortch, J. M., Caffee, M. W., Dietsch, C., Fuchs,M., Haneberg, W. C., Sharma, M. C., and Townsend-Small, A.: Timing andclimatic drivers for glaciation across monsoon-influenced regions of theHimalayaneTibetan orogen, Quaternary. Sci. Rev., 88, 159–182,https://doi.org/10.1016/j.quascirev.2014.01.013, 2014.
Oerlemans, J., Anderson, B., Hubbard, A., Huybrechts, Ph., Jóhannesson,T., Knap, W. H., Schmeits, M., Stroeven, A. P., van de Wal, R. S. W., and Zuo,Z.: Modelling the response of glaciers to climate warming, Clim. Dynam., 14, 267–274,https://doi.org/10.1007/s003820050222, 1998.
Owen, L. A.: Latest Pleistocene and Holocene glacier fluctuations in theHimalaya and Tibet, Quaternary. Sci. Rev., 28, 2150–2164,https://doi.org/10.1016/j.quascirev.2008.10.020, 2009.
Owen, L. A. and Dortch, J. M.: Nature and timing of Quaternary glaciation inthe Himalayan-Tibetan orogen, Quaternary. Sci. Rev., 88, 14–54,https://doi.org/10.1016/j.quascirev.2013.11.016, 2014.
PAGES 2k-PMIP3 group: Continental-scale temperature variability in PMIP3 simulations and PAGES 2k regional temperature reconstructions over the past millennium, Clim. Past, 11, 1673–1699,https://doi.org/10.5194/cp-11-1673-2015, 2015.
Parkes, D. and Goosse, H.: Modelling regional glacier length changes over the last millennium using the Open Global Glacier Model, The Cryosphere, 14, 3135–3153,https://doi.org/10.5194/tc-14-3135-2020, 2020.
Pelto, B. M., Maussion, F., Menounos, B., Radić, V., and Zeuner, M.:Bias-corrected estimates of glacier thickness in the Columbia River Basin,Canada, J. Glaciol., 66, 1051–1063,https://doi.org/10.1017/jog.2020.75, 2020.
Peng, X., Chen Y., Liu, G., Liu, B., Li, Y., Liu, Q., Han, Y., Yang, W., andCui, Z.: Late Quaternary glaciations in the Cogarbu valley, BhutaneseHimalaya, J. Quaternary. Sci., 34, 40–50,https://doi.org/10.1002/jqs.3079, 2019.
Peng, X., Chen, Y., Li, Y., Liu, B., Liu, Q., Yang, W., and Liu, G.: LateHolocene glacier fluctuations in the Bhutanese Himalaya, Global. Planet. Change, 187, 103137,https://doi.org/10.1016/j.gloplacha.2020.103137, 2020.
Pronk, J. B., Bolch, T., King, O., Wouters, B., and Benn, D. I.: Contrasting surface velocities between lake- and land-terminating glaciers in the Himalayan region, The Cryosphere, 15, 5577–5599,https://doi.org/10.5194/tc-15-5577-2021, 2021.
Qiao, B. and Yi, C.: Reconstruction of Little Ice Age glacier area andequilibrium line attitudes in the central and western Himalaya, Quatern. Int., 444, 65–75,https://doi.org/10.1016/j.quaint.2016.11.049, 2017.
Qureshi, M. A., Li, Y., Yi, C., and Xu, X.: Glacial changes in the HunzaBasin, western Karakoram, since the Little Ice Age, Palaeogeogr. Palaeocl., 562, 110086,https://doi.org/10.1016/j.palaeo.2020.110086, 2021.
Rampino, M. R. and Self, S.: Historic Eruptions of Tambora (1815), Krakatau(1883), and Agung (1963), their Stratospheric Aerosols, and Climatic Impact,Quatern. Res., 18, 127–143,https://doi.org/10.1016/0033-5894(82)90065-5, 1982.
RGI Consortium: Randolph Glacier Inventory (RGI)-A Dataset of GlobalGlacier Outlines: Version 6.0,https://doi.org/10.7265/N5-RGI-60, 2017.
Saha, S., Owen, L. A., Orr, E. N., and Caffee, M. W.: Timing and nature ofHolocene glacier advances at the northwestern end of the Himalayan-Tibetanorogen, Quaternary. Sci. Rev., 187, 177–202,https://doi.org/10.1016/j.quascirev.2018.03.009, 2018.
Saha, S., Owen, L. A., Orr, E. N., and Caffee, M. W.: High-frequency Holoceneglacier fluctuations in the Himalayan-Tibetan orogen, Quaternary Sci. Rev., 220, 372–400,https://doi.org/10.1016/j.quascirev.2019.07.021, 2019.
Schmidt, G. A., Jungclaus, J. H., Ammann, C. M., Bard, E., Braconnot, P., Crowley, T. J., Delaygue, G., Joos, F., Krivova, N. A., Muscheler, R., Otto-Bliesner, B. L., Pongratz, J., Shindell, D. T., Solanki, S. K., Steinhilber, F., and Vieira, L. E. A.: Climate forcing reconstructions for use in PMIP simulations of the last millennium (v1.0), Geosci. Model Dev., 4, 33–45,https://doi.org/10.5194/gmd-4-33-2011, 2011.
Shafeeque, M. and Luo, Y.: A multi-perspective approach for selecting CMIP6scenarios to project climate change impacts on glacio-hydrology with a casestudy in Upper Indus River basin, J. Hydrol., 599, 126466,https://doi.org/10.1016/j.jhydrol.2021.126466, 2021.
Sigdel, S.R., Zhang, H., Zhu, H., Muhammad, S., and Liang, E.: Retreatingglacier and advancing forest over the past 200 years in the CentralHimalayas, J. Biogeogr., 125, e2020JG005751.https://doi.org/10.1029/2020JG005751, 2020.
Solomina, O. N., Bradley, R. S., Hodgson, D. A., Ivy-Ochs, S., Jomelli, V.,Mackintosh, A. N., Nesje, A., Owen, L. A., Wanner, H., Wiles, G. C., and Young,N. E.: Holocene glacier fluctuations, Quaternary. Sci. Rev., 111, 9–34,https://doi.org/10.1016/j.quascirev.2014.11.018, 2015.
Taylor, K., Stouffer, R., and Meehl, G.: An Overview of CMIP5 and theExperiment Design, B. Am. Meteorol. Soc., 93, 485–498,https://doi.org/10.1175/BAMS-D-11-00094.1,2012.
WGMS: Fluctuations of Glaciers Database, World Glacier Monitoring Service, Zurich, Switzerland,https://doi.org/10.5904/wgms-fog-2021-05, 2021.
Winkelmann, R., Martin, M. A., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., and Levermann, A.: The Potsdam Parallel Ice Sheet Model (PISM-PIK) – Part 1: Model description, The Cryosphere, 5, 715–726,https://doi.org/10.5194/tc-5-715-2011, 2011.
Xu, X. and Yi, C.: Little Ice Age on the Tibetan Plateau and its borderingmountains: Evidence from moraine chronologies, Global. Planet. Change., 116, 41–53,https://doi.org/10.1016/j.gloplacha.2014.02.003, 2014.
Yan, Q., Owen, L. A., Wang, H., and Zhang, Z.: Climate constraints onglaciation over High-Mountain Asia during the last glacial maximum,Geophys. Res. Lett., 45, 9024–9033,https://doi.org/10.1029/2018GL079168, 2018.
Yan, Q., Owen, L. A., Zhang, Z., Jiang, N., and Zhang, R.: Deciphering theevolution and forcing mechanisms of glaciation over the Himalayan-Tibetanorogen during the past 20,000 years, Earth. Planet. Sc. Lett., 541, 116295,https://doi.org/10.1016/j.epsl.2020.116295, 2020.
Yan, Q., Owen, L. A., Zhang, Z., Wang, H., Wei, T., Jiang, N., and Zhang,R.: Divergent evolution of glaciation across High-Mountain Asia during thelast four glacial-interglacial cycles, Geophys. Res. Lett., 48, e2021GL092411,https://doi.org/10.1029/2021GL092411, 2021.
Yang, B., Achim, B., and Shi, Y.: Late Holocene temperature fluctuations onthe Tibetan Plateau, Quaternary. Sci. Rev., 22, 2335–2344,https://doi.org/10.1016/S0277-3791(03)00132-X, 2003.
Yang, W., Li, Y., Liu, G., and Chu, W.: Mapped glacier region in BH during LIA, Zenodo [data set],https://doi.org/10.5281/zenodo.7033379, 2022.
Yi, C., Chen, H., Yang, J., Liu, B., Fu, P., Liu, K., and Li, S.: Review ofHolocene glacial chronologies based on radiocarbon dating in Tibet and itssurrounding mountains, J. Quaternary. Sci., 23, 533–543,https://doi.org/10.1002/jqs.1228,2008.
Zekollari, H. and Huybrechts, P.: On the climate–geometry imbalance,response time and volume–area scaling of an alpine glacier: insights from a3-D flow model applied to Vadret da Morteratsch, Switzerland, Ann. Glaciol., 56, 51–62,https://doi.org/10.3189/2015AoG70A921, 2015.
Zhang, Q., Yi, C., Dong, G., Fu, P., Wang, N., and Capolongo, D.: Quaternaryglaciations in the Lopu Kangri area, central Gangdise Mountains, southernTibetan Plateau, Quaternary. Sci. Rev., 201, 470–482,https://doi.org/10.1016/j.quascirev.2018.10.027, 2018a.
Zhang, Q., Yi, C., Fu, P., Wu, Y., Liu, J., and Wang, N.: Glacier change inthe Gangdise Mountains, southern Tibet, since the Little Ice Age,Geomorphology, 306, 51–63,https://doi.org/10.1016/j.geomorph.2018.01.002, 2018b.





