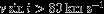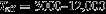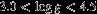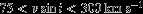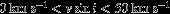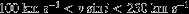1. INTRODUCTION
Stellar multiplicity is an inevitable and common outcome of star formation, with roughly half of all solar-type field stars in binary or multiple systems (Raghavan et al.2010) and an even higher fraction as the stellar mass increases (Zinnecker & Yorke2007). Young stellar associations and clusters tend to have even higher multiplicity (Duchêne & Kraus2013), indicating that stars often form in multiple systems that are subsequently destroyed by dynamical interactions as the cluster dissociates.
The overall multiplicity rate and the distributions of the mass ratio, period, and eccentricity of a binary star population place important constraints on the mode of binary star formation. While the period and eccentricity are altered by dynamical processing in the birth cluster, the present-day mass ratio of a binary system is a direct result of its formation (Parker & Reggiani2013). Most binary stars are thought to form via core fragmentation (Boss & Bodenheimer1979; Boss1986; Bate et al.1995), in which a collapsing core fragments into two or more individual protostars. The number and initial masses of the fragments are set by the total core mass, as well as its rotation, turbulence, and its temperature and density structure. If the fragments are well separated ( AU), they will evolve independently of each other, accreting mass from the core material onto their own protostellar disks and then onto the protostars themselves. However, close fragments (
AU), they will evolve independently of each other, accreting mass from the core material onto their own protostellar disks and then onto the protostars themselves. However, close fragments ( AU) will interact with each other; the protostellar disk may be truncated, destabilized, or form into a circumbinary disk if the separation is small enough (Bate & Bonnell1997). In addition, an unstable disk can fragment to form low-mass companions (Kratter & Matzner2006; Stamatellos & Whitworth2011). The mass ratios of close companions formed via either mechanism should be affected by preferential accretion. Most work has suggested that the disk material will preferentially accrete onto the lower mass companion (Bate & Bonnell1997; Bate et al.2002); however, recent work has indicated that magnetic disk braking may result in preferential accretion onto the more massive component (Zhao & Li2013) instead. In either case, we would expect to find a mass-ratio distribution for companions inside a few 100 AU that differs from that of companions on wider orbits where preferential accretion does not occur.
AU) will interact with each other; the protostellar disk may be truncated, destabilized, or form into a circumbinary disk if the separation is small enough (Bate & Bonnell1997). In addition, an unstable disk can fragment to form low-mass companions (Kratter & Matzner2006; Stamatellos & Whitworth2011). The mass ratios of close companions formed via either mechanism should be affected by preferential accretion. Most work has suggested that the disk material will preferentially accrete onto the lower mass companion (Bate & Bonnell1997; Bate et al.2002); however, recent work has indicated that magnetic disk braking may result in preferential accretion onto the more massive component (Zhao & Li2013) instead. In either case, we would expect to find a mass-ratio distribution for companions inside a few 100 AU that differs from that of companions on wider orbits where preferential accretion does not occur.
The mass ratio, period, and eccentricity distributions are well-known for solar-type stars (Duquennoy & Mayor1991; Raghavan et al.2010) and cooler stars (Fischer & Marcy1992; Delfosse et al.2004). Interestingly, Reggiani & Meyer (2011), and later Reggiani & Meyer (2013), found that the mass-ratio distribution of field solar-type and M-dwarf stars is invariant to separation. The field M-dwarf semimajor axis distribution peaks near ∼5 AU (Duchêne & Kraus2013), with very few companions at a separation the 27 stars used in the analysis by Reggiani & Meyer (2011) are insufficient to compare the mass-ratio distribution inside ∼100 AU with that outside it. However, the solar-type period distribution peaks near 45 AU (Raghavan et al.2010), with roughly 40% of binary systems on orbits wider than 100 AU. The nondetection of a difference in mass-ratio distribution is significant, although with only 30 stars in the field sample it is difficult to completely rule out that such a difference exists.
the 27 stars used in the analysis by Reggiani & Meyer (2011) are insufficient to compare the mass-ratio distribution inside ∼100 AU with that outside it. However, the solar-type period distribution peaks near 45 AU (Raghavan et al.2010), with roughly 40% of binary systems on orbits wider than 100 AU. The nondetection of a difference in mass-ratio distribution is significant, although with only 30 stars in the field sample it is difficult to completely rule out that such a difference exists.
All of the orbital distributions are much less certain for more massive stars. The reason for this is two-fold: first, more massive stars tend to be more distant than sunlike or low-mass stars, meaning many of the companions are angularly close to the primaries and difficult to detect with imaging techniques. Second, the primary stars tend to be rapid rotators, which limits radial velocity precision to and causes the spectral lines of double-lined systems to blend. Radial velocity monitoring can only measure a mass ratio if spectral lines from both components are visible and separable; this typically suffers from the same flux ratio difficulty as imaging techniques.
and causes the spectral lines of double-lined systems to blend. Radial velocity monitoring can only measure a mass ratio if spectral lines from both components are visible and separable; this typically suffers from the same flux ratio difficulty as imaging techniques.
Nonetheless, De Rosa et al. (2014) performed an adaptive optics imaging survey of nearby A-type stars, and found that the mass-ratio distribution is well-described by a power law with a large slope, indicating a very strong preference for low-mass companions. They also found initial evidence that the mass-ratio distribution for companions inside 125 AU has a much shallower power law slope than that of wide companions, and is consistent with being flat. Their close companion subsample contained only 18 binary systems, and the result is complicated by the inherent difficulty of detecting close companions with low mass ratios in an imaging survey.
Radial velocity monitoring surveys can detect much closer companions than imaging surveys, but are typically only complete to low-mass companions if the primary is a slow rotator. Chemically peculiar Am stars are typically associated with binary companions, and are slow rotators due to tidal braking; they thus form a highly biased sample of intermediate-mass stars. Nonetheless, it is interesting to note that they have a mass-ratio distribution which peaks near (Vuissoz & Debernardi2004), an entirely different form than the distribution found around chemically normal stars at wide separations.
(Vuissoz & Debernardi2004), an entirely different form than the distribution found around chemically normal stars at wide separations.
In this paper, we describe a spectroscopic survey of nearby chemically normal, main-sequence intermediate-mass stars ( ). We search for companions using the direct spectral detection technique (Gullikson et al.2016), which has a separation-invariant detection rate for all separations inside
). We search for companions using the direct spectral detection technique (Gullikson et al.2016), which has a separation-invariant detection rate for all separations inside . We describe the stellar sample and data used for the survey in Section2, as well as the data reduction steps. Next, we describe the direct spectral detection method and tabulate the companion detections in Section3. We estimate the mass and age of the sample stars in Section4, and discuss the survey completeness in Section5. Finally, we end with a derivation of the mass-ratio distribution from our sample in Section6 and discuss its implications for binary formation in Section7.
. We describe the stellar sample and data used for the survey in Section2, as well as the data reduction steps. Next, we describe the direct spectral detection method and tabulate the companion detections in Section3. We estimate the mass and age of the sample stars in Section4, and discuss the survey completeness in Section5. Finally, we end with a derivation of the mass-ratio distribution from our sample in Section6 and discuss its implications for binary formation in Section7.
2. OBSERVATIONS AND DATA REDUCTION
The stellar sample for this survey is defined by the following criteria:
- 1.
 mag.
mag. - 2.
 .
. - 3.Spectral type A or B with the following additional constraints
- i.Main sequence.
- ii.No spectral peculiarities except for “n,” which denotes broad lines.
The magnitude limit ensures that a sufficiently high signal-to-noise ratio (S/N) can be achieved in a short period of time. It does introduce a Malmquist bias in the derived mass ratio, which we discuss and correct for in Section6. Likewise, the limit makes accounting for the primary star spectrum in the companion search trivial; since most A- or B-type stars are rapid rotators, the cutoff removes less than half of the stars from the potential sample. We exclude pre-main-sequence stars because both the primary and the companion mass would depend very strongly on young and uncertain (
limit makes accounting for the primary star spectrum in the companion search trivial; since most A- or B-type stars are rapid rotators, the cutoff removes less than half of the stars from the potential sample. We exclude pre-main-sequence stars because both the primary and the companion mass would depend very strongly on young and uncertain ( Myr) evolutionary models. Finally, we exclude post-main-sequence stars from our sample because the binary flux ratio would be even less favorable to companion detection in an evolved star. Most of the spectral peculiarities denote narrow lines, which are already removed from the sample by the
Myr) evolutionary models. Finally, we exclude post-main-sequence stars from our sample because the binary flux ratio would be even less favorable to companion detection in an evolved star. Most of the spectral peculiarities denote narrow lines, which are already removed from the sample by the cut. The sample is given in Table1. The spectral type, coordinates, V-magnitude, and parallax are all adopted from the Simbad Database (Wenger et al.2000), while the stellar effective temperature, surface gravity, masses, and ages are discussed in Section4.
cut. The sample is given in Table1. The spectral type, coordinates, V-magnitude, and parallax are all adopted from the Simbad Database (Wenger et al.2000), while the stellar effective temperature, surface gravity, masses, and ages are discussed in Section4.
Table 1. Sample Properties
| star | SpT | R.A. | Decl. | V | parallax | Teff | 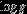 | Mass | Age | References |
|---|---|---|---|---|---|---|---|---|---|---|
| (mas) | (K) | (cgs) | (M⊙) | (Myr) | ||||||
| HIP 813 | B9Vn | 00:10:02.20 | +11:08:44.93 | 5.537 | 10.68 | 12,516 ± 426 | 4.3 ± 0.14 | 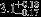 | 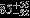 | (1) |
| HIP 1191 | B8.5V | 00:14:54.52 | -09:34:10.45 | 5.757 | 9.63 | 12,000 ± 1000 | 4.5 ± 0.25 | 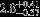 |  | (2) |
| HIP 1366 | A2V | 00:17:05.50 | +38:40:53.89 | 4.610 | 10.56 | 9371 ± 319 | 4.0 ± 0.14 | 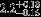 | 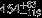 | (1) |
| HIP 1647 | B9V | 00:20:39.04 | −69:37:29.68 | 5.498 | 10.25 | 11,393 ± 387 | 4.0 ± 0.14 | 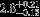 | 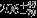 | (1) |
| HIP 2381 | A3V | 00:30:22.65 | −23:47:15.65 | 5.190 | 18.83 | 8364 ± 284 | 4.0 ± 0.14 | 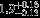 | 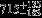 | (1) |
| HIP 2505 | B8Vn | 00:31:46.36 | +54:31:20.23 | 4.732 | 8.64 | 12,000 ± 1000 | 4.0 ± 0.25 | 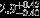 |  | (2) |
| HIP 2548 | B9.5 V | 00:32:23.78 | +06:57:19.66 | 5.698 | 12.35 | 11,864 ± 403 | 4.4 ± 0.14 |  | 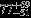 | (1) |
| HIP 3300 | B2V | 00:42:03.90 | +50:30:45.09 | 4.810 | 2.28 | 18,000 ± 1000 | 4.0 ± 0.25 |  |  | (2) |
| HIP 3478 | B5V | 00:44:26.19 | +47:51:50.34 | 5.646 | 5.23 | 18,000 ± 1000 | 4.5 ± 0.25 | 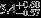 | 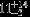 | (2) |
| HIP 5131 | A1Vn | 01:05:40.96 | +21:28:23.45 | 5.317 | 11.86 | 11,956 ± 406 | 4.4 ± 0.14 |  |  | (1) |
Notes. Spectral types, coordinates, V-band magnitudes, and parallax measurements are taken from the Simbad database; the spectral type given is that of the brightest star if part of a known multiple system. The “References” column denotes the reference for the stellar effective temperature, surface gravity, mass, and age.
References. (1) David & Hillenbrand2015; (2) this study.
Only a portion of this table is shown here to demonstrate its form and content. Amachine-readable version of the full table is available.
Download table as: DataTypeset image
The sample, being comprised of early-type stars, is heavily biased toward young stars. The estimated ages range from about 10 Myr to 1 Gyr, with most falling in the range of a few tens or hundreds of Myr. The sample also mostly contains nearby stars, although the magnitude limit provides a greater extent than a volume-limited survey would. The parallactic distances in our sample range from pc. The maximum detectable separation, which we define as the point at which the companion is no longer guaranteed to fall on the spectrograph slit (see Section2.1 for a description of the spectrographs we use), is
pc. The maximum detectable separation, which we define as the point at which the companion is no longer guaranteed to fall on the spectrograph slit (see Section2.1 for a description of the spectrographs we use), is . The median parallactic distance in our sample is 95 pc, corresponding to a projected separation of ∼200 AU. Most of the companions we are able to detect are close enough to have been impacted by the circumprimary disk, with 85% of the sample sensitive to companions inside 100 AU.
. The median parallactic distance in our sample is 95 pc, corresponding to a projected separation of ∼200 AU. Most of the companions we are able to detect are close enough to have been impacted by the circumprimary disk, with 85% of the sample sensitive to companions inside 100 AU.
2.1. Spectroscopic Data
We use several high spectral resolution, cross-dispersed échelle spectrographs for this survey. We use the CHIRON spectrograph (Tokovinin et al.2013) on the 1.5 m telescope at Cerro Tololo Inter-American Observatory for most southern targets. This spectrograph is an spectrograph with wavelength coverage from 450–850 nm, and is fed by a
spectrograph with wavelength coverage from 450–850 nm, and is fed by a optical fiber. The data are automatically reduced with a standard CHIRON data reduction pipeline, but the pipeline leaves residuals of strong lines in adjacent orders. We therefore bias-correct, flat-field, and extract the spectra with the optimum extraction technique (Horne1986) using standard IRAF3 tasks, and use the wavelength calibration from the pipeline reduced spectra.
optical fiber. The data are automatically reduced with a standard CHIRON data reduction pipeline, but the pipeline leaves residuals of strong lines in adjacent orders. We therefore bias-correct, flat-field, and extract the spectra with the optimum extraction technique (Horne1986) using standard IRAF3 tasks, and use the wavelength calibration from the pipeline reduced spectra.
For the northern targets, we use a combination of the High Resolution Spectrograph (HRS; Tull1998) on the Hobby-Eberly Telescope, and the Tull coudé (TS23; Tull et al.1995) and IGRINS (Park et al.2014) spectrographs, both on the 2.7 m Harlan J. Smith Telescope. All three northern instruments are at McDonald Observatory. For the HRS, we use theR = 60,000 setting with a fiber, and with wavelength coverage from 410–780 nm. We bias-correct, flat-field, and extract the spectra using an IRAF pipeline very similar to the one we use for the CHIRON data. The HRS spectra are wavelength-calibrated using a Th–Ar lamp observed immediately before or after the science observations.
fiber, and with wavelength coverage from 410–780 nm. We bias-correct, flat-field, and extract the spectra using an IRAF pipeline very similar to the one we use for the CHIRON data. The HRS spectra are wavelength-calibrated using a Th–Ar lamp observed immediately before or after the science observations.
For the TS23 spectrograph, we use a slit in combination with the E2 échelle grating (53 grooves/mm, blaze angle 65◦), yielding a resolving power ofR = 60,000 and a wavelength coverage from 375–1020 nm. We reduce the data using an IRAF pipeline very similar to the ones we use for CHIRON and HRS, and wavelength calibrate using a Th–Ar lamp observed immediately before the science observations.
slit in combination with the E2 échelle grating (53 grooves/mm, blaze angle 65◦), yielding a resolving power ofR = 60,000 and a wavelength coverage from 375–1020 nm. We reduce the data using an IRAF pipeline very similar to the ones we use for CHIRON and HRS, and wavelength calibrate using a Th–Ar lamp observed immediately before the science observations.
IGRINS has a single setting withR = 40,000. It has complete wavelength coverage from 1475–2480 nm, except in the telluric water band from 1810–1930 nm. Each star is observed in an ABBA nodding mode, and reduced using the standard IGRINS pipeline (Lee2015). The standard pipeline uses atmospheric OH emission lines as well as a Th–Ar calibration frame to calibrate the wavelengths; we further refine the wavelength solution using telluric absorption lines in the science spectrum.
After reducing the data, we fit and remove the telluric spectrum using the TelFit code (Gullikson et al.2014). We fit each échelle order affected by telluric absorption independently from each other to obtain the best removal. The telluric correction is critical for IGRINS spectra, where every order is dominated by telluric absorption lines. For the optical spectra, it is less critical but allows us to use some of the redder orders than we otherwise would be able to. For unsaturated lines, the best-fit telluric model reproduces the data to within ∼1%–5% of the continuum level.
We give the spectroscopic observation log in Table2. We calculate the S/N for the optical instruments (CHIRON, TS23, and HRS) as the median of the extracted flux divided by its uncertainty for each pixel from the échelle order nearest 675 nm. For the IGRINS instrument, we calculate the S/N from the order nearest 2200 nm.
Table 2. Spectroscopic Observation Log
| Star | MJD | Instrument | exptime | S/N |
|---|---|---|---|---|
| (JD-2450000) | (s) | |||
| HIP 813 | 6618.58 | TS23 | 557 | 1810 |
| HIP 1191 | 6552.60 | CHIRON | 1200 | 320 |
| HIP 1366 | 6585.73 | TS23 | 274 | 1790 |
| HIP 1647 | 6510.74 | CHIRON | 1105 | 630 |
| HIP 2381 | 6874.71 | CHIRON | 505 | 580 |
| HIP 2505 | 6586.71 | TS23 | 235 | 1700 |
| HIP 2505 | 6962.71 | TS23 | 804 | 1960 |
| HIP 2505 | 6945.71 | IGRINS | 224 | 210 |
| HIP 2548 | 7240.93 | IGRINS | 360 | 100 |
| HIP 2548 | 6516.84 | HRS | 412 | 1070 |
Note. See Section2.1 for details of the S/N calculation.
Only a portion of this table is shown here to demonstrate its form and content. Amachine-readable version of the full table is available.
Download table as: DataTypeset image
2.2. Imaging Data
As part of the follow-up effort, we used the NIRI instrument behind the Altair adaptive optics system on the Gemini North Telescope. For each star listed in Table3, we obtained 25 images in five dithering positions. We used the K-continuum band centered on and a variety of exposure times and dates (listed in Table3). Because the targets are all extremely bright, we used the high read noise and high flux detector settings to allow for very short co-add exposure times and to prevent saturation. We reduced the data using the Gemini set of IRAF tasks, which include steps for nonlinearity correction, flat-fielding, sky subtraction, and co-addition of the dither frames.
and a variety of exposure times and dates (listed in Table3). Because the targets are all extremely bright, we used the high read noise and high flux detector settings to allow for very short co-add exposure times and to prevent saturation. We reduced the data using the Gemini set of IRAF tasks, which include steps for nonlinearity correction, flat-fielding, sky subtraction, and co-addition of the dither frames.
Table 3. NIRI Observation Log
| Star | K | Date | Exposure | ρ | θ |  |  | a (AU) |
|---|---|---|---|---|---|---|---|---|
| HIP 22833 | 4.83 | 2015 Mar 29 | 50 × 0.3 | 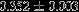 | 14.1 ± 0.7 | 3.04 ± 0.06 |  | 25.1 ± 0.24 |
| HIP 22958 | 5.79 | 2015 Oct 19 | 52 × 0.4 | 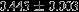 | 65.0 ± 0.3 | 2.57 ± 0.05 | 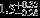 | 124.1 ± 0.81 |
| HIP 26093 | 5.96 | 2015 Mar 23 | 33 × 0.6 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 26126 | 5.07 | 2015 Mar 29 | 40 × 0.4 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 29735 | 5.10 | 2015 Mar 22 | 83 × 0.2 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 31278 | 5.46 | 2015 Mar 28 | 29 × 0.6 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 38538 | 4.66 | 2015 Oct 19 | 75 × 0.2 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 39847 | 4.66 | 2015 Mar 27 | 50 × 0.3 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 75178 | 5.49 | 2015 Mar 24 | 29 × 0.6 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 88116 | 4.47 | 2015 Mar 22 | 50 × 0.3 | 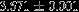 | 242.99 ± 0.02 | 3.9 ± 0.4 | 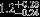 | 467.7 ± 0.18 |
| HIP 91118 | 5.67 | 2015 Oct 16 | 43 × 0.4 | 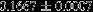 | 41.7 ± 0.2 | 1.77 ± 0.01 | 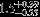 | 36.4 ± 0.16 |
| HIP 100221 | 5.70 | 2015 Oct 18 | 26 × 0.7 |  | 346.8 ± 0.92 | 2.28 ± 0.04 | 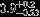 | 28.5 ± 0.24 |
| HIP 100907 | 5.41 | 2015 Oct 16 | 43 × 0.4 | 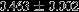 | 335.4 ± 0.30 | 2.91 ± 0.04 |  | 37.7 ± 0.16 |
| HIP 101909 | 6.47a | 2015 Oct 16 | 39 × 0.5 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 109139 | 4.40 | 2015 Apr 26 | 50 × 0.3 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 109521 | 4.96 | 2015 Apr 25 | 40 × 0.4 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| HIP 115115 | 4.96 | 2015 Oct 18 | 40 × 0.4 | 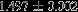 | 313.14 ± 0.08 | 2.54 ± 0.04 |  | 120.0 ± 0.17 |
Note.
aThere is no K-magnitude tabulated in the Simbad Database. The value quoted here is estimated from the spectral type of the star and its V-band magnitude.Amachine-readable version of the table is available.
Download table as: DataTypeset image
We measure the flux and position of both stars by fitting a 2D Moffat function (Moffat1969) to both stars simultaneously, constraining the shape parameters for both functions to be the same. The ratio of the amplitudes gives the magnitude difference, and the pixel locations along with the detector pixel scale gives the separation and position angle between the stars. We note that the goal of these images was confirmation and we did not observe any reference targets to make a distortion map and correct the image rotation. The uncertainty in position angle and to a lesser degree separation quoted in Table3 is likely underestimated.
3. COMPANION SEARCH
We search for stellar companions to our sample stars using the direct spectral detection technique, described in detail in Gullikson et al. (2016). In short, we unsharp-mask each spectrum using a Gaussian filter with width proportional to the primary star to remove the broad lines from the primary star. We then cross-correlate each échelle order of each filtered spectrum against a large grid of Phoenix model spectra (Husser et al.2013) with the following parameters:
to remove the broad lines from the primary star. We then cross-correlate each échelle order of each filtered spectrum against a large grid of Phoenix model spectra (Husser et al.2013) with the following parameters:
- 1.
 K, in steps of 100 K.
K, in steps of 100 K. - 2.[Fe/H] = −0.5, 0.0, +0.5.
- 3.
 .
.
In order to be sensitive to hot companions, we additionally cross-correlate the spectra against a second grid of Kurucz model spectra (Castelli & Kurucz2003). The change in model is necessary because the Phoenix model library does not extend beyond . The Kurucz grid is defined as follows:
. The Kurucz grid is defined as follows:
- 1.
 K, in steps of 1000 K.
K, in steps of 1000 K. - 2.[Fe/H] = −0.5, 0.0, +0.5.
- 3.
 .
.
We combine the cross-correlation functions (CCFs) for all orders using both a simple average and the maximum-likelihood weighting scheme (Zucker2003). A companion detection is denoted by a strong peak in the combined CCF. While the maximum-likelihood scheme produces detections with much higher significance, it also magnifies spurious peaks and so has a larger false-positive rate. For this reason, we use the simple average CCFs in all further analysis.
The peak height in the CCF as a function of the stellar model acts in a similar way to the more typical map of parameter space. More concretely, as the stellar model template approaches the true companion spectrum, the CCF peak becomes higher. We can therefore measure the companion temperature and, to a lesser degree its metallicity and
map of parameter space. More concretely, as the stellar model template approaches the true companion spectrum, the CCF peak becomes higher. We can therefore measure the companion temperature and, to a lesser degree its metallicity and , in a single spectrum. We calculate the measured temperature (Tm) and variance (
, in a single spectrum. We calculate the measured temperature (Tm) and variance ( ) as a weighted sum near the grid point with the highest CCF peak value, weighting by the peak CCF height at each temperature (Ci):
) as a weighted sum near the grid point with the highest CCF peak value, weighting by the peak CCF height at each temperature (Ci):


Typical uncertainties are on the order of 200 K. In the case of multiple observations for the same star, we use the variance-weighted mean of the individually measured temperatures.
Imperfect stellar models cause a bias between the true companion temperature and the measured temperature (Tm). This bias is most pronounced at low temperatures, where the difficult-to-model molecular absorption becomes important. We correct for the bias by applying the linear calibrations developed in Gullikson et al. (2016). These calibrations are only valid for companions with for detections at hotter temperatures we assume that the temperature which produces the maximum CCF peak is anunbiased estimator of the true companion temperature.
for detections at hotter temperatures we assume that the temperature which produces the maximum CCF peak is anunbiased estimator of the true companion temperature.
We list the companion detections in Table4, and report the estimate of the companion temperature, , and metallicity derived from the model parameters which produce the largest CCF peak. The
, and metallicity derived from the model parameters which produce the largest CCF peak. The and metallicity values do not have uncertainties and should only be taken as a rough estimate of the true value. The mean and standard deviation of the companion metallicities is −0.29 ± 0.30; the marginal bias toward low metallicities is most likely a measurement bias and does not reflect the true companion population (Gullikson et al.2016). We show the detection CCFs and a plot of peak CCF height as a function of model temperature for HIP 109139 in Figure1. Similar figures for all companions are available in the supplementary files.
and metallicity values do not have uncertainties and should only be taken as a rough estimate of the true value. The mean and standard deviation of the companion metallicities is −0.29 ± 0.30; the marginal bias toward low metallicities is most likely a measurement bias and does not reflect the true companion population (Gullikson et al.2016). We show the detection CCFs and a plot of peak CCF height as a function of model temperature for HIP 109139 in Figure1. Similar figures for all companions are available in the supplementary files.

Figure 1.
Left: CCFs between the observed spectra of HIP 109139 and a Phoenix model spectra. The detections on two dates show significant velocity variation, indicating orbital motion with a short period. Right: peak CCF height as a function of Phoenix model spectra template temperature. The maxima of the curves indicate the temperature of the companion. (The complete figure set (62 images) isavailable in the supplementary data.)
Download figure:
Standard imageHigh-resolution image
Figure 1.
Left: CCFs between the observed spectra of HIP 109139 and a Phoenix model spectra. The detections on two dates show significant velocity variation, indicating orbital motion with a short period. Right: peak CCF height as a function of Phoenix model spectra template temperature. The maxima of the curves indicate the temperature of the companion. (The complete figure set (62 images) isavailable in the supplementary data.)
Download figure:
Standard imageHigh-resolution imageTable 4. Companion Detections
| Star | Component | Nobs | Used in | Teff |  | [Fe/H] | Mass (M⊙) | |
|---|---|---|---|---|---|---|---|---|
| Analysis | (K) | (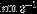 ) ) | (dex) | Isochrone | Spectral Type | |||
| HIP 2548 | Aa,Ab | 2 | yes | 5732 ± 112 | 30 | −0.5 |  |  |
| HIP 5348 | AB | 1 | no | 12,000 ± 1000 | 75 | 0.0 |  | 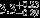 |
| HR 545 | Aa,Aba | 3 | yes | 4312 ± 87 | 5 | −0.5 |  |  |
| HR 604 | AB | 1 | no | 4736 ± 150 | 5 | 0.5 | 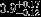 |  |
| HIP 10732 | ABa | 2 | yes | 5578 ± 109 | 5 | 0.0 | 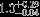 |  |
| HIP 12332 | ABa | 2 | yes | 5551 ± 107 | 10 | 0.0 |  |  |
| HIP 12706 | AB | 2 | yes | 6051 ± 107 | 10 | 0.0 |  | 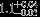 |
| HIP 13165 | Aa,Ab | 1 | no | 5773 ± 163 | 5 | −0.5 | 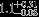 |  |
| HIP 13327 | ABa | 1 | yes | 5524 ± 150 | 5 | −0.5 | 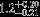 |  |
| HIP 14043 | Aa,Aba | 1 | yes | 11,500 ± 500 | 20 | 0.5 |  | 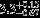 |
| HIP 14764 | ABa | 2 | yes | 5623 ± 150 | 5 | −0.5 | 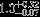 |  |
| HIP 16147 | AB | 1 | yes | 13,000 ± 1000 | 1 | 0.0 |  | 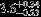 |
| HIP 16244 | AB | 2 | yes | 5592 ± 107 | 5 | −0.5 |  |  |
| HIP 16340 | ABa | 1 | yes | 6214 ± 150 | 5 | −0.5 | 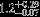 |  |
| HIP 16611 | AB | 1 | yes | 11,500 ± 1000 | 75 | 0.0 |  | 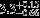 |
| HIP 19949 | ABa | 1 | yes | 6492 ± 155 | 20 | −0.5 |  | 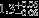 |
| HIP 20380 | ABa | 2 | yes | 6492 ± 109 | 20 | −0.5 | 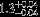 | 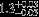 |
| HIP 21589 | Aa,Ab | 1 | yes | 4562 ± 154 | 5 | 0.0 | 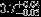 |  |
| HIP 22833 | AB | 2 | yes | 4745 ± 107 | 10 | 0.0 |  | 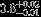 |
| HIP 22958 | Aa,Ab | 2 | yes | 5762 ± 158 | 30 | −0.5 | 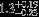 |  |
| HIP 23362 | ABa | 1 | yes | 6283 ± 158 | 5 | −0.5 | 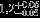 | 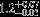 |
| HIP 24902 | AB | 1 | yes | 5679 ± 154 | 30 | 0.0 | 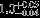 |  |
| HIP 26126 | AB? | 3 | yes | 5841 ± 91 | 5 | −0.5 |  | 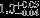 |
| HIP 28691 | AB | 1 | no | 15,000 ± 1000 | 1 | 0.5 | 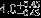 | 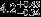 |
| HIP 28691 | AC | 1 | no | 12,000 ± 1000 | 1 | 0.5 | 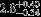 | 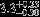 |
| HIP 32607 | ABa | 3 | yes | 5068 ± 91 | 5 | −0.5 |  | 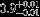 |
| HIP 37322 | AB | 1 | yes | 8157 ± 147 | 30 | −0.5 | 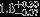 | 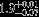 |
| HIP 37450 | ABa | 1 | yes | 16,000 ± 1000 | 30 | 0.0 | 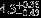 | 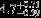 |
| HIP 38538 | AB | 1 | no | 6576 ± 150 | 75 | 0.0 |  | 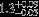 |
| HIP 38593 | ABa | 2 | yes | 5398 ± 112 | 5 | −0.5 |  | 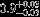 |
| HIP 38846 | ABa | 1 | yes | 6595 ± 158 | 10 | 0.0 | 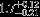 | 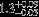 |
| HIP 39847 | Aa,Aba | 2 | no | 5750 ± 107 | 10 | −0.5 |  |  |
| HIP 40881 | ABa | 1 | yes | 4562 ± 154 | 10 | −0.5 |  | 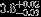 |
| HIP 42129 | AB | 1 | yes | 5241 ± 158 | 10 | −0.5 |  | 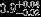 |
| HIP 46283 | AB? | 3 | yes | 9268 ± 85 | 10 | 0.5 |  |  |
| HIP 52678 | ABa | 2 | yes | 5033 ± 112 | 10 | −0.5 | 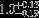 | 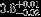 |
| HIP 63945 | AC | 1 | no | 7038 ± 162 | 10 | −0.5 | 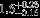 | 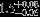 |
| HIP 72154 | ABa | 1 | yes | 4918 ± 162 | 30 | −0.5 |  | 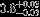 |
| HR 5605 | AB | 1 | no | 16,000 ± 1000 | 10 | 0.0 |  |  |
| HR 5605 | AC | 1 | no | 14,000 ± 1000 | 10 | 0.0 | 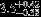 | 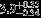 |
| HIP 74117 | AB | 1 | no | 14,000 ± 1000 | 10 | 0.0 |  | 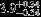 |
| HIP 76267 | AB | 1 | yes | 5449 ± 158 | 5 | −0.5 | 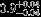 | 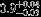 |
| HIP 77336 | ABa | 2 | yes | 6407 ± 112 | 20 | 0.0 | 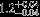 |  |
| HIP 77516 | AB | 1 | yes | 6825 ± 141 | 5 | 0.5 | 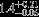 | 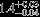 |
| HIP 78820 | AB | 1 | no | 5658 ± 158 | 5 | 0 |  | 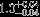 |
| HIP 78918 | AB | 1 | yes | 9000 ± 500 | 120 | −0.5 | 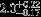 | 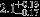 |
| HIP 79199 | AB | 1 | no | 4616 ± 158 | 5 | −0.5 |  |  |
| HIP 79404 | ABa | 2 | yes | 4773 ± 112 | 10 | −0.5 | 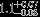 | 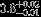 |
| HIP 80460 | AB | 1 | yes | 6391 ± 155 | 10 | 0.0 | 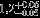 | 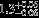 |
| HIP 82673 | ABa | 2 | yes | 4668 ± 112 | 5 | 0.5 |  | 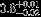 |
| HIP 84606 | AB | 1 | yes | 5476 ± 154 | 10 | −0.5 | 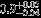 | 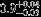 |
| HIP 88116 | ABa | 2 | yes | 5293 ± 112 | 5 | 0.0 | 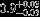 |  |
| HIP 88817 | Ba,Bba | 1 | yes | 3647 ± 154 | 20 | 0.0 |  |  |
| HIP 88818 | Aa,Ab | 3 | yes | 5296 ± 91 | 20 | −0.5 | 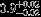 | 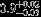 |
| HIP 91118 | AB | 1 | yes | 6492 ± 155 | 10 | −0.5 |  | 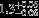 |
| HIP 93225 | AB | 2 | yes | 14,000 ± 700 | 10 | 0.5 | 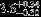 |  |
| HIP 93805 | Aa,Aba | 2 | yes | 4054 ± 109 | 5 | −0.5 |  |  |
| HIP 96840 | AB | 1 | yes | 9942 ± 152 | 10 | 0.0 | 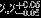 | 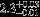 |
| HIP 100221 | AB | 1 | yes | 5273 ± 154 | 20 | −0.5 |  | 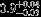 |
| HIP 100907 | ABa | 2 | yes | 5222 ± 109 | 10 | 0.0 |  | 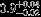 |
| HIP 103298 | Aa,Ab | 3 | yes | 4615 ± 90 | 5 | −0.5 |  | 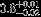 |
| HIP 109139 | AB | 2 | yes | 5710 ± 112 | 20 | −0.5 | 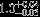 |  |
| HIP 109521 | Aa,Aba | 3 | yes | 4412 ± 87 | 10 | 0.0 | 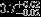 | 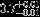 |
| HIP 115115 | AB | 3 | yes | 4943 ± 91 | 5 | −0.5 | 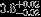 |  |
Note.
aNewly discovered companions.Amachine-readable version of the table is available.
We have follow-up spectroscopy for 15/23 of the new companions to confirm their existence. In most cases, there is a clear shift in the radial velocity of the companion, indicating that it is orbiting the target star and is not a foreground or background contaminant (See Figure1). Two of the new detections (companions to HIPs 38593 and 79404) were detected twice but not in a third attempt, most likely because the third spectrum had low S/N. The companion to HIP 93805, at ∼4000 K, was detected twice with near-infrared IGRINS but not the optical CHIRON instrument which is less sensitive to cool companions than IGRINS. Two of the companions with only one detection were observed at least twice (HIPs 19949 and HIP 23362); both of the non-detections are from the IGRINS instrument, which is less sensitive to hot companions with rapid rotation speeds because there are far fewer spectral lines of the companion in the near-infrared than there are in the optical.
In addition to the spectroscopic follow-up, we obtained Gemini/NIRI adaptive optics imaging data for 18 of the northern companions, and were able to resolve 7 of them. We show the separation, position angle, and magnitude difference measurements in Table3, and display the images in Figure2. We also derive the projected separation in AU and the companion mass from the images. We calculate the separation from the measured angular separation and the Hipparchos parallax (van Leeuwen2007). We calculate the companion mass and uncertainties from 1000 samples of the magnitude difference measurement and the primary star mass, temperature, age, and radius (see Section4). For each sample, we use a grid of Kurucz stellar model spectra (Castelli & Kurucz2003) and the pysynphot code4 to determine the companion temperature needed to replicate the observed magnitude difference. We estimate the companion radius by interpolating solar metallicity Dartmouth isochrones (Dotter et al.2008) from the companion temperature and system age sample. We convert the best temperature to a companion mass using the same isochrone grid. The masses derived from the imaging data have very large uncertainties because the primary star property estimates that they depend on are very uncertain. The imaging masses agree with the spectroscopically derived masses in Table4, with the exception of HIP 115115 which has a much higher mass from the imaging data than the spectroscopic data. The spectroscopic masses for all stars are more reliable, since they are less model-dependent.

Figure 2. Detection images for all stars in which we detect a companion in the follow-up NIRI data. There are several nearby sources for HIP 88116, none of which are the source we detect in the spectroscopic data (see Section3).
Download figure:
Standard imageHigh-resolution imageOne star in the imaging sample, HIP 88116, has several nearby sources in the image. We quote the magnitude difference and separation of the brightest source in Table3, but stress thatnone of the visible sources is likely to be the companion we see in the spectroscopic data. The two epochs of spectroscopic data show a radial velocity shift of over the course of roughly one year; this orbital motion is much too large to be consistent with any of the companions visible in the image (all with separations
over the course of roughly one year; this orbital motion is much too large to be consistent with any of the companions visible in the image (all with separations and projected separations
and projected separations AU).
AU).
4. SAMPLE STAR PARAMETERS
In order to convert from companion temperature to mass ratio, we first need an estimate of the primary mass. In addition, since the primary stars in our survey have short main-sequence lifetimes, some companions may still be contracting onto the main sequence and so an age estimate for the system is necessary to convert from companion temperature to mass.
About half of our sample stars have robust mass and age estimates from Strömgren uvbyβ photometry (David & Hillenbrand2015). For those that do not, we estimate the mass and age of the system from our spectra. We first cross-correlate the data against a grid of solar metallicity Kurucz model spectra (Castelli & Kurucz2003) spanning
- 1.
 in steps of
in steps of for
for , and in steps of
, and in steps of for hotter templates.
for hotter templates. - 2.
 in steps of 0.5 dex.
in steps of 0.5 dex. - 3.
 in steps of
in steps of .
.
For the optical data, we use the blue échelle orders ( ). We ignore the strong hydrogen Balmer lines in the spectrum because they span several échelle orders and make continuum normalization very difficult, potentially biasing the result. There are sufficient metal lines in the optical spectra that the resulting CCF always has a very strong peak at the radial velocity of the primary star. The near-infrared IGRINS spectra have very few strong metal lines; we use the subset from
). We ignore the strong hydrogen Balmer lines in the spectrum because they span several échelle orders and make continuum normalization very difficult, potentially biasing the result. There are sufficient metal lines in the optical spectra that the resulting CCF always has a very strong peak at the radial velocity of the primary star. The near-infrared IGRINS spectra have very few strong metal lines; we use the subset from that is dominated by hydrogren Brackett lines for these spectra. Similar to the companion search, we estimate the temperature and surface gravity of the stars from the CCF with the largest peak. We adopt the following errors on the temperature and surface gravity, which are based on the grid step size and are somewhat more pessimistic than typical uncertainties seen in the literature for A- and B-type stars (e.g., Aydi et al.2014; David & Hillenbrand2015):
that is dominated by hydrogren Brackett lines for these spectra. Similar to the companion search, we estimate the temperature and surface gravity of the stars from the CCF with the largest peak. We adopt the following errors on the temperature and surface gravity, which are based on the grid step size and are somewhat more pessimistic than typical uncertainties seen in the literature for A- and B-type stars (e.g., Aydi et al.2014; David & Hillenbrand2015):


The IGRINS parameters are less reliable because they rely almost solely on the hydrogren Brackett lines that span an entire échelle order, so we double the uncertainty on the IGRINS-derived temperature and surface gravity. Additionally, we throw out the IGRINS parameters if the star was also observed by one of the optical instruments in our survey. For stars observed multiple times, we use the average parameters and reduce the uncertainties accordingly.
Next, we use Padova stellar evolutionary tracks (Bressan et al.2012) and the isochrones code (Morton2015) to estimate the mass and age of the system from the measured temperature and surface gravity. As a consistency check, we also interpolate from a table of stellar properties as a function of spectral type (Pecaut & Mamajek2013) to estimate the primary mass from the published spectral types. We show the comparison in Figure3. We estimate uncertainties in the spectral-type mass by assuming a spectral-type uncertainty of ±0.5 spectral types and propagating to mass. There is excellent agreement between the masses we measure and the spectral-type masses.

Figure 3. Comparison of primary star masses derived from our cross-correlation analysis and Padova isochrones (Bressan et al.2012) with those expected from the published spectral type. There is excellent agreement between the two measures across the entire range of masses.
Download figure:
Standard imageHigh-resolution imageWe show the temperature, surface gravity, mass, and age estimates for most of our sample stars in Table1. We do not give parameters for the few stars that show strong discrepancies with the spectral-type estimate, most of which are early B-stars that have temperatures higher than the maximum grid temperature of 30,000 K.
5. SURVEY COMPLETENESS
The detectability of a companion mostly depends on its temperature: cooler companions emit much less light and so are increasingly lost in the Poisson noise from the primary star spectrum. A companion with a high rotation rate is also more difficult to detect because the CCF obtains most of its power from narrow spectral lines.
5.1. Injection and Recovery Tests
To quantify the detection rate as a function of companion temperature and , we performed a series of injection and recovery experiments. We started by creating synthetic binary star observations from each of our observed spectra. We made two distinct grids of companion stars: a low temperature grid spanning
, we performed a series of injection and recovery experiments. We started by creating synthetic binary star observations from each of our observed spectra. We made two distinct grids of companion stars: a low temperature grid spanning
- 1.
 in steps of
in steps of ;
; - 2.
 in steps of
in steps of ;
;
and a high temperature grid spanning
- 1.
 in steps of
in steps of ;
; - 2.
 in steps of
in steps of .
.
For each grid point, we added a solar metallicity Phoenix model spectrum to the observed data after scaling to replicate the expected flux between a main-sequence companion of the model temperature and the known target star spectral type. If the target star had known companions within , we included the expected flux from the companion when computing the flux ratio. We repeated each grid point at different radial velocities spanning
, we included the expected flux from the companion when computing the flux ratio. We repeated each grid point at different radial velocities spanning in
in steps to sample the noise properties of the spectra and estimate a probability of detection at each point.
steps to sample the noise properties of the spectra and estimate a probability of detection at each point.
Next, we cross correlated all of the synthetic observations against the Phoenix model template that was used to construct them. We counted the companion as detected if the highest point in the resulting CCF was found at the correct radial velocity, and if the peak had a significance of , whereσ is the standard deviation of the CCF for points more than
, whereσ is the standard deviation of the CCF for points more than away from the peak. We combined all of the radial velocity trials for each grid point to estimate a probability of detection at that grid point:
away from the peak. We combined all of the radial velocity trials for each grid point to estimate a probability of detection at that grid point:

where is the number of radial velocity trial points.
is the number of radial velocity trial points.
Finally, we interpolated between the grid points using a linear radial basis function interpolator (Figure4). In order to extrapolate from our grids to estimate the detection rate at high temperature and low and at low temperature and high
and at low temperature and high , we made the following assumptions about the shape of the two-dimensional detection rate surface. First, we assume that if no companions are detected at temperatureT and rotation speed
, we made the following assumptions about the shape of the two-dimensional detection rate surface. First, we assume that if no companions are detected at temperatureT and rotation speed , then no companions will be detected at the same temperature and faster rotation speeds (upper left points in Figure4). Likewise, we assumed that if all companions are detected at temperatureT = 6500 K and rotation speed
, then no companions will be detected at the same temperature and faster rotation speeds (upper left points in Figure4). Likewise, we assumed that if all companions are detected at temperatureT = 6500 K and rotation speed , then all companions with the same
, then all companions with the same and higher temperature will also be detected (lower right points in Figure4). The detection rate of hot companions is affected by two factors: the increased flux from the companion makes detection easier, while the decreasing number of spectral lines in the companion spectrum makes detection more difficult. If the latter factor is more important, then the assumption we made about the shape of the detection surface is incorrect. We therefore tested the assumption with a small subset of injection and recovery tests, and found that the second assumption we make is valid.
and higher temperature will also be detected (lower right points in Figure4). The detection rate of hot companions is affected by two factors: the increased flux from the companion makes detection easier, while the decreasing number of spectral lines in the companion spectrum makes detection more difficult. If the latter factor is more important, then the assumption we made about the shape of the detection surface is incorrect. We therefore tested the assumption with a small subset of injection and recovery tests, and found that the second assumption we make is valid.

Figure 4. Detection rate as a function of companion temperature and for HIP 24244. All companions that are shaded yellow are detectable, while companions in the purple region are never detectable. The grids of squares in the lower left and upper right show the low temperature and high temperature grid points we used in the sensitivity analysis. The remaining squares come from assumptions about the shape of the detection rate surface and allow us to fully interpolate (see text for details).
for HIP 24244. All companions that are shaded yellow are detectable, while companions in the purple region are never detectable. The grids of squares in the lower left and upper right show the low temperature and high temperature grid points we used in the sensitivity analysis. The remaining squares come from assumptions about the shape of the detection rate surface and allow us to fully interpolate (see text for details).
Download figure:
Standard imageHigh-resolution imageFigure4 shows a clear diagonal dividing line between hot, slow rotators that are always detected and cool, fast rotators that never are. Additionally the figure shows that very fast rotators are never detected, regardless of their temperature, because the signal is completely removed when we unsharp-mask the data (see Section3).
5.2. Marginalization
By sampling a suitable distribution of values for a star of each temperature, we marginalize over the rotation speed:
values for a star of each temperature, we marginalize over the rotation speed:

where is the surface plotted in Figure4 andvk are the samples from the distribution of
is the surface plotted in Figure4 andvk are the samples from the distribution of . For
. For K, we sample
K, we sample using the gyrochronology relation given in Barnes (2010):
using the gyrochronology relation given in Barnes (2010):

In Equation (7),kC andkI are constants fit to data with known ages and rotation periods,P andP0 are, respectively, the current and zero-age main-sequence rotation periods,τ is the convective turnover timescale, andt is the current age of the star. We use the same values that Barnes (2010) used for the constants:
- 1.kC = 0.646 day Myr−1;
- 2.
 day−1.
day−1.
We estimate the convective timescale (τ) by interpolating Table 1 of Barnes & Kim (2010). We then randomly draw a system aget from its probability distribution function (PDF) (see Section4 and Table1). Young stars have rotation periods in the range of 0.2–10 days (Bouvier et al.2014, p. 433), so we randomly choose an initial rotation periodP0 from a log-uniform distribution in this range for each age sample. Equation (7) then gives a current rotation period for each sample, which we convert to an equatorial velocity with the stellar radiusR. We estimateR by interpolating Dartmouth pre-main-sequence isochrones (Dotter et al.2008) using the companion temperature and system age. We finally convert to projected velocity by randomly sampling a uniform distribution for the inclination
by randomly sampling a uniform distribution for the inclination .
.
The gyrochronology relations are invalid for stars with , the canonical limit at which the convective zone is too small to efficiently remove angular momentum to the stellar wind and spin down the star (Pinsonneault et al.2001). Zorec & Royer (2012) fit Maxwellian distributions to the equatorial velocity of A- and B-type stars in several mass bins. For
, the canonical limit at which the convective zone is too small to efficiently remove angular momentum to the stellar wind and spin down the star (Pinsonneault et al.2001). Zorec & Royer (2012) fit Maxwellian distributions to the equatorial velocity of A- and B-type stars in several mass bins. For , we linearly interpolate the fit parameters as a function of mass and sample the resulting Maxwellian probability density function.
, we linearly interpolate the fit parameters as a function of mass and sample the resulting Maxwellian probability density function.
Typical velocities from the gyrochronology relationships are , while the Maxwellian velocity distributions have typical velocities
, while the Maxwellian velocity distributions have typical velocities . We transition between the two regimes for temperatures in the range
. We transition between the two regimes for temperatures in the range by first estimating the equatorial velocities from the gyrochronology relationship (Equation (7)) at
by first estimating the equatorial velocities from the gyrochronology relationship (Equation (7)) at . We then fit the velocities to a Maxwellian distribution, and add the result to the tabulated parameters from (Zorec & Royer2012). With the extended table, we treat stars in the transition range the same way we treat hot stars.
. We then fit the velocities to a Maxwellian distribution, and add the result to the tabulated parameters from (Zorec & Royer2012). With the extended table, we treat stars in the transition range the same way we treat hot stars.
We show the marginalized detection rate and mean value of as a function of temperature in Figure5. Both the detection rate and the average
as a function of temperature in Figure5. Both the detection rate and the average are smoothly varying, and show the expected behavior with temperature. The detection rate falls with hotter temperatures because the companions are expected to be fast rotators, which are more difficult to detect.
are smoothly varying, and show the expected behavior with temperature. The detection rate falls with hotter temperatures because the companions are expected to be fast rotators, which are more difficult to detect.

Figure 5. Marginalized detection rate for the same star as shown in Figure4. The fall in detection rate toward hotter stars is caused by the increase in typical rotational speeds.
Download figure:
Standard imageHigh-resolution image5.3. Conversion to Mass Ratio
The result of the previous analysis is a series of estimates for the detection rate as a function of companion temperature for each observation of each star. We convert companion temperature to mass by interpolating Table 5 of Pecaut & Mamajek (2013). Next, we estimate the primary mass for each star as the median of the mass samples developed in Section4. We then convert each detection rate curve to be a function of mass ratio (Qj(q), wherej denotes thejth star in the sample), and linearly interpolate onto a grid in mass ratio from . Finally, we combine the detection rate curves for each starwith no companion detection in our data into an estimate of the survey-wide completeness by taking the average of the detection rate for all stars:
. Finally, we combine the detection rate curves for each starwith no companion detection in our data into an estimate of the survey-wide completeness by taking the average of the detection rate for all stars:

In the equation above,Ni is the number of sample stars that contain an estimate for without extrapolating. For
without extrapolating. For ,Ni is near the total sample size. However,Ni falls for both low and highq, since a
,Ni is near the total sample size. However,Ni falls for both low and highq, since a /
/ companion has a mass ratio
companion has a mass ratio for an A9V primary, but
for an A9V primary, but for a B0V primary. Our sensitivity analysis therefore does not sample large mass ratios around the very early-type primary stars in the sample, and does not sample very low mass ratios around late-type primary stars.
for a B0V primary. Our sensitivity analysis therefore does not sample large mass ratios around the very early-type primary stars in the sample, and does not sample very low mass ratios around late-type primary stars.
Table 5. Mass-ratio Distribution Parameters
| Model | Parameter | Median Value | 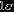 Credible Interval Credible Interval | |
|---|---|---|---|---|
| Lower | Upper | |||
| Histogram | 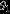 | 0.50 | 0.18 | 1.00 |
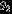 | 1.53 | 1.14 | 1.89 | |
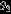 | 2.17 | 1.80 | 2.65 | |
 | 1.42 | 0.98 | 1.81 | |
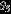 | 0.74 | 0.40 | 1.12 | |
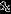 | 0.29 | 0.10 | 0.55 | |
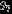 | 0.16 | 0.06 | 0.33 | |
| Lognormal | μ | −0.99 | −1.06 | −0.92 |
| σ | 0.46 | 0.40 | 0.54 | |
| maximuma | 0.30 | 0.27 | 0.33 | |
| Power Law | γ | 0.29 | 0.15 | 0.42 |
Note.
aThis parameter is derived from the mean and standard deviation, not fit.Download table as: ASCIITypeset image
Gullikson et al. (2016) used a very similar method to search for known companions to A- and B-type stars, and found that the detection rate is high for G- and K-dwarf companions but very low for hot companions. The search grid used in this work includes much hotter temperatures, and we have several detections of hot companions (see Table4). We test to determine if the completeness is reasonable at large mass ratios by comparing to known binary systems. We detect 15 of the 25 stars in our sample with a hot ( ) companion in either the Washington Double Star Catalog (Mason et al.2014) or the Ninth Catalog of Spectroscopic Binary Orbits (Pourbaix et al.2009). The completeness function for hot, roughly equal-mass companions suggests the probability of detection is
) companion in either the Washington Double Star Catalog (Mason et al.2014) or the Ninth Catalog of Spectroscopic Binary Orbits (Pourbaix et al.2009). The completeness function for hot, roughly equal-mass companions suggests the probability of detection is , which is still incompatible with our low detection rate. The discrepancy may be due to an underestimate of the typical rotation rates for hot stars, which we use when marginalizing out the dependence on
, which is still incompatible with our low detection rate. The discrepancy may be due to an underestimate of the typical rotation rates for hot stars, which we use when marginalizing out the dependence on . Additionally, rapidly rotating companions, especially when they have a similar temperature to the primary, are more difficult to detect if they have a small radial velocity offset from the primary star. While the injection and recovery experiments do sample velocity space to account for this, they may be over-sampling companions with very large velocity offsets and producing anomalously high detection rates. We account for the discrepancy by introducing a scaling factor: we multiply the estimated detection rate for all companions with
. Additionally, rapidly rotating companions, especially when they have a similar temperature to the primary, are more difficult to detect if they have a small radial velocity offset from the primary star. While the injection and recovery experiments do sample velocity space to account for this, they may be over-sampling companions with very large velocity offsets and producing anomalously high detection rates. We account for the discrepancy by introducing a scaling factor: we multiply the estimated detection rate for all companions with byf = 0.8.
byf = 0.8.
We show the resulting total survey completeness in Figure6. The completeness falls very rapidly toward low mass ratios, although we are still complete atq = 0.1. The slow fall-off toward large mass ratios is caused by a combination of the scale factor described above and the inherent difficulty of detecting rapidly rotating companions (see Figure5). The detection rate at large mass ratios is now ∼0.6–0.7, which is consistent with our 15/25 empirical detection rate.
complete atq = 0.1. The slow fall-off toward large mass ratios is caused by a combination of the scale factor described above and the inherent difficulty of detecting rapidly rotating companions (see Figure5). The detection rate at large mass ratios is now ∼0.6–0.7, which is consistent with our 15/25 empirical detection rate.

Figure 6. Survey completeness as a function of mass ratio (q).
Download figure:
Standard imageHigh-resolution image6. MASS-RATIO DISTRIBUTION
We are now finally in a position to estimate the mass-ratio distribution for our sample. We estimate the mass for each detected companion star by sampling the temperatures given in Table4 as a Gaussian, and converting each temperature sample into a mass sample. We do the conversion to mass both by interpolating Table 5 from Pecaut & Mamajek (2013), and by interpolating from temperature and system age (see Section4) to mass with Dartmouth isochrones (Dotter et al.2008). Both methods give similar results in most cases. Since the isochrone masses are more accurate at young ages, we use them throughout the analysis that follows. We sample the mass ratio of the system by dividing the companion mass samples by samples of the primary mass (Section4). We denote thenth mass-ratio sample for thekth star as , and denote the number of these samples asNk.
, and denote the number of these samples asNk.
We do not use systems with more than one companion, unless the wider companion is separated by from the primary star. We mark the 50 companions we use in the mass-ratio analysis with the fourth column of Table4. Many of the companions we use in the analysis only have one detection in our data; 26/36 of these are previously known companions and so do not need follow-up to confirm. The remaining ten are new and unconfirmed detections; these all have very strong CCF signals and are likely to be confirmed with follow-up spectroscopy or imaging. Their inclusion does not significantly change the results.
from the primary star. We mark the 50 companions we use in the mass-ratio analysis with the fourth column of Table4. Many of the companions we use in the analysis only have one detection in our data; 26/36 of these are previously known companions and so do not need follow-up to confirm. The remaining ten are new and unconfirmed detections; these all have very strong CCF signals and are likely to be confirmed with follow-up spectroscopy or imaging. Their inclusion does not significantly change the results.
6.1. Fitting Methodology
We use the methodology developed in Foreman-Mackey et al. (2014) to perform Bayesian inference on the shape and form of the mass-ratio distribution. The log-likelihood function in this formalism is derived from modeling the survey as a draw from the inhomogeneous Poisson process with rate density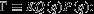

In the above equation, denotes the data for stark, and
denotes the data for stark, and denotes the parameters for the model we are fitting.K = 50 is the number of stars used in the analysis,Q(q) is the completeness function shown in Figure6, and
denotes the parameters for the model we are fitting.K = 50 is the number of stars used in the analysis,Q(q) is the completeness function shown in Figure6, and is the likelihood function for the mass ratio given the model parameters. We fit the data to three distinct distributions: a histogram (P1), a lognormal distribution (P2), and a power law (P3):
is the likelihood function for the mass ratio given the model parameters. We fit the data to three distinct distributions: a histogram (P1), a lognormal distribution (P2), and a power law (P3):



The constantA in the lognormal distribution is a renormalization factor such that the distribution is only defined from :
:

We fit all distributions via importance nested sampling with the MultiNest code (Feroz et al.2013). Following Foreman-Mackey et al. (2014), we apply a smoothing prior on the parameters for the histogram model:
for the histogram model:


The smoothing prior is an seven-dimensional Gaussian with meanm and covariance matrixKij, and encodes our belief that the mass-ratio distribution is a smoothly varying function while leaving enough flexibility to let the data drive the shape of the function. Since we have introduced three new hyperparameters ( ), we must apply a prior to them and marginalize over them when estimating the bin heights. We choose log-uniform priors for
), we must apply a prior to them and marginalize over them when estimating the bin heights. We choose log-uniform priors for , and
, and , and a uniform prior for the meanm. The full posterior probability distribution for the histogram model is:
, and a uniform prior for the meanm. The full posterior probability distribution for the histogram model is:

The lognormal distribution only has two parameters ( ), and was chosen because it has a similar shape to the histogram resulting from the first model. We use uniform priors on bothμ andσ, although we note thatμ is compared to
), and was chosen because it has a similar shape to the histogram resulting from the first model. We use uniform priors on bothμ andσ, although we note thatμ is compared to and so acts like a log-uniform prior. The power law has only one parameter (γ); we use a uniform prior in the fit.
and so acts like a log-uniform prior. The power law has only one parameter (γ); we use a uniform prior in the fit.
6.2. Malmquist Bias Correction
We are trying to recover the intrinsic distribution from an observed sample, so we must fit the data to the PDF for mass ratio,given that we observed the star: . In a volume-limited sample, this is equal to
. In a volume-limited sample, this is equal to . However, our sample is magnitude-limited and therefore suffers from Malmquist bias. There is a higher probability for equal-mass binary systems to occur in our survey because they contribute twice the flux and are therefore more likely to fall under the magnitude limit. We can calculate the PDF for mass ratio, given that we observed the system, from Bayes’ theorem:
. However, our sample is magnitude-limited and therefore suffers from Malmquist bias. There is a higher probability for equal-mass binary systems to occur in our survey because they contribute twice the flux and are therefore more likely to fall under the magnitude limit. We can calculate the PDF for mass ratio, given that we observed the system, from Bayes’ theorem:

We already know (Equations (10)–(12)). We estimate
(Equations (10)–(12)). We estimate by simulating a very large sample of binary stars via these steps:
by simulating a very large sample of binary stars via these steps:
- 1.Draw random primary star masses from the Kroupa initial mass function (IMF) (Kroupa2002)
- 2.Draw a random distance for each star from a disk with infinite extent and scale height of 150 pc (the approximate scale height of the Milky Way disk for A-type stars, Binney & Merrifield1998).
- 3.For eachq from 0 to 1, in steps of 0.01:Add a companion star to each primary with the appropriate mass to make a binary system with mass ratioq.Calculate the combined absolute V-magnitude by interpolating Table 5 of Pecaut & Mamajek (2013).Calculate apparent magnitudeV from the absolute magnitude and distance.Find fraction of stars (f(q)) with apparent
 .
. - 4.Fit the sampled fractionsf(q) to a fifth-order polynomial.
With the fitted Malmquist-correction polynomial, we then substitute everywhere
everywhere appears in Equation (9).
appears in Equation (9).
We summarize the parameters in Table5, and show the resulting fits in Figure7. The uncertainties in the bin heights from the histogram model are shown as error bars, and we overplot 300 samples of the lognormal distribution fit to show the spread allowed by the data. The best-fit power law is plotted with a red dot–dashed line. We also estimate the mass-ratio distribution expected from random pairing of the Kroupa IMF, and show the result in yellow. We estimate the distribution by drawing 100,000 primary stars from the IMF with masses between
uncertainties in the bin heights from the histogram model are shown as error bars, and we overplot 300 samples of the lognormal distribution fit to show the spread allowed by the data. The best-fit power law is plotted with a red dot–dashed line. We also estimate the mass-ratio distribution expected from random pairing of the Kroupa IMF, and show the result in yellow. We estimate the distribution by drawing 100,000 primary stars from the IMF with masses between . We then draw companions from the same IMF, with the restriction that the companion has a lower mass than the primary. The result plotted in yellow in Figure7 is a Gaussian kernel density estimate of the resulting mass ratios, with a bandwidth of 0.05.
. We then draw companions from the same IMF, with the restriction that the companion has a lower mass than the primary. The result plotted in yellow in Figure7 is a Gaussian kernel density estimate of the resulting mass ratios, with a bandwidth of 0.05.

Figure 7. Mass-ratio distribution for our sample. The data were fit to a histogram, a lognormal distribution, and a power law. The histogram is shown in the solid blue blocks, with uncertainties marked with error bars. The variance of the lognormal fit is shown with 300 samples from the posterior probability distribution for the parameters in green. We also show the best-fit power law and the mass-ratio distribution resulting from random pairing of the Kroupa IMF. Finally, we display the raw mass-ratio measurements with associated uncertainties in the cluster of data points near the top of the figure.
uncertainties marked with error bars. The variance of the lognormal fit is shown with 300 samples from the posterior probability distribution for the parameters in green. We also show the best-fit power law and the mass-ratio distribution resulting from random pairing of the Kroupa IMF. Finally, we display the raw mass-ratio measurements with associated uncertainties in the cluster of data points near the top of the figure.
Download figure:
Standard imageHigh-resolution image7. DISCUSSION
Previous measurements of the mass-ratio distribution find that the data are well fit by a power law. Kouwenhoven et al. (2007) compiled spectroscopic, imaging, and astrometric observations of binary stars with intermediate-mass primaries in the Scorpius OB association, and derived a power law index of −0.45 ± 0.15. More recently De Rosa et al. (2014) performed an adaptive optics and common proper motion search for companions to field A-type stars. They found that the distribution for companions on wide ( ) orbits has a very steep power law index of
) orbits has a very steep power law index of , while the distribution for close (
, while the distribution for close ( ) companions is consistent with flat.
) companions is consistent with flat.
7.1. Model Comparison
The most striking feature of the mass-ratio distribution shown in Figure7 is the turnover or flattening at intermediateq. The maximum of the lognormal distribution occurs at and is an estimate of the characteristic scale.
and is an estimate of the characteristic scale.
Although the power law fit and the Kroupa IMF are visually very poor fits to the data, we formally compare the models to ensure that the different form is not an artifact of binning or simple noise. We make the comparison using the posterior odds:

The integrals are estimated as part of the nested sampling algorithm in the MultiNest code. The odds ratio comparing the lognormal distribution to power law fit is , indicating a very strong preference for the lognormal distribution model. We also compare to the mass-ratio distribution expected for random pairing from the Kroupa IMF and to a uniform distribution (a special case of the power law). In these cases, there are no free parameters so the evidence integral just becomes the likelihood function (Equation (9)). The corresponding odds ratios are
, indicating a very strong preference for the lognormal distribution model. We also compare to the mass-ratio distribution expected for random pairing from the Kroupa IMF and to a uniform distribution (a special case of the power law). In these cases, there are no free parameters so the evidence integral just becomes the likelihood function (Equation (9)). The corresponding odds ratios are and
and . Both of these again demonstrate a very strong preference for the lognormal distribution.
. Both of these again demonstrate a very strong preference for the lognormal distribution.
The extreme unlikeliness of the Kroupa IMF model also indicates that our sample is not significantly biased by foreground or background contaminants. In fact, the present-day background star mass function is more bottom heavy than the IMF because some of the massive stars have evolved to white dwarfs or ended their lives in a supernova. The comparison to a Kroupa IMF thereforeunderestimates the likelihood of background star contamination.
7.2. Comparison to Previous Results
Our mass-ratio distribution appears to be in tension with the results of the VAST survey (De Rosa et al.2014), which finds a nearly flat distribution for close companions. However, their subsample of close companions only includes 18 binaries, so it is possible that the different forms are just a result of small number statistics. To assess the degree of tension, we use the Anderson–Darling test (Anderson & Darling1954) to find the probability that both their close companion subsample and our companions are drawn from the same parent distribution. We only use companions from this work with mean because the VAST survey subsample makes the same cut. The VAST survey also only included stars with projected separations
because the VAST survey subsample makes the same cut. The VAST survey also only included stars with projected separations in their close companion subsample. Since we cannot estimate the separation from our data, we do not make such a cut. We could make a cut using themaximum possible separation, set by the distance and spectrograph slit width, but doing so vastly reduces the number of detections and does not affect the result.
in their close companion subsample. Since we cannot estimate the separation from our data, we do not make such a cut. We could make a cut using themaximum possible separation, set by the distance and spectrograph slit width, but doing so vastly reduces the number of detections and does not affect the result.
To account for measurement uncertainties in the mass ratios, we draw from both our mass-ratio samples ( , see Section6) and the VAST mass-ratio values many times and compute the Anderson–Darling test statistic each time. Since De Rosa et al. (2014) do not quote uncertainties, we assume uncertainties of
, see Section6) and the VAST mass-ratio values many times and compute the Anderson–Darling test statistic each time. Since De Rosa et al. (2014) do not quote uncertainties, we assume uncertainties of for all of their measurements. The result is
for all of their measurements. The result is we cannot reject the hypothesis that both samples come from the same distribution.
we cannot reject the hypothesis that both samples come from the same distribution.
7.3. Theoretical Implications
The mass-ratio distribution derived in this work has a very different form than the power law found for companions at wide separations. This is likely a result of disk interactions as the two components are accreting. The close companions that we detect may form with similar masses to their counterparts at large separations ( ), but preferentially accrete matter from the dense primary star disk. The result would be a depletion of low mass-ratio companions as they become intermediate to high mass-ratio companions. The characteristic scale of ∼0.3 that we see in Figure7 would then be related to the disk timescale, since with enough time the preferential accretion would push all companions toq = 1.0.
), but preferentially accrete matter from the dense primary star disk. The result would be a depletion of low mass-ratio companions as they become intermediate to high mass-ratio companions. The characteristic scale of ∼0.3 that we see in Figure7 would then be related to the disk timescale, since with enough time the preferential accretion would push all companions toq = 1.0.
It is also possible that some of the companions found in this work were formed from a gravitationally unstable disk (e.g., Kratter & Matzner2006; Stamatellos & Whitworth2011). Being a completely different formation mechanism than the way wide companions form, we would expect the initial companion mass function to differ. Such companions would undergo the same preferential accretion discussed above.
Large scale simulations are likely needed to distinguish between the two scenarios and fully interpret the results of this survey. A significant amount of work has already been put toward this end in the form of radiation hydrodynamic simulations of giant molecular clouds (Bate2012; Krumholz et al.2012). However, the present simulations do not generate enough stars more massive than the Sun to quantitatively compare binary and multiple star statistics to observations.
8. SUMMARY
In this work, we described a binary survey of 341 bright A- and B-type stars. We used the direct spectral detection method (Gullikson et al.2016) to find the spectral lines of 64 companions with temperatures ranging from 3600–16,000 K. We used the CCFs to estimate the temperature and surface gravity of most of our sample stars, and converted to mass and age by interpolating Padova stellar evolutionary tracks (Bressan et al.2012). Likewise, we convert the companion temperature measurements to mass by using solar metallicity Dartmough evolutionary tracks (Dotter et al.2008).
We then use the formalism introduced in Foreman-Mackey et al. (2014), which self-consistently accounts for measurement errors, to infer the form of the mass-ratio distribution (shown in Figure7). Unlike most previous work, we find that a power law is a poor descriptor of the data and find that a lognormal distribution performs much better. This result, which only includes close companions since it is a spectroscopic technique, is consistent with the 18 close companions found in the VAST survey (De Rosa et al.2014). However, this result shows much more detail due to a larger number of companions.
We interpret the mass-ratio distribution in terms of formation mechanism in Section7.3. It is likely that the mass-ratio distribution we find is largely a result of preferential accretion onto the secondary star, which largely stops when the circumprimary or circumbinary disk dissipates.
In the effort of open and reproducible research, we have made several data products freely available to the community. All of the reduced and telluric-corrected spectra used in this study are available athttps://zenodo.org/record/46340. Samples of the primary and companion mass and system age posterior distributions are available athttps://zenodo.org/record/48073, as are the posterior distributions for the parameters fit in Section6 and every CCF generated in our analysis. We additionally provide a series of python libraries and jupyter notebooks with the computer code we used for the analysis on github:https://github.com/kgullikson88/BinaryInference.
We would like to thank the anonymous referee for their helpful comments, which have notably improved this work. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013). It was supported by a start-up grant to Adam Kraus as well as a University of Texas Continuing Fellowship and a Dissertation Writing Fellowship to Kevin Gullikson.
This work used the Immersion Grating Infrared Spectrograph (IGRINS) that was developed under a collaboration between the University of Texas at Austin and the Korea Astronomy and Space Science Institute (KASI) with the financial support of the US National Science Foundation under grant AST-1229522, of the University of Texas at Austin, and of the Korean GMT Project of KASI.
The Hobby-Eberly Telescope (HET) is a joint project of the University of Texas at Austin, the Pennsylvania State University, Stanford University, Ludwig-Maximilians-Universität München, and Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly.
Based on observations at Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory (NOAO Prop. IDs: 13A-0139, 13B-0112, 2014A-0260, 14A-0260, 15A-0245; PI: Kevin Gullikson), which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation.