lstsq#

scipy.linalg.lstsq(a,b,cond=None,overwrite_a=False,overwrite_b=False,check_finite=True,lapack_driver=None)[source]#

Compute least-squares solution to the equationa@x=b.

Compute a vector x such that the 2-norm|b-Ax| is minimized.

The documentation is written assuming array arguments are of specified“core” shapes. However, array argument(s) of this function may have additional“batch” dimensions prepended to the core shape. In this case, the array is treatedas a batch of lower-dimensional slices; seeBatched Linear Operations for details.

Parameters:

a(M, N) array_like

Left-hand side array

b(M,) or (M, K) array_like

Right hand side array

condfloat, optional

Cutoff for ‘small’ singular values; used to determine effectiverank of a. Singular values smaller thancond*largest_singular_value are considered zero.

overwrite_abool, optional

Discard data ina (may enhance performance). Default is False.

overwrite_bbool, optional

Discard data inb (may enhance performance). Default is False.

check_finitebool, optional

Whether to check that the input matrices contain only finite numbers.Disabling may give a performance gain, but may result in problems(crashes, non-termination) if the inputs do contain infinities or NaNs.

lapack_driverstr, optional

Which LAPACK driver is used to solve the least-squares problem.Options are'gelsd','gelsy','gelss'. Default('gelsd') is a good choice. However,'gelsy' can be slightlyfaster on many problems.'gelss' was used historically. It isgenerally slow but uses less memory.

Added in version 0.17.0.

Returns:

x(N,) or (N, K) ndarray

Least-squares solution.

residues(K,) ndarray or float

Square of the 2-norm for each column inb-ax, ifM>N andrank(A)==n (returns a scalar ifb is 1-D). Otherwise a(0,)-shaped array is returned.

rankint

Effective rank ofa.

s(min(M, N),) ndarray or None

Singular values ofa. The condition number ofa iss[0]/s[-1].

Raises:

LinAlgError

If computation does not converge.

ValueError

When parameters are not compatible.

See also

scipy.optimize.nnls

linear least squares with non-negativity constraint

Notes

When'gelsy' is used as a driver,residues is set to a (0,)-shapedarray ands is alwaysNone.

Examples

Try it in your browser!

>>>importnumpyasnp>>>fromscipy.linalgimportlstsq>>>importmatplotlib.pyplotasplt

Suppose we have the following data:

>>>x=np.array([1,2.5,3.5,4,5,7,8.5])>>>y=np.array([0.3,1.1,1.5,2.0,3.2,6.6,8.6])

We want to fit a quadratic polynomial of the formy=a+b*x**2to this data. We first form the “design matrix” M, with a constantcolumn of 1s and a column containingx**2:

>>>M=x[:,np.newaxis]**[0,2]>>>Marray([[  1.  ,   1.  ],       [  1.  ,   6.25],       [  1.  ,  12.25],       [  1.  ,  16.  ],       [  1.  ,  25.  ],       [  1.  ,  49.  ],       [  1.  ,  72.25]])

We want to find the least-squares solution toM.dot(p)=y,wherep is a vector with length 2 that holds the parametersa andb.

>>>p,res,rnk,s=lstsq(M,y)>>>parray([ 0.20925829,  0.12013861])

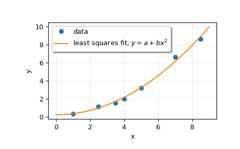
Plot the data and the fitted curve.

>>>plt.plot(x,y,'o',label='data')>>>xx=np.linspace(0,9,101)>>>yy=p[0]+p[1]*xx**2>>>plt.plot(xx,yy,label='least squares fit, $y = a + bx^2$')>>>plt.xlabel('x')>>>plt.ylabel('y')>>>plt.legend(framealpha=1,shadow=True)>>>plt.grid(alpha=0.25)>>>plt.show()

Go BackOpen In Tab