numpy.interp¶

numpy.interp(x,xp,fp,left=None,right=None,period=None)[source]¶

One-dimensional linear interpolation.

Returns the one-dimensional piecewise linear interpolant to a functionwith given discrete data points (xp,fp), evaluated atx.

Parameters:	x:array_like The x-coordinates at which to evaluate the interpolated values. xp:1-D sequence of floats The x-coordinates of the data points, must be increasing if argumentperiod is not specified. Otherwise,xp is internally sorted afternormalizing the periodic boundaries withxp=xp%period. fp:1-D sequence of float or complex The y-coordinates of the data points, same length asxp. left:optional float or complex corresponding to fp Value to return forx < xp[0], default isfp[0]. right:optional float or complex corresponding to fp Value to return forx > xp[-1], default isfp[-1]. period:None or float, optional A period for the x-coordinates. This parameter allows the properinterpolation of angular x-coordinates. Parametersleft andrightare ignored ifperiod is specified. New in version 1.10.0.
Returns:	y:float or complex (corresponding to fp) or ndarray The interpolated values, same shape asx.
Raises:	ValueError Ifxp andfp have different lengthIfxp orfp are not 1-D sequencesIfperiod == 0

Notes

Does not check that the x-coordinate sequencexp is increasing.Ifxp is not increasing, the results are nonsense.A simple check for increasing is:

np.all(np.diff(xp)>0)

Examples

>>>xp=[1,2,3]>>>fp=[3,2,0]>>>np.interp(2.5,xp,fp)1.0>>>np.interp([0,1,1.5,2.72,3.14],xp,fp)array([ 3. ,  3. ,  2.5 ,  0.56,  0. ])>>>UNDEF=-99.0>>>np.interp(3.14,xp,fp,right=UNDEF)-99.0

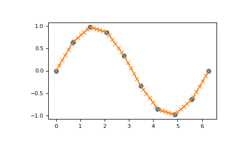
Plot an interpolant to the sine function:

>>>x=np.linspace(0,2*np.pi,10)>>>y=np.sin(x)>>>xvals=np.linspace(0,2*np.pi,50)>>>yinterp=np.interp(xvals,x,y)>>>importmatplotlib.pyplotasplt>>>plt.plot(x,y,'o')[<matplotlib.lines.Line2D object at 0x...>]>>>plt.plot(xvals,yinterp,'-x')[<matplotlib.lines.Line2D object at 0x...>]>>>plt.show()

Interpolation with periodic x-coordinates:

>>>x=[-180,-170,-185,185,-10,-5,0,365]>>>xp=[190,-190,350,-350]>>>fp=[5,10,3,4]>>>np.interp(x,xp,fp,period=360)array([7.5, 5., 8.75, 6.25, 3., 3.25, 3.5, 3.75])

Complex interpolation:

>>>x=[1.5,4.0]>>>xp=[2,3,5]>>>fp=[1.0j,0,2+3j]>>>np.interp(x,xp,fp)array([ 0.+1.j ,  1.+1.5j])