numpy.random.Generator.exponential#

method

random.Generator.exponential(scale=1.0,size=None)#

Draw samples from an exponential distribution.

Its probability density function is

\[f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta}),\]

forx>0 and 0 elsewhere.\(\beta\) is the scale parameter,which is the inverse of the rate parameter\(\lambda = 1/\beta\).The rate parameter is an alternative, widely used parameterizationof the exponential distribution[3].

The exponential distribution is a continuous analogue of thegeometric distribution. It describes many common situations, such asthe size of raindrops measured over many rainstorms[1], or the timebetween page requests to Wikipedia[2].

Parameters:

scalefloat or array_like of floats

The scale parameter,\(\beta = 1/\lambda\). Must benon-negative.

sizeint or tuple of ints, optional

Output shape. If the given shape is, e.g.,(m,n,k), thenm*n*k samples are drawn. If size isNone (default),a single value is returned ifscale is a scalar. Otherwise,np.array(scale).size samples are drawn.

Returns:

outndarray or scalar

Drawn samples from the parameterized exponential distribution.

References

[1]

Peyton Z. Peebles Jr., “Probability, Random Variables andRandom Signal Principles”, 4th ed, 2001, p. 57.

[2]

Wikipedia, “Poisson process”,https://en.wikipedia.org/wiki/Poisson_process

[3]

Wikipedia, “Exponential distribution”,https://en.wikipedia.org/wiki/Exponential_distribution

Examples

Try it in your browser!

Assume a company has 10000 customer support agents and the time between customer calls is exponentially distributed and that the average time between customer calls is 4 minutes.

>>>scale,size=4,10000>>>rng=np.random.default_rng()>>>time_between_calls=rng.exponential(scale=scale,size=size)

What is the probability that a customer will call in the next 4 to 5 minutes?

>>>x=((time_between_calls<5).sum())/size>>>y=((time_between_calls<4).sum())/size>>>x-y0.08  # may vary

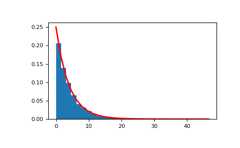
The corresponding distribution can be visualized as follows:

>>>importmatplotlib.pyplotasplt>>>scale,size=4,10000>>>rng=np.random.default_rng()>>>sample=rng.exponential(scale=scale,size=size)>>>count,bins,_=plt.hist(sample,30,density=True)>>>plt.plot(bins,scale**(-1)*np.exp(-scale**-1*bins),linewidth=2,color='r')>>>plt.show()

Go BackOpen In Tab