You saw in theprevious exercise that just addinghidden layers to our network wasn't sufficient to represent nonlinearities.Linear operations performed on linear operations are still linear.

How can you configure a neural network to learnnonlinear relationships between values? We need some way to insert nonlinearmathematical operations into a model.

If this seems somewhat familiar, that's because we've actually appliednonlinear mathematical operations to the output of a linear model earlier inthe course. In theLogistic Regression module, we adapted a linear regression model to output a continuous value from 0to 1 (representing a probability) by passing the model's output through asigmoid function.

We can apply the same principle to our neural network. Let's revisit our modelfromExercise 2 earlier, but this time, beforeoutputting the value of each node, we'll first apply the sigmoid function:

Try stepping through the calculations of each node by clicking the>| button(to the right of the play button). Review the mathematical operations performedto calculate each node value in theCalculations panel below the graph.Note that each node's output is now a sigmoid transform of the linearcombination of the nodes in the previous layer, and the output values areall squished between 0 and 1.

Here, the sigmoid serves as anactivation functionfor the neural network, a nonlinear transform of a neuron's output valuebefore the value is passed as input to the calculations of the nextlayer of the neural network.

Now that we've added an activation function, adding layers has more impact.Stacking nonlinearities on nonlinearities lets us model very complicatedrelationships between the inputs and the predicted outputs. In brief, each layeris effectively learning a more complex, higher-level function over the rawinputs. If you'd like to develop more intuition on how this works,seeChris Olah's excellent blog post.

Common activation functions

Three mathematical functions that are commonly used as activation functions aresigmoid, tanh, and ReLU.

The sigmoid function (discussed above) performs the following transform on input$x$, producing an output value between 0 and 1:

\[F(x)=\frac{1} {1+e^{-x}}\]

The termsigmoid is often used more generally torefer to any S-shaped function. A more technically precise term for the specificfunction $F(x)=\frac{1} {1+e^{-x}}$ islogistic function.

Here's a plot of this function:

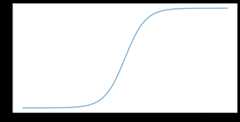
The tanh (short for "hyperbolic tangent") function transforms input $x$ toproduce an output value between –1 and 1:

\[F(x)=tanh(x)\]

Here's a plot of this function:

Note that the range of the sigmoid function is 0 to 1, andthe range of the tanh function is –1 to 1

Therectified linear unit activation function (orReLU, forshort) transforms output using the following algorithm:

• If the input value $x$ is less than 0, return 0.
• If the input value $x$ is greater than or equal to 0, return the input value.

ReLU can be represented mathematically using the max() function:

$$F(x)=max(0,x)$$

Here's a plot of this function:

ReLU often works a little better as an activation function than a smoothfunction like sigmoid or tanh, because it is less susceptible to thevanishing gradient problemduringneural network training. ReLU is also significantly easierto compute than these functions.

Other activation functions

In practice, any mathematical function can serve as an activation function.Suppose that \(\sigma\) represents our activation function.The value of a node in the network is given by the followingformula:

Keras provides out-of-the-box support for manyactivation functions.That said, we still recommend starting with ReLU.

Summary

The following video provides a recap of everything you've learned thus farabout how neural networks are constructed:

Now our model has all the standard components of what people usuallymean when they refer to a neural network:

• A set of nodes, analogous to neurons, organized in layers.
• A set of learned weights and biases representing the connections betweeneach neural network layer and the layer beneath it. The layer beneath may beanother neural network layer, or some other kind of layer.
• An activation function that transforms the output of each node in a layer.Different layers may have different activation functions.

A caveat: neural networks aren't necessarily always better thanfeature crosses, but neural networks do offer a flexible alternative that workswell in many cases.

• Activation function
• Sigmoid function
• Vanishing gradient problem