Page Summary

outlined_flag

• This module explores neural networks, a model architecture designed to automatically identify nonlinear patterns in data, eliminating the need for manual feature cross experimentation.

• You will learn the fundamental components of a deep neural network, including nodes, hidden layers, and activation functions, and how they contribute to prediction.

• The module covers the training process of neural networks, using the backpropagation algorithm to optimize predictions and minimize loss.

• Additionally, you will gain insights into how neural networks handle multi-class classification problems using one-vs.-all and one-vs.-one approaches.

• This module builds on prior knowledge of machine learning concepts such as linear and logistic regression, classification, and working with numerical and categorical data.

• Explain the motivation for building neural networks, and the use cases they address.
• Define and explain the function of the key components of a deep neural network architecture:
  • Nodes
  • Hidden layers
  • Activation functions
• Develop intuition around how neural network predictions are made, by stepping through the inference process.
• Build a high-level intuition of how neural networks are trained, using the backpropagation algorithm.
• Explain how neural networks can be used to perform two types of multi-class classification: one-vs.-all and one-vs.-one.

• Introduction to Machine Learning
• Linear regression
• Logistic regression
• Classification
• Working with numerical data
• Working with categorical data
• Datasets, generalization, and overfitting

You may recall from theFeature cross exercisesin theCategorical data module,that the following classification problem is nonlinear:

"Nonlinear" means that you can't accurately predict a label with amodel of the form \(b + w_1x_1 + w_2x_2\). In other words, the"decision surface" is not a line.

However, if we perform a feature cross on our features $x_1$ and $x_2$, we canthen represent the nonlinear relationship between the two features using alinear model:$b + w_1x_1 + w_2x_2 + w_3x_3$ where $x_3$ is the feature cross between$x_1$ and $x_2$:

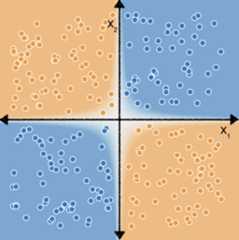
Now consider the following dataset:

You may also recall from theFeature cross exercisesthat determining the correct feature crosses to fit a linear model to this datatook a bit more effort and experimentation.

But what if you didn't have to do all that experimentation yourself?Neural networks are a familyof model architectures designed to findnonlinearpatterns in data. During training of a neural network, themodel automaticallylearns the optimal feature crosses to perform on the input data to minimizeloss.

In the following sections, we'll take a closer look at how neural networks work.

• Activation function
• Hidden layer
• Linear model
• Model
• Neural network
• Nodes
• Nonlinear