Page Summary

outlined_flag

• Embeddings are low-dimensional representations of high-dimensional data, often used to capture semantic relationships between items.

• Embeddings place similar items closer together in the embedding space, allowing for efficient machine learning on large datasets.

• The distance between points in an embedding space represents the relative similarity between the corresponding items.

• Real-world embeddings can encode complex relationships, like those between countries and their capitals, allowing models to detect patterns.

• Static embeddings like word2vec represent all meanings of a word with a single point, which can be a limitation in some cases.

Anembedding is avector representation of data inembedding space. Generallyspeaking, a model finds potential embeddings by projecting the high-dimensionalspace of initial data vectors into a lower-dimensional space.For a discussion of high-dimensional versuslow-dimensional data, see theCategorical Datamodule.

Embeddings make it easier to do machine learning on largefeature vectors, suchas the sparse vectors representing meal items discussed in theprevious section. Sometimes the relative positions of items inembedding space have a potential semantic relationship, but often the process offinding a lower-dimensional space, and relative positions in that space, is notinterpretable by humans, and the resulting embeddings are difficult tounderstand.

Still, for the sake of human understanding, to give an idea of how embeddingvectors represent information, consider thefollowing one-dimensional representation of the disheshot dog,pizza,salad,shawarma, andborscht,on a scale of "least like asandwich"to "most like a sandwich." The single dimension is an imaginary measure of"sandwichness."

Where on this line would anapple strudelfall? Arguably, it could be placed betweenhot dog andshawarma. But applestrudel also seems to have an additional dimension ofsweetnessordessertness that makes it very different from the other options.The following figure visualizes this by adding a "dessertness" dimension:

An embedding represents each item inn-dimensional space withnfloating-point numbers (typically in the range –1 to 1 or 0 to 1).The embedding in Figure 3 represents each food in one-dimensional spacewith a single coordinate, while Figure 4 represents each food intwo-dimensional space with two coordinates. In Figure 4, "apple strudel"is in the upper-right quadrant of the graph and could beassigned the point (0.5, 0.3), whereas "hot dog" is in the bottom-rightquadrant of the graph and could be assigned the point (0.2, –0.5).

In an embedding, the distance between any two items can be calculatedmathematically, and can be interpreted as a measure of relative similaritybetween those two items. Two things that are close to each other, likeshawarma andhot dog in Figure 4, are more closely related in the model'srepresentation of the data than two things more distant from eachother, likeapple strudel andborscht.

Notice also that in the 2D space in Figure 4,apple strudel is much fartherfromshawarma andhot dog than it would be in the 1D space, which matchesintuition:apple strudel is not as similar to a hot dog or a shawarma as hotdogs and shawarmas are to each other.

Now consider borscht, which is much more liquid than the other items. Thissuggests a third dimension,liquidness, or how liquid a food might be.Adding that dimension, the items could be visualized in 3D in this way:

Where in this 3D space wouldtangyuan go? It'ssoupy, like borscht, and a sweet dessert, like apple strudel, and mostdefinitely not a sandwich. Here is one possible placement:

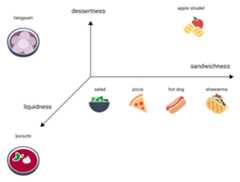
Notice how much information is expressed in these three dimensions.You could imagine adding additional dimensions, like how meaty orbaked a food might be, though 4D, 5D, and higher-dimensional spaces aredifficult to visualize.

Real-world embedding spaces

In the real world, embedding spaces ared-dimensional, whered is muchhigher than 3, though lower than the dimensionality of the data, andrelationships between data points are not necessarily as intuitive as in thecontrived illustration above. (For word embeddings,d is often 256, 512, or1024.1)

In practice, the ML practitioner usually sets the specific task and the numberof embedding dimensions. The model then tries to arrange the trainingexamples to be close in an embedding space with the specified number ofdimensions, or tunes for the number of dimensions, ifd is not fixed.The individual dimensions are rarely as understandable as"dessertness" or "liquidness." Sometimes what they "mean" can be inferredbut this is not always the case.

Embeddings will usually be specific to the task, and differ from each otherwhen the task differs. For example, the embeddings generated by a vegetarianversus non-vegetarian classification model will be different from theembeddings generated by a model that suggests dishes based on time ofday or season. "Cereal" and "breakfast sausage" would probably be closetogether in the embedding space of a time-of-day model but far apart in theembedding space of a vegetarian versus non-vegetarian model, for example.

Static embeddings

While embeddings differ from task to task, one task has somegeneral applicability: predicting the context of a word. Models trained topredict the context of a word assume that words appearing in similar contextsare semantically related. For example, training data that includes thesentences "They rode a burro down into the Grand Canyon" and "They rode a horsedown into the canyon" suggests that "horse" appears in similar contexts to"burro." It turns out that embeddings based on semantic similarity work wellfor many general language tasks.

While it's an older example, and largely superseded by other models, theword2vec model remains useful for illustration.word2vec trains on acorpus of documents to obtain a singleglobal embedding per word. When each word or data point has a single embeddingvector, this is called astatic embedding. The following video walksthrough a simplified illustration ofword2vec training.

Research suggests that these static embeddings, once trained, encode somedegree of semantic information, particularly in relationships between words.That is, words that are used in similar contexts will be closer to each otherin embedding space. The specific embeddings vectors generatedwill depend on the corpus used for training.See T. Mikolov et al (2013),"Efficient estimation of word representations in vector space",for details.

• Embedding vector
• Embedding space