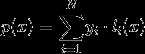Explanation
In this task you'll be given a set ofN points(x1,y1),…,(xN,yN) with distinctxi values and your task is to interpolate a polynomial through these points. If you know what Lagrange interpolation is you can skip this section.
The goal of apolynomial interpolation is to construct the (unique) polynomialp(x) with degreeN-1 (for higher degrees there are infinite solutions) for whichp(xi) = yi for alli = 1…N. One way to do so is to constructN Lagrange basis polynomials and form a linear combination. Such a basis polynomial is defined as follows:
As you can see if you evaluateli at the points x1,…,xi-1,xi+1,…,xN it is 0 by construction and 1 for xi, multiplying by yi will only change the value at xi and set it to yi. Now having N such polynomials that are 0 in every point except one we can simply add them up and get the desired result. So the final solution would be:
Challenge
- the input will consist ofN data points in any reasonable format (list of tuples, Points, a set etc.)
- the coordinates will all be of integer value
- the output will be a polynomial in any reasonable format: list of coefficients, Polynomial object etc.
- the output has to be exact - meaning that some solutions will have rational coefficients
- formatting doesn't matter (
2/2instead of1or1 % 2for1/2etc.) as long as it's reasonable - you won't have to handle invalid inputs (for example empty inputs or input wherex coordinates are repeated)
Testcases
These examples list the coefficients in decreasing order (for example[1,0,0] corresponds to the polynomialx2):
[(0,42)] -> [42][(0,3),(-18,9),(0,17)] -> undefined (you don't have to handle such cases)[(-1,1),(0,0),(1,1)] -> [1,0,0][(101,-42),(0,12),(-84,3),(1,12)] -> [-4911/222351500, -10116/3269875, 692799/222351500, 12]3 Answers3
Enlist, 25 bytes
Ḣ‡ḟ¹‡,€-÷_Ḣ¥€§æc/§₱W€$↙·ṪMonadic link takes an array of length 2 (e.g.,[[101,0,-84,1],[-42,12,3,12]]) as input. The first element of the array is list of x value, the second is list of y value. Output as list of coefficient in increasing degree.
Because @HyperNeutrino forgot to wrap numbers in rational wrapper if it is evaluated in list, (Try it online!) the argument must be hardcoded in the code.
The↙ is necessary because HyperNeutrino make some mistake in implementing· I don't know (or is this a feature? Not sure)
Equivalent Mathematica code:
Expand[ Table[ Times @@ ((z - #)/(xi - #) & /@ DeleteCases[x, xi]) , {xi, x}] . y]wherex andy are list of coordinates. This prints the polynomial.
What Enlist have for this challenge:
- Built in rational number support
- Convolution
æc(my feature request)
- 1\$\begingroup\$If you need a rational number version of Jelly,M might be worth a shot\$\endgroup\$2017-12-23 00:47:41 +00:00CommentedDec 23, 2017 at 0:47
Python, withnumpy, 301 bytes
Seethis notebook for how it works.
Golfed version. 301 bytes, it can be golfed much more.Attempt this online!
import numpy as npfrom itertools import combinations as Cfrom numpy.polynomial import Polynomial as Pdef l(k,x):return P([sum([np.prod(x) for x in C(np.delete(x,k),i)])*(-1)**(i+1)/np.prod(np.delete(x,k)-x[k]) for i in range(len(x))][::-1])def f(x,y):return sum(l(k,x)*y[k] for k in range(len(y)))Ungolfed version.Attempt this online!
import numpy as npfrom itertools import combinations from numpy.polynomial import Polynomial# get the Lagrange basis functiondef l(k, x): n = len(x) assert (k < len(x)) x_k = x[k] x_copy = np.delete(x, k) denominator = np.prod(x_copy - x_k) coeff = [] for i in range(n): coeff.append(sum([np.prod(x) for x in combinations(x_copy, i)]) * (-1)**(i+1) / denominator) coeff.reverse() return Polynomial(coeff)def f(x,y):return sum(l(k,x)*y[k] for k in range(len(y)))x=[101,0,-84,1]y=[-42,12,3,12]print(f"{l(0,x)=}\n")print(f"{l(1,x)=}\n")print(f"{l(2,x)=}\n")print(f"{l(3,x)=}\n")print("y[0]*l(0,x)+y[1]*l(1,x)+y[2]*l(2,x)+y[3]*l(3,x)== f(x):")print(f(x,y))Explore related questions
See similar questions with these tags.