サクサク読めて、
アプリ限定の機能も多数!
Generic data structures (vectors, queues,maps, trees, and so on) seem to be the hottopic if you are evaluating a new language. One of the most frequent questions we've had aboutGo is where the generics are.It seems like there are three basic approaches to generics: (The C approach.) Leave them out. This slows programmers. Butit adds no complexity to the language. (TheC++ approach.) Compile-t
なぜ、動的型付けスクリプト言語の流行りから、再び静的型付けの言語が注目されているのか。 型付けの歴史を振り返り、これからの「型」のありかた、それを実装した処理系のありかたについて考えます。

I stumbled upon this amazing video called "The Unreasonable Effectiveness of Dynamic Typing for Practical Programs"It's about 50mins long and unfortunatelyvimeo has no fast playback options like youtube so I'd suggest you downloadit and viewit inVLC then click Ctrl+ or Cmd+ to speed up In any case he makes a very compelling argument that static typing isn't really all that. His argument is LO
カリー=ハワード同型(Curry-Howard isomorphism)は数学の一見無関係に思えるふたつの領域、型理論と構造論理を結びつける実に驚くべき関係である。 これよりカリー=ハワード同型は単に C-H と表記する。C-H が示しているのは、定理の本質を反映するような型を構築し、それからその型を持つ値を見つけさえすれば、どんな数学的定理をも証明することができる、ということだ。これは最初は極めて不思議に思える。型と定理にどんな関係があるというのだろうか?しかしながら、以下に述べるように、このふたつは非常に近しい関係にあるのである。はじめる前に簡単に注意しておくが、導入の章ではerror や undefinedのような 表示的意味論 が ⊥ である式の存在は無視する。これらはとても重要な役割を果たすのだが、これらについては後ほど別に考えることにする。また、unsafeCoerce#のよ
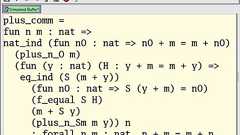
関数型プログラムとして書かれた証明:自然数の加法に関する交換律のCoqによる証明。 カリー=ハワード同型対応(カリー=ハワードどうけいたいおう、英語: Curry–Howard correspondence)とは、プログラミング言語理論と証明論において、計算機プログラムと証明との間の直接的な対応関係のことである。「プログラム=証明」(proofs-as-programs)・「型=命題」(formulae-as-types)などとしても知られる。これはアメリカの数学者ハスケル・カリーと論理学者ウィリアム・アルヴィン・ハワード(英語版)により最初に発見された形式論理の体系とある種の計算の体系との構文論的なアナロジーを一般化した概念である。通常はこの論理と計算の関連性はカリーとハワードに帰属される。しかしながら、このアイデアはブラウワー、ハイティング、コルモゴロフらが定式化した直観主義論理の操作
科学はその方法論上のイメージよりもはるかに”ぞんざい”かつ”非合理的”なものである。 Paul Feyerabend著『Against Method(方法への挑戦)』(1975年) プログラミング言語は魅力的な分野です。それは、計算機科学(と論理)を 社会学や人間とコンピュータの相互作用 、科学的に定量化できない直感や嗜好、そして(良くも悪くも)政治などを含む分野と結び付けてくれるからです。 プログラミング言語を話題にする場合、たいてい何らかの客観的な真実を追求する科学的議論になってしまいます。科学は完璧のオーラに包まれているため、科学的本質の核心部だけに集中し、他の部分を無視するのが正しいプログラミング言語の考え方だと単純に思ってしまうのも無理ありません。 しかし、これではプログラミング言語を面白くしている多くのものが除外されてしまいます。この隙間を埋める1つの方法は、科学の哲学に目を向

Creating aprogramming language is apparently all the rage these days, andit’sgot me thinking about what I would really like to see in one. I’m starting to suspect the things I want are either impossible or mutually incompatible, so I’d better write them down and let smarter people tell me why I can’t have everything and also a pony. I’m strongly influenced by my love ofPython, my aversion to C

ラムダ計算でEither Either型の値をパターンマッチする状況を考えます。 「データコンストラクタのパターンマッチ」は,下図のようにしてラムダ計算で表現できます。 ラムダ計算でBool 今度は,Bool型の値をパターンマッチする状況を考えます。 TrueやFalseには引数が無いので,(3)や(4)はλで囲みません。 パターンマッチ = 「データコンストラクタを他の関数に置き換えること」 パターンマッチによって,Leftがlに置き換わります。以下同様です。 「データコンストラクタを置き換える」という概念について,もう少し詳しく考えていきます。 データコンストラクタの置き換え方は2種類ある リストのような再帰的なデータ型では,データコンストラクタの置き換え方が2種類あります。 data List a = Cons a (List a) | Nil (1) 全てのデータコンストラクタを置

以前書いた(C言語についての) メモリ安全性について定義した記事 について、型安全性について説明する記事も投稿してほしいというコメントがありました。型安全性についてはかなりよく知られてきていると思いますが、ズバリこうだと簡単に定義できるほどにはまだ理解が浸透していません。特に誰かが”Javaは型安全な言語だ”と言った場合、これは厳密に何を意味するのでしょう。全ての型安全な言語はある意味”同じ”と言えるでしょうか。ある特定の言語について、そして一般的な意味で、あなたを悩ませる型安全性とは何でしょうか。 実際のところ、型安全性が何を意味するのかは言語の型システムの定義によります。最もシンプルなケースでは、型安全性はプログラムの動作が正しく定義されるように保証します。もっと一般的な話をすると(この記事ではそのあたりをカバーするつもりですが)、言語の型システムはそのプログラムの正確さと安全性を推論

誰? minamiyama1994です、不審者です これは何? comb meet up!というLT大会で発表した型! 型!という同名のスライドに関する補足記事的なものです U22が中心ですが、中高生から社会人まで幅広く参加する勉強会ということで基本的なことを説明しました、分かる人にはつまらない話かと思います まず、型って何よ? 「TAPLの第1章読め」の一言で済む話なのですが、それではあまりに無慈悲なので少し解説します(TAPL読めって言ってたらそもそもこの発表や記事なくてもいいもんね) 型というのは 値の取りうる集合 データに対するメタ情報 です ……何を言っているかわからないと思うので具体例を出します 「0」は「整数型」です 「"hoge"」は「文字列型」です 「http://b-world.org」は「URL型です」です 要するにこういうのが型です 「値の取りうる集合」とは? 例え

We support business-critical transformation within the world’s leading financial markets participants, enabling them to meaningfully differentiate themselves and successfully navigate a shifting landscape. Digital disruptionBlockchain andCryptoProduct innovationSimplificationBig dataCloudRegulationDigital disruptionThe digitalization of financial markets is transforming service distribution and d
Understanding Clojure transducers through types Aug 7, 2014 · 9 minute read · 18 Comments Clojuretransducerstypeshigher-rank typesHaskellmonadstype classesScalaRich HickeyJohn LaunchburySimon Peyton Jones Yesterday, Rich Hickey published ablog post, “Transducers are Coming”, which attracted a lot of attention. I have a confession to make, which I have made before: I findit very difficult to unde
本稿はPython に型アノテーションを追加するという PEP 483 - The Theory of Type Hinting の提案で参照されている Jeremy Siek (@jeremysiek) 氏と Walid Taha 氏が開発した漸進的型付けについての入門記事の翻訳です。 What is Gradual TypingPython 3.5 で導入された型アノテーションについて興味がある方は以下を参考にしてください。Python と型ヒント (Type Hints) と #pyconjp [翻訳] PEP 0484 -- 型ヒント (Type Hints) Revenge of the Types: 型の復讐 私自身、型システムに明るくないため、一部未訳の部分があったり、勘違いや誤訳もあると思います。そういった誤りを見つけたら編集リクエストを送ってもらえると助かります。

いま論理学とか集合論とかを勉強してるので、クラスって何かという話のときも集合論として考えてた。 なので、そのとき考えたことをまとめておく。 まず、「なにか」があるとする。「なにか」はなんでもいい。 そして、その「なにか」の集合を考える。たとえば"aaa"や"bbb"を要素とするStringという集合を考える。3とか5とかを要素とするIntegerという集合を考える。 ここで、その集合がなにを扱うかという規則をどうするかというのがオブジェクト指向としては大切になるかもしれないけど、今回はそこには触れないでおく。 とにかく、「なにか」と『「なにか」の集合』を考えることをここでは大切にする。 これで『「なにか」の集合』を考えたところで、『「なにか」の集合』を要素とする集合を考えて、この集合をクラスとする。つまり、クラスという集合は、StringやIntegerといった集合を要素にもつ。 ここで、

Deleted articles cannot be recovered. Draft of this article would be also deleted. Are you sure you want to delete this article? この記事は http://www.cl.cam.ac.uk/~srk31/blog/2014/10/07/ この文書の和訳である。原文も別に個人的には興味深いとは言い難いし、CSについての専門知識は全然ないので適任でもなんでもないのだが、例によって「POSTD」の日本語訳( http://postd.cc/7-deadly-sins-of-talking-about-types/ )が余りにも余りなので、私にわかる限りでもう少しマトモな翻訳にするとどうなるか試してみる。Markdownの脚注と[ ]内は訳者の(余計な)補足である。 型を

私の小論 “In Search of Types” では、プログラミングで使われる“型”という言葉の概念や目的、考え方について、公平な批評を心がけました。所々で、私の真剣さを感じ取っていただけるはずです。このブログ記事では逆に、思い切って堂々と批評していきます。いくつかの意見や考え方に、私は苛立ちを隠せません。先日参加したStrange Loopでも、このような状況に陥りました(補足しますが、すばらしいコンファレンスでした)。この機会に、“型”について多くの人が(誤って)語った“重大な誤り”をリストアップしていきます。 ここで話す内容は、説得力のあるものです。私が苛立ちを覚えるのは、人々が正当かつ透明性のある議論を行っていないことに対してです。結論に誤りがあってはいけません。私は、OCamlである程度の数のプログラミングを行っており、それは型チェックから多くの価値を得ることができるシンプル

Marcelo Cantos gave a prettygood explanation, but I thinkit can be made slightly more precise. A type of thing is composable when several instances can be combined in a certain way to produce the same type of thing. Control structure composability. Languages like C make a distinction between expressions, which can be composed using operators to produce new expressions, and statements, which can
リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く