サクサク読めて、
アプリ限定の機能も多数!
下記の文章は、私が今年の某月某日に熊本県立熊本高校で1年生向けの講演をしたときの講演原稿に少し手を加えたものです。講演には特にタイトルはありませんでしたので、上のタイトルは後で私が付けました。講演の依頼及び原稿の掲載に同意して頂いた熊本高校の諸先生に感謝致します。 皆さん、こんにちは。今日は「世界の中の日本」という視点から今後の学問のあるべき姿や、そんな中で「頭を使う」とはどういうことかについてお話しするようにご依頼を受けています。これらについて、まずは私自身の経験から始めようと思います。 私は今から30年前、1995年の6月から1ヶ月半ほど、初めて数学の研究のための旅行でヨーロッパを数カ国旅しました。当時私は京大の博士課程の学生で、特にグラントやフェローシップもなかったので、自費で旅行しました。自費だったところが、実はよかったと思っています。いろいろ吸収しようと本気で頑張らざるを得ないで


2要素認証などでよくみる6桁のワンタイムパスワードですが、個人的に何となく気になっていることがありました。 それは 同じ数字が並ぶことが多いな と感じるということです。 この記事では 「同じ数字が並ぶ」という直感が正しいのか? 何かの目的 (例: 入力を楽にする) があってこうなっているのか? ワンタイムパスワードの生成アルゴリズム的にこういう偏りが生まれやすくなるのか? という素朴な疑問を解決すべく調査・検証してみました。 ワンタイムパスワードの仕様 6桁のワンタイムパスワード(以下、OTP)は、実は国際的に標準化された仕様に基づいて生成されています。 RFC 4226 - HOTP: An HMAC-Based One-Time Password Algorithm RFC 6238 - TOTP: Time-Based One-Time Password Algorithm HOTP

この記事は 古代エジプト人は3:4:5の比を辺をもつ三角形を使って直角を作図した ピュタゴラスは三平方の定理を証明した 古代ギリシャで無理数(量)の研究は禁止されていた 無理量を口外した者はピュタゴラス教団に殺された アルキメデスは「私の円を乱すな」と言った キリスト教徒のせいでギリシャ数学は滅びた デカルトは「デカルト座標」を発明した 古代ギリシャ人は三大作図問題を解けなかった 古代エジプト人は円周率を計算していた 以上のような数学史上の俗説を検証するものです.全文無料公開ですが,注釈(本文で ³ のような上付きの数字で示されている箇所の脚注を読めます)を含めたPDFは有料となっております.さらに学びを深めたい方はご購入ください.それでは始めます. 序.数学史に関する書物で,原典を調べもせずに,他の書物から無批判にその主張を受け売りしている例,お伽噺のようなことが「あまねく知られた事実」


教育界の大谷翔平(英数社3教科教員免許持ち) @BH79Ca4YNT6112 昔、東進ハイスクールの林修先生が「もう時効なんで言えるんですけど」と前置きした上でされていた興味深い話。 林修先生がまだ数学の先生だった頃、ある日の授業の予習をしていないことを、その授業の直前に気がついたそうです。その日は東大の過去問を解説する回でした。 林修先生は授業に対して徹底した準備をして臨みます。しかしその日の授業の準備はもう間に合いません。生徒に申し訳ないからと、その日の授業は休みにしようと塾に電話をしようとしたそうです。 しかしここで「今自分が1番やるべきことは、授業に穴をあけないこと」と思い直し、その日は授業の準備を殆どせずに、授業に臨むことになりました。 いよいよ授業が始まり、生徒は林修先生の解説を聞く準備ができています。解説するはずだった問題は殆ど初見の問題。そこで林修先生は、あーでもない、こー

If you really look closely, most overnight successes took a long time. Steve Jobs (本気でじっくり見てみると、あっという間にできてしまったように見えることのほとんどが、実はすごく時間を掛けて成し遂げられたことだとわかるだろう) スティーブ・ジョブズ(米の起業家、アップルの共同創業者) 91年の2月の終わり頃(当時44歳)、「(その年の)夏にNHK教育テレビで放送する、高校生(受験生)向けの数学講座に出演してくれないか」と、出演依頼が舞い込んできた。 「従来、NHK教育テレビでは、教科書に準拠した数学講座を放送してきたのだが、今年は少し冒険して、今までとはまったく異なる数学講座を視聴者に提供したい」とのことだった。 駿台でやってきた授業を形にして残そうと、『発見的教授法による数学シリーズ』(全7巻)を出版したが


背景Twitter(X.com)で掛け算の順序指導を少しでも支持するや否や罵詈雑言のリンチに遭う状態が10年以上継続しているようだ。 真面目で誠実な小学校の先生等の教育関係者は悪意ある反順序(順序指導否定派)とも向き合い、そして傷ついたことであろう。お疲れ様でした。 私は1年以上この界隈をウォッチしてきた順序肯定派であるが、反順序な意見や反順序指導はそれはそれで尊重するという立場である。 概要・目的まず、議論という構造を俯瞰し、討論はどうやるべきかを説明する。 そして、反順序の思想に触れつつ、彼らの議論や討論が破綻していることを見る。 これと関連づけて反順序がどういう人々なのかをまとめる。 以上をもって、殆どの反順序は討論の作法に反するので無視しても構わない、ということを読者に納得いただくことを目指す。 反順序に絡まれたときに「貴方がこの記事の通りでないなら話聞くよ」とフィルターとしても使




科学や教育に関するさまざまな話題を動画で解説するYouTubeチャンネル・Veritasiumが、「なぜ民主主義は数学的に不可能なのか」と題し、選挙における投票システムについて動画で解説しています。 Why Democracy Is Mathematically Impossible - YouTube 民主主義における最も単純な選挙方法として、有権者に投票用紙で一人の候補者を選ばせる方式があります。この方式は「単純小選挙区制」として知られており、単に最多得票の候補者が勝利します。この方法は古代にまでさかのぼり、14世紀からイギリスの下院議員選出に使用され、現在も世界44カ国で指導者選出に用いられています。 しかし、単純小選挙区制には問題があります。議会の代表者を選ぶ場合、国の大多数が権力を握る政党に投票していないという状況が頻繁に発生します。過去100年間で、イギリス議会で単一政党が議席


古代ギリシャのヘルメス @kodaigirisyano 【お願い】数学史に関心のある方は… 三村太郎『数学の歴史』を読んで! 三村太郎『数学の歴史』を読んで! 三村太郎『数学の歴史』を読んで!数学の歴史を通じて「科学」という営みがどうやって誕生したのかを学べる凄い本ですよ! 実は今年一番楽しみにしていた本なのですが,期待以上でした! pic.x.com/3EicCUKhMF 2025-03-14 20:44:54 古代ギリシャのヘルメス @kodaigirisyano 同名の三浦伸夫『数学の歴史』とはまったく異なる内容ですから,こちらを読んでいる方ももちろん楽しめる本になっています…というか両方とも読みましょう😂 pic.x.com/S4ZNnzYF0a 2025-03-14 20:45:55 古代ギリシャのヘルメス @kodaigirisyano アルゴスの殺し手は古代の思想に関心

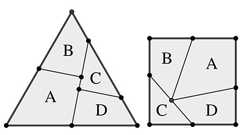
北陸先端科学技術大学院大学(JAIST)と米マサチューセッツ工科大学の研究チームは3月10日、120年以上未解決だった古典パズル「デュードニーの裁ち合わせパズル」の証明に成功したと発表した。 与えられた多角形をなるべく少ないピースに切り分け、並べ替えて別の多角形に変えるパズルは「裁ち合わせパズル」といわれる。そのうちの有名な問題の一つが、デュードニーの裁ち合わせパズルだ。これは“正三角形を4つのピースに切り分けて正方形を作る”という問題で、4ピースよりも少ない解があるかは120年以上未解決のままだった。 研究チームは数年間この問題に取り組み、JAIST所属の鎌田斗南助教が新しい証明技法を考案。このパズルの最適解は4ピースであり、3ピース以下の解が存在しないことを証明した。 研究チームの証明技法では、まず3分割の方法となり得る組み合わせを列挙。そのうち実現の可能性がある組み合わせのみに絞り込
Orange Juice @PaxRomana_CA ちなみに、細かい公式を忘れたとかの話ではなくて 例えば分数に全く普段触れない人でも、1/2+1/3は?と聞かれて、仮に分子同士、分母同士足して2/5と一回しちゃっても、あれ、なんか違うかったよね?とストッパーがかかると思うんですが そういうストッパーが全くかからないんですよね。。。 2025-03-04 19:04:40 Orange Juice @PaxRomana_CA 私の表現が悪かったようで補足ですが、別に日本の高校生の数学力と比較する趣旨は一切ないです。単に彼らに基本の理解がごっそり抜けていたと言いたかっただけで それでも紛らわしい場合、「日本の高校2年の数学の教科書初級レベル」を「米国の高校のAP数学のレベル」とでも読み替えていただければ! 2025-03-05 06:50:40


セガが手掛ける線形代数の解説書籍『セガ的 基礎線形代数講座』、2025年1月30日(木)に日本評論社より発売 セガが2021年6月に公開した社内勉強会用の資料を書籍化したものゲーム開発などで必須な線形代数について、基礎の振り返りから、3次元回転の表現に関する「クォータニオン」なども解説 セガの開発技術部課長である山中 勇毅氏が執筆した、ゲーム開発領域などで必要な線形代数の知識を解説した書籍『セガ的 基礎線形代数講座』が、日本評論社より発売されます。 発売日は2025年1月30日(木)。総ページ数は256ページ、価格は2,970円(税込)。Amazon.co.jpなど各種ECサイトにて予約を受付中です。 線形代数はゲーム開発領域を含む幅広い理工系技術の基礎を担う分野で、ゲーム開発では主に3DCG技術の基礎として活用されています。本書は、仕事で数学を活用する人や、改めて数学を学び直したい人に

このコーナーでは、2014年から先端テクノロジーの研究を論文単位で記事にしているWebメディア「Seamless」(シームレス)を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。 X: @shiropen22023年、米国の高校生ネキヤ・ジャクソンさんとカルセア・ジョンソンさんは、地元の高校のコンテストで驚くべき成果を披露した。それは、三角関数を用いてピタゴラスの定理を証明するという方法の発見であった。 「a^2+b^2=c^2」で表されるピタゴラスの定理は、よく知られている数学の基本定理である。この式は、直角三角形において、最も長い辺(斜辺)の2乗が、残りの二辺の2乗の和に等しいことを示している。 これまで数多くの数学者たちが代数学や幾何学を用いてこの定理を証明してきたが、三角関数による証明はより難しかった。三角関数の基本公式自体がピタゴラスの定理を前



藤原京左京七条一坊跡(奈良県橿原市上飛騨町)から2001年に出土した飛鳥時代末期の木簡1点を奈良文化財研究所(奈文研)が再調査した結果、当時の役人が使っていた「九九早見表」の一部とみられることが分かり、同研究所紀要で4日公表した。担当した桑田訓也・主任研究員(古代史)によると、最古級の九九早見表の確認例。律令国家で九九が広く用いられたことを示す貴重な史料という。 木簡は長さ16・2センチ、幅1・2センチ。縦書きで1行に文字群が3段分書かれ、肉眼で「十一」「六」「六八」の計5文字のみ判別できた。奈文研は当初、1段目を「九々(くく)八十一」、3段目を「六八卌(しじゅう)八」と推定。九九を練習したメモ代わりの木簡と解釈した。

この記事では、MEGA BIGくじの最適な賭け額、最適な賭け額の算出方法について説明する。 ※この記事の内容は間違っている可能性があるので注意してください。間違いがあればご指摘いただけると嬉しいです。できれば専門家にレビューしてほしいです。 ※この記事はMEGA BIGの購入を薦めているわけではありません。 MEGA BIG 祭2024/8/30、MEGA BIG祭が突如発生した。 MEGA BIGは通常期待値がマイナスであるが、台風の影響でサッカーの試合が一部中止になり第1476回のMEGA BIGの期待値が1を超える可能性があるという投稿があったのだ。 toto MEGA BIGが熱い。 対象の12試合中4試合が中止(自動的中扱い)なので、8試合分当たれば1等というレイドイベント発生。現在キャリーオーバー61億円。 公営ギャンブルとしてはありえない期待値。 なおtoto BIG/100

正直なところ言及したくない話題なのですが、最近あまりにもひどい動きが散見されるので今の私の考えを書き留めておくことにします。 予めこの記事で「しないこと」について記しておきます: 丁寧な背景説明 現行の教育方針に対する是・非の判断 何が問題なのか? 客観的な事実 数 a と数 b があったとき、a\times b と b\times a は同じ結果をもたらします。両者は等号で結ばれるものであり、両者に数学的な違いは存在しません。これ自体は疑いようのない事実であり、誰の目にも明らか[1]です。 注意すべきなのは、このことを理解するために高度な数学の知識は全く必要がないということです。つまりここで「実数体の乗算の性質が」とか「可換環が」とか言い出すのは追加の情報を与えないので無意味な行為です。 そしてそれは同時に、高度な数学の知識を有していることがこの問題に向き合うにあたってアドバンテージにな

リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く