サクサク読めて、
アプリ限定の機能も多数！
アプリで開く
セミのなかには、毎年姿を現すものもあれば、一定の周期でしか姿を現さない「周期ゼミ」もいる。2024年の春は、米国の南東部から中西部で、周期ゼミの2つの大きな集団が同時発生する見込みだ。（PHOTOGRAPH BY REBECCA HALE, NAT GEO IMAGE COLLECTION） 2024年の4月下旬から6月にかけて、米国の南東部から中西部で、200年の時を超えて大自然の交響曲が奏でられる。周期ゼミの2つの集団が221年ぶりに同時に姿を現しはじめるのだ。「今年はとても重要な年になるでしょう。神秘的で驚くべき出来事です」と、「虫博士」として知られる米ミズーリ大学のタマラ・リオール氏は言う。（参考記事：「17年ゼミの大発生始まる、動物たちの反応は？」） 221年ぶりなのは、2つの集団の周期がそれぞれ13年と17年だから。前回同時に姿を現したのは1803年のこと。米国大統領はトーマス
【▲図: 今回の研究で予言されたネスターは、グラバスターの入れ子構造となっています。 (ImageCredit: Daniel Jampolski & Luciano Rezzolla,Goethe-Universität) 】 「ブラックホール」は現代物理学が破綻する領域であるため、それを回避するための理論的な提案がいくつも出されています。代表的な回避策の1つは「グラバスター（Gravastar）」です。 ライプツィヒ大学理論物理学研究所のDaniel Jampolski氏とLuciano Rezzolla氏は、「アインシュタイン方程式」を解くことで現れるグラバスターについて研究し、「グラバスターの中にグラバスターがある天体」が存在可能であることを示しました。この入れ子構造は何重にも可能であるため、両氏はこの天体を「ネスター（Nestar）」と名付けました。 ネスターが実際に存在する
佐久間ちゃん @2_wykipedia 昔、アメリカで飛行機内で微分方程式を解いていた男性が怪しまれて通報された事件の話を聞いて、京王井の頭線で「代数多様体のblow-upを繰り返して特異点を解消して」等と早口で数学の話をしているイカ東たちが暗号めいた言葉で爆破テロを計画してるのではないかと疑われて通報されないか心配になった 2024-01-16 14:33:28 佐久間ちゃん @2_wykipedia 昔、アメリカで飛行機内で微分方程式を解いていた男性が怪しまれて通報された事件の話を聞いて、京王井の頭線で「代数多様体のblow-upを繰り返して特異点を解消して」等と早口で数学の話をしているイカ東たちが暗号めいた言葉で爆破テロを計画してるのではないかと疑われて通報されないか心配になった 2024-01-16 14:33:28
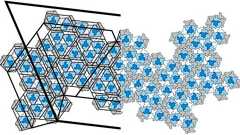
あるあるですよね。 実はこの多面体はどう頑張っても作れません。正六角形でなくとも、六角形のみで多面体を構成することは不可能です。 詳しく知りたい人は、オイラーの多面体定理が参考になるでしょう。 (2023-12-19 追記) 穴が空いてたり、六角形がくぼんでたりすると作れるっぽいことがわかりました。 というわけで、何かしらの誤魔化しがなされています。集めて観察してみよう。 平面的に配置し切り取っているもの 葬送のフリーレン第3話よりおそらく平面に敷き詰めた六角形を歪ませて円状に切り取り擬似的に見せてると推測します。煙で少し隠されている上部での輪郭の回りこみに違和感があり、立体としては不自然だと感じました。(違ったらごめん) 参考:フラーレン このカットは煙によって一瞬しか映らないことで気付きにくいよう工夫されています。こんなのにわざわざ気付くの自分くらいだろうというくらいには一瞬だったので
$$\newcommand{a}[0]{\alpha} \newcommand{Aut}[0]{\operatorname{Aut}} \newcommand{b}[0]{\beta} \newcommand{C}[0]{\mathbb{C}} \newcommand{d}[0]{\delta} \newcommand{dis}[0]{\displaystyle} \newcommand{e}[0]{\varepsilon} \newcommand{F}[4]{{}_2F_1\left(\begin{matrix}#1,#2\\#3\end{matrix};#4\right)} \newcommand{farc}[2]{\frac{#1}{#2}} \newcommand{G}[0]{\Gamma} \newcommand{g}[0]{\gamma} \newcommand{Gal}[0]
ある数学愛好家が発見した帽子に似た図形に数学界が沸き立っている 英ヨークシャー在住の数学愛好家スミス（David Smith）が，とある13角形を発見した。数学者による探索を何十年もかいくぐってきた図形だ。いかつい帽子に似たその形（次ページの図で太線で描かれている図形）は，ドイツ語で「1個の石」を意味する「アインシュタイン」という名で呼ばれている。アインシュタイン・タイルを使うと浴室の床を隙間なく敷き詰めることができ，しかも同じパターンが繰り返されることが決してない。浴室の床だけでなく，どんな平面でも，それが無限に広がっていても，これが可能だ。 非周期的にしか敷き詰められないタイル数学者は長年，敷き詰めが必ず非周期的になる「強非周期的タイル張り」を実現するタイル形状を探し求めてきた。まず見つかったのは形状が様々に異なるタイルのセットだった。1964年に発見された最初のセットは2万426種
Rootport🔥 @rootport 作家・マンガ原作者／好きな言葉は「群盲撫象」／TIME誌「世界で最も影響力のあるAI業界の100人」選出(2023年版)／📝rootport.hateblo.jp／質問箱 marshmallow-qa.com/rootport or mond.how/ja/Rootport youtube.com/channel/UCp6RK… Rootport🔥 @rootport 「60を半分で割って20を足したらいくつ？（正解：22）」って算数の問題が流れてきたけど、日本語を商売道具にしている人間としては見過ごせませんよ!? ヒトの脳は自動的に文章を校正しちゃうので、「60を〝その〟半分で割って」と書かないと伝わりません。「60を半分〝に〟割って」と校正しちゃう。2023-09-26 08:57:23 Rootport🔥 @rootport 「60を
スタンフォード大学の教授で数学者の時枝正（ときえだ・ただし）は、「おもちゃ」を使って数学や物理の定理を解き明かす。スープ皿や木のレール、大きなコインを手に、「ショー」とも呼べそうな講義をいかにも楽しげに始めるその姿に、聴衆は一瞬にして心を惹きつけられるという。数学者には二つのタイプがいるという──。一つは、チョークを握り黒板に向かう、理論派タイプ。もう一つは、フェルトペンとホワイトボードを使う、どちらかというと応用数学系の人である。 その伝でいうと、時枝正は第三のタイプの数学者である。しかもこの第三のタイプは、世界広しといえども彼一人だけの可能性がある。 時枝は仕事道具をどれも煎餅の空箱から取り出すのだが、箱は「すべて同じブランドのもの」なのだそうだ。たとえばその中身は、見かけはそっくりなのに、転がるものと転がらないものがある二つの不思議な構造物。ひもや輪ゴム、クリップの扱い方は、まるで
高校分野の解法を使って円周率の新しい求め方を証明した（左から）中山啓太さん、丸尾祐希さん、田中陸人さん、宮本陣弥さんと指導した宮寺良平教諭＝西宮市高座町 西宮市立西宮高校（兵庫県西宮市高座町）３年の４人が「三角比の定理」などを用いて証明した「円周率の新しい求め方」が、オーストラリアの大学が発行する数学雑誌に掲載された。授業の一環で取り組んだ。高校までで学ぶ公式などを使って証明することは困難とされており、新たな証明方法として評価された。大学受験と部活に励む生徒たちは「答えのない研究だったが、成果を出せて安心した」と快挙を喜んでいる。（久保田麻依子） メンバーは、同校グローバル・サイエンス科の田中陸人さん（１７）▽中山啓太さん（１７）▽丸尾祐希さん（１７）▽宮本陣弥さん（１８）。臨時講師の宮寺良平教諭（６７）が指導した。 研究を始めたのは１年生だった２０２１年９月。身近な疑問を出発点に深く探究
アメリカ数学会で2人の10代の少女がピタゴラスの定理について新しい証明方法をプレゼンテーションしたことが話題になっています。応用数学の専門家であるキース・マクナルティ氏は「性別、民族、社会人口学的背景に関係なく、喜びと情熱があれば誰でも、研究分野での卓越性は達成可能であることを示す素晴らしい出来事」と評しているほか、その証明方法自体が波紋を呼んでいます。 Here’s How Two New Orleans Teenagers Found a New Proof of the Pythagorean Theorem | by Keith McNulty | Apr,2023 | Medium https://keith-mcnulty.medium.com/heres-how-two-new-orleans-teenagers-found-a-new-proof-of-the-pytha
この画像を大きなサイズで見る 何十年も探し求められた「アインシュタイン」のタイルがついに発見されたそうだ。 それは13の辺を持つジグソーパズルのような図形で、どれだけ並べても、絶対に同じパターンが繰り返されることはない。数学の世界で「非周期的モノタイル」と呼ばれるこの形状の発見は、数学の歴史の革新的発見（ブレイクスルー）と称されている。 この図形の不思議さとすごさ、面白さを説明していこう。 非周期的タイルとは何か？ 「アインシュタイン」とは言っても、あの天才物理学者アルベルト・アインシュタインのことではない。ドイツ語で「1つの石」のことで、つまりは1枚のタイルであることを意味するものだ。 これについて、発見者の1人であるカナダ、ウォータールー大学のクレイグ・カプラン教授は、「私たちは史上初の本物の”非周期的モノタイル”を紹介しています」と声明で述べている。 「非周期的タイル」とは何か？
InnovativeTech： このコーナーでは、テクノロジーの最新研究を紹介するWebメディア「Seamless」を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。Twitter: ＠shiropen2 英国の数学者らと、カナダのウォータールー大学と米アーカンソー大学に所属する研究者らが発表した論文「An aperiodic monotile」（プレプリント）は、繰り返しパターンを作らず、2次元の表面を無限に敷き詰めることができる単一のタイル形状を発見した研究報告である。 このような図形を非周期的なタイルと呼び、2次元の平面にタイルを隙間なく敷き詰めるが決して周期的ではない形状を指す。 非周期的なタイルの最初の集合は、1966年に発見された2万種類以上のタイルの組み合わせだった。その後、タイルの種類を減らす方向に研究が進んだ結果、最も有名な非周期的なタ
東京大学は12月9日、理論的に虚数の角速度を考えて虚回転する高温物質が、クォーク閉じ込めの性質を持つことを示したと発表した。 同成果は、東大大学院 理学系研究科の陳実大学院生、同・嶋田侑祐大学院生、同・福嶋健二教授らの共同研究チームによるもの。詳細は、米国物理学会が刊行する機関学術誌「Physical Review Letters」に掲載された。 自然界には電磁気力、弱い力、強い力、重力の4つがある。そのうち強い力は、原子核を構成するクォークとグルーオンの相互作用のことで、量子色力学(QCD)という場の量子論に従う。もしQCDを解くことができれば、もともとほとんど質量のないクォークとグルーオンから構成される中性子や陽子などの粒子が、実験で観測されるような質量を獲得するメカニズムを、理論的に解明することができると考えられている。 ところが強い力は、ほかの3つの力とは違って結合定数が大きいため
子Aと子Bがいるとして「Aが男のときBが女の確率は？」なら答は1/2。「ABのどちらか片方が男のときもう片方が女の確率は？」なら答は2/3。 これの前者の意味がさっぱり分からないんだけど誰かマジで説明してくれ。勝手に生まれた順だと決め付けて子Aが男だった場合お姉ちゃんがいるケースを省いてるって事？ 追記 生まれた順は関係なくて、性別が確定したのが「特定の個人」か「不特定の個人」かで、もう1人の性別の確率は変わるのです。 一番わかりやすかったです。ありがとう。元ブコメは勘違いしてすまんかった。
タンパク質設計問題を解決する数学公式を名古屋大学が発見、圧倒的な高速化を実現 大学ジャーナルオンライン編集部 名古屋大学大学院の高橋智栄博士後期課程学生らの研究グループは、シミュレーションや実験をせずにタンパク質設計をするための数学公式を世界で初めて導出することに成功した。この数学公式により、膨大な計算量のシミュレーションの必要がなくなり、圧倒的に高速な設計が可能になった。 研究グループは昨年、タンパク質進化に関する新しい仮説と機械学習の手法を組み合わせることで、従来手法に比べて圧倒的に高速なタンパク質設計を実現することに成功していた。今回さらに、複雑系物理学・情報統計力学の理論を適用することにより、シミュレーションが不要なアミノ酸配列の推定のための数学公式を導出することに成功した。 これにより、タンパク質設計にかかる時間を昨年発表した効率的な設計手法を用いた場合より、さらに10分の1 程
AIが科学を新たな次元に押し上げています。 どんなに賢い犬であっても、ニュートンやアインシュタインの方程式を理解することはできません。 その理由は犬という種族の脳の限界によるものです。 では人間にも同様に理解できる理論の限界があるのでしょうか？ 人間の認知力を超えた英知は得られないのでしょうか？ 新たに行われた研究によれば、AIの持つ「機械の知性」を活用することで、ある程度の限界突破が可能であることが示されています。 米国のフラットアイアン研究所（Flatiron Institute）で行われた研究によれば、訓練を積んだAIによって、10万個の方程式を用いて記述される量子問題を、わずか4個の方程式に変換することに成功した、とのこと。 数個の方程式を同じ意味を持つ1つの方程式に統合することは人間の数学者でも可能ですが、10万個を4個に圧縮するのは人間を超えた機械の知性が必要となります。 研究
リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く
