サクサク読めて、
アプリ限定の機能も多数！
アプリで開く
筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第8回です。前回は、独立性の検定を紹介しました。例えば、出身地域と麺類の好みは独立しているか（＝関係がないか）どうかを調べました。 今回は相関係数の検定を取り上げます。独立性の検定では名義尺度であるカテゴリの度数（人数など）を基に検定を行いましたが、相関係数の検定では間隔尺度である変
Deleted articles cannot be recovered. Draft of this article would be also deleted. Are you sure you want to delete this article? はじめに 今回は、「新しい相関係数」と銘打ったインパクトのある論文を紹介します。 この論文で定義を見ただけだとイマイチぴんと来ないかもしれないので、図を使ってわかりやすく説明します。 紹介する論文はこちら： Chatterjee, Sourav. "A new coefficient of correlation." Journal of the American Statistical Association 116.536 (2021): 2009-2022. Stanford大の重鎮による単著で、統計学4大誌のJASAに掲載。この
はじめに あるデータの組み合わせが手元にあるとき、それらがどれほど依存関係にあるのか？というのはデータを触っていると自然に湧いてくる疑問だと思う。 データの依存関係を見る時、「相関係数」なるものを計算するのは大半の人が行うと思うが、この相関係数は「ピアソンの相関係数」を指すことがほとんどであろう。この相関係数は Y = aX + b という線形の関係を捉えることはできる。 と、ここまで書いてたのだが、つい先日 Qiita にこんな記事が投稿された。 まさにこういう話をしたかったので完全に先を越されてしまった。悔しい… だがせっかくなので、実はこの相関係数は「バイアス」があると指摘した論文についてでも紹介しようかと思う。以下はarXivに投稿されたワーキングペーパーをベースにしたものである 注意：以下は夜中に勢いで書いたので、構成とか変わる可能性がある (12/10) 新しいセクションを追加
筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第7回です。前回は、番外編として、G*Powerという便利なツールを使って検定に必要なサンプルサイズを求める方法を紹介しました。今回は独立性の検定と呼ばれる検定を取り上げます。例えば、出身地域と麺類の好みは独立している（＝出身知識と麺類の好みには関係がない＝出身地域によって麺類の好み
無料で「統計データの活用法」を学べるオンライン講座、総務省が受講生募集：学習期間は4週間、受講の前提条件は？ 総務省統計局は、統計リテラシー向上とデータサイエンス人材育成を目的に、無料で学べるオンライン講座「誰でも使える統計オープンデータ」を2026年1月13日から開講する。
筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第6回です。前回は、正規分布する2つの母集団の分散が等しいかどうかを調べるために、分散の比の検定を行う方法を解説しました。前回までで、母平均の検定、母平均の差の検定、母分散の検定、母分散の比の検定という、よく使われる4つの検定について見てきました。併せて、それぞれの検定における適切な
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。 この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト（MicrosoftExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。 必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。 筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一
筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第4回です。前回は、正規分布する2つの母集団の平均に差があるかどうかを検定する方法を解説しました。今回は正規分布する母集団の分散（母分散）が、ある値よりも小さいか（あるいは大きいか／異なるか）を検定する方法を見ていきます。 母分散の検定についての基本的な考え方 前々回と前回は、母平均
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。 この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト（MicrosoftExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。 必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。 筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一
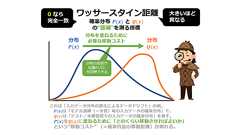
2つの確率分布間の“距離”を測る指標で、「ある分布をもう一方に重ねるために、どれだけ“確率質量”を動かす必要があるか」を表す。値が0なら「完全一致」、大きいほど「異なる」ことを意味する。主に統計学や機械学習で使われ、データドリフト検出や生成モデル（WGAN）などに応用される。別名「アースムーバー距離」。 連載目次 用語解説 統計学／機械学習におけるワッサースタイン距離（Wasserstein distance）とは、2つの確率分布の“距離”を測るための指標である。数理最適化の分野で研究されてきた最適輸送理論に基づいて定義されており、その特徴は「分布の形状」や「分布の位置のズレ」を自然に反映できる点にある。直感的には「ある分布をもう一方の分布に重ね合わせるために、どれだけ“確率質量”（＝分布における確率）を移動させる必要があるか」を表す（図1）。 別名として「アースムーバー距離（EMD：Ea
ちょっと前に、回帰分析における多重共線性に関する解説記事を2本ほど書いたわけですが。 多重共線性そのものの問題点はこれでもかと論じている割に、その対処法についてはあまり触れていなかったなと気付いたのでした。ということで、今回の記事では遅ればせながら多重共線性への対処法をある程度網羅的に挙げていこうと思います。 データセット VIFで多重共線性に寄与する変数を特定した上で削除orマージ（第一選択）PCAで変数を削除orマージ（要件次第） L1正則化で変数選択（要件次第） L2正則化で回帰係数同士のバランスをとる（非推奨） ベイズ回帰で事前分布を設定することで多重共線性によるバイアスを軽減させる（事前分布の蓋然性次第） コメントなど データセット まず、x1-5の5つの説明変数から成るデータセットを用意します。真の回帰係数はそれぞれ1, 2, -2, 5, -3.5とし、サンプルサイズは10
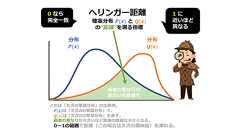
詳しい計算方法は後述するが、平方根を含む数式定義により、数式の形は「ユークリッド距離」に近く、分布Pと分布Qの違いを直感的に理解しやすい“距離”として捉えられるのが特徴だ。 用途 ヘリンガー距離は「確率分布同士の違い」を評価できるため、主に統計学や機械学習の分野で、次のような場面に利用される。 ベイズ推定／統計的検定： モデルの事前分布と事後分布の差、または推定分布と理論分布の差を評価する。 クラスタリング： 各クラスタを確率分布で表現し、それらの距離を測る。 生成モデルの評価： 実データ分布と生成データ分布の距離を測る。 情報検索／類似度検索： 文書の単語分布間や頻度分布間の距離を測る。
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。 この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフト（MicrosoftExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。 必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。 筆者紹介：IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一
が好評でしたので、2025年版を作りましたよ。今年も好著連発なため、追いきれてない本もあります。おいおい追記編集します。本記事のめあてIT系の技術者の方がデータ分析関連の仕事をするために役立つ本を紹介する（私が学び始めた時にあれば欣喜雀躍したであろう）記事として書いております本記事作者の青木はバイオインフォマティクス（ゲノムデータのDB化中心・Perl・MySQL）からRで時系列分析→Pythonでデータ分析一般と業務をしてまいりました ですので研究者目的の本はありません。また、データ分析の基礎は主にRで学んだのですが、昨今の流行に合わせて理論のほかはほぼPython本のみにしています こういうリストを挙げる奴は大抵読んでいない、と過去にも言われたのですが、未読本は削除しました 最近好著連発なので読んでいる途中だけど挙げている本はあります（初版を読んだが改訂版が出てそちらは読んでいな
Excelで学ぶ、やさしいデータ分析【仮説検定編】 ～ 考え方とP値の基礎：やさしい推測統計（仮説検定編） 初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ第4弾がスタート。第1回は仮説検定の考え方や知っておくべきキーワード、今後の連載予定を紹介します。データ分析を実践的に役立てるための基礎をしっかり学んでみませんか？ 連載目次データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載『社会人1年生から学ぶ、やさしいデータ分析』のシリーズとして、「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続いて、今回から「推測統計（仮説検定編）」を開始します。2023年から始まった連載もおかげさまでいよいよ第4シーズンに突入です。 これからのお話は、仮説検定と呼ばれる分野に関するものとなります。そこで、仮説検定の考え方や留意点を簡単にお話
最近、趣味で統計の勉強を始めた。 働いてるから夜に少しずつしか進められないけど、統計って面白いな。 あと有意水準が5%なのも明確な意味があると思っていたけど、実際にはフィッシャーが「5%ぐらいなら現実的だろ」って提案して広まっただけと知って驚いた。 この5％っていうのは慣習で決まった社会的ルールみたいなものなんだってね。 統計って数理的なもの。だからそういったものはないと思ってたから…意外だったよ。
「ポテトチップスの袋に入っている量って、 毎回ちょっとずつ違うかも？」 「“100年に1人の天才”って、本当にそんなペースで現れてるの？」 「チケット抽選、“三度目の正直”で当選！ ただの幸運？ それとも確率の力？」 ――そんな“あるある”な疑問を、Excelで楽しく解き明かしてみませんか？ 無料の電子書籍『Excelで学ぶ、やさしい確率分布』では、データの“分布”（グラフ）を通じて身近な現象を分析する方法をやさしく学べます。本書は、＠ITのDeep Insiderで連載された『やさしいデータ分析』シリーズ『確率分布編』をまとめたものです。“確率分布”という真面目なテーマにもかかわらず、連載は想定を大きく上回る反響を呼び、多くの読者から注目を集めました。編集部としても、データ分析に初めて触れる方にこそ手に取ってほしい、“入門編”として自信を持ってお薦めできる一冊です。本書は、確率分布
リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く
